Interactions Dominate the Dynamics of Visual Cognition

Abstract

Many cognitive theories have described behavior as the summation of independent contributions from separate components. Contrasting views have emphasized the importance of multiplicative interactions and emergent structure. We describe a statistical approach to distinguishing additive and multiplicative processes and apply it to the dynamics of eye movements during classic visual cognitive tasks. The results reveal interaction-dominant dynamics in eye movements in each of the three tasks, and that fine-grained eye movements are modulated by task constraints. These findings reveal the interactive nature of cognitive processing and are consistent with theories that view cognition as an emergent property of processes that are broadly distributed over many scales of space and time rather than a componential assembly line.

Interactions Dominate the Dynamics of Visual Cognition

Cognition is the product of a large, complex system. Like any complex system, the cognitive system consists of components (i.e., constituent parts) that interact with one another. Much of cognitive science has concerned itself with understanding the parts or components: Is there a face recognition module? Does language processing require a rule module? Etc. Other researchers have focused on the interactions and the structure that emerges from those interactions. Clearly, understanding cognition requires understanding both the components and their interactions, but where to begin? That is, should cognition be regarded as component-dominant or interaction-dominant?

The distinction between component-dominance and interaction-dominance is a matter of organization (Van Orden, Holden, & Turvey, 2003). In a system dominated by components, cognitive labor is divided among constituent parts. Specialized functions are locally encapsulated, and cognition is the summed activity of all constituent parts. When interactions dominate, organization is emergent and context-dependent. Functions are not encapsulated – the constituent parts arrange themselves according to the current demands of context. That is, components may flexibly bind together or break down to suit the changing conditions for a given task (Kay, 1988). Here, organization is an emergent coordination, and rather than obeying local divisions into parts, this coordination emerges in response to ongoing changes in information flow (Kelso, 1995).

Controversy in cognitive science

Cognitive science has traditionally focused on identifying the constituent parts of the cognitive architecture. For example, visual cognition would be divided among an attention component, a feature detection component, a recognition component, a feature integration component, etc., and each component would have a separate context-independent function (Treisman, 1993). Each component receives information from the last and, having processed the information in its specialized manner, passes the information on to the next component. The amount of time that it takes to find the target is the sum of processing time needed by each component along the way. Performance differences due to experimental manipulations or individual differences can be reduced to changes within specific components. This formulation remains an influential way to think about cognition (e.g., Coltheart, 1999; Dietrich & Markman, 2003; Marr, 1982; Wagenmakers, Farrell, & Ratcliff, 2004).

However, throughout the history of cognitive science, alternative perspectives have emphasized the role of emergence. Component-dominance makes for concise schematics of cognitive process, but the evidence suggests that components may not be so rigidly specialized and that the interactions may be more fundamental for cognition. For instance, Lashley (1950) and Hebb (1949) argued that learning could not be localized within a specific part of the brain but is encoded as distributed patterns of activation and connection among individual neurons. Based on neuropsychological data, Luria (1973a, 1973b) argued that cognition was based on distributed “functional systems”, rather than components, and that these systems could reorganize. More recently, Parallel Distributed Processing (PDP) has taken up the pursuit of interactivity and emergent structure as the foundation for cognition. PDP stresses interactions among simple processing elements (e.g., microfeatures) and the emergent properties of such systems (e.g., Elman, Bates, Johnson, Karmiloff-Smith, Parisi, & Plunkett, 1996; Rumelhart, McClelland, & the PDP Research Group, 1986). PDP networks begin with a finite set of microfeatures, such as “has wings”, “is yellow”, and “can sing” for canary (e.g., Rogers & McClelland, 2004; McRae, Cree, Seidenberg, & McNorgan, 2005). The emergent structure is limited to the interactions among these microfeatures; thus, the use of microfeatures in PDP may credit undue influence to components. Although the combinatoric variety of emergence is somewhat limited in this case (Boogerd, Bruggeman, Richardson, Stephan, & Westerhoff, 2005; Cariani, 1997), PDP serves as a well-known example of an interaction-based account of cognition.

Distinguishing component-dominance and interaction-dominance

Cognitive scientists interested in the role of interactions have gained new inspiration from work in statistical mechanics on the properties of complex systems. Indeed, even the PDP approach was significantly influenced by work in physics and thermodynamics (Ackley, Hinton, & Sejnowski, 1985; Hopfield, 1982, 1984). More recent complex-systems perspectives on cognition have adopted methods from complexity science in order to distinguish component-dominant dynamics from interaction-dominant dynamics in cognitive behavior. These methods involve assessing the statistical distributions of system behavior (Holden, Van Orden, & Turvey, 2009; Van Orden et al., 2003). We now briefly describe one such method, involving the test of a continuum of distributions. After briefly reviewing the existing evidence of interaction-dominance in cognition, we present new evidence of interaction-dominant dynamics in three classic visual cognitive tasks.

In order to use statistical mechanics techniques to distinguish between component-dominance and interaction-dominance, we take a step away from cognitive issues for a moment and consider the dynamics of random variables. Random variables represent the components composing a system and may assume a variety of values within an arbitrary domain. The behavior of the system depends on the current value of the random variables and the relationship that links them together. In a mathematical description, the two basic relationships are addition and multiplication. Hence, outcomes of system behavior are due to the addition or multiplication of random variables within the system.

These two different mathematical relations lead to different distributions of outcomes. To illustrate this difference, let us consider a system whose outcomes depend only on two random variables at a time, a and b. In the first case, a and b are each independently selected from the domain and then added together. The resulting numbers range from the sum of the two smallest possible values of a and b to the sum of the two largest possible values of a and b. After very many sums of pairs of random variables, the sums will tend to aggregate most heavily half-way between the two extremes. The extremely small sums and extremely large sums will both be rare compared to the median sums. A plot of these frequencies would give us a normal distribution. Most important for our purposes, the role of each participating number is always the same: to increase the sum by a specific amount. That is, addends invariantly serve the same role, much like the parts in a component-dominant theory of cognitive processes.

Now, consider the second case in which a and b are independently selected as before but are now multiplied rather than added together. As before with sums, the products range from the product of the smallest pair of random variables to the product of the largest pair of random variables. However, the landscape between these two extremes is now quite different from the normal distribution. Specifically, the mode and median have shifted to lower values and the tail has become longer: smaller products tend to be more frequent than the larger products and the upper limit on products is much higher than the upper limit on sums. The frequencies of products are best described by a lognormal distribution, a positively skewed curve with a relatively thick tail (e.g., Limpert, Stahel, & Abbt, 2001). This skewed result arises from the fact that the effect of multiplication depends nonlinearly on the values of the elements. Furthermore, the impact of one variable is not independent of the impact of the other: Outcomes due to either random variable can be radically different depending on the current value of the other variable. Just like in an interaction term for a regression, the magnitude of one random variable’s effect will be moderated by the value of the other (e.g., the effect of spelling-sound regularity depends on word frequency: Seidenberg, Waters, Barnes, & Tanenhaus, 1984; Taraban & McClelland, 1987). The behavior of the system in this interaction-dominated situation depends much more on context (i.e., the context of the other variable).

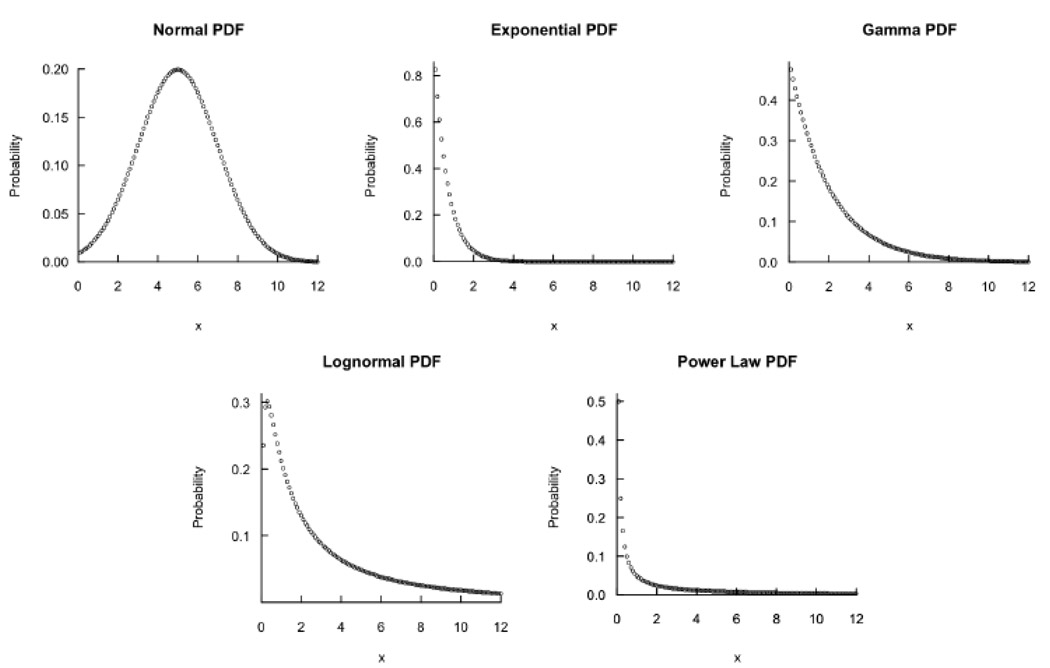
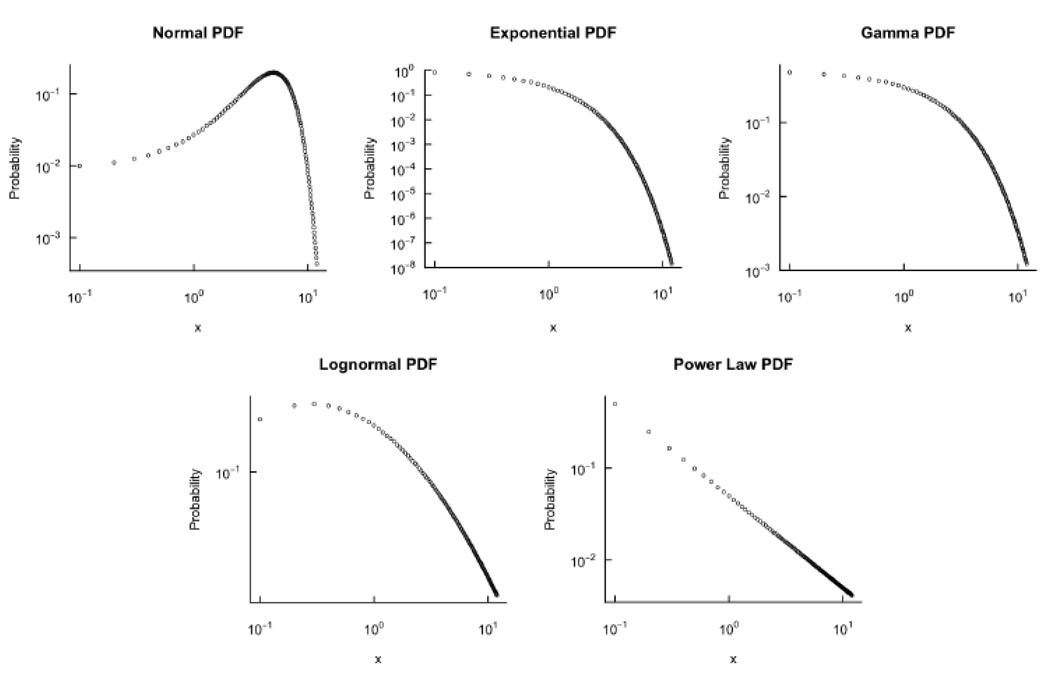
Thus, the test between component-dominance and interaction-dominance boils down to a distinction between additive and multiplicative distributions, respectively. We now describe a continuum from pure additivity/component-dominance to pure multiplicativity/interaction-dominance (Holden et al., 2009; West & Deering, 1995). This set of distributions is not exhaustive (see Nakatani & van Leeuwen, 2008) but captures a broad range of dynamics that might be found in cognition. We describe this continuum in mathematical terms of graded additivity and graded multiplicativity without a theoretical view as to whether systems may fundamentally belong to one or another distribution. At this point, whether cognitive dynamics are additive or multiplicative and how the distributions are influenced by context remain empirical questions. Thus, we take an agnostic position and consider the conventional range of possible distributions from various mixtures of additivity and multiplicativity (Edwards et al., 2007). For the purposes of illustration, Figure 1 shows the probability density functions (pdfs) for each distribution. In cases of strong skew, empirical distributions can be difficult to distinguish visually. Logarithmically scaling both axes can present a more easily legible picture; Figure 2 shows the same pdfs as in Figure 1, only on logarithmic axes.

Figure 1.

Probability distribution functions (pdfs) for continuuum distributions described in the text. Top row depicts pdfs for additive distributions (i.e., normal, exponential, and gamma, from left panel to right panel). Bottom row depicts pdfs for multiplicative distributions (i.e., lognormal and inverse power law, from left to right).

Figure 2.

Probability distribution functions (pdfs) on double-log plots. Top row depicts pdfs for additive distributions (i.e., normal, exponential, and gamma, from left panel to right panel). Bottom row depicts pdfs for multiplicative distributions (i.e., lognormal and inverse power law, from left to right).

Pure additivity: The normal distribution

The quintessential portrait of component-dominant dynamics is the normal distribution (Figure 1–Figure 2: top row, left panel). The normal distribution arises when independently-selected distinct components are added as described above. Because distributions of observed behavior are usually skewed (Engbert, Neuthman, & Kliegl, 2007; Andrews & Heathcote, 2001), the normal distribution serves here only as the anchor for the remaining continuum of distributions.

Skewed additivity: The gamma and exponential distributions

Modest multiplicative distortion will turn a symmetric additive model into a skewed distribution (Arellano-Valle, Branco, & Genton, 2006). For example, the exponential (Figure 1–Figure 2) and the gamma distributions (Figure 1–Figure 2: top row, middle and right panels) both reflect summations of independent components (Edwards et al., 2007; Kendal, 2001). The exponential distribution exhibits slightly greater skew. Both exponential and gamma distributions are often used in models of reaction times (Luce, 1986; Miller & Ulrich, 2003) as well as fixation durations (Engbert & Kliegl, 2001).

Multiplicativity among components: The lognormal distribution

The lognormal distribution describes a normal distribution of logarithmically scaled values (Figure 1–Figure 2: bottom row, left panel). Whereas the normal distribution expresses probability p as the sum of two random variables a and b

$$p=a+b,$$ (1)

the lognormal distribution expresses the probability p as the sum of logarithmically scaled random variables

$$p=\text{log}a+\text{log}b.$$ (2)

Because the sum of logarithms is equal to a logarithm of the product:

$$p=\text{log}(a\times b),$$ (3)

the lognormal distribution arises from multiplicativity. The lognormal distribution retains the independence of individual components but reflects a constrained variety of interaction-dominant dynamics (Farmer, 1990; Holden et al., 2009). The increased multiplicativity is apparent in the greater skew of the lognormal across x in Figure 1–Figure 2 relative to the gamma and the exponential.

Multiplicativity with feedback: The (inverse) power-law distribution

This most-skewed distribution is a multiplicative process in which probabilities decay by a constant ratio (Figure 1–Figure 2: bottom row, right panel; Montroll & Shlesinger, 1982). Power laws entail the weakest role for independent components and the strongest role for interactions, exhibited in the shallowest decay compared to other distributions. The dependence of random variables in the power-law case can be considered a result of resonant feedback dynamics. Under feedback dynamics, the occurrence of an event increases the probability that it will occur again; that is, once a random value is selected, the same (or similar) values for a random variable will be selected multiple times in sequence. The power law distribution arises due to exponentiation of random variables (i.e., a^b). Exponentiation relies on multiplication, but now the elements that are multiplied are not independent: small values are multiplied by small values and large values are multiplied by large values. Consequently, the range of the products is amplified. Power laws have been found in a variety of cognitive processes, from word naming reaction times (Van Orden et al., 2003), to self-paced tapping (Lemoine, Torre, & Delignières, 2006), to forgetting curves (Anderson & Schooler, 1991).

In summary, normal distributions reflect pure addition of independent variables, gamma and exponential distributions reflect addition of independent variables with slight multiplicative distortion, lognormal distributions reflect multiplication of independent variables, and power law distributions reflect multiplication of non-independent variables.

Cognitive behavior reflects interaction-dominant dynamics

Recent evidence suggests that interactions dominate cognitive behavior. For instance, variability in cognitive tasks repeated over time may exhibit power-law structure. Specifically, variability over time may exhibit 1/f noise, the power-law decay across frequencies in the power spectrum. That is, response times oscillate over long ranges, and the power (i.e., squared amplitude) of these oscillations diminishes very slowly as the frequency of these oscillations increases. This pattern has been found in response times for mental rotation (Gilden, 2001) and word naming (Van Orden et al., 2003; Holden et al., 2009). Speech appears to follow the same pattern: syllable utterance duration, acoustic power of vocalization at a variety of frequency bandwidths, and intervals between turns taken in a conversational setting all exhibit 1/f noise (Kello, Anderson, Holden, & Van Orden, 2008). In a set of findings convergent with the power-law structure in 1/f noise, the aggregate pdfs of response times in reading printed words aloud followed power-law and lognormal distributions, as well as mixtures of these two distributions (Holden et al., 2009). Task factors such as word ambiguity lengthened reaction times and shifted the distributions to be more like power law than lognormal.

Interaction-dominance in visual cognition

Aks and colleagues have found similar results in visual cognition. For instance, when participants looked at the reversible figure commonly known as the Necker cube, the time intervals between reversals (i.e., perceived changes in the Necker cube’s orientation) exhibited 1/f noise (Aks & Sprott, 2003). In order to manipulate depth cues and duration viewing conditions, participants viewed the Necker cube through red-blue anaglyph eyeglasses for a variety of durations. The Necker cube was presented for 15, 30, or 60 minutes in red and blue contours offset by 0, 1, 2, and 4 seconds of visual arc. Stronger depth cues and briefer viewing conditions increased the exponent of the power-law decay in the power spectrum. In a visual search task that required participants to find an upright “T” amidst rotated “Ts,” Euclidean distances between consecutive gaze positions (sampled at 500 Hz) exhibited 1/f noise (Aks, Zelinsky, & Sprott, 2002).

Stephen, Mirman, Magnuson, and Dixon (2009) examined the dynamics of eye movements while participants followed spoken instructions to click on one of four images presented on a computer screen (i.e., the visual world paradigm, or VWP; Tanenhaus, Spivey-Knowlton, Eberhard, & Sedivy, 1995). Eye movements were sampled at a relatively coarse grain (50 Hz). The aggregate pdf of Euclidean distances between consecutive gaze positions was better fit by a power-law distribution than by a gamma or exponential distribution. Such interaction-based, nonlinear dynamics have been critical to previous – namely PDP – accounts of visual search (e.g., Spivey & Dale, 2004) and VWP (e.g., Magnuson, Tanenhaus, Aslin, & Dahan, 2003).

Previous to Holden et al.’s (2009) inclusion of the lognormal distribution, interaction-dominance in cognitive tasks had been described largely in terms of power laws. So far, there has been a similar reliance upon the power law in tests of interaction-dominance in visual cognition (Aks & Sprott, 2003; Aks et al., 2002; Stephen et al., 2009). This focus on the power-law has led to a dichotomous view in which cognition is either interaction-dominant (and fits the power law distribution) or it is not. As reviewed above, there is a potential continuum of interaction dominance, and the lognormal distribution is a critical point in that continuum that reflects interaction-dominance under constraints, possibly from biological and physical properties. Indeed, lognormal distributions often appear to be more realistic models of biological and neural dynamics than power-law distributions (Hyman et al., 1995; Limpert et al., 2001; Qian & Bassingthwaighte, 2000).

The visual cognitive tasks

We examined where eye movement dynamics fall on a continuum of interaction-dominance in three classic visual cognitive tasks: two visual search tasks (e.g., Treisman & Gelade, 1980) and the VWP. We examined distributions of gaze steps: the Euclidean pixel distance displacements between consecutive gaze positions sampled by an eye-tracking device (as in previous studies: Aks & Sprott, 2003; Aks et al., 2002; Stephen et al., 2009). If cognitive dynamics are interaction-dominant, the observed distributions of gaze steps should be better fit by power-law and lognormal distributions than exponential and gamma distributions.

We also examined how task differences influenced the kind of distributions that unfold. The two visual search tasks were quite similar in nature, requiring the participant to search among distractors for a target that was distinguished by either a single visual feature or the conjunction of two features. The consistency among the targets and the distractors may constitute a constraint, pushing the system toward additive distributions in eye movements. A VWP task was chosen to be a considerably different visual cognitive task: participants were asked to mouse-click the picture of an animal among a set of four pictures (one target picture of an animal and three pictures of non-animal objects). The variety of targets (“animal” for VWP vs. “O” or “green N” for feature and conjunction search) and distractors (non-animal objects vs. brown “Ns” and green “Xs”) was much greater in the VWP task than in the visual search tasks. This wider variety of targets and distractors may place weaker constraints on the participant’s eye movements and thus allow greater interactivity to unfold in their visual exploration, much like ambiguity (spelling-pronunciation inconsistency) shifted distributions of reading times closer to power-law functions (Holden, 2002). Under this hypothesis, the distribution of gaze steps in the VWP task should tend closer to power-law distributions than those in the visual search tasks.

Methods

Participants

Six participants completed the experiment as one option to fulfill a course requirement. All participants reported normal or corrected-to-normal vision. Participants gave informed consent as required by the Institutional Review Board of the University of Connecticut.

Equipment and procedure

Participants were seated with their eyes approximately 27” from a 20” screen with 1024 × 768 resolution. Participants completed three tasks in counterbalanced order: two search tasks (single-feature and conjunction) and one VWP task. Gaze positions were recorded by a remote SR EyeLink 1000 eye-tracker at 500 Hz.

Visual search tasks

Participants completed 24 trials of each visual search task. In the single feature search task, participants had to indicate whether or not the letter “O” was present among distractors that were letters “N” and “X”. In the conjunction search task, participants had to indicate whether or not a green letter “N” was present among distractors that were green “X’s” and brown “N’s”. There were six trials for each set size (1, 5, 15, and 30 letters), and the target letter was present in half of the trials.

VWP task

Participants completed 30 trials of the VWP task. Participants were instructed at the start of the block to mouse-click on the image of an animal in each display. Each display consisted of images of 3 common non-animal objects (e.g., jukebox, mug, plum) and one image of an animal (e.g., gorilla). Each of the four images was displayed near one of the screen corners and the position of each image was randomized.

Data Analysis

Traditional inferential statistical tests (t-test and ANOVA) were used for behavioral data analysis. For distribution fitting, we used the MATLAB Statistics Toolbox for maximum likelihood (ML) estimation. Whereas ordinary least-squares (OLS) evaluates model fit with r-squared, ML evaluates model fit with log-likelihood. For a candidate distribution, ML estimation fits parameters that maximize log-likelihood. The candidate distribution with the highest log-likelihood is taken to be the best fitting distribution (Edwards et al., 2007; Sims et al., 2008). Of course, empirical data are unlikely to conform precisely to any model distribution; rather, we define a sample of candidate distributions and take the best-fitting (that is, most likely) distribution to be the best approximation of the empirical data (Burnham & Anderson, 2002; Schunn & Wallach, 2005). If the best-fitting distribution is additive, this is evidence of component-dominance. If it is multiplicative, it is evidence of interaction-dominance. The relative goodness-of-fit of one distribution over another is expressible by the difference in log-likelihoods of the distributions in question.¹ Because the difference of logarithms equals the logarithm of a ratio (i.e., log(b) − log(c) = log(b/c)), this difference in log-likelihoods is called the log ratio (Singer & Willett, 2003).

Results

Behavioral results

Accuracy

All six participants completed all tasks at 87.5% accuracy or higher, and the differences in accuracy among participants were not statistically reliable, F(2, 15) = 2.39, p > .05. (see Table 1)

Table 1.

Accuracy by participant and by task.

	Task
Participant	VWP	Simple-Feature	Conjunction
1	100.00%	87.50%	100.00%
2	100.00%	100.00%	95.83%
3	100.00%	95.83%	87.50%
4	100.00%	95.83%	91.67%
5	100.00%	100.00%	100.00%
6	100.00%	100.00%	100.00%

Reaction time

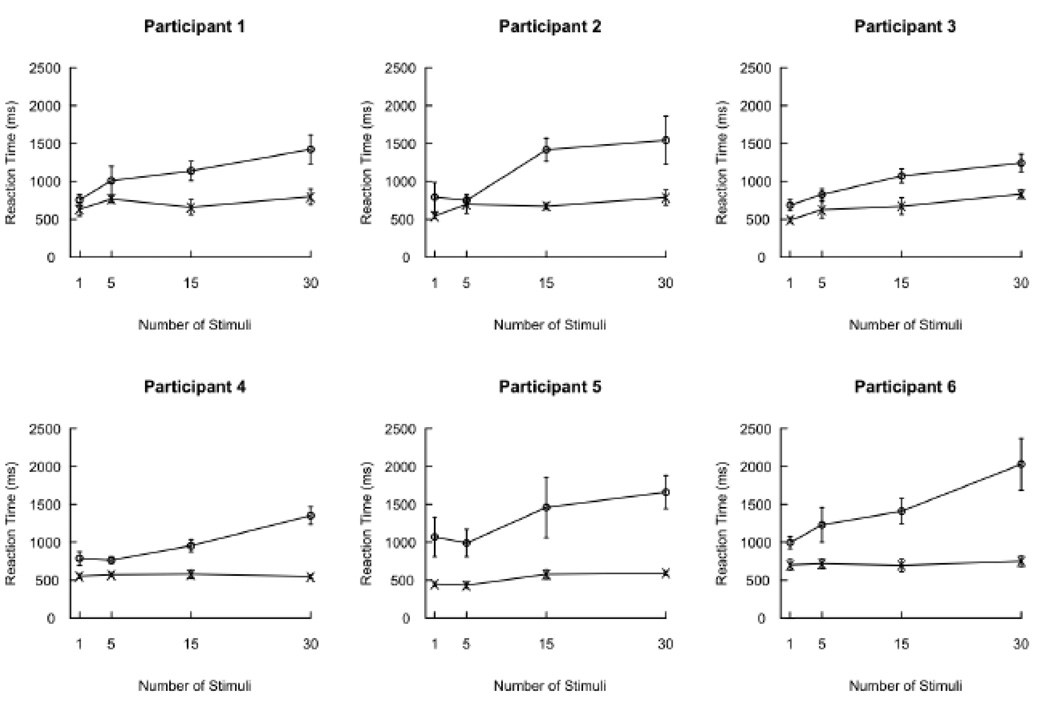
Reaction times were not significantly different between the VWP task and the visual search tasks, t(12) = .10, p > .05. For the visual search tasks, there were main effects of task, F(1, 5) = 39.67, p < .01, and set size, F(3, 15) = 45.11, p < .0001, and a significant interaction of task with set size, F(3, 15) = 20.66, p < .0001. Figure 3 shows the mean reaction times for each participant across the two different visual search tasks. The interaction reflects the strong effect of set size on conjunction-feature search and relatively weak effect of set size on single-feature search – a replication of the classic visual-search result (e.g., Triesman & Gelade, 1980).

Figure 3.

Plots of reaction times by set size for each participant in the Treisman and Gelade (1980) search tasks. The bottom curve on each set of axes indicates reaction times in the single-feature search; the top curve on each set of axes indicates reaction times in the conjunction search.

Relative likelihood estimation

Gaze step size

Gaze steps for the VWP task (M = 2.45, SE = .14) were marginally (F(2, 10) = 3.73, p = .06) larger than for the single-feature search task (M = 1.98, SE = .35) or the conjunction search task (M = 1.84, SE = .23).

Probability distribution functions

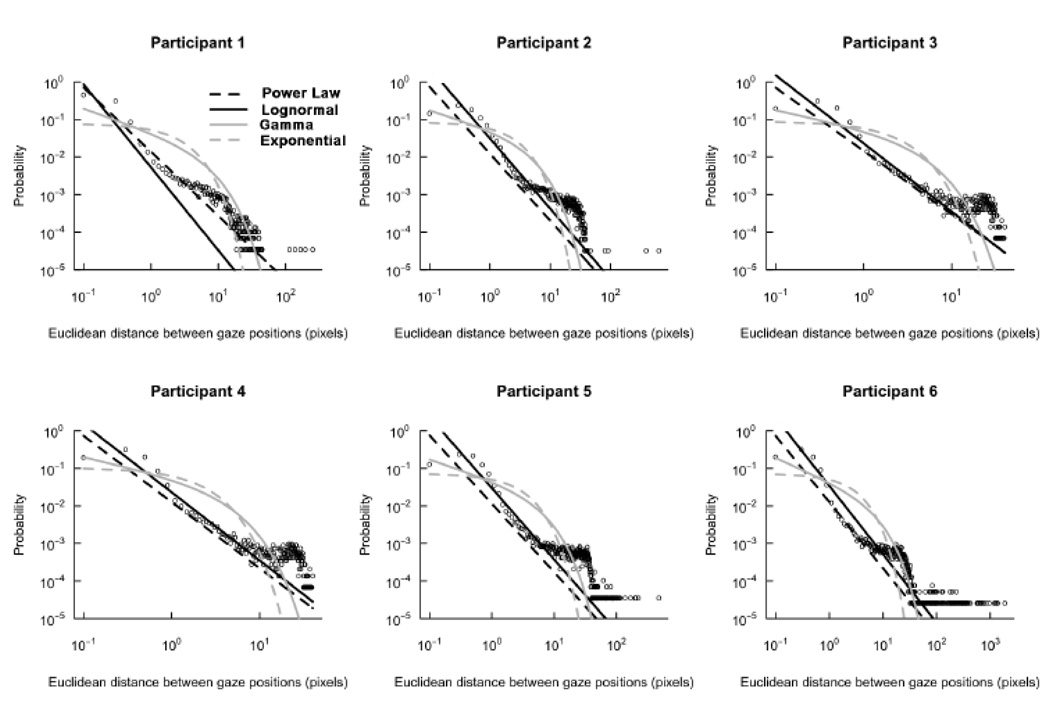
Figure 4–Figure 6 show empirical pdfs by participant for the VWP task, the single-feature search task, and the conjunction search task, respectively. Logarithmic axes are used for ease of visualization.

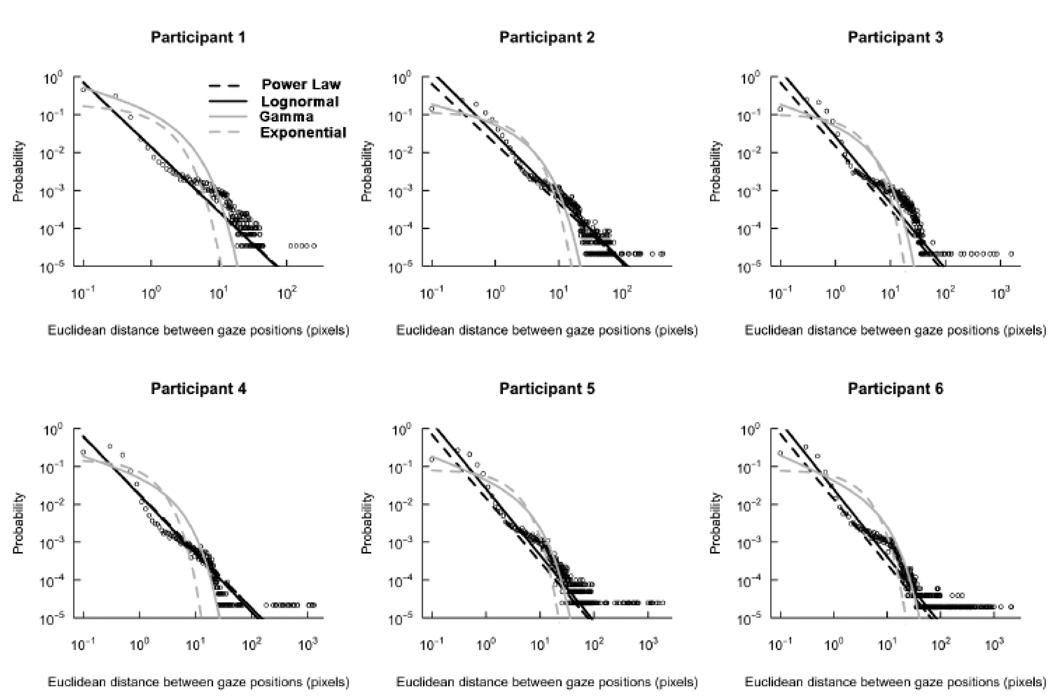
Figure 4.

Empirical probability distribution functions (pdfs) of gaze steps in the visual world paradigm (VWP) task by participant on double-log plots. Distribution fits are shown for inverse power law (dashed black curve), lognormal (solid black curve), gamma (solid gray curve), and exponential (dashed gray curve).

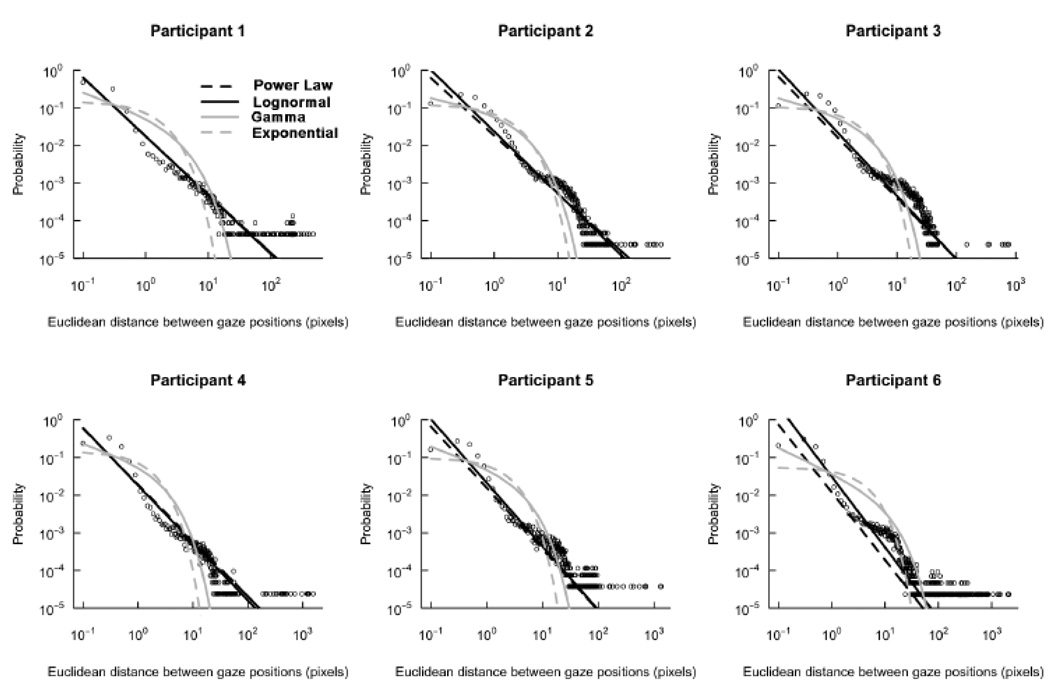
Figure 6.

Empirical probability distribution functions (pdfs) of gaze steps in the conjunction search task by participant on double-log plots. Distribution fits are shown for inverse power law (dashed black curve), lognormal (solid black curve), gamma (solid gray curve), and exponential (dashed gray curve). As in Figure 5, lognormal and inverse power-law fits for Participants 1 and 4 are sufficiently close to one another that the lognormal curve eclipses the inverse power-law curve.

Basic model fits

We tested the model fit of exponential, gamma, lognormal, and power-law distributions to the distributions of gaze steps for each task. Table 2 shows the log-likelihood for each fit by task and by participant. Higher log-likelihood indicates better model fit. For the VWP task, one participant exhibited power-law-distributed gaze steps, and five participants exhibited lognormal-distributed gaze steps. For visual search, gaze steps were all lognormal-distributed. These multiplicative distributions of eye movements suggest that interactions dominate cognition in these tasks. Fits for the four distributions tested are shown on the same axes as empirical pdfs in Figure 4–Figure 6: lognormal and power-law distributions were better fits than gamma and exponential distributions. Often, the best fitting lognormal and power-law distributions were quite similar on simply visual inspection.

Table 2.

Log-likelihoods for model fits of gamma, exponential, Pareto (power-law), and lognormal distributions.

		Distribution
Participant	Task	Gamma	Exponential	Lognormal	Pareto
1	VWP	−38312.27	−50889.10	27925.59	−27532.58*
	S-F	−25010.68	−31945.15	−10978.22*	−12496.94
	Conj	−19414.35	−28503.78	−3140.16*	−4973.41
2	VWP	−50987.68	−57705.02	−39835.88*	−40853.14
	S-F	−65568.10	−70883.54	−48376.19*	−51439.16
	Conj	−58913.71	−62164.20	−44955.34*	−48016.11
3	VWP	−48481.12	−54565.41	−35671.84*	−36997.10
	S-F	−68171.09	−76503.19	−49796.42*	−52119.44
	Conj	−63501.46	−68963.30	−47271.86*	−49988.98
4	VWP	−20099.90	−23791.34	−13920.05*	−14375.34
	S-F	−50106.03	−59003.13	−24100.57*	−28385.39
	Conj	−45057.44	−54031.50	−19867.38*	−23923.36
5	VWP	−48844.32	−57470.51	−36892.35*	−37408.63
	S-F	−62020.48	−74280.42	−41675.59*	−43407.09
	Conj	−38120.47	−45336.28	−24246.53*	−25622.05
6	VWP	−59391.24	−78970.37	−35907.80*	−36646.79
	S-F	−72909.36	−96165.02	−42515.25*	−44195.32
	Conj	−69789.61	−97055.82	−42278.09*	−42790.18

Task differences

The distributions of gaze steps were influenced by task, suggesting that they were not simply generic products of oculomotor dynamics. We examined the log ratio between lognormal and power-law fit to reveal how task influenced the dynamics of eye movements.

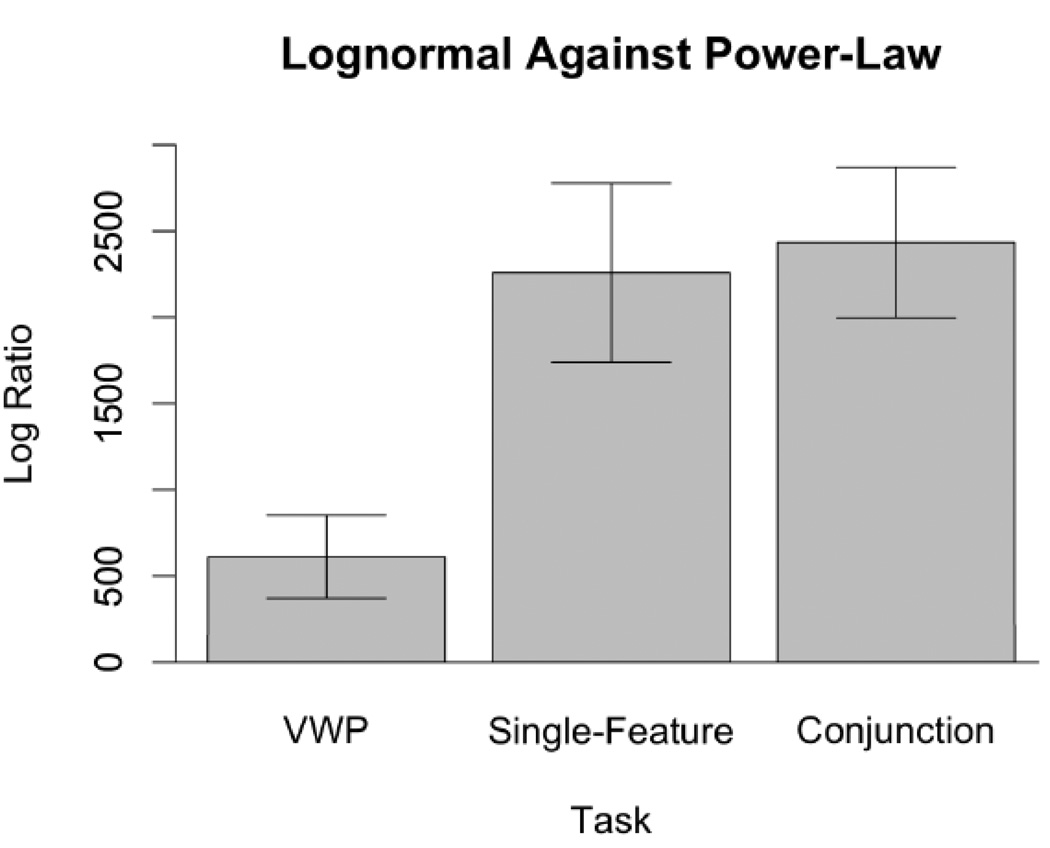
Figure 7 shows that the difference in log-likelihoods favoring lognormal over power-law fit was significantly lower in the VWP task (M = 610.01, SE = 240.34) than in either the single-feature search task (M = 2259.10, SE = 519.48) or the conjunction search task (M = 2433.67, SE = 437.10). An F-test comparing these differences in average log-likelihood by task was significant, F(2, 10) = 11.37, p < .01. That is, relative to visual search, the cognitive dynamics underlying performance in the VWP task were closer to power-law. Far from being an outlier, Participant 1 reflected a general tendency for gaze-step distributions to move towards power-law structure in the VWP task. This result is consistent with the hypothesis that cognitive behavior appears more interaction-dominant when performing a less constrained task.

Figure 7.

Log-ratios between indicating the relative strength of lognormal fit to power-law fit. The single-feature and conjunction search tasks indicate similar log-ratios. Although the gaze steps elicited by the VWP task were still predominantly lognormal, the gaze steps tended closer towards power-law fit.

The distributions were equally lognormal for both single-feature and conjunction search (t(4) = .257, p > .40), consistent with interactive models that propose the same underlying process for both types of search (e.g., Spivey & Dale, 2004), rather than componential models that propose fundamentally different processes (e.g., Triesman & Gelade, 1980). Note also that the heavier tail of a power-law distribution would produce the slightly larger average gaze step size found for VWP than visual search.

Discussion

The present research examined the dynamics of the cognitive system during three visual cognitive tasks. The distributions of gaze steps were best fit by lognormal or power-law distributions, which is consistent with the hypothesis that cognitive dynamics are interaction-dominant. We also found task-specific differences in the shape of gaze step distributions, indicating that task differences shifted cognitive dynamics along a continuum of interaction-dominance between lognormal and power-law distributions, consistent with previous work suggesting that the apparent degree of interaction-dominance depends on task constraints (Aks & Sprott, 2003; Kello et al., 2008). These findings of lognormal distributions in gaze steps and task-modulation of distribution shape provide new evidence of system-wide interactivity in visual cognition.

Interactions appear to dominate the dynamics of visual cognition

The classic description of visual perception and cognition rests on a componential division of labor. Light hits the retina, progresses through a sequence of ever more abstract levels of processing that elicit the intention to shift gaze, and this intention is then executed by the peripheral oculomotor system. Under a strictly componential view, information from these different levels would be combined in an additive manner, eventually producing an additive distribution of eye-movements indicative of component-dominant processing. There is, however, tremendous evidence of interactivity in the visual system: from extra-classical receptive fields (e.g., Angelucci et al., 2002) to visual illusions (e.g., Lee & Nguyen, 2001) to context effects on object recognition (e.g., Bar, 2004). Interaction-dominant dynamics suggest a major departure from the classic description. Under interaction-dominant dynamics, the structure of the cognitive system is emergent and the organization is fluidly dependent on the ongoing flow of information through the system. The individual parts of the visual system assume functions and relationships that may change dramatically depending on context.

Borrowing analytical techniques from statistical mechanics and complexity science, we present a different perspective on components and interactions in cognitive systems. A system of stable, independent components – as described in traditional cognitive science theories, particularly those that emphasize modularity (e.g., Coltheart, 1999; Dietrich & Markman, 2003; Fodor, 1983; Marr, 1982; Wagenmakers, Farrell, & Ratcliff, 2004) – would produce additive normal distributions of behavior. A system of relatively stable but highly interactive components would produce multiplicative lognormal distributions; and an interactive system with broad interdependence and feedback among components would produce power-law distributions. The present findings of lognormal and power-law distributions and task sensitivity in eye movement dynamics suggest that cognition (at least visual cognition) is dominated by interactive processes and emergent structure. This view is closely related to perspectives in which cognition is an emergent property of interactions of simple processing components rather than the sum of independent sub-systems.

It is important to stress the conceptual distance between empirical and theoretical distributions. Although lognormal distributions were generally the best fitting distribution, there were small but systematic departures of the empirical distributions from the best-fitting theoretical distributions. The peaks fell short of the fitted curves (i.e. to the left), and the extreme ends of the tails tended to sprawl above and beyond the fitted curves (i.e., to the right). First, there is no guarantee that an empirical distribution will be fit perfectly by any theoretical distribution (Schunn & Wallach, 2005). Second, if we permit the possibility that the cognitive system may exhibit behavior falling along a continuum of distributions, there must necessarily be mixtures of distributions as the cognitive system moves from one mode to another. It is possible that, as Holden et al. (2009) found in distributions of response time, these distributions of gaze steps are mixtures of power law and lognormal functions. We were interested only in demonstrating the generally interaction-dominated structure. Future work might investigate the relative advantage of such mixtures, with the caveat that systems whose dynamics generally reflect multiplicativity may not simply be the added sum of two multiplicative distributions but may involve multiplications of constituent distributions.

Interactivity and strategies for computational models of cognition

An emphasis on emergent structure is found in a range of theories of cognitive processing, particularly those that fall within the PDP framework. Interactivity and nonlinear (multiplicative) processing are central principles in the PDP framework (e.g., McClelland, 1993) and one critical motivation for the development of PDP models of cognition has been to provide an account of cognition in which structure is emergent rather than stipulated (e.g., McClelland, Plaut, Gotts, & Maia, 2003). Although these models have typically been applied to task-specific performance scores, the approach we have taken here examined fine-grained (i.e., densely sampled, at 500 Hz) dynamics of eye-movements and yielded new evidence of interaction-dominance in visual cognition.

Despite the shared theme of interactivity, interaction-dominant dynamics makes a few substantial departures from the PDP approach. For instance, the framework of interaction-dominant dynamics is purposefully agnostic about specifying a preexisting architecture. The reason for this agnosticism is the very point that interaction-dominated systems are inherently context specific: architecture will evolve based on the flow of information. In the PDP framework, a baseline or input/output structure is specified and the focus is on the emergent mediating (often called “hidden level”) structure. Interaction-dominant dynamics take this one step further to allow the architecture itself to emerge. Information flow stirs a structurally uncommitted system into an orchestra of subsystems and parts. In this sense, interaction-dominant approaches are slightly more similar to computational modeling in liquid state machines (LSMs; Maass, Natschläger, & Markram, 2002). Whereas PDP networks are built to solve specific tasks, LSMs are neural nets that are built without predesigned functions or predetermined networks of connectivity between nodes (Morse & Aktius, 2009). Nodes in LSMs are connected randomly but recurrently, prone to any of a wide number of possible large-scale nonlinearities in the presence of activation. The architecture is uncommitted, and the flow of activation (i.e., information) governs the coordinations between nodes.

Concluding remarks

A componential division of labor would predict additive distributions and no modulation by task (e.g., oculomotor control mechanisms independently executing cognitive commands). Component-dominant theories describe cognition as the driver at the wheel of a biological automobile: the fine-grained mechanics of the engine, the valves, and the wheels remain the same no matter the destination, and the driver only changes the broader scales of dynamics. In contrast, we found multiplicative distributions and modulation by task. That is, cognition extended far beyond the intentional, abstract levels of processing -- even the biological nuts and bolts of motor periphery showed sensitivity to task. These results indicate that cognition is broadly distributed over many anatomical scales and that looking behavior is an emergent property of the entire system.

Figure 5.

Empirical probability distribution functions (pdfs) of gaze steps in the single-feature search task by participant on double-log plots. Distribution fits are shown for inverse power law (dashed black curve), lognormal (solid black curve), gamma (solid gray curve), and exponential (dashed gray curve). Lognormal and inverse power-law fits for Participants 1 and 4 are sufficiently close to one another that the lognormal curve eclipses the inverse power-law curve.