Effect of Membrane Thickness on Conformational Sampling of Phospholamban from Computer Simulations

Abstract

The conformational sampling of monomeric, membrane-bound phospholamban is described from computer simulations. Phospholamban (PLB) plays a key role as a regulator of sarcoplasmic reticulum calcium ATPase. An implicit membrane model is used in conjunction with replica exchange molecular dynamics simulations to reach μs-ms timescales. The implicit membrane model was also used to study the effect of different membrane thicknesses by scaling the low-dielectric region. The conformational sampling with the membrane model mimicking dipalmitoylphosphatidylcholine bilayers is in good agreement overall with experimental measurements, but consists of a wide variety of different conformations including structures not described previously. The conformational ensemble shifts significantly in the presence of thinner or thicker membranes. This has implications for the structure and dynamics of PLB in physiological membranes and offers what we believe to be a new interpretation of previous experimental measurements of PLB in detergents and microsomal membrane.

Introduction

Calcium plays an essential role in muscle contractions. During muscle relaxation, sarcoplasmic/endoplasmic reticulum (SR/ER) calcium ATPase (SERCA) pumps Ca²⁺ from the cytosol to the lumen across the SR/ER membrane (1). The activity of the cardiac isoform of Ca²⁺-ATPase, SERCA2a, is regulated by phospholamban (PLB), a 52-amino acid transmembrane (TM) protein (2). The interaction with unphosphorylated PLB is believed to lock SERCA into the reduced calcium affinity E2 form thereby inhibiting Ca²⁺ transport (3). Inhibition is released when PLB is phosphorylated at S16 and/or T17 (4). Phosphorylation of PLB is proposed to either result in dissociation of PLB from SERCA or in an altered interaction between PLB and SERCA so that SERCA can switch from the inactive E2 form to the active E1 form with high Ca²⁺ affinity. However, details of this regulatory mechanism remain unclear (5). The importance of PLB in heart muscle function is underscored by a link between PLB mutations and heart failure in humans (6).

As a first step toward understanding the inhibitory mechanism of PLB, many studies have focused on the structural analysis of PLB without SERCA. PLB shows a strong tendency to oligomerize and in particular to form pentamers (7,8). However, most experimental evidence based on electron paramagnetic resonance, (9) fluorescence (10), and mutagenesis (3,8) studies suggests that the monomeric form of PLB is primarily responsible for inhibition of SERCA. Therefore, most studies of PLB are concerned with the monomeric form.

The C41F mutant of PLB has a low propensity to form pentamers but retains biological activity. NMR studies of this mutant in CHCl₃/MeOH indicate the presence of two α-helices connected by a β-turn suggesting an L-shaped structure (11). Solid-state NMR (SSNMR) studies of the triple mutant in a mixed bilayer (12) suggest an interhelical angle of 80 ± 20° consistent with L- or T-shaped conformations. A slightly different value of ∼66° was obtained using multidimensional SSNMR (13). Furthermore, solution NMR-derived structures of C36A/C41F/C46A mutants in dodecylphosphocholine (DPC) micelles show three distinct structural domains for PLB (14): a short cytoplasmic (CP) helix (domain Ia, residues 1–16), a hinge with a β-turn type III conformation (residues 17–22), and a long hydrophobic TM helix (domains Ib, 23–30, and II, 31–52 (17)) also with an interhelical angle of 80° (15). Further studies of PLB with multidimensional SSNMR and hybrid solution NMR and SSNMR suggest that the CP helix adopts angles of 93–102° with respect to the membrane normal whereas the TM helix is tilted with an angle of 22–24°(13,16).

The static models of PLB described so far are contrasted by evidence of significant conformational dynamics. There is evidence of two topologies for the TM domain from solution NMR (17). Two well-resolved conformational states of the CP domain have also been observed in solution NMR, electron paramagnetic resonance spectroscopy (18,19), and SSNMR (13). One conformation, called the T state, is ordered and in direct contact with the membrane surface whereas the other conformation, the R state, is dynamically disordered and detached from the membrane. Furthermore, fluorescence resonance energy transfer measurements suggest that the CP domain of PLB in the absence of SERCA assumes a wide range of structures relative to the TM domain (20).

Molecular dynamics (MD) simulations provide atomistic insight into the structural information and dynamics of PLB. Several MD simulations of partial or full length PLB in different environments have been reported (21–25). One of the first MD simulations of full length PLB in dipalmitoylphosphatidylcholine (DPPC) bilayer, water, and methanol maintained the two well-defined TM and CP helical domains over 5–10 ns, and showed large-amplitude rigid-body motions of these domains, in particular for the CP domain (21). The average interhelical angles in methanol and water were found to be 54° and 63°, respectively, and 130° in the lipid bilayer (21) in disagreement with NMR results. Replica exchange MD simulations of the CP domain of PLB and phosphorylated PLB as well as the R9C mutant in explicit water showed the importance of P21 in maintaining the local helical structure of the CP domain of PLB (22). Constant-temperature MD simulations of full-length PLB and phosphorylated PLB for 30 ns, suggested that the TM helix and the lipid bilayer have only a minor effect on the conformational sampling of the CP domain of PLB (23). Furthermore, a 15-ns MD simulation of PLB in palmitoyl oleoyl phosphatidyl choline bilayer confirmed the presence of dynamic motions involving the CP domain of PLB and preservation of mostly helical structures for the CP and TM domains (24). Finally, a recent MD simulation study (over 15 ns) of PLB in explicit palmitoyl oleoyl phosphatidyl choline bilayer confirmed the helix-hinge-helix structure of PLB but found that the interhelical angle and the position of the CP helix relative to the membrane are highly dependent on the starting structure indicating that simulations of PLB over 10-ns timescales are not sufficient to describe fully the conformational dynamics of PLB (25).

We describe replica exchange simulations of monomeric PLB with an implicit membrane model that effectively cover at least μs timescales and provide a more comprehensive view of PLB dynamics than simulations reported previously. Implicit membrane simulations have been used before to cover long-time dynamics in the interaction of peptides with membranes (26–31). The use of an implicit membrane also offers the unique advantage that the membrane thickness can be varied easily. For what we believe to be the first time, our simulation results suggest that the conformational sampling of PLB may indeed differ for very thin and very thick membranes, which has important consequences for the interpretation of conflicting experimental data and offers new insights into the mechanism by which PLB regulates SERCA.

Methods

MD simulations of phospholamban

Replica exchange MD simulations (32) of monomeric PLB with the wild-type sequence were started from model 1 of the NMR ensemble for the C36A/C41F/C46A PLB mutant in DPC micelles (PDB entry 1N7L (15)). Standard protonation states (pH = 7) and zwitterionic termini were used. The initial structure was oriented in the implicit membrane with the TM helix (domain II) parallel to the membrane normal and the CP helix (domain Ia) parallel to and above the membrane surface. The CHARMM22 all-atom force field (33) in combination with the CMAP correction term (34) was used to describe intramolecular interactions along with the heterogeneous dielectric generalized Born (HDGB) implicit membrane model to reflect the membrane environment. No cutoffs were applied to nonbonded interactions. Temperature replica exchange MD simulations were started from the energy-minimized initial structure with eight replicas spanning a temperature range of 300–400 K in an exponential fashion. Exchanges were attempted every 500 MD steps. The acceptance ratio between adjacent replicas was between 22% and 33%. A time step of 1.5 fs was used to maintain stable simulations with the implicit membrane model (35). Langevin dynamics (36) was used with a friction coefficient of 10 ps⁻¹ (37) for all nonhydrogen atoms to control the temperature of the system. The SHAKE algorithm was used to constrain bond lengths involving hydrogen atoms (38). All of the simulations were carried out with CHARMM (39), version 34a2 in combination with the MMTSB Tool Set (40) to facilitate the replica exchange simulations and analyze the simulation results.

Implicit membrane model

An implicit model of the phospholipid bilayer is applied to reach long timescales that are otherwise inaccessible with conventional explicit lipid simulations. Implicit models reduce the computational time per time step but the more significant advantage comes from instant relaxation of the environment that would otherwise incur kinetic barriers with an explicit representation, especially in lipid bilayer environments. To obtain a realistic representation of the physical characteristics of membrane environments, the HDGB model (41) consisting of a variable dielectric continuum along the membrane normal is applied. This model is based on the generalized Born (GB) formalism and involves a modified description of the electrostatic component of ΔG_solvation (42):

$${\Delta G}_{\text{electrostatic}}=-166\sum _{\text{i}=1}^{\text{n}}\sum _{\text{j}=1}^{\text{n}}\left[1-\frac{1}{(1/2)({\varepsilon }_{\text{i}}-{\varepsilon }_{\text{j}})}\right]\frac{q_{\text{i}}{q}_{\text{j}}}{\sqrt{r_{\text{ij}}^2+{\alpha }_{\text{i}}\left({\varepsilon }_{\text{i}}\right){\alpha }_{\text{j}}\left({\varepsilon }_{\text{j}}\right)\exp \left[-r_{\text{ij}}^2/8{\alpha }_{\text{i}}\left({\varepsilon }_{\text{i}}\right){\alpha }_{\text{j}}\left({\varepsilon }_{\text{j}}\right)\right]}},$$ (1)

where q_i are atomic charges, n is the number of atoms, r_ij are interatomic distances, and α_i are the effective atomic Born radii. The dielectric constant (ɛ) for each atom in Eq. 1 varies as a function of z, along the membrane normal, and reflects the effective dielectric constant at a certain membrane insertion depth. The ɛ profile was generated initially by solving the Poisson equation for a spherical probe at different locations in a system composed of dielectric slabs (41) and subsequently optimized to match free energies of insertion from experiment and explicit membrane simulations as described below (see Fig. S1 in Supporting Material). Other parameters of the GB model were set as described previously (35,41–43).

The nonpolar component of the solvation free energy is described by the solvent accessible area model:

$${\Delta G}_{\text{nonpolar}}=\gamma \sum _{\text{i}=1}^{\text{n}}S\left(z_{\text{i}}\right)A_{\text{i}},$$ (2)

where A_i is the solvent accessible surface area of the i^th atom, z_i is the distance of atom i from the membrane center along the membrane normal, γ is the empirical surface tension parameter set to 0.015 kcal/mol (41), and S(z) is a switching function to reflect the change of the surface tension along membrane normal. The S(z) function was determined initially from explicit lipid simulations for the insertion of O₂ into lipid bilayers (41,44) and subsequently optimized along with the ɛ profile to match insertion free energies (see Fig. S1).

Analysis of simulation results

The weighted histogram analysis method (45) was used to generate potential of mean force (PMF) maps from the replica exchange trajectories. The angle between the CP and the TM helices (interhelical angle, θ) and the distance between the center of mass of the CP helix and the projection onto the TM helical axis (d-COM) were chosen as the reaction coordinates for generating the PMFs (Fig. 1). The helices were described by residues 4–12 and 25–40 for the CP and TM helices, respectively. Only part of the complete TM helix was used in this definition to reduce the effect of local bending within the TM helix on the calculated θ. Other structural properties were calculated using slightly different definitions to match experimental data as described in the caption of Table 1. Clustering of PLB conformations was carried out with the K-means method implemented in the MMTSB Tool Set (40). PyMOL was used to visualize the simulation results and generate molecular graphics (46).

Figure 1.

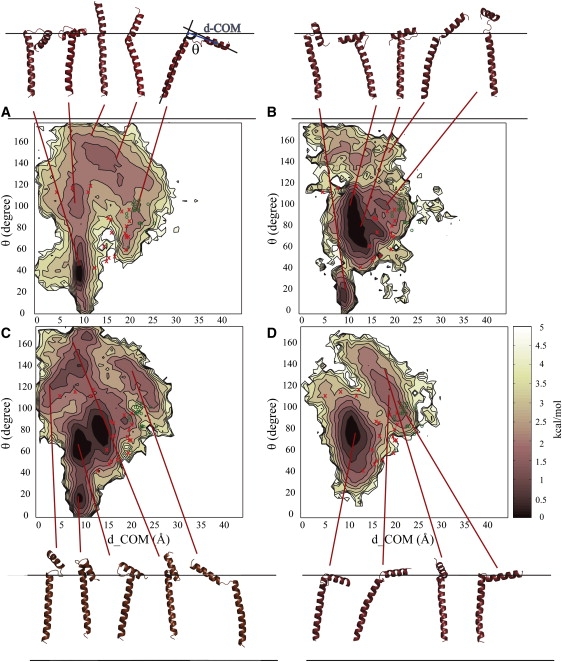
Energy landscape for PLB in different membrane models; (A) MM1, (B) MM2, (C) MM3, and (D) MM4. Representative structures for the clusters corresponding to the minima are shown in cartoon representation. NMR structures with PDB codes 1N7L and 2KB7 are mapped and shown as red x and green o, respectively (15,16).

Table 1.

Average structural properties of PLB calculated from simulations with different membrane models

Membrane model	MM1	MM2	MM3	MM4	Experiment
Interhelical angle, θ (°)	81 ± 13	87 ± 11	83 ± 12	82 ± 10	68 ± 23 (11)
					80 ± 20 (12)
TM tilt, αTM (°)	19.5 ± 2.7	13.3 ± 1.9	13.6 ± 1.8	13.0 ± 1.7	21.2 ± 2 (13)
					24 ± 2 (16)
CP tilt, αCP (°)	96.4 ± 14	96.4 ± 12	101.2 ± 14	98.6 ± 18	93 ± 6 (13)
					97 (16)
Interdomain distance (Å)	16.1 ± 1.7	18.4 ± 1.4	15.1 ± 1.4	13.4 ± 1.4	∼20 (5)
TM insertion (Å)	7.3 ± 0.7	5.6 ± 0.6	5.8 ± 0.6	5.7 ± 0.6	5.5 ± 0.5 (16)∗
CP insertion (Å)	27.8 ± 1.6	30.1 ± 1.2	31.3 ± 1.2	29.5 ± 1.3	16.2 ± 0.8 (16)∗
TM rotation, ρTM (°)	213 ± 14	196 ± 10	215 ± 8	208 ± 7	∼198 (16)
CP rotation, ρCP (°)	187 ± 16	209 ± 16	136 ± 8	229 ± 8	92 ± 3 (16)∗

Experimental values in DPC micelles (15), mixed DOPC/DOPE or DOPC lipid bilayers (12,13,16), and liposomes consisting of SR lipids (5) are given for comparison. Tilt angles α_TM and α_CP are with respect to membrane normal, the interdomain distance is the distance between C_α atoms of residues Y6 and C24 (5), TM and CP insertion depths are based on the center of mass for residues 23–52 (TM helix) and residues 1–16 (CP helix) relative to the membrane center (z = 0), and rotation angles ρ_CP and ρ_TM are defined as described previously (16) with helical axes obtained by averaging backbone N(i) − O(i + 4) vectors for residues 23–38 (TM helix) and residues 3–10 (CP helix). Only the upper part of the TM helix was considered to avoid artifacts due to TM helix bending. Errors for simulation results are obtained from comparing block averages.

^∗Values reported in Traaseth et al. (16) as a result of refinement instead of direct experimental measurements.

Results

Optimization of implicit membrane model

The HDGB implicit membrane model was initially parameterized based on limited reference data from experiments and explicit lipid insertion profiles. Since the original publication of the HDGB model, additional high-quality amino acid side chain analog insertion profiles from explicit lipid bilayer simulations have become available (47). These data were used to optimize the ɛ and nonpolar profiles published previously (41). The resulting optimized profiles are depicted in Fig. S1 and a comparison of implicit and explicit membrane insertion profiles is shown in Fig. S2. Overall, the agreement between the implicit and explicit insertion profiles is remarkably good, especially when the OPLS force field (48) is used with HDGB method to match the explicit lipid profiles that also used the OPLS force field. At the same time, the free energies of insertion predicted with the implicit model agree well with experimental water-cyclohexane transfer free energies (49). There are some discrepancies for polar residues that exhibit interfacial minima ∼15 Å due to the development of water defects in explicit lipid simulations (47). Although water defects are not possible in the HDGB model, this is expected to be less of a problem for peptides and proteins interacting with the lipid bilayer where the development of water defects around a polar residue is likely to be discouraged by neighboring hydrophobic residues.

The optimized profiles shown in Fig. S1 are appropriate for DPPC bilayer, but stretched or compressed profiles can be generated through simple scaling to examine the effect of different membrane thicknesses. The profiles in Fig. S1 have a thickness of 26 Å for the ɛ profile (the value of z where the bulk value of ɛ is reached), and 26 Å for the nonpolar profile (the value of z where the nonpolar function, S(z), reaches 1). Three additional profiles were considered with dielectric/nonpolar profile thicknesses of 24.5/24 Å (MM1), 25.5/24 Å (MM2), and 26.5/27 Å (MM4) to model membranes that are thinner or thicker than DPPC bilayers. MM2 may be representative of phospholipid bilayers with shorter fatty acid tails than DPPC. MM1 is even thinner and may represent bilayers consisting of extremely short fatty acid tails like detergent molecules whereas MM4 may represent phospholipid bilayers with longer fatty acid tails as often present in physiological membranes (50). The resulting ɛ and nonpolar profiles are shown in Fig. S3. Amino acid insertion profiles changed only moderately as a result of the shifted ɛ and nonpolar profiles (see example in Fig. S4).

Replica exchange simulations of PLB with implicit membrane

Replica exchange simulations of PLB with different implicit membrane profiles were carried out for 30,000 cycles (22.5 ns/replica) each. The first 10,000 cycles were discarded as equilibration and the last 20,000 cycles (15 ns) of each simulation were used for analysis. To improve statistical convergence further, two separate simulations were run for each system rather than extending the time for a single simulation. Fig. S5 shows a comparison of PMFs generated from two separate replica exchange simulations for MM1. The PMFs are qualitatively similar, but the quantitative differences between the two PMFs suggest an error of up to 1 kcal/mol in the less populated regions that translates into a maximum error of 0.7 kcal/mol when combining two PMFs according to standard error analysis. Consequently, all of the subsequent PMFs are averaged from two independent replica exchange simulations.

Fig. 1 C shows the sampling of PLB as a function of θ, the interhelical angle, and d-COM, the TM axis-CP helix distance, for the DPPC membrane model (MM3). A broad range of conformations is sampled, including the structures from the NMR ensembles in DPC micelles (PDB id: 1N7L (15)) and recently refined models based on SSNMR data in DOPC bilayer (PDB id: 2KB7 (16)) that have been mapped onto the PMFs based on their reaction coordinate values. The simulated PLB structures were clustered and the conformations closest to the cluster centers corresponding to minima in the PMF are shown in cartoon representation. The predominant minima correspond to L- and T-shaped conformations with T-shaped conformations being more prominent whereas the NMR ensembles emphasize L-shaped conformations more. The combination of solution NMR and lipid bilayer SSNMR in the 2KB7 ensemble has led to a shift in populations toward larger d-COM values, still within the range of structures sampled in the simulations but clearly distinct from the main minima of the simulated structures.

To compare further with the primary experimental data, average chemical shift anisotropy (CSA) and ¹H-¹⁵N dipolar couplings (DC) were calculated from the simulations and compared against the experimental values (see Fig. S6 and Fig. S7). Overall, the simulation results with the DPPC model are in good agreement with the SSNMR data. Average CSA values for the CP domain are slightly higher than experimental values as a result of sampling some structures with large θ (Fig. 1). Deviations in the TM region also include a shift to slightly larger values (corresponding to slightly less tilted TM helices in the simulations). We also find that the averages from the simulations underestimate the amplitude of the periodic variations of both CSA and DC values. However, this is not an indication of significantly different structural ensembles because the amplitude is highly sensitive to the helical tilt angle and the average orientation of the N-H vector with respect to the helical axis (51).

In other conformations seen in the simulations the CP helix interacts less strongly with the membrane interface because of a more extended configuration or it inserts partially into the head-group region of the membrane in an almost parallel orientation relative to the TM helix. The latter conformation has not been described previously by experiments or any of the simulation studies. Based on our simulations, it is estimated that this compact conformation would be populated ∼8% of the time and may therefore not be easily detectable in experimental studies or in short simulations. However, in the absence of clear experimental evidence, we cannot rule out that this conformation is an artifact of the simulation methodology used here.

Effect of membrane thickness on PLB sampling

Implicit membrane models with stretched or compressed profiles were used to examine the effect of membrane thickness on PLB sampling. Fig. 1 shows the PMFs generated with four different membrane models. It can be seen that the structures with small interhelical angles (θ) of 0–50° are increasingly populated at reduced membrane thickness model (MM1) and vanish in the model with the thickest membrane (MM4). At the same time, the pronounced broad minimum with θ = 60–120° is present in all but MM1. Structures with large values of θ where the CP helix points away from the membrane surface are present in all profiles, but in the thickest membrane these structures are less populated and there are more partially bent structures with θ near 120° rather than fully extended structures with θ near 180°. The structures from the NMR ensembles overlap reasonably well with the simulated distributions for MM2-4 but less so for the thinnest membrane model, MM1, where L-shaped conformations are largely missing. The average DC values from the simulations agree well with the SSNMR restraints for all models, but CSA values deviate significantly for the CP part in MM1 and for residues 15–18 in MM2 and MM4.

Average values of θ, tilt and rotation angles and insertion depths for the CP and TM helices, and the interdomain distance (between Y6 and C24) are reported in Table 1. The simulation results can be compared with experimental values for θ, the TM tilt and rotation angles, the CP tilt angle, and the interdomain distance (5,12,13,15,16). The other properties are compared against the reported values for the structural ensemble that resulted from optimization in a simple membrane potential (52) in the context of experimental restraints (16). Overall, the agreement is quite good and there are only modest differences between the four membrane models despite significant differences in the conformational sampling suggesting that the averages are not very sensitive to the actual structural ensembles. We note that the TM tilt angle is reduced in the simulations as evident already from the DC and CSA data described above. Furthermore, the interdomain distance seems to be reduced in the simulated structures compared to the experimental data. However, there are uncertainties in the exact interpretation of the fluorescence resonance energy transfer experiments that were carried out to obtain these data (5). The largest discrepancy between the simulated structures and the ensemble derived from experiments is in the CP insertion depth. In the simulations, the center of the CP helix is located at the membrane-water interface at ∼30 Å from the membrane center whereas the structures from the recent NMR ensemble (2KB7) have a much more deeply inserted CP helix. However, although the exact insertion depth was not measured experimentally, the reported value of ∼16 Å seems to be at least in part a result of the simple E_z membrane potential that was used during structure optimization. We found that optimization of representative structures extracted from our simulations with the E_z potential generally led to orientations with more deeply inserted CP helices suggesting that deep insertion of CP helices into the lipid bilayer is more favorable with the E_z potential than with our energy function.

An analysis of the distributions of the TM and CP helix tilt angles (see Fig. S10), the interdomain distances (see Fig. S11), and the CP and TM rotation angles (see Fig. S9) indicates that the average values from the simulations are in fact a result of broad conformational ensembles that consist of multiple states. For example, the average CP tilt angle does not vary much between the different membrane models. However, the actual distribution is quite different for MM1 compared to MM2 and MM4. In MM2 and MM4 there is a single peak near the average value whereas MM1 has two separate peaks corresponding to the extended and compact states with tilt angles of 120° and 40°, respectively. The distribution for MM3 seems to be intermediate between MM1 and MM2/MM4. The distributions of the interdomain distances and helix rotation angles are more complex as a result of the broad ensemble of structures that are sampled in the simulations highlighting again that simple averages as measured experimentally may not fully capture the structural diversity of the actual structural ensembles of monomeric PLB. In the case of the TM helix rotation we find multiple states, a major state with a rotation angle of ∼220° and minor states at ∼120° and ∼50°. In addition, there is another state with a rotation angle of ∼270° that is predominantly populated with the MM1 model. The CP helix rotation angle seems to be very sensitive to the membrane model. With the MM3 model, the CP helix is predominantly rotated such that the hydrophobic residues A11, V4, and A15 are facing the membrane (ρ_CP < 180), whereas those residues mostly face the solvent with the MM2 and MM4 models (ρ_CP > 180).

The interaction of the helices in the membrane was further analyzed by examining the distribution of the insertion depths of the TM and CP helices. The corresponding data for the four membrane models are shown in Fig. 2. The insertion depths of the CP helix with MM2-4 follow similar Gaussian-like distributions with a peak ∼30 Å. This means that the CP helix for the most part remains close to the membrane-water interface despite a significant fraction of structures with large interhelical angles. This is accomplished in part by tilting the TM helix and by the formation of compact linker structures that allow the CP helix to stay close to the membrane as evident from the conformations shown in Fig. 1. In contrast, the insertion depth distribution for the CP helix exhibits a much broader distribution with MM1 where one peak is located ∼25 Å and an additional broad feature extends from 35–48 Å. The first peak corresponds to compact structures with small values of θ, whereas the second feature reflects extended structures with large values of θ. Thus, only with the thinnest membrane we observe extended conformations where the CP helix is located far above the membrane.

Figure 2.

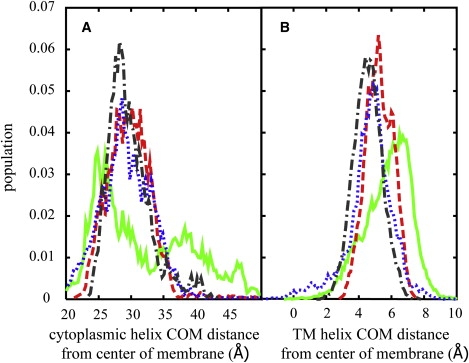
(A) Distribution of CP helix insertion. (B) Distribution of the TM helix (residues 25–52) insertion for different membrane models: MM1 (green solid line), MM2 (red dashed line), MM3 (blue dotted line), MM4 (black dash-dot line).

The TM helix is generally shifted toward the CP side of the membrane (Fig. 2 B). Again, MM2-4 show similar distributions of the distances from the center of the membrane, whereas MM1 stands out. The center of mass of the TM helix is on average 5 Å away from the membrane center with models 2–4 but in the thinnest membrane its COM is displaced further to ∼7 Å from the membrane center. The larger displacement of the TM helix with the thinnest membrane is possible because of the hydrophobic mismatch and results in the hinge region being pushed further above the membrane-water interface. With the hinge region away from the membrane, the CP helix can form compact structures with small values of θ where the polar N-terminus points toward the membrane but is still not inserted significantly into the hydrophobic core of the membrane. At the same time, the sampling of more extended structures with the CP helix far from the membrane interface as described above is facilitated by the raised hinge region, and L- and T-shaped structures are not especially favorable with the CP helix far from the membrane-water interface in those conformations.

Finally, distributions of the average helicity for the CP domain and full length PLB are given in Fig. S8. The CP domain is largely helical in our simulations with a small subset of partially helical conformations. These results are in agreement with most experimental studies except for a study by Andronesi et al., who interpreted dynamics in the CP domain as sampling of nonhelical conformations (53).

Discussion

The conformational analysis of membrane-bound peptides has been challenging with both experimental and computational methods. Experimental methods often do not provide full atomistic resolution and/or have to compromise on the systems that can be studied (e.g., mutated PLB in DPC micelles versus wild-type PLB in phospholipid bilayers). At the same time computational methods are limited by compromises between force field accuracy and the extent of sampling that can be achieved. Here, the new implicit membrane model, HDGB, is used to overcome sampling limitations in explicit lipid simulations. The implicit model offers significantly improved conformational sampling, in particular because the kinetic barriers due to lipid rearrangements in response to conformational changes of a given solute are absent. Because of the nature of implicit solvent, the increased computational efficiency comes at the cost of reduced accuracy. In particular, specific lipid-peptide interactions cannot be fully represented with an implicit approach. However, the implicit model has been optimized carefully to reflect the mean-field energetics of explicit all-atom lipid bilayer environments whereas previous simulations of peptides and proteins with implicit membranes (26–31,54) have resulted in good agreement with experimental data.

It is estimated that μs-ms timescales can be accessed with our simulations that is much longer than the timescales covered in previous simulation studies. The use of implicit solvent with Langevin dynamics and a small friction coefficient by itself has been shown to accelerate the crossing of barriers in aqueous solvent by a factor 2-10 (37) whereas temperature replica exchange sampling is expected to accelerate barrier crossings further by at least a factor of 10. This means that our replica exchange implicit solvent simulations with ∼20 ns/replica should be equivalent to at least μs timescale sampling. Furthermore, the mean-field energetics provided by the implicit membrane model avoids kinetic barriers due to lipid relaxation processes that may occur on timescales ranging from ns to seconds (55). Therefore, μs timescale implicit membrane simulations are probably equivalent to ms or longer explicit membrane simulations. Indeed, we found significant conformational sampling of a wide range of structures that far exceeds the conformational variety observed in previous simulation studies and agrees with the experimental finding of significant conformational dynamics in PLB (19).

The use of an implicit model also offers the unique advantage of being able to easily change the membrane thickness. Here, four different thicknesses were considered to examine the effect of membrane thickness on PLB sampling. It was found that sampling of PLB differs significantly between the thinnest and thickest membranes. With the thickest membranes PLB predominantly samples L- and T-shaped conformations as well as semi-extended structures, but in all cases the CP helix closely interacts with the membrane surface. With the thinnest membrane, most of the sampling involves compact structures with small interhelical angles where the CP and TM helices are nearly parallel. In addition, fully extended structures are sampled where the CP helix is located far above the membrane interface.

The intermediate model MM3 was parameterized to reflect DPPC bilayer. From a comparison of MD simulations of DPC micelles (56) and DPPC bilayers (57), the overall membrane thickness is slightly reduced with DPC over DPPC as in the MM2 model. The thinnest model, MM1, may then be representative of detergents such as the C₁₂E₈ detergent with even shorter hydrocarbon tails. On the other hand, the physiological cardiac sarcoplasmic reticulum membrane with an average fatty acid chain length of 18.1 carbon atoms (58) compared to DPPC with 16 carbon atom tails corresponds best to the thickest membrane model (MM4). It should be emphasized, however, that only MM3 was optimized to model a specific membrane, DPPC, and that the other models are introduced simply to study the general effect of reduced or increased membrane thickness on PLB sampling. To model other specific types of lipid environments, further optimizations would be required. In this study, we are also neglecting the possible impact of membrane curvature that may be important to accurately model micellar systems.

The conformational sampling with MM2 (Fig. 1 B) is in good agreement with the structural NMR ensemble in DPC micelles but the results for MM2 and MM3 are similar, suggesting that PLB sampling in DPC micelles and DPPC bilayers may not be significantly different and that DPC micelles may be good mimics for DOPC/DPPC bilayers in experimental or computational studies. In contrast, there are more significant differences between MM2/MM3 and MM4 suggesting that experimental results obtained in DPC detergents or DOPC/DPPC bilayers may not be fully reflective of the behavior of PLB in native SR membranes.

The original NMR ensemble in DPC micelles was recently re-refined by applying a geometric restraints from new SSNMR measurements of PLB in DOPC (that is similar to DPPC) (16) along with an empirical membrane potential (52). The resulting ensemble still consists of mostly L-shaped structures but the CP domain is generally further extended and more inserted into the lipid bilayer compared to the originally reported ensemble. It may seem that the shift in the structural ensemble as a result of the SSNMR data in DOPC bilayers suggests genuine differences in the conformational sampling between DPC micelles and DOPC bilayers. However, neither set of data (NOE restraints from solution NMR in DPC micelles and SSNMR data in DOPC bilayers) are sufficient to unambiguously describe the conformation of PLB and even when both data sets are combined significant uncertainties remain, especially with respect to the insertion of the CP domain into the bilayer. Furthermore, it should be kept in mind, that structures consistent with the time- and ensemble-averaged NMR data are not necessarily expected to agree with the actual conformational distribution on sub-ms timescales.

An interesting observation is that fully extended conformations with the CP helix located far above the membrane surface are only sampled with the thinnest membrane. PLB has been previously suggested to interact with SERCA in an extended form. This idea is based primarily on the observation of a cross-link between K3 of PLB and K400 of SERCA in C₁₂E₈ detergent (59). Such an interaction is only possible when PLB is fully extended. However, this cross-link could not be reproduced by other groups especially the Jones group, who used insect cell microsomes instead of detergent (60,61). Our simulations offer an explanation for this apparent controversy. C₁₂E₈ detergent has a very short lipid tail consisting of only 12 carbon atoms and is best modeled with a thin membrane similar to MM1. At the same time, microsomal membranes are thicker than DPPC bilayers according to electron microscopy measurements (50,57) and are best modeled by MM4. Our simulations show that PLB conformations with a fully extended CP helix are not observed in thicker membranes but are a feature of very thin membranes. Therefore, it seems that the observation of the PLB-K400 cross-link (59) may be a result of the particular detergent that was used. Because native SR membranes are also thicker, this finding has implications for the role of extended conformations of PLB in interactions with SERCA. Based on our result (see Fig. 1 D) PLB assumes primarily T- and L-shaped conformations in the thickest membrane with two main basins, one consisting of more compact T-shaped structures, the other one consisting of more extended, but still mostly L-shaped conformations. Therefore, one may conclude that in SR membranes PLB interacts with SERCA primarily in one of those conformations instead of a fully extended form as suggested earlier. At the same time, it has been known for a long time that membrane thickness affects SERCA activity. In particular, long chain, unsaturated fatty acids maximize calcium transport across SR membranes (62,63). Whereas this may be a direct consequence of lipid-protein interactions, it is also possible, based on our findings, that SERCA activity is diminished in thinner membranes because of increased inhibition by PLB under the assumption that PLB does in fact inhibit SERCA more readily in the extended form. To address these possibilities in more detail, future studies will need to focus on the actual interactions between PLB and SERCA. Furthermore, the effect of phosphorylation on PLB structure in the context of different membranes and in interactions with SERCA has not been considered here and will also need to be addressed in more detail in future studies to arrive at a complete understanding of SERCA regulation by PLB.

Conclusion

The conformational sampling of PLB on ns-μs timescale was investigated with an implicit membrane model. Significant conformational dynamics were observed that are in overall good agreement with experimental measurements. Furthermore, different membrane thicknesses were modeled by appropriate scaling of the implicit membrane model. Membrane model mimicking DPPC bilayers results in conformational ensembles with a high population of T- and L-shaped structures as well as more extended structures with larger interhelical angles. In addition, a small, but significant population of compact, highly bent structures was found that have not been described previously. The sampling of compact and fully extended structures is enhanced with the thinnest membrane model whereas those conformations are suppressed with the thickest membrane model that resembles the actual physiological SR membranes most closely. These findings suggest that partially extended conformations rather than the fully extended ones may play a significant role in PLB-SERCA interactions under physiological conditions.

Supporting Material

Eleven figures are available at http://www.biophysj.org/biophysj/supplemental/S0006-3495(09)01743-3.