Statistics and Physical Origins of pK and Ionization State Changes upon Protein-Ligand Binding

Abstract

This work investigates statistical prevalence and overall physical origins of changes in charge states of receptor proteins upon ligand binding. These changes are explored as a function of the ligand type (small molecule, protein, and nucleic acid), and distance from the binding region. Standard continuum solvent methodology is used to compute, on an equal footing, pK changes upon ligand binding for a total of 5899 ionizable residues in 20 protein-protein, 20 protein-small molecule, and 20 protein-nucleic acid high-resolution complexes. The size of the data set combined with an extensive error and sensitivity analysis allows us to make statistically justified and conservative conclusions: in 60% of all protein-small molecule, 90% of all protein-protein, and 85% of all protein-nucleic acid complexes there exists at least one ionizable residue that changes its charge state upon ligand binding at physiological conditions (pH = 6.5). Considering the most biologically relevant pH range of 4–8, the number of ionizable residues that experience substantial pK changes (ΔpK > 1.0) due to ligand binding is appreciable: on average, 6% of all ionizable residues in protein-small molecule complexes, 9% in protein-protein, and 12% in protein-nucleic acid complexes experience a substantial pK change upon ligand binding. These changes are safely above the statistical false-positive noise level. Most of the changes occur in the immediate binding interface region, where approximately one out of five ionizable residues experiences substantial pK change regardless of the ligand type. However, the physical origins of the change differ between the types: in protein-nucleic acid complexes, the pK values of interface residues are predominantly affected by electrostatic effects, whereas in protein-protein and protein-small molecule complexes, structural changes due to the induced-fit effect play an equally important role. In protein-protein and protein-nucleic acid complexes, there is a statistically significant number of substantial pK perturbations, mostly due to the induced-fit structural changes, in regions far from the binding interface.

Introduction

Protein-ligand binding is central to many fundamental cellular functions such as gene regulation, enzyme catalysis, molecular recognition by the immune system, and signal transduction (1). Understanding the mechanism behind the binding process requires detailed knowledge of the nature and origins of changes in the physical state of proteins that occur in protein-ligand binding. Such knowledge is also important for many practical applications such as biotechnology (2) and structure-based drug design (3). In particular, early stages of the structure-based drug discovery process often involve identifying a ligand that binds to the target protein with high affinity. It is well known that structural complementarity plays a critical role in the ligand binding process, and so it is not surprising that structural rearrangements that can accompany protein-ligand binding have been extensively explored (4–6). Structure-energy relationships in the binding process have also been systematically investigated (7–10).

At the same time, relatively little is known about the magnitude, prevalence, and detailed physical origins of changes in the charge state of receptor proteins upon ligand binding. These changes are intimately related to the changes in pK values and ionization states of the ionizable residues (amino acids) in the receptor protein. The question of whether changes in protein charge state occur often in the process of ligand binding, or if they are so rare that this possibility can be safely neglected in most cases, is important, because the charge state can have a profound effect upon ligand binding. In particular, it was shown both experimentally (11,12) and theoretically (13) that altering the charge state of the binding interface via specific mutations can affect protein-ligand binding affinity, and can even be used to design complexes with higher affinity (14,15). Properly accounting for possible changes in the charge state upon binding may also be important for structure-based drug design. For example, it was demonstrated, based on quantum-mechanical calculations, that docking accuracy (16) and binding affinity predictions (17) improve when the energy model accounts for the redistribution of ligand charges upon binding. In another recent study (18), it was shown that accurate prediction of ionization states is a prerequisite for the accurate prediction of binding affinities between HIV protease and some inhibitors.

Changes in pK values and ionization states of ionizable residues in proteins can be obtained experimentally, usually by NMR methods, but at the moment only a handful of experimental data points are available for protein-protein (19), protein-small molecule (20), and protein-nucleic acid complexes (21). Moreover, these experimentally reported pK and ionization states changes appear to be limited to a relatively small group of proteins, such as HIV protease, and so it is not clear to what extent the observed trends might be general. It is also not clear whether substantial changes occur only in the immediate vicinity of the binding interface, or if the binding can alter pK and ionization states of more distant residues. A long distance effect can be important in, for example, allosteric regulation in which a stimulus in one side is transmitted to a distant side (22).

What the available data does suggest is that the pK changes (ΔpK) upon ligand binding may be substantial, considerably larger than 1 pK unit (23). For example, the data set of experimental pK changes assembled in this study has a root-mean-square value of |ΔpK| = 2.97 pK units (see Validation in the Supporting Material). With this large ΔpK, the energetic cost of misassigning the ionization state of just one residue would already be well above the ∼1 pK unit error margin of experiments that measure ligand binding affinity. Ideally, computational methods should strive to achieve the same level of accuracy as the corresponding experiment (24), which would not be possible in the above example without properly accounting for the possibility of ionization state change.

Given the scarcity of the experimental data, computational methods become particularly valuable in addressing the questions of prevalence and origins of pK and ionization state changes in protein-ligand binding. Over the past decade, several computational studies (25–27) made noticeable progress in investigating ionization state and pK changes of ionizable residues in proteins upon ligand binding. However, those earlier studies focused on a small number of specific proteins and residues, and it was not until very recently that computational works based on large sets of computed pKs—thousands of data points—began to appear (28,29). These recent studies explore and quantify statistical trends in addition to analyzing individual cases in detail. Perhaps the most intriguing finding that has emerged is that changes in pK and ionization states of titratable amino acids occur quite commonly in protein-protein binding, which has so far been the focus of these large-scale studies. Do the same statistical trends occur in other types of complexes? What is the level of false-positive noise in such estimates? The last question is particularly critical for any computational approach.

In this work we have applied a well-established computational methodology (30–33) based on the continuum solvent framework (34) to study, on an equal footing, ionization state and pK changes upon ligand binding in a statistically significant set of molecular complexes. The set of structures consists of 20 protein-protein, 20 protein-small molecule, and 20 protein-nucleic acid complexes; the complexes contain a total of 5899 ionizable residues, and are selected from different databases based on the quality of the structures.

We also explore physical origins of the pK and ionization state changes. Specifically, our methodology allows us to study the relative roles of two major contributions responsible for pK changes upon ligand binding to proteins: electrostatic perturbations and conformational changes. The role of each of the contributions is investigated as a function of the distance from the binding site, which provide an estimate of how far pK changes due to binding propagate. An important feature of this work is the inclusion of an extensive error analysis. Uncertainties in the input structures are always propagated into errors in the computed pK values; a careful and systematic error analysis is necessary to provide realistic and robust conclusions.

The rest of this article is organized as follows. First, we present the methodology employed to calculate pK changes due to binding. Results contains the overall statistics for pK and ionization state changes upon ligand binding. We also discuss the relative roles of electrostatic perturbations and conformational changes in pK changes upon ligand binding, and give a thorough analysis of both the systematic and random errors. Our findings are summarized in the Discussion. In addition, an extensive Validation section is presented in the Supporting Material.

Methods

Our methodology is summarized in the flow chart shown in Fig. 1. It includes the following three components:

• 1.Collection of protein-ligand complexes from three different databases, as described below.
• 2.Computation of pK values for every ionizable residue separately in the complexed and the unligated structures.
• 3.Determination of ionization state and pK change upon ligand binding.

Figure 1.

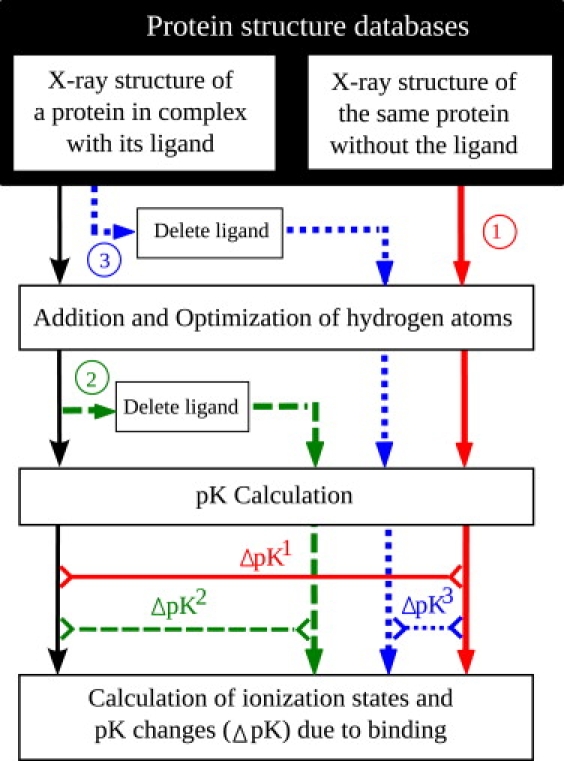
Flowchart of the overall computational methodology. (Thick color lines running from the top to the bottom of the diagram) Three procedures employed to obtain unligated protein structures. (Solid red lines) Overall procedure (1); (dashed green lines) electrostatics-only procedure (2); and (dotted blue lines) structural-changes-only procedure (3). (Thin horizontal lines at the bottom part of the diagram) Pairs of protein structures used to compute ΔpK values corresponding to each computational procedure.

For each analyzed complex, two types of experimental structures were used in subsequent computations:

• 1.Protein structures in complex with their ligands; and
• 2.Protein structures in the absence of ligands (unligated proteins).

We based our analysis only on those complexes for which both types of structures were experimentally available. In addition to the experimentally determined unligated structures, two other structures of unligated proteins were computationally prepared for each protein-ligand complex. The corresponding computational procedures are schematically illustrated in Fig. 1; their details are provided below. These different procedures helped us elucidate the relative roles of various physical effects involved.

Collection of structures

Protein-ligand complexes were collected from three different sources of experimental structures: The Benchmark 2.0 Database (35) for protein-protein (84 complexes); the LPDB Database (36) for protein-small molecule (262 complexes); and the NPIDB database (37) for protein-nucleic acid complexes (1932 complexes). From these combined sources we selected those complexes for which the x-ray structures of proteins in the absence of ligands were also available in the Protein Databank (PDB; http://www.rcsb.org). Because accuracy of pK calculations depend critically on quality of the input structure, we have chosen the 20 highest quality structures of complexes from each category, based on the following criteria: no missing residues; and 2.5 Å or better resolution. The same selection criteria also applied to the corresponding structures of proteins in absence of ligands. The 60 complexes thus selected contain a total of 5899 ionizable residues, a statistically significant number for the purpose of our analysis. The PDB codes and the number of ionizable residues per structure are given in the Supporting Material.

Methodology used to compute pK values

We used the H++ server (http://biophysics.cs.vt.edu/H++) to prepare the input structures required to compute the pK values of all ionizable residues in the proteins. The details of the computational protocols are given in Gordon et al. (38) and references therein. A brief summary of key methods and steps is presented below.

Structure preparation

Before each pK calculation, H++ removes all atoms, including explicit ions, in the input structure that are not part of amino acids, nucleic acids, or small molecule ligands. Sequence continuity is also verified and used to filter out structures with missing residues. Continuity is important because pK estimation depends critically on structure details. Next, H++ server adds hydrogen atoms to the input structures. The standard AMBER (39) templates are used to add hydrogen atoms for peptide, DNA, and RNA molecules, and the BABEL (40) software package (Ver. 1.1) is used for other types of ligand molecules. All ionizable residues are initially set to their standard protonation states based on AMBER charges for amino and nucleic acids. The positions of the hydrogen atoms are then optimized using a combination of minimization and simulated annealing based on the standard AMBER force field. For small molecule ligands, generalized AMBER force-field parameters (41) are used for optimizing the positions of the hydrogens added to the ligand. Generalized AMBER force field includes force-field parameters for the organic chemical space beyond the biological molecules covered by the traditional AMBER force-field parameters. The partial atomic charges are calculated semiempirically by AM1-BCC method available in the ANTECHAMBER (42) module of AMBER. For all the small molecule ligands considered in this study, partial atomic charges were assigned assuming a net ligand charge of zero.

pK estimates

The energetics of proton transfer is calculated by the standard continuum electrostatics methodology (30) available in H++. Unless otherwise stated, the protein and its ligand are treated as a low dielectric medium ɛ_in = 6, whereas the surrounding solvent is assigned a high dielectric constant ɛ_out = 80. The electrostatic screening effects of (monovalent) salt enter via the Debye-Hückel screening parameter κ = 0.128 Å⁻¹, which roughly corresponds to a physiological concentration of [NaCl] = 0.15 M. A summary of the methodology is presented in the Supporting Material.

Preparation of unligated structures: the three procedures

As noted above, we employed three different computational procedures, represented by thick color lines in Fig. 1, to obtain the unligated protein structure corresponding to each complex.

The first procedure is denoted by solid red lines (and label 1) in Fig. 1. The unligated protein structures used for this computational procedure are experimentally determined x-ray structures of proteins in the absence of ligands. The corresponding procedure for computing the overall statistics of pK changes upon ligand binding as a single number for the two residues is called “overall”. Within our computational model, this procedure takes into account all effects that can cause pK changes upon binding. The resulting values of pK changes can be directly compared with the experiment (see Validation in the Supporting Material).

For the second procedure (shown by dashed green lines and label 2 in Fig. 1), each unligated structure was obtained by removing the ligand atoms from the corresponding protein-ligand complex after the initial addition and preoptimization of hydrogen atoms. This sequence of steps guaranteed that the conformation of the unligated protein used in subsequent pK estimates was exactly the same as the conformation of the protein in the corresponding complex, thus eliminating the effects of conformational changes upon the computed ΔpK. This procedure was used to quantify the electrostatic effects and is called the “electrostatics-only” procedure.

Within the first and second procedures, the reported ΔpK for a given residue in a protein was calculated as the difference between the pK value of this residue in the protein in complex with its ligand, and the corresponding unligated form of the protein prepared according to the procedures described above.

For the third procedure (dotted blue lines, and label 3 in Fig. 1), each unligated structure was obtained by first removing the ligand atoms from the original PDB file of the corresponding protein-ligand complex, and then following the same computational protocol as in the overall procedure. Thus, the resulting structure contains all of the structural changes the binding process may have induced in the receptor protein. The ΔpK reported for this procedure was computed relative to the corresponding naturally unligated receptor protein structure obtained via the overall procedure 1. In contrast to procedures 1 and 2, procedure 3 computes ΔpK between two unligated proteins. Thus, this ΔpK is caused solely by conformational changes induced in the receptor protein by the binding of the ligand. The procedure directly probes the influence of the induced-fit effect upon pK. We call it the “structural-changes-only” procedure.

Note that although the overall procedure roughly corresponds to the net combined effects of the electrostatics-only and structural-changes-only, exact additivity in the number of residues with substantial pK change is not guaranteed. For example, a given residue can be identified as having substantial pK change by both procedures independently.

Definitions used in the calculation of ionization state and pK changes

For determining changes in ionization state we consider only the residues with substantial pK change (|ΔpK| > 1.0), and assume a standard environment pH value of 6.5. An ionizable residue is assumed to change its charge state upon binding if its pK value changes from being greater (or less) than the environment pH to a value that is less (or greater) than the environment pH.

We also report statistics of substantial pK changes, but only in the biologically relevant pH range of 4–8. Namely, we consider the ΔpK of a specific ionizable residue to be biologically relevant if the ΔpK between the two conformational states (complexed or unligated) is >1, and one of the following three conditions is satisfied:

• 1.The pK value in both states is inside the pH range.
• 2.The pK value in the unligated state is outside/inside the pH range and changes to a value that is inside/outside the pH range.
• 3.The pK value in the unligated state is below/above the pH range and changes to a value that is above/below the pH range.

The interface region is defined by the protein residues located within contact distance (6 Å) from the ligand. These distances are calculated as the minimum distance between the atoms of the given amino acid and the ligand atoms.

Results

Overall statistics of changes in pK and ionization states upon ligand binding

The pK and ionization state changes were calculated for our dataset of all 60 complexes using the overall computational procedure in which unligated proteins were taken as experimental x-ray structures of proteins obtained in the absence of ligands. Our findings are as follows. For a standard pH value of 6.5, 60% of all protein-small molecule complexes, 90% of all protein-protein complexes, and 85% of all protein-nucleic acid complexes present at least one ionizable residue that changes its ionization state upon binding. Moreover, considering the biologically relevant pH range from 4 to 8, all of the complexes present at least one ionizable residue with substantial pK change due to binding. Additional statistics are shown in Table 1; the effect of pK changes upon binding is, on average, significant. The variance of the change is large: the maximum and minimum number of residues affected per complex can be as high as 24% of all ionizable residues for some complexes, and possibly negligible (1.5%) for others.

Table 1.

Percentages of ionizable residues per complex that exhibit substantial pK changes (|ΔpK| > 1) in the biologically relevant pH range from 4 to 8

Complex type	Minimum	Average	Maximum
Protein-protein (20)	1.5%	8.7%	16.7%
Protein-small molecule (20)	2.1%	5.7%	12.5%
Protein-nucleic acid (20)	5.6%	12.3%	24.4%

Considering all 5899 ionizable residues in our dataset, ∼9% of them present a substantial and potentially biologically relevant pK change upon ligand binding. In what follows, we show that this number is safely above the false-positive level that can result from structural and methodological uncertainties.

Origins of pK changes upon ligand binding

In general, pK changes upon ligand binding are caused by perturbations of the ionizable residues environment. Within our methodological framework we distinguish two major causes contributing to such perturbations: direct electrostatic field perturbation and protein conformational changes.

Direct electrostatic perturbation

Ionizable residues located at the binding interface experience major perturbations in their electrostatic environment due to ligand binding. Before binding, interface residues are in contact with the high dielectric solvent. After binding, these residues may become completely buried in the low dielectric medium of the ligand and the protein itself. Another way in which the electrostatic environment of an ionizable residue is perturbed by ligand binding is by direct electrostatic interactions—as the ligand approaches a protein, the electrostatic field inside that protein is perturbed by ligand charges. Note that within this mechanism, a pK change can occur even if no conformational change occurs in either the ligand or the protein upon binding.

Protein conformational change

Proteins often adjust their conformation during the process of ligand binding, according to the Induced-fit model (43). This conformational change modifies the microenvironment of the amino acids, possibly affecting their pK values.

To quantify relative roles of each of these two perturbations on pK changes, we introduced three different computational procedures designed to separate out contributions from each type of perturbation (see Methods for more details). The first—i.e., the overall—procedure corresponds to all of the perturbations combined. The second procedure is used to quantify the electrostatic perturbation only, and is called electrostatics-only. The third procedure called structural-changes-only is used to quantify the induced-fit effect on pK changes.

We begin our analysis by considering the spatial distribution of residues with substantial pK change in the protein due to the combined effect of all the perturbations. To this end, we divide protein structures into five spatial regions according to the distance from the ligand, and compute the percentage of residues with substantial pK changes in each region. Each percentage is computed relative to the total number of ionizable residues found in the given region. The results are presented in Fig. 2, where the solid red bars show the distance distribution of all ionizable residues with substantial pK change in the biologically relevant range; there is one bar for each spatial region. In the interface region, the percentage of residues with substantial pK changes is almost 20% in all three types of protein-ligand complexes. Notably, there are also residues with substantial pK changes located outside the interface region, some of them well beyond the interface, more than 24 Å from the ligand. One may wonder if all residues with substantial pK change in regions far from the ligand belong to a small group of complexes that are unique in some way. Our statistics show that this is not the case: 58 out of 60 complexes present at least one residue with substantial pK change located outside the interface region. Thus, the occurrence of substantial pK changes far from the binding interface appears to be a general property of the ligand-binding process.

Figure 2.

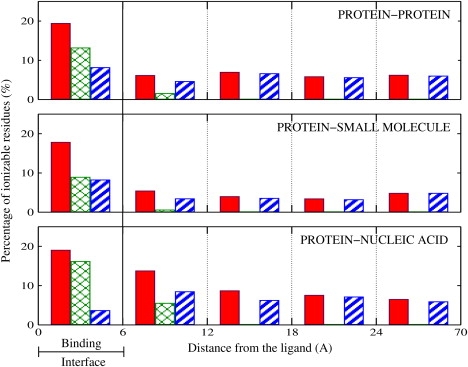
Distance distribution of ionizable residues with substantial and biologically relevant pK change upon binding of the ligand in protein-protein, protein-small molecule, and protein-nucleic acid complexes. (Solid red bars) Overall procedure; (cross-hatched green bars) electrostatics-only procedure; and (striped blue bars) structural-changes-only procedure. The percentage reported for each region is relative to the total number of ionizable residues located in that region.

pK changes at the binding interface

In the previous subsection we have shown that the percentages of residues in the protein-ligand interface region that experience substantial pK change upon ligand binding are approximately the same for all three types of complexes considered. This apparent equivalence is noteworthy, considering the fact that the binding regions of the three types of complexes are likely to be physically different; for example, the protein-nucleic acid interface may be expected to be more highly charged compared to the protein-protein interface. This difference in physical characteristics of binding interfaces reveals itself in the difference between the relative contributions of electrostatic effects and conformational changes to ΔpKs. The cross-hatched green bars in Fig. 2 represent the distance distribution of residues with substantial ΔpK computed via the electrostatics-only procedure, whereas the striped blue bars show the distance distribution of the same quantity obtained by the structural-changes-only procedure. In the protein-nucleic acid complexes, interface residues with substantial pK changes are seen as affected mostly by electrostatic effects, in accord with the intuition, whereas in the protein-small molecule complexes the contribution of electrostatics effects and conformational changes are approximately the same. In the protein-protein complexes the contribution of electrostatic effects is slightly higher than the contribution of induced-fit conformational change. However, the net effect of all the contributions (solid red bars, overall) is approximately the same for all three types of complexes. Thus, irrespective of the type of ligand, approximately one in every five ionizable residues of the interface region in the receptor protein is expected to change its pK value by more than one unit due to ligand binding.

Although the electrostatics-only influence on pK values is relatively short-ranged (cross-hatched green bars in Fig. 2), this type of perturbation does influence ionizable residues located in the region immediately outside the binding interface (in the range of 6 Å–12 Å from the ligand). The percentage of such residues is larger in protein-nucleic acid complexes compared to those of protein-protein and protein-small molecules complexes. This is likely due to a relatively large charge associated with nucleic acid ligands compared to that of proteins and small molecule ligands, which are, on average, neutral.

pK changes far from the binding interface

In many cases, the pK changes upon ligand binding propagate to regions located far from the ligand (beyond 12 Å, Fig. 2). In this region, the pK values are seen to be affected mainly by induced-fit conformational changes (represented by the striped blue bars in Fig. 2). The percentages of such residues are smaller in the protein-small molecule complexes compared to those of protein-nucleic acid and protein-protein complexes. Presumably, this is because structural perturbations caused by small molecules in the receptor proteins are weaker compared to those exerted by larger ligands.

Error estimates: false-positive levels

An important issue is the level of uncertainty in the computational estimates shown in Fig. 2. In general this uncertainty has two components: the systematic and the random error. A comparison with experimentally observed pK changes upon ligand binding (see Validation in the Supporting Material) shows that the systematic (average) error of our computational |ΔpK| estimates is 0.34 pK units, which is safely below the threshold level of 1 pK unit we have set to define substantial pK changes reported here. However, there still exists a nonzero probability for any such substantial change to be a statistical false-positive. Here we estimate the level of such false-positive noise in our calculations of the relative number of ionizable residues with substantial pK changes shown in Fig. 2.

Within our methodological framework, the computed pK values are directly determined by the atomic-resolution input structure, and are known to be sensitive to structural details (44). Uncertainties in the input x-ray structure will be propagated into errors in the computed pKs. To estimate this type of error we have analyzed the variation in computed pK values that results from structural deviations between several x-ray structures corresponding to the same protein. We selected, from the protein-protein data set, those proteins that have more than one experimentally determined x-ray structure in the unligated form available (see Table S2 in the Supporting Material). There were seven of such proteins whose unligated structures also satisfy the selection criteria we used before: resolution ≤2.5 Å and no missing residues. For each such protein, we computed the pK values in all of their available x-ray structures. The difference between computed pK values of the same residue that result from differences in the x-ray structures corresponding to the same biological molecule characterizes the random error of the methodology. To obtain a statistically meaningful value, we computed ΔpK for all possible pairs of x-ray structures of each protein. Substantial pK changes (|ΔpK| > 1.0) in the biologically relevant pH range were identified as described in Methods. Without this structural noise, the number of such substantial changes would be zero, as the two structures in each pair would be identical; the nonzero value we obtained is the false-positive noise we set to estimate.

The open bars in Fig. 3 represent the distance distribution, as in Fig. 2, of the false-positive pK changes due to the structural noise. To facilitate comparison with Fig. 2, we also show the distance distribution of the pK changes obtained using the overall procedure for protein-protein complexes (solid red bars from Fig. 2).

Figure 3.

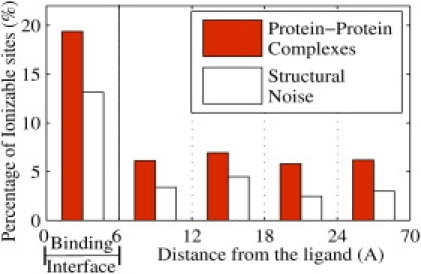
Distance distribution of ionizable residues with substantial pK change in the biologically relevant pH range. (Solid red bars) Overall procedure in protein-protein complexes; (open bars) false-positive pK changes due to structural noise. The percentage in each region is relative to the number of residues located in that region.

Clearly, the level of the false-positive structural noise is the highest in the interface region. This may be attributed to the fact that in the unligated forms, most of the interface residues are in the surface of the protein where structural fluctuations are expected to be higher compared to that of the deeply buried ionizable residues. Nevertheless, the number of residues in the interface with substantial pK change due to noise is appreciably smaller than the signal for all three types of complexes. This validates our conclusions regarding the prevalence of substantial pK changes in the interface region. Also note that the results of the electrostatics-only procedure shown as cross-hatched green bars in Fig. 2 do not contain any structural noise, thus providing an independent support for the claim that most pK changes in the interface region are indeed a consequence of the ligand binding process, beyond the noise level.

In all the regions outside the binding interface (>6 Å), the level of structural noise (false-positives) is safely below the estimate of the number of ionizable residues with substantial pK change in protein-protein and protein-nucleic acid complexes. Thus, substantial pK changes upon binding do indeed occur far away from the interface in these types of complexes. However, in protein-small molecule complexes the level of false-positives is comparable to our estimates of the percentages of substantial pK changes upon binding.

To obtain quantitative statistical estimates, we performed a t-test to compare the mean (average) of the number of pK changes due to structural noise (noise sample) to the mean of the number of pK changes due to ligand binding (signal samples). Details of the t-test can be found in the Supporting Material. In this analysis, we considered only the residues in regions outside the interface. The results of the t-test rejected the hypothesis that the noise sample is identical to the protein-protein sample and protein-nucleic acid samples, with a probability of 0.95. In these complexes the pK changes upon binding outside the interface are clearly statistically significant. In contrast, the probability that the noise sample and the protein-small molecule sample are identical is 0.56. Thus, based on our computations, we cannot confirm or reject the possibility of statistically substantial pK changes outside the binding interface in protein-small molecule complexes.

Sensitivity of the computed ΔpKs to the uncertainty in the choice of solute dielectric constant

Within the traditional continuum solvent framework employed here, the protein is treated as a low dielectric medium with internal dielectric constant ɛ_in, surrounded by a solvent that has high dielectric constant ɛ_out. There is no ambiguity as to the value of ɛ_out = 80 for water. However, in the case of ɛ_in, substantial uncertainty exists: different values from 4 to 10 and even higher have been employed (45–47). Higher values of ɛ_in may be more suitable for amino acids close to the surface whereas lower values may be more suitable for buried amino acids, but no unambiguous rule exists for choosing an optimal ɛ_in. The situation is even more complicated in the process of protein-ligand binding, as the degree of burial of some interfacial residues in the receptor protein, and thus the optimal ɛ_in for these residues, may change substantially upon binding—thus introducing additional uncertainties into the choice of optimal ɛ_in. One might consider using separate ɛ_in values for complexes and unligated structures as a remedy, but it is also far from perfect, as many residues do not change their degree of burial upon binding. Several of these options are explored in Table 2, which shows percentages of ionizable residues with substantial pK changes for different set of values of ɛ_in of complexes and unligated structures taken from the protein-protein dataset; unligated proteins were obtained using the overall procedure. As expected, higher ɛ_in yields lower percentages of substantial pK changes and vice versa, but overall there is a tolerable variation in the predicted percentages of ionizable residues with substantial pK change upon binding. Throughout the rest of the work, we chose to use a single value of ɛ_in = 6 for both the complex and unligated structures as the middle ground between the high and the low ɛ_in values, which provides conservative estimates of the percentage of pK changes due to binding. We believe that such a choice provides greater internal consistency (and accuracy) for estimating the percentages of substantial pK changes.

Table 2.

Variation in the computed percentage of ionizable residues with substantial (|ΔpK| > 1.0) pK change as a function of the protein dielectric constant ɛ_in

ɛin		Percentage of ionizable residues
Complex	Unligated
4	4	12%
6	6	8.7%
10	10	6.5%
4	10	12.1%

Discussion

A detailed knowledge of the protein-ligand binding process is important for both fundamental and applied sciences, but several aspects of changes in physical state of receptor proteins that can occur upon ligand binding have not yet been fully characterized. Specifically, one phenomenon that is often ignored by atomistic methods that model protein-ligand binding properties is the possibility of changes in the receptor protein charge (ionization) state due to ligand binding.

In this work, we have used the standard continuum solvent methodology to study changes in charge states and pK values of ionizable residues that occur in receptor proteins in the process of protein-ligand binding in three types of complexes: protein-protein, protein-small molecule, and protein-nucleic acid. In total, we have analyzed 5899 ionizable residues, which makes our results statistically meaningful. For each protein-ligand complex used in our analysis, the experimentally determined x-ray structure of the corresponding unligated protein is also available. In addition, only complete (no missing residues), relatively high-resolution structures have been used. We believe that these methodological restrictions minimize the inevitable uncertainties inherent in such computations.

According to our estimates, 9% of all ionizable residues (averaged over all complex types) present a substantial pK change (|ΔpK| > 1.0) due to ligand binding. The majority of receptor proteins, 47 out of 60, present at least one ionizable residue that changes its charge state at a standard pH of 6.5. These estimates are conservative; we report only statistically significant trends for which the signal is well above the noise level. Our approach provides general insights into what can be expected in the majority of cases, and elucidates prevalent physical mechanisms involved. We conclude that substantial changes in ionization states and pKs occur due to ligand binding to proteins, and this effect is statistically significant in all three types of complexes considered. This conclusion is consistent with that of two other recent computational studies (28,29) of large sets of ionizable residues in protein-protein complexes. Importantly, methods of pK estimation used in those works are different from ours.

Overall, substantial pK changes due to binding occur most often in protein-nucleic acid complexes and least often in complexes of proteins with small molecules. Not surprisingly, the effect is the strongest—20% of available ionizable residues change their pK substantially—in the immediate binding interface, which is within 6 Å of the ligand. In this region, the electrostatic effects are predominant in affecting pKs upon ligand binding in protein-nucleic acid complexes, whereas in protein-small molecule and protein-protein complexes, both induced-fit and electrostatic effects play an equally important role. The effect of the electrostatic perturbation is generally short-ranged, only causing significant pK changes in residues located within ∼6 Å away from the ligand in the majority of protein-protein and protein-small molecule complexes, and weakly extending to 12 Å from the ligand in the case of binding of highly charged nucleic acids. At the same time, our results indicate that pK perturbations due to induced-fit structural rearrangements propagate well beyond the immediate interface region in a statistically significant number of cases.

The possibility that ligand binding can induce substantial pK changes far from the binding interface is important. We speculate that this distant residue pK coupling effect might play a key role in allosteric regulation: subtle changes on one side of the receptor protein may affect ligand-binding properties on the other side. We suggest that the phenomenon be further explored, both experimentally and computationally. Our computations suggest (see Supporting Material) that there is no single dominant structural mechanism responsible for such distant pK changes. However, among the three structures with the largest number of substantial pK changes (6Q21, 1GJR, and 1E1N), we find these distant pK changes to correlate with at least three types of structural rearrangements described previously in different contexts (48–50):

Collective motion of defined secondary structures

This refers to movements of an entire helix (or β-sheet) in the complexed form relative to the unligated form. Fig. S4 A in the Supporting Material shows an example of this mechanism. These movements can induce breaking/formation of salt bridges and hydrogen bonds between secondary structures modifying protein stability.

Disorder/order transition

Ligand binding can make a disordered region acquire an ordered secondary structure or vice versa through formation/breaking of hydrogen bonds, especially in regions close to a secondary structure. These transitions can modify the microenvironment of some ionizable residues affecting their pK values. An example of a β-sheet to random-coil transition is depicted in Fig. S4 B.

Structural disorder

Random coils and the terminal region of protein chains are expected to be very flexible. This flexibility may affect the pK values of ionizable residues located in these regions (see an example in Fig. S4 C).

It is important to note that these specific mechanisms are related to a small set of ionizable residues with substantial pK changes, and by no means represent the general causes for all pK perturbations computed in this work.

The inevitable uncertainty of our estimates may come from several sources. Note, for example, that the average conformation of a protein in the crystal may be different from that in solution, and may, along with the computed pK, depend on specific experimental conditions. Another source of uncertainty, especially in regions far away from the interface, may be crystal contacts which can produce conformational changes in the complexed structure that differ from those of unligated structures. The combined effect of these types of uncertainties on the computed pK values is included in our estimate of structural noise. The estimates helped us support the conclusion that not only does ligand binding cause substantial pK changes in the interface region, but the changes are statistically significant outside this region in the case of protein-protein and protein nucleic acid complexes. In the case of protein-small molecule complexes we do not have enough statistical significance to confirm (beyond the noise level) or reject the possibility of substantial changes outside the binding interface region. Further analysis of this intriguing possibility would require either a substantially larger set of structures, or a detailed analysis of individual protein-small molecule complexes in which this effect is well pronounced.

The magnitude and extent of changes of pK values and ionization states upon protein ligand binding indicate that this effect should be taken into account by atomic-level methods aimed at quantitative prediction of protein-ligand binding affinities and related properties. Several approaches may be considered. Although a search through all 2^N protonation states is the most rigorous approach, it is probably computationally intractable for most but the smallest structures. The computational complexity may be drastically reduced by a careful partitioning of the set of ionizable residues into strongly interacting clusters (51–53) or by the use of Monte Carlo method to sample the states (54); both techniques have been successfully employed in the context of pK calculations. Even a simple consistency check—whether the assumed ionization states change or remain the same after docking—is a better strategy than the current practice of completely ignoring the possibility.

Supporting Material

Six tables and four figures are available at http://www.biophysj.org/biophysj/supplemental/S0006-3495(09)01744-5.