Mouse Fibroblast Cell Adhesion Studied by Neutron Reflectometry

Abstract

Neutron reflectometry (NR) was used to examine live mouse fibroblast cells adherent on a quartz substrate in a deuterated phosphate-buffered saline environment at room temperature. These measurements represent the first, to our knowledge, successful visualization and quantization of the interface between live cells and a substrate with subnanometer resolution using NR. NR data, attributable to the adhesion of live cells, were observed and compared with data from pure growth medium. Independently of surface cell density, the average distance between the center of the cell membrane region and the quartz substrate was determined to be ∼180 Å. The membrane region (∼80 Å thick) contains the membranes of cells that are inhomogeneously distributed or undulating, likely conforming to the nonplanar geometry of the supporting adherence proteins. A second region of cell membranes at a greater distance from the substrate was not detectable by NR due to the resolution limits of the technique employed. Attachment of the live cell samples was confirmed by interaction with both distilled water and trypsin. Distinct changes in the NR data after exposure indicate the removal of cells from the substrate.

Introduction

Cellular adhesion is an essential biological process that has been investigated with great interest for several decades. Beginning with studies by Curtis (1) in 1964 using interference reflection microscopy (IRM), many measurements have been made to determine the spatial range of adhesion forces, utilizing a wide range of resolution limits. The measurement techniques used include IRM (also known as reflection interference contrast microscopy (RICM) (1–5)), fluorescence interference contrast microscopy (FLIC) (6–8), total internal reflection fluorescence microscopy (TIRFM) (9–13), and surface plasmon resonance microscopy (SPRM) (14,15). Collectively, these studies have established an accepted range for cell adhesion focal contact of 100–300 Å. The optical microscopy techniques used in these studies have evolved to the point where it is now possible to transcend the diffraction limit set by the wavelength of light by making use of the distance-dependent characteristics of optical probes. In a departure from these optical microscopy studies, we report neutron reflectometry (NR) measurements with subnanometer resolution of the adhesion of live mouse fibroblast cells to quartz.

NR commonly is used to probe thin films with thicknesses of 5–5000 Å at various buried interfaces. Over the past two decades, this technique has evolved to become key in the characterization of biological and biomimetic thin films (16,17). Typically, NR measurements are performed on model systems in which samples are homogeneous over large areas, including phospholipid monolayers at the air-liquid interface (18), pure and hybrid phospholipid bilayers on silicon and quartz substrates (19–22), and phospholipid bilayers on novel support systems designed to more closely mimic biological membranes (23,24). Because live cells adherent to a solid substrate are complex and exhibit inhomogeneity over large areas, they represent a radical departure from a typical system measured via NR, and their measurement establishes a precedent for in situ NR measurements of more biologically relevant objects than their surrogate counterparts.

Materials and Methods

Preparation of cells

HK-03 mouse fibroblast cells were obtained from Dr. Keith Laderoute (Stanford Research Institute, Stanford, CA) and grown in Dulbecco's modified Eagle's medium (DMEM; Life Technologies, Carlsbad, CA) with 5.0% (vol:vol) calf serum (Cosmic Calf Serum; HyClone, Logan, UT) in a 5.0% CO₂ atmosphere at 37°C on 150 cm² flasks. The cells were removed from the dishes by adding 3 mL of a 0.25% trypsin solution in a phosphate buffer with 1 mM EDTA and 25 mM HEPES (pH 7.4) onto the cell monolayer for 1 min. After washing over the cell surface, the trypsin solution was removed by aspiration, and an additional 3 mL of trypsin solution were added. After 1 min the side of the flask was rapped. The flask was set aside for an additional minute and then rapped again to help dislodge the cells from the surface. This process was repeated at 1 min intervals until microscopic examination showed that the cells had been released from the growth surface. Then 5 mL of cold, complete medium were added, and the cell suspension was mixed by repeated pipetting to separate cell clumps. The cell suspension was then centrifuged (1000 rpm for 10 min). The trypsin/medium solution was removed by aspiration, and the cell pellet was resuspended in 7 mL of cold, complete medium. An aliquot of the cells was then counted on an electronic particle count and size analyzer (model Z2; Beckman Coulter, Miami, FL) with a 100 μm aperture. Three counts were performed on a measured volume of 0.5 mL and averaged. The particle counter also provided a distribution of cell volumes, which was used both to eliminate acellular debris from the counts and to provide an estimate of the mean cell volume (25). The cells were then centrifuged again (as above), resuspended in complete medium at a concentration designed to give the proper coverage of the quartz substrate, and finally seeded onto quartz substrates as described below.

Seeding of cells onto substrates

HK-03 cells and DMEM media with 5.0% fetal calf serum were seeded onto 7.6 cm diameter quartz monocrystals (pure c-cut, alpha quartz, density 2.64–2.65 g-cm⁻³; Institute of Electronic Materials Technology, Warsaw, Poland) and allowed to incubate in a 5.0% CO₂, 37°C incubator for 12 h. Before seeding was performed, the substrates were placed in 250 cm² glass petri dishes in the incubator for 1 h to equilibrate their temperatures. Cells were seeded at 90% and 100% confluence. Determination of the number of cells required to achieve confluence was based on data from a growth curve of HK-03 cells in monolayer culture on standard tissue culture dishes, which showed that the cells reached confluence at a density of 1.52 × 10⁵ cells/cm². Given the surface area of the quartz monocrystal (45.6 cm²), confluence would be obtained with 6.9 × 10⁶ cells seeded onto the surface. Confluence of the cell monolayer was also confirmed by microscopic examination of the quartz surface at the end of the 12 h culture period.

Preparation of substrates for NR

The cell-coated quartz substrate was measured in a solid-liquid interface cell (Fig. 1). The setup was composed of a quartz substrate against a Macor ceramic disk (Ceramic Products, Palisade Park, NJ) containing SiO₂:MgO:Al₂O₃:K₂O:B₂O₃:F in a weight ratio of 46:17:16:10:7:4. Between the substrate and Macor disk was a 0.2–0.3 mm thick liquid reservoir created by an o-ring. The entire sample environment was held in place with clamps and screws. The Macor disk was cleaned by rinsing with chloroform, isopropanol, and ethanol, and placed into an ultraviolet ozone cleaner for 45 min. A solution of phosphate-buffered saline (PBS) in heavy water (deuterated PBS (dPBS)) was injected into the reservoir in the assembled solid-liquid interface cell. The dPBS solution was prepared according to the recipe for Dulbecco's PBS (1×) in D₂O (99.8% isotopic purity; Cambridge Isotope Laboratories, Andover, MA) and used to provide neutron scattering contrast among quartz, the hydrogen-rich cells, and the bulk solution. All NR measurements were performed at 23°C.

Figure 1.

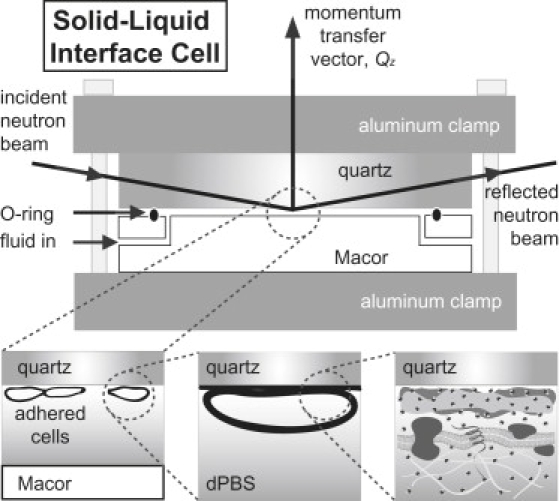
Schematic of the solid-liquid interface cell used in NR measurements. The quartz substrate with adherent cells is clamped against a Macor disk with a 0.2–0.3 mm thick gap created by an o-ring. The subphase, in this case dPBS, is injected into the gap. The neutron beam penetrates the lateral face of the quartz substrate to reach the solid-liquid interface where the cells reside.

Neutron reflectometry

NR experiments were performed on the Surface Profile Analysis Reflectometer (SPEAR), a time-of-flight reflectometer at the Los Alamos National Laboratory Neutron Science Center (http://www.lansce.lanl.gov/lujan/instruments/SPEAR/index.html). SPEAR receives neutrons from a polychromatic, pulsed source that have passed through a partially coupled liquid hydrogen moderator at 20 K to shift their energy spectrum. Through the use of choppers and frame-overlap mirrors, neutrons that reach the sample have a wavelength range of 2–16 Å. In time-of-flight measurements, the wavelength of incident neutrons is determined by measuring the time it takes for a neutron to travel from its source to the detector.

NR data are acquired by measuring the ratio of reflected to incident intensity of neutrons striking the sample at a small angle, θ, and elastically and specularly scattered. This ratio is the reflectivity, R, and is measured as a function of the momentum transfer vector Q_z, where Q_z = 4πsin[θ]λ⁻¹ and λ is the neutron wavelength. Analysis of reflectometry data provides information regarding the coherent scattering length density (SLD) distribution normal to a sample's surface. The reflectometry data presented here are multiplied by Q_z⁴ to compensate for the sharp decrease in reflectivity as described by Fresnel's law: R α Q_z ⁻⁴ (26).

The neutron beam is collimated with a series of slits to create a footprint on the sample of 10 mm × 50 mm. The acquired data are an average of the reflectivity from each 1 × 100 μm coherent area of the neutron beam that makes up the footprint. Because the average intensity over a large area is measured, the reflectivity may be sensitive to the surface coverage of cells. Based on the cell number at confluence (1.52 × 10⁵ cells/ cm²), the average surface area of a single attached HK-03 cell is 660 μm². Thus, each coherent area of the neutron beam (100 μm²) corresponds to a measurement from a small region (∼15%) of the bottom surface of a single cell. Using similar calculations, the average intensity from the entire neutron beam footprint represents the measurement of ∼7.5 × 10⁵ cells. Thus, the averaged NR signal recorded in these experiments would not be greatly affected by localized differences in cell coverage, but would be altered by differences in the cell coverage between experiments (see below). NR is also a time-averaged measurement, and conditions such as sample environment, sample homogeneity, and beam intensity can dictate the duration of an experiment. Using SPEAR, reflectivities as small as R ≈ 5 × 10⁻⁷ and a range in Q_z from 0 to 0.25 Å⁻¹ typically can be acquired in as little as 60 min. The reflectometry data shown here were acquired over 2–3 h and have a limited maximum Q_z value because extreme inhomogeneity in the samples leads to increased surface roughness and weak scattering.

The resulting reflectometry data are reduced using the incident neutron intensity spectrum. The intensity of the specular reflectivity and its real-space interpretation are related by a nonlinear inverse transformation. As a result, a unique transformation does not exist for a single experiment because only intensities (and no phase information) are acquired (27). Instead, the data presented here were analyzed using model-independent B-spline profiles (28) and a model-dependent Parratt fitting algorithm (29). Model-independent fitting requires less a priori knowledge of the system as compared to model-dependent fitting. Both methods provide a best least-squares fit to the NR data and a corresponding SLD profile. SLD is a value unique to a particular chemical composition and is the sum of the coherent scattering length of the constituent elements, divided by the volume they occupy. The SLD profile is shown as a function of distance from the interface in the direction normal to the sample surface.

B-spline profiles

The result of model-independent fitting is a real-space interpretation of the NR data that is less biased by the experimenters' expectations of the SLD distribution. The SLD profile is composed of cubic or parametric B-splines (27,28,30). Starting from an initial B-spline curve, a theoretical reflectivity profile is calculated and compared with the measured NR data. The B-spline curve is then modified and the process is repeated until the corresponding theoretical reflectivity profile reproduces the measured NR data. The fitting procedure requires input of the following parameters: Δρ, the difference in SLD of the substrate and subphase (in this case, quartz and deuterated buffer); n, the number of B-splines; d, the distance between the substrate and subphase; and β, a damping factor. Additional parameters employed to optimize computation include A₁, a function to determine the smoothness of the solution with a weight w₁; A₂, a biasing function to bias the solution toward an expected average SLD; and w₂, a second weight parameter to balance these two functions (A₁/A₂). The resulting SLD curves are refined by adjusting the parameters β, n, and d to obtain the best least-squares fit with physical relevance. Although the output of the model-independent fitting procedure is a single SLD profile, the entire process can be run iteratively to produce many SLD profiles within a range of χ² values. The criterion used here was to calculate a family of SLD profiles with χ² values in the range of ${\chi }_{\min }^2\pm {\chi }_{\min }$, where ${\chi }_{\min }^2$ was the minimum value found.

Box models

Model-dependent fitting is performed by comparing the NR profile with a model reflectivity profile generated using the Parratt recursion formalism (29), and adjusting the model using genetic optimization and the Levenberg-Marquardt nonlinear least-squares method to obtain the best least-squares fit (31). This approach is said to generate “box models” because the SLD distribution is described by a sequence of n boxes, each of constant SLD and thickness. Two adjoining layers, i and i+1, are connected by an error function centered at their interface to describe the roughness between the layers. The roughness includes contributions from static roughness and dynamic undulations. We utilized the simplest possible model of physical relevance, the model with the fewest parameters, to mimic the SLD profile obtained from the model-independent fitting.

Results and Discussion

Media

NR measurements were first performed on quartz substrates coated in only media to later aid in differentiation between these profiles and the NR profiles acquired from substrates coated with cells grown on media. The cell growth media contained proteins, sugars, and salts. The reflectivity profile from a media-coated substrate was fit with a model-dependent, two-box model, and this result is shown with the corresponding SLD profile in Fig. 2. Also shown in Fig. 2 is a cartoon interpretation of the SLD profile. Two boxes were required to model the media, signifying two length scales. The first length corresponds to the region of moderately dense, hydrogen-rich material adjacent to the quartz substrate, and the second corresponds to the subsequent, slightly less dense region, which gradually diffuses into the bulk solution. The high SLD values of the media indicate a large volume fraction of dPBS buffer. Typical SLD values of proteins and sugars are on the order of 1.0–2.0 × 10⁻⁶ Å⁻². Mixing with dPBS (SLD ∼6.2 × 10⁻⁶ Å⁻²) raises the SLD of the media.

Figure 2.

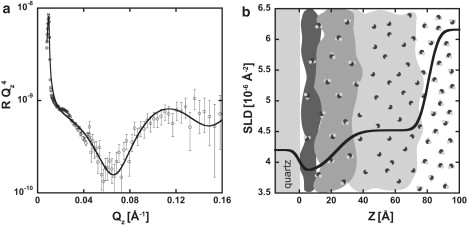
NR data and SLD profile for a media-coated quartz substrate. (a) The NR profile for the media sample with no cells present. The model-dependent fit based on the simplest, physically relevant box model is in black, and the data are shown with open circles and error bars indicating 1 standard deviation (SD). (b) The corresponding SLD profile (black line) is depicted on top of an interpretation of the media distribution at the interface. Large regions in grayscale represent varying concentrations of the proteins, salts, and sugars that reside in the media. Concentration is highest close to the quartz and gradually diffuses into the subphase with increasing distance from the substrate. Small D₂O molecules represent the increasing volume fraction of water as a function of distance from the quartz substrate.

High cell surface density

NR data from live cells incubated with media on a quartz substrate are shown in Fig. 3. Differences in the reflectivity from samples seeded with cells and the bare media are immediately visible, confirming that adherent cells were measured. The high degree of complexity of this living system places greater emphasis on model-independent fitting to provide an unbiased interpretation of the NR data. Fitting was performed with the use of both model-independent and model-dependent fitting procedures as described above. Iteratively running the model-independent fitting procedure and accepting all SLD profiles that were within χ of the best χ² profile produced a family of SLD profiles shown as a ribbon in Fig. 3 b. Model-dependent fitting was performed in an attempt to mimic this profile using the simplest possible box model. Both fitting methods provided very similar SLD profiles.

Figure 3.

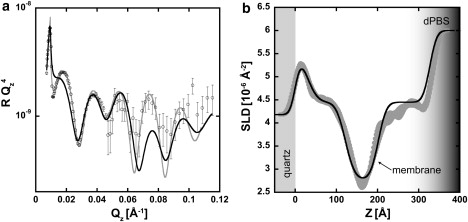
NR data and SLD profile for a high cell surface density sample. (a) NR data are shown with open circles and error bars that indicate 1 SD. The model-dependent fit is shown in black and the model-independent fit is shown in gray. (b) The corresponding SLD profiles for each fitting method. The model-independent method produces a family of SLD profiles (gray ribbon) where no curve differs from the lowest found χ² value by more than χ. The shading between 300 and 400 Å (b) represents the transition from hydrogen-rich material adjacent to the membrane to bulk dPBS in the cells' interior.

An interpretation of the high cell surface density SLD profile is shown in Fig. 4. The 80 Å dip in SLD (to ∼2.7 × 10⁻⁶ Å⁻²) centered at ∼180 Å from the quartz substrate represents the hydrocarbon tails of the cell membrane. The thickness of the hydrocarbon component of a pure phospholipid bilayer is typically ∼40 Å, the length of two hydrophobic tails. A membrane region twice this thick suggests that the membranes of the adhering cells are not organized as a homogeneous plane uniformly spaced from the quartz substrate. Instead, the membrane is likely either undulating or inhomogeneously distributed due to the surface topography of the underlying media and adherence proteins. Immediately at the quartz interface is a thick layer of proteins, ∼120 Å thick. The SLD in this region is different from that for the pure media sample. When cells are present, the SLD is higher due to a higher volume fraction of dPBS or a depleted presence of hydrogen-rich proteins. Though the exact composition of this region is unclear, it is important to recognize the differences in this region, 0–120 Å from the quartz substrate, between samples with and without cells. This difference may provide evidence that the cells are indeed producing proteins to adhere to the substrate, changing the composition of the cell-substrate interface. The interior of the cell region (200–350 Å from the substrate) contains some hydrogen-rich material in the vicinity of the membrane, but transitions to the SLD of pure dPBS over ∼150 Å. One might expect to see the other leaflet of the cell membrane visible at a much greater distance from the quartz substrate; however, using SPEAR, the largest resolvable feature measurable for an extremely homogeneous sample is 5000 Å. Based on the cell surface area calculations given above (660 μm² per cell) and the mean volume of a single HK-03 cell (1870 μm³), the thickness of a cell adherent to the substrate can be estimated at 2.8 μm. This is ∼5 times the distance from the quartz surface over which SPEAR measurements can be made.

Figure 4.

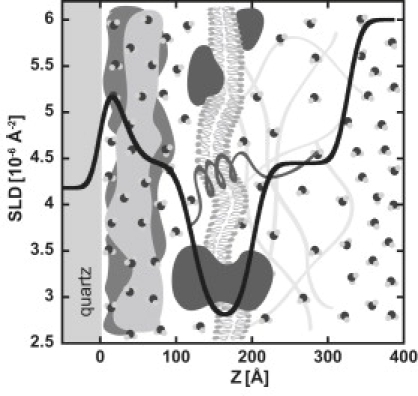
SLD profile of the highest surface concentration of cells depicted on top of a cartoon representation of how the cell behaves in the adherence region. Immediately adjacent to the quartz substrate is a layer of adherence proteins (∼120 Å thick), on top of which sits the membrane region (∼80 Å thick), followed by a diffuse profile representing the interior of the cell. Because of instrument limitations, the more distant cell membrane is not visible. Small D₂O molecules represent the water content as a function of distance from the quartz substrate.

Low cell surface density

Samples with low cell surface density were also prepared. NR data from a representative low-density sample are depicted along with data from a high cell surface density in Fig. 5. A comparison of the high and low cell surface density NR profiles shows that the overall shape of the scattering curve is preserved, indicating that the length scales are similar between the two samples. However, the overall reflected intensity is lower for the sample with lower cell surface density. The SLD profile for the low cell density data was generated by model-dependent fitting with the intent to mimic the one obtained for higher cell surface density. As shown in Fig. 5 b, the length scales of the two systems are almost identical, but in the lower cell surface density case, the overall SLD in the region between 30 and 350 Å is increased, suggesting a larger volume fraction of dPBS at lower cell surface density.

Figure 5.

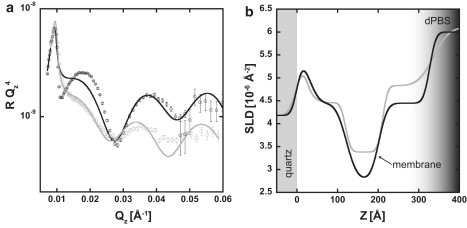
NR profiles (a) and corresponding SLD profiles (b) for high (black) and low (gray) cell surface densities. NR data are shown by open circles, and error bars indicate 1 SD. The lower surface cell density is evident from the decreased scattering intensity (a) and the increased SLD in the membrane region (120–200 Å) and interior of the cell (200–320 Å) (b).

Effect of distilled water and trypsin on adhered cells

To further confirm the accuracy of our NR measurements on live cells, we measured the effects of distilled water and trypsin on our cell samples. Both distilled water and trypsin are expected to disrupt the cells on the substrate. Fig. 6 a shows NR profiles of a low cell surface density sample before and after the introduction of distilled water into the subphase. After the initial NR measurement of the sample, 5 mL of distilled H₂O were injected, and allowed to interact with the system for 5 min. Then 5 mL of dPBS were injected and the sample was remeasured. Fig. 6 b compares the SLD profiles of the sample before and after the introduction of distilled water. After exposure to distilled water, the SLD profile (one-box model) shows a featureless transition from the SLD of the quartz substrate to the SLD of the bulk dPBS subphase, indicating that the distilled water effectively removed both the cells and media from the substrate.

Figure 6.

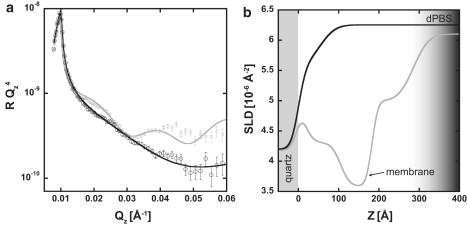
NR data (a) and corresponding SLD profiles (b) show changes to the cell sample due to the introduction of distilled water. Data obtained before (gray) and after (black) exposure to distilled water are shown by open circles and error bars indicating 1 SD. After modeling, the changes in the NR data indicate that the introduction of distilled water effectively removed almost all material from the substrate. The grayscale gradient (300–400 Å) only corresponds to the SLD profile before the introduction of distilled water.

Another cell sample was characterized using NR, and then 5 mL of trypsin were injected and given 5 min to interact with the sample. Next, 5 mL of media were introduced, followed by an additional 5-min incubation. Finally, the cell subphase was replaced with 5 mL of dPBS and the sample was remeasured. Trypsin is a serine protease that is responsible for protein digestion, and it is expected to digest the proteins that facilitate adhesion of the cell to the substrate. Fig. 7 compares the NR profiles before and after the introduction of trypsin into the subphase. In similarity to the interpretation of the distilled water data, the disappearance of features in the NR profile after the introduction of trypsin indicates that the cells are no longer adherent. A two-box SLD model was sufficient to fit the NR data. In the post-trypsin SLD profile depicted in Fig. 7 b, trace amounts of protein are visible on the quartz surface (0–30 Å), but the SLD profile rapidly approaches the SLD of the bulk subphase (dPBS).

Figure 7.

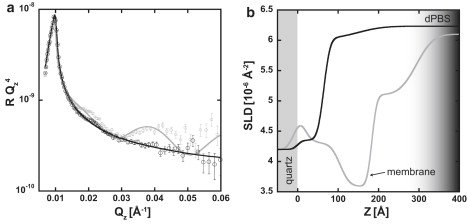
NR and SLD profiles before and after introduction of trypsin. NR data (a) and corresponding SLD profiles (b) before (gray curve) and after (black curve) exposure. NR data are shown with open circles and error bars indicating 1 SD. The gray curves show typical low cell surface density profiles. After the introduction of trypsin, the changes in the NR data suggest that trypsin has digested most of the adherence proteins, leaving only trace amounts of protein on the quartz surface. The grayscale gradient (300–400 Å) only corresponds to the SLD profile before the introduction of trypsin.

Conclusions

We have described a series of experiments that represent, to our knowledge, the first successful visualization and quantization of the interface between live cells and a substrate using NR. We observed a clear signal attributable to live HK-03 mouse fibroblast cells, as confirmed by comparison with samples of pure media. The average distance from the center of the membrane region to the quartz substrate was determined to be ∼180 Å. This offers support for measurements of cell adhesion focal contact made by numerous other techniques and determined to be in the range of 100–300 Å (1–15). The membrane region, ∼80 Å, contains inhomogeneously distributed or undulating membranes that likely conform to the nonplanar geometry of the supporting adherence proteins. The cell membranes that are farther from the quartz substrate are too distant to be resolvable with the instrument used. Measurements of many different cell densities demonstrated that the length scale of adherence proteins is independent of surface cell density. We confirmed the attachment of the live cell samples by successfully removing them from the substrate by interaction with distilled water or trypsin.

The measurement of live cells with NR represents a significant new direction for the study of highly complex biological systems. Historically, NR measurements have been limited to homogeneous model systems, and the ability to extract information from a system as complicated as live cells will enable many similar measurements to be made in the future. A major benefit of our method is that NR measurements can be made on viable cells in liquid medium. This configuration makes it possible to examine the attachment region of cells under a variety of conditions, such as different compositions of the substrate and extracellular matrix or biochemical or genetic alteration of the cellular expression of attachment molecules. Thus, NR measurements of viable, attached cells could be a very powerful means of probing the detailed structure and biophysics of cell attachment in situ with minimum measurement disturbance.