Microscopic Basis for the Mesoscopic Extensibility of Dendrimer-Compacted DNA

Abstract

The mechanism of DNA compaction by dendrimers is key to the design of nanotechnologies that can deliver genetic material into cells. We present atomistic simulations, mesoscopic modeling and single-molecule pulling experiments describing DNA dendrimer interactions. All-atom molecular dynamics were used to characterize pulling-force-dependent interactions between DNA and generation-3 PAMAM amine-terminated dendrimers, and a free energy profile and mean forces along the interaction coordinate are calculated. The energy, force, and geometry parameters computed at the atomic level are input for a Monte Carlo model yielding mesoscopic force-extension curves. Actual experimental single-molecule curves obtained with optical tweezers are also presented, and they show remarkable agreement with the virtual curves from our model. The calculations reveal the microscopic origin of the hysteresis observed in the phase transition underlying compaction. A broad range of ionic and pulling parameters is sampled, and suggestions for windows of conditions to probe new single-molecule behavior are made.

Introduction

Polyamidoamine (PAMAM) dendrimers (1) are functionalized nanoparticles that hold promise for use in several biomedical applications involving the targeted delivery of drugs and genetic material into the cell. Due to their chemical similarity to DNA-binding proteins, they are also instructive model systems for the hierarchical organization of genes (2). PAMAM dendrimers consist of an ethylene diamine core with four branched units (Fig. 1). Their size and surface chemistry can be easily controlled by adding successive generations of branches with different functional groups (3), allowing the dendrimers to be targeted to specific cell types. Dendrimers have been shown to bind DNA and be effective vectors for transfection (4), i.e., for the delivery inside the cell of therapeutic genes, antisense oligonucleotides, or ribozymes. As such, a detailed quantitative analysis of the physical interactions between dendrimers and nucleic acids is a crucial first step in understanding the delivery mechanisms.

Figure 1.

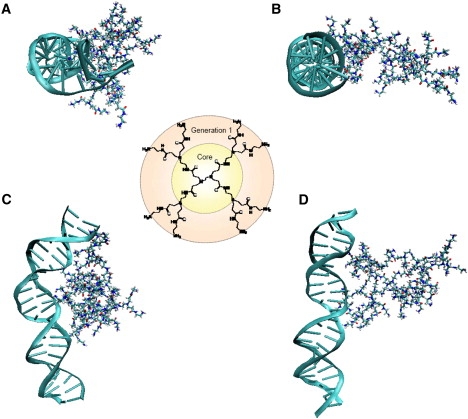
Dendrimer structure of the core and first branching generation (center) and four atomic snapshots of the two orientations simulated with MD. (Top and side views) Complexed structure for orientation 1 (A and C) and orientation 2 (B and D).

The basic process that makes dendrimers capable of transfecting DNA is the very substantial compaction of the DNA molecule that takes place upon cooperative dendrimer binding. For example, a μm-long DNA in extended form can, in the presence of dendrimers, be condensed to a size of tens of nm; this results in a dramatic increase in the density of DNA segments by several orders of magnitude.

Because the amine terminations of the dendrimers are protonated at physiological pH, their positive charge allows them to effectively bind negatively charged DNA. The interaction between dendrimers and double-stranded DNA has been studied by a variety of experimental techniques (5–8). Relatively fewer theoretical studies have been reported, including a molecular dynamics simulation of dendrimers interacting with single stranded DNA (9) and mathematical modeling of the electrostatics of duplex DNA-dendrimer interactions (10,11). Dynamic light scattering (12,13) and single molecule data (14) on the interaction between amine dendrimers and DNA indicate that DNA may be condensed by low generation dendrimers, or may wrap around higher generation dendrimers, but details of the respective compaction mechanisms are absent.

The most forthright means yet of probing dendrimer-DNA interaction comes from a detailed single molecule manipulation study by Ritort et al. (14), the data for which we use herein. In that study, single DNA molecules (a 7.2 μm-long, λ-phage DNA fragment was used) condensed by dendrimers of a particular generation are pulled from their ends using optical tweezers; the experiment is repeated with different generations and in various ionic conditions. The force at the ends of the DNA as a function of the end-to-end distance, the so-called force-extension curves (FEC), is measured. These curves reveal characteristic force plateaus and hysteresis between pulling and relaxation (see Fig. 2), indicating the existence of a first-order transition between an extended and a condensed state of the DNA (states which are confirmed, in the same study, by AFM visualization). The optical tweezer manipulations do show that DNA condenses around dendrimers and are able to measure characteristic forces, but whether the dendrimers induce structural changes in the DNA or interact with multiple segments, or both, is unknown (14). Moreover, the interplay among various components such as electrostatic interactions, solvent structure, and dynamical changes upon binding at the microscopic level has not been described until now. It is also not known whether the dendrimer terminations only interact with the phosphate groups on DNA or if they can interact with the basepairs as well. Also lacking is a microscopic understanding of the decondensation transition and the hysteresis observed in the macroscopic (or, more accurately, mesoscopic) pulling data. To determine the structural details of the dendrimer-DNA complex, including the deformation of the DNA and possibly the dendrimer as well as the free energies of complex formation, we set up to run atomistic molecular dynamics simulations and free energy calculations on a dendrimer-dsDNA system. We chose a generation-3 (G3) dendrimer because it is expediently small for intracellular delivery purposes, flexible enough to be interesting (otherwise large dendrimers are almost rigid and bind like spheres), and because it is computationally feasible, so that convergence in the calculation of free energy (a notoriously difficult computation for large systems) can be achieved with available computational resources. For quantitative comparison of our computational study, we then use the actual experimental single molecule data reported in Ritort et al. (14); via a Monte Carlo model, we scale up the microscopic observables derived from our atomistic MD simulation to generate macroscopic force-extension theoretical curves that can be directly compared with the measured force-extension curves obtained by optical tweezer pulling.

Figure 2.

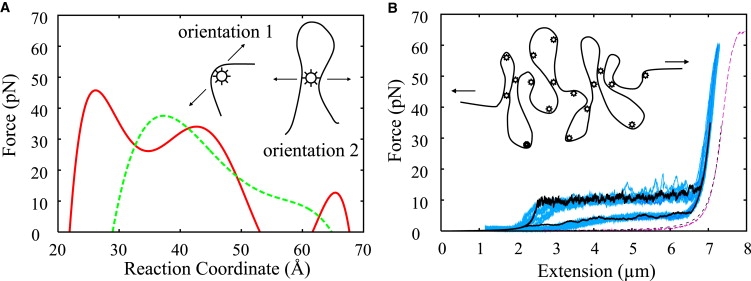
(A) Mean forces versus separation for the two orientations derived from the numerical derivative of the PMFs computed for orientation 1 (solid) and 2 (dashed). Insets (in both panels A and B) depict the two possible mechanisms of DNA condensation. Arrows indicate the direction of pulling force. The relative detachment force felt by the dendrimer will depend on the structure of the DNA-dendrimer complex. (B) Experimental single-molecule force-extension curves (blue, data from (14)) and theoretical curve (black) computed for an entire DNA molecule with N = 300 contacts, using the parameters derived from the umbrella sampling free energy calculations for an individual dendrimer DNA contact (see text). Experimental curve for naked DNA and a fitted EWLC (see Eq. 1) are shown in red and black dotted curves, respectively.

Dendrimer-DNA systems

All-atom molecular dynamics simulations in combination with umbrella sampling (15) were used to study the details of PAMAM dendrimer-DNA interactions. The calculations mapped out a free energy profile (a potential of mean force, PMF) along the approach coordinate. A DNA-dendrimer system in two distinct relative orientations was studied in our simulations. Interactions were examined for a double-stranded, 24-basepair segment of DNA, a two-times' repeat of the Dickerson-Drew dodecamer sequence (16), and a G3 dendrimer with 32 amine terminations. The dendrimer was placed initially so that the side with the greatest surface area faced the DNA. Because the dendrimer may also approach the DNA sideways, which can result in a distinct microscopic interaction, a second orientation was also studied. The dendrimer was rotated 90° with respect to the core so that the smallest surface area faced the DNA. The two dendrimer orientations that we set up are the two representative ones for the prototypical subset of possible approach geometries, given the structure of the branches.

The amine termination has a large positive charge at neutral pH (all-protonated G3 has charge +32) and the DNA has a large number of negatively charged groups. It is therefore expected that the interaction will be driven largely by electrostatics (as confirmed by the salt-dependence of the FEC, see below). However, the relative contribution of nonelectrostatic interactions such as hydrogen bonding and van der Waals interactions, as well as the role of solvent, are also to be assessed.

Simulation Methods

Multiple starting structures were generated for the all-amine dendrimer-DNA system, with the molecules' centers of mass at 30 Å, 50 Å, and 70 Å for the first orientation, and 45 Å, 60 Å, and 70 Å, for the 90° rotation. The DNA-dendrimer systems were fully solvated using TIP3P water molecules (17) in a box of dimensions 108 × 95 × 95 ų and 108 × 125 × 95 ų, and 108 × 145 × 95 ų, respectively. The periodic cells were designed such that the minimum distance between the molecules and the edge of the water box was 14 Å. Our results indicate that the DNA and dendrimer do not interact at edge-to-edge distances >∼23 Å, thus we expect the size of the cell is sufficient to prevent interaction between molecules in neighboring cells. Forty-six sodium ions were added to the system to balance the charge of the DNA, and then 32 chloride ions were also added, yielding electrically neutral unit cells. Simulations were run using constant number of particle, volume, and temperature conditions and all used periodic boundary conditions. Simulations were run in NAMD using the CHARMM 27 parameter set (18) with a timestep of 2 fs using SHAKE (19). Electrostatics were calculated using the particle-mesh Ewald method (20). Nonbonded interactions had a real-space cutoff of 14 Å. The systems were minimized for 1000 steps of steepest-descent minimization with the DNA and dendrimer held fixed and, subsequently, for 4000 steps of the adopted-basis Newton-Raphson method with decreasing harmonic restraints on the dendrimer and DNA. Each system was then equilibrated for 50 ps with dendrimer and DNA fixed with a harmonic restraint of 0.5 kcal/mol/Ų applied to the heavy atoms of the dendrimer and DNA, so that only the solvent and ions were free to move. Each system was then equilibrated for another 50 ps with temperature-coupling to a heat bath of 300 K (21,22) under constant volume conditions with no restraints. In all simulations, the relative displacement of basepairs at the ends of the DNA segment was restrained with a harmonic potential to prevent fraying. Although fraying is physically possible for short stretches of DNA duplexes, this boundary restraint on the end basepairs was deemed appropriate to model the interaction of the dendrimer with stretched DNA for longer than we could include in the atomistic simulation.

For umbrella sampling simulations, the reaction coordinate used was the distance between the center-of-mass of the dendrimer and the center of the DNA, defined as the center-of-mass of the middle two basepairs. A harmonic potential with a force constant of 2.5 kcal/mol/Ų was applied to this reaction coordinate over a series of windows starting from the initial structures and progressing along the reaction coordinate in 1 Šincrements. Each window was run for 200 ps of simulation, yielding total simulation times ranging from 11.4 ns to 20.8 ns. The free energy profiles were calculated using the weighted histogram analysis method (23). Two parallel sets of umbrella sampling simulations that differed by initial structures and seeds were run to increase sampling. In all simulations, a structure from the previous window was used to start each successive window. Coordinates were saved every picosecond.

Results

Structural details of DNA-dendrimer complex

The simulation snapshots shown in Fig. 1 highlight the structural effect of complexation for the two orientations. The bound structures show that orientation 1 has the greatest effect on the structure of both molecules in complex. In this case, the dendrimer stretches out to cover as much of the DNA as possible, bending the DNA in the process. The total degree of the bend, measured as the cumulative angle formed by adjacent basepair normals, ranges from 19.91° to 108.81°, with an average value of 51.78°. Orientation 2 of the dendrimer does not bend the helical axis significantly. Most likely, this is because the second orientation is characteristic of a lateral binding mode in which each of the two lobes binds a distinct helical fragment (i.e., the dendrimer straddles two duplex-DNA segments that are close in space but distant in sequence), whereas orientation 1 likely corresponds to a dendrimer bound to a single, bent DNA segment. These two modes are sketched in the inset of Fig. 3 a. For both orientation 1 and 2, the dendrimer-binding contour length for DNA from the simulation (between 10 and 18 basepairs) is in accord with contour lengths derived from ethidium bromide fluorescence titration experiments on low-generation dendrimer-DNA complexes (24). Moreover, similarly to what was observed for other cationic polyamines, namely, spermidine³⁺ and spermine⁴⁺ (25), our simulation shows that G3 binding does not perturb basepairing; this is of crucial importance if low-generation PAMAM dendrimers are to be used for gene compaction predelivery.

Figure 3.

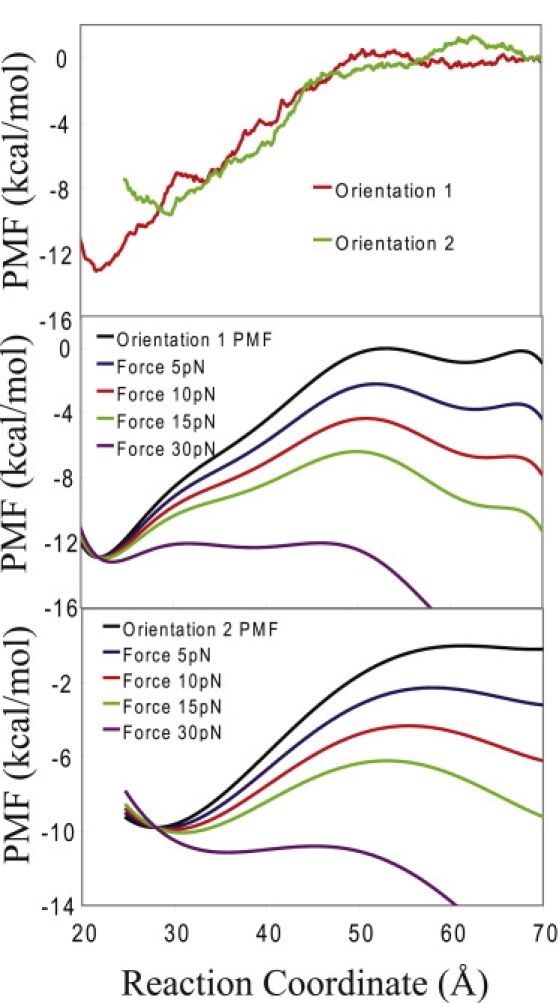
(A) Potentials of mean force for the two orientations of dendrimer. A Monte Carlo bootstrap error analysis estimates a maximum standard deviation for these PMFs of 0.035 kcal/mol (data not shown). (B) Relative PMFs under various pulling forces for orientation 1. (C) Relative PMFs for orientation 2.

It is of interest to compare the DNA bend angle upon dendrimer binding to structural knowledge regarding DNA-binding proteins that bend DNA to varying degrees as part of their biological function. Examples of such proteins are histones (26), viral DNA packing proteins (27), and many transcription factors; they can induce bend angles ranging from ∼20 to 130° (28).

It is known that dendrimers condense DNA and that this condensation is necessary to promote transfection (29). However, G3 does not appear to pack DNA in the same fashion as do nucleosomes. The latter bend DNA into a circular structure around large protein complexes (26). In contrast, the dendrimer only induces a small local bend in the DNA. It is more likely that dendrimers condense DNA by multiple discrete bends (as in our orientation 1) and by binding to straddle two segments nonadjacent in sequence (14) (as in our orientation 2). In this way dendrimers are more like other DNA packing proteins, such as the mitochondrial protein Abf2p (30), a 20-kDa protein that organizes DNA in the yeast mitochondria by bending the molecule at multiple sites by an average of 78° (30). Furthermore, recent simulations between DNA strands in the presence of monovalent ions (31) and multivalent ions (32) have shown that even small counterions can neutralize DNA strands to the point where they can be brought into close contact, with interstrand distances of ∼24 Å.

A structural analysis of the type of atomic contacts detected in our simulations indicates that the interaction between dendrimers and DNA is predominantly nonspecific and driven by electrostatic contacts between oppositely charged groups. However, we note in passing that a significant part of the free energy for the interaction between the all-amine terminated dendrimer and DNA is mediated by ordered waters, an effect that appears to be orientation-dependent (data not shown), with strong implication for the existence of substantial long-range interactions. There are very few interactions between the dendrimer and the base moieties and no obvious specificity to those interactions. A more detailed analysis of the influence of dendrimer terminations by considering neutrally charged acetamide and mixtures of dendrons will be reported elsewhere. Hereafter, we focus on the energetics and forces of the dendrimer DNA complex with particular emphasis on the single molecule pulling measurements of DNA-amine-dendrimer compaction.

Interaction free energy profiles

In the limit of infinite sampling, the potential of mean force we computed is the free energy of the system as a function of the reaction coordinates (33). This, by definition, involves integration over all other degrees of freedom. For a spherically asymmetrical molecule (as is the dendrimer), all the relative rotational orientations cannot be sampled within reasonable computation time. Although the PMFs reported here are for a given interaction geometry without rotational averaging, they report on the contribution of each respective configurational orientation. To mitigate the orientation effects, we have run two sets of simulations with dendrimer orientations that represent two extremes. In the first orientation, the dendrimer is positioned so that its widest side faces the DNA, whereas in the second orientation the dendrimer is positioned so that its smallest side faces the DNA. This approximates well the free energy for an interaction in which the molecules would be free to rotate, i.e., would yield an ergodic average. An important point to make here, however, involves a discussion of nonergodicity, which can manifest not only in the simulation when perpendicular degrees of freedom are not sampled, but also in the actual experiments when pulling is fast. Of particular relevance is the hysteresis in the single molecule study (14) for finite pulling rates; a similar hysteresis was observed for a different polycation-compacted DNA conglomerate (34). The hysteresis is indicative of the coexistence of an extended and a condensed phase. This involves not only metastability through trapping in average energy minima along the pulling coordinate but also for individual single molecules, trapping in different dendrimer-DNA orientations that may not be averaged over in the conglomerate. The latter, the perpendicular noise, is the source of heterogeneity in the different single-molecule traces and will be modeled by random force directions in our Monte Carlo model (see below).

The free energy profiles (the PMFs) along the approach coordinates for the two orientations are shown in Fig. 3. The first orientation, with its largest side facing the DNA, has the most favorable change in free energy, −13.5 kcal/mol. The other orientation of the all-amine dendrimer has a relatively lower total free energy change, of −10.9 kcal/mol. The overall shape of the PMFs reveals the typical profile of long-range attraction, a minimum, and a steep repulsion at short distances. Comparison with a distinct free energy profile calculation where the dendrimer had the charge neutralized by half (results not shown) point to an electrostatically driven interaction as the dominant contribution. The slight differences in the location of the free energy minima have to do with the structural changes of the dendrimers upon interaction with the DNA in the two geometries.

The interaction free energy per cationic charge computed for the 32+ charged G3 dendrimer was 0.028 kT/bp and 0.024 kT/bp for the two orientations. This compares favorably with data from two independent single-molecule experiments on DNA condensed by the polycation spermidine³⁺, reporting an intramolecular attraction per charge of 0.0277 kT/bp (35) and 0.02 kT/bp (36)—data also consistent with osmotic stress measurements in bulk condensed DNA. Additionally, our computed free energies falls within the range of yet other experimental free energy per charge estimates of 0.0175–0.036 kT/bp inferred for spermine⁴⁺ and spermidine³⁺, respectively (37,38).

Forces of interaction

The negative gradient of the PMF is, by definition, the mean force (39). The forces of interaction of the dendrimer-DNA systems, shown in Fig. 2, were hence calculated from the free energy plots by taking the numerical derivative of the PMF with respect to the reaction coordinate. This sets the so-called adiabatic limit for the detachment force, i.e., this is the equilibrium force needed to maintain a certain DNA dendrimer separation when the other degrees of freedom have had time to relax (i.e., upon pulling slowly). This limit can be exceeded, however, when pulling faster than diffusive relaxation (40). As seen in Fig. 2, the PMFs reveal a distribution of forces in accord to the corresponding experimental study (14). For example, the ∼20–60 pN force range computed from our PMFs (Fig. 3) is in accord with the force range to break dendrimer DNA interactions, from the easily detachable to the more resilient ones, observed in the pulling experiments.

Although we do see bending of the DNA, it is likely that its mesoscopic collapse is also the result of lateral interactions involving two DNA duplexes joined by a dendrimer and not just of elastic buckling; similar lateral interactions were inferred from experiments on DNA collapse by trivalent cations (35)). The characteristic force plateau seen in the experiments is therefore most likely the result of contacts being broken between the dendrimer and one of the two DNA strands being bridged. As such, we projected the mean forces computed from the PMF along the direction of DNA dendrimer separation as schematized in Fig. 2. A force applied to pull the DNA-dendrimer system will lower the free energy of the extended states (see Fig. 3, C and D). It will also tilt the computed PMF for each dendrimer-DNA contact by −Fx∗, where F is the magnitude of the force in the direction of pulling, and x∗ is a characteristic length scale (which may be, in principle, F-dependent; see Concluding Discussion) ascribed to the distance from the reactant region to the transition state. Each dendrimer-DNA contact can thus be thought of as a two-state system: a detached (extended) state and a collapsed state. In the presence of dendrimers and a relatively high external force, the detached DNA dendrimer state is favored; however, upon decreasing the magnitude of the force, the stretched polymer will collapse when the attractive free energy is lower than the free energy of the detached state. Because there are many contacts per DNA molecule, it is expected that there will exist a coexistence curve with both detached and collapsed contacts, indicative of a first-order phase transition. The FECs observed in the single-molecule data (Fig. 2) clearly follow this predicted behavior, as indicated by the existence of the force plateau.

Atomistic-to-mesoscopic extrapolation: from PMFs to FECs

Given our atomistic, MD-calculated PMF (and its two associated geometries) for the separation of a single DNA-dendrimer contact, we can go to the experimentally relevant mesoscopic length (μm) of an entire DNA molecule with N dendrimers bound by using a stochastic model for the attachment/detachment kinetics. We employ an elastically coupled two-level system of contacts, used previously to describe the unfolding of proteins and carbohydrates (41), that evolves according to a Monte Carlo (MC) procedure. A similar stochastic model was used by Ritort et al. (14) to interpret experimental data in terms of a dynamical equilibrium between an extended and a condensed state. The resulting FEC from our combined MD/MC simulations are shown in Fig. 2, together with an experimental FEC containing the actual data reported in Ritort et al. (14) (data kindly provided by Professor F. Ritort).

The Monte Carlo model works as follows. For DNA, the FEC, i.e., the dependence of the force F on the extension x is given by an elastic version of the wormlike chain model (EWLC),

$$F(x,L)=\frac{k_{\text{B}}T}{p}\left(\frac{1}{4{(1+\frac{\text{F}}{\gamma }-\frac{\text{x}}{\text{L}})}^2}-\frac{1}{4}+\frac{x}{L}\right),$$ (1)

where p is the persistence length (in our case 20 nm), γ is Young's modulus (2000 pN), and L is the effective contour length, i.e., the length of DNA free to extend without breaking a contact (7.2 μm for the fully extended DNA molecule used in the experiment, with an initial value of 2.7 μm to account for the amount of slack existent in the fully condensed DNA). We note that the persistence length chosen for our model is lower than the standard value of 50 nm. It has been shown that the presence of multivalent cations significantly decreases the persistence length of DNA (35,42). Concentrations of cobalt hexamine just below the threshold required to condense DNA reduce the persistence length to 20 nm (43), and higher concentrations of this trivalent cation result in a persistence length as low as 15 nm (44). It is reasonable to assume that highly charged molecules such as dendrimers would also have this effect, and so the value of 20 nm is in fact more suitable for our system than 50 nm would be.

Unlike in typical applications of the EWLC, here the dependence on L of F is made explicit because L changes upon each dendrimer binding/detachment event. Equation 1 describes accurately the naked DNA FEC, i.e., the force for a given length L of DNA without any dendrimer bound. However, it fails to capture the essential features (plateaus and hysteresis) of dendrimer-condensed DNA FECs. To model these, the effect of the pulling force on the rates of contact breaking/formation (α(F), β(F)) need to be incorporated. In the simplest approach, they are given by the Bell model (45),

$$\mathit{\alpha }\left(F\right)=\mathit{\omega }{e}^{-(\Delta G_{\text{E}}-F{x}_{\text{E}}^{\ast })/k_{\text{B}}T)},$$ (2)

$$\mathit{\beta }\left(F\right)=\mathit{\omega }{e}^{-(\Delta G_{\text{C}}+F{x}_{\text{C}}^{\ast })/k_{\text{B}}T)},$$ (3)

where ΔG_E and ΔG_C are the free energy barriers to break or form a contact, i.e., to extend or to compact, respectively, x∗_E and x∗_C are characteristic widths of the free energy wells, and ω = 5 × 10⁴ s is the reciprocal of the diffusive relaxation time. For our model, the variables determining the force-dependency of the rates were derived directly from our PMFs using the average of the two orientations, ΔG_E = 12.2 kcal/mol and ΔG_C = 0 and x∗_E = 3.1 nm. To account for the elastic linkage that creates a transient capture-well for rebinding (see Evans (40) for details), x_C was set to δL = 15 nm, the average increase of contour length upon each detachment event (see below). This is expected to be a lower estimate because diffusion away from the DNA binding site limits the ability of the dendrimer to recombine; even so, for forces beyond 10 pN contact-breaking probability dominates and reformation of contacts becomes negligibly small. Moreover, although the recombination at zero force is barrierless in our PMF (as it should be for a short DNA duplex), a possible refinement of our model may include of a recombination barrier in orientation 2 to account for long-scale DNA looping (34). Although this will not change the barrier to cause it to break a contact because both reactant and transition state will be raised by the same amount (and hence will not modify the upper FEC plateaus), it may somewhat improve the fit for the lower, equilibrium curve.

The extension advances linearly with time, x = vt, with v the velocity; in practice, a discretization t_i = iδt is used. The evolution of contact counts is given by first-order kinetics,

$$d{N}_c/dt=-d{N}_E/dt=-\alpha \left(F\right)N_c+\beta \left(F\right)N_E,$$

where N_C is the number of intact contacts and N_E is the number of broken (extended) contacts, with their sum a constant, N_C + N_E = 300, a value consistent with the experimental data (14). At each time step, a Monte Carlo acceptance-rejection scheme is used to determine whether a given contact changes its state, according to the probabilities α(F)δt and β(F)δt of a contact being either broken or, respectively, reformed between t_i and t_i + δt. If a contact is broken, then the contour length, L in Eq. 1, is increased by δL = 15 nm, i.e., by the average contour length per contact; x in the same equation, which stands for modeling the cantilever motion, continues to increase linearly without a jump. Conversely, if a contact is formed, the contour length is decreased by the same amount. In either case, with the new values of x and L, the force F(x, L) for the next step is recalculated using Eq. 1. For each contact, the angle of the DNA bend for orientation 1 or the geometry of the straddling complex for orientation 2 (note that both of these orientations modulate the direction of the force felt by the dendrimer) can be different. The effect of the resulting disorder (or structural noise) on the force along the pulling direction, averaged over all contacts, was modeled by multiplying the force in Eqs. 2 and 3 by the cosine of a Gaussian-distributed angle with zero mean and standard deviation of 30°. This structural noise could alternatively be calculated by using a distribution of values for the free energy barrier instead of the pulling angle, as was done in the original experimental fit. Ritort et al. (14) used an exponential distribution of the free energy with a mean of ∼11.79 kcal/mol and variance 5.95 kcal/mol to fit the data, which is in good agreement with our two extreme free energy values. The upper FEC plateau of the curve was calculated with v = 0.2 μm/s, the actual velocity used in the experiment. For calculation of the lower curve, the necessary free energy values (those for contact formation) were not available from our simulations. Instead, v was decreased to 0.01 μm/s, under an assumption of equilibrium in which all contacts were given the chance of breaking at each time step (akin to sending v to zero). As the velocity approaches zero, the system approaches equilibrium, the upper plateau approximates the condensation curve, and the hysteresis disappears. Fig. 2 shows the remarkable similarity between such calculated FECs and the experimental single-molecule FECs. We get directly from the umbrella sampling free energy calculations, i.e., without fitting, values for ΔG values and x∗ values that, when translated in to FECs, yield curves comparable to the ones derived by the experiments of Ritort et al. (14). This result shows that our simulations validate the assumption of the two state, extended-collapsed system used in the interpretation of the experimental FECs.

It is of interest to consider the effect of solution ions on the FECs in connection to the single molecule data measured at various ionic concentrations. Fig. 4 shows the our calculation of the binding free energy for G5 at various ion concentrations of NaCl. For these calculations, we do not have estimates for ΔG_E from simulations. Instead, we varied the value of ΔG_E so that results of the corresponding MC runs, using the elastically coupled two-state model, yield FECs that fit the experimental curves. For these calculations, we assumed a priori that the salt concentration would have no effect on the length to the top of the free energy barrier, although in reality this may not be exactly the case, and used the same value as in the previous fit. We find that the relationship between ion concentration and free energy is linear for concentrations between 50 mM and 500 mM, with increasing ion concentration corresponding to lower free energy of interaction. The linear relationship breaks down at the lowest ion concentration, 10 mM. This relationship is in agreement with experiments on the effect of ion concentration on the free energy of interaction for DNA and a nonspecific DNA-binding protein (46), which also found a linear relationship between salt concentration and binding free energy for all but very low salt concentrations. This makes intuitive sense if the interaction is primarily driven by electrostatics, as one would expect the ions to screen molecular charges. In separate PMF calculations, amine-acetamide mixed-termination dendrimers (results not shown) had ΔG_E values of 3.6 kcal/mol for a dendrimer with randomly distributed charges and 4.6 kcal/mol for a dendrimer with amine charges on one lobe and acetamide on the other. These values are below even the energy value fit to the highest ion concentration (7 kcal/mol at 500 mM) based; on that we would predict that the lower-charge dendrimers would not be able to condense DNA, because at 500 mM the DNA acts like the naked DNA curve.

Figure 4.

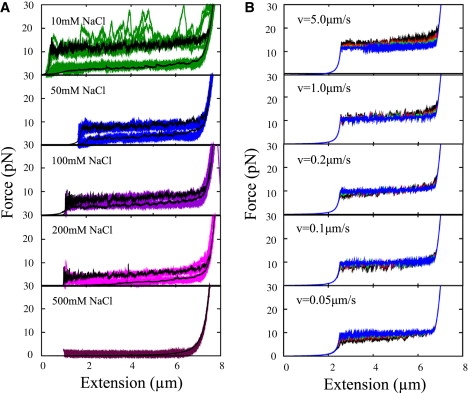
(A) Experimental force curves for G5 at various ion concentrations with theoretical curves in black. Theoretical curves were calculated using ΔG_E 13.6 kcal/mol (10 mM NaCl), 11.5 kcal/mol (50 mM NaCl), 11 kcal/mol (100 mM NaCl), 10 kcal/mol (200 mM NaCl), and 7 kcal/mol (500 mM NaCl). (B) The effect of velocity of pulling on the force plateau for DNA-condensation by dendrimers. At the velocity used in experiments, v = 0.2 μm/s, the several ΔG_E and x^∗_E values yield virtually indistinguishable plateaus, but at different velocities the plateaus begin to separate. The curves shown are for (ΔG_E, x^∗_E) = (20 k_BT, 3 nm) black, (25 k_BT, 5 nm) red, (30 k_BT, 7 nm) green, and (35 k_BT, 9 nm) blue (in this order from top to bottom in the top panel).

An intriguing finding stemming from the experiments and our microscopic simulations collectively is that the upper plateau of the hysteretic curves for G5, G6, and G7 studied experimentally, as well as the G3 dendrimer in the MD-based MC modeling, all seem, remarkably, to superimpose, despite their difference in size and overall charge (see Figs. 2 and 4 herein and Fig. 2 in Ritort et al. (14)). The only variables that affect the height of the plateau, as opposed to the length or EWLC fit in Eq. 1, are ΔG_E (plateau goes up as ΔG_E increases), x∗_E (plateau goes down as x∗_E increases), and velocity v. The overlap between FECs of dendrimers of substantially different charge and size may be explained by the effect of the force-dependent rates if ΔG_E increases with larger dendrimer size are offset by the concomitant increase in x∗_E. To explore whether this seeming universality is preserved across various pulling speeds, we used our MC model to gauge the effect of v on the force curve for DNA-condensation by dendrimers. As seen in Fig. 4, at the velocity used in the actual experiments, one can fit several values of ΔG and x∗_E to give virtually indistinguishable FECs, but at different velocities the curves begin to separate out. Experiments done on the different dendrimer sizes at varying speeds could help elucidate the degree to which PMFs are similar (as implied by the single-molecule study) or the extent of ΔG_E and x∗_E increase with dendrimer size.

Concluding Discussion

Using all-atom molecular dynamics simulations and free energy calculations, we have performed an atomistic study of aspects concerning the structural changes and driving forces involved in DNA interacting with generation-3 PAMAM amine-terminated dendrimers from which we derived a mesoscopic model for the extensibility of dendrimer-condensed DNA. A free energy profile along the interaction coordinate was calculated, as well as the mean forces as a function of DNA-dendrimer separation. Using energy, force, and geometry parameters computed at the atomic level, a Monte Carlo model for a mesoscopic force-extension curve was constructed that generated a force extension curve that reproduced, to a high degree of accuracy, the experimental single-molecule curves on DNA-dendrimer conglomerates.

Of the two orientations we studied, only the first orientation of the dendrimer induced a substantial structural deformation of the DNA locally, decreasing the end-to-end distance for the DNA by almost 15 Å and leading to an average bend angle of 51.8°. On the other hand, the second orientation most likely serves as a bridge between adjacent DNA molecules. This would lead to what is usually referred to as DNA looping in the context of protein-DNA interactions. The sawtooth-shaped peaks visible in both the experimental and simulated force extension curves are similar in character to the sawtooth patterns observed experimentally in single-molecule force-extension measurements with known DNA looping proteins (47,48) and serve as potential evidence for such looping in the DNA-dendrimer system. Our simulations uncovered two additional aspects, both of electrostatic nature, which may be of interest for further exploration.

Firstly, the dendrimer also deforms appreciably during the interaction. In addition to the mesoscopic contraction of the DNA molecule on scales comparable to its persistence length (as revealed with AFM in visualization mode), one also observes a local contraction of the dendrimer itself on microscopic scales comparable to its size, which we deem to be driven by a change in the local electrostatic environment.

Secondly, a study of the local order of water molecules in the simulation, using orientational correlation functions (data not shown), revealed an unexpectedly large role for ordered water dipolar contribution to the long-range interactions between the amine terminated dendrimer and DNA, which may lead to a refinement of a dipolar electrostatic steered-diffusion mechanism.

We have used several simplifications in our determination of the force-extension curve for this system. In principle, they may affect the results, so we discuss their validity. A recent work by Dudko et al. (49) has shown that the Bell model, which we use in these calculations, is not the most accurate description of the relationship between free energy and force. Their work shows that Kramer's theory of diffusive barrier crossing can be used to model a more accurate relationship between free energy and force than the relatively simpler Bell model. The improvement is especially evident in free energy surfaces that resemble the cusp model. However, for linear-cubic free energy profiles and low-to-intermediate pulling rates, the results of the Bell model are close to those of the more robust Kramer's theory model. As the experimental velocity was in the intermediate range and our free energy surface is roughly cubic in shape, the Bell model should still give reasonable results for our system. For a free energy surface that is cusplike, these types of calculations are better done with the Kramer's theory method described in Dudko et al. (49). Another potential problem with our calculations using this simple model is the assumption that the applied force affects the barrier height, ΔG_E, and it does not affect the barrier length, x. Close inspection of the plots in Fig. 3 reveals that this is in fact not true; as increasing force is applied to the system, the barrier of the free energy surface drifts to the left. This change, however, is minor, amounting to ∼1–3 Å for the forces used in the experiment, and we therefore assume that our use of a force-independent x_E is a reasonable approximation that should not substantially affect our results. A more accurate calculation would take into account the effect of force on x_E, as in Dudko et al. (49).

By changing the parameters in the MC model we revealed the microscopic origin of the hysteresis observed in the first-order phase transition between the extended and compacted DNA forms. Moreover, the broad range of ionic and pulling parameters sampled with the model can be used to offer suggestions for windows of conditions to probe new single-molecule behavior in future experiments.