Abstract
Channelrhodopsins are light-gated ion channels that mediate vision in phototactic green algae like Chlamydomonas. In neurosciences, channelrhodopsins are widely used to light-trigger action potentials in transfected cells. All known channelrhodopsins preferentially conduct H+. Previous studies have indicated the existence of an early and a late conducting state within the channelrhodopsin photocycle. Here, we show that for channelrhodopsin-2 expressed in Xenopus oocytes and HEK cells, the two open states have different ion selectivities that cause changes in the channelrhodopsin-2 reversal voltage during a light pulse. An enzyme kinetic algorithm was applied to convert the reversal voltages in various ionic conditions to conductance ratios for H+ and divalent cations (Ca2+ and/or Mg2+), as compared to monovalent cations (Na+ and/or K+). Compared to monovalent cation conductance, the H+ conductance, α, is ∼3 × 106 and the divalent cation conductance, β, is ∼0.01 in the early conducting state. In the stationary mixture of the early and late states, α is larger and β smaller, both by a factor of ∼2. The results suggest that the ionic basis of light perception in Chlamydomonas is relatively nonspecific in the beginning of a light pulse but becomes more selective for protons during longer light exposures.
Introduction
Channelrhodopsins (ChRs) of Chlamydomonas reinhardtii are of wide interest because they are prototypes of light-gated channels that initiate vision in phototactic algae (1) and are widely used as neurophysiological tools to trigger action potentials by light in ChR2-transfected cells (2). In both respects, the selectivity of these channels is crucial. All known ChRs preferentially conduct H+, but in physiological conditions and external pHe between 6 and 8, Na+, K+, and Ca2+ can significantly contribute to the current (3–6). The relative preference of H+ over Na+ and K+ has been estimated approximately (>106) from stationary currents at a fixed voltage and various ion concentrations (5,7).
Fig. 1 summarizes the known electrophysiological properties of ChR2. Typically, during a bright light stimulus of a few hundred milliseconds, the current decreases from an early peak to a stationary level (Fig. 1 A) (7,8). This feature, and the finding that the peak is smaller upon a second light pulse after a brief dark period (7,9), led to the proposal of a branched photocycle with two conducting (open) states, O1 and O2, and two nonconducting (closed) states, C1 and C2 (Fig. 1 B) (9,10). Because the transition from C2 to C1 is irreversible, the model in Fig. 1 B dictates that in the first instant of illumination after a long dark period, only O1 will be occupied before O2 is populated from O1 and C2. Thus, the initial current, I0, obtained by extrapolation of the current relaxation from peak to stationary level to time zero (see Fig. 1 A), can be assigned solely to the early state O1, whereas the peak itself already comprises some conversion of O1 to O2, because the peak marks the time when the decrease of the current through O1 and the increase of the current through O2 cancel each other to yield zero temporal slope of the total current. At low-intensity light pulses, the peak current appears later due to successive ChR activation and is smaller due to low occupancy of the O2 state. In fact, when our analysis below was carried out using the peak currents instead of the initial currents (results not shown), the qualitative features were similar but not as strongly expressed as from the actual analysis presented here. Compared to I0, the stationary current, I∞, reflects a mixture of currents through O1 and O2 but with more contribution from O2. For a given voltage, the model allows identification of time courses of occupancy for all four states, and conductivity for the two open states (9,10), but does not allow conclusions to be drawn with respect to their ionic selectivity. Strictly speaking, C1 and C2 represent the ensemble of several nonconducting states that were previously identified by spectroscopy (3,11,12).
Figure 1.
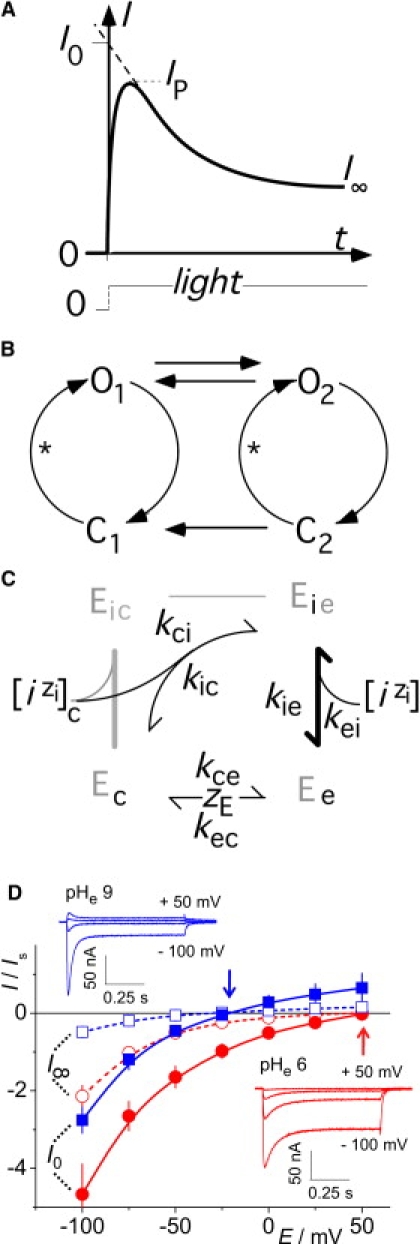
Definitions, recapitulation, and reaction schemes of the working hypothesis. (A) Typical time course of ChR2 photocurrent upon a bright, rectangular light pulse: after an early peak (IP), the current relaxes to a stationary level, I∞; extrapolation of the steepest slope to t = 0 yields the initial current, I0. (B) Simplified photocycle of ChR (6,7) with early and late conducting (open) states O1 and O2, respectively, plus two nonconducting (closed) states, C1 and C2. Asterisks indicate photoisomerization steps. Due to the irreversible step from C2 to C1, the steady-state occupation probabilities, p, of the four states are pC1 = 1, and pO1 = pO2 = pC2 = 0 in the dark; hence, I0 can be assigned to state O1 exclusively. (C) Reaction scheme for experiments with concentration changes of external ions; bold line indicates rapid equilibria. Derivation of three-state model from standard four-state model (gray) for uniport of one substrate i through enzyme E when no internal concentration changes take place. Subscripts c and e represent cytoplasmic and external measures, respectively. In the global model, n ion species, i, with their specific valencies, zi, compete for the empty binding site with charge zE, resulting in n three-state cycles sharing reorientation of the empty binding site between the cytoplasmic and external sides. (D) Current-voltage relationships for current amplitudes of I0 and I∞ versus holding voltage, recorded at pHe 9 and 6. IS is the reference current at pHe 7.5 with 100 mM external Na+, for standardizing results from various preparations. Arrows indicate the estimated reversal voltages, and insets show individual current tracings at the indicated holding voltages.
The aim of this study is a systematic investigation of the selectivities of the two ChR2 conducting states. Previous reports of other ion channels with states of different ion selectivity were merely qualitative and based on current amplitudes at a fixed holding voltage (13). In contrast, Lin et al. considered reversal voltages for ChR2, but did not discriminate between early and late currents (6). This study is based on reversal voltages and a quantitative selectivity analysis based on the enzyme kinetic reaction scheme in Fig. 1 C. The benefit of this model is that the reversal voltage is expressed by only one substrate parameter per ion species. In contrast, the more familiar model of a substrate binding site between two barriers requires three independent parameters per ion species.
Fig. 1 D illustrates previous observations regarding ChR photocurrents as they occur upon stimulation with bright light pulses (7,8), showing the sensitivity of the initial current (I0) and the stationary currents (I∞) to external pH, pHe, and transmembrane voltage, E, over wide ranges: The ratio I0/I∞ is quite variable but always >1 in response to pulses of bright light. This ratio decreases with acidic pHe and positive voltages. These striking features of the current amplitudes are of minor interest in this study, as they do not help the observer to draw conclusions about the relative selectivities of O1 and O2. Thus, we focus on conditions where the currents reverse their sign at the reversal voltages, Er.
The positive shift of the reversal voltages upon external acidification (Fig. 1 D, arrows) identifies H+ as the prevalent charge carrier of the ChR2 photocurrents. Differences between reversal voltages Er0, determined from initial currents, and Er∞ from stationary currents, are barely discernable from plots such as those in Fig.1 D. However, such differences could exist and indicate different ion selectivities of those two states. These differences could, in fact, be assessed by more detailed investigations of photocurrents near the reversal voltage in various ionic conditions.
Since different ion species will not move independently through ChR2 and since Ca2+can also pass ChR2 (5–7), it is, to our understanding, illegitimate to convert the reversal voltages to conductance ratios by the familiar formalism of the Goldman equation, although this has been done by Lin and colleagues (6) using a modified GHK algorithm according to Chang (14). We used instead an alternate, enzyme kinetic algorithm, which is presented in detail below. The use of an enzyme kinetic model with a defined binding site instead of a single barrier is necessary, because all transportable ion species will compete for passage through the selectivity filter and impede the passage of alternate ions by temporal occupation of the binding site(s).
One simple model to account for competition would be one binding site between two barriers. A quantitative treatment of the selectivity problem with this model would require three independent parameters for each translocated species (not illustrated), i.e., nine free parameters for the three different ion species investigated here. As an alternative, our applied model (Fig. 1 C) with fast binding equilibria and slow reorientation steps requires only one species-specific parameter for a quantitative treatment of the selectivity problem (see Theoretical, in Materials and Methods).
Material and Methods
Experimental
Voltage-clamp experiments on heterologously expressed ChR2 were carried out in Xenopus oocytes and HEK293 cells (here, HEK cells), as described previously (4,7).
Experiments in Xenopus oocytes were carried out under various ionic conditions (in mM): 0.1 CaCl2, 2 MgCl2, and 100 NMGCl or 100 NaCl at pH 9 (5 glycine), pH 7.5 (5 MOPS), or pH 6 (5 MES). For an increase of Ca2+, 1 mM NMG was replaced by 1 mM CaCl2. Detailed voltage-clamp recordings of initial and stationary currents were carried out at holding voltages, EC, in the vicinity of reversal voltages; Er was determined as the intersection of the regression line with zero current line.
An HEK293 cell line expressing ChR2-WT(1–307) inducible by adding 1 μM tetracycline was the kind gift of E. Bamberg (MPI Frankfurt, Frankfurt, Germany). Cells were cultured in Dulbecco's minimal essential medium supplemented with 10% (v/v) fetal bovine serum, 2 mM glutamine (Biochrome, Berlin, Germany), 175 μM penicillin, 68 μM streptomycin, 120 μM blasticidine, and 175 μM zeocine. Cells were seeded on coverslips at a concentration of 0.4 × 106 cells/ml. One day after seeding, cells were induced by 1 μM tetracycline. At 20 h postinduction, currents in cells were recorded with a conventional whole-cell patch-clamp method with an Axopatch200B and a Digidata 1440 (Molecular Devices, Sunnyvale, CA). The external solution contained (in mM) 100 NaCl, 2 CaCl2, and 2 MgCl2 with 10 HEPES (pHe 7.5), 10 Tris (pHe 9.0), or 10 MES (pH 6.0). The internal cytoplasmic solution contained (in mM) 120 NaCl, 10 EGTA, 2 MgCl2, 2 CaCl2, and 10 HEPES (pHc was adjusted to 7.3 using either CsOH or HCl). In all experiments, salt bridges were used to keep the electrodes at 100 mM NaCl under all conditions.
A 75-W xenon lamp (Jena Instruments, Jena, Germany) combined with a fast shutter (Uniblitz T132; Vincent Associates, Rochester, NY) was used for light pulses. Blue light was selected with a dichroic mirror reflecting 450–490 nm light through the objective onto the sample. 100% light intensity corresponded to 4.5 × 1021 photons m−2 s−1 at the cell surface.
Theoretical
The formalism of the Goldman equation applies not only to independent electrodiffusion but also to cases where several ion species compete for the main binding site of a charge-translocating enzyme (15). However, this holds only if the competing ion species have the same valency. Here, we develop an algorithm that makes it possible to determine selectivity relations from reversal voltages as well as for enzymatic translocation of ions with different valencies.
Formalism
Let us assume a standard four-state transport cycle (Fig. 1 C) with fast binding equilibria and slow reorientation steps. If the internal medium is not changed during experimentation, only the parameters of a three-state model can be identified from steady-state current-voltage relationships, whereby the inner equilibrium and the reorientation of the loaded state is lumped as a pair of gross rate constants (16).
Fig. 1 C illustrates this scenario for n ion species i with valencies zi. When zi is different for the different species, the reversal voltage depends on the fundamental rate constants kce0 and kci0, and on the ion concentrations on both sides in the following manner. Reorientation of the empty binding site is defined as
| (1a) |
| (1b) |
where subscripts “c” and “e” stand for cytoplasmic and external, respectively, and superscript “0” identifies reference conditions (0 mV, 1 mM). The reduced membrane voltage, u, is defined as u = EF/(RT). Rate constants are expressed in s−1.
Gross rate constants for binding/unbinding and reorientation of the occupied binding site are written
| (1c) |
| (1d) |
Rapid, external binding equilibria are Ki = kei/kie at kei, kie >> kci, kic, kec, kce with
| (2a) |
| (2b) |
because of microscopic reversibility.
We use auxiliary weighting variables, F, for King-Altman determination of state probabilities (17). Derivation and application of these weighting variables is demonstrated by the following example: with two assumed substrates, 1 and 2, Fig. 1 C becomes a four-state model, i.e., two three-state cycles sharing the empty site with its two orientation states c and e, plus the two loaded states E1 and E2 (n = 2). For each of the four states, there are eight product combinations of three rate constants, which feed the population of the respective state at the expense of the other three states; and the sum of these combinations amounts to the respective weighting factor, F. For state c, these combinations are keck1ck2c, keck1ck2e, keck2ck1e, keck1ek2e, k1eke2k2c, k2eke1k1c, k1ck2cke1, and k1ck2cke2; corresponding combinations hold for the other states. Because of condition 2, ke1, k1e, ke2, k2e >> kc1, k1c, k2c, kc2, kce, kec, five of these eight combinations can be ignored, leaving three relevant combinations, namely keck1ek2e, k1eke2k2c, and k2eke1k1c, for state c, with corresponding combinations for the other states. Dividing all terms by the products of the fast reactions k1ek2e and substituting K1 = ke1/k1e and K2 = ke2/k2e yields the sum Fc = kec + k1cK1 + k2cK2 as a weighting variable for state c, with corresponding sums for the other three states. Application of these rules for n substrates i yields
| (3a) |
| (3b) |
| (3c) |
To normalize the system to a total occupation probability of 1, we form the denominator
| (4) |
which allows us to calculate the individual state probabilities as
| (5a) |
| (5b) |
| (5c) |
The currents through the individual limbs are
| (6) |
for the empty binding site, where e is the elementary charge and zE the charge number of the empty binding site, and
| (6i) |
for the loaded sites. So the total current is
| (7) |
This sum does not reflect independence among the various ion species; instead, Eq. 6i indicates the interaction, as all rate constants of the system enter the occupation probability, p, of each state (Eq. 5) via Eqs. 3, a–c, and 4.
The following relationships prove that the reversal voltage, Er = EI=0, is independent of kec, kic, and zE. For zero current, IE + ΣIi = 0, we use Eq. 6. to write
| (8a) |
Dividing both terms by e and Den yields the net fluxes through the n + 1 pathways
| (8b) |
or the net charge fluxes, rightward minus leftward,
| (8c) |
which, when F is substituted by Eq. 3, becomes
| (8d) |
Introducing the voltage and concentration dependences of Eqs. 1 and 2. and using the symbols e0 = exp(zEu/2), ei = exp(ziu/2), and eI = exp((zE + zi)u/2) for momentaneous writing economy, yields
| (9) |
Multiplication of both sides (left side first, then right side) by kce0/kec0, shortening by kic0 and e0, and subtraction of the zE expressions from both sides yields
| (10) |
In this form, zE and the fundamental rate constants kec0 and kic0 do not appear any more. Q.E.D.
For zi = constant, kce0 drops out as well, and Eq. 10 assumes the form of the Goldman equation after some rearrangement:
| (11) |
confirming Eq. 97 in Andersen (15).
Results and Discussion
Qualitative observations
ChR2 was expressed in Xenopus oocytes and photocurrents were recorded under various ionic and voltage conditions in response to bright light pulses of 450 nm. To examine a possible anion conductance, the 100-mM external Cl− was partially or totally replaced by alternate anions, like glutamate, aspartate, or sulfate, which were assumed to have an even smaller conductance in ChR2 than Cl−. All three ions reduced the current amplitudes up to 25% at concentrations between 0 and 5 mM. However, none of the ions caused Er to become more positive. Similar experiments were repeated in ChR2-expressing HEK cell lines. Again, partial exchange of cytoplasmic Cl− by aspartate did not affect Er, so a significant anion conductance of ChR2, especially for Cl−, was excluded.
In contrast, partial or total replacement of inorganic cations in oocytes and HEK cells in the bath by the large organic NMG+, caused Er to become more negative throughout, confirming the observations from studies cited above. Since K+ and Na+ had similar effects (5–7), for quantitative purposes, we subsumed these ions under M+, meaning the sum of the monovalent ions K+ and Na+.
Likewise, a major increase of external Ca2+ or Mg2+ from 2 to 20 mM, caused noticable depolarization, especially at pHe 9 in the absence of external M+. Since the conductances of Ca2+ and Mg2+ could not be distinguished in a first series of experiments, we subsumed these divalent cations under D2+ for quantitative considerations. For maintaining the stability of the preparations, external D2+ could not totally be replaced.
Quantitative aspects
To determine the reversal voltages precisely, we recorded the current-voltage relationship of ChR2 in the vicinity of the reversal voltages with small voltage intervals. Typical results of this approach are shown in Fig. 2 for ChR2 in Xenopus oocytes. In the absence of external Na+ (Fig. 2 A), the initial reversal voltage and the stationary reversal voltage can hardly be distinguished at any pHe. However, in the presence of 100 mM external Na+, the differences are obvious. The stationary reversal voltages are more negative than those for the initial current and this difference is most pronounced at pHe 9. The more negative reversal voltage indicates an increased H+ selectivity in the stationary state compared to the initial one, because the Nernst equilibrium voltage for H+, EH = RT/F × ln([H+]e/[H+]c) was near −100 mV at pHe 9, whereas EM and ED were close to zero.
Figure 2.
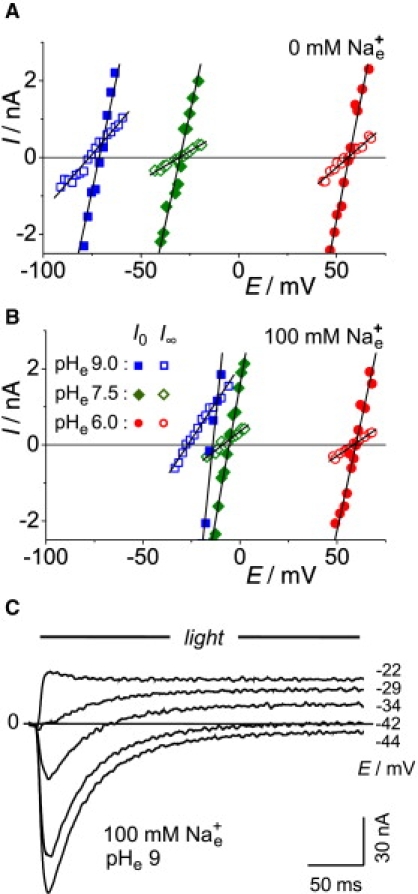
Typical experiment for determination of reversal voltages Er0 and Er∞ of ChR2 in Xenopus oocytes under various ionic conditions (in mM): internal, ∼120 Na+, ∼40 Cl−, pHc 7.3; external, 0.1 CaCl2, 2 MgCl2, and 100 mM NMGCl (A) or 100 mM NaCl (B). Voltage-clamp recordings of initial and stationary currents, I, were carried out at holding voltages, EC, in the vicinity of reversal voltages. Readings of Er are from intersections of regression lines with the zero-current line in the absence of external Na+ (A), and in the presence of 100 mM external Na+ (B) (for statistical evidence, see Fig. 4D; for quantitative analysis, see Table 1). (C) Original photocurrent records, measured at the indicated holding voltages. Note change of current sign in middle tracing (−34 mV), indicating change of reversal voltage and selectivity during a light pulse. Since the experiments in A–C were from different oocytes, the current scale in C was adjusted to match A and B.
Consequently, the time courses of the photocurrents at clamp voltages near the reversal voltage are of particular interest (Fig. 2 C). Data for pHe 9 in Fig. 2 B indicate that for certain holding voltages between the initial and the stationary reversal voltage, the initial current will be negative and the stationary current positive, with a change of sign in between. This scenario is well represented by the current tracing at a holding voltage of −34 mV in Fig. 2 C.
Another interesting case is the current record for −42 mV in Fig. 2 C, where the holding voltage equals the stationary reversal voltage, yielding zero stationary current: whereas the initial currents are assigned to the early state O1 exclusively, according to the model of Fig. 1 B, the stationary current is a mixture of currents through both states, O1 and O2. Consequently, zero total stationary current implies equal amounts of 1), M+- and D2+-dominated inward current through O1, and 2), H+-dominated outward current through O2.
Electrophysiological studies in Xenopus oocytes bear some uncertainty, because the actual ionic composition of cytoplasmic medium is not known exactly but has to be assumed from the literature (18). To avoid this disadvantage, similar experiments were performed with HEK cells as well, where the experimenter sets the ionic composition of the internal medium. The results of such a typical experiment are shown in Fig. 3. Here, the reversal voltages, especially those in the alkaline pHe range, are more positive than those from Xenopus ooytes (see Eq. 1).
Figure 3.
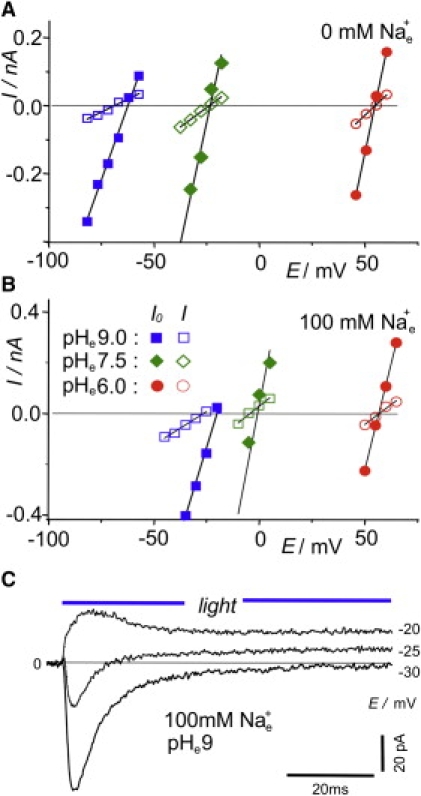
Typical experiment for determination of reversal voltages Er0 and Er∞ of ChR2 in HEK cells under various ionic conditions (in mM): internal, 120 NaCl, 10 Hepes, 2 MgCl2, 10 EGTA, and 2 CaCl2, pHc 7.3; and external, 2 CaCl2, 2 MgCl2, and 100 mM NMGCl (A) or 100 mM NaCl (B). Voltage-clamp records of initial and stationary currents, I, are shown at holding voltages, EC, in the vicinity of reversal voltages. Readings of Er are from intersections of regression lines with the zero-current line. in the absence of external Na+ (A), and with 100 mM added external Na+ (B). The predominant result was Er∞ < Er0 throughout, indicating increased H+ selectivity in the stationary state compared to the initial state (for statistical evidence, see Fig. 4A, and for quantitative analysis, see Table 1). (C) Original photocurrent records. Note change of current sign in the middle tracing (−25 mV), indicating change of reversal voltage and selectivity during a light pulse. The current scale was adjusted to match A and B.
The main conclusions of this study are based on the differences between the initial and the stationary reversal voltages, Er0 and Er∞. The differences in HEK cells are smaller than for ChR2 in oocytes, and the significance of these differences is not evident in Fig. 4, A and B. Therefore, these differences are plotted with statistical support by Fig. 4, C and D, for the ionic condition pHe 9. These panels show significantly more negative Er∞ than Er0 in the presence of 100 mM Na+e. This shift toward the dashed reference line (EH) in Fig. 4, A and B, indicates an increased H+ selectivity.
Figure 4.
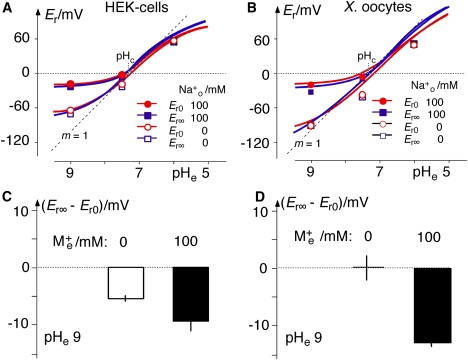
Initial (red) and stationary (blue) reversal voltages, Er0 and Er∞, of ChR2 as a function of pHe, recorded with and without 100 mM external Na+ in HEK cells and Xenopus oocytes. Values are means of n ≥ 3 independent recordings. (A) Absolute Er values in HEK cells (internal ion concentrations, in mM: 120 NaCl, 10 Hepes, 2 MgCl2, 2 CaCl2, and 10 EGTA, pHc 7.3); small SEs of 0.5–5.7 mV (n = 3) not illustrated. dotted line: theoretical Nernstian EH(pHe) with slope m = 1 (here, rounded 60 mV/pH unit); solid lines: theoretical relationships according to Eq. 10 with mean conductance ratios α and β from Table 1 at pHe 9.0, with and without 100 mM Na+e. (B) Same as A, but for Xenopus oocytes (internal ion concentrations, in mM: 120 Na+, 40 Cl−, pHc 7.4; data taken from Zhang and Prigge (4); small SEs of 1.0–5.0 mV (n = 3–7) are not shown. (C and D) Statistically supported differences, Er∞ − Er0, at pHe 9, for HEK cells and Xenopus oocytes, respectively.
Before the observed changes of the reversal voltages are quantitatively analyzed in terms of selectivity, alternative explanations should be considered. In particular, it is conceivable that the concentration terms in Eq. 10 change during continuous current clamping because of formation of unstirred depletion and accumulation layers in the close vicinity of membranes. Fortunately, a major bias by this mechanism can be excluded, because measurements of Er in flowing or stagnant media resulted in Er changes of only a few percentage points both in Xenopus oocytes and in HEK-cells, rendering these effects irrelevant in our context.
The mean experimental data of the pHe- and [M+]e-dependent reversal voltages of ChR2 in HEK cells are plotted versus pHe in Fig. 4 A. The dashed auxiliary line with the reference slope m = 1 of 59 mV/pH unit, marks the Nernst equilibrium voltage for protons, EH = RT/F × ln([H+]e/[H+]c), at different pHe values. This reference line crosses the Er = 0 line when pHe = pHc.
The data points at pHe 9 in the absence of external M+ are more positive than EH marked by the dotted reference line. Since at [M+]e = 0, EM is more negative than EH, the observed deviation must be due to an EX > EH, where X might be Cl− (ECl ≈ 0 mV), Ca2+ (ECa ≈ +120 mV), or Mg2+ (EMg ≈ 0 mV) in these conditions. Since a significant role of anions has already been excluded, and since the impact of Mg2+ and Ca2+ is similar (see qualitative observations above), we assign this difference to the global selectivity of divalent ions, D2+ (Mg2+ and Ca2+), compared to monovalent ions, M+ (K+ and Na+), by the selectivity coefficient β = kcD0/kcM0 for divalent cations, in analogy with the selectivity coefficient α = kcH0/kcM0, for H+.
In principle, the coefficient γ (kce0/kcM0) for the empty binding site is equivalent in interest to α (kcH0/kcM0) and β (kcD0/kcM0). Fig. 5 A shows the theoretical impact of increasing and decreasing coefficients α, β, and γ, on the Er(pCa) relationship of ChR2, where the reference curve with rounded parameters (Fig. 5 A, inset) basically reflects the experimental results. These changes need not be discussed here in full detail. However one feature worth noting in our specific scenario is that increases of γ can hardly be distinguished from decreases of β. Therefore, γ = 1 was fixed for numerical analysis by Eq. 10.
Figure 5.
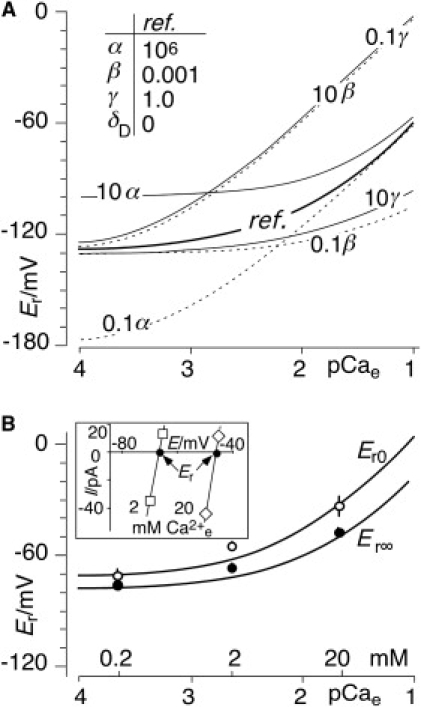
Effect of divalent cations, D2+ (Mg2+ + Ca2+), on Er. (A) Theoretical relations: impact of 10-fold increase and decrease of conductance ratios α (kcH0/kcM0), β (kcD0/kcM0), and γ (kce0/kcM0) on Er([D2+]e) relationships compared to reference configuration (inset). Note that increase of γ and decrease of β are almost equivalent in this configuration ([M+]c = 120 mM (100 mM K+ and 20 mM Na2+), [D2+]c = 2 mM (2 mM Mg2+ and 0.25 μM Ca2+), pHc 7.3, pHe [M+]e = 0, [D2+]c as marked by pCae on abscissa). To circumvent corresponding fluctuations in fits, γ was arbitrarily fixed at γ = 1 for numerical analysis. (B) Experimental results (symbols, means ± SE) and fits (solid lines) of Er at various external [Ca2+]; cytoplasmic ions, γ = 1, [M+]e = 0, pHe 9.0, as in A. To obtain fair fits, an ad hoc correction, δD, was introduced to account for the impact of external Mg2+: [D2+]e = δD + [Ca2+]e (see numerical results in Table 2). (Inset) Example of original current-voltage data for ChR2 in HEK cells (pHe 9, [M+]e = 0, internal solution, as in main figure) showing [Ca2+]e dependency of Er.
It is of interest that the Er values in Fig. 4, A and B, show a correspondingly negative deviation from EH at acidic pHe. This observation reflects the scenario of Fig. 1 C and Eq. 10, when ions with different valencies compete with each other for translocation, whereas the familiar formalism of the Goldman equation would show an asymptotic approach of Er to EH for large and increasing [H+]e.
The simple observation that the Er∞ values from the stationary currents (Fig. 4, blue line) are closer to the dotted reference line, EH, than are the Er0 values from the initial currents (red) already indicates a higher H+ selectivity of ChR2 after longer illumination. The close coincidence of the fitted curves with the experimental data in Fig. 4 A confirms the validity of the analysis. It is pointed out that the numerical analysis was based only on the data at pHe 9 and revealed good predictions for the measurements at pHe 7.5 and pHe 6.
To determine whether the results from experiments in HEK cells are representative for ChR2 or are biased by the particular expression system, analysis corresponding to that in Fig. 4 A has been carried out with ChR2 expressed in Xenopus oocytes. These results are plotted in Fig. 4 B and show basic agreement with those in Fig. 4 A, although in the absence of external Na+, the deviation of the reversal voltages from the EH is significantly smaller in Xenopus oocytes (Fig. 1 B) than in HEK cells (Fig. 4 A). This deviation is explained by the different concentrations of external Ca2+ in the two preparations: 2 mM Ca2+ in the HEK cell experiments, and 0.2 mM in the oocyte experiments. Taking this into account, similar conductance ratios were calculated for ChR2 in both expression systems (Table 1). The fact that the fits and predictions in Fig. 4 B are not as good as those in Fig. 4 A is explained by the uncertainties of the actual ionic composition of the cytoplasm in Xenopus oocytes, whereas in HEK cells, this composition was fully controlled by the experimenter.
Table 1.
ChR2 conductance ratios α, β, and γ in HEK cells and Xenopus oocytes
| HEK cells | Xenopus oocytes | |
|---|---|---|
| α0 | 4.5 × 106 ± 15% | 3.0 × 106 ± 8% |
| α∞ | 6.5 × 106 ± 16% | 8.6 × 106 ± 13% |
| α0/α∞ | 0.71 ± 2% | 0.36 ± 6% |
| β0 | 18 × 10−3 ± 28% | 5.5 × 10−3 ± 29% |
| β∞ | 12 × 10−3 ± 31% | 2.7 × 10−3 ± 37% |
| β0/β∞ | 1.56 ± 6% | 2.2 ± 6% |
α = kcH0/kcM0 for H+ over M+ (Na+ + K+); β = kcD0/kcM0 for D2+ (Ca2+ + Mg2+) Ca2+ over M+; and γ = kce0/kcM0 = 1 in Xenopus oocytes and HEK-cells, determined by fitting Eq. 10 to pairs of reversal voltages, Er, at pHe 9.0 with and without 100 mM external Na+, using experimental data presented in Fig. 4, A and C. Cytoplasmic cation concentrations were 120 mM M+ (100 mM K+ + 20 mM Na+) and 2 mM D2+ (2 mM Mg2+ + 0.25 μM Ca2+), pHc 7.3. Subscripts 0 and ∞ indicate values from initial and stationary currents, respectively. Values are expressed as means ± percent error, 100·SE/mean from independent experiments in n = 3 HEK cells and n = 6 Xenopus oocytes. Ratios α0/α∞ and β0/β∞ are the means of ratios from n cells, not ratios between two means.
The experimental results described in Fig. 4 directly demonstrate the behavior of the H+ and M+ conductances, whereas the role of D2+, which was not changed during the experimentation, was only an indirect result of the analysis. This deficit was accounted for by direct demonstration of the depolarizing effect of [Ca2+]e on Er (Fig. 5 B). The numerical analysis of these Er data was not as straightforward as that from Fig. 4, because the uncertain relations between Mg2+ and Ca2+ were changing, and the condition [D2+]e = 0 could not be carried out for stability reasons. Nevertheless, after adjustment of kcD0[D2+] for selectivity variations between Ca2+ and Mg2+ by introducing δD, as described in the legend to Fig. 5 B, good fits of Eq. 10 to the experimental data in Fig. 5 B were achieved, whereby the amounts and temporal changes of the resulting conductance ratios α and β (Table 2) agree reasonably well with those in Table 1 taken from the experimental results in Fig. 4.
Table 2.
ChR2 conductance ratios α, β, and δD in HEK cells
| α0 | 2.3 × 106 ± 16% |
| α∞ | 3.8 × 106 ± 9% |
| α0/α∞ | 0.63 ± 8% |
| β0 | 12 × 10−3 ± 20% |
| β∞ | 5 × 10−3 ± 16% |
| β0/β∞ | 2.3 ± 8% |
| δD0/mM | 4.7 ± 16% |
| δD∞/mM | 7.3 ± 9% |
| δD0/δD∞ | 0.64 ± 8% |
α = kcH0/kcM0 for H+ over M+; β = kcD0/kcM0 for D2+ (Ca2+ + Mg2+) over M+; and δD = correction for [D2+]e determined in HEK cells, from experiments with different concentrations of external Ca2+. Eq. 10 was fit to reversal voltages, Er, at [D2+]e = δD + 0.2, 2.0, and 20 mM [Ca2+]o, at pHe 9.0, and to data from experiment in Fig. 5B. Cytoplasmic cation concentrations were 120 mM M+ (100 K+ + 20 Na+) and 2 mM D2+ (2 mM Mg2+ + 0.25 μM Ca2+), pHc 7.3. Subscripts 0 and ∞ indicate values from initial and stationary currents, respectively. Values are expressed as means ± percent error, 100·SE/mean from independent experiments in three HEK cells.
The numerical results of the selectivity relations of ChR2 are compiled in Table 1, for expression in both Xenopus oocytes and HEK cells. These results can be summarized as follows:
-
1.
The selectivity relations of ChR2 are similar in both expression systems. This result confirms the notion (7) that i), the protein expresses its typical features, independent of the particular expression system, and ii), the lack of the knowledge of the exact ionic composition in Xenopus oocytes does not severely affect the validity of our analysis.
-
2.
Upon a bright light pulse, the initial selectivity α for H+ over M+ is ∼3 × 106 and increases by a factor of ∼2 to its stationary value.
-
3.
Correspondingly, the initial selectivity β for D2+ (Mg2+ and/or Ca2+) over M+ is ∼0.01 and decreases by a factor of ∼2 to its stationary value.
-
4.
With respect to H+, the decrease of β means another increase of the H+ selectivity. A temporal increase of the H+ selectivity during illumination is the global experimental result of this study.
It is expected that changes of the ionic composition of the cytoplasmic medium will reveal consistent conductance ratios. For technical reasons, this could only be examined in HEK cells, for instance, by reducing the internal Na+ concentration from 120 to 5 mM. The theory for our scenario predicts that this ionic change would shift Er by about +10 mV toward EH at pHe 6.0, i.e., closer to the dashed reference line in the positive branches of Fig. 4 A. Corresponding measurements at pHe 6.0 with and without external Na+ (n = 4 independent samples; data not shown explicitly) confirmed this expectation quantitatively and yielded α ≈ 3 × 106 and β ≈ 10−2 by fitting Eq. 10 to them, which agrees well with the conductance ratios listed in Tables 1 and 2.
The observed selectivity increase within the photocycle of ChR2 is paralleled by a known decrease of the total conductance (see slopes in Figs. 1 D, 2, and 3). This combination suggests that the physiological benefit of this sensory device is that it functions quickly, by employing a rather nonselective conductance at the expense of accuracy initially, and hence more precisely in the case of sufficient stimulus quantity.
The photophobic response of the alga is triggered by sudden light intensity changes and a large transient photoreceptor current that is carried by several ionic species mainly conducted by the open state O1 (19–21). The same O1 state should carry in the alga the photoreceptor current responsible for phototaxis at low light, where most of the ChR is in the C1 state. In contrast, in continuous light of high intensity, the photocurrent is reduced by two regulatory factors: first, by accumulation of late nonconducting photocycle intermediates (3,11,12), and second, by a reduced M+ and D2+ conductance of the O2 state. Thus, the cell saves energy at high light intensity by restricting the inward photoreceptor current (21,22).
Acknowledgments
We thank Maila Reh for technical support and preparation of the Xenopus oocytes. We thank Dale Sanders for critical reading of the manuscript. We are also indebted to E. Bamberg for sharing the ChR2-HEK cell line with us.
A.B. is supported by a Leibniz Graduate School fellowship. This work was supported by a Deutsche Forschungsgemeinschaft grant (to P.H.).
Footnotes
Dietrich Gradmann's present address is A.-v.-Haller-Institut der Universität, 37073 Göttingen, Germany.
Contributor Information
Dietrich Gradmann, Email: dgradma@gwdg.de.
Peter Hegemann, Email: hegemape@rz.hu-berlin.de.
References
- 1.Hegemann P. Algal sensory photoreceptors. Annu. Rev. Plant Biol. 2008;59:167–189. doi: 10.1146/annurev.arplant.59.032607.092847. [DOI] [PubMed] [Google Scholar]
- 2.Zhang F., Aravanis A.M., Deisseroth K. Circuit-breakers: optical technologies for probing neural signals and systems. Nat. Rev. Neurosci. 2007;8:577–581. doi: 10.1038/nrn2192. [DOI] [PubMed] [Google Scholar]
- 3.Ernst O.P., Sánchez Murcia P.A., Hegemann P. Photoactivation of channelrhodopsin. J. Biol. Chem. 2008;283:1637–1643. doi: 10.1074/jbc.M708039200. [DOI] [PubMed] [Google Scholar]
- 4.Zhang F., Prigge M., Deisseroth K. Red-shifted optogenetic excitation: a tool for fast neural control derived from Volvox carteri. Nat. Neurosci. 2008;11:631–633. doi: 10.1038/nn.2120. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Tsunoda S.P., Hegemann P. Glu 87 of channelrhodopsin-1 causes pH-dependent color tuning and fast photocurrent inactivation. Photochem. Photobiol. 2009;85:564–569. doi: 10.1111/j.1751-1097.2008.00519.x. [DOI] [PubMed] [Google Scholar]
- 6.Lin J.Y., Lin M.Z., Tsien R.Y. Characterization of engineered channelrhodopsin variants with improved properties and kinetics. Biophys. J. 2009;96:1803–1814. doi: 10.1016/j.bpj.2008.11.034. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Nagel G., Szellas T., Bamberg E. Channelrhodopsin-2, a directly light-gated cation-selective membrane channel. Proc. Natl. Acad. Sci. USA. 2003;100:13940–13945. doi: 10.1073/pnas.1936192100. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Ishizuka T., Kakuda M., Yawo H. Kinetic evaluation of photosensitivity in genetically engineered neurons expressing green algae light-gated channels. Neurosci. Res. 2006;54:85–94. doi: 10.1016/j.neures.2005.10.009. [DOI] [PubMed] [Google Scholar]
- 9.Hegemann P., Ehlenbeck S., Gradmann D. Multiple photocycles of channelrhodopsin. Biophys. J. 2005;89:3911–3918. doi: 10.1529/biophysj.105.069716. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Nikolic K., Grossman N., Degenaar P. Photocycles of channelrhodopsin-2. Photochem. Photobiol. 2009;85:400–411. doi: 10.1111/j.1751-1097.2008.00460.x. [DOI] [PubMed] [Google Scholar]
- 11.Bamann C., Kirsch T., Bamberg E. Spectral characteristics of the photocycle of channelrhodopsin-2 and its implication for channel function. J. Mol. Biol. 2008;375:686–694. doi: 10.1016/j.jmb.2007.10.072. [DOI] [PubMed] [Google Scholar]
- 12.Ritter E., Stehfest K., Bartl F.J. Monitoring light-induced structural changes of channelrhodopsin-2 by UV-visible and Fourier transform infrared spectroscopy. J. Biol. Chem. 2008;283:35033–35041. doi: 10.1074/jbc.M806353200. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Zheng J., Sigworth F.J. Selectivity changes during activation of mutant Shaker potassium channels. J. Gen. Physiol. 1997;110:101–117. doi: 10.1085/jgp.110.2.101. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Chang D.C. Dependence of cellular potential on ionic concentrations. Data supporting a modification of the constant field equation. Biophys. J. 1983;43:149–156. doi: 10.1016/S0006-3495(83)84335-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Andersen O.S. Kinetics of ion movement mediated by carriers and channels. Methods Enzymol. 1989;171:62–112. doi: 10.1016/s0076-6879(89)71007-7. [DOI] [PubMed] [Google Scholar]
- 16.Gradmann D., Klieber H.G., Hansen U.P. Reaction kinetic parameters for ion transport from steady-state current-voltage curves. Biophys. J. 1987;51:569–585. doi: 10.1016/S0006-3495(87)83382-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.King E.L., Altman C. A schematic method of deriving the rate laws for enzyme-catalyzed reactions. J. Phys. Chem. 1956;60:1375–1378. [Google Scholar]
- 18.Barish M.E. A transient calcium-dependent chloride current in the immature Xenopus oocyte. J. Physiol. Lond. 1983;342:309–325. doi: 10.1113/jphysiol.1983.sp014852. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Nonnengässer C., Holland E.M., Hegemann P. The nature of rhodopsin-triggered photocurrents in Chlamydomonas. II. Influence of monovalent ions. Biophys. J. 1996;70:932–938. doi: 10.1016/S0006-3495(96)79636-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Holland E.M., Harz H., Hegemann P. Control of phobic behavioral responses by rhodopsin-induced photocurrents in Chlamydomonas. Biophys. J. 1997;73:1395–1401. doi: 10.1016/S0006-3495(97)78171-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Sineshchekov O.A., Govorunova E.G. Rhodopsin-mediated photosensing in green flagellated algae. Trends Plant Sci. 1999;4:58–63. doi: 10.1016/s1360-1385(98)01370-3. [DOI] [PubMed] [Google Scholar]
- 22.Harz H., Hegemann P. Rhodopsin-regulated calcium currents in Chlamydomonas. Nature. 1991;351:489–491. [Google Scholar]


