FAST MOLECULAR SOLVATION ENERGETICS AND FORCE COMPUTATION

Abstract

The total free energy of a molecule includes the classical molecular mechanical energy (which is understood as the free energy in vacuum) and the solvation energy which is caused by the change of the environment of the molecule (solute) from vacuum to solvent. The solvation energy is important to the study of the inter-molecular interactions. In this paper we develop a fast surface-based generalized Born method to compute the electrostatic solvation energy along with the energy derivatives for the solvation forces. The most time-consuming computation is the evaluation of the surface integrals over an algebraic spline molecular surface (ASMS) and the fast computation is achieved by the use of the nonequispaced fast Fourier transform (NFFT) algorithm. The main results of this paper involve (a) an efficient sampling of quadrature points over the molecular surface by using nonlinear patches, (b) fast linear time estimation of energy and inter-molecular forces, (c) error analysis, and (d) efficient implementation combining fast pairwise summation and the continuum integration using nonlinear patches.

1. Introduction

Most of the protein molecules live in the aqueous solvent environment and the stabilities of the molecules depend largely upon their configuration and the solvent type. Since the solvation energy term models the interaction between a molecule and the solvent, the computation of the molecular solvation energy (also known as molecule - solvent interaction energy) is a key issue in molecular dynamics (MD) simulations, as well as in determining the inter-molecular binding affinities “in-vivo” for drug screening. Molecular dynamics simulations where the solvent molecules are explicitly represented at atomic resolution, for example as in the popular package NAMD [1], provide direct information about the important influence of solvation. Moreover, as the total number of atoms of solvent molecules far outnumber the atoms of the solute, a larger fraction of the time is spent on computing the trajectory of the solvent molecules, even though the primary focus of the simulation is the configuration and energetics of the solute molecule. Implicit solvent models, attempt to considerably lower the cost of computation through a continuum representation (mean-field approximation) of the solvent [2]. In the implicit model, the solvation free energy G_sol which is the free energy change to transfer a molecule from vacuum to solvent, consists of three components: the energy to form a cavity in the solvent which is also known as the hydrophobic interactions, the van der Waals interactions between the molecule and the solvent, and the electrostatic potential energy between the molecule and the solvent (also known as polarization energy), G_sol = G_cav + G_vdw + G_pol. Based on the Weeks-Chandler-Andersen (WCA) perturbation theory [3, 4], the non-polar solvation energies are of the form G_cav + G_vdw = G^(rep) + G^(rep). In [5], G_(rep) is described as the weighted sum of the solvent-accessible surface area A_i of the atoms. In [31], a volume term is added: $G^{(\text{rep})}={\sum }_{i=1}^M{\gamma }_i{A}_i+pV$, where p is the solvent pressure parameter and V is the solvent-accessible volume. In [6], the attractive van der Waals dispersion energy $G^{(\text{att})}={\sum }_{i=1}^M{G}_i^{(\text{att})}$, where $G_i^{(\text{att})}={\rho }_0\int u_i^{(\text{att})}({\mathbf{x}}_i,\mathbf{y})\theta (\mathbf{y})\text{d}\mathbf{y}$, ρ₀ is the bulk density, $u_i^{(\text{att})}({\mathbf{x}}_i,\mathbf{y})$ is the van der Waals dispersive component of the interaction between atom i in the solute and the volume of solvent at y, θ(y) is a density distribution function for the solvent. Hence the non-polar solvation energies

$$G_{\text{cav}}+G_{\text{vdw}}=\sum _{i=1}^M{\gamma }_i{A}_i+pV+{\rho }_0\int u_i^{(\text{att})}({\mathbf{x}}_i,\mathbf{y})\theta (\mathbf{y})\text{d}\mathbf{y}.$$ (1.1)

The electrostatic solvation energy is caused by the induced polarization in the solvent when the molecule is dissolved in the solvent, therefore

$$G_{\text{pol}}=\frac{1}{2}\int {\phi }_{\text{reaction}}(\mathbf{r})\rho (\mathbf{r})\text{d}\mathbf{r},$$ (1.2)

where φ_reaction = φ_solvent − φ_gas-phase, φ(r) and ρ(r) are the electrostatic potential and the charge density at r, respectively.

The Poisson-Boltzmann (PB) model was developed to compute the electrostatic solvation energy by solving the equation −∇(ε(x)∇φ(x)) = ρ(x) for the electrostatic potential φ. Numerical methods to solve the equation include the finite difference method [7, 8], finite element method [9, 10], and boundary element method [11]. However the PB methods are prohibitive for large molecules such as proteins due to the limited computational resources. As an alternative, (1.2) is approximated by a generalized Born (GB) model which is in the form of discrete sum [12]

$$G_{\text{pol}}=-\frac{\tau }{2}\sum _{i,j}\frac{q_i{q}_j}{{\left[r_{ij}^2+R_i{R}_{j}exp(-\frac{r_{ij}^2}{4R_i{R}_j})\right]}^{\frac{1}{2}}},$$ (1.3)

where $\tau =\frac{1}{{\epsilon }_p}-\frac{1}{{\epsilon }_w}$, εp and εw are the solute (low) and solvent (high) dielectric constants, q_i and R_i are the charge and effective Born radius of atom i, respectively, and r_{i j} is the distance between atoms i and j. The solvation force acting on atom α, which is part of the forces driving dynamics is computed as

$${\mathbf{F}}_{\alpha }^{\text{sol}}=-\frac{\partial G_{\text{sol}}}{\partial {\mathbf{x}}_{\alpha }}.$$ (1.4)

Because the GB calculation is much faster than solving the PB equation, the GB model is widely used in the MD simulations. Programs which implement the GB methods include CHARMM [13], Amber [14], Tinker [15], and Impact which is now part of Schrodinger, Inc.’s FirstDiscovery program suite. Even though the GB computation is much faster than the PB model, the computation of the Born radius R_i is still slow. During the MD simulation, the Born radii need to be frequently recomputed at different time steps. Because this part of computation is too time-consuming, there are attempts to accelerate the MD simulation by computing the Born radii at a larger time step. For example, in [16] in their test of a 3 ns GB simulation of a 10-base pair DNA duplex, they change the time step of computing the Born radii and long-range electrostatic energy from 1 fs to 2 fs. This reduces the time of carrying out the simulation from 13.84 hours to 7.16 hours. From this example we can see that the calculation of the Born radii takes a large percentage of total computation time in the MD simulation. In the long dynamic runs, this decrease in the frequency of evaluating the effective Born radii are not accurate enough to conserve energy which restricts the MD simulation of the protein folding process to small time scale [17]. Hence it is demanding to calculate the Born radii and the solvation energy accurately and efficiently.

In this paper we develop a method for fast computation of the GB solvation energy, along with the energy derivatives for the solvation forces, based on a discrete and continuum model of the molecules (Figure 1.1). An efficient method of sampling quadrature points on the nonlinear patch is given. We also show that the error of the Born radius calculation is controlled by the size of the triangulation mesh and the regularity of the periodic function used in the fast summation algorithm. The time complexity of the forces computation is reduced from the original O(MN +M²) to nearly linear time O(N +M +n³ logn +M logM), where M is the number of atoms of a molecule, N is the number of integration points that we sample on the surface of the molecule when we compute the Born radius for each atom, and n is a parameter introduced in the fast summation algorithm. The fast summation method shows its advantage when it is applied to the Born radius calculations for macromolecules, where there could be tens of thousands or millions of atoms, and N could be even larger. In the fast summation method, one only need to choose a small n which is much smaller than M and N to get a good approximation, which makes the new fast summation based GB method more efficient.

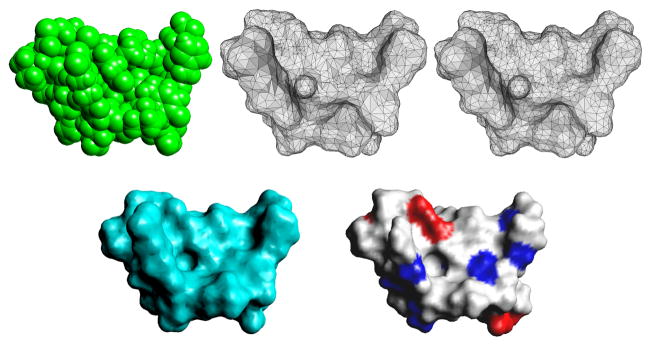
Fig. 1.1.

Top left: the discrete van der Waals surface model (436 atoms); top middle: the triangulation of the continuum Gaussian surface model with 6004 triangles; top right: the regularized triangular mesh where the quality of the elements is improved (making each as close as possible to an equilateral triangles); bottom left: the continuum ASMS model generated from the triangular mesh up right; bottom right: the molecular surface rendered according to the interaction with the solvent where red means strong and blue means weak interaction.

The rest of the paper is organized as follows: in Section 2 we explain the geometric model that our energy and force computation are based on; we discuss in detail the energy computation in Section 3 and the force computation in Section 4; some implementation results are shown in Section 5; some details such as the fast summation algorithm and the NFFT algorithm are discussed in the appendix.

2. Geometric model

2.1. Gaussian surface

The electron density and shape are used in a similar sense in the literature with respect to the modeling of molecular surfaces or interfaces between the molecule and its solvent. The electron density of atom i at a point x is represented as a Gaussian function: $f(\mathbf{x})=e^{\beta (\frac{\mid \mathbf{x}-{\mathbf{x}}_i{\mid }^2}{r_i^2}-1)}$ where x_i, r_i are the position of the center and radius of the atom k. If we consider the function value of 1, we see that it is satisfied at the surface of the sphere (x: |x − x_i| = r_i). Using this model, the electron density at x due to a protein with M atoms is just a summation of Gaussians:

$$f(\mathbf{x})=\sum _{i=1}^M{e}^{\beta (\frac{\mid \mathbf{x}-{\mathbf{x}}_i{\mid }^2}{r_i^2}-1)}$$ (2.1)

where β is a parameter used to control the rate of decay of the Gaussian and known as the blobbiness of the Gaussian. In [18] β = −2.3, isovalue = 1 is indicated as a good approximation to the molecular surface.

2.2. Triangular mesh

The triangular mesh of the Gaussian surface is generated by using the dual contouring method [19, 20]. In the dual contouring method a top-down octree is recursively constructed to enforce that each cell has at most one isocontour patch. The edges whose endpoints lie on different side of the isocontour are tagged as sign change edges. In each cube that contains a sign change edge, we compute the intersection points (and their unit normals) of the isocontour and the edges of the cube, denoted as p_i and n_i, and compute the minimizer point in this cube which minimizes the quadratic error function (QEF) [21]:

$$\text{QEF}(x)=\sum _i{[n_i·(x-p_i)]}^2.$$

Since each sign change edge is shared by either four cubes (uniform grid) or three cubes (adaptive grid), connecting the minimizer points of these neighboring cubes forms a quad or a triangle that approximates the isocontour. We divide the quads into triangles to generate the pure triangular mesh.

2.3. Algebraic spline molecular surface (ASMS)

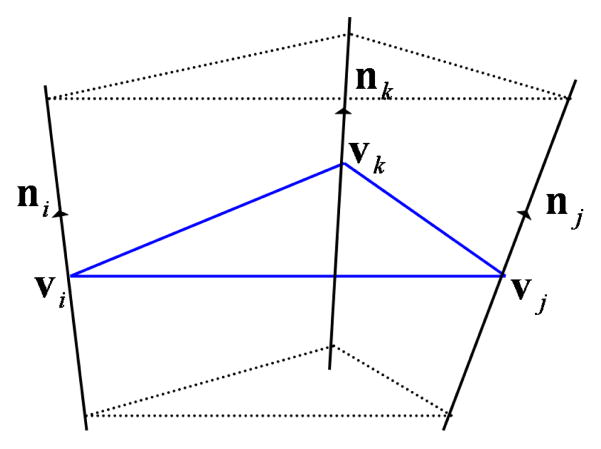
The triangular mesh is a linear approximation to the Gaussian surface. In our solvation energy computation, we generate another higher order approximation called ASMS model (Figure 2.3(f)) based on the triangular mesh to improve accuracy and efficiency [22]. Starting from the triangular mesh, we first construct a prism scaffold as follows. Let [v_iv_jv_k] be a triangle of the mesh where v_i, v_j, v_k are the vertices of the triangle and n_i, n_j, n_k be their unit normals. Define v_l(λ) = v_l + λn_l. Then the prism is define as

Fig. 2.3 .

(a) is the discrete van der Waals model of protein 1BGX with 19,647 atoms; (b) and (c) are the zoom-in views of the the initial triangulation of the continuum surface with 85656 triangles; (d) and (e) are the zoom-in views of the quality improved mesh; (f) is the a continuum ASMS model generated based on the quality improved mesh.

$$D_{\mathit{ijk}}:=\{\mathbf{p}:\mathbf{p}=b_1{\mathbf{v}}_i(\lambda )+b_2{\mathbf{v}}_j(\lambda )+b_3{\mathbf{v}}_k(\lambda ),\lambda \in I_{\mathit{ijk}}\},$$

where b₁, b₂, b₃ ∈ [0, 1], b₁ + b₂ + b₃ = 1, and I_ijk is a maximal open interval such that (i) 0 ∈ I_ijk, (ii) for any λ ∈ I_ijk, v_i(λ), v_j(λ) and v_k(λ) are not collinear, and (iii) for any λ ∈ I_ijk, n_i, n_j and n_k point to the same side of the plane P_ijk(λ):= {p: p = b₁v_i(λ) + b₂v_j(λ) + b₃v_k(λ)} (Figure 2.1).

Fig. 2.1 .

A prism D_ijk constructed with a triangle [v_iv_jv_k] as a basis.

Next we define a function over the prism D_ijk in the cubic Bernstein-Bezier (BB) basis:

$$F(b_1,b_2,b_3,\lambda )=\sum _{i+j+k=3}{b}_{\mathit{ijk}}(\lambda )B_{\mathit{ijk}}^3(b_1,b_2,b_3),$$ (2.2)

where $B_{\mathit{ijk}}^3(b_1,b_2,b_3)=\frac{3!}{i!j!k!}{b}_1^i{b}_2^j{b}_3^k$. The ASMS denoted as Γ is the zero contour of F. The scheme for defining the coefficients b_ijk are defined is described in detail in [22]. In short they are defined such that

• the vertices of the triangular mesh are points on Γ;

• Γ is C¹ at the vertices of mesh;

• Γ is C¹ at the midpoints of the mesh edges.

Later, given the barycentric coordinates of a point (b₁, b₂, b₃) in triangle [v_iv_jv_k], we solve the equation F(b₁, b₂, b₃, λ) = 0 for λ by Newton’s method. In this way we can get the corresponding point (x,y,z) on Γ:

$${(x,y,z)}^{\text{T}}=b_1{\mathbf{v}}_i(\lambda )+b_2{\mathbf{v}}_j(\lambda )+b_3{\mathbf{v}}_k(\lambda ).$$ (2.3)

We have proved in [22] that the ASMS model is C¹ everywhere if the normals of the mesh satisfy certain symmetry conditions. The error between the ASMS and the Gaussian surface is bounded and we have shown that the ASMS converges to the Gaussian surface at the rate of O(h³) where h is the maximum edge length of the mesh.

3. Fast solvation energy computation

3.1. Method

Similarly to what is done for other GB models, we use (1.3) as the electrostatic solvation energy function. Before we compute (1.3), we need to first compute the effective Born radius R_i for every atom which reflects the depth a charge buried inside the molecule (Figure: 3.1). An atom buried deep in a molecule has a larger Born radius, whereas an atom near the surface has a smaller radius. Hence surfactant atoms have a stronger impact on the polarization. Given a discrete van der Waals (vdW) atom model, as long as we know R_i for each atom, we can compute (1.3) by using the fast multipole method (FMM) [23] with the time complexity O(M logM). However the Born radii computation is not easy and is very time-consuming. There are various ways of computing the Born radius as summarized in [24]. These methods can be divided into two categories: volume integration based methods and surface integration based methods. In general, the surface integration methods are more efficient than the volume integration methods due to the decreased dimension. So we adopt the surface integration method given in [25] to compute the Born radius:

$$R_i^{-1}=\frac{1}{4\pi }{\int }_{\mathrm{\Gamma }}\frac{(\mathbf{r}-{\mathbf{x}}_i)·\mathbf{n}(\mathbf{r})}{\mid \mathbf{r}-{\mathbf{x}}_i{\mid }^4}\text{d}Si=1,\dots ,M,$$ (3.1)

where Γ is the molecule-solvent interface, x_i is the center of atom i, and n(r) is the unit normal on the surface at r and we use ASMS as the model of Γ.

Fig. 3.1 .

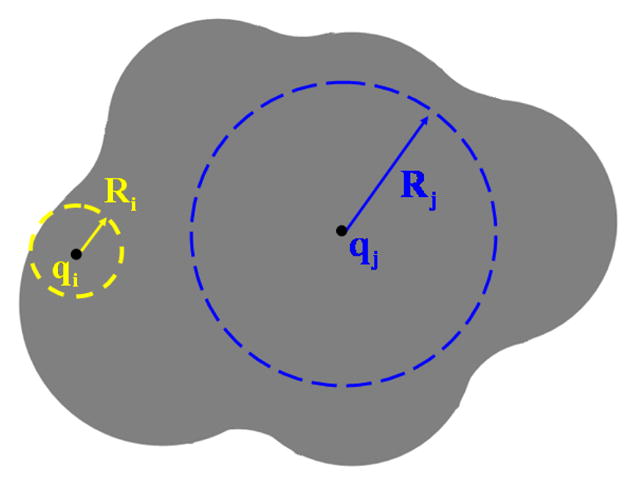
The effective Born radius reflects how deep a charge is buried inside the molecule. The Born radius of an atom is small if the atom is close to the surface of the molecule, otherwise the Born radius is large therefore has weaker interaction with the solvent.

Applying the Gaussian quadrature, We compute (3.1) numerically:

$$R_i^{-1}=\frac{1}{4\pi }\sum _{k=1}^N{w}_k\frac{({\mathbf{r}}_k-{\mathbf{x}}_i)·\mathbf{n}({\mathbf{r}}_k)}{\mid {\mathbf{r}}_k-{\mathbf{x}}_i{\mid }^4}i=1,\dots ,M,$$ (3.2)

where w_k and r_k are the Gaussian integration weights and nodes on Γ (Figure 3.2). r_k are computed by mapping the Gaussian nodes of a master triangle to the algebraic patch via the transformation 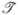. Let ${\mathbf{r}}_k^0$ and $w_k^0$ be one of the Gaussian nodes and weights on the master triangle. Then the corresponding node r_k and weight w_k are 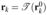and 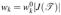where |J(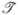)| is the Jacobian determinant of .

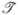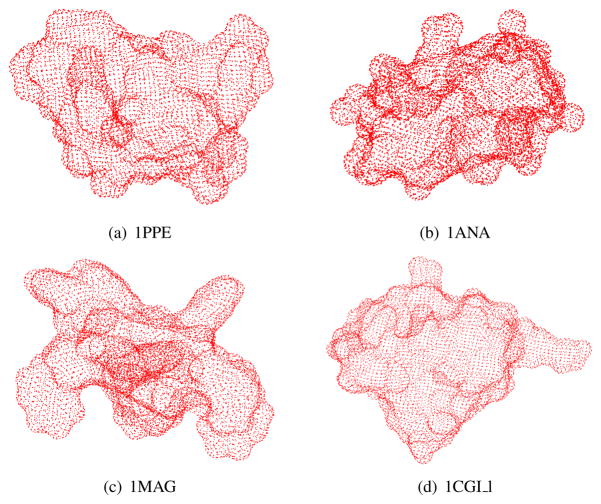
Fig. 3.2 .

Gaussian integration points on the surface of protein (a) 1PPE, (b) 1ANA, (c) 1MAG, and (d) 1CGI l. The surfaces are partitioned into 24244 triangular patches for (a), 28620 triangular patches for (b), 30624 triangular patches for (c), and 29108 triangular patches for (d). There are three Gaussian quadrature nodes per triangle. The nodes are then mapped onto the ASMS to form the red point cloud.

We formalize (3.2) in two steps. First we split it into two parts:

$$R_i^{-1}=\frac{1}{4\pi }\sum _{k=1}^N\frac{w_k{\mathbf{r}}_k·\mathbf{n}({\mathbf{r}}_k)}{\mid {\mathbf{r}}_k-{\mathbf{x}}_i{\mid }^4}-\frac{1}{4\pi }\sum _{k=1}^N\frac{w_k{\mathbf{x}}_i·\mathbf{n}({\mathbf{r}}_k)}{\mid {\mathbf{r}}_k-{\mathbf{x}}_i{\mid }^4}.$$ (3.3)

Then we split the second summation in (3.3) into three components:

$$\sum _{k=1}^N\frac{w_k{\mathbf{x}}_i·\mathbf{n}({\mathbf{r}}_k)}{\mid {\mathbf{r}}_k-{\mathbf{x}}_i{\mid }^4}=x_i\sum _{k=1}^N\frac{w_k{n}_x^k}{\mid {\mathbf{r}}_k-{\mathbf{x}}_i{\mid }^4}+y_i\sum _{k=1}^N\frac{w_k{n}_y^k}{\mid {\mathbf{r}}_k-{\mathbf{x}}_i{\mid }^4}+z_i\sum _{k=1}^N\frac{w_k{n}_z^k}{\mid {\mathbf{r}}_k-{\mathbf{x}}_i{\mid }^4}.$$ (3.4)

The first summation in (3.3) and the three summations in (3.4) without the coefficients in front are of the common form:

$$G({\mathbf{x}}_i)=\sum _{k=1}^N{c}_{k}g({\mathbf{x}}_i-{\mathbf{r}}_k)i=1,\dots ,M,$$ (3.5)

with the kernel function $g(\mathbf{x}-{\mathbf{r}}_k)=\frac{1}{\mid \mathbf{x}-{\mathbf{r}}_k{\mid }^4}$ and the coefficient c_k = w_kr_k · n(r_k), $w_k{n}_x^k,w_k{n}_y^k,w_k{n}_z^k$, respectively. (3.5) can be efficiently computed by using the fast summation algorithm introduced in [26] with complexity O(M + N + n³ logn), where n is a parameter used in the fast summation algorithm.

3.2. Fast summation

The fast summation algorithm is published in [26]. For convenience, we discuss this algorithm in this section briefly. The fast summation algorithm is often applied to compute the summations of the form

$$G({\mathbf{x}}_i)=\sum _{k=1}^N{c}_{k}g({\mathbf{x}}_i-{\mathbf{r}}_k),i=1,\dots ,M,$$ (3.6)

where the kernel function g is a fast decaying function. Cutting off the tail of g, one can assume that the support of g is bounded. In our Born radii computation, since the distance between x_i and r_k is no less than the smallest radius of the atoms, there is no singularity in g. Without loss of generality, we assume $\mathbf{x}-{\mathbf{r}}_k\in \mathrm{\Pi }:={[-\frac{1}{2},\frac{1}{2}]}^3$. After duplicating g in the other intervals, g can be extended to be a periodic function of period one in ℝ³ and this periodic function can be decomposed into the Fourier series:

$$g(\mathbf{x}-{\mathbf{r}}_k)=\sum _{\mathit{\omega }\in I_{\infty }}{g}_{\mathit{\omega }}{e}^{2\pi i\mathit{\omega }·(\mathbf{x}-{\mathbf{r}}_k)},$$ (3.7)

where I_∞:= {(ω₁, ω₂, ω₃) ∈ ℤ³} and g_ω = ∫_Π g(x)e^−2πiω·x dx. We approximate (3.7) by a truncated series:

$$g(\mathbf{x}-{\mathbf{r}}_k)\approx \sum _{\mathit{\omega }\in I_n}{g}_{\mathit{\omega }}{e}^{2\pi i(\mathbf{x}-{\mathbf{r}}_k)·\mathit{\omega }},$$ (3.8)

where $I_n:=\{({\omega }_1,{\omega }_2,{\omega }_3)\in {\mathbb{Z}}^3:-\frac{n}{2}\le {\omega }_i<\frac{n}{2}\}$. We compute the Fourier coefficients g_ω numerically by

$$g_{\mathit{\omega }}=\frac{1}{n^3}\sum _{\mathbf{j}\in I_n}g(\frac{\mathbf{j}}{n})e^{-2\pi i\mathit{\omega }·\mathbf{j}/n},\mathit{\omega }\in I_n.$$ (3.9)

by using the fast Fourier transform (FFT) algorithm with complexity O(n³ logn).

Plugging (3.8) into (3.6), we get

$$\begin{array}{l}G({\mathbf{x}}_i)\approx \sum _{k=1}^N{c}_k\left(\sum _{\mathit{\omega }\in I_n}{g}_{\mathit{\omega }}{e}^{2\pi i({\mathbf{x}}_i-{\mathbf{r}}_k)·\mathit{\omega }}\right)=\sum _{\mathit{\omega }\in I_n}{g}_{\mathit{\omega }}\left(\sum _{k=1}^N{c}_k{e}^{-2\pi i\mathit{\omega }·{\mathbf{r}}_k}\right)e^{2\pi i\mathit{\omega }·{\mathbf{x}}_i}\\ =\sum _{\mathit{\omega }\in I_n}{g}_{\mathit{\omega }}{a}_{\mathit{\omega }}{e}^{2\pi i\mathit{\omega }·{\mathbf{x}}_i}\end{array}$$ (3.10)

where

$$a_{\mathit{\omega }}=\sum _{k=1}^N{c}_k{e}^{-2\pi i\mathit{\omega }·{\mathbf{r}}_k}.$$ (3.11)

(3.10) is computed by using the NFFT algorithm with complexity O(n³ logn +M) and (3.11) is computed by the NFFT^T algorithm with complexity O(n³ logn +N). Hence the total complexity of computing (3.6) is O(N + M + n³ logn), which is significantly faster than the the trivial O(MN) summation method once the number of terms in the Fourier series n is much smaller than M and N. We explain the NFFT algorithm and the NFFT^T algorithm in Appendix A and B, respectively.

3.3. Error analysis

The numerical analysis of the error introduced during the computation of (3.1) can be decomposed as follows: (i) the sum of a quadrature error E_Q; (ii) some “fast computation” error in the evaluation of the quadrature itself. The latter error is then decomposed in three terms, which correspond to different steps in the numerical procedure. They are the truncation error E_FS when we truncate the Fourier series (3.7) into finite terms, NFFT^T errors E_ω when we compute the coefficients (3.11), and an NFFT error E_NFFT when we finally evaluate (3.10) by the NFFT algorithm.

Let I_i and Ĩ_i denote the exact integration and the numerical output of (3.1) for atom i, respectively. Then We have

$$I_i={\stackrel{\sim }{I}}_i+E_{\text{NFFT}}+E_{{\text{NFFT}}^{\text{T}}}+E_{\text{FS}}+E_{\text{Q}}.$$

Let ${\left|\right|E\left|\right|}_{\infty }=\underset{i}{max}\mid I_i-{\stackrel{\sim }{I}}_i\mid$. We have

$${\left|\right|E\left|\right|}_{\infty }\le {\left|\right|E_{\text{Q}}\left|\right|}_{\infty }+{\left|\right|E_{\text{FS}}\left|\right|}_{\infty }+{\left|\right|E_{\text{NFFT}}\left|\right|}_{\infty }+{\left|\right|E_{{\text{NFFT}}^{\text{T}}}\left|\right|}_{\infty }.$$ (3.12)

Next we will analyze each individual error ||E_Q||_∞, ||E_FS||_∞, ||E_NFFT||_∞, and ||E_NFFT^T||_∞.

3.3.1. Quadrature error

Let Γ_e be one of the algebraic patches on the molecular surface Γ. Suppose Γ_e is built based on a triangle e:= [v_i, v_j, v_k]. Any point (b₁, b₂, b₃) ∈ e can be mapped to a point r(b₁, b₂) ∈ Γ_e. The integration (3.1) over Γ_e is

$$\begin{array}{l}{I}_e={\int }_{{\mathrm{\Gamma }}_e}\frac{(\mathbf{r}-{\mathbf{x}}_i)·\mathbf{n}(\mathbf{r})}{\mid \mathbf{r}-{\mathbf{x}}_i{\mid }^4}\text{d}S\\ ={\iint }_{{\mathrm{\Omega }}_0}\frac{(\mathbf{r}(b_1,b_2)-{\mathbf{x}}_i)·\mathbf{n}(\mathbf{r}(b_1,b_2))}{\mid \mathbf{r}(b_1,b_2)-{\mathbf{x}}_i{\mid }^4}\mid J\mid \text{d}{b}_1\text{d}{b}_2\end{array}$$ (3.13)

where Ω₀ is the canonical triangle, (b₁, b₂, b₃) is the barycentric coordinates of the points in Ω₀ and |J| is the Jacobian. Let f (b₁, b₂) denote the integrand in (3.13). As we discuss in Appendix C, f (b₁, b₂) ∈ C^∞(Ω₀). Suppose we use an s-th order quadrature rule on element e, then

$$I_e={\iint }_{{\mathrm{\Omega }}_0}f(b_1,b_2)\text{d}{b}_1\text{d}{b}_2=\sum _{k=1}^{s_e}{w}_{k}f(b_1^k,b_2^k)+E.$$ (3.14)

We expand f(b₁, b₂) in a Taylor series around a point $(b_1^{\prime },b_2^{\prime },b_3^{\prime })\in {\mathrm{\Omega }}_0$:

$$f(b_1,b_2)=P_s(b_1,b_2)+R_s(b_1,b_2),$$ (3.15)

where P_s(b₁, b₂) is a polynomial of degree s:

$$P_s(b_1,b_2)=f(b_1^{\prime },b_2^{\prime })+\frac{1}{s!}{[(b_1-b_1^{\prime })\frac{\partial }{\partial b_1}+(b_2-b_2^{\prime })\frac{\partial }{\partial b_2}]}^{s}f(b_1^{\prime },b_2^{\prime })$$ (3.16)

and the residue R_s is

$$R_s(b_1,b_2)=\frac{1}{(s+1)!}{[(b_1-b_1^{\prime })\frac{\partial }{\partial b_1}+(b_2-b_2^{\prime })\frac{\partial }{\partial b_2}]}^{s+1}f(b_1^{\ast },b_2^{\ast }),(b_1^{\ast },b_2^{\ast })\in {\mathrm{\Omega }}_0.$$ (3.17)

Then the error E becomes

$$E={\iint }_{{\mathrm{\Omega }}_0}{R}_s(b_1,b_2)\text{d}{b}_1\text{d}{b}_2-\sum _{k=1}^{s_e}{w}_k{R}_s(b_1^k,b_2^k).$$

Let W_k = max(|w_k|), we get

$$\mid E\mid \le {\iint }_{{\mathrm{\Omega }}_0}\mid R_n(b_1,b_2)\mid \text{d}{b}_1\text{d}{b}_2+W_k\sum _{k=1}^3\mid R_n(b_1^k,b_2^k)\mid .$$

Within Ω₀, $\mid b_1-b_1^{\prime }\mid \le 1$ and $\mid b_2-b_2^{\prime }\mid \le 1$, hence

$$\mid R_s(b_1,b_2)\mid \le \frac{1}{(s+1)!}{[\mid \frac{\partial }{\partial b_1}\mid +\mid \frac{\partial }{\partial b_2}\mid ]}^{s+1}f(b_1^{\ast },b_2^{\ast }),$$ (3.18)

where $\mid \frac{\partial }{\partial b}\mid ·$ denotes $\mid \frac{\partial ·}{\partial b}\mid$. By the chain rule,

$$\frac{\partial }{\partial b_1}=\frac{\partial }{\partial x}\frac{\partial x}{\partial b_1}+\frac{\partial }{\partial y}\frac{\partial y}{\partial b_1}+\frac{\partial }{\partial z}\frac{\partial z}{\partial b_1}.$$

According to (2.3), we have $\frac{\partial x}{\partial b_1}=v_1^x-v_3^x+\lambda (n_1^x-n_3^x)$. Let h_max be the maximum edge length of the triangular mesh, λ_max = max{|λ |}, and h = max(h_max, λ_max). Then we have $\mid \frac{\partial x}{\partial b_1}\mid \le 2h$. Similarly, we can get the same bound for the derivatives of x, y, z with respect to b₁ and b₂. Therefore

$$\mid R_s(b_1,b_2)\mid \le \frac{{(2h)}^{s+1}}{(s+1)!}{[\mid \frac{\partial }{\partial x}\mid +\mid \frac{\partial }{\partial y}\mid +\mid \frac{\partial }{\partial z}\mid ]}^{s+1}\stackrel{\sim }{f}(x^{\ast },y^{\ast },z^{\ast })\le C\frac{{(2h)}^{s+1}}{(s+1)!}$$ (3.19)

where $(x^{\ast },y^{\ast },z^{\ast })=b_1^{\ast }{\mathbf{v}}_i(\lambda )+b_2^{\ast }{\mathbf{v}}_j(\lambda )+b_3^{\ast }{\mathbf{v}}_k(\lambda ),\stackrel{\sim }{f}(x^{\ast },y^{\ast },z^{\ast })=f(b_1^{\ast },b_2^{\ast })$, and the constant $C=\underset{(x,y,z)\in \mathrm{\Gamma }}{max}\mid D^{s+1}\stackrel{\sim }{f}(x,y,z)\mid <\infty$. Noticing that the area of Ω₀ is 1/2, we can write

$$\mid E\mid \le (\frac{1}{2}+s_e{W}_k)\frac{2^{s+1}}{(s+1)!}{Ch}^{s+1}.$$ (3.20)

Even though a greater number of quadrature nodes correspond to the higher order of accuracy, the increase in complexity is a limiting factor. Meanwhile, since the ASMS error is of the order h³, there is no point in a very accurate approximation of (3.20) to too high an order. As a trade-off, we use a two dimensional 3-point Gaussian quadrature over the triangle Ω₀ which is of order 2 [27]. So s = 2 and s_e = 3. The nodes are ( $\frac{1}{6},\frac{1}{6},\frac{1}{3}$) and its permutations. $W_k=\frac{1}{3}$ for k = 1,2,3. Then

$$\mid E\mid \le 2{Ch}^3.$$ (3.21)

Suppose there are N_e patches on Γ, then |E_Q| ≤ 2N_eCh³. So we have the same bound

$${\left|\right|E_{\text{Q}}\left|\right|}_{\infty }\le 2N_e{Ch}^3.$$ (3.22)

3.3.2. Fast summation error

According to the fast summation method described in Section 3.2, the Fourier series is truncated into a finite series

$$E_{\text{FS}}^i:=\sum _{k=1}^N{c}_k\left(\sum _{\mathit{\omega }\in I_{\infty }\backslash I_n}{g}_{\mathit{\omega }}{e}^{2\pi i\mathit{\omega }·({\mathbf{x}}_i-{\mathbf{r}}_k)}\right)=\sum _{k=1}^N{c}_k{T}_k^i$$

where $T_k^i$ denotes the truncation error of the Fourier series. Hence

$$\mid E_{\text{FS}}^i\mid \le {\left|\right|\mathbf{c}\left|\right|}_{\infty }\sum _{k=1}^N\mid T_k^i\mid$$ (3.23)

where ${\left|\right|\mathbf{c}\left|\right|}_{\infty }:=\underset{k=1,\dots ,N}{max}\mid c_k\mid$,

$$\mid T_k^i\mid =\mid \sum _{\mathit{\omega }\in I_{\infty }\backslash I_n}{g}_{\mathit{\omega }}{e}^{2\pi i\mathit{\omega }·({\mathbf{x}}_i-{\mathbf{r}}_k)}\mid \le \sum _{\mathit{\omega }\in I_{\infty }\backslash I_n}\mid g_{\mathit{\omega }}\mid$$ (3.24)

with

$$g_{\mathit{\omega }}={\int }_{\mathrm{\Pi }}g(\mathbf{x})e^{-2\pi i\mathit{\omega }·\mathbf{x}}\text{d}\mathbf{x}$$ (3.25)

and g being the the kernel function in the fast summation. In the Born radii calculation, $g(\mathbf{x})=\frac{1}{\mid \mathbf{x}{\mid }^4}$. As defined in Section 3.2, Π is bounded and excludes 0. Let ω = (ω₁, ω₂, ω₃). Then we rewrite Σ_ω∈I∞\In|g_ω| as

$$\sum _{\mathit{\omega }\in I_{\infty }\backslash I_n}\mid g_{\mathit{\omega }}\mid =\sum _{i,j,k,=0,1}\sum _{{\omega }_1=n+1}^{\infty }\sum _{{\omega }_2=n+1}^{\infty }\sum _{{\omega }_3=n+1}^{\infty }\mid g_{{(-1)}^i{\omega }_1{(-1)}^j{\omega }_2{(-1)}^k{\omega }_3}\mid .$$ (3.26)

By successive integration by parts for each dimension, we get

$$g_{{\omega }_1{\omega }_2{\omega }_3}={\left(\frac{-i}{2\pi {\omega }_1}\right)}^{m_1}{\left(\frac{-i}{2\pi {\omega }_2}\right)}^{m_2}{\left(\frac{-i}{2\pi {\omega }_3}\right)}^{m_3}{\int }_{\mathrm{\Pi }}{D}^{m}g(\mathbf{x})e^{-2\pi i\mathit{\omega }·\mathbf{x}}\text{d}\mathbf{x},$$

where m = m₁ + m₂ + m₃ and $D^{m}g=(\frac{{\partial }^{m_1}}{\partial x^{m_1}}+\frac{{\partial }^{m_2}}{\partial y^{m_2}}+\frac{{\partial }^{m_3}}{\partial z^{m_3}})g$. Therefore

$$\mid g_{{\omega }_1{\omega }_2{\omega }_3}\mid \le \frac{1}{{(2\pi )}^m{\omega }_1^{m_1}{\omega }_2^{m_2}{\omega }_3^{m_3}}{\int }_{\mathrm{\Pi }}\mid D^{m}g(\mathbf{x})\mid \text{d}\mathbf{x}.$$

Let μ_m = ∫_Π |D^mg(x)| dx. We obtain $\mid g_{{\omega }_1{\omega }_2{\omega }_3}\mid \le \frac{{\mu }_m}{{(2\pi )}^m{\omega }_1^{m_1}{\omega }_2^{m_2}{\omega }_3^{m_3}}$. For the other terms in (3.26) we have the same upper bound. If we assume m₁, m₂, m₃ ≥ 2, then

$$\begin{array}{l}\mid T_k^i\mid \le \frac{8{\mu }_m}{{(2\pi )}^m}\left(\sum _{{\omega }_1=n+1}^{\infty }\frac{1}{{\omega }_1^{m_1}}\right)\left(\sum _{{\omega }_2=n+1}^{\infty }\frac{1}{{\omega }_2^{m_2}}\right)\left(\sum _{{\omega }_3=n+1}^{\infty }\frac{1}{{\omega }_3^{m_3}}\right)\\ \le \frac{8{\mu }_m}{{(2\pi )}^m}\left({\int }_n^{\infty }\frac{1}{{\omega }_1^{m_1}}\text{d}{\omega }_1\right)\left({\int }_n^{\infty }\frac{1}{{\omega }_2^{m_2}}\text{d}{\omega }_2\right)\left({\int }_n^{\infty }\frac{1}{{\omega }_3^{m_3}}\text{d}{\omega }_3\right)\\ =\frac{8{\mu }_m}{{(2\pi )}^m(m_1-1)(m_2-1)(m_3-1)n^{m-3}}.\end{array}$$

For m₁ = m₂ = m₃, we have

$$\mid T_k^i\mid \le \frac{8{\mu }_6}{{(2\pi )}^6{n}^3}.$$ (3.27)

Then for (3.24), we have

$$\mid E_{\text{FS}}^i\mid \le {\left|\right|\mathbf{c}\left|\right|}_{\infty }\frac{8{\mu }_{6}N}{{(2\pi )}^6{n}^3}.$$ (3.28)

In fact, the right hand side of (3.28) is independent of i. Therefore we get

$${\left|\right|E_{\text{FS}}\left|\right|}_{\infty }\le {\left|\right|\mathbf{c}\left|\right|}_{\infty }\frac{8{\mu }_{6}N}{{(2\pi )}^6{n}^3}.$$ (3.29)

3.3.3. NFFT error

The error analysis of the NFFT algorithm is thoroughly discussed at the end of Appendix A. This error estimation is derived based on the analysis in [28]. In summary, the NFFT error is split into the aliasing error $E_{\text{NFFT}}^1$ and the truncation error $E_{\text{NFFT}}^2$ [28]:

$${\left|\right|E_{\text{NFFT}}\left|\right|}_{\infty }\le {\left|\right|E_{\text{NFFT}}^1\left|\right|}_{\infty }+{\left|\right|E_{\text{NFFT}}^2\left|\right|}_{\infty }.$$

The error bounds of $E_{\text{NFFT}}^1$ and $E_{\text{NFFT}}^2$ are

$${\left|\right|E_{\text{NFFT}}^1\left|\right|}_{\infty }\le {\left|\right|\widehat{G}\left|\right|}_1\underset{\mathit{\omega }\in I_n}{max}\sum _{\mathbf{i}\in {\mathbb{Z}}^3\backslash \{0\}}\mid \frac{C_{\mathit{\omega }+\mathbf{i}\sigma n}(\xi )}{C_{\mathit{\omega }}(\xi )}\mid ,$$ (3.30)

$${\left|\right|E_{\text{NFFT}}^2\left|\right|}_{\infty }\le \frac{1}{{\sigma }^3{n}^3}\underset{\mathit{\omega }\in I_n}{max}(C_{\mathit{\omega }}^{-1}(\xi )){\left|\right|\widehat{G}\left|\right|}_1\underset{i}{max}\sum _{\mathbf{l}\in I_{\sigma n}}\mid \xi ({\mathbf{x}}_i-\frac{\mathbf{l}}{\sigma n})-\eta ({\mathbf{x}}_i-\frac{\mathbf{1}}{\sigma n})\mid ,$$ (3.31)

where ξ is a 1-periodic window function defined in Appendix A, C_ω (ξ) are the Fourier co-efficients of ξ, and η is a truncated version of ξ. In the fast summation method (3.10), ||Ĝ||₁ = Σ_ω∈In|g_ωa_ω|, where g_ω and a_ω are defined in Section 3.2. Combining (3.30) and (3.31), one obtains

$${\left|\right|E_{\text{NFFT}}\left|\right|}_{\infty }\le C(\xi ,m,\sigma ){\left|\right|\widehat{G}\left|\right|}_1.$$ (3.32)

In [26], the coefficient C(ξ, m, σ) is given for some special ξ. They are

• Gaussian, ξ(x) = (πb)^−1/2e^{−||σnx||2/b}, where $b:=\frac{2\sigma }{2\sigma -1}\frac{m}{\pi }$, the coefficient C(ξ, m, σ) = 4e^{−mπ(1−1/(2σ−1))};

• cardinal central B-splines [29], ξ(x) = M_2m(σnx), the coefficient $C(\xi ,m,\sigma )=4{(\frac{1}{2\sigma -1})}^{2m}$;

• powers of sinc function, $\xi (\mathbf{x})=\frac{n(2\sigma -1)}{2m}{\text{sinc}}^{2m}\left(\frac{(2\sigma -2)n\pi \mathbf{x}}{2m}\right)$, the coefficient $C(\xi ,m,\sigma )=\frac{1}{m-1}\left(\frac{2}{{\sigma }^{2m}}+{(\frac{\sigma }{2\sigma -1})}^{2m}\right)$;

• Kaiser-Bessel function [30]

  $$\begin{array}{l}\xi (\mathbf{x})=\frac{1}{\pi }\{\begin{array}{cc}\frac{sinh(b\sqrt{m^2-{(\sigma n)}^2{\left|\right|\mathbf{x}\left|\right|}^2})}{\sqrt{m^2-{(\sigma n)}^2{\left|\right|\mathbf{x}\left|\right|}^2}},& \left|\right|x\left|\right|\le \frac{m}{\sigma n},\\ \frac{sinh(b\sqrt{{(\sigma n)}^2{\left|\right|\mathbf{x}\left|\right|}^2-m^2})}{\sqrt{{(\sigma n)}^2{\left|\right|\mathbf{x}\left|\right|}^2-m^2}},& \text{otherwise},\end{array}\\ C(\xi ,m,\sigma )=5{\pi }^2{m}^{3/2}\sqrt[4]{1-\frac{1}{\sigma }}{e}^{-m2\pi \sqrt{1-1/\sigma }}.\end{array}$$

3.3.4. NFFT^T error

As we mentioned in Section 3.2, (3.11) is computed by the NFFT^T algorithm and then they are plugged in (3.10) for the following evaluation of the summation. So the NFFT error E_NFFT^T is

$$E_{{\text{NFFT}}^{\text{T}}}=\sum _{\mathit{\omega }\in I_n}{g}_{\mathit{\omega }}{E}_{\mathit{\omega }}{e}^{2\pi i\mathit{\omega }·{\mathbf{x}}_i},$$ (3.33)

where E_ω denotes the error of the NFFT^T algorithm and g_ω is the same as is defined in (3.25). Then we have

$$\mid E_{{\text{NFFT}}^{\text{T}}}\mid \le \sum _{\mathit{\omega }\in I_n}\mid g_{\mathit{\omega }}{E}_{\mathit{\omega }}\mid \le \underset{\mathit{\omega }\in I_n}{max}\mid E_{\mathit{\omega }}\mid \sum _{\mathit{\omega }\in I_n}\mid g_{\mathit{\omega }}\mid ={\left|\right|E_{\mathit{\omega }}\left|\right|}_{\infty }{\left|\right|g\left|\right|}_1$$ (3.34)

with ${\left|\right|E_{\mathit{\omega }}\left|\right|}_{\infty }:=\underset{\mathit{\omega }\in I_n}{max}\mid E_{\mathit{\omega }}\mid$ and ${\left|\right|g\left|\right|}_1:={\displaystyle \sum _{\mathit{\omega }\in I_n}}\mid g_{\mathit{\omega }}\mid$.

As we discussed in Appendix B, the NFFT^T error E_ω is decomposed into the aliasing error ( $E_{\mathit{\omega }}^1$) and the truncation error $(E_{\mathit{\omega }}^2),E_{\mathit{\omega }}=E_{\mathit{\omega }}^1+E_{\mathit{\omega }}^2$. So

$${\left|\right|E_{\mathit{\omega }}\left|\right|}_{\infty }\le {\left|\right|E_{\mathit{\omega }}^1\left|\right|}_{\infty }+{\left|\right|E_{\mathit{\omega }}^2\left|\right|}_{\infty },$$

where ${\left|\right|E_{\mathit{\omega }}^1\left|\right|}_{\infty }=\underset{\mathit{\omega }\in I_n}{max}\mid E_{\mathit{\omega }}^1\mid$ and ${\left|\right|E_{\mathit{\omega }}^2\left|\right|}_{\infty }=\underset{\mathit{\omega }\in I_n}{max}\mid E_{\mathit{\omega }}^2\mid$. Based on the error bounds derived in Appendix B,

$${\left|\right|E_{\mathit{\omega }}^1\left|\right|}_{\infty }\le {\left|\right|\mathbf{c}\left|\right|}_1\underset{\mathit{\omega }\in I_n}{max}\sum _{\mathbf{i}\in {\mathbb{Z}}^3\backslash \{0\}}\frac{C_{\mathit{\omega }+\mathbf{i}\sigma n}(\xi )}{C_{\mathit{\omega }}(\xi )}$$ (3.35)

and

$${\left|\right|E_{\mathit{\omega }}^2\left|\right|}_{\infty }\le \frac{1}{{(\sigma n)}^3}{\left|\right|\mathbf{c}\left|\right|}_1\underset{\mathit{\omega }\in I_n}{max}(C_{\mathit{\omega }}^{-1}(\xi ))\underset{k}{max}\sum _{\mathbf{l}\in I_{\sigma n}}\mid \xi (\frac{\mathbf{l}}{\sigma n}-{\mathbf{r}}_k)-\eta (\frac{\mathbf{l}}{\sigma n}-{\mathbf{r}}_k)\mid$$ (3.36)

where ${\left|\right|\mathbf{c}\left|\right|}_1={\mathrm{\sum }}_{k=1}^N\mid c_k\mid$. Comparing (3.35) with (3.30) and comparing (3.36) with (3.31) yield the error estimation of E_ω which is similar to E_NFFT:

$${\left|\right|E_{\mathit{\omega }}\left|\right|}_{\infty }\le C(\xi ,m,\sigma ){\left|\right|\mathbf{c}\left|\right|}_1.$$

Hence

$$\mid E_{{\text{NFFT}}^{\text{T}}}\mid \le C(\xi ,m,\sigma ){\left|\right|\mathbf{c}\left|\right|}_1{\left|\right|g\left|\right|}_1.$$ (3.37)

The inequality (3.37) is independent of i, therefore,

$${\left|\right|E_{{\text{NFFT}}^{\text{T}}}\left|\right|}_{\infty }\le C(\xi ,m,\sigma ){\left|\right|\mathbf{c}\left|\right|}_1{\left|\right|g\left|\right|}_1.$$ (3.38)

4. Fast solvation force computation

The solvation force acting at the center of atom α, which is part of the forces driving dynamics is

$${\mathbf{F}}_{\alpha }^{\text{elec}}=-\frac{\partial G_{\text{sol}}}{\partial {\mathbf{x}}_{\alpha }}.$$ (4.1)

Partition the solvation energy into polar and non-polar parts:

$$\frac{\partial G_{\text{sol}}}{\partial {\mathbf{x}}_{\alpha }}=\frac{\partial }{\partial {\mathbf{x}}_{\alpha }}(G_{\text{cav}}+G_{\text{vdw}})+\frac{\partial G_{\text{pol}}}{\partial {\mathbf{x}}_{\alpha }}=\gamma \frac{\partial S_A}{\partial {\mathbf{x}}_{\alpha }}+\frac{\partial G_{\text{pol}}}{\partial {\mathbf{x}}_{\alpha }}.$$ (4.2)

The non-polar force is proportional to the derivatives of the volume and/or the surface area with respect to the atomic coordinates. There has been previous work on analytically computing the derivatives of the area/volume [31, 32, 33]. To compute the polar force, we first define

$$G_{ij}=q_i{q}_j/{(r_{ij}^2+R_i{R}_{j}exp(-\frac{r_{ij}^2}{4R_i{R}_j}))}^{1/2}.$$ (4.3)

Then

$$G_{\text{pol}}=-\tau \sum _{i=1}^M\sum _{j=i+1}^M{G}_{ij}-\frac{\tau }{2}\sum _{i=1}^M{G}_{ii}.$$ (4.4)

Differentiating (4.4) w.r.t. x, one gets

$$\frac{\partial G_{\text{pol}}}{\partial {\mathbf{x}}_{\alpha }}=-\tau \sum _{i=1}^M\sum _{j=i+1}^M\frac{\partial G_{ij}}{\partial {\mathbf{x}}_{\alpha }}-\frac{\tau }{2}\sum _{i=1}^M\frac{\partial G_{ii}}{\partial {\mathbf{x}}_{\alpha }},$$ (4.5)

where

$$\frac{\partial G_{ij}}{\partial {\mathbf{x}}_{\alpha }}=\frac{\partial G_{ij}}{\partial r_{ij}}\frac{\partial r_{ij}}{{\mathbf{x}}_{\alpha }}+\frac{\partial G_{ij}}{\partial R_i}\frac{\partial R_i}{{\mathbf{x}}_{\alpha }}+\frac{\partial G_{ij}}{\partial R_j}\frac{\partial R_j}{{\mathbf{x}}_{\alpha }}.$$ (4.6)

From (4.3), one can easily compute $\frac{\partial G_{ij}}{\partial r_{ij}}$ and $\frac{\partial G_{ij}}{\partial R_i}$, which are

$$\begin{array}{l}\frac{\partial G_{ij}}{\partial r_{ij}}=q_i{q}_j{\left(r_{ij}^2+R_i{R}_j{e}^{-\frac{r_{ij}^2}{4R_i{R}_j}}\right)}^{-\frac{3}{2}}\left(\frac{1}{4}{e}^{-\frac{r_{ij}^2}{4R_i{R}_j}}-1\right)r_{ij},\\ \frac{\partial G_{ij}}{\partial R_i}=-\frac{q_i{q}_j}{8R_i}{\left(r_{ij}^2+R_i{R}_j{e}^{-\frac{r_{ij}^2}{4R_i{R}_j}}\right)}^{-\frac{3}{2}}{e}^{-\frac{r_{ij}^2}{4R_i{R}_j}}(4R_i{R}_j+r_{ij}^2).\end{array}$$

$\frac{\partial r_{ij}}{\partial {\mathbf{x}}_{\alpha }}$ is nonzero if i or j = α which will be $\frac{\partial r_{\alpha j}}{\partial {\mathbf{x}}_{\alpha }}=\frac{{\mathbf{x}}_{\alpha }-{\mathbf{x}}_j}{r_{\alpha j}}$. In (4.6) the computation of $\frac{\partial R_i}{{\mathbf{x}}_{\alpha }}$ for i = 1,…,M is not trivial. Because Γ depends on the position of the atoms, it is not easy to compute the derivative of R_i directly from (3.1). To solve this problem, we convert the integration domain back to the volume:

$$R_i^{-1}=\frac{1}{4\pi }{\int }_{\text{ex}}\frac{1}{\mid \mathbf{r}-{\mathbf{x}}_i{\mid }^4}\text{d}\mathbf{r}.$$ (4.7)

Then by defining a volumetric density function to distinguish the exterior from the interior of the molecule, we may have an integration domain that is independent of {x_i}. One way of defining the volumetric function is given in [34] where they first define a density function for each of the atoms

$${\chi }_i(\mathbf{r})=\{\begin{array}{ll}1,\hfill & \left|\right|\mathbf{r}-{\mathbf{x}}_i\left|\right|\le a_i\hfill \\ 0,\hfill & \left|\right|\mathbf{r}-{\mathbf{x}}_i\left|\right|>a_i\hfill \end{array}$$

and then define the volumetric function by following the inclusion-exclusion principle

$$\rho (\mathbf{r})=\sum _i{\chi }_i-\sum _{i<j}{\chi }_i{\chi }_j+\sum _{i<j<k}{\chi }_i{\chi }_j{\chi }_k-\sum _{i<j<k<l}{\chi }_i{\chi }_j{\chi }_k{\chi }_l+\dots .$$ (4.8)

There are some nice properties of this model. For example, the exterior region of the molecule is well characterized by ρ = 0 and two atoms i and j are disconnected if for any r ∈ ℝ³, χ_i(r)χ _j(r) = 0. The drawback of this model is that function χ is not smooth, which makes it inapplicable to the derivative computation. Therefore we smoothen χ by introducing a cubic spline near the atom boundary:

$${\rho }_i(x)=\{\begin{array}{ll}1,\hfill & x\le a_i\hfill \\ \frac{2}{w^3}{(x-a_i)}^3-\frac{3}{w^2}{(x-a_i)}^2+1,\hfill & a_i<x<a_i+w\hfill \\ 0,\hfill & x\ge a_i+w\hfill \end{array}$$ (4.9)

with x =|| r − x_i||. The region defined by ρ_i ≠ 0 is regarded as the interior of atom i and this region converges to the van der Waals volume of the atom as w goes to 0. In the SES model, two atoms are considered to be completely separated if the distance between the centers is greater than the sum of the radii plus the probe diameter. Otherwise they can be connected by the reentrant surface of the rolling probe. By setting w = 1.4 Å, atoms i and j are disconnected in the same sense as in the SES model iff ρ_i(r)ρ_j(r) = 0, for any r ∈ ℝ³. In addition to this modification, we neglect the cases that more than four atoms overlap simultaneously. Therefore the molecular volumetric density function becomes

$$\rho (\mathbf{r})=\sum _i{\rho }_i-\sum _{i<j}{\rho }_i{\rho }_j+\sum _{i<j<k}{\rho }_i{\rho }_j{\rho }_k-\sum _{i<j<k<l}{\rho }_i{\rho }_j{\rho }_k{\rho }_l.$$ (4.10)

We define the complementary function ρ̄ = 1 − ρ. It is easy to show that within the VWS of the molecule, ρ̄ is always 0, beyond the SAS, ρ̄ is always 1, in between, 0 < ρ̄ < 1. Then (4.7) can be rewritten as

$$R_i^{-1}=\frac{1}{4\pi }{\int }_{{ℝ}^3}\frac{\overline{\rho }(\mathbf{r},\{{\mathbf{x}}_j\})}{\mid \mathbf{r}-{\mathbf{x}}_i{\mid }^4}\text{d}\mathbf{r}.$$ (4.11)

Differentiating both sides of (4.11), one gets

$$-\frac{1}{R_i^2}\frac{\partial R_i}{\partial {\mathbf{x}}_{\alpha }}=\frac{1}{4\pi }{\int }_{{ℝ}^3}\frac{\partial }{\partial {\mathbf{x}}_{\alpha }}\left(\frac{\overline{\rho }(\mathbf{r},\{{\mathbf{x}}_j\})}{\mid \mathbf{r}-{\mathbf{x}}_i{\mid }^4}\right)\text{d}\mathbf{r}.$$ (4.12)

So

$$\frac{\partial R_i}{\partial {\mathbf{x}}_{\alpha }}=-\frac{R_i^2}{4\pi }\left({\int }_{{ℝ}^3}\frac{\frac{\partial }{\partial {\mathbf{x}}_{\alpha }}\overline{\rho }(\mathbf{r},\{{\mathbf{x}}_j\})}{\mid \mathbf{r}-{\mathbf{x}}_i{\mid }^4}\text{d}\mathbf{r}+{\int }_{\text{ex}}\frac{\partial }{\partial {\mathbf{x}}_{\alpha }}\frac{1}{\mid \mathbf{r}-{\mathbf{x}}_i{\mid }^4}\text{d}\mathbf{r}\right).$$ (4.13)

For the first integral in (4.13),

$$\frac{\partial }{\partial {\mathbf{x}}_{\alpha }}\overline{\rho }=-\frac{\partial }{\partial {\mathbf{x}}_{\alpha }}\rho =-\frac{\partial {\rho }_{\alpha }}{\partial {\mathbf{x}}_{\alpha }}\left(1-\sum _j{\rho }_j+\sum _{j<k}{\rho }_j{\rho }_k-\sum _{j<k<l}{\rho }_j{\rho }_k{\rho }_l\right)=-\frac{\partial {\rho }_{\alpha }}{\partial {\mathbf{x}}_{\alpha }}{g}_{\alpha },$$

where j, k, l are the atoms overlapping with atom α, g = 1 − Σ_j ρ_j + Σ_j<k ρ_jρ_k − Σ_j<k<l ρ_jρ_kρ_l, and

$$\frac{\partial {\rho }_i}{\partial {\mathbf{x}}_{\alpha }}(\mathbf{r})=\{\begin{array}{ll}0,\hfill & x\le a_{\alpha }\hfill \\ (\frac{6}{w^3}{(x-a_{\alpha })}^2-\frac{6}{w^2}(x-a_{\alpha }))\frac{{\mathbf{x}}_{\alpha }-\mathbf{r}}{x},\hfill & a_{\alpha }<x<a_{\alpha }+w\hfill \\ 0,\hfill & x\ge a_{\alpha }+w\hfill \end{array}$$

with x = ||r − x_α||. Noticing that $\frac{\partial {\rho }_{\alpha }}{\partial {\mathbf{x}}_{\alpha }}\ne 0$ only if a_α < |r − x_α| < a_α + w, the first integral in (4.13) is simplified as

$${\int }_{\mid \mathbf{r}-{\mathbf{x}}_{\alpha }\mid =a_{\alpha }}^{\mid \mathbf{r}-{\mathbf{x}}_{\alpha }\mid =a_{\alpha }+w}-\frac{\partial {\rho }_{\alpha }}{\partial {\mathbf{x}}_{\alpha }}{g}_{\alpha }(\mathbf{r})\frac{1}{\mid \mathbf{r}-{\mathbf{x}}_i{\mid }^4}\text{d}\mathbf{r}.$$ (4.14)

The integration domain of (4.14) is a regular spherical shell of the width w around atom α (Figure 4.1(a)). We switch to the spherical coordinate system:

$$\{\begin{array}{l}x=x_{\alpha }+(a_{\alpha }+r)cos\theta sin\phi \hfill \\ y=y_{\alpha }+(a_{\alpha }+r)sin\theta sin\phi \hfill \\ z=z_{\alpha }+(a_{\alpha }+r)cos\phi \hfill \end{array}$$

where (r, θ, φ) ∈ [0, w] × [0, 2π] × [0, π]. We sample r, θ, φ by using the 2-point Gaussian quadrature nodes in each dimension. For all the atoms in the molecule, they share the same set of sampling points (r, θ, φ).

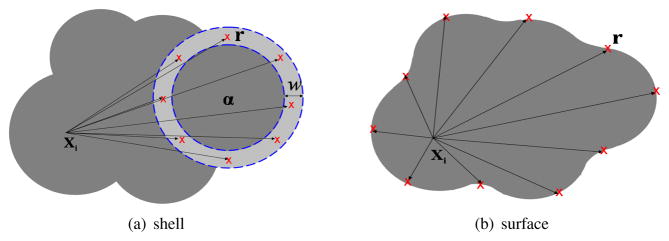
Fig. 4.1 .

When computing the derivatives of the Born radii $\frac{\partial R_i}{\partial {\mathbf{x}}_{\alpha }}$, the quadrature points of the first integral are points within a spherical shell around atom α, as shown in (a), whereas the second integral is necessary when i ≡ α and the quadrature points are points on the surface, as shown in (b). The dark region represents the molecule, the light grey region is the shell of width w around atom α.

The second integral in (4.13) is nonzero if i ≡ α. In that case

$${\int }_{\text{ex}}\frac{\partial }{\partial {\mathbf{x}}_i}\frac{1}{\mid \mathbf{r}-{\mathbf{x}}_i{\mid }^4}\text{d}\mathbf{r}=-{\int }_{\text{ex}}\frac{\partial }{\partial \mathbf{r}}\frac{1}{\mid \mathbf{r}-{\mathbf{x}}_i{\mid }^4}\text{d}\mathbf{r}.$$ (4.15)

We compute each component of (4.15) individually and convert to the surface integration (Figure: 4.1(b)) by the divergence theorem:

$$-{\int }_{\text{ex}}\frac{\partial }{\partial x}\frac{1}{\mid \mathbf{r}-{\mathbf{x}}_i{\mid }^4}\text{d}\mathbf{r}={\int }_{\mathrm{\Gamma }}\frac{n_x(\mathbf{r})}{\mid \mathbf{r}-{\mathbf{x}}_i{\mid }^4}\text{d}S\simeq \sum _{k=1}^N\frac{w_k{n}_x^k}{\mid {\mathbf{r}}_k-{\mathbf{x}}_i{\mid }^4},$$ (4.16)

$$-{\int }_{\text{ex}}\frac{\partial }{\partial y}\frac{1}{\mid \mathbf{r}-{\mathbf{x}}_i{\mid }^4}\text{d}\mathbf{r}={\int }_{\mathrm{\Gamma }}\frac{n_y(\mathbf{r})}{\mid \mathbf{r}-{\mathbf{x}}_i{\mid }^4}\text{d}S\simeq \sum _{k=1}^N\frac{w_k{n}_y^k}{\mid {\mathbf{r}}_k-{\mathbf{x}}_i{\mid }^4},$$ (4.17)

$$-{\int }_{\text{ex}}\frac{\partial }{\partial z}\frac{1}{\mid \mathbf{r}-{\mathbf{x}}_i{\mid }^4}\text{d}\mathbf{r}={\int }_{\mathrm{\Gamma }}\frac{n_z(\mathbf{r})}{\mid \mathbf{r}-{\mathbf{x}}_i{\mid }^4}\text{d}S\simeq \sum _{k=1}^N\frac{w_k{n}_z^k}{\mid {\mathbf{r}}_k-{\mathbf{x}}_i{\mid }^4},$$ (4.18)

where the quadrature weights and points (w_k, r_k) and the unit normals ( $n_x^k,n_y^k,n_z^k$) are the same as those used in Section 3. We compute (4.16), (4.17), and (4.18) by directly applying the fast summation method with the coefficients $c_k=w_k{n}_x^k,w_k{n}_y^k,w_k{n}_z^k$, respectively. Since the same algorithm is used in the Born radius derivative calculation, the error analysis is similar to the error analysis of the Born radius calculation except that a quadrature error of the integration over the shell region needs to be added.

To compute the force acting on each of the M atoms, we need to compute (4.15) for i = 1, …, M. By using the fast summation algorithm, the computational complexity of this part is O(N + M + n³ log n), the same as the energy computation. To compute (4.14), since the shell integration domain is narrow, only a small number of atoms have non-zero densities in this region, therefore the complexity of computing (4.14) for a fixed α for i = 1, …, M is O(M). Moreover, since the integrand in (4.14) is very small if atom i and atom α are far apart, we use a cut-off distance d₀ in our computation and compute (4.14) only if d(i, α) ≤ d₀. Therefore the overall time complexity of computing (4.13) is O(N +M +n³ log n).

5. Results

We compare the polarization energy computed based on the fast summation algorithm and the trivial summation in Table 5.1 for four proteins (PDB ID: 1CGI_l, 1BGX, 1DE4, 1N2C). An ASMS model is constructed for each protein with N_e number of patches. A three-point Gaussian quadrature is used on each algebraic patch. We also compare the overall computation time of the two methods. As we see from the table, for the small proteins (e.g. 1CGI_l), the fast summation method is slower than the trivial summation. However as the protein size gets larger (e.g. 1BGX, 1DE4, 1N2C), the fast summation is apparently faster than the trivial summation without losing too much accuracy. The relative error ε between the fast summation and the trivial summation is small. As for the trade-off between efficiency and accuracy, since in the current research of the MD simulation efficiency is more concerned, the fast-summation-based GB is superior to the trivial GB method.

Table 5.1.

Comparison of the electrostatic solvation energy G_pol (kcal/mol) and computation time (second) of the fast summation method (A) and the trivial summation method (B). M is the number of atoms. N_e is the number of patches, N is the number of integration points. n, σ, and m are parameters in the fast summation method. ε is the relative percentage error $\mid (G_{\mathit{pol}}^A-G_{\mathit{pol}}^B)/G_{\mathit{pol}}^B\mid$.

Protein ID		1CGI_l	1BGX	1DE4	1N2C
M		852	19,647	26,003	39,946
Ne		29,108	112,636	105,288	83,528
N		116,432	450,544	421,152	334,112
n		100	100	100	100
σ		2	2	2	2
m		4	4	4	4
A	Gpol	−1380.988	−19734.848	−25754.552	−41408.959
	timing	86	358	863	631
B	Gpol	−1343.150	−19297.528	−25388.455	−40675.383
	timing	49	4327	5368	9925
ε		2.8%	2.3%	1.4%	1.8%

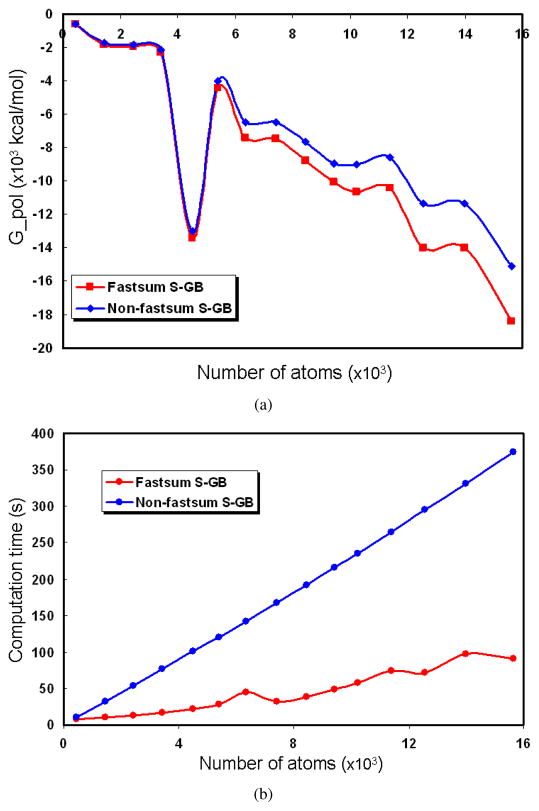
In Figure 5.1 we compare G_pol computed by the fast summation based GB and the trivial summation method along with their computation time for proteins of various sizes. For all these proteins, we generate the ASMS of the same number of patches (in our test we use 20,000 patches for each protein). We choose the fixed parameters n = 30, m = 4, and σ = 2 for all the proteins. We observe that the G_pol computed by the fastsum GB is close to that computed by the trivial GB methods and the error gets larger as the molecule gets bigger. Even though the error analysis in Section 3.3 does not show that the error depends on the size of the molecule, the analysis is based on the assumption that the kernel function is defined on the domain ${[-\frac{1}{2},\frac{1}{2}]}^3$. To ensure that x_i − r_k, i = 1, …, M, k = 1, …, N are all within this range, we scale the molecule. The larger the molecule, the larger the scaling factor. Later on when we scale back to the original coordinates by multiplying the scaling factor, the error gets amplified. As we expect, computation time of the fastsum GB increases as M becomes large but is much faster than the traditional GB method.

Fig. 5.1 .

In (a) we compare G_pol computed by the fastsum GB and the non-fastsum GB for various proteins containing different number of atoms. In (b) we compare the computation time of the two methods.

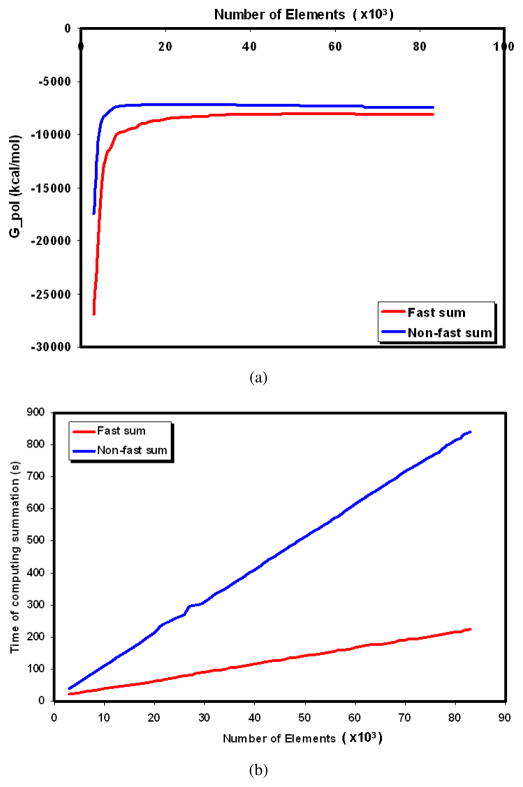
In Figure 5.2, we compare G_pol computed by the fast summation based GB versus the trivial summation method and the computation time for a test protein 1JPS where we generate the ASMS with different numbers of patches. We use the same values for the parameters n, m, and σ as in the previous test. As shown in the figure, as the triangular mesh becomes denser, the fast summation result converges rapidly to the result of the trivial method but takes less computation time.

Fig. 5.2 .

For protein 1JPS, in (a) we compare G_pol computed by the fastsum GB and the non-fastsum GB with various number of surface elements. In (b) we compare the computation time of the two methods.

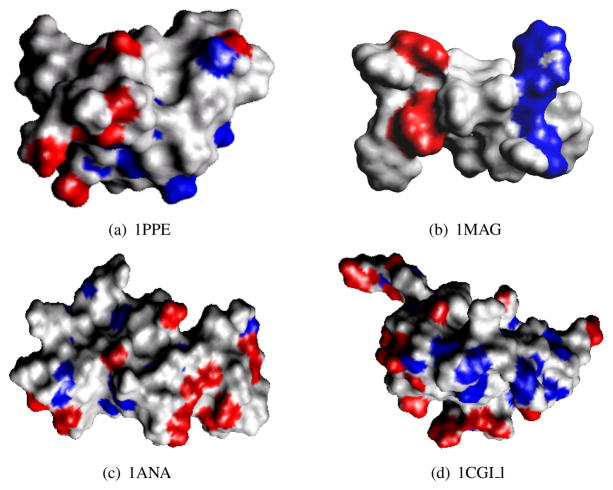
For the test proteins 1ANA, 1MAG, 1PPE_l, 1CGI_l, we compute the solvation force ${\mathbf{F}}_{\alpha }^{\text{elec}}$, for α = 1, …, M. We show the timing results in Table 5.2. In general, if an atom has a strong solvation force, this atom is in favor of being polarized, and hence is an active atom. On the contrary, if an atom has a weak solvation force, it is more likely to be an inactive atom. For every test protein, after we compute the solvation force for each atom, we sort the forces based on their magnitude and choose the top most active atoms and the top inactive atoms. As shown in Figure 5.3, the top 5% of the most active atoms are rendered in red and the bottom 5% of the atoms are rendered in blue. This provides a convenient and cheaper way, alternative to the experimental method, to help the biologists quickly find an active site of a protein.

Table 5.2.

Force calculation timing: M is the number of atoms, N is the number of triangles in the surface triangular mesh, t₁ is the time (in seconds) for computing (4.15) for i = 1, …, M and t₂ is the time for computing the rest of the terms in (4.6) for i, j, α = 1,…, M. T_total is the overall timing.

Protein ID	M	N	t1 (s)	t2 (s)	Ttotal (s)
1ANA	249	6,676	66.05	0.14	66.19
1MAG	544	7,328	69.58	0.23	69.81
1PPE_l	436	5,548	59.55	0.56	60.11
1CGI_l	852	6,792	68.71	3.27	71.98

Fig. 5.3 .

Atoms that have the greatest electrostatic solvation force (top 5%) are colored in red; atoms that have the weakest electrostatic solvation force (bottom 5%) are colored in blue.

6. Conclusion

We introduce a fast summation based algorithm to calculate the effective Born radii and their derivatives in the generalized Born model of implicit solvation. The algorithm relies on a variation of the formulation for the Born radii and an additional analytical volumetric density function for the derivatives. For a system of M atoms and N sampling points on the molecular surface, the trivial way of computing the Born radii requires O(MN) arithmetic operations, whereas with the aids of the Fourier expansion of the kernel functions of the Born radii (and their derivatives) and the NFFT algorithm which essentially approximates the complex exponentials in the NDFT by the DFT of a fast decaying smooth window function, the Born radii as well as their derivatives can be obtained at cost of (M +N +n³ log n) where n is the number of frequencies in the Fourier expansion. We show that the error of the algorithm decreases as the mesh gets denser, or as any of the parameters σ, m, n increase. Other than the Born model developed with a Coulomb field approximation, there has been other models for the Born radii evaluation, for example the Kirkwood-Grycuk model [35] where $R_i^{-1}={\left(\frac{3}{4\pi }{\int }_{\text{ex}}\frac{1}{\mid \mathbf{r}-{\mathbf{x}}_i{\mid }^6}\text{d}\mathbf{r}\right)}^{1/3}$. This model is recently applied to the GBr⁶NL model which approximates the solvation energy of the nonlinear Poisson-Boltzmann equation [36]. It is interesting to note that we can utilize a similar quadrature point generation via ASMS and the fast summation algorithm to speed up this GBr⁶NL computation. In fact, by the divergence theorem, ${\int }_{\text{ex}}\frac{1}{\mid \mathbf{r}-{\mathbf{x}}_i{\mid }^6}\text{d}\mathbf{r}=\frac{1}{3}{\int }_{\mathrm{\Gamma }}\frac{(\mathbf{r}-{\mathbf{x}}_i)·\mathbf{n}(\mathbf{r})}{\mid \mathbf{r}-{\mathbf{x}}_i{\mid }^6}\text{d}\mathbf{r}$ and the rest follows similar to the methods in this paper.

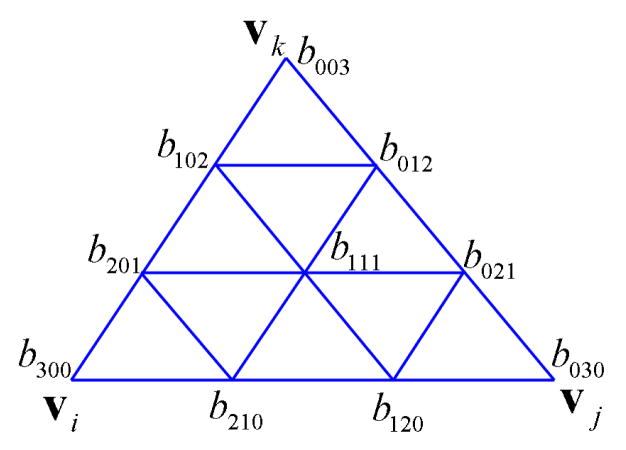
Fig. 2.2 .

The control coefficients of the cubic Bernstein-Bezier basis of function F

Appendix A. NFFT

The NFFT [28] is an algorithm for fast computation of multivariate discrete Fourier transforms for nonequispaced data in spacial domain (NDFT¹). The NDFT¹ problem is to evaluate the trigonometric polynomials

$$G({\mathbf{x}}_j)=\sum _{\mathit{\omega }\in I_n}{G}_{\mathit{\omega }}{e}^{2\pi \text{i}\mathit{\omega }·{\mathbf{x}}_j}j=1,\dots ,M,$$ (A.1)

where $I_n=\{({\omega }_1,{\omega }_2,{\omega }_3)\in {\mathbb{Z}}^3:-\frac{n}{2}\le {\omega }_i\le \frac{n}{2}\}$. Without loss of generality, we assume ${\mathbf{x}}_j\in {[-\frac{1}{2},\frac{1}{2}]}^3$. Instead of computing the summations in (A.1) directly, one can approximate G by a function s(x) which is a linear combination of the shifted 1-periodic kernel function ξ:

$$s(\mathbf{x}):=\sum _{\mathbf{l}\in I_{\sigma n}}{g}_{\mathbf{l}}\xi (\mathbf{x}-\frac{\mathbf{l}}{\sigma n}),$$ (A.2)

where $I_{\sigma n}:=\{(l_1,l_2,l_3):l_i\in [-\frac{\sigma n}{2},\frac{\sigma n}{2}]\cap \mathbb{Z},\sigma >1\}$ and $\frac{\mathbf{l}}{\sigma n}:=\{(\frac{l_1}{\sigma n},\frac{l_2}{\sigma n},\frac{l_3}{\sigma n})\}$. We have σ > 1 because of the error estimation discussed in Section 3.3.3.

The kernel function ξ is defined as

$$\xi (\mathbf{x}):=\sum _{\mathbf{i}\in {\mathbb{Z}}^3}{\xi }_0(\mathbf{x}+\mathbf{i}),\text{where}{\xi }_0\in L_2({ℝ}^3).$$

Good candidates for ξ₀ include Gaussian, B-spline, sinc, and Kaiser-Bessel functions. Expand the periodic kernel function ξ by its Fourier series

$$\xi (\mathbf{x})=\sum _{\mathit{\omega }\in {\mathbb{Z}}^3}{C}_{\mathit{\omega }}(\xi )e^{2\pi i\mathit{\omega }·\mathbf{x}},$$ (A.3)

with the Fourier coefficients

$$C_{\mathit{\omega }}(\xi ):={\int }_{{[-\frac{1}{2},\frac{1}{2}]}^3}\xi (\mathbf{x})e^{-2\pi i\mathit{\omega }·\mathbf{x}}\text{d}\mathbf{x}={\int }_{{ℝ}^3}{\xi }_0(\mathbf{x})e^{-2\pi i\mathit{\omega }·\mathbf{x}}\text{d}\mathbf{x}={\widehat{\xi }}_0(\mathit{\omega }).$$

Cut off the higher frequencies in (A.3), one can get

$$\xi (\mathbf{x})=\left(\sum _{\mathit{\omega }\in I_{\sigma n}}+\sum _{\mathit{\omega }\in {\mathbb{Z}}^3\backslash I_{\sigma n}}\right)C_{\mathit{\omega }}(\xi )e^{2\pi i\mathit{\omega }·\mathbf{x}}\approx \sum _{\mathit{\omega }\in I_{\sigma n}}{C}_{\mathit{\omega }}(\xi )e^{2\pi i\mathit{\omega }·\mathbf{x}}.$$ (A4.)

Plug (A.4) into (A.2), we get

$$\begin{array}{l}s({\mathbf{x}}_j)\approx \sum _{\mathbf{l}\in I_{\sigma n}}{g}_{\mathbf{l}}\sum _{\mathit{\omega }\in I_{\sigma n}}{C}_{\mathit{\omega }}(\xi )e^{2\pi i\mathit{\omega }·({\mathbf{x}}_j-\frac{\mathbf{l}}{\sigma n})}\\ =\sum _{\mathit{\omega }\in I_{\sigma n}}{\stackrel{\sim }{G}}_{\mathit{\omega }}{C}_{\mathit{\omega }}(\xi )e^{2\pi i\mathit{\omega }·{\mathbf{x}}_j},\end{array}$$ (A.5)

with the coefficients

$${\stackrel{\sim }{G}}_{\mathit{\omega }}:=\sum _{\mathbf{l}\in I_{\sigma n}}{g}_{\mathbf{l}}{e}^{-2\pi i\mathit{\omega }·\frac{\mathbf{l}}{\sigma n}}.$$ (A.6)

By defining

$${\stackrel{\sim }{G}}_{\mathit{\omega }}:=\{\begin{array}{ll}\frac{G_{\mathit{\omega }}}{C_{\mathit{\omega }}(\xi )}\hfill & \text{for}\mathit{\omega }\in I_n,\hfill \\ 0\hfill & \text{for}\mathit{\omega }\in I_{\sigma n}\backslash I_n,\hfill \end{array}$$ (A.7)

one can immediately get

$$s({\mathbf{x}}_j)\approx \sum _{\mathit{\omega }\in I_n}{G}_{\mathit{\omega }}{e}^{2\pi \text{i}\mathit{\omega }·{\mathbf{x}}_j}=G({\mathbf{x}}_j).$$ (A.8)

The next problem is to compute g_l. From (A.6), one can compute the coefficients g_l which are also coefficients in (A.8) by the discrete Fourier transform

$$g_{\mathbf{l}}=\frac{1}{{\sigma }^3{n}^3}\sum _{\mathit{\omega }\in I_{\sigma n}}{\stackrel{\sim }{G}}_{\mathit{\omega }}{e}^{2\pi \text{i}\mathit{\omega }·\frac{\mathbf{l}}{\sigma n}}=\frac{1}{{\sigma }^3{n}^3}\sum _{\mathit{\omega }\in I_n}\frac{G_{\mathit{\omega }}}{C_{\mathit{\omega }}(\xi )}{e}^{2\pi \text{i}\mathit{\omega }·\frac{\mathbf{l}}{\sigma n}},\mathbf{l}\in I_{\sigma n},$$ (A.9)

with complexity O(n³ log n) by the FFT algorithm.

Since the function ξ drops very fast, one can further reduce the computation complexity of (A.8) by cutting off the tail of ξ. Define a function η₀:

$${\eta }_0:={\xi }_0(\mathbf{x}){\chi }_{{[-\frac{m}{\sigma n},\frac{m}{\sigma n}]}^3}(\mathbf{x})\text{where}m\ll \sigma n,m\in \mathbb{N}.$$

Construct the one-periodic function η the same way as ξ is constructed:

$$\eta (\mathbf{x})=\sum _{\mathbf{i}\in {\mathbb{Z}}^3}{\eta }_0(\mathbf{x}+\mathbf{i}).$$

Replacing ξ with η in (A.8), we obtain that

$$G({\mathbf{x}}_j)\approx \sum _{\mathbf{l}\in I_{\sigma n,m}({\mathbf{x}}_j)}{g}_{\mathbf{l}}\eta ({\mathbf{x}}_j-\frac{\mathbf{l}}{\sigma n}),$$ (A.10)

where I_σn,m(x_j) = {(l₁, l₂, l₃): σnx_j,i − m ≤ l_i ≤ σnx_j,i + m, i = 1, 2, 3}. There are at most (2m + 1)³ nonzero terms in (A.10). Therefore the complexity of evaluating (A.10) for j = 1, …, M is O(m³M). Adding the complexity of computing the coefficients g_l, the overall complexity of NFFT algorithm is O(n³ log n + m³M).

Remark

If we reorganize the above equations, it is not hard to see that, in fact, (A.1) is approximately computed by the expression

$$G({\mathbf{x}}_j)=\sum _{\mathit{\omega }\in I_n}{G}_{\mathit{\omega }}\left(\frac{1}{{(\sigma n)}^3{C}_{\mathit{\omega }}(\xi )}\sum _{\mathbf{l}\in I_{\sigma n}}\eta ({\mathbf{x}}_j-\frac{\mathbf{l}}{\sigma n})e^{2\pi \text{i}\mathit{\omega }·\frac{\mathbf{l}}{\sigma n}}\right).$$ (A.11)

From a linear algebra point of view, equation (A.11) can be written as the product of a matrix and a vector. For example, for a one dimensional NFFT, (A.11) is equivalent to

$$\mathbf{g}=\mathrm{\Xi }FD\widehat{\mathbf{g}}$$ (A.12)

with vectors

$$\mathbf{g}:={[G(x_i)]}_{i=1}^M,\widehat{\mathbf{g}}:={[G_{\omega }]}_{\omega =-\frac{n}{2}}^{\frac{n}{2}-1}.$$

Ξ is a sparse matrix

$$\mathrm{\Xi }:={\left[\eta (x_i-\frac{l_j}{\sigma n})\right]}_{M\times \sigma n},$$

F is the classical Fourier matrix

$$F:={\left[e^{2\pi \text{i}{\omega }_j\frac{l_i}{\sigma n}}\right]}_{\sigma n\times n},$$

and D is an n × n diagonal matrix with the iith element being $\frac{1}{\sigma n{C}_{{\omega }_i}(\xi )}$. For a multi-dimensional NFFT, it is the same as the 1D case as long as one orders the indices of the multi-dimension into one dimension.

As discussed in [28], in the first approximation (A.8), we see that s is equal to G after its higher frequencies in the Fourier series are cut off. Hence the error introduced in (A.8) which is known as the aliasing error is

$$\begin{array}{l}{E}_{\text{NFFT}}^1:=\sum _{\mathbf{l}\in I_{\sigma n}}{g}_{\mathbf{l}}\xi ({\mathbf{x}}_j-\frac{\mathbf{l}}{\sigma n})-G({\mathbf{x}}_j)\\ =\sum _{\mathbf{i}\in {\mathbb{Z}}^3\backslash \{0\}}\sum _{\mathit{\omega }\in I_{\sigma n}}{\stackrel{\sim }{G}}_{\mathit{\omega }+\mathbf{i}\sigma n}{C}_{\mathit{\omega }+\mathbf{i}\sigma n}(\xi )e^{2\pi \text{i}(\mathit{\omega }+\mathbf{i}\sigma n)·{\mathbf{x}}_j}.\end{array}$$ (A.13)

Note that from (A.6), we have the condition G̃_ω+iσn = G̃_ω, for i ∈ ℤ³ and ω ∈ I_σn. By the definition (A.7), one obtains

$$\mid E_{\text{NFFT}}^1\mid \le \sum _{\mathbf{i}\in {\mathbb{Z}}^3\backslash \{0\}}\sum _{\mathit{\omega }\in I_n}\mid G_{\mathit{\omega }}\frac{C_{\mathit{\omega }+\mathbf{i}\sigma n}(\xi )}{C_{\mathit{\omega }}(\xi )}\mid .$$ (A.14)

Let ${\left|\right|\widehat{G}\left|\right|}_1={\displaystyle \sum _{\mathit{\omega }\in I_n}}\mid G_{\mathit{\omega }}\mid$. Then

$$\mid E_{\text{NFFT}}^1\mid \le {\left|\right|\widehat{G}\left|\right|}_1\underset{\mathit{\omega }\in I_n}{max}\sum _{\mathbf{i}\in {\mathbb{Z}}^3\backslash \{0\}}\mid \frac{C_{\mathit{\omega }+\mathbf{i}\sigma n}(\xi )}{C_{\mathit{\omega }}(\xi )}\mid .$$ (A.15)

In the second approximation (A.10), since ξ is replaced by η, the so caused error, known as the truncation error, is

$$\begin{array}{l}{E}_{\text{NFFT}}^2:=\sum _{\mathbf{l}\in I_{\sigma n}}{g}_{\mathbf{l}}\xi (\mathbf{x}-\frac{\mathbf{l}}{\sigma n})-\sum _{\mathbf{l}\in I_{\sigma n,m}}{g}_{\mathbf{l}}\eta (\mathbf{x}-\frac{\mathbf{l}}{\sigma n})\\ =\sum _{\mathbf{l}\in I_{\sigma n}\backslash I_{\sigma n,m}}{g}_{\mathbf{l}}[\xi (\mathbf{x}-\frac{\mathbf{l}}{\sigma n})-\eta (\mathbf{x}-\frac{\mathbf{l}}{\sigma n})]\\ =\sum _{\mathbf{l}\in I_{\sigma n}\backslash I_{\sigma n,m}}\frac{1}{{\sigma }^3{n}^3}\sum _{\mathit{\omega }\in I_n}\frac{G_{\mathit{\omega }}}{C_{\mathit{\omega }}(\xi )}{e}^{2\pi i\mathit{\omega }·\frac{\mathbf{l}}{\sigma n}}[\xi (\mathbf{x}-\frac{\mathbf{l}}{\sigma n})-\eta (\mathbf{x}-\frac{\mathbf{l}}{\sigma n})].\end{array}$$ (A.16)

Thus

$$\begin{array}{l}\mid E_{\text{NFFT}}^2\mid \le \frac{1}{{\sigma }^3{n}^3}\sum _{\mathbf{l}\in I_{\sigma n}}\mid \frac{G_{\mathit{\omega }}}{C_{\mathit{\omega }}(\xi )}[\xi (\mathbf{x}-\frac{\mathbf{l}}{\sigma n})-\eta (\mathbf{x}-\frac{\mathbf{l}}{\sigma n})]\mid \\ \le \frac{1}{{\sigma }^3{n}^3}\underset{\mathit{\omega }\in I_n}{max}(C_{\mathit{\omega }}^{-1}(\xi )){\left|\right|\widehat{G}\left|\right|}_1\sum _{\mathbf{l}\in I_{\sigma n}}\mid \xi (\mathbf{x}-\frac{\mathbf{l}}{\sigma n})-\eta (\mathbf{x}-\frac{\mathbf{l}}{\sigma n})\mid .\end{array}$$ (A.17)

Appendix B. NFFT^T

The NFFT^T algorithm deals with the fast computation of multivariate discrete Fourier transforms for nonequispaced data in frequency domain (NDFT²):

$$a(\mathit{\omega })=\sum _{k=1}^N{c}_k{e}^{-2\pi \text{i}\mathit{\omega }·{\mathbf{r}}_k},\mathit{\omega }\in I_n.$$ (B.1)

Define a function

$$A(\mathbf{x}):=\sum _{k=1}^N{c}_k\xi (\mathbf{x}-{\mathbf{r}}_k),$$ (B.2)

where ξ is defined as same as in Appendix A. The Fourier series of A(x) is:

$$A(\mathbf{x})=\sum _{\mathit{\omega }\in {\mathbb{Z}}^3}{C}_{\mathit{\omega }}(A)e^{2\pi \text{i}\mathit{\omega }·\mathbf{x}}.$$ (B.3)

On the other hand,

$$\sum _{k=1}^N{c}_k\xi (\mathbf{x}-{\mathbf{r}}_k)=\sum _{k=1}^N{c}_k\sum _{\mathit{\omega }\in {\mathbb{Z}}^3}{C}_{\mathit{\omega }}(\xi )e^{2\pi i\mathit{\omega }·(\mathbf{x}-{\mathbf{r}}_k)}.$$ (B.4)

Hence we get the relationship of Fourier coefficients of A and ξ:

$$C_{\mathit{\omega }}(A)=\sum _{k=1}^N{c}_k{e}^{-2\pi \text{i}\mathit{\omega }·{\mathbf{r}}_k}{C}_{\mathit{\omega }}(\xi ),\mathit{\omega }\in {\mathbb{Z}}^3.$$ (B.5)

Comparing (B.5) with (B.1) one obtains

$$a(\mathit{\omega })=\frac{C_{\mathit{\omega }}(A)}{C_{\mathit{\omega }}(\xi )},\mathit{\omega }\in I_n.$$ (B.6)

It remains to compute C_ω (A). By definition,

$$\begin{array}{l}{C}_{\mathit{\omega }}(A)={\int }_{{[-\frac{1}{2},\frac{1}{2}]}^3}A(\mathbf{x})e^{-2\pi \text{i}\mathit{\omega }·\mathbf{x}}\text{d}\mathbf{x}\\ ={\int }_{{[-\frac{1}{2},\frac{1}{2}]}^3}\left(\sum _{k=1}^N{c}_k\xi (\mathbf{x}-{\mathbf{r}}_k)\right)e^{-2\pi \text{i}\mathit{\omega }·\mathbf{x}}\text{d}\mathbf{x}\\ =\sum _{k=1}^N{c}_k{\int }_{{[-\frac{1}{2},\frac{1}{2}]}^3}\xi (\mathbf{x}-{\mathbf{r}}_k)e^{-2\pi \text{i}\mathit{\omega }·\mathbf{x}}\text{d}\mathbf{x}.\end{array}$$ (B.7)

Discretizing the integration in (B.7) by the left rectangular rule leads to

$$a(\mathit{\omega })\approx \frac{1}{C_{\mathit{\omega }}(\xi )}\sum _{k=1}^N{c}_k\frac{1}{{(\sigma n)}^3}\sum _{\mathbf{l}\in I_{\sigma n}}\xi (\frac{\mathbf{l}}{\sigma n}-{\mathbf{r}}_k)e^{-2\pi \text{i}\mathit{\omega }·\frac{\mathbf{l}}{\sigma n}}.$$ (B.8)

Replacing ξ with η yields

$$a(\mathit{\omega })\approx \frac{1}{{(\sigma n)}^3}\frac{1}{C_{\mathit{\omega }}(\xi )}\sum _{\mathbf{l}\in I_{\sigma n}}{\widehat{g}}_{\mathbf{l}}{e}^{-2\pi \text{i}\mathit{\omega }·\frac{\mathbf{l}}{\sigma n}},$$ (B.9)

where

$${\widehat{g}}_{\mathbf{l}}:=\sum _{k=1}^N{c}_k\eta (\frac{\mathbf{l}}{\sigma n}-{\mathbf{r}}_k),\mathbf{l}\in I_{\sigma n}.$$ (B.10)

To compute ĝ_l, if one scans the r_k list, then for each r_k there are at most (2m + 1)³ grid points (l) that contribute nonzero η. Hence, the complexity of computing ĝ_l is O(m³N). After computing ĝ_l one can easily evaluate (B.9) by the FFT algorithm at the complexity of O(n³ log n). Lastly the complexity of computing (B.6) is O(n³). So the overall complexity of the NFFT^T algorithm is O(m³N +n³ log n).

Remark

Similar to the NFFT algorithm, we may write the one-line formula for computing (B.1) by the NFFT^T:

$$a(\mathit{\omega })=\sum _{k=1}^N{c}_k\left(\frac{1}{{(\sigma n)}^3{C}_{\mathit{\omega }}(\xi )}\sum _{\mathbf{l}\in I_{\sigma n}}\eta (\frac{\mathbf{l}}{\sigma n}-{\mathbf{r}}_k)e^{-2\pi \text{i}\mathit{\omega }·\frac{\mathbf{l}}{\sigma n}}\right),$$ (B.11)

which in one dimension is equivalent to the linear system:

$$\widehat{\mathbf{a}}=D^{\text{T}}{F}^{\ast }{\mathrm{\Xi }}^{\text{T}}\mathbf{c}$$ (B.12)

with vectors

$$\widehat{\mathbf{a}}:={[a(\omega )]}_{\omega =-\frac{n}{2}}^{\frac{n}{2}},\mathbf{c}:={[c_k]}_{k=1}^N.$$

Matrix Ξ is similar to that defined in Appendix A

$$\mathrm{\Xi }:={\left[\eta (\frac{l_j}{\sigma n}-r_i)\right]}_{N\times \sigma n}.$$

F^* is the conjugate transpose of the Fourier matrix F, and D is the same as that defined in Appendix A. From the matrix expression, we see why the algorithm is called the “transpose” of NFFT.

Let E_ω designate the error of a(ω). E_ω can also be split into the aliasing error $E_{\mathit{\omega }}^1$ introduced in (B.8) and the truncation error $E_{\mathit{\omega }}^2$ introduced in (B.9), $E_{\mathit{\omega }}=E_{\mathit{\omega }}^1+E_{\mathit{\omega }}^2$, for ω ∈ I_σn. By taking the Fourier expansion of ξ, we get form (B.8), so

$$\begin{array}{l}{E}_{\mathit{\omega }}^1=a(\mathit{\omega })=\frac{1}{C_{\mathit{\omega }}(\xi )}\sum _{k=1}^N{c}_k\frac{1}{{(\sigma n)}^3}\sum _{\mathbf{l}\in I_{\sigma n}}\left(\sum _{\mathbf{j}\in {\mathbb{Z}}^3}{C}_{\mathbf{j}}(\xi )e^{2\pi \text{i}(\frac{\mathbf{l}}{\sigma n}-{\mathbf{r}}_k)·\mathbf{j}}\right)e^{-2\pi \text{i}\mathit{\omega }·\frac{\mathbf{l}}{\sigma n}}\\ =a(\mathit{\omega })-\frac{1}{C_{\mathit{\omega }}(\xi )}\sum _{k=1}^N{c}_k\sum _{\mathbf{j}\in {\mathbb{Z}}^3}{C}_{\mathbf{j}}(\xi )e^{-2\pi \text{i}{\mathbf{r}}_k·\mathbf{j}}\frac{1}{{(\sigma n)}^3}\sum _{\mathbf{l}\in I_{\sigma n}}{e}^{2\pi \text{i}(\mathbf{j}-\mathit{\omega })·\frac{\mathbf{l}}{\sigma n}}.\end{array}$$

Since

$$\frac{1}{{(\sigma n)}^3}\sum _{\mathbf{l}\in I_{\sigma n}}{e}^{2\pi \text{i}(\mathbf{j}-\mathit{\omega })·\frac{\mathbf{l}}{\sigma n}}=\{\begin{array}{ll}1,\hfill & \text{if}\mathbf{j}-\mathit{\omega }=\mathbf{i}\sigma n,\mathbf{i}\in {\mathbb{Z}}^3,\hfill \\ 0,\hfill & \text{otherwise},\hfill \end{array}$$

we have,

$$E_{\mathit{\omega }}^1=a(\mathit{\omega })-\frac{1}{C_{\mathit{\omega }}(\xi )}\sum _{k=1}^N{c}_k\sum _{\mathbf{i}\in {\mathbb{Z}}^3}{C}_{\mathit{\omega }+\mathbf{i}\sigma n}(\xi )e^{-2\pi \text{i}{\mathbf{r}}_k·(\mathit{\omega }+\mathbf{i}\sigma n)}.$$ (B.13)

By (B.1),

$$E_{\mathit{\omega }}^1=\frac{1}{C_{\mathit{\omega }}(\xi )}\sum _{k=1}^N{c}_k\sum _{\mathbf{i}\in {\mathbb{Z}}^3\backslash \{0\}}{C}_{\mathit{\omega }+\mathbf{i}\sigma n}(\xi )e^{-2\pi \text{i}{\mathbf{r}}_k·(\mathit{\omega }+\mathbf{i}\sigma n)}.$$ (B.14)

Define ${\left|\right|\mathbf{c}\left|\right|}_1={\sum }_{k=1}^N\mid c_k\mid$. Then we have

$$\mid E_{\mathit{\omega }}^1\mid \le {\left|\right|\mathbf{c}\left|\right|}_1\sum _{\mathbf{i}\in {\mathbb{Z}}^3\backslash \{0\}}\frac{C_{\mathit{\omega }+\mathbf{i}\sigma n}(\xi )}{C_{\mathit{\omega }}(\xi )}.$$ (B.15)

In (B.9), the truncation error

$$E_{\mathit{\omega }}^2=\sum _{k=1}^N{c}_k\left(\frac{1}{{(\sigma n)}^3{C}_{\mathit{\omega }}(\xi )}\sum _{\mathbf{l}\in I_{\sigma n}}[\xi ({\mathbf{r}}_k-\frac{\mathbf{l}}{\sigma n})-\eta ({\mathbf{r}}_k-\frac{\mathbf{l}}{\sigma n})]e^{-2\pi \text{i}\mathit{\omega }·\frac{\mathbf{l}}{\sigma n}}\right),$$ (B.16)

which has the bound

$$\mid E_{\mathit{\omega }}^2\mid \le \frac{1}{{(\sigma n)}^3}{\left|\right|\mathbf{c}\left|\right|}_1\frac{1}{C_{\mathit{\omega }}(\xi )}\underset{k}{max}\sum _{\mathbf{l}\in I_{\sigma n}}\mid \xi (\frac{\mathbf{l}}{\sigma n}-{\mathbf{r}}_k)-\eta (\frac{\mathbf{l}}{\sigma n}-{\mathbf{r}}_k)\mid .$$ (B.17)

Appendix C. Continuity of f

As defined in Section 3.3.1,

$$f=\frac{(\mathbf{r}-{\mathbf{x}}_i)·\mathbf{n}(\mathbf{r})}{\mid \mathbf{r}-{\mathbf{x}}_i{\mid }^4},$$ (C.1)

where r ≠ x_i and n = ∇F with F given in (2.2). r(b₁, b₂, λ) is simply defined in (2.3). In this appendix, we mainly discuss the continuity of n. As derived in [22],

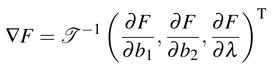(C.2)

where

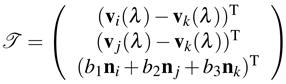is a nonsingular matrix. Hence n is well defined. Consider ( $\frac{\partial \mathbf{n}}{\partial b_1},\frac{\partial \mathbf{n}}{\partial b_2}$):

$$\left(\frac{\partial \mathbf{n}}{\partial b_1},\frac{\partial \mathbf{n}}{\partial b_2}\right)=\left(\begin{array}{lll}{F}_{xx}\hfill & F_{xy}\hfill & F_{xz}\hfill \\ F_{xy}\hfill & F_{yy}\hfill & F_{yz}\hfill \\ F_{xz}\hfill & F_{yz}\hfill & F_{zz}\hfill \end{array}\right)\left(\begin{array}{cc}\frac{\partial x}{\partial b_1}& \frac{\partial x}{\partial b_2}\\ \frac{\partial y}{\partial b_1}& \frac{\partial y}{\partial b_2}\\ \frac{\partial z}{\partial b_1}& \frac{\partial z}{\partial b_2}\end{array}\right).$$

Let $\nu ={\left(\frac{\partial F}{\partial b_1},\frac{\partial F}{\partial b_2},\frac{\partial F}{\partial \lambda }\right)}^{\text{T}}$. We have

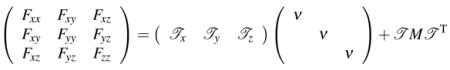(C.3)

where 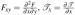, and

$$M=\left(\begin{array}{lll}{F}_{b_1{b}_1}\hfill & F_{b_1{b}_2}\hfill & F_{b_1\lambda }\hfill \\ F_{b_1{b}_2}\hfill & F_{b_2{b}_2}\hfill & F_{b_2\lambda }\hfill \\ F_{b_1\lambda }\hfill & F_{b_2\lambda }\hfill & F_{\lambda \lambda }\hfill \end{array}\right).$$ (C.4)

To show 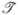is differentiable, we take the first row of 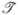and compute its derivative with respect to x, i.e. ( $\frac{{\partial }^2{b}_1}{\partial x^2}\frac{{\partial }^2{b}_2}{\partial x^2}\frac{{\partial }^2\lambda }{\partial x^2}$) as an example. We write (2.3) in the form of

$$\{\begin{array}{l}x=x(b_1,b_2,\lambda ),\hfill \\ y=y(b_1,b_2,\lambda ),\hfill \\ z=z(b_1,b_2,\lambda ).\hfill \end{array}$$ (C.5)

Taking the second derivatives of both sides of (C.5) with respect to x, we get

$$0=C_f+\frac{\partial x}{\partial b_1}\frac{{\partial }^2{b}_1}{\partial x^2}+\frac{\partial x}{\partial b_2}\frac{{\partial }^2{b}_2}{\partial x^2}+\frac{\partial x}{\partial \lambda }\frac{{\partial }^2\lambda }{\partial x^2},$$ (C.6)

$$0=C_g+\frac{\partial y}{\partial b_1}\frac{{\partial }^2{b}_1}{\partial x^2}+\frac{\partial y}{\partial b_2}\frac{{\partial }^2{b}_2}{\partial x^2}+\frac{\partial y}{\partial \lambda }\frac{{\partial }^2\lambda }{\partial x^2},$$ (C.7)

$$0=C_h+\frac{\partial z}{\partial b_1}\frac{{\partial }^2{b}_1}{\partial x^2}+\frac{\partial z}{\partial b_2}\frac{{\partial }^2{b}_2}{\partial x^2}+\frac{\partial z}{\partial \lambda }\frac{{\partial }^2\lambda }{\partial x^2}.$$ (C.8)

where

$$\begin{array}{l}{C}_f=\left(\begin{array}{c}\frac{\partial b_1}{\partial x}\\ \frac{\partial b_2}{\partial x}\\ \frac{\partial \lambda }{\partial x}\end{array}\right)·\left(\begin{array}{c}\frac{{\partial }^{2}x}{\partial b_1^2}\frac{\partial b_1}{\partial x}+\frac{{\partial }^{2}x}{\partial b_1\partial b_2}\frac{\partial b_2}{\partial x}+\frac{{\partial }^{2}x}{\partial b_1\partial \lambda }\frac{\partial \lambda }{\partial x}\\ \frac{{\partial }^{2}x}{\partial b_1\partial b_2}\frac{\partial b_1}{\partial x}+\frac{{\partial }^{2}x}{\partial b_2^2}\frac{\partial b_2}{\partial x}+\frac{{\partial }^{2}x}{\partial b_2\partial \lambda }\frac{\partial \lambda }{\partial x}\\ \frac{{\partial }^{2}x}{\partial b_1\partial \lambda }\frac{\partial b_1}{\partial x}+\frac{{\partial }^{2}x}{\partial b_2\partial \lambda }\frac{\partial b_2}{\partial x}+\frac{{\partial }^{2}x}{\partial {\lambda }^2}\frac{\partial \lambda }{\partial x}\end{array}\right),\\ C_g=\left(\begin{array}{c}\frac{\partial b_1}{\partial x}\\ \frac{\partial b_2}{\partial x}\\ \frac{\partial \lambda }{\partial x}\end{array}\right)·\left(\begin{array}{c}\frac{{\partial }^{2}y}{\partial b_1^2}\frac{\partial b_1}{\partial x}+\frac{{\partial }^{2}y}{\partial b_1\partial b_2}\frac{\partial b_2}{\partial x}+\frac{{\partial }^{2}y}{\partial b_1\partial \lambda }\frac{\partial \lambda }{\partial x}\\ \frac{{\partial }^{2}y}{\partial b_1\partial b_2}\frac{\partial b_1}{\partial x}+\frac{{\partial }^{2}y}{\partial b_2^2}\frac{\partial b_2}{\partial x}+\frac{{\partial }^{2}y}{\partial b_2\partial \lambda }\frac{\partial \lambda }{\partial x}\\ \frac{{\partial }^{2}y}{\partial b_1\partial \lambda }\frac{\partial b_1}{\partial x}+\frac{{\partial }^{2}y}{\partial b_2\partial \lambda }\frac{\partial b_2}{\partial x}+\frac{{\partial }^{2}y}{\partial {\lambda }^2}\frac{\partial \lambda }{\partial x}\end{array}\right),\\ C_h=\left(\begin{array}{c}\frac{\partial b_1}{\partial x}\\ \frac{\partial b_2}{\partial x}\\ \frac{\partial \lambda }{\partial x}\end{array}\right)·\left(\begin{array}{c}\frac{{\partial }^{2}z}{\partial b_1^2}\frac{\partial b_1}{\partial x}+\frac{{\partial }^{2}z}{\partial b_1\partial b_2}\frac{\partial b_2}{\partial x}+\frac{{\partial }^{2}z}{\partial b_1\partial \lambda }\frac{\partial \lambda }{\partial x}\\ \frac{{\partial }^{2}z}{\partial b_1\partial b_2}\frac{\partial b_1}{\partial x}+\frac{{\partial }^{2}z}{\partial b_2^2}\frac{\partial b_2}{\partial x}+\frac{{\partial }^{2}z}{\partial b_2\partial \lambda }\frac{\partial \lambda }{\partial x}\\ \frac{{\partial }^{2}z}{\partial b_1\partial \lambda }\frac{\partial b_1}{\partial x}+\frac{{\partial }^{2}z}{\partial b_2\partial \lambda }\frac{\partial b_2}{\partial x}+\frac{{\partial }^{2}z}{\partial {\lambda }^2}\frac{\partial \lambda }{\partial x}\end{array}\right).\end{array}$$

So we get

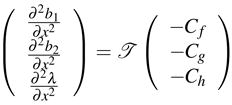(C.9)

Using the same method, we can get the other rows of 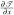, matrices 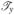and 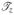by changing C_f, C_g, C_h in (C.9). Therefore is differentiable. Similarly, we can compute the higher order derivatives of and prove that ∈ C^∞, thus prove F ∈ C^∞ (Ω₀), where Ω₀ defined in Section 3.3.1 is the canonical triangle. Therefore, as defined in (C.1), f ∈ C^∞(Ω₀).