Abstract
The expanding spectrum of applications of single-molecule fluorescence imaging ranges from fundamental in vitro studies of biomolecular activity to tracking of receptors in live cells. The success of these assays has relied on progresses in organic and non-organic fluorescent probe developments as well as improvements in the sensitivity of light detectors. We describe a new type of detector developed with the specific goal of ultra-sensitive single-molecule imaging. It is a wide-field, photon-counting detector providing high temporal and high spatial resolution information for each incoming photon. It can be used as a standard low-light level camera, but also allows access to a lot more information, such as fluorescence lifetime and spatio-temporal correlations. We illustrate the single-molecule imaging performance of our current prototype using quantum dots and discuss on-going and future developments of this detector.
Keywords: single-molecule, quantum dot, fluorescence lifetime, photon-counting, widefield detector, particle tracking, phasor analysis, TCSPC, FCS
1. Introduction
1.1. Single-molecule fluorescence imaging and spectroscopy
Single-molecule fluorescence detection has grown from a cutting-edge capability confined to a few pioneering groups to one advertised by microscope or camera manufacturers, and used by an increasing number of research groups. Its applications range from single-molecule tracking in live cells using total internal reflection fluorescence (TIRF) microscopy to single-molecule fluorescence resonance energy transfer (FRET) studies of macromolecule conformation or enzyme activity (reviewed in ref. 1-4). More recently, single-molecule detection has achieved public fame thanks to its use in super-resolution imaging techniques such as photoactivated localization microscopy (PALM)5 or stochastic optical reconstruction microscopy (STORM)6 (reviewed in ref. 7). In practice, many technical aspects involved in single-molecule detection are similar to those encountered in the detection of faint astronomical objects: it can be achieved only in low light background conditions; it is next to impossible near bright objects and it requires optimized optics and detectors. New detector developments have therefore been and will remain essential for the progresses of single-molecule fluorescence detection, but unlike in astrophysics, where the observable light sources have been created eons ago and cannot be modified, single-molecule biophysicists have the possibility to design and synthesize molecules with properties tailored for single-molecule detection. In other words, performance optimization can be achieved by a constant feedback between detector development and fluorescent probe development. The purpose of this report is to describe our collaborative efforts towards the development of a new type of detector taking advantage of and tailored for quantum dots (QDs), a new type of bright and stable fluorescent probes used in single-protein imaging in live cells (reviewed in ref. 8).
1.2. Current detector limitations
Single QDs can be seen with the naked eyes under a standard fluorescence microscope and therefore can be imaged with any reasonably sensitive detector. In practice, standard video cameras are perfectly capable of detecting QDs, albeit with a poor signal-to-noise ratio. The current detector of choice for QD imaging is the EMCCD camera, which combines exceptional sensitivity (up to 90% quantum efficiency in the visible spectrum) with an electron-multiplying gain mechanism that overcomes the noise of the readout electronics. One limitation of current EMCCD cameras is their limited readout rates. As pixels are read sequentially, the maximum achievable readout rate is proportional to the number of pixels. At ~100 ns per pixel (10 MHz digitization rate), a 512 × 512 pixel camera needs 26.2 ms to digitize a frame, which limits the frame rate to approximately video rate (30 frames per second or 30 fps) when the transfer time to the computer is taken into account. As discussed in more detail below, the same readout electronics allows a 128 × 128 pixel EMCCD camera to achieve close to 500 fps, with sufficient signal-to-noise ratio (SNR) to detect single-QD blinking and track individual QDs with ~30 nm resolution. However, the requirement to have each QD’s image cover a few pixels limits the effective field of view to ~ 10-20 μm, which is barely sufficient to image a typical cell.
Novel detectors such as electron-bombarded (EB) or intensified camera based on CMOS sensors rather than CCDs could in principle overcome the pixel number limitation of small but fast EMCCDs, since some CMOS cameras can achieve over 1,000 fps (1 kfps) for sensors with over 1 million pixels. However obtaining such large frame rates currently comes at a cost, both literally and in terms of flexibility, as the corresponding data transfer bandwidth requires intermediate storage in an on-board memory. Depending on the amount of memory on the camera controller board (counted in gigabytes, Gb), the total duration of an acquisition is of the order of a few sec only (1 Gb = 1,024 × 1,024 pixels × 2 bytes × 500 frames). Although this might be sufficient for some applications, this is a serious limitation in many others.
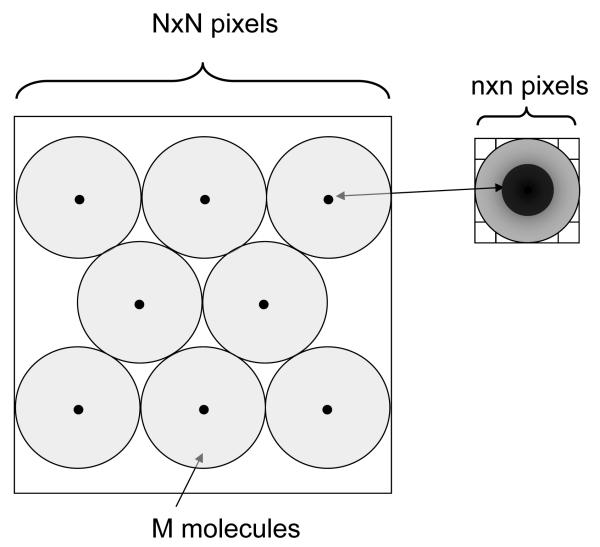
If we return to the application discussed in this article, that of single-molecule imaging, and more specifically, single-QD imaging, it appears that detectors based on a complete readout of the whole sensor area at a fixed (albeit fast) rate are wasting data transfer bandwidth. Indeed, single-molecule imaging is, as the analogy with astronomy reminds us, sparse imaging. As illustrated in Fig. 1, if we observed M single molecules, each covering n × n pixels (with typically n = 3 to 5), each frame contains only M × n2 useful pixels of information out of the total N × N (with typically N = 512 or 1,024). The maximum number of easily distinguishable immobile spots per frame, Mmax, is therefore of the order of ~ (N/n)2, i.e. Mmax ~ 10,000 spots for a 512 × 512 pixel detector and 5 × 5 pixel per single-molecule image. In the case of mobile spots, a larger spacing between spots would be needed to avoid trajectory crossing, resulting in Mmax of a few hundreds (see Appendix). This means that in most cases the useful information is contained in at most a few percents of all pixels. Readout schemes that could figure out where the useful information is (for instance based on simple thresholding) and only digitize and/or transmit these pixel values could therefore result in a gain of a few orders of magnitude in bandwidth. Taking into account that some CMOS cameras are already equipped with Field Programmable Gate Arrays (FPGAs), the constantly improvement in FPGA speed and capabilities makes such a prospect realistic.
Fig. 1.
Single-molecule imaging. M molecules (black dots) imaged by a detector with N2 pixels, each molecule’s image (point-spread-function or PSF) occupying n2 pixels. Here the pixel size a has been chosen such that the FWHM of the PSF equals 2.5 pixels (detail on the right hand side). An ideal detector comprises enough pixels to allow the simultaneous observation of M well separated individual spots (distance between spots > spot size). It should provide enough pixels to image each spot with enough resolution to allow high-resolution tracking of diffusing molecules. The pale gray circles indicate the radius of diffusion of each molecule after a finite time.
However, these potential developments will eventually face two fundamental limits. The first limit is signal-to-noise ratio. Achieving faster frame rates by reducing the number of pixels read will eventually reach a regime where the number of photo-electrons accumulated per pixel will be comparable with the readout noise, rendering the data reduction scheme alluded to before inefficient. The second limit is related to the relaxation time of the intensification mechanism. In current image intensifiers, a phosphorescent layer is used to convert incoming amplified photo-electrons into photons detectable by the CCD or CMOS sensor. This layer has a recovery time which can vary between a few tens of ms (P43 phosphor) to a few tens of μs (P46 phosphor) to mention only material emitting in a wavelength range of maximum CMOS and CCD sensitivity. This may limit the achievable artifact-free acquisition rate from a few kHz to a few 100 kHz.
The latter value is still far from what single-pixel (or point) detectors such as Single-Photon Counting Avalanche Photodiode (SPAD) or Hybrid Photodetectors (HPD) are capable of9. These detectors are used in point illumination geometries (typically, confocal microscopy) and are capable of sustaining high local count rates (> MHz) as well as providing high resolution temporal information for each detected photon (~100 ps). However, they have no position-sensing capabilities (i.e. are single pixel units). Although recent developments in CMOS SPAD detectors have led to the prospect of building relatively large arrays of individual photon counting detectors10, their effective sensitive area occupies only a small percentage of the whole array (small fill factor) due to various technological constraints, which makes them inefficient imagers. Additionally, arrays comprised of a large number of individual pixels are currently prohibitively complex to readout in parallel, resulting in readout schemes that limit the information per pixel to a mere number of detection events per unit time. The latter is fixed by the time necessary to readout the whole array and in part by the data transfer bandwidth10.
2. H33D detector
2.1. H33D detector history
To address the limitations of current detectors discussed in the previous section, we launched a collaborative effort in 2001 to develop a time-resolved wide-field single-photon detector addressing the needs of single-molecule imaging in 2001. This detector, dubbed H33D detector (pronounced “heed”) for High spatial resolution, High temporal resolution and High throughput 2+1 Dimensional detector will be described briefly in the next section. In practice, it functions as a time-resolved photon counting camera. Our collaboration combined the expertise of single-molecule biophysicists at UCLA, astrophysicists at the Space Sciences Laboratory (SSL) at UCB, experts in photon-counting detectors development and fast analog electronics experts from the Lawrence Berkeley National Laboratory (later Lawrence Livermore National Laboratory). This effort was initially funded by the National Institute of Health (NIH grant 5R21 RR17414) and is currently funded by the National Science Foundation (NSF grant DBI-0552099) and the NIH (grant 5R01 GM084327). A first proof-of-principle prototype, used in the studies described later in the paper, was released in 2004. A second prototype with better performance is currently under development.
2.2. H33D detector principle
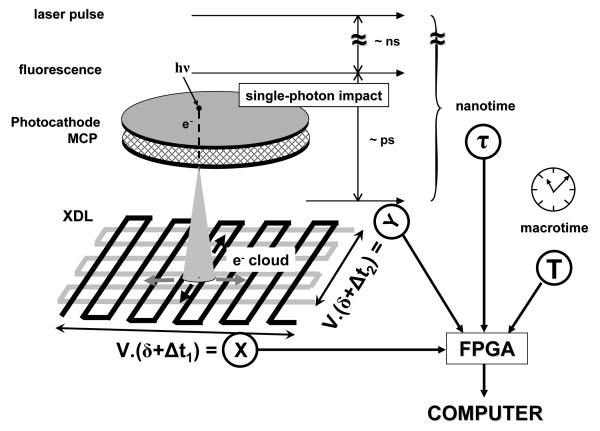
The H33D detector principle has already been described in detail in previous publications (ref. 11-14 and Fig. 2). Briefly, it is comprised of a photocathode sensitive in the visible spectrum, followed by a microchannel plate (MCP) stack amplifying each photo-electron by a factor 106-107 by successive emission of secondary electrons upon impact on the walls of the microchannel capturing the photo-electron. The resulting electron cloud is proximity-focused onto a position-sensing anode used to determine the location of the initial photon impact on the photocathode. The short pulse generated by the passage of millions of electrons in the MCP is used to obtain the arrival time of each photon with respect to a reference signal (such as an laser excitation pulse) using a time-do-digital converter (TDC). The resulting nanotime information (τ) has a typical accuracy of a few 100 ps but is limited to a finite time window set by the range of the TDC (from 50 ns to few 100 ns). The nanotime is useful to measure fluorescence lifetime decay, but does not keep track of the order in which the photons have been detected. To be able to assign an absolute arrival time to each photon, a second piece of information (the macrotime T) is obtained from a stable clock signal such as an internal clock in the readout electronics or a counter of the number of laser excitation pulses since the beginning of the experiment. The macrotime has a typical accuracy of a few tens or hundreds of nanoseconds depending on which clock source is used.
Fig. 2.
Principle of operation of the H33D detector. A fluorescence photon emitted a few ns after the excitation pulse is collected by the imaging optics and interacts with the photocathode (PC), creating a photoelectron with a wavelength-dependent probability QE. The photoelectron is amplified by an apposed MCP stack, generating an electron cloud (cone shape). When pulsed laser excitation is used to excite the fluorescence, the measurement of the delay between the charge pulse at the back of the MCP and the laser pulse performed with a TDC gives the nanotime τ. A position-sensitive anode determines the position of the electron cloud. Here a cross-delay line anode (as implemented in our Gen I H33D prototype) is represented: the charges propagate through the delay lines and are collected at both ends of each line. A timing electronics converts the differences in arrival time into position information (X or Y). A internal clock provides a 4th coordinate, the macrotime T. The 4 coordinates of each photon (12 bits per spatial coordinate, 12 bits for the nanotime, 32 bits for the macrotime) are collected by an FPGA and asynchronously sent to a computer for storage and processing. δ: fixed time delay. V > 1 mm/ns: signal propagation velocity.
The position sensitive anode needs to be capable of registering the location of the center of mass of the electron cloud with reasonable accuracy. Since the path of the secondary electrons is constrained within a single straight microchannel (or a succession of straight microchannels in the case of a MCP stack), the maximum achievable resolution is equal to the size of a microchannel (10 μm). Such accuracy is achievable if enough secondary electrons are collected by the anode. In practice, a trade-off needs to be found between the position accuracy and the detector throughput, as a larger number of secondary electrons (larger gain) reduces the maximum achievable local detection rate.
An interface electronics based on a field-programmable gate array (FPGA) checks for the synchronous availability of nanotime τ and position (X, Y) information, associates them with macrotime information T and passes this (X, Y, T, τ) set of coordinate to a computer via a first-in-first-out (FIFO) buffer.
2.3. H33D Gen I performance
Our first H33D detector (Gen I) prototype was based on a 27 mm diameter photocathode, whose material composition had a modest sensitivity in the visible spectrum range (multialkali S20) and was manufactured in the SSL facility. Its typical quantum efficiency (QE) was about 10% at 500 nm, decreasing quasi-linearly at larger wavelengths (ref). A stack of 3 MCP across which a potential difference of −3,500 V was applied resulted in a gain > 106. The position-sensitive anode was a cross-delay line (XDL) anode, consisting of two orthogonal zigzagging transmission lines separated by an insulating layer. Position determination along a given line was achieved by measuring the difference between arrival times of the intercepted electron charges at both ends of the lines. A position accuracy of ~50 μm was measured resulting in ~500 effective resolution elements (pixels) along one diameter. A commercial TDC with ps timing resolution was used to measure the nanotime. The measured instrument response function (IRF) of the detector plus electronics assembly showed a full-width at half-maximum (FWHM) of less than 200 ps (ref). The (X, Y, T, τ) coordinate of each photon was encoded in two 32 bits words and transmitted to a PC via a commercial high-speed digital I/O board.
The readout electronics speed limited the global event throughput to ~500K events per second (expressed in kHz). The high gain necessary to achieve good spatial resolution limited the local detection rate to ~10 kHz.
This detector allowed us to demonstrate proof-of-principle time-gated imaging13, lifetime imaging14, 15 and in this article, single-quantum dot imaging.
3. Single quantum dot imaging
3.1. Single quantum dot photophysics
Quantum dots have several advantages over organic fluorophores that make them attractive probes for biological imaging and other biomedical applications8. Their emission spectrum is tunable and very symmetric, allowing the synthesis of many different colors in the visible and near-infrared spectral range. Their absorption spectrum extends far into the blue-ultraviolet range of the spectrum, allowing a single excitation wavelength to be used for multiple probes, greatly simplifying multicolor imaging. Finally, they are significantly brighter and more photostable than organic fluorophores, which makes them very good single-molecule probes. For this reason, the simplest way to observe QDs is by direct eye observation under the microscope.
Single QD fluorescence has been studied quantitatively with a variety of methods and detectors including cooled CCD camera, electron-multiplied CCD (EMCCD) camera, single-photon counting avalanche photodiodes (SPAD), photomultipliers (PMT) or hybrid photodetectors (HPD)9.
A characteristic feature apparent from all these studies with greatly variable temporal resolution is the phenomenon of blinking, or fluorescence intermittency16. Blinking in QDs is believed to be due to charge trapping and Auger recombination17. It is characterized by a typical power law distribution of on (emitting) and off (non-emitting) states18. There are several practical consequences of blinking for the use of single QDs as biological probes. First and foremost, since the distribution of off times is a power law distribution with exponent smaller than −1, there is no well defined “average off time” (it depends on the duration over which this average is computed) and long off times can be observed with a significant probability. In other words, single QDs often turn off for a long time, limiting their use for single particle tracking. On the other hand, blinking is a convenient signature that one is observing a single QD rather than a cluster of two or more (in which case the likelihood to observe a synchronous extinction of all QDs is small). Recent developments have resulted in non-blinking QDs by increase of their shell thickness19, 20. This could be used advantageously in some studies, although this comes at the price of larger probes.
A second important property of QDs is their rather long fluorescence lifetimes compared to standard organic fluorophores21. This characteristic is actually a bit more subtle, as it appears that individual QDs are characterized by multiple fluorescence lifetimes, which may alternate over time22. However, the existence of long decays in QDs (>10 ns) allows in principle a simple distinction between their fluorescence and that of other fluorophores, such as for instance cell protein autofluorescence, by time-gating13, 21.
In summary, QDs have a number of interesting properties that may allow pushing the limits of single molecule imaging in biology. However, as we will argue in the remainder of this article, this can only be taken advantage of in a limited way with current detectors.
3.2. Single QD blinking
As mentioned previously, single QD blinking can be observed with almost any kind of detectors. The temporal resolution of this observation will however greatly depend on the detector used. Wide-field detectors such as cameras have a finite readout speed which is set by the digitization and transfer processes. Limiting the acquisition to a small region of the sensor, it is possible to boost this readout speed, but the reduced signal collected during the short integration time will eventually become comparable to the readout noise, thus diminishing the signal-to-noise ratio. A standard way to compensate for the large readout noise of cameras is to amplify the signal before readout, as in intensified CCDs or electron multiplying CCDs. The effect of this amplification is to diminish the relative importance of the readout noise, usually at the expense of increasing the statistical noise affecting the signal as discussed in some detail in ref. 23. This effect is usually modeled by a device-specific excess noise factor (ENF) F:
| (1) |
where G is the amplification gain, σin represents the standard deviation of the input signal and σamp that of the amplified signal.
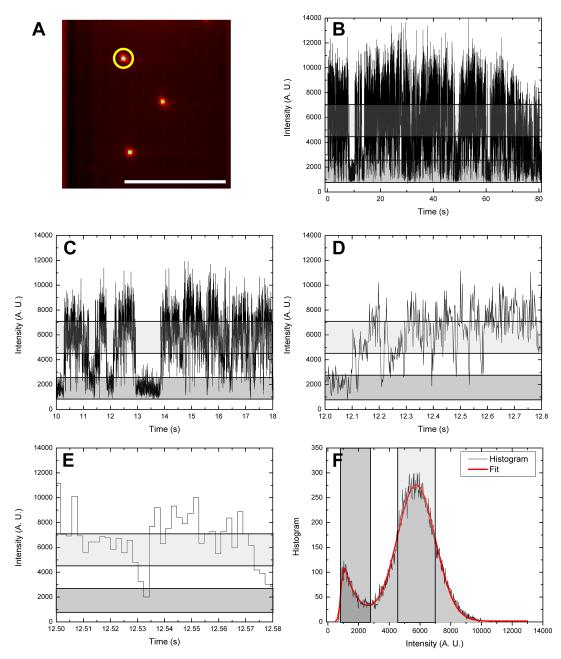
Currently, the most efficient camera technology with a gain mechanism is the EMCCD (with G up to several hundreds). EMCCDs possess the superb quantum efficiency (QE) of silicon devices in the visible (and near-infrared) range and have a reasonable ENF of only 1.4 (compared to ENF of ~ 1.8 or more for ICCDs, which have the additional drawback of having lower QE). Fig. 3 shows an intensity time trace of a single 620 nm emitting QD obtained with 2.04 ms per frame (maximum full frame readout rate of the model used in this experiment) at maximum EM gain. The SNR for this time trace is SNR2 ms = 3.2.
Fig. 3.
Intensity time trace of a single 620 nm emitting QD acquired with a fast electron-multiplying CCD (EMCCD). A: Average intensity image over the 40,000 frames of the movie, with the studied QD circled in yellow. Scale bar: 10 μm. B-E: 80 s, 8 s, 800 ms and 80 ms time windows of a single-QD trace (2.04 ms/frame) exhibiting the well-know scale-free blinking pattern characteristic of colloidal QDs. The gray and light gray bands correspond to intensity ranges defined in E, indicating the off state (background level) and on state, respectively. F: Count histogram for the whole time trace shown in B, with a fit a Gaussian distribution (on state: M1 = 5752, σ1 = 1236) and an exponentially modified Gaussian distribution (off state: M2 = 852.3, σ2 = 122.4, τ2 = 907.2). The gray and light gray vertical boxes correspond to intervals centered on the mean of each distribution and half-width equal to one standard deviation of each distribution.
As can be seen from successively zooming in to shorter time windows, the absence of a characteristic timescale for blinking is quite apparent down to the camera time resolution of 2.04 ms. However, the histogram of counts corresponding to this time trace shows another important characteristic of EMCCDs, which is the significant effect of the EM gain mechanism on the signal statistics24. In particular, the part of the histogram corresponding to background (which should be Poisson distributed) is best fitted with an asymmetric exponentially modified Gaussian distribution (M2 = 852.3, σ2 = 122.4, τ2 = 907.2). The departure from Poisson statistics for the on state signal is in part due to the EN gain mechanism (Eq. (1) above), but also to the power law distribution of on and off states25.
To achieve higher temporal resolution, researchers have for a long time resorted to photon-counting detectors such as SPADs, which output brief voltage pulses after each photon-detection event26. The height and width of these pulses depend on the precise model, but is typically a TTL (transistor-transistor-logic) or NIM (Nuclear Instrumentation Module) signal, which needs to be detected and time-tagged by a separate electronics (counter unit or time-correlated single-photon-counting –TCSPC-unit). Each photon can thus be timed with an absolute accuracy depending on the readout electronics but ultimately limited by the time-jitter of the entire experimental setup (including the detector). For simple counting applications, accuracy of a few ns can easily be achieved. For experiments involving pulsed laser excitation, in which one might be interested in addition to measure the separation between fluorescence excitation and emission, relative accuracies of a few ps may be achieved in the best cases. In all cases, the achievable temporal resolution per photon is much better than that could be obtained with camera used in photon-counting mode. However, this does not necessarily translate into a better temporal resolution at the intensity time trace level.
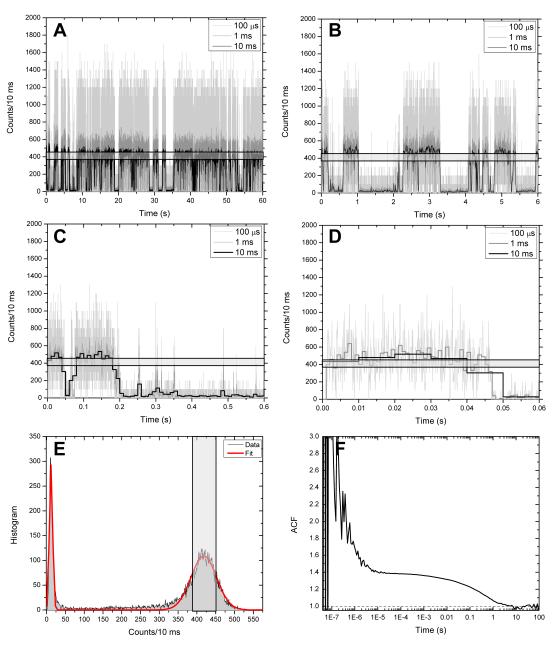
Fig. 4A-D show a time trace from a single QD obtained by first acquiring a raster-scanned confocal image of the sample and then parking the QD of interest in the confocal excitation spot. The collected signal consists in a train of photon arrival times, which can be binned with arbitrary resolution to form intensity time traces. As before, blinking at all time scales is apparent with a clear distribution in two intensity levels (on and off) as shown by the histogram of counts per 10 ms (Fig. 4 E). A peak at ~11 counts corresponding to the off state is reasonably well fitted with a Gaussian with mean M1 = 11.7 and standard deviation σ1 = 4.4. The departure from a Poisson distribution (σ = √11 = 3.3 expected for shot-noise limited background) is due to the presence of nearby QDs, which are weakly excited by the focused laser spot 27. The main peak corresponding to the on state is reasonably well fitted by a Gaussian with M2 = 418.3 and σ2 = 31.4. The strong departure from a shot-noise limited signal (σ = √418.3 = 20.5) is again due to the power law distribution of on and off states.
Fig. 4.
Intensity time trace of a single 585 nm emitting QD acquired with a single-photon counting avalanche photodiode (SPAD). A-D: 60 s, 6 s, 600 ms and 60 ms time windows of a single-QD trace at different timing resolution (light gray: 100 μs, dark gray: 1 ms, black: 10 ms). The light gray band corresponds to the on state intensity range defined in E. E: Count histogram of the 10 ms-resolution time trace (gray) and corresponding fit (red curve). A peak at ~11 counts corresponding to the off state is reasonably well fitted with a Gaussian with mean M1 = 11.7 and standard deviation σ1 = 4.4. The main peak corresponding to the on state is reasonably well fitted by a Gaussian with M2 = 418.3 and σ2 = 31.4. The light gray vertical box corresponds to an interval centered on M2 and width σ2. F: FCS curve corresponding to the time trace shown in A. The amplitude decays around a time scale of 100 ms, corresponding to the typical on (or off) state duration for this particular time trace. The increased amplitude at time scales below 1 μs is due to the SPAD afterpulsing.
The availability of a time stamp for each photon detected by the SPAD allows going beyond time trace analysis and looking at the autocorrelation function (ACF) of the intensity down to the detector temporal resolution (SPAD deadtime ~ 40 ns). Fig. 4F shows the ACF corresponding to the time trace represented in Fig. 4A down to 40 ns. Two well-known features can be observed in this curve. First, the ACF amplitude increases below 10 μs due to the phenomenon of SPAD afterpulsing, making analysis of fluorescence fluctuations below this timescale problematic, unless two SPADs and a Hanbury Brown-Twiss geometry are used26. Second, the ACF decays towards its asymptotic limit of 1 around a time scale of 0.1 s. As noted previously by Messin et al., this time scale is related to the particular on and off time distribution observed in this time trace, but is itself not very informative due to the non-ergodicity of QD blinking28.
As expected, the SNR decreases as the binning interval decreases (SNR10 ms = 13.0, SNR1 ms = 2.8, SNR0.1 ms = 0.9). In fact, despite the large ENF of the EMCCD (F = 1.4) compared to the SPAD (no ENF or F = 1), both achieve similar SNR at a similar temporal resolution of ~1 ms.
This in itself is an interesting result, despite the following differences between the two experiments:
The extinction coefficients of the two QDs are different: the common 488 nm excitation used in both experiments excites 620 nm emitting QDs more efficiently than 585 nm emitting QDs. A rough estimation gives a ratio of ~5.5 in favor of the red QD.
The excitation powers are different: the TIRF excitation for the EMCCD experiment was ~ 1 μW/μm2 whereas the confocal excitation for the SPAD experiment was ~ 18 μW/μm2, i.e. a factor of 20 in favor of the green QD.
The QE of the detectors are different: the EMCCD is ~ 30-40% more sensitive than the SPAD in the relevant spectral range, giving a factor of ~1.4 in favor of the red QD.
Overall, it appears that the emission count rate in both experiments is similar within a factor of 2-3. Therefore, the previous results show that similar data quality may be obtained with either detector despite the fact that one is a noiseless photon-counting detector and the other a noisier and non photon-counting one. However, one technique allows observing several QDs at once (3 in the case of Fig. 3A but more could have fitted in the field of view), while the other allows temporal correlations within the time trace (or, with pulsed excitation, fluorescence lifetime decay analysis) on a single QD.
As a final element of comparison between the two types of experiments, let us consider the data file size generated by each.
The single, ~42 kHZ-emitting QD SPAD recording of 140 s (60 first seconds shown in Fig. 4) occupies ~18 megabytes (MB) of disk space. Indeed, each photon’s information is encoded on one 32 bits word (4 bytes): 42.103 × 4 × 140 = 22.5 MB. The difference is easily explained by the percentage of off times, which is ~25% in this particular trace (left histogram peak in Fig. 4B). More generally, a ~100 kHz emitting non-blinking QD SPAD recording should generate ~ 22.9 MB/min. The same recording duration, regardless of the number of QDs or count rate per QD will occupy 2 × 1282 × 60 / (2.04 10−3) = 919.1 MB with a 16 bits EMCCD camera with 128 ×128 pixels run at maximum speed (2.04 ms/frame). This is the space occupied by 40 single-QD SPAD recordings as estimated before. In principle, therefore, it would be advantageous both in terms of disk space and throughput to record single-QD data with an EMCCD above a few dozen QDs (40 QDs on 1282 pixels represents 202 pixels per QD, which is reasonable if each QD is well separated from the others, but may results in overlaps if the distribution of QD is completely random). Disk space considerations might of course become irrelevant as disk space cost decreases or if efficient data compression algorithms are implemented.
In summary, these two experiments show that current state-of-the-art wide-field detectors (fast EMCCD) and photon-counting detectors (SPAD) can achieve very comparable results in terms of signal-to-noise ratio and disk space consumption although:
The SPAD has a low throughput, does not allow fast imaging, but allows TCSPC studies.
The EMCCD has a high throughput and is capable of limited imaging but is incapable of providing TCSPC information.
Let us now examine how our prototype widefield photon detector fares in similar conditions.
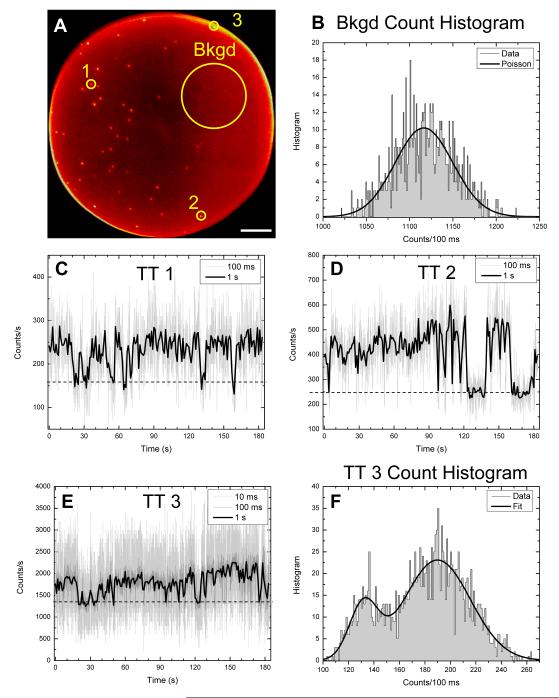
Fig. 5A (see also Movie 1) shows a 70 μm wide field of view of 577 nm emitting QDs spin-cast on a glass coverslip, as recorded by the Gen I H33D detector. The image consists of ~ 3.1.106 photons collected over a period of ~ 3 min (mean count rate: 170 kHz). Photon coordinates (coded on 12 bits) were binned by a factor 8, resulting in a circular imaging area ~ 400 pixels in diameter. Individual QDs are clearly resolved and their intensity time trace can be reconstructed with arbitrary time resolution. The time traces corresponding to 3 of the recorded spots in Fig. 5C-E (labeled 1-3 in Fig. 5A) are shown with time resolution 100 ms (gray) and 1 s (black), clearly showing blinking of the QD on top of a significant background level. The background is likely due to autofluorescence and possibly laser excitation leakage, as a powerful pulsed laser excitation at 532 nm was used. Interestingly, as shown in Fig. 5B, the histogram of counts per 100 ms recorded in a background only region shows a perfect Poisson behavior with a mean signal of 1116.9 counts per 100 ms, as expected for a shot-noise limited constant source recorded by a photon-counting detector. In contrast, the histogram of time trace 3 is best fitted with two Gaussian distributions of mean (M) and standard deviation (σ): M1 = 131.7, σ1 = 11.0 (off state), M2 = 189.8, σ2 = 26.0 (on state). Note that √M1 = 11.5 and √M2 = 13.8, showing that the first distribution is almost Poissonian (as expected for background) whereas the second is clearly non Poissonian (as expected for a QD).
Fig. 5.
Intensity time traces (TT) of single QDs imaged with the H33D detector. A: Accumulated image of individual 577 nm emitting QDs spin-cast on a glass coverslip corresponding to a 3 min acquisition. The 3 circled QDs (1, 2, 3) and the large QD-free area (Bkgd) are studied in the remainder of the figure. Scale bar: 10 μm. B: Histogram of background photon counts over the duration of the acquisition for 100 ms frames. The black curve indicates a fit with a Poisson distribution of mean 1116.9 counts per 100 ms. C, D: Intensity time trace corresponding to a 10 × 10 pixel region around QD 1 (resp. QD 2). The gray curve corresponds to 100 ms per frame, while the black curve corresponds to 1 s/frame. The dashed horizontal line indicates background level. Clear on/off transitions are observable, indicative of single QDs. E: Time trace corresponding to QD 3 in A, located at the rim of the sensitive area. The larger count rate allows binning the time trace down to 10 ms/frame while still preserving a good contrast (light gray curve). The dark gray (100 ms) and black (1 s) curves confirm that a single QD is observed. F: Histogram of counts per 100 ms corresponding to the dark gray curve of E (100 ms binning), fitted with two Gaussian distributions of mean (M) and standard deviation (σ): M1 = 131.7, σ1 = 11.0, M2 = 189.8, σ2 = 26.0.
Obviously, compared to the data of Fig. 3 and Fig. 4, the detected signal is much lower, because of the lower QE of the Gen I detector (nominally about 10-fold less efficient than the SPAD around 580 nm but potentially less after several years of tube aging) and the less efficient excitation wavelength (the absorption cross-section decreases by a factor 1.6 from 488 nm to 532 nm for 585 nm emitting QDs, which provides a good estimate of the relative excitation efficiency in both experiments). The measured SNR of QD 3’s time traces: 1.1 (10 ms), 2.2 (100 ms), 5.5 (1 s) reflect these differences.
In summary, taking into account that our current prototype has a low QE in the wavelength range of interest, the wide-field photon-counting detector demonstrates single QD sensitivity and an excellent spatial resolution. We discuss this latter aspect in more detail in the following section.
3. Widefield and single point source imaging
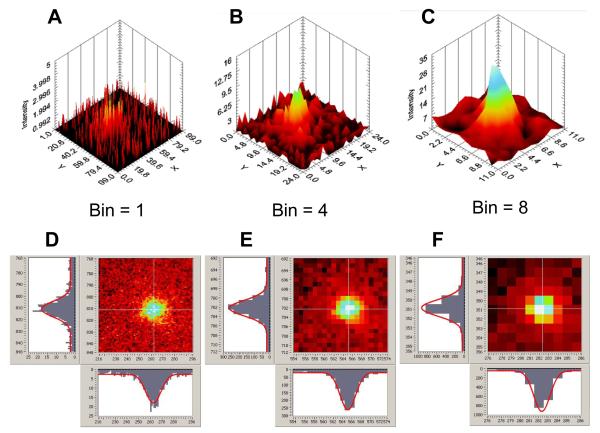
Fig. 5A demonstrated the widefield imaging capabilities of the H33D detector. The image was binned by a factor of 8 to minimize file size, but small regions of interest can of course be imaged with a smaller binning factor. Fig. 6 shows a detail around QD 2 of Fig. 5A displayed with increasing spatial resolution. However, contrary to Fig. 5A, which was constructed with all photons collected during the ~ 3 min acquisition time, these images correspond to a single frame of Movie 1, binned with 1 s temporal resolution. Movies limited to this small region (with different spatial binning) are provided as Supporting Information (Movie 2: binning = 8, Movie 3: binning = 4, Movie 4: binning = 1). The effect of decreasing spatial binning (i.e. increasing spatial resolution) is evident in Fig. 6C, which illustrates the photon-counting nature of our detector: most pixels have value 0 or 1, with only a few pixels exhibiting larger values, indicating the faint presence of a QD. According to the criterion discussed in the Appendix, an appropriate pixel size for accurate localization of the QD would be a = σ = 84 nm for a perfectly focused QD, provided we had enough photons to use a Gaussian fitting approach. Using a calibrated reticle image, we measured a = 100 nm for a binning factor 4 (Fig. 6B). Fitting the intensity distribution in Fig. 6B to a Gaussian results in a parameter σ = 145 nm, indicating that the QD was probably slightly out of focus. At this temporal resolution (1 s) or in other words, for this number of collected photons per QD (N ~ 200, Fig. 5D), a binning factor of 4 to 8 is therefore ideal 29. This, however, depends on the available number of photons in the image. Fig. 6D-F show images of the same region but using all photons accumulated during the ~ 3 min of acquisition. Those images contain ~ 180 more photons than the previous ones, allowing an accurate fitting at all resolutions (including when no binning is performed, Fig. 6F). For all binning values, a perfect Gaussian fit is obtained, with identical parameter σ ~ 175 nm.
Fig. 6.
Spatial resolution of the H33D detector. A-C: Representative 1 s frame of a region of interest (ROI) encompassing QD 2 of Fig. 5, with increasing spatial binning factor (A: 1, B: 4, C: 8). For a binning factor of 8, the pixel size represents 200 nm in the object plane. The localization accuracy of QD shown in C can be estimated as described in the text to be ~50 nm. Standard PSF fitting methods are not appropriate to localize the QD as imaged in A (with no binning), where the photon-counting nature of the detector is most apparent. Corresponding movies 2-4 show the whole sequence of images for different spatial binning of the data (1, 4, 8) of the time trace shown in Fig. 5D. D-F: Images of the same region obtained using all photons accumulated during the ~ 3 min acquisition, with the corresponding Gaussian fit profiles shown along two orthogonal directions. The fitted Gaussian parameter is σ ~ 175 nm at all resolutions.
In theory, our localization accuracy is given by Eq. (5) (Appendix): δx ~ 12 nm for 1 s integration images comprised of ~ 200 photons per QD. However, as discussed elsewhere, this theoretical estimate needs to be interpreted with caution30, 31. A more reliable estimate can be obtained by computing the average localization accuracy along the trajectory. To do this, we fitted the position of QD 2 in the ~180 frames of the 1 s/frame movie, generating a QD trajectory. We then computed the corresponding mean-square displacement (MSD) curve32. In addition to providing information on random diffusion and drift during the acquisition, the MSD curve provides an estimate of the average localization uncertainty. Applying this analysis to QD 2, we obtained δx = 49 nm, which is less flattering than the previous value, but is probably more realistic due to the variance in QD intensity (and photon distribution) during the whole acquisition. Note that the same analysis applied to the QD imaged at 490 frames/s with a fast EMCCD (Fig. 3A) results in a similar localization uncertainty of δx = 42 nm (pixel size a = 130 nm). This is consistent with the fact that a similar SNR was measured in both cases.
This discussion demonstrates that the H33D detector provides both a very wide field of observation and spatial resolution matching that of conventional detectors.
4. Single particle tracking
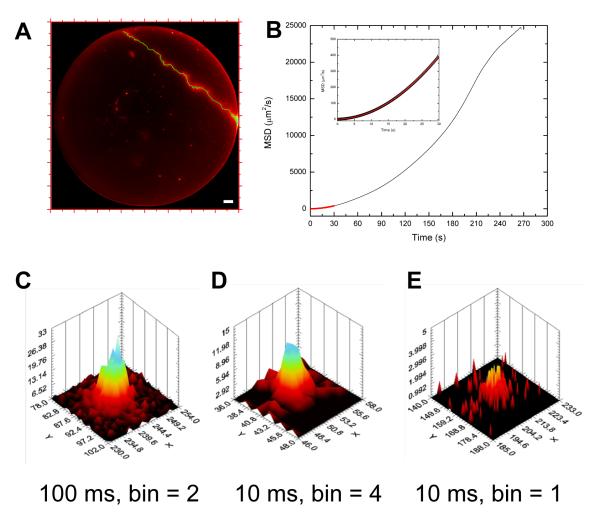
Fig. 7A shows an image corresponding to a ~ 5 min acquisition of immobile single QD fluorescence (isolated spots visible throughout the field of view) during which a bright particle (most likely a cluster of QD suspended in the solution) drifted through the field of view. Movie 5 shows the whole event with 1 s time resolution. Although not a single QD, the tracked particle provides an interesting illustration of the capability of our detector, as its average luminosity was ~ 10 kHz, the nominal maximum local count rate of our Gen I H33D detector (almost two orders of magnitude larger than the single-QD intensities studied in Fig. 5).
Fig. 7.
Single-particle tracking with the H33D detector. A: Accumulated image corresponding to a ~ 5 min observation of QDs bound to a glass coverslip (isolated spots visible within the disk-shaped imaging area). A wandering QD-cluster is also observed to transit through the field of view (streak in the upper right corner). The tracked trajectory (100 ms/frame) is indicated in green. Scale bar: 10 μm. B: Mean square displacement (MSD) curve corresponding to the trajectory shown in A. Inset: zoom in on the first 10% of the curve showing the fit to a model of diffusion superimposed with a drift at constant velocity: MSD(t) = 4σ2 + 4Dt + (Vt)2, where σ = 68 nm is the localization error, D = 0.13 μm2/s is the diffusion constant and v = 0.65 μm/s is the velocity. C-E: Example of images of the moving particle at t = 100 s obtained with different settings.
Superimposed onto the streak generated by the diffusing particle is the fitted 2D trajectory obtained at 100 ms resolution. Although the particle evidently goes in and out of focus, we treated its trajectory as purely 2-dimensional. The resulting MSD curve (Fig. 7B) was fitted with a model of directed motion (linear drift at constant velocity v) with a superimposed Brownian motion (diffusion constant D) and an average localization uncertainty σ. The fitted parameters were σ = 68 nm, D = 0.13 μm2/s and v = 0.65 μm/s.
A 10 kHz signal represents ~ 1,000 photons per 100 ms, which is plenty to achieve an average 68 nm localization accuracy. However, 100 ms is a frame duration which is easily achieved with a large area EMCCD. To test the limits of our detector, we generated an image sequence with 10 ms integration per frame (~ 100 photons per spot) and checked whether decent localization accuracy was still achievable. As indicated in Fig. 7C-E, at the native resolution of the detector (bin = 1), a 100-photons spot has very few counts per pixel and cannot be fitted to a Gaussian using a simple non-linear least square fitting approach. However, by binning the image by a factor 4, it is possible to obtain an intensity distribution that can satisfactorily be fitted with a Gaussian function (Fig. 6E). The first ~22,000 10 ms frames were fitted as before and a trajectory reconstructed. The computed MSD was essentially superimposable to that obtained from the 100 ms movie except at very short time scale (data not shown). The fitted parameters (obtained from the first 1 % of the curve) were: σ = 258 nm, D = 0.14 μm2/s and v = 0.66 μm/s. The only difference between these results and those of the 100 ms trajectory is the localization accuracy, which is obviously lower due to the reduced SNR. The ratio σ10 ms/σ100 ms = 3.8 is indeed close to the ratio of SNR (SNR100 ms/SNR10 ms ~ √10 = 3.3).
This demonstrates the trade-off which can be made between temporal and spatial resolution. Since the data from the H33D can be rebinned multiple ways in post-processing, a dataset can be used to obtain either very high localization accuracy at larger timesteps, or very high temporal resolution with a reduction in spatial localization. As shown, this approximately follows the expected relationship of the spatial localization improving by the square root of the frame time.
In summary, provided a moving particle emits enough photons to generate a 10 kHz signal on the H33D detector, it is possible to track it with high spatial resolution with a temporal resolution of at least 10 ms, without sacrificing on the size of the field of view. As discussed in the next section, there is much more to learn about this particle using the H33D detector.
5. Lifetime analysis
The main specificity of the H33D detector is its ability to detect, localize and time-tag every photon individually. As discussed earlier, two types of temporal information are associated with each photon: its macrotime T and its nanotime τ. The macrotime T has been used up to now in order to bin the data in “frames” of constant duration 10 ms, 100 ms or 1 s. Its resolution depends on whether the electronics uses the laser excitation pulses as an external clock or a fixed rate, internal clock. For instance, the data of Fig. 5 and Fig. 6 was acquired in the latter mode using a 40 MHz clock (hence a 25 ns resolution), whereas the data of Fig. 7-9 was acquired in the former mode (repetition rate 4.75 MHz, hence a 210.5 ns resolution).
Fig. 9.
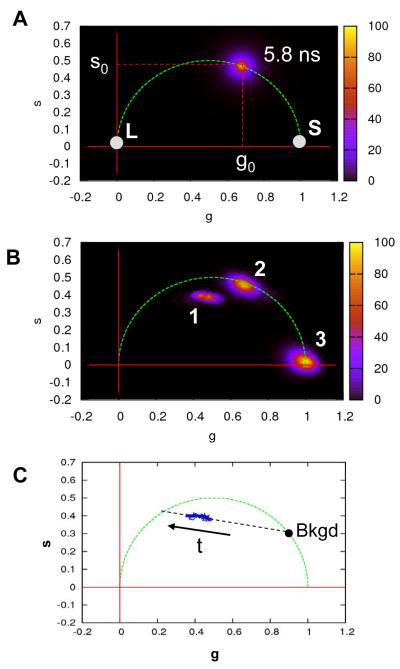
A: Principle of the phasor plot. Single exponential lifetimes are located on the universal semicircle (dashed green curve), short lifetimes are located near the bottom right intersection with the horizontal (g) axis (white dot: S), and long lifetimes are located near the origin (white dot: L). Samples with multiple lifetimes are located within the half disk below the universal circle. The color coded histogram shown is for a sample with lifetime τ0 ~ 5.8 ns. B: Phasor plot showing the QD sample studied here (1), a fluorescent bead sample (2) and a dye (3) with a very short lifetime (Erythrosin B: 80 ps). Each individual histogram was normalized to facilitate comparison of the three samples. C: Phasor trajectory of the QD cluster (blue). The black dot indicates the phasor value of the background. The trajectory indicates a linear combination (black dashed line) between a long lifetime component and the short lifetime of the backround (~ 3 ns). The arrow indicates the direction of the evolution of the phasor coordinates along the trajectory.
When the recorded fluorescence is excited with a pulsed laser rather than a continuous wave laser, the H33D also provides nanotime information, which is the separation between the photon emission (more precisely, its detection) and the next excitation pulse. As usual in this kind of configuration where the laser pulse is used as the stop signal, care must be taken to match the TDC time window to the typical fluorescence decay time and/or to the laser repetition period, whichever is longer. In favorable cases, the nanotime information allows a straightforward extraction of the interesting information, which is the separation between the excitation pulse and the corresponding fluorescence photon emission, henceforth called the fluorescence decay time.
This information can be used in two different ways, as discussed in the following sections.
5.1. Time domain analysis
The standard way of using fluorescence decay time information is to histogram all values and fit the histogram with a fluorescence decay model26. In the simplest case, the histogram is the convolution of the instrument response function (IRF) and a single exponential function with parameter τ0, the fluorescence lifetime.
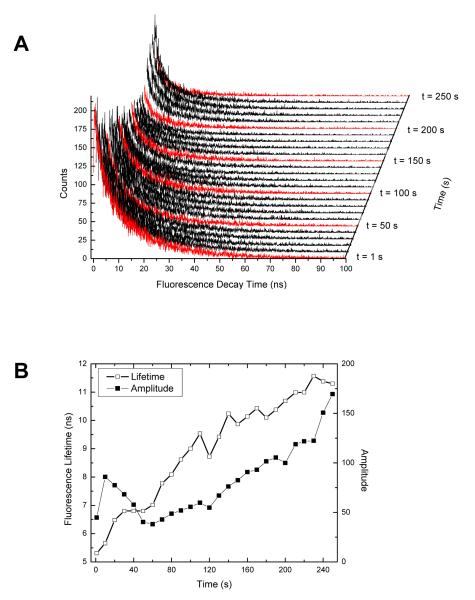
Building fluorescence decay time histograms is straightforward and rapid, but it becomes cumbersome when done for multiple objects in an image. For instance, Fig. 8 shows a waterfall representation of fluorescence decay histograms obtained at 10 s intervals along the trajectory of the drifting particle described in the previous sections. Each histogram corresponds to 1 s worth of data. This representation makes it clear that there are variations in spot intensity (the spot becoming dimmer towards the middle of the trace due to the particle going out of focus), as seen from the variable peak heights. Fitting each histogram with a single exponential decay recovers a best fit fluorescence lifetime at each time point along the trajectory, as represented in Fig. 8B. Fig. 8B suggests a progressive increase of the fluorescence lifetime of the particle, but its strong correlation with the fitted amplitude indicates that it could merely be an artifact of the intensity increase. Indeed, a careful look at the histogram fits shows that a single exponent model fails to capture the full complexity of the decays. In particular, a second, longer lifetime component appears necessary for a fully satisfactory fit of the decays. There is no need to go into the details of this analysis in this particular context, as there is not much interesting to expect from a diffusing QD cluster. Suffice it to say that this problem is illustrative of the potential pitfalls of fluorescence decay analysis: poor signal limits the analysis to a single exponent decay, when the underlying photophysics might require two or more exponents to be considered. On the other hand, when the signal is sufficient to fit the decays with multiple exponents, data representation and analysis becomes an issue, since multiple exponents (and amplitudes) need to be studied simultaneously. For these reasons, it appears that a different type of analysis may be more appropriate when multiple spots are tracked over time.
Fig. 8.
A: Fluorescence lifetime decay curves of the diffusing QD-cluster corresponding to 1 s frames separated by 10 s along the trajectory. Curves in red are separated by 50 s from one another. B: Corresponding fitted single exponent lifetimes (open circles) and decay amplitudes (filled squares) showing an increase in lifetime.
5.2. Phasor (or frequency domain) analysis
Phasor analysis of fluorescence decay time is inspired from techniques developed for frequency domain studies of fluorescence decay15, 33-35. In this approach, a set of fluorescence decay time data is transformed into a coordinate pair (g, s) called a phasor. Phasor data corresponding to different sets of fluorescence decay time data are then represented in a two-dimensional histogram called a phasor plot, as shown in Fig. 9A. A phasor plot turns out to be a convenient visual representation of the distribution of lifetime values of multiple data sets, as single exponent decays appear on a so-called universal semicircle, and multi-exponent decays appear within the corresponding half-disk. A preliminary report on the advantages of this approach for H33D data representation and analysis has recently been published, and we refer the interested reader to it for a detailed description of the method15. Fig. 9B shows the respective locations of the QD sample studied in this section, a fluorescent bead sample and a short fluorescent lifetime dye (Erythrosin B). Each sample, characterized by very different lifetimes appear at very distinct locations on the phasor plot. In particular, the fact that QD sample is localized below the universal semicircle emphasizes that its fluorescence decay is characterized by a distribution of lifetimes.
In the current experiment, we are interested in analyzing the evolution of the fluorescence decay of the moving particle along the trajectory. The fluorescence decay time histogram of photons emitted by the particle during a given frame can be transformed into a single phasor data point. Each of these points can thus be viewed as an instantaneous “phasor coordinate” of the QD cluster, and the series of such points as a “phasor trajectory”, visually depicting the evolution of the QD cluster fluorescence decay along its actual physical trajectory. The result of this analysis is shown in Fig. 9C and clearly indicates two things: (i) the fluorescence decay of the particle consists of several components at all time points (the phasor data is located within the half-disk) and (ii) the contribution of the longer component increases as time progresses. In particular, when the phasor value of the background fluorescence is computed, it is found to be around the phasor coordinate (0.85, 0.3), which lies on the extension of the line formed by the QD trajectory. Thus the QD trajectory can be seen to be an intensity-dependent linear combination between the background component and the phasor value of the QD itself. This analysis makes clear the relationship that was ambiguously suggested by the more tedious fluorescence decay time analysis of the previous section.
Phasor analysis therefore appears as a very simple way of monitoring changes in the fluorescence decay of individual particles (or single molecules). For the QD cluster studied here, such changes might be due to different causes (such as photobrightening of QDs for instance), which we did not investigate further, our purpose being to illustrate the capabilities of the H33D detector.
Translated at the single-molecule level however, the capability of monitoring the fluorescence decay without the requirement of fitting the fluorescence decay with any specific model would be of tremendous interest. Indeed, the fluorescence lifetime of an individual fluorophore is sensitive to its electronic environment, and can therefore be affected by the presence of nearby molecules. Fluorescence resonance energy transfer, electron transfer or the presence of an interface are examples of phenomena affecting fluorescence lifetime which have been extensively studied at the single-molecule level (reviewed in ref. 3, 4). The H33D detector combined with phasor analysis thus provides a tool for performing this type of analysis on moving single-molecules, which will be explored in future work.
6. Perspectives
In this work, we demonstrated the promising capabilities of our prototype photon-counting camera (Gen I H33D detector) for time-resolved single-molecule imaging. Due to the limited sensitivity of our current prototype, we limited ourselves to single QD imaging and presented examples of single QD blinking monitored down to 10 ms resolution, single QD tracking with 1 s resolution and illustrated the capabilities of our detector by tracking a bright particle with 10 ms time resolution over a large field of view. In addition to allowing faster tracking of a single particle over a larger area than current detectors are capable of, the H33D detector is capable of providing accurate timing information for each photon. We illustrated this capability by reporting the evolution of the fluorescence lifetime of a single particle along its trajectory, analyzed with both a standard fluorescence decay time analysis and the phasor approach.
We are currently developing a new version of the H33D detector with a different photocathode material having improved QE in the visible spectrum (in particular in the red part of the spectrum). This better sensitivity should further increase the temporal resolution by reducing the time required to accumulate the signal level necessary for a given localization accuracy. The new prototype will also sustain higher local count rate (up to 100 kHz compared to the current 10 kHz), which will allow tracking brighter particles down to 1 ms over large fields of view. Our next photocathode will not, however, exhaust the margin for improvements, as materials such as GaAs or GaAsP may provide up to 10-fold increase in QE in the visible range.
We are therefore confident that high sensitivity widefield single-photon counting will eventually allow monitoring the evolution of the fluorescence lifetime of single diffusing fluorescent probes in live cells. As fluorescence lifetime directly reports on the environment of a fluorophore, this could be used to study the heterogeneous and dynamic structure of the cell membrane without the need for staining the membrane or to study the interaction of individual receptor proteins with their partners in the initial stages of signal transduction pathways, among many other outstanding questions.
7. Material and Methods
Quantum dots
Three different samples of quantum dots were used. (i) Peptide-coated 620 nm emitting CdSe/ZnS QDs were synthesized as described36. Surface immobilized QDs were observed in Ham Kaighn’s F12K medium after overnight incubation. (ii) 585 nm emitting streptavidin-functionalized CdSe/ZnS QDs were purchased from Invitrogen (Carlsbad, CA). (iii) 577 nm emitting QDs were purchased from Ocean Nanotech (Springdale, AR) as powder and diluted in butanol.
Microscopy and data acquisition
Samples were imaged on a modified inverted microscope (IX71, Olympus, Center Valley, PA) equipped with a 60X, NA 1.45 oil immersion objective lens. Fluorescence excitation was performed with three different lasers: (i) the 488 nm line of a continuous wave Ar ion laser (ILT 5490A, Midwest Laser Products, Frankfort, IL), (ii) a 532 nm pulsed laser (IC-532-1000 ps, High Q Lasers, Watertown, MA) emitting 8 ps pulses at 68 MHz. Both lasers were coupled to a single-mode fiber. (iii) a frequency-doubled, pulsed-picked Ti:Sa laser (Mira 900, Coherent, Santa Clara, CA) emitting 100 fs-pulses at 460 nm and 4.75 MHz.
For confocal imaging, a 3-axis piezostage was used to move the sample (Nano-View, MadCityLabs, Madison, WI) and a SPAD was used to collect the emitted fluorescence (SPCM-AQR14, Perkin-Elmer Optoelectronics, Vaudreuil, QC, Canada). Software programmed in LabVIEW (ScanX) was used to control the acquisition. CW laser power was ~500 nW at the back of the objective lens, which converts into an incident intensity on the focused QD of ~ 20 μW/μm2.
For TIRF imaging, the Ar ion laser (620 nm QD EMCCD imaging) or 532 nm laser (577 nm QD H33D imaging) were used. The single-mode fiber was attached to the TIRF port of the microscope and the incidence angle adjusted to obtain maximum excitation intensity and lowest background level. The measured power out of the objective lens was ~ 6 mW (CW 488 nm) or ~11 mW (pulsed 532 nm). The illuminated area had a diameter ~ 200 μm.
For EMCCD imaging, an Ixon 860 camera (Andor Technology, South Windsor, CT) was used and acquisition controlled by the open source MicroManager software (www.micromanager.org). For H33D imaging, custom software written in LabVIEW and C (IdefiX) was used.
For epifluorescence imaging (QD cluster H33D imaging), the 460 nm pulsed laser excitation was used, with an incident power at the back of the objective lens of ~ 200 μW. For each acquisition, appropriate dichroic mirrors and emission filters were used.
Data analysis
Data analysis was performed with a series of custom software written in LabVIEW and C. Single-particle tracking was done using custom LabVIEW software (AsteriX). Some data representation and fitting was performed with Origin 8 (OriginLab, Northampton, MA) or GnuPlot. FCS calculation was performed in LabVIEW using a DLL gracefully provided by Dr. Ted Laurence37.
Supplementary Material
Movie 1: Blinking of single QDs corresponding to Fig. 5. Acquisition: 1 fps, 200 nm/pixel. The movie is sped up 8 times.
Movie 2: 3D representation of the temporal evolution of the intensity image of a single QD discussed in Fig. 6A. Spatial binning: none, temporal binning: 1 s. The movie is sped up 8 times. 1 pixel = 25 nm.
Movie 3: 3D representation of the temporal evolution of the intensity image of a single QD discussed in Fig. 6B. Spatial binning: 4, temporal binning: 1 s. The movie is sped up 8 times. 1 pixel = 100 nm.
Movie 4: 3D representation of the temporal evolution of the intensity image of a single QD discussed in Fig. 6C. Spatial binning: 8, temporal binning: 1 s. The movie is sped up 8 times. 1 pixel = 200 nm.
Movie 5: Diffusion of a QD cluster corresponding to Fig. 7. Acquisition: 1 fps, 513 nm/pixel. The movie is sped up 8 times.
8. Acknowledgments
This work was funded by the NIH (grant 5R01 GM-084327) and the NSF (grant DBI-0552099). We thank Dr. Ted Laurence for providing his LabVIEW correlation function calculation code.
Appendix: Optimal detector size and resolution
To obtain an order of magnitude of the size of a region that can be imaged with good resolution with the 128 × 128 pixel EMCCD, it is convenient to refer to a simple criterion used in high-resolution localization38. For a pixilated detector, the best localization resolution of a point source (at a given input number N of photons) is obtained when the detector pixel size a is equal to:
| (2) |
where σ is the standard deviation of the Gaussian fitted to the point source image and b the standard deviation of the readout noise per pixel (corrected here by a factor G as in Eq. (1)). Using b = 46 e− rms (as reported by the vendor of our camera) it can be verified that Eq. (2) results in values between 0.16 (N = G = 1,000) and 0.89 (N = G = 100) for values of 100 < N, G < 1,000. In other words, an optimal pixel size is such that a < σ.
It can be shown that for an Airy disk (ideal image of a perfectly focused point source):
| (3) |
where λ is the emission wavelength and NA the numerical aperture of the objective lens. The full width at half maximum (FWHM) of the Airy disk is:
| (4) |
For λ = 600 nm and NA = 1.45, σ = 87 nm and FWHMAiry = 211 nm. The actual dimension of the imaged PSF might be larger than this value if imaging is not perfect (for instance, if the image is out of focus).
These values allow us to estimate the field of view of the 128 × 128 pixel EMCCD used in optimal conditions (pixel ~ σ = 87 nm) to be of the order of 11.4 μm wide. This is quite small and in particular not very well adapted to whole cell imaging, which would require more pixels.
Another important consideration is spot separation (Fig. 1). Using a pixel size defined for optimal localization, each spot occupies approximately a 5 × 5 pixel area. For immobile spots, tight packing would allow quite a large number of spots to be imaged on a 128 × 128 pixel sensor: for instance, if each spot is distant by at least 3 FWHM from the next to allow easy localization, ~300 spots can be easily fitted. For mobile spots, however, such a criterion is not sufficient to avoid paths crossing after a finite time t, resulting in confusion between spots or even spot overlap. Taking as a typical diffusion constant of single membrane protein the value D = 10−2 μm2/s (ref Traffic), a minimal separation d = 2 × √4Dt is necessary between spots as illustrated in Fig. 1. For observation duration of 1 min, this results in a minimum separation between spots of ~ 14 FWHM. In this case, a 128 × 128 pixel sensor could only accommodate a dozen such spots.
Therefore, it appears that realistic single-molecule tracking in live cells requires sensors several 100 pixels wide. Such sensors exist, as EMCCD with 512 × 512 or more pixels are available, but they are correspondingly slow, achieving at most video rate.
Note that up to now, we have discussed a detector with readout noise. Different considerations apply for detectors without readout noise, such as the photon-counting detector discussed in this article. For such a detector, the localization resolution δx is given approximately by:
| (5) |
which in principle becomes better as the pixel size a decreases. However, for very small pixel sizes, the signal per pixel becomes very low (at fixed counts N), preventing the fitting approach underlying this localization resolution theory to be applied successfully. Assuming that N is large enough for the fitting approach to work in all situations, the resolution improvement by decreasing a from a = σ to a = σ/2 is only ~ 3 %, with a maximum resolution obtained (theoretically) for a = 0, reaching only 4 % compared to the reference case a = σ. For all practical purposes, a choice of a = σ is therefore appropriate.
References
- 1.Weiss S. Science. 1999;283:1676–1683. doi: 10.1126/science.283.5408.1676. [DOI] [PubMed] [Google Scholar]
- 2.Weiss S. Nature Structural Biology. 2000;7(9):724–729. doi: 10.1038/78941. [DOI] [PubMed] [Google Scholar]
- 3.Michalet X, Weiss S. Comptes Rendus Physique. 2002;3(5):619–644. [Google Scholar]
- 4.Michalet X, Weiss S, Jäger M. Chem. Rev. 2006;106(5):1785–1813. doi: 10.1021/cr0404343. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Betzig E, Patterson GH, Sougrat R, Lindwasser OW, Olenych S, Bonifacino JS, Davidson MW, Lippincott-Schwartz J, Hess HF. Science. 2006;313(5793):1642–1645. doi: 10.1126/science.1127344. [DOI] [PubMed] [Google Scholar]
- 6.Bates M, Huang B, Dempsey GT, Zhuang X. Science. 2007;317(5845):1749–1753. doi: 10.1126/science.1146598. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Hell SW. Science. 2007;316(5828):1153–1158. doi: 10.1126/science.1137395. [DOI] [PubMed] [Google Scholar]
- 8.Michalet X, Pinaud FF, Bentolila LA, Tsay JM, Doose S, Li JJ, Sundaresan G, Wu AM, Gambhir SS, Weiss S. Science. 2005;307:538–544. doi: 10.1126/science.1104274. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Michalet X, Cheng A, Antelman J, Suyama M, Arisaka K, Weiss S. Proceedings of SPIE. 2008;6862:68620F. doi: 10.1117/12.763449. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Guerrieri F, Tisa S, Zappa F. Proceedings of SPIE. 2009;7249:72490U. [Google Scholar]
- 11.Siegmund OHW, Michalet X, Vallerga JV, Jelinsky P, Weiss S. IEEE Nuclear Symposium Conference Record. 2005;N14-55:448–452. [Google Scholar]
- 12.Michalet X, Siegmund OHW, Vallerga JV, Jelinsky P, Millaud JE, Weiss S. Nucl. Instr. Meth. Phys. Res. A. 2006;567:133–136. doi: 10.1016/j.nima.2006.05.155. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Michalet X, Siegmund OHW, Vallerga JV, Jelinsky P, Millaud JE, Weiss S. SPIE Proc. 2006;6092:60920M. doi: 10.1117/12.646482. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Michalet X, Siegmund OHW, Vallerga JV, Jelinsky P, Pinaud FF, Millaud JE, Weiss S. Proceedings of SPIE. 2006;6372:63720E. doi: 10.1117/12.686429. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Colyer R, Siegmund O, Tremsin A, Vallerga J, Weiss S, Michalet X. Proceedings of SPIE. 2009;7185:71850T. doi: 10.1117/12.809496. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Nirmal M, Dabbousi BO, Bawendi MG, Macklin JJ, Trautman JK, Harris TD, Brus LE. Nature. 1996;383:802–804. [Google Scholar]
- 17.Efros AL, Rosen M. Physical Review Letters. 1997;78(6):1110–13. [Google Scholar]
- 18.Kuno M, Fromm DP, Hamann HF, Gallagher A, Nesbitt DJ. Journal of Chemical Physics. 2000;112:3117–3120. [Google Scholar]
- 19.Chen Y, Vela J, Htoon H, Casson JL, Werder DJ, Bussian DA, Klimov VI, Hollingsworth JA. Journal of the American Chemical Society. 2008;130(15):5026–5027. doi: 10.1021/ja711379k. [DOI] [PubMed] [Google Scholar]
- 20.Mahler B, Spinicelli P, Buil S, Quelin X, Hermier JP, Dubertret B. Nature Materials. 2008;7(8):659–664. doi: 10.1038/nmat2222. [DOI] [PubMed] [Google Scholar]
- 21.Dahan M, Laurence T, Pinaud F, Chemla DS, Alivisatos AP, Sauer M, Weiss S. Optics Letters. 2001;26(11):825–828. doi: 10.1364/ol.26.000825. [DOI] [PubMed] [Google Scholar]
- 22.Schlegel G, Bohnenberger J, Potapova I, Mews A. Physical Review Letters. 2002;88(13):137401. doi: 10.1103/PhysRevLett.88.137401. [DOI] [PubMed] [Google Scholar]
- 23.Michalet X, Siegmund OHW, Vallerga JV, Jelinsky P, Millaud JE, Weiss S. J. Mod. Opt. 2007;54:239–282. doi: 10.1080/09500340600769067. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Ulbrich MH, Isacoff EY. Nature Methods. 2007;4(4):319–321. doi: 10.1038/NMETH1024. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Verberk R, van Oijen AM, Orrit M. Physical Review B. 2002;66:233202. [Google Scholar]
- 26.Becker W. Advanced time-correlated single photon couting techniques. Springer; Berlin: 2005. [Google Scholar]
- 27.We checked that for a constant illumination source (attenuated room light), our SPAD recorded Poisson-distributed time traces.
- 28.Messin G, Hermier JP, Giacobino E, Desbiolles P, Dahan M. Optics Letters. 2001;26(23):1891–1893. doi: 10.1364/ol.26.001891. [DOI] [PubMed] [Google Scholar]
- 29.An additional factor makes using very fine binning somewhat useless. Indeed, the absolute localization accuracy of the H33D was estimated to be of the order of ~50-100 μm (ref. 23). Since the sensitive area of diameter 27 mm is represented by ~ 400 pixels when binning with a factor 8, each pixel represents a square of the detector with side ~ 68 μm. Since this is close to the expected localization accuracy, there is not much localization improvement to expect by using binning factors of 2 or 1.
- 30.Antelman J, Wilking-Chang C, Weiss S, Michalet X. 2009. submitted. [DOI] [PMC free article] [PubMed]
- 31.Michalet X, Lacoste TD, Weiss S. Methods. 2001;25(1):87–102. doi: 10.1006/meth.2001.1218. [DOI] [PubMed] [Google Scholar]
- 32.Pinaud F, Michalet X, Iyer G, Margeat E, Moore H-P, Weiss S. Traffic. 2009 doi: 10.1111/j.1600-0854.2009.00902.x. in press. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Clayton AHA, Hanley QS, Verveer PJ. Journal of Microscopy. 2004;213(1):1–5. doi: 10.1111/j.1365-2818.2004.01265.x. [DOI] [PubMed] [Google Scholar]
- 34.Redford GI, Clegg RM. Journal of Fluorescence. 2005;15(5):805–815. doi: 10.1007/s10895-005-2990-8. [DOI] [PubMed] [Google Scholar]
- 35.Digman MA, Caiolfa VR, Zamai M, Gratton E. Biophysical Journal. 2008;94(2):L14–L16. doi: 10.1529/biophysj.107.120154. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Iyer G, Michalet X, Chang Y-P, Pinaud FF, Matyas SE, Payne G, Weiss S. Nano Letters. 2008;8:4618–4623. doi: 10.1021/nl8032284. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Laurence TA, Fore S, Huser T. Optics Letters. 2006;31(6):829–831. doi: 10.1364/ol.31.000829. [DOI] [PubMed] [Google Scholar]
- 38.Thompson RE, Larson DR, Webb WW. Biophys. J. 2002;82:2775–2783. doi: 10.1016/S0006-3495(02)75618-X. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Movie 1: Blinking of single QDs corresponding to Fig. 5. Acquisition: 1 fps, 200 nm/pixel. The movie is sped up 8 times.
Movie 2: 3D representation of the temporal evolution of the intensity image of a single QD discussed in Fig. 6A. Spatial binning: none, temporal binning: 1 s. The movie is sped up 8 times. 1 pixel = 25 nm.
Movie 3: 3D representation of the temporal evolution of the intensity image of a single QD discussed in Fig. 6B. Spatial binning: 4, temporal binning: 1 s. The movie is sped up 8 times. 1 pixel = 100 nm.
Movie 4: 3D representation of the temporal evolution of the intensity image of a single QD discussed in Fig. 6C. Spatial binning: 8, temporal binning: 1 s. The movie is sped up 8 times. 1 pixel = 200 nm.
Movie 5: Diffusion of a QD cluster corresponding to Fig. 7. Acquisition: 1 fps, 513 nm/pixel. The movie is sped up 8 times.