Electric field dependence of nonlinearity parameters and third order elastic constants of 0.70Pb(Mg_1∕3Nb_2∕3)O₃–0.30PbTiO₃ single crystal

Abstract

Through second harmonic measurements, the ultrasonic nonlinearity parameters of [001]_c and [111]_c polarized 0.70Pb(Mg_1∕3Nb_2∕3)O₃–0.30PbTiO₃(PMN–0.3PT) single crystals have been measured as a function of bias electric field. It was found that the nonlinearity parameter increases almost linearly with field at low field but shows a drastic increase near the coercive field. The [111]_c polarized single domain crystal has much smaller nonlinearity parameter than that of the [001]_c polarized multidomain crystal. Based on effective symmetries of these crystals, we were able to derive the field dependence of several third order elastic constants, which are important parameters for high field applications.

(1−x)Pb(Mg_1∕3Nb_2∕3)O₃–xPbTiO₃(PMM–xPT) single crystals have attracted a lot of attention in recent years because of its ultrahigh piezoelectric constants and electromechanical coupling factors, which can lead to revolutionarily changes in electromechanical devices, such as ultrabroadband ultrasonic transducers, very large displacement actuators, etc. Researchers have been trying to understand the mechanism of domain engineering method that can produce ultrahigh piezoelectric and dielectric constants.^{1, 2, 3, 4} It was demonstrated that the domain engineering method can also greatly enhance the functional properties in traditional ferroelectric single crystals, such as BaTiO₃.^{5, 6, 7} Studies had demonstrated that the achieved functional properties in PMN–xPT single crystals depend on the composition, applied electric field, and temperature.^{8, 9}

In practical applications, particularly in applications requires high driving field, the performance of domain engineered crystals often degrade and their behavior could not be explained by linear theory. Therefore, it is critical to understand the nonlinear behavior of these crystals and quantify their field dependence. There are a few published works studying the piezoelectric nonlinearity of ceramics and crystals.^{10, 11, 12, 13} For the acoustic nonlinearity, Jiang and Cao¹⁴ had studied PMN–PT ceramics and found its nonlinearity parameter to be twice as large compared with ordinary piezoelectric materials. Harmonic generation of transverse acoustic waves in LiNbO₃ crystals and PZT ceramics were also studied.^{15, 16}

In ferroelectric materials, very strong nonlinear phenomena can be found accompanied with domain switching process. In fact, Yin and Cao^{17, 18} had used the onset of steep nonlinearity rise to judge the degree of polarization switching in 0.955Pb(Zn_1∕3Nb_2∕3)O₃–0.045PbTiO₃(PZN–PT) crystals.

Nonlinearity parameter quantifies the degree of nonlinear physical phenomena, such as wave distortion and second harmonic generation. In ferroelectric materials, acoustic nonlinearity are often closely linked to other type of nonlinear phenomena, such as nonlinear dielectric and piezoelectric responses.¹⁹ In this letter, we report an experimental study on the acoustic nonlinearity parameter of PMN-0.30PT single crystal and its electric field dependence. Based on effective symmetries of the multidomain crystals, we were also able to calculate the field dependence of a few third order elastic constants, which were never reported before. Our experimental results showed that the change of nonlinearity parameter induced by external field directly reflects the change of domain structures.

The PMN–0.30PT crystals used in this work were grown by TRS Ceramics (State College, PA 16801) using a modified Bridgeman method. The crystallographic orientations were determined by a DX-4 x-ray single-crystal orientation unit with an accuracy of ±0.5°. One crystal was cut into a cuboid of 15.88×13.33×14.18 mm³ with orientations of [100]_c∕[010]_c∕[001]_c, where the subscript “c” refers to cubic coordinates. Another crystal was a 15.05 mm long cylinder with a diameter of 14.87 mm and the orientation along the cylindrical axis is [111]_c.

The experimental setup was similar to the one used in Ref. 14. The samples were immersed in silicon oil for better electric insulation. A tone burst signal from an arbitrary generator (Wavetek) was fed into a power amplifier (LogiMetrix), and the output was applied to a 5 MHz transmitting transducer. After the signal traveled through the sample along [001]_c or [100]_c for the cuboid sample, or along [111]_c for the cylinder sample, it was detected by a broadband transducer, which can detect both the 5 and 10 MHz signals. A low-pass filter (whose cutoff frequency is 5 MHz) was used after the signal was amplified by the power amplifier in order to eliminate the nonlinearity noise of the measurement system. The received signals were sent to a digital oscilloscope and downloaded to a computer for further signal processing. High voltage (Bertan high voltage supply) was applied incrementally along [001]_c for the cuboid sample and along [111]_c for the cylinder sample, respectively, to find the field dependence.

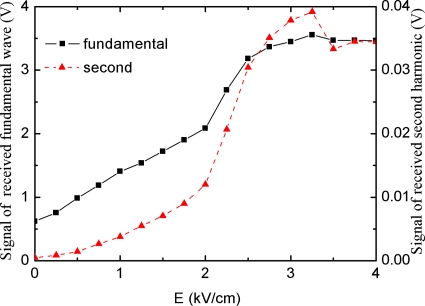
The receiver was calibrated carefully²⁰ so that we can measure the absolute amplitude of the received signal. An aluminum sample was tested using our setup and the measured nonlinearity parameter is 5.3, which agrees well with the reported result of Ref. 21. The magnitude of the received signal traveling along [001]_c through the cuboid PMN-0.30PT sample increased with the applied electric field along [001]_c and became saturated at about 3 kV∕cm (Fig. 1), which means that the sound attenuation of the sample continues to decrease as the number of domains are reduced during the poling process. For the [001]_c poled case, all downward domains with polarizations along ${\left[11\overline{1}\right]}_{\text{c}}$, ${\left[1\overline{1}\overline{1}\right]}_{\text{c}}$, ${\left[\overline{1}1\overline{1}\right]}_{\text{c}}$, and ${\left[\overline{1}\overline{1}\overline{1}\right]}_{\text{c}}$ have been eliminated but the domain states with polarization along [111]_c, ${\left[\overline{1}11\right]}_{\text{c}}$, ${\left[1\overline{1}1\right]}_{\text{c}}$, and ${\left[\overline{1}\overline{1}1\right]}_{\text{c}}$ remain. For the cylinder sample, only the [111]_c domain survived at very high field.

Figure 1.

Field dependence of the received fundamental and second harmonic signals for PMN-0.30PT with the electric field along [001]_c.

Domain wall regions have lower crystal symmetry and they have many special properties. Therefore, one could use domain boundary engineering to realize functionality that are not allowed in the underlying crystal symmetry.²² Near the coercive field, these domain walls become extremely active so that they contribute substantially to the nonlinear response. As the number of domains being eliminated with increasing field, active domain walls are reduced. When the samples are fully polarized, the remaining domain walls are not mobile type (neutral wall oriented along the field direction while charged walls perpendicular to the field direction) so that they will have almost no contributions to the nonlinearity observed.

As shown in Fig. 1, the second harmonic component of the received signal increased with the applied electric field at low field level and reached its maximum when the electric field was about 3.25 kV∕cm, then showed a slight decrease.

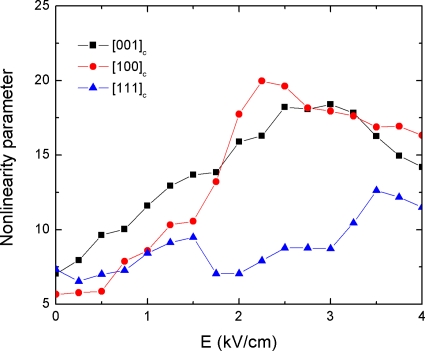
The measured acoustic nonlinearity parameter versus applied electric field along [001]_c is given in Fig. 2. At low field level from 0 to 1.75 kV∕cm, the acoustic nonlinearity parameter changes almost linearly with the applied electric field. For field level beyond 1.75 kV∕cm, the nonlinearity parameter increased faster and reached a peak near 3.0 kV∕cm. This drastic change of the nonlinearity parameter indicated the onset of domain switching. The change of the acoustic nonlinearity parameter of the cuboid PMN-0.30PT crystal in the transverse direction [100]_c is also shown in Fig. 2, for which the wave propagation direction is along [100]_c and the field was applied along [001]_c. One can see that the field dependence is more nonlinear but the basic trend is similar to the previous case. There is also a peak value of the nonlinearity parameter near 2.2 kV∕cm. It should be mentioned that the same sample was used for these two measurements but the sample was depoled completely through high temperature annealing after each round of measurement.

Figure 2.

Electric field dependence of the nonlinearity parameter along [001]_c and [100]_c for [001]_c poled, and along [111]_c for [111]_c poled PMN-0.30PT single crystals.

The rhombohedral PMN-0.30PT single crystal has eight ⟨111⟩ family domain states, which are randomly distributed before poling. As the electric field is increased along the [001]_c direction, domain switching occurred at a critical threshold and eventually the four downward domains were eliminated. The nonlinearity parameter changed moderately when the electric field was less than the coercive field (E_c≅2.2–3.0 kV∕cm),^{23, 24} and the field dependence is almost linear. Above the coercive field (E=2.5 kV∕cm), the nonlinearity parameter exhibited more drastic change with the electric field due to domain switching. As more and more domains are being switched, the nonlinearity parameter starts to decrease after reaching a peak value but the nonlinearity at the fully polarized situation is still more than the zero-field situation.

In order to confirm domain and domain wall contributions to the nonlinearity parameter, we also did the same experiment for a cylinder PMN-0.30PT sample with the axial orientation to be [111]_c. The field and wave propagation directions are both along [111]_c. We found that the acoustic nonlinearity parameter was much smaller in this case because the process will eventually produce a single domain state. The coercive field is higher along [111]_c than along [001]_c (Ref. ²⁵) so that the nonlinearity increase associated with domain switching occurred at a larger field level (∼3 kV∕cm). (Fig. 2).

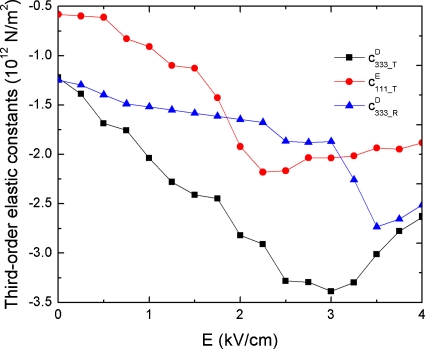
We can derive three third order elastic constants from the measured nonlinearity parameter β. For a single crystal poled along [001]_c, the macroscopic symmetry is tetragonal 4mm, while for a crystal poling along [111]_c, the single domain symmetry is rhombohedral 3mm. Therefore, the nonlinearity parameter for the [001]_c poled sample can give us 2 third-order elastic constants for the tetragonal symmetry: $c_{333\text{\_T}}^D=-\left(3+\beta \right)c_{33\text{\_T}}^D$ and $c_{111\text{\_T}}^E=-\left(3+\beta \right)c_{11\text{\_T}}^E$, respectively, while for the [111]_c poled sample, we have $c_{333\text{\_R}}^D=-\left(3+\beta \right)c_{33\text{\_R}}^D$, where c_{ij_T} and c_{ij_R} are the corresponding second elastic constants for the tetragonal and rhombohedral symmetries, respectively. The calculated field dependence of the third-order elastic constants is showed in Fig. 3 for the 3 third-order elastic constants. One can see that the absolute value of the third order elastic constants all increase with bias field at low field level, reach a peak value, then show slight decrease in the fully poled samples. Specifically, $\left|c_{333\text{\_T}}^D\right|$ peaks at 3 kV∕cm, $\left|c_{111\text{\_T}}^E\right|$ peaks at 2.25 kV∕cm and $\left|c_{333\text{\_R}}^D\right|$ peaks at 3.5 kV∕cm.

Figure 3.

Electric field dependence of the effective third-order elastic constants $c_{333\text{\_T}}^D$, $c_{111\text{\_T}}^E$, and $c_{333\text{\_R}}^D$.

In summary, using a specially designed second harmonic generation setup, we were able to measure the filed dependence of the nonlinearity parameter and found the correlation to domain switching. The field dependence of the acoustic nonlinearity parameter and the nonlinear elastic constants obtained in this work can provide useful input parameters for the design of piezoelectric devices using domain engineered PMN-0.30PT single crystals, particularly for those devices operating at high field.