Monte Carlo evaluation of object shape effects in iodine-131 SPET tumor activity quantification

Abstract

In our clinical iodine-131 single-photon emission tomography (SPET) quantification for radioimmunotherapy, calibration and partial volume correction are based on measurements with phantoms containing spheres to simulate patient tumors even though real tumors are frequently nonspherical. In this study, Monte Carlo simulation was used to evaluate how object shape influences “spill-out” and “spill-in”, which are major sources of quantification error associated with the poor spatial resolution of ¹³¹I SPET. Objects that varied in shape (spheres, cylinders, and an irregular structure) but were identical in activity and volume were simulated. Iterative reconstruction employed both attenuation and triple-energy-window scatter compensation. VOIs were defined in the reconstructed images both using physical boundaries and using expanded boundaries to allow for the limited resolution. When physical boundaries were used, both spill-out and spill-in were more significant for nonspherical structures than for spherical structures. Over the range of object volumes (50–200 ml) and at all background levels, VOI counts in cylinders were lower than VOI counts in spheres. This underestimation increased with decrease in object size (for the cold background −18% at 200 ml and −39% at 50 ml). It also decreased with increase in background activity because spill-in partially compensated for spill-out. It was shown that with a VOI larger than physical size, the results are independent of object shape and size only in the case of cold background. Activity quantification was carried out using a procedure similar to that used in our clinic. Quantification of nonspherical objects was improved by simple sphere-based partial volume correction, but the error was still large in some cases (for example, −39% for a 50-ml cylinder in a cold background and −35% for a 200-ml irregular structure defined on the basis of a typical tumor outlined on an X-ray computed tomography scan of a patient with non-Hodgkin’s lymphoma). Partial volume correction by patient-specific Monte Carlo simulation may provide better quantification accuracy.

Introduction

Single-photon emission tomography (SPET) imaging is often used to quantify iodine-131 tumor uptake in patients following radiopharmaceutical therapy [1, 2, 3, 4]. SPET quantification accuracy is affected by many factors, including attenuation, scatter, and finite spatial resolution. The last-mentioned is a major concern in ¹³¹I SPET because typically collimators optimized for higher energy isotopes have poor spatial resolution. Commercial ¹³¹I collimators are designed with thicker septa and larger hole size in order to limit penetration while keeping the sensitivity acceptable, and a trade-off is poor resolution. Tumor activity quantification is affected by the spread or blurring of regional counts to surrounding areas owing to the finite spatial resolution of the system. The “spill-out” of counts from the target to the background decreases the tumor activity estimate as the source structure gets smaller while the “spill-in” contribution from the background to the target increases the tumor activity estimate. The spill-out depends on the shape and size of the source structure and the system resolution while spill-in depends on these parameters as well as the activity level and distribution in the background. The term “partial volume effect” (PVE) is used in this work to describe both aspects of poor resolution (that is, both spill-out and spill-in).

PVEs in emission tomography are well understood. However, studies addressing the magnitude of the problem in SPET activity quantification are limited, particularly with respect to object shape and nontarget activity. In addition to the work by our group with ¹³¹I [5, 6], there have been two recent studies on effects of object size on technetium-99m quantification and the use of recovery coefficients (RCs) in SPET [7, 8]. In these two studies the partial volume correction models proposed by Hoffman et al. [9] and Kessler et al. [10] for position emmission tomography (PET) were assessed for SPET quantification of spherical objects. Hot spot RCs (to correct for spill-out) and cold spot RCs (to correct for spill-in) were determined in calibration experiments using spheres of different sizes. Zito et al. used these RCs to correct measured radioactivity concentrations in spheres for a range of object sizes and showed good agreement with the true radioactivity concentration [8]. On the other hand the work of Geworski et al. demonstrated that while partial volume correction based on physical phantom studies is feasible in PET, it is subject to serious difficulties in the case of SPET [7]. They concluded that this was due to imperfections in the scatter and attenuation correction methods that were used. Our group previously reported on the effect of object size on ¹³¹I SPET quantification evaluated by Monte Carlo simulation of phantoms containing spheres [5]. The previous study, where the object size varied from 20 to 200 ml and where no partial volume correction was used, showed that quantification accuracy depends strongly on object size and background activity. All of the above-mentioned studies involved spherical objects and to our knowledge there has been only one previous investigation in which the effect of object shape on SPET activity quantification was specifically addressed [11]. In that work, ^99mTc and ¹³¹I phantom experiments were carried out to evaluate the effect of activity, volume, shape, and uniformity of activity on both volume and activity determination. Shape effects were evaluated using objects that were cylindrical, cuboidal, conic, and spherical in shape. In all cases, object volume was relatively large (300 ml) and no background activity was present. Using the quantification technique defined in the publication, which included a thresholding method for VOI determination, it was shown that activity assessment is unaffected by shape. However, these shape-independent results were obtained only after expanding the boundary of the threshold-determined VOI (by up to 18 mm) to make allowance for the limited SPET resolution [12].

At the University of Michigan our group has developed a clinical SPET tumor quantification procedure for non-Hodgkin’s lymphoma (NHL) patients undergoing ¹³¹I radioimmunotherapy (RIT) [1]. A background-dependent calibration factor is determined from measurements carried out using a 200-ml ¹³¹I-filled sphere centered in an elliptical phantom at several background activity levels. To account for spatial resolution effects, volume-dependent RCs are determined based on measurements with spherical objects of various sizes situated in uniform background levels [6]. Irrespective of the patient tumor shape, the sphere-based calibration factor and RCs are used when quantifying uptake. Although a sphere can be a fairly good approximation of tumor shape in some cases, sometimes tumor shapes are very irregular. Since PVEs are dependent on object shape, we can expect significant error when sphere-based RCs are used for activity quantification of nonspherical structures. In this work we study object shape effects in quantitative ¹³¹I SPET using Monte Carlo simulation of tumor phantoms. We evaluate how VOI counts vary in reconstructed SPET images of objects that vary in shape but are identical in activity and volume. In our evaluation a range of object volumes and background activities are considered. Using a quantification procedure similar to that used in the clinic, we also evaluate quantification accuracy in nonspherical structures.

Materials and methods

SPET system and Monte Carlo model

The SPET camera modeled in this work was a Picker Prism XP3000 with an ultra-high-energy general-purpose (UHEGAP) collimator. In a previous study we showed that the ultra-high-energy collimator substantially reduces ¹³¹I septal penetration compared with the commonly used high-energy collimator [5]. The NaI crystal measured 24 cm×40 cm×0.95 cm. The measured energy resolution at 364 keV was 10.2% (FWHM). SPET simulations employed 360°, 60 angles, a 20% photopeak window at 364 keV, two 6% adjacent scatter correction windows, and a 64×64 matrix with a pixel size of 7.2 mm.

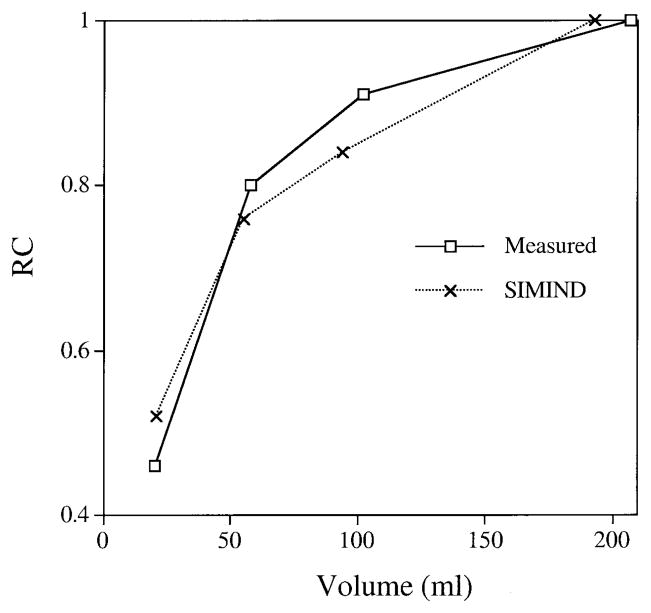
All Monte Carlo simulations were carried out using the well-established SIMIND code [13]. The version of the code that is used here is coupled to a collimator routine [14] that explicitly models collimator scatter and penetration. The camera model includes a 5-cm glass layer behind the NaI crystal to model backscatter. Note that for ease of implementation the collimator routine is restricted to a rectangular hole shape. The hexagonal hole shape UHEGAP collimator was approximated in the simulation by a square hole collimator that has the same open area and lead content as proposed by de Vries et al. [14]. Previously we have extensively validated SIMIND for ¹³¹I SPET by showing good agreement between measurement and simulation for both point source and phantom geometries [5, 15]. As a further validation particularly relevant to the present work, measured and simulated RCs are compared in Fig. 1. The RCs were defined as in the section below on absolute quantification. At all sphere volumes there is good agreement between measurement and simulation, giving us confidence that the Monte Carlo modeling reflects reality within an acceptable level of error. Note that the data of Fig. 1 correspond to a high-energy collimator and not to the UHEGAP collimator because measured data for this case already existed from a previous study [6].

Fig. 1.

Comparison of recovery coefficients (RC) from measurement and Monte Carlo simulation (SIMIND)

Phantom simulations

SPET projection data were generated by Monte Carlo simulation of the phantom and camera. A large number of emitted photons (more than 10⁸ per projection) were simulated to produce low-noise projection images. Spherical objects were compared with other objects that differed in shape but were equal in volume and activity. In all cases the simulated SPET acquisition time was the same and true activity within each object was 1 MBq. The radius of rotation was 26 cm.

Analytical phantom

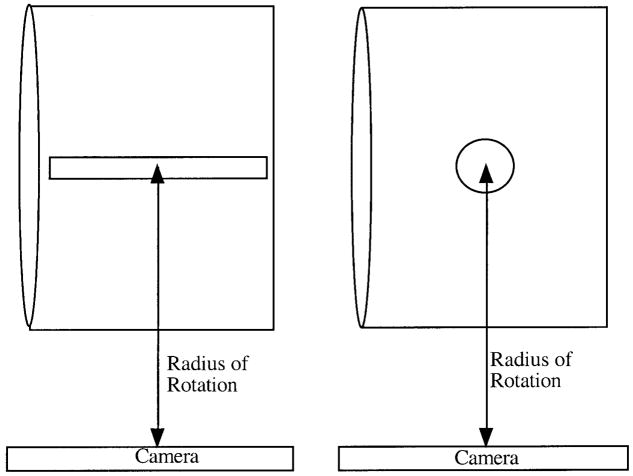
The tumors were modeled as spherical structures or thin long cylindrical structures centered in a water-filled elliptical phantom representing the rest of the body (Fig. 2). The elliptical phantom was 23 cm×31.5 cm and 20.5 cm in height. The sphere and cylinder volumes were 50 ml, 100 ml, and 200 ml. At each volume the cylinder radius was set at one-half that of the sphere and the height was determined such that the sphere and the cylinder had the same volume. The dimensions of the simulated structures are given in Table 1. In the first case, the ¹³¹I-filled hot objects were in a cold background. Next, to assess the effect of spill-in, the above six structures were also simulated in the presence of background ¹³¹I activity in the elliptical phantom. The background to tumor activity concentration ratio, b, was 1/5 and 1/3.

Fig. 2.

Cylindrical and spherical objects in the elliptical phantom as modeled in the Monte Carlo simulation

Table 1.

Dimensions of the spherical and cylindrical shaped objects used in the simulation

Volume (ml)	Sphere	Cylinder
	Radius, r (cm)	Radius, r (cm)	Height, h (cm)
50	2.29	1.14	12.14
100	2.88	1.44	15.35
200	3.63	1.8	19.65

Voxel phantom

Tumors were defined within the “voxel-man,” which is a digitized anthropomorphic phantom [16] that has been coupled to the SIMIND code. We added a feature that allows activities to be assigned to arbitrary-shaped structures that can be superimposed onto the activity distributions of the voxel-man. An irregular structure was defined based on a typical tumor outlined on an X-ray computed tomography (CT) scan of an NHL patient who underwent ¹³¹I RIT at our clinic. Using the X-ray CT images as a guide, the tumor shape and location were reproduced closely and superimposed onto the voxel-man. Two typical slices of the voxel-man density map are shown in Fig. 3, including the tumor outline on these slices. The total tumor volume was 202 ml and it was simulated in a cold background. For comparison, a voxel-man simulation with a sphere that had the same volume, activity, and location as the irregular structure was also carried out.

Fig. 3.

Typical density maps of the voxel-man phantom including the outline of the simulated tumor

Reconstruction and definition of VOI

Phantom projections were reconstructed using a space alternating generalized expectation-maximization algorithm (SAGE) [17]. The algorithm employed an attenuation-weighted-strip-integral and incorporated scatter estimates based on the triple-energy window (TEW) method into the Poisson statistical model. In the case of the analytical phantom, the attenuation coefficient of water at 364 keV (0.11 cm⁻¹) and the actual dimensions of the elliptical phantom were used to generate the attenuation map. For the voxel-man, attenuation coefficient maps were generated based on the registered density images.

In the reconstructed images the VOIs corresponding to the simulated structures were defined in two ways. In the first case, a tight boundary corresponding to the physical size and location of each structure was used to define the VOI. The use of physical VOIs is consistent with our clinical SPET procedure, where patient tumor outlines are drawn on a CT scan and superimposed onto the SPET image following CT-SPET registration [1]. In the second approach the above physical VOIs were expanded to allow for the limited spatial resolution of SPET. In the analytical phantoms the expanded VOIs were defined by increasing the radii of the spheres and the radii and heights of the cylinders by either 1 pixel (0.72 cm) or 2 pixels (1.44 cm) from their true value. In voxel-man the expanded VOI was defined by carrying out a 2-pixel dilation operation on the physical VOI.

Absolute quantification

At each background level of the elliptical phantom, (1) the calibration factor (counts per second per MBq) was determined based on VOI counts corresponding to the 200-ml sphere and the known true activity, (2) SPET-estimated activities of the other spheres were determined using the calibration, and (3) the RC defined as the ratio between the SPET-estimated activity and the true activity was determined for each sphere size. The SPET-estimated activities of the nonspherical structures were determined using these sphere-based calibration and RCs. The procedure used here to convert VOI counts to activity is similar to that used in our clinic for ¹³¹I SPET studies. Note that instead of using separate corrections for spill-out (using a hot spot RC) and spill-in (using a cold spot RC) we carry out an “effective” partial volume correction that considers both object size and contrast.

Results

VOI counts

Analytical phantom

Table 2 compares the VOI counts in the reconstructed images corresponding to the two different objects. Note that in all cases the activity simulated within each object was the same and ideally the VOI counts should also be the same. First consider the case where physical VOIs were used. The cylinder VOI counts are consistently lower than the sphere VOI counts and the difference becomes less significant as object volume increases and background activity increases. Results of Table 2 also show the effect of object size on VOI counts. For example, in the cold background as the object volume decreases from 200 ml to 50 ml, the sphere counts decrease from 541 to 422 and the cylinder counts decrease from 457 to 303. When background activity is present, the decrease in VOI counts with decrease in volume is less significant.

Table 2.

Counts corresponding to the analytical phantoms with the VOI defined as specified

Volume (ml)	b	Physical VOI		Expanded VOI (r,h increased by 1 pixel)		Expanded VOI (r,h increased by 2 pixels)
		Sphere counts	Cylinder counts	Sphere counts	Cylinder counts	Sphere counts	Cylinder counts
50	0	422	303 (−39%)	625	562 (−11%)	766	730 (−5%)
100	0	465	360 (−29%)	657	617 (−6%)	777	755 (−3%)
200	0	541	457 (−18%)	711	638 (−11%)	788	762 (−3%)
50	1/5	479	381 (−25%)	768	818 (6%)	1,132	1,279 (11%)
100	1/5	495	417 (−19%)	744	809 (8%)	1,042	1,167 (11%)
200	1/5	548	502 (−9%)	781	746 (−5%)	960	1,050 (9%)
50	1/3	512	429 (−19%)	859	982 (13%)	1,365	1,647 (17%)
100	1/3	512	452 (−13%)	800	936 (15%)	1,212	1,424 (15%)
200	1/3	551	529 (−4%)	826	816 (1%)	1,071	1,239 (14%)

The values in parentheses are the percentage difference between sphere and cylinder counts

With the expanded VOIs, when there is no background present the underestimation of counts in the cylinder compared with the sphere is greatly reduced. For all of the volumes evaluated, the sphere and cylinder counts agree to within 5% with the VOI expanded by 2 pixels. The use of the expanded VOIs also reduces the dependence of VOI counts on object size for the case of the cold background. In this case, for both the cylinder and the sphere, the VOI counts vary by <5% as the object volume is varied. However, in the presence of background activity, use of expanded VOIs does not result in either shape-independent or size-independent results. With expanded VOIs the difference between sphere and cylinder VOI counts is generally reduced (compared with results for physical VOIs) at all background levels. But, use of expanded VOIs greatly increases the dependence of VOI counts on the background activity level for both the cylinder and the sphere at all volumes. For example, for the 200-ml sphere when b is increased from 0 to 1/3, the physical VOI counts increase by only 3% (from 541 to 551) whereas the expanded VOI counts increase by 36% (from 788 to 1,071). Because of this very large dependency on background activity, it was decided to only use physical boundaries for the activity quantification described in the next section. Use of physical boundaries is also consistent with our present clinical quantification procedure.

Voxel phantom

When physical boundaries were used, the VOI counts for the sphere and the irregular-shaped tumor were 578 and 399 respectively. This is an underestimation of 45% for the irregular structure VOI counts compared with the sphere VOI counts. With the expanded VOI, the counts for the sphere and the irregular-shaped tumor were 769 and 632 respectively, reducing the underestimation to 22%.

Absolute activity

Counts in the physical VOIs given in columns 3 and 4 of Table 2 were used for activity quantification. The sphere-based calibration factor in units of counts per second per MBq was 541, 548, and 551 at b=0, 1/5, and 1/3 respectively. The RCs for each sphere volume are given in Table 3 for the different background levels. Note that the RC is unity at 200 ml because the calibration factor was also determined from this simulation. Table 3 also gives quantification results for each cylinder both with and without partial volume correction. With no partial volume correction, quantification error was in the range −4% to −79%. With the use of sphere-based partial volume correction, quantification error was in the range −4% to −39%.

Table 3.

Cylinder activity quantification

Cylinder volume (ml)	b	Recovery coefficient (from spheres)	Activity without RC (MBq)	Activity with RC (MBq)
50	0	0.78	0.56 (−79%)	0.72 (−39%)
100	0	0.86	0.67 (−50%)	0.77 (−29%)
200	0	1.00	0.85 (−18%)	0.85 (−18%)
50	1/5	0.87	0.70 (−44%)	0.80 (−25%)
100	1/5	0.90	0.76 (−32%)	0.84 (−19%)
200	1/5	1.00	0.91 (−9%)	0.91 (−9%)
50	1/3	0.93	0.78 (−28%)	0.84 (−19%)
100	1/3	0.93	0.82 (−22%)	0.88 (−13%)
200	1/3	1.00	0.96 (−4%)	0.96 (−4%)

The values in parentheses are the percentage difference between the estimated activity and the true value of 1 MBq. VOIs were defined using physical boundaries

For voxel-man, using the physical VOI counts and the calibration factor determined above, the activity for the irregular-shaped structure was estimated as 0.74 MBq. This is an error of −35% compared with the true simulated activity of 1 MBq. Note that the RC for this tumor is unity because its volume is approximately 200 ml.

Discussion

The purpose of this work was to evaluate PVEs in ¹³¹I SPET activity quantification in different object shapes. In a paper on anatomical effects in PET quantitation it was reported that objects that are circular suffer less from PVEs than irregular structures [18]. Our present results showed that spill-out is more significant in non-spherical structures than in spherical structures. This is evident from the fact that when physical boundaries were used to define the VOI, counts corresponding to non-spherical structures were significantly underestimated compared with spherical objects in the case of the cold background. This underestimation became less severe as background activity increased because spill-in from the background is also more significant for nonspherical structures than for spherical structures. The spill-in from background to object partially compensates for spill-out from object to background, and the level of compensation increases with increase in background. For example, for the 200-ml volume the cylinder VOI counts were 18% lower than the sphere VOI counts at b=0 but this difference was reduced to 4% at b=1/3. The present results also showed that both spill-out and spill-in effects increase with decreasing object size. The difference between VOI counts in spherical objects compared with nonspherical objects of the same volume and activity is especially significant to our ¹³¹I clinical SPET quantification procedure, where the calibration factor and RCs are determined by measurements with spherical phantoms [1]. The present Monte Carlo evaluation shows that use of the sphere-based RCs irrespective of the patient tumor shape can result in large quantification error. Partial volume correction substantially improved activity estimation but the error was still large in some cases (up to −39% for cylinders and −35% for the irregular structure). In order to improve quantification accuracy we are presently developing a 3-D depth-dependent collimator response correction in the reconstruction algorithm to minimize resolution effects [19]. Another approach to shape-independent activity quantification is partial volume correction using co-registered anatomical information. This method has been investigated for SPET using co-registered X-ray CT images [3] and for brain PET using co-registered MR images [20]. We are presently considering the feasibility of determining tumor-specific RCs using Monte Carlo simulation. As was done in the present work, simulations using the voxel-man phantom can be carried out for each patient with arbitrarily shaped tumors defined on the basis of patient X-ray CT. Alternatively, the simulation can be made more patient-specific by using the X-ray CT to create a voxel phantom of the patient with activity distributions determined from the patient SPET. Carrying out a simulation for each patient is computationally very tedious but is feasible using the version of the SIMIND code that we recently implemented on a parallel architecture [15].

In the analytical phantoms, use of expanded VOIs minimized both object shape and size effects only for the case of the cold background. The shape-independent activity assessment using expanded VOIs reported by Alaamer et al. was also carried out with a cold background [11]. By expanding the VOI it is possible to include counts that otherwise would be blurred out to pixels outside the physical boundary owing to the limited resolution. If the VOI is sufficiently large, all counts that spill out can be captured, eliminating the need for partial volume correction. However, when there is nontarget activity, the extra pixels will also capture background counts, which makes the total VOI counts very dependent on the background activity level and distribution. To avoid inclusion of nontarget counts, accurate background compensation is needed. Accurate background compensation is difficult to implement when the background activity is nonuniform, as is typically the case. Subtraction of the spill-in contribution using a cold spot RC as proposed by Kessler et al. [10] was not investigated in the present work. Our analysis here as well as our clinical procedure does not involve explicit background subtraction. We account for spill-in using an “effective” RC that depends on both object size and contrast. One advantage of this choice over subtraction is that there is no noise amplification.

The optimum definition of the VOI will also depend on whether quantification of activity or activity concentration is desired. Based on the results of the present study, for total activity quantification in intravenously administered ¹³¹I RIT, where nontarget uptake is significant, we recommend the use of tight VOIs defined following the physical edge of the tumor. In contrast, for quantification of activity concentration, which was not addressed in this study, the smallest possible VOI is typically used. In phantom studies, Links et al. [20] and Geworski et al. [7] determined RCs for three different regions: the single pixel within the sphere with the maximum value, a circular region with a diameter equal to the system FWHM, and a circular region with a diameter equal to the true sphere diameter. The highest recovery was achieved using the maximum pixel content but because of noise considerations they concluded that use of a single pixel value is clinically unrealistic. As a compromise between precision and accuracy when quantifying activity concentration they recommended selecting a region corresponding to the resolution unit of the system [21].

In conclusion: PVEs significantly influence ¹³¹I SPET tumor quantification accuracy. The spill-in and spill-out contributions depend not only on object size but also on the object shape. In general our results show that spherical objects were less influenced by PVEs compared with nonspherical structures of equal volume. Use of simple sphere-based partial volume correction for nonspherical structures improved ¹³¹I quantification accuracy but the error was still large (up to 39%) because shape effects were not considered in the correction.