A parallel Monte Carlo code for planar and SPECT imaging: implementation, verification and applications in ¹³¹I SPECT

Abstract

This paper reports the implementation of the SIMIND Monte Carlo code on an IBM SP2 distributed memory parallel computer. Basic aspects of running Monte Carlo particle transport calculations on parallel architectures are described. Our parallelization is based on equally partitioning photons among the processors and uses the Message Passing Interface (MPI) library for interprocessor communication and the Scalable Parallel Random Number Generator (SPRNG) to generate uncorrelated random number streams. These parallelization techniques are also applicable to other distributed memory architectures. A linear increase in computing speed with the number of processors is demonstrated for up to 32 processors. This speed-up is especially significant in Single Photon Emission Computed Tomography (SPECT) simulations involving higher energy photon emitters, where explicit modeling of the phantom and collimator is required. For ¹³¹I, the accuracy of the parallel code is demonstrated by comparing simulated and experimental SPECT images from a heart/thorax phantom. Clinically realistic SPECT simulations using the voxel-man phantom are carried out to assess scatter and attenuation correction.

1. Introduction

There has been renewed interest in quantification of ¹³¹I for internal dosimetry due to the recent success of radioimmunotherapy (RIT) in treating B-cell non-Hodgkin’s lymphoma (NHL) here at the University of Michigan and at other institutions [1,2]. ¹³¹I quantification is carried out both by planar imaging [3,4] and by SPECT [5–7] but, the latter is the preferred method when imaging tumors in the presence of significant activity in overlying tissue. The multiple high-energy gamma-ray emissions of ¹³¹I make imaging and quantification more difficult compared to common nuclear medicine isotopes such as ⁹⁹Tc^m. Monte Carlo simulation is a valuable tool for assessing the problems associated with ¹³¹I imaging such as scatter, penetration and attenuation. Monte Carlo codes typically used in nuclear medicine do not explicitly model collimator scatter and penetration. Although computationally tedious, including collimator interactions is a prerequisite for accurate simulation of high-energy photon emitters such as ¹³¹I. There have been a few recent codes that include complete photon transport through both the phantom and collimator [8–11] but, one of the limitations of these codes is the speed even when variance reduction is utilized.

All of the above mentioned Monte Carlo codes are serial codes, i.e. they have been developed to run on scalar single processor computers with the exception of the code by de Vries et al. which utilizes an array processor within a Unix workstation to perform some computations. Due to the recent increase in accessibility of advanced computer architectures there has been much interest in vectorized and parallel Monte Carlo codes. The Monte Carlo method for particle simulation is inherently parallel because each particle history is independent of any other particle’s history [12]. The conventional scalar Monte Carlo algorithm is history based, that is, photon histories are computed sequentially one photon at a time. A parallel history based algorithm can be developed with minimal changes to the existing serial code. A large number of particles, needed to reduce the standard deviation in Monte Carlo simulations, are distributed equally among available processors and are combined at the end to calculate the final result. A critical part of a history based parallel algorithm is a good parallel random number generator, which provides uncorrelated random number streams to each processor. Then each processor’s simulation is statistically independent of one another, making the combined result statistically equivalent to one large run with the same total number of histories. Unlike the conventional Monte Carlo algorithms the vectorized algorithms are event based. In the event based approach the simulation of many histories is broken up into a collection of events, such as tracking and boundary crossing, which are similar and can be processed in a vectorized manner [13]. Significant gains in performance can be attained with the vectorized algorithm but total restructuring of the scalar Monte Carlo algorithm is required for compatibility with the vector architecture. In review articles on Monte Carlo techniques in nuclear medicine imaging [14] and in medical radiation physics [15], parallel processing is recognized as the ideal solution for such simulations. However, development of either vectorized or parallel Monte Carlo codes for nuclear medicine imaging applications has been very limited [16,17].

We previously reported on ¹³¹I simulations using the SIMIND Monte Carlo code combined with a collimator routine which model scatter and penetration [18]. In this reference we quote modest CPU times of 1–6 days on a 500 MHz DEC Alpha XP1000 workstation for SPECT simulations of simple analytical phantoms. However even with this relatively fast code which includes variance reduction, when modeling clinically realistic voxel-based phantoms the time for obtaining statistically acceptable SPECT data becomes unrealistic (several months). Note that in the case of SPECT, typically 60 projection sets must be simulated as opposed to the two sets required in a planar study. In order to speed up SPECT simulations of higher energy photon emitters the SIMIND Monte Carlo code was implemented on a distributed memory parallel architecture as described here. Verification and applications of the parallel version of the code are also presented here for ¹³¹I SPECT imaging with voxel based anthropomorphic phantoms.

2. Implementation of SIMIND on the parallel system

2.1. Parallel architecture

Parallel processing utilizes multiple CPUs operating independently and asynchronously on one application. The two major parallel architectures are the shared memory multiprocessor and the distributed memory multiprocessor. In the shared memory concept a collection of CPUs share a common memory via an internal network, usually bus- or cross-bar based. In the distributed memory concept each processor has its own local memory and communication among processors takes place via message passing. The parallel SI-MIND code was implemented on the RS/6000 Scalable Power Parallel 2 (SP2) system from IBM [19]. The distributed memory architecture of the IBM SP2 is based on a ‘shared nothing’ model with each processor having its own CPU, memory and disk. The RS/6000 systems are implementations of a Reduced Instruction Set Computer (RISC) architecture. The SP2 software architecture is based on the AIX/6000 operating system, IBM’s implementation of Unix. The SP2 system used in the present work is located at the Center for Parallel Computing at the University of Michigan. This system has 48 160-MHz processors with 1 GByte of memory on each processor. Each processor has a peak performance of 640 MFLOPS (millions of floating point operations per second). A high-performance networking switch provides high-bandwidth, low-latency inter-processor communication with a peak bi-directional data transfer rate of 110 MB/s between each processor pair.

2.2. Parallel random number generator

Before explaining issues related to parallel random number generators it is worthwhile to mention that an ideal serial random number generator should produce sequences that are uniformly distributed, are uncorrelated, have a long period and are reproducible. For practical purposes we only require that the period of the random number stream be larger than the total number of random numbers needed by an application, and that the correlation be sufficiently weak. There are many different iterative schemes to generate random number streams of which the Linear Congruential Generator (LCG) is the most commonly used [20]. The linear recursion underlying the LCG can be written as:

$$X_n=a^{\ast }{X}_{n-1}+c(modm)$$ (1)

where m is the modulus, a the multiplier, and c the additive constant. The size of the modulus constrains the period, and for implementational reasons it is chosen to be a prime or a power-of-two. When a, c, and m are chosen appropriately, one can obtain a random number sequence with a maximum period equal to m.

A parallel random number generator must satisfy all the criteria for an acceptable serial random number generator. In addition, the parallel random number sequences should have no inter-processor correlation, should be reproducible independent of the number of processors used, and should be generated with minimal or no inter-processor communication. The most common approaches to generating parallel sequences of random numbers from serial random number generators are sequence splitting, Lehmer tree and parameterization. In the sequence splitting method, a serial random number stream is partitioned into non-overlapping contiguous subsequences that are then used on individual parallel processors. In the Lehmer tree approach, N starting seeds are generated by one random number generator which are then used by each of the N processors to generate random sequences with a second generator. Recent research has focussed on development of parallel random number generators based on parameterization. This method identifies a parameter in the underlying recursion of a serial random number generator that can be varied. Each valid value of this parameter leads to a recursion that produces a unique, full-period stream of random numbers [21].

In the present work, we use a parallel LCG from the recently developed software library SPRNG which contains six different parallel random number generators [22]. The selected generator is linked in at compile time. The period of the LCG in SPRNG is 2⁴⁸. Parameterization is carried out by having different prime numbers as the addend c in Equation 1. The number of distinct streams is ~2¹⁹. The independent, reproducible streams are produced without performing any inter-processor communication. The same seed is used to initialize all the streams in one particular computational run. In order to get a different sequence in a different run, this common seed can be changed.

2.3. Parallelization

When photon histories are independent of one another as in the present application there are several ways to partition the photons among the processors. Here we use the simplest and most efficient approach referred to as natural partitioning by Martin et al. [23]. The photons are equally distributed among the processors in such a way as to equalize the workload and minimize communication. Each processor performs the entire simulation for all the photons assigned to it, and reports its results to one of the processors called the host processor. The host processor sums up the results from all processors and calculates the final result. Since the random number streams in the different processors are uncorrelated the standard deviation of the combined results is improved by the ratio 1/√N, where N is the number of processors. The natural partitioning approach may lead to excessive memory requirements since each processor must know the entire problem domain. Two alternative approaches, partitioning by geometry and partitioning by photon energy do reduce the memory requirements, but lead to increased communications and increased difficulty in equalizing the workload among processors [23].

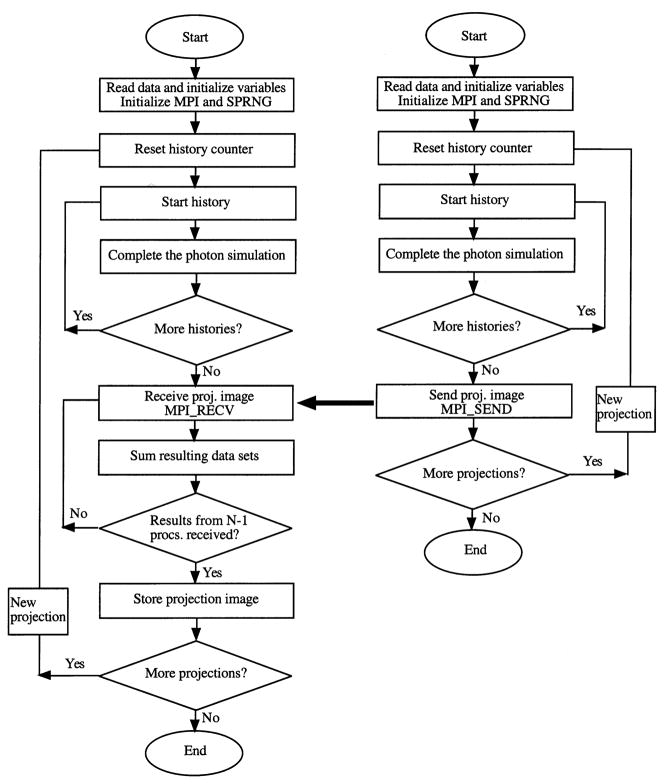
Our parallelization approach required minimal changes to the original serial SIMIND code [24], which is written in Fortran90. The code was replicated in each processor since each processor is performing the complete simulation. A simplified flow chart of the parallel algorithm for generating a SPECT image is given in Fig. 1 with the diagram for the host processor on the left and the diagram for all other processors on the right. The host contributes a complete image set just like the other processors, but has the additional task of summing the image sets to generate the global image. As the flow chart indicates there is no inter-processor communication until the simulations are complete. For inter-processor communication we utilized the MPI library for message passing which is available on almost all parallel machines in C and Fortran [25]. At the start of the program each processor carries out the MPI initialization which returns the total number of processors, N, and the processor’s rank (i.e. identification number which goes from 0 to N−1). In the SPRNG initialization, each stream number is associated with the processor’s rank and thus unique streams are produced on each processor. The same number of histories specified in the input file is assigned to each processor. Photon transport in the phantom, collimator and scintillation detector is carried out as in the serial code, which is well described in the literature on the SIMIND code and in the literature on the collimator routine [8]. When simulation of a projection angle is complete the host and the other N−1 processors communicate via the MPI send and receive commands. Because the processors operate asynchronously it is necessary for all processors to synchronize prior to starting the simulation of a new projection angle. Synchronization is achieved by calling the MPI_BARRIER command, which blocks the calling processor until all other processors join at the barrier point of the code. Typically, SIMIND simulations include generation of energy spectra and calculation of parameters such as sensitivity and scatter fraction, which are not included in Fig. 1. When all SPECT projections have been completed there are send and receive commands and a summation of partial results associated with each of these parameters.

Fig. 1.

Flow chart of the parallel simulation. The diagram for the host processor is on the left and the diagram for all other processors is on the right.

It is worth noting that the MPI commands were implemented such that they are included only at the linking stage. Therefore, it was possible to have only one version of SIMIND for both the serial and parallel implementations which is convenient because the code is constantly been developed. We are presently working on a another version of the parallel algorithm (not described here), that would split the simulation of the different SPECT projection angles among the processors.

3. Materials

For all of the ¹³¹I measurement and simulation results presented here the SPECT camera used was a Picker Prism XP3000 equipped with an Ultra High Energy General-Purpose collimator. The NaI crystal measured 24×40×0.95 cm. The measured energy resolution at 364 keV was 10.2% (FWHM). SPECT acquisitions employed 360°, 60 angles, a 64×64 matrix with a pixel size of 0.72 cm and a 20% photopeak window at 364 keV. Reconstruction was by a space-alternating generalized expectation-maximization algorithm, SAGE [26]. To carry out the triple energy window (TEW) scatter correction two additional 6% windows were included adjacent to the photopeak window. For attenuation correction a registered attenuation coefficient map based on the voxel-man density images was used.

Included in SIMIND is access to the following two voxel-based anthropomorphic phantoms which were utilized in the present work: (1) the voxel-man phantom [27]; and (2) the Radiological Support Devices (RSD) heart/thorax phantom [28]. The voxel-man closely resembles the anatomy of a typical male and consists of 243 byte-coded images, which include 58 organs. The RSD phantom is a computerized version of a commercially available fully tissue-equivalent experimental phantom made up of a basic thorax, heart, lungs, liver and a realistic skeleton. The computerized version of the phantom consisting of 132 byte-coded images was created recently specifically to be used with the SIMIND code. SIMIND also allows for activities to be assigned to spherical tumors, which can be superimposed onto the activity distributions of the voxel man or the voxel RSD phantom. The organ and tumor relative activity concentration ratios used in the phantom simulations below were realistic values obtained from planar images of typical NHL patients who underwent ¹³¹I RIT at our clinic.

4. Results and discussion

4.1. Timing results

For the timing evaluation one SPECT projection of the voxel-man phantom was simulated. Table 1 shows the performance results as a function of the number of processors and the problem size (i.e. the number of photons simulated). The total time is the CPU time for the entire simulation including the time required for I/O operations. The measured speed-up, S_N, and efficiency, ε_N, were defined as

Table 1.

Measured timing results on the SP2 as a function of the number of processors and problem size

N	Small (8.4×107 photons/projection)			Medium (8.4×108 photons/projection)
	Time (s)	Speedup	Efficiency	Time (s)	Speedup	Efficiency
1	17131	1.000	1.000	171640	1.000	1.000
2	8581	1.997	0.998	85922	1.998	0.999
4	4298	3.986	0.996	42959	3.995	0.999
8	2162	7.923	0.990	21598	7.947	0.993
16	1085	15.785	0.987	10749	15.968	0.998
32	547	31.304	0.978	5408	31.739	0.992

$$S_N=\frac{\text{execution}\text{time}\text{for}\text{a}\text{single}\text{processor}}{\text{execution}\text{time}\text{using}N\text{processors}}$$ (2)

and

$${\epsilon }_N=\frac{S_N}{N}$$ (3)

Since S_N ≤N, we have ε_N ≤1. When perfect speedup of S_N =N, referred to as linear speed-up, is achieved ε_N =1. In almost any algorithm there are operations that must be executed on one processor at a time, thereby decreasing the efficiency. The fraction of such operations is referred to as the ‘serial fraction’. Other factors that degrade speed-up include synchronization of tasks, and communication between processors and are referred to as the ‘parallelization overhead’.

The results of Table 1 indicate near linear speed-up. This is to be expected because in the present implementation, both the serial fraction and inter-processor communication is minimal. There is a very small degradation in speed-up and efficiency with the number of processors because of increased parallelization overhead. The speedup and efficiency values in Table 1 are somewhat better when the problem size is larger because the serial fraction gets smaller as the photon histories increase while overhead for communication and synchronization remains fixed.

4.2. Validation of the parallel code

Validations for planar imaging were carried out by comparing ¹³¹I energy spectra and point source images obtained with the parallel version of SI-MIND to those obtained with the serial code and by experimental measurement. We have previously validated the serial code for planar imaging by showing good agreement between measurement and simulation [18]. The parallel code results were in close agreement with those obtained with the serial code but were not identical because the two versions use different random number generators. The normalized mean square error (NMSE) between the parallel code and serial code results for ¹³¹I was 0.12% for the energy spectra and 0.18% for the point source images. Validation of the SIMIND code for ¹³¹I SPECT imaging has not been carried out previously. Here we perform the SPECT validation by carrying out both experimental measurement and simulation of the RSD heart/thorax phantom. The physical phantom was augmented by inserting a 100-ml water filled plastic sphere close to the liver to represent a tumor. In both the experimental measurement and simulation ¹³¹I activities were distributed with the following relative concentration ratios: tumor, 124; liver, 50; left lung, 17, right lung, 9; heart chambers, 94; myocardial wall, 122; background (thoracic cavity), 6. We simulated 1.6×10⁹ photons/projection using 16 processors of the IBM SP2 with a run time of 214 h for the entire simulation consisting of 60 projection images. Both the experimental data and the simulated data were reconstructed without scatter and attenuation correction. There was good agreement between the measured and simulated images as demonstrated in Fig. 2, which compares a typical reconstructed slice and line profile across the center of the tumor. The figure also shows the true activity distribution corresponding to the reconstructed slice. The NMSE between measured and simulated images calculated on a pixel-by-pixel basis was 5.5%.

Fig. 2.

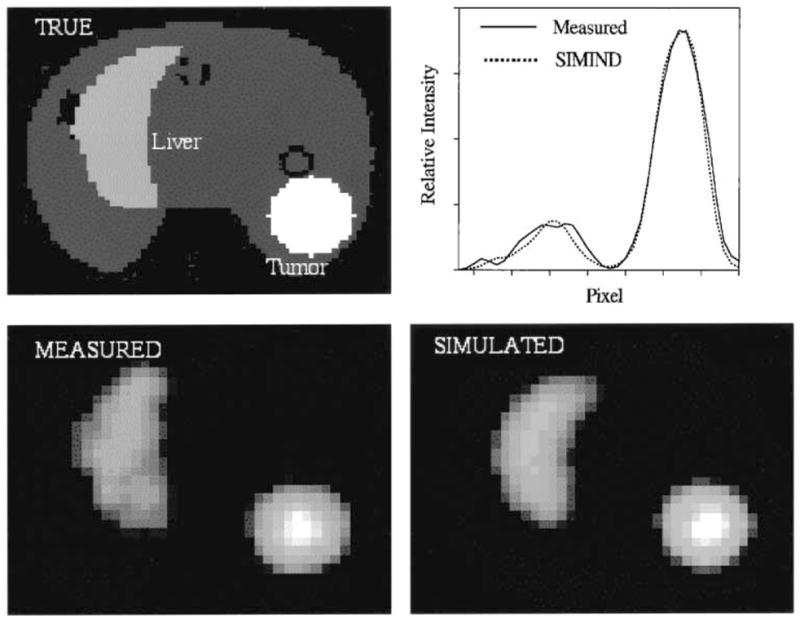
Images and profiles corresponding to a typical slice of the RSD heart/thorax phantom. The true activity distribution as well as the measured and simulated reconstructed images are shown. The line profile is across the center of the tumor.

4.3. Anthropomorphic phantom simulations

Here we demonstrate an application of the parallel SIMIND code where simulations of the voxel-man phantom was used to evaluate ¹³¹I SPECT scatter and attenuation correction. We have previously used the scalar SIMIND code to evaluate SPECT quantification but due to the prohibitive computational time the previous study was limited to a simple analytical elliptical phantom with uniform scattering and attenuating media [18]. The speed-up achieved in the present work made it feasible to model a highly realistic imaging situation using the voxel-man phantom. In the abdominal region ¹³¹I activities were distributed in several organs including three 200 ml spherical tumors according to the following concentration ratios: tumor 1, 100; tumor 2, 100; tumor 3, 100; kidneys, 81; liver, 26; lungs, 26; spleen, 53; blood-pool, 48. We simulated 1.1×10⁹ photons/projection using 16 processors of the IBM SP2 with a run time of 226 h for the entire simulation consisting of 60 projection images.

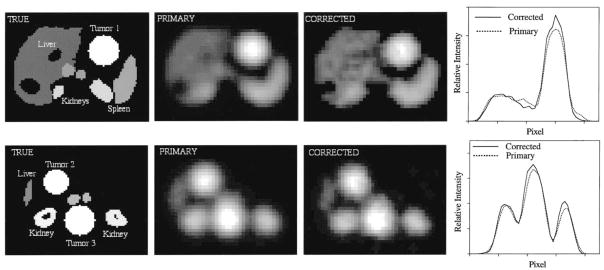
To evaluate scatter and attenuation two sets of projection data were obtained: (1) case with scatter (phantom and collimator) and attenuation events included; and (2) ideal case with no scatter or attenuation (primary events only). The first set of projections was reconstructed with attenuation and scatter correction to obtain the corrected image while the latter set was reconstructed without any correction to obtain the primary image. Slices of the reconstructed images and the corresponding profile curves are compared qualitatively in Fig. 3. The compensated images show good agreement with the primary images giving us confidence in our clinical SPECT quantification procedure where TEW scatter compensation and patient specific attenuation maps are used [5]. In a future study results from parallel simulations will be used to optimize the window width and location for the TEW method as well as to carry out a quantitative assessment of scatter correction methods for ¹³¹I. Activity quantification can also be evaluated since the true simulated activities of the tumors are known.

Fig. 3.

Images and profiles corresponding to two slices of the voxel-man simulation. The true activity distribution as well as the primary and corrected images are shown. The line profiles are across Tumor 1 and Tumor 3.

5. Summary and conclusions

In this work a parallel version of the SIMIND Monte Carlo code for planar and SPECT imaging was successfully implemented and verified on the IBM SP2 distributed memory parallel machine. Photons were equally partitioned among the processors and the measured speedup was very close to linear. The present parallel code is easily portable to any other distributed memory parallel computer system, which supports MPI and has an operating structure similar to the SP2. Recently we successfully ran the code on a SGI Origin 2000 parallel system configured with 100 300 MHz processors at Lund University, Sweden.

SPECT simulations of higher energy photon emitters are computationally tedious and can greatly benefit from the speedup achieved by running the code in a parallel architecture. In this work, we demonstrated the use of the parallel code in ¹³¹I SPECT simulations involving clinically realistic voxel-based anthropomorphic phantoms. For these simulations even though 16 processors of the SP2 were used the computational time to obtain statistically acceptable data was long (~10 days). However, as parallel processing speed and power are steadily increasing, we can expect the computational time for such simulations to rapidly decrease. The IBM SP2 at University of Michigan is presently being upgraded to 128 processors. Recently the San Diego Supercomputing Center acquired the new IBM Teraflops RS/6000 SP configured with 1152 Power3 processors, each running at 222 MHz. This new parallel machine has a combined peak performance of 1 TFLOP (10¹² floating-point operations per second). The above supercomputing facilities are accessible to researchers at other institutions via the National Partnership for Advanced Computational Infrastructure (NPACI) [29]. In conclusion, the recent increase in availability of advanced computer architectures and the speed-up demonstrated by the present parallel implementation makes it feasible to carry out accurate clinically realistic SPECT simulations of higher energy photon emitters.