A Longitudinal Analysis of Family Migration and the Gender Gap in Earnings in the United States and Great Britain

Abstract

This article uses longitudinal data for the United States and Great Britain to examine the impact of residential mobility and childbirth on the earnings of women, their family earnings, and the related division of earnings by gender. This project is the first to compare explicitly the impact of childbirth and family migration on women’s earnings, and it extends prior cross-sectional and longitudinal studies on isolated countries by providing a direct contrast between two major industrialized nations, using comparable measures. The results indicate that families respond in similar ways in both countries to migration and childbirth. In response to both migration and childbirth, women’s earnings fall at the time of the event and recover slowly afterward, but the magnitude of the impact is roughly twice as large for childbirth as for migration. However, migration—but not the birth of a child—is also associated with a significant increase in total family earnings because of increased husbands’ earnings. As a result, the effect of migration on the relative earnings of wives to husbands is similar to the effect of childbirth. These results suggest that family migration should be given consideration in the literature on the gender earnings gap.

Women earn less than men do. Comparative research has documented that in the 1990s, the female-to-male earnings ratio for full-time workers was 76% in the United States (US) and 75% in the United Kingdom (UK) (Blau and Kahn 2000). Various factors influence this earnings gap between men and women, with most empirical research focusing on differences in rates of pay influenced by relative levels of human capital, the degree of labor market involvement, gender-based occupational segregation, parental status, discrimination, general wage inequality, and the institutional framework of labor force participation. In particular, many recent studies emphasized the role of childbearing on earnings, the negative effects of which continue to be borne almost entirely by women (see Anderson, Binder, and Krause 2003; Budig and England 2001; Joshi, Paci, and Waldfogel 1999; Waldfogel 1997, 1998; Winslow-Bowe 2006).

The literature on the gender earnings gap has not recognized that family migration may contribute to the gender earnings gap, despite a large body of research demonstrating that the migration of families tends to harm the employment and earnings of married women. The purpose of this study is to evaluate the contribution of migration to the gender gap in earnings and to compare its relative influence with the contribution of childbearing. The well-established effects of childbearing on labor market interruptions and earnings provide a useful reference for establishing the relative importance of migration as a contributor to the gender gap in earnings.

The study is cross national, allowing us to compare the importance of moving and bearing children in Great Britain (GB) and the US. The data are drawn from harmonized versions of the Panel Study of Income Dynamics (PSID) and the British Household Panel Study (BHPS), equivalent subsets of which are included in the Cross-National Equivalency File (CNEF). This longitudinal analysis is a natural extension of a body of cross-national, cross-sectional studies of family migration conducted during the late 1990s and early 2000s in GB and the US that focused on labor market implications of family migration (Boyle et al. 1999, 2001, 2002, 2003).

LITERATURE REVIEW

The literature on the gender pay gap is concerned with explaining the difference in pay between men and women and whether these differences change over time. Blau and Kahn (2000) and Gregory (forthcoming) provided excellent surveys of this literature. As described in these reviews, a common empirical approach is to estimate models of men’s and women’s earnings as a function of education, experience, industry, occupation, race, and union membership. Standard decomposition techniques attribute differences in earnings to the differing distributions of men and women across these categories and to gender differences in pay within these categories. For example, Blau and Kahn (2006) found that women’s full-time wages in 1998 were about 80% of men’s; however, after adjusting for differing distributions across the previously listed categories, women’s full-time wages were 91% of men’s. Discrimination or other unmeasured differences between men and women may account for the remaining 9%.

The role of family and parental status has also been examined using similar methods. For example, Blau and Kahn (1992) conducted a cross-national analysis in the UK and the US of gender differences in earnings, using data sources from the mid- to late 1980s. After adjusting for hours worked, single women who were employed full-time earned 95% (UK) and 96% (US) of comparable single men’s earnings. However, for married female workers, this ratio was 60% in the UK and 59% in the US. Because these data represented full-time workers, the results reflect different rates of pay as opposed to different numbers of hours worked. Thus, recent research on the gender gap in earnings has rightfully focused on the role of marriage—and, more specifically, on the effects of having a child (see Anderson et al. 2003; Budig and England 2001; Joshi et al. 1999; Waldfogel 1997, 1998; Winslow-Bowe 2006). As Waldfogel (1998:505) stated, “In the United States and Britain, there is a ‘family gap’ between the wages of mothers and other women. Differential returns to marital and parental status explain 40%–50% of the gender gap. Another 30%–40% is explained by women’s lower levels of work experience and lower returns to experience.”

Beyond the extension of standard decomposition techniques to consider the impact of marital status and the presence of children on the wage gap, others have also examined the impact of parental roles in different institutional settings. Blau and Kahn (2003) related differences in family leave and child-care support legislation to cross-national patterns of gender wage gaps. They also explained how cross-national differences in inequality that are related to broad market phenomena—rather than to gender, per se—may also help explain variation across countries in the male-female wage gap.

Curiously, the role of family migration has remained unexplored in this body of literature (see Cooke [2008] for a recent review of the family migration literature). In the 1970s, DaVanzo (1972, 1976), Sandell (1977), and Mincer (1978) each developed very similar theories regarding family migration based upon human capital theory (Becker 1974; Sjaastad 1962). The exact impetus for this development is unclear, but there is some indication that by the early 1970s, increasing female labor force participation was depressing family migration rates (Long 1974), necessitating a consideration of how families make migration decisions. The essence of the human capital model of family migration is that “. . . couples pool information on their joint utilities and weigh both in the final decision. However, since total family utility is assumed to be measured best by total monetary income, the spouse who can contribute the most to this total may have his/her prospects weighed most heavily in the decision” (Spitze 1984:22). Based upon these arguments, Mincer (1978:758) concluded that moving is likely to have a negative effect on the economic status of women:

Indeed, within the family, higher market earning powers of husbands induce a lesser market participation, lower market earnings and a diminished migration payoff for the wife . . . In view of the smaller gains from migration, wives are more likely to be tied movers in migration families, while husbands, if they are tied at all, are more likely to be tied stayers than tied movers. Of course, the larger the wife’s contribution to family earnings, and the stronger her job attachment, the greater the deterrent effect on family mobility.

The overwhelming empirical evidence demonstrates that being a tied migrant harms labor force participation and employment (e.g., Cooke and Speirs 2005), that wives are more likely than men to be tied migrants (e.g., Bielby and Bielby 1992; Lichter 1982; Shihadeh 1991; Spitze 1986), and that migration reduces both wives’ time in employment (e.g., Cooke and Bailey 1996; Lichter 1980) and their earnings (e.g., Cooke 2003; Jacobsen and Levin 1997; LeClere and McLaughlin 1997; Shauman and Noonan 2007).

There is also a temporal dimension to this effect (e.g., Lichter 1983; Spitze 1984). For example, Clark and Withers (2002) found that migration reduces the employment of married women in dual-employment marriages by up to 10% in the months leading up to migration and by over 20% immediately after migration, and that recovery to premigration employment levels takes nearly one year. In contrast, family migration does not affect the employment of husbands. It seems likely that several moves over time might cause a significant decline in actual labor market experience. This suggests that the impact of migration on married women’s earnings may be due as much to a reduced rate of human capital accumulation as it is to the disruptive effects of being a tied migrant.

The disruptive effects of migration on the accumulation of trailing wives’ human capital extend beyond actual labor market experience into education and job-specific skills. The migration event severs job-specific skills in the migration origin that may not be transferable to a new job in the migration destination (Bonney and Love 1991). As well, the search for employment in the destination is limited by poorly developed job-information networks and by responsibilities for reestablishing the household in the new locale (McCollum 1990). Trailing wives may, therefore, become underemployed relative to their skill levels (Markham 1986). Employers may also use recent mobility as a signal for lower productivity or as a signal that the applicant may be willing to accept a lower wage (Halfacree 1995). One strategy that may be used is for women to enter into occupations for which job skills are easily transferred across firms (e.g., nursing, education, real estate; Hanson and Pratt 1995). The net effect is that family migration reduces trailing wives’ earnings not only because of the disruptive effects of migration on employment but also because of the loss of accumulated work experience, declining job-specific skills, and lower returns to human capital investments.

The literature on family migration has spent much less time conceptualizing and measuring how family migration affects the human capital and earnings of married men, but it is not too difficult to see that the negative effects of migration for women discussed earlier have positive effects for men. As leading migrants, migration can be used by married men as a strategy to increase human capital that is specific to a particular firm or occupation, and migration may be used as a signal of higher productivity to employers. Thus, not only may migration reduce the accumulation of human capital, the returns to human capital, and the earnings of married women, but it may also increase the accumulation of human capital, the returns to human capital, and the earnings of married men, all of which would contribute to the gender pay gap.

To conclude, despite numerous studies that clearly demonstrate that the migration of families harms the employment and earnings of married women, research on the gap in earnings between men and women has overlooked the role that migration may have in contributing to that gap. The current study evaluates the importance of migration for explaining gender differences in earnings and places these negative effects into their larger context. Specifically, we directly compare the effects of moving with the effects of having a child on married women’s earning trajectories. Because the negative effect of having a child on women’s earnings is widely acknowledged, this provides a useful reference point for assessing the relative contribution of migration to the gender earnings gap. This research is primarily descriptive and simply seeks to establish whether family migration may contribute to the gender earnings gap. If so, the next steps are to consider how migration affects the accumulation of human capital and to integrate migration directly into models of the gender earnings gap.

DATA AND METHODS

For both the US and GB, fixed-effects models are estimated for women’s earnings, total family earnings, and the intrafamily gender pay gap. For each of these dependent variables, two models are estimated. The first includes basic demographic information and a set of independent variables designed to measure the trajectory of earnings, family earnings, and the gender pay gap after a birth and after a move. The second adds more-detailed human capital information. Because the analysis is primarily concerned with describing (rather than explaining) the trajectories in the dependent variables after a birth or after a move, the first, more simplified model is the primary focus. The second model provides a test of the robustness of the first model with respect to the addition of human capital variables.

The data for this study are drawn from the Cross-National Equivalency Files (CNEF), which include harmonized data from four panel studies: the BHPS, PSID, the German Socio-Economic Panel (GSOEP), and the Canadian Survey of Income and Labour Dynamics (SLID) (for information on the CNEF, see Burkhauser et al. 2005; and Frick et al. 2007). To facilitate cross-national studies, the CNEF includes and rectifies the most commonly used variables across the five panel studies. Consistent with previous cross-national, crosssectional studies on family migration in the US and GB (Boyle et al. 1999, 2001, 2002, 2003), this analysis focuses on the BHPS and PSID extracted from the CNEF.

There are several benefits to using a cross-national study. The role of economic structure and institutional arrangements in shaping the gender earnings gap can be uncovered through cross-national analyses (see Pettit and Hook 2005). Most cross-national studies comparing the social and economic characteristics of Western countries have found that the US and GB are more similar than dissimilar in comparison with other Western countries (e.g., Esping-Andersen 1990). Indeed, previous cross-national, cross-sectional studies on family migration in the US and GB (Boyle et al. 1999, 2001, 2002, 2003) found remarkable similarities in the effect of moving on women’s employment. Thus, the effect of moving in the US and GB should be similar. However, GB provides much more generous parental leave than that in the US (Waldfogel 1998). Because parental leave replaces lost earnings and provides job protection in GB, the birth of a child may lead to a greater decline in women’s earnings and family earnings, and a greater increase in the gender earnings gap in GB than in the US. However, both Ruhm (1998) and Blau and Kahn (2003) argued that the effect may not be so straightforward because parental leave protection may also increase job attachment.

This research uses a fixed-effects approach to model these panel data, which has the benefit of offering a general solution to unobserved heterogeneity and selection bias (see Hsiao 2003). The advantages of a fixed-effects approach are demonstrated by first considering the following model:

$$y_{it}={\mu }_t+\beta {\text{x}}_{\text{i}\text{t}}+\gamma {\text{z}}_{\text{i}}+{\alpha }_i+{\epsilon }_{it},$$

where y_it is the dependent variable, μ_t is an intercept that varies with time, β and γ are vectors of coefficients, x_it is a vector of independent variables that vary over time, z_i is a vector of independent variables that do not vary over time, α_i reflects unobserved independent variables that also do not vary over time, and ɛ_it is a random component. If the unobserved independent variables, α_i, are correlated with any of the observed characteristics, x_it, then estimates of β are biased (Heckman 1979). The fixed-effects approach takes advantage of information present in panel data to eliminate this bias by subtracting each variable from its corresponding individual mean:

$$y_{it}-{\overline{y}}_i=\left(u_t-\overline{u}\right)+\left(\beta {\text{x}}_{\text{i}\text{t}}-\beta {\overline{\text{x}}}_{\text{i}}\right)+\left(\gamma {\text{z}}_{\text{i}}-\gamma {\overline{\text{z}}}_{\text{i}}\right)+\left({\alpha }_i-{\overline{\alpha }}_i\right)+\left({\epsilon }_{it}-{\overline{\epsilon }}_i\right),$$

which reduces to

$$y_{it}-{\overline{y}}_i=\left(u_t-\overline{u}\right)+\beta \left({\text{x}}_{\text{i}\text{t}}-{\overline{\text{x}}}_{\text{i}}\right)+\left({\epsilon }_{it}-{\overline{\epsilon }}_i\right),$$

and which then can then be rewritten as

$$y_i^{*}=u^{*}+\beta x_i^{*}+{\epsilon }_i^{*},$$

where the asterisk indicates difference scores. The advantage here is that the effect of fixed individual-level characteristics and unobserved variables have been removed, implying that the estimates of β are unbiased.

The specific dependent and independent variables are described in Table 1. The dependent variables are (1) women’s earnings, (2) total family earnings, and (3) the intrafamily gender earnings gap (the difference between the husband’s and the wife’s earnings). All earnings variables are adjusted for inflation by using the country-specific indexes (Bureau of Labor Statistics 2007; Office for National Statistics 2006) to 2005 for the US and to 2006 for GB. These three variables are analyzed because it is not adequate to focus only on the effects of family migration on women’s earnings. The human capital model of family migration emphasizes that even if women’s earnings decline because of migration, total family earnings should increase. If this is the case, then the husband’s earnings must be increasing, and the wife’s earnings must be decreasing. This should result in an increase in the intrafamily gender earnings gap.

Table 1.

Variable Names, Definitions, and Descriptive Statistics

Variable Name	Variable Definition	United States		Great Britain
		Mean	SD	Mean	SD
Model 1 Variables
Wife’s Earnings	Labor earnings include wages and salary from all employment, including training, primary and secondary jobs, and self-employment, plus income from bonuses, overtime, and profit sharing.	17,977.67	20,718.32	8,038.90	9,169.39
Total Family Earnings	Wife’s Earnings plus Husband’s Earnings (as defined above).	60,542.00	52,907.48	25,197.57	20,374.21
Gender Earnings Gap	Wife’s Earnings less Husband’s Earnings.	–24,586.66	46,692.43	–9,119.78	18,849.20
Child Born This Year	If the number of children in the household increased since last year, then this variable equals 1; otherwise, this variable equals 0.	0.14	0.35	0.06	0.24
Number of Children	This variable is based on a CNEF variable indicating number of children in the household and may include stepchildren or adopted children. In some cases, the number of children might decrease as children leave the household.	1.35	1.20	1.25	1.20
Age of Youngest Child	Years since last child was born (as defined above).	3.19	4.29	3.13	4.34
Moved This Year	Change in state (US) or region (GB) of residence from since last year.	0.03	0.18	0.01	0.11
Number of Previous Moves	Cumulative number of moves (moves are defined as above). Set to zero at the first observed person-year.	0.23	0.66	0.08	0.34
Years Since Last Move	Years since last move (moves are defined as above).	0.51	1.82	0.17	0.93
Wife’s Age	Wife’s age.	33.03	9.29	38.94	9.92
Wife’s Age, Squared	Wife’s age, squared.	1,177.21	705.38	1,614.50	818.98
Wife’s Years of Education	This variable indicates the number of years of education completed at the time of the survey for individuals in the household, as reported by the householder.	13.00	2.17	13.18	2.44
Husband’s Earnings	See Wife’s Earnings.	42,564.33	45,392.11	17,158.68	17,352.89
Model 1 Sample Size (person-years)		37,970		19,722
Additional Model 2 Variables
Wife Employed Part-Time Last Year	If the individual had positive wages and worked at least 52 hours but fewer than 1,820 hours last year, then the individual was employed part-time.	0.41	0.49	0.43	0.50
Wife Employed Full-Time Last Year	If the individual had positive wages and worked at least 1,820 hours last year (35 hours per week on average), then the individual was employed full-time.	0.35	0.48	0.29	0.46
Husband’s Age	Husband’s age.	34.22	8.68	39.85	9.20
Husband’s Age, Squared	Husband’s age, squared.	1,246.52	665.56	1,672.58	768.50
Husband Employed Part-Time Last Year	See Wife Employed Part-Time Last Year.	0.17	0.37	0.21	0.41
Husband Employed Full-Time Last Year	See Wife Employed Part-Time Last Year.	0.79	0.40	0.66	0.47
Husband’s Years of Education	See Wife’s Years of Education.	13.10	2.31	13.62	2.55
Model 2 Sample Size (person-years)		30,716		15,366

Notes: Figures are unweighted statistics. Both models also include dummy variables for year in the panel (1981 through 1997, excluding 1980, for the PSID; 1992 to 2002, excluding 1991, for the BHPS).

The focus centers on a set of independent variables designed to measure the trajectory in earnings, family earnings, and the gender earnings gap after either a birth or after a move. This modeling approach is similar to that taken in job dislocation literature, which focuses on the temporal effects of mass layoffs on earnings (see Couch 2001; Jacobson, LaLonde, and Sullivan 1993). In these studies, there tends to be a relative dip in earnings for dislocated workers relative to the continuously employed in the time leading up to a mass layoff, a significant drop in the year of the mass layoff, and then a recovery over several years as laid-off workers find new jobs. Empirically, the job displacement literature uses panel data models with a timing variable for each observed person-year, indicating the set of years before or after an impending layoff that measures the dip, drop, and recovery periods. Analogously, this analysis focuses on panel data models that include variables designed to measure and compare the relative drop and recovery in earnings attributable to childbirth and migration, relative to women who do not experience these events.

More specifically, the three earnings trajectories are estimated as a function of three sets of corresponding variables (see Table 1 for additional information). First, we include two dummy variables that indicate a birth (Child Born This Year) or a move (Moved This Year) between t and t – 1. Within the regressions, these variables capture the immediate effect of a birth or a move in the year in which it occurred. Second, we include two variables that indicate the cumulative number of births (Number of Children) or moves (Number of Previous Moves) ever experienced. These variables change in the year of a birth or a move but remain fixed at that value until the next birth or move. These variables indicate the long-term effect of a birth or a move on earnings. Third, we include two more variables that indicate the number of years since the last birth (Age of Youngest Child) or last move (Years Since Last Move). These variables, which are reset to zero in the year of a new birth or a next move, indicate the rate at which earnings recover following a birth or a move. Finally, migration is defined as a move within the 50 U.S. states or within the 18 regions of GB.

For each dependent variable, two models are specified (see Table 1 for additional information). Model 1 includes basic demographic information and a set of independent variables designed to measure the trajectory of earnings, family earnings, and the gender pay gap after a birth and after a migration. Model 1 also includes a set of dummy variables for panel year.1 Model 2 adds more-detailed human capital variables: years of education and last year’s employment status. Note that because of missing data, the sample sizes for the second model are smaller than those for the first model.

The sampling strategy is to select women who are living in nuclear families and are continuously married to their spouse.2 Observation-years prior to the marriage and after the end of the marriage are not included in the sample. Also deleted are all individuals (including those during their years of marriage) for whom there were any missing person-years or missing variables during those continuous years of marriage, or for whom the spouse was not present at any time during their years of marriage. This results in a sample of 35,839 person-years from 1980 to 1997 for the PSID and 19,772 person-years from 1991 to 2002 for the BHPS.

One descriptive statistic from Table 1 deserves discussion. The reported rate of migration in both the US and GB (3% and 1% per person-year, respectively) is much lower than the rate of childbirth (14% and 6% per person-year, respectively). One conclusion that can be drawn from this is that even if migration is shown to have a negative effect on married women’s earnings, its relative rarity would indicate that its aggregate effect on the gender earnings gap would be minimal. However, these estimates are unweighted and are based upon interstate (US) and interregional (GB) migration. In the US, the annual rate of intercounty migration among married couple households in 2006 was 5.3% in 2006 (U.S. Census Bureau 2006), and the birth rate for married women aged 15–45 was 85.5 per 1,000 (8.6%) (Dye 2005). In GB, the inter-ward migration rate was 8.3% in 2000 (Office for National Statistics 2008), and the fertility rate for married women aged 15–44 was 93.8 (9.4%) in 2006 (Office for National Statistics 2007). Thus, in both the US and GB, the true incidence of migration and childbirth are similar.

RESULTS

Women’s Earnings

The basic model considers the effects of a birth or a move on women’s earnings. This is the type of analysis considered in most family migration research. Tables 2 and 3 present the estimates of the effect of both the birth of a child and moving on women’s earnings in the US and GB. The following discussion is based entirely on the estimates from Model 1, but note that the estimates from Model 2 are similar in sign, significance, and size.

Table 2.

Models of Wife’s Earnings

Variable	United States		Great Britain
	Model 1	Model 2	Model 1	Model 2
Child Born This Year	769.88**	–111.61	1,586.69**	611.28**
	(3.41)	(0.43)	(9.02)	(3.42)
Number of Children	–3,946.87**	–2,664.66**	–3,640.97**	–2,323.60**
	(24.70)	(14.68)	(29.35)	(15.89)
Age of Youngest Child	163.75**	138.06**	82.75**	42.27*
	(5.96)	(4.54)	(5.11)	(2.43)
Moved This Year	–455.36	–876.89	–148.66	–386.01
	–0.97	–1.79	(0.35)	(0.85)
Number of Previous Moves	–1,401.51**	–821.19**	–1,073.41**	–952.22**
	(5.72)	(3.09)	(3.39)	(2.80)
Years Since Last Move	248.65**	235.55**	–51.28	42.32
	(3.53)	(3.28)	(0.63)	(0.51)
Age	1,347.10**	1,128.67**	1,373.75**	1,220.73**
	(6.41)	(4.82)	(8.01)	(6.20)
Age, Squared	–20.05**	–13.48**	–15.06**	–12.51**
	(13.37)	(8.09)	(15.51)	(11.21)
Husband’s Earnings	0.02**	0.02**	0.01	0.02**
	(6.45)	(6.48)	(1.87)	(5.10)
Employed Part-Time Last Year		6,243.64**		1,559.47**
		(25.58)		(10.47)
Employed Full-Time Last Year		11,911.70**		6,195.46**
		(40.89)		(31.44)
Years of Education		1,072.61**		216.14**
		(5.01)		(2.74)
Constant	8,519.66	–17,369.54	–15,774.46*	–21,268.94**
	(1.11)	(1.90)	(2.30)	(2.69)
Number of Person-Years	37,970	30,716	19,772	15,366
Number of Persons	6,080	4,555	4,337	3,641
R2	0.05	0.11	0.07	0.15

Notes: Absolute values of t statistics are in parentheses. Parameters for yearly dummy variables are not shown but are available upon request.

^*p < .05;

^**p < .01

Table 3.

Combined Effects of Birth and Migration on Wife’s Earnings

Effect on Wife’s Earnings	United States		Great Britain
	Model 1	Model 2	Model 1	Model 2
Year of Birth	–$3,176.99	–$2,776.27	–£2,054.28	–£1,712.32
	(.00)	(.00)	(.00)	(.00)
Year After Birth	–$3,783.12	–$2,526.61	–£3,558.22	–£2,281.34
	(.00)	(.00)	(.00)	(.00)
Each Additional Year After Birth	$163.75	$138.05	£82.75	£42.27
	(.00)	(.00)	(.00)	(.02)
Year of Move	–$1,856.87	–$1,698.08	–£1,222.07	–£1,338.23
	(.00)	(.00)	(.00)	(.00)
Year After Move	–$1,152.86	–$585.64	–£1,124.69	–£909.90
	(.00)	(.02)	(.00)	(.00)
Each Additional Year After Move	$248.65	$235.55	–£51.28	£42.32
	(.00)	(.00)	(.53)	(.61)

Notes: Estimates are based on sums of model estimates. Probability values, shown in parentheses, are based on standard errors calculated from an error-covariance matrix.

With respect to the birth of a child, the parameter associated with the Child Born This Year variable indicates an increase in earnings in the year of a birth of $770 (P > |t| = .001) in the US and £1,587 (P > |t| = .000) in GB (Table 2). However, this increase is offset by the parameter associated with the Number of Children variable, which indicates a statistically significant decrease in earnings for each child born of $3,947 (P > |t| = .000) in the US and £3,641 (P > |t| = 0000) in GB. The parameter associated with Age of Youngest Child indicates that the negative effect of childbirth is reduced each year by $164 (P > |t| = .000) in the US and £83 (P > |t| = .000) in GB.

Table 3 indicates that the net effect of these parameters on women’s earnings in the US is as follows3: a woman’s earnings declines by $3,177 (P > |t| = .000) in the year of a birth and by $3,783 (P > |t| =.000) in the year after a birth. In each year thereafter, a woman’s earnings increases by only $164 (P > |t| =.000). A similar pattern emerges in GB: a woman’s earnings declines by £2,054 (P > |t| = .000) in the year of a birth and by £3,558 (P > |t| = .000) in the year after a birth. In each year thereafter, a woman’s earnings increases by only £83 (P > |t| = .000) per year.

Returning to Table 2, with respect to moving, the parameter associated with the Moved This Year variable indicates a statistically insignificant effect on earnings of a move in the same year in both the US and GB. The Number of Previous Moves variable indicates a decrease in earnings for each move of $1,402 (P > |t| = .000) in the US and £1,073 (P > |t| = .001) in GB. The parameter associated with Years Since Last Move indicates that the negative effect of a move is reduced by $249 (P > |t| = .000) each year in the US, but the GB parameter is statistically insignificant.

Table 3 indicates that the net effect of these parameters on women’s earnings in the US is as follows: a woman’s earnings declines by $1,857 (P > |t| = .000) in the year of a move and by $1,153 (P > |t| = .000) in the year after the move. In each year thereafter, a woman’s earnings increases by only $249 (P > |t| = .000). A similar pattern emerges in GB: a woman’s earnings declines by £1,222 (P > |t| = .002) in the year of a move and by £1,125 (P > |t| = .000) in the year after a move (P > |t| =.000).

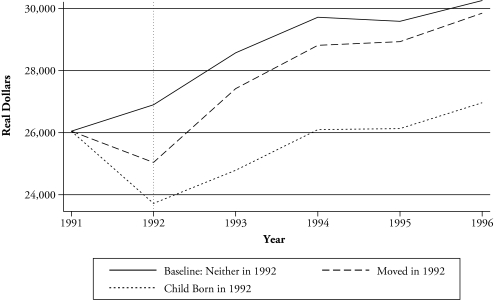
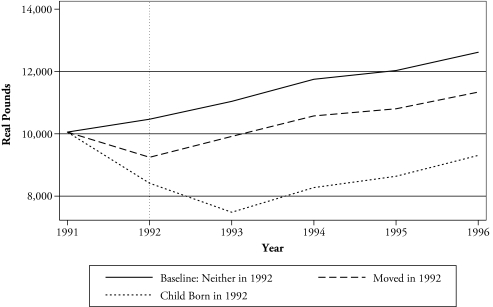
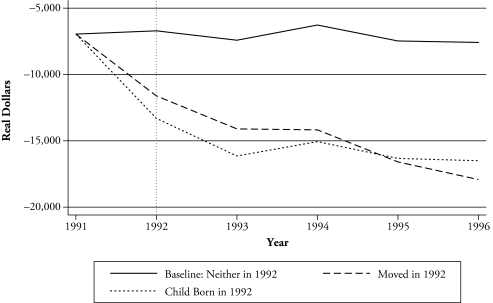
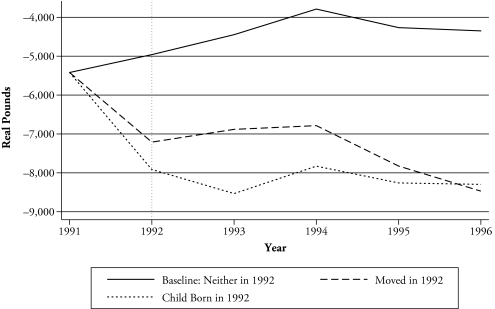
Figures 1 and 2 present estimates for the effect of moving and the birth of a child in the US and in GB, respectively.4 These estimates are for a birth or a move in 1992 for a woman who was 31 years old in 1991 and whose a husband’s inflation-adjusted earnings were equal to two-thirds of median household earnings in each year. (Median household earnings variables are available in the CNEF data.) The baseline represents the estimated earnings for a similar woman who neither moved nor had a child. In the US, there is a dramatic effect on earnings from both moving and having a child, relative to the baseline, with the effect of having a child nearly twice the effect of moving. Migrants recover to nearly the baseline level after several years, but no recovery is in sight for mothers. It is important to note, however, that the recovery of a migrant’s earnings to the baseline level about four years after a move does not constitute a recovery of lost earnings in the previous years but simply indicates a recovery to the baseline earnings of 1996. In GB, the effect of having a child is greatest two years after the birth of a child; and, as in the US, the effect of a move is about one-half that of having a child. However, in contrast to the US, there appears to be no convergence in the earnings of mothers or migrants after a move. The initial impact is comparable between GB and the US, but the long-term implications seem more serious in GB.

Figure 1.

Predicted Effect of a Birth or a Move on Wife’s Earnings: United States

Figure 2.

Predicted Effect of a Birth or a Move on Wife’s Earnings: Great Britain

The patterns in Figures 1 and 2 demonstrate that migration has an impact on married women’s earnings that is similar in pattern to the birth of a child. In both the US and GB, a significant decline in earnings is noted for both the year after a move and the year after a birth, with a relatively slow recovery in earnings. However, as expected, the scale of the effect of a birth of a child in both the US and GB is greater than the effect of a move.

Family Earnings

It is important to place these estimates into their family context. Tables 4 and 5 present results from estimating models of total family earnings, using the same sample of married women as in the previous model and as a function of the same variables, except that the variable Spouse’s Earnings is excluded from the model. Again, note that the following discussion is based entirely on the estimates from Model 1, but the results for Model 2 are similar to the results for Model 1.

Table 4.

Models of Total Family Earnings

Variable	United States		Great Britain
	Model 1	Model 2	Model 1	Model 2
Child Born This Year	–563.32	–1,122.11	2,001.04**	1,041.08*
	(0.96)	(1.53)	(4.43)	(2.31)
Number of Children	913.58*	1,195.39*	–3,143.40**	–2,054.46**
	(2.20)	(2.27)	(9.86)	(5.41)
Age of Youngest Child	398.15**	293.53**	119.75**	71.39
	(5.55)	(3.33)	(2.88)	(1.55)
Moved This Year	–1,506.84	–1,550.96	82.15	395.15
	(1.23)	(1.10)	(0.07)	(0.34)
Number of Previous Moves	2,792.60**	3,394.13**	–263.44	–911.59
	(4.37)	(4.49)	(0.32)	(1.05)
Years Since Last Move	1,758.73**	1,783.01**	465.98*	1,036.64**
	(9.59)	(8.76)	(2.22)	(4.70)
Age	3,428.20**	–1,895.94*	4,144.28**	800.97
	(6.25)	(2.15)	(9.41)	(1.18)
Age, Squared	–38.54**	32.85**	–45.51**	–8.31
	(9.85)	(3.56)	(18.34)	(1.46)
Employed Part-Time Last Year		3,064.21**		1,483.41**
		(4.36)		(3.71)
Employed Full-Time Last Year		6,053.29**		5,531.28**
		(7.21)		(10.53)
Years of Education		1,561.32*		244.57
		(2.49)		(1.16)
Spouse’s Age		3,533.70**		2,324.02**
		(4.32)		(3.37)
Spouse’s Age, Squared		–39.03**		–32.44**
		(4.46)		(5.77)
Spouse Employed Part-Time Last Year		10,016.14**		542.70
		(6.74)		(0.97)
Spouse Employed Full-Time Last Year		16,386.97**		5,913.03**
		(11.17)		(10.61)
Spouse’s Years of Education		685.89		–286.71
		(1.19)		(1.45)
Constant	–345.40	–26,983.06	–56,976.08**	–24,734.95
	(0.02)	(0.78)	(3.24)	(0.95)
Number of Person-Years	37,970	27,891	19,772	12,380
Number of Persons	6,080	3,962	4,337	2,921
R2	.16	.18	.05	.10

Notes: Absolute values of t statistics are in parentheses. Parameters for yearly dummy variables are not shown but are available upon request.

^*p < .05;

^**p < .01

Table 5.

Combined Effects of Birth and Migration on Total Family Earnings

Effect on Total Family Earnings	United States		Great Britain
	Model 1	Model 2	Model 1	Model 2
Year of Birth	$350.25	$73.28	–£1,142.36	–£1,013.38
	(.58)	(.92)	(.01)	(.03)
Year After Birth	$1,311.73	$1,488.92	–£3,023.65	–£1,983.07
	(.00)	(.01)	(.00)	(.00)
Each Additional Year After Birth	$398.15	$293.53	£119.75	£71.39
	(.00)	(.00)	(.00)	(.12)
Year of Move	$1,285.76	$1,843.17	–£181.29	–£516.44
	(.29)	(.20)	(.86)	(.64)
Year After Move	$4,551.33	$5,177.14	£202.54	£125.05
	(.00)	(.00)	(.79)	(.88)
Each Additional Year After Move	$1,758.73	$1,783.01	£465.98	£1,036.64
	(.00)	(.00)	(.03)	(.00)

Notes: Estimates are based on sums of model estimates. Probability values, shown in parentheses, are based on standard errors calculated from error-covariance matrix.

The significance of specific variables differs between the US and GB, as does the aggregate picture. Table 4 indicates that with respect to the birth of a child, the parameter associated with the Child Born This Year variable is statistically insignificant in the US; n GB, there is a statistically significant increase in family earnings in the year of birth of £2,001 (P > |t| = 0.000). The parameter associated with the Number of Children variable indicates a statistically significant increase of $914 (P > |t| = .028) in family earnings for each child born in the US—but a decline of £3,143 (P > |t| = .000) in GB. The parameter associated with Age of Youngest Child indicates that in each subsequent year, family earnings increases by $398 (P > |t| = .000) in the US and by £120 (P > |t| = .004) in GB.

Turning to Table 5, the net effect of these parameters on women’s earnings in the US is as follows: there is no statistical change in family earnings in the year of a birth but a significant increase of $1,312 (P > |t| = .002) in the year after a birth. In each year thereafter, family earnings increase by $398 (P > |t| = .000). A different pattern emerges in GB: family earnings decline by £1,142 (P > |t| = .011) in the year of a birth and by £3,024 (P > |t| = .000) in the year after a birth. In each year thereafter, family earnings increase by only £120 (P > |t| = .004).

Returning to Table 4, with respect to moving, the parameter associated with Moved This Year is statistically insignificant in both the US and GB. However, the Number of Previous Moves variable indicates a statistically significant increase of $2,793 (P > |t| = .000) in family earnings in the US for each move but no significant effect in GB. The parameter associated with Years Since Last Move is statistically significant and positive in the US (= $1,759 (P > |t| = .000)) and GB (= £466 (P > |t| = .027)).

Table 5 indicates that the net effect of these parameters on family earnings in the US is as follows: family earnings are not affected by migration in the year of a move (P > |t| = .286) but increase by $4,551 (P > |t| = .000) in the year after a move and by $1,759 each year thereafter. A different pattern emerges in GB: family earnings are unaffected by migration in the year of a move (P > |t| = .860) or the year after a move (P > |t| = .786) but increase by £466 (P > |t| = .027) each year thereafter.

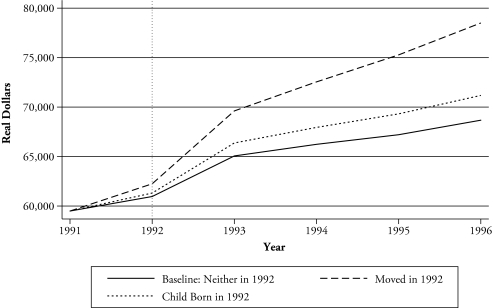
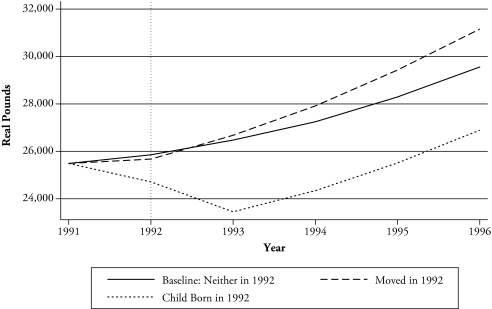
These patterns are displayed graphically in Figures 3 and 4, which are constructed in the same way as Figures 1 and 2. In the US (Figure 3), the birth of a child has very little effect on family earnings. However, migration has a significant and long-term positive effect on family earnings. With respect to migration, the situation in GB (Figure 3) is somewhat similar to the US. There appears to be a long-term positive effect of moving, relative to the baseline, on family earnings. However, the effect of having a child on family earnings in GB is significantly negative. One explanation for the loss in earnings in GB relative to the US is the wider availability of parental leave benefits in GB (see Waldfogel 1998), which may compensate for the loss of earnings after childbirth.

Figure 3.

Predicted Effect of a Birth or a Move on Total Family Earnings: United States

Figure 4.

Predicted Effect of a Birth or a Move on Total Family Earnings: Great Britain

Thus, with respect to the effect of moving on women’s earnings, it appears as if the consistent finding of a negative effect of moving on women’s earnings must be placed within the context of net family gain. Migration in both the US and GB may result in a decline in women’s earnings, but these losses appear to be compensated for by gains in family earnings, especially in the US.

Family Gender Gap

An important additional issue, however, is the degree to which a wife’s loss is viewed negatively or positively. In isolation, the effect of moving on women’s earnings is not a positive event, but within the context of a net gain in family earnings, the “wife’s sacrifice” may not be entirely negative. Tables 6 and 7 explore this further by focusing on the effect of moving and having a child on the difference between the husband’s and wife’s earnings. Once more, the following discussion is based entirely on the estimates from Model 1 because of the similarity in results between Models 1 and 2.

Table 6.

Models of the Gender Earnings Gap (wife’s earnings less husband’s earnings)

Variable	United States		Great Britain
	Model 1	Model 2	Model 1	Model 2
Child Born This Year	2,063.10**	822.37	1,177.61**	266.65
	(3.59)	(1.16)	(2.63)	(0.62)
Number of Children	–8,661.58**	–6,663.77**	–4,132.22**	–2,738.47**
	(21.36)	(13.10)	(13.10)	(7.56)
Age of Youngest Child	–63.62	–29.12	46.22	7.43
	(0.91)	(0.34)	(1.12)	(0.17)
Moved This Year	564.59	109.70	–376.53	–125.59
	(0.47)	(0.08)	(0.35)	(0.11)
Number of Previous Moves	–5,469.86**	–4,859.33**	–1,873.08*	–1,094.16
	(8.79)	(6.64)	(2.32)	(1.33)
Years Since Last Move	–1,216.16**	–1,244.35**	–561.98**	–552.17**
	(6.80)	(6.32)	(2.70)	(2.63)
Age	–671.61	2,819.41**	–1,361.56**	4,112.07**
	(1.26)	(3.30)	(3.13)	(6.38)
Age, Squared	–2.11	–44.61**	15.00**	–42.50**
	(0.55)	(4.99)	(6.11)	(7.85)
Employed Part-Time Last Year		9,454.81**		1,739.26**
		(13.92)		(4.56)
Employed Full-Time Last Year		17,863.74**		6,567.03**
		(22.00)		(13.11)
Years of Education		878.15		268.60
		(1.45)		(1.34)
Spouse’s Age		–3,113.24**		–4,994.47**
		(3.93)		(7.59)
Spouse’s Age, Squared		27.35**		62.59**
		(3.23)		(11.67)
Spouse Employed Part-Time Last Year		–10,813.42**		–630.84
		(7.52)		(1.18)
Spouse Employed Full-Time Last Year		–17,562.46**		–6,369.79**
		(12.38)		(11.99)
Spouse’s Years of Education		–807.27		361.69
		(1.45)		(1.91)
Constant	17,118.91	26,587.86	24,903.42	–16,997.42
	(0.87)	(0.80)	(1.43)	(0.69)
Number of Person-Years	37,970	27,891	19,772	12,380
Number of Persons	6,080	3,962	4,337	2,921
R2	.13	.17	.03	.10

Notes: Absolute values of t statistics are in parentheses. Parameters for yearly dummy variables are not shown but are available upon request.

^*p < .05;

^**p < .01

Table 7.

Combined Effects of Birth and Migration on the Gender Earnings Gap

Effect on Gender Earnings Gap	United States		Great Britain
	Model 1	Model 2	Model 1	Model 2
Year of Birth	–$6,598.48	–$5,841.40	–£2,954.61	–£2,471.82
	(.00)	(.00)	(.00)	(.00)
Year After Birth	–$8,725.21	–$6,692.88	–£4,086.00	–£2,731.03
	(.00)	(.00)	(.00)	(.00)
Each Additional Year After Birth	–$63.62	–$29.12	£46.22	£7.43
	(.36)	(.73)	(.26)	(.87)
Year of Move	–$4,905.27	–$4,749.63	–£2,249.62	–£1,219.76
	(.00)	(.00)	(.03)	(.24)
Year After Move	–$6,686.02	–$6,103.68	–£2,435.06	–£1,646.33
	(.00)	(.00)	(.00)	(.03)
Each Additional Year After Move	–$1,216.16	–$1,244.35	–£561.98	–£552.17
	(.00)	(.00)	(.01)	(.01)

Notes: Estimates are based on sums of model estimates. Probability values, shown in parentheses, are based on standard errors calculated from error-covariance matrix.

Table 6 indicates that with respect to the birth of a child, the parameter associated with the Child Born This Year variable indicates a decrease in the intrafamily gender earnings gap of $2,063 (P > |t| = .000) in the US and £1,178 (P > |t| = .008) in GB in the year of a birth. The parameter associated with the Number of Children variable indicates an increase in the gender earnings gap of $8,662 (P > |t| = .000) in the US and £4,132 (P > |t| = .000) in GB for each child born. In both cases, the Age of Youngest Child variable is insignificant, indicating that this gap does not change after the birth of a child.

The net effect of these parameters on the gender earnings gap in the US is shown in Table 7. There is a significant increase in the gender earnings gap in the year of a birth of $6,598 (P > |t| = .000) and of $8,725 in the year after a birth (P > |t| = .000). In GB, the family gender earnings gap increases by £2,955 in the year of a birth (P > |t| = .000) and by £4,086 in the year after a birth (P > |t| = .000).

With respect to moving, the parameter associated with Moved This Year is statistically insignificant in both the US and GB (see Table 6). However, the Number of Previous Moves variable indicates a statistically significant increase in the gender earnings gap of $5,470 (P > |t| = .000) in the US and £1,873 (P > |t| = .020) in GB. The parameter associated with Years Since Last Move is statistically significant in both the US and GB, indicating that the gender earnings gap increases each year after a move by $1,216 (P > |t| = .000) in the US and by £562 (P > |t| = .007) in GB.

Table 7 shows that the net effect of these parameters on the gender gap in earnings is as follows: in the US, the gender earnings gap increases by $4,905 (P > |t| = .000) in the year of a move and by $6,686 (P > |t| = .000) in the year after a move. In GB, the gender earnings gap increases by £2,250 (P > |t| = .027) in the year of a move and by £2,435 (P > |t| = .001) in the year after a move. These effects increase over time.

Thus, Figure 5 for the US and Figure 6 for GB indicate that for both countries, migration and the birth of a child have similar long-term impacts on the intrafamily gender earnings gap. Although the negative effect on women’s earnings of moving is not nearly as strong as the negative effect on women’s earnings of having a child, the increase in the husband’s earnings after a move (see Figure 3) means that over time, migrant women earn significantly less than their husbands as a result of moving.

Figure 5.

Predicted Effect of a Birth or a Move on the Gender Earnings Gap: United States

Figure 6.

Predicted Effect of a Birth or a Move on the Gender Earnings Gap: Great Britain

CONCLUSIONS

To summarize, this longitudinal study places the well-accepted negative effect of moving on married women’s earnings into a greater temporal and social context. The results demonstrate clearly that family migration has a significant impact on the earnings of married women for several years following a move. In GB, earnings never return to their pre migration level. Although they do return to premigration levels in the US, the recovery takes several years, and the lost earnings are never recouped. This study also places the earnings loss into its cultural context by using a cross-national study design. Like previous cross-sectional, cross-national studies (Boyle et al. 1999, 2001, 2002, 2003), the results for GB and the US are quite similar. However, the negative effects of childbirth and migration for women are much stronger and more permanent in GB than in the US, suggesting that despite all the gender-equality promoting policies that the UK government employs, GB is still way behind the US in realizing economic mobility among women. More importantly, this study places the earnings loss within the context of the family. In both GB and the US, the effect of migration on the wife’s earnings is compensated for by gains in total family earnings. However, because the husband’s earnings increase and the wife’s earnings decline, the net effect is that family migration causes an increase in the intrafamily gender earnings gap. Finally, this study places these results alongside the effects of childbirth on women’s earnings. In this case, the effect of moving on women’s earnings is about one-half of the effect of childbirth. However, because migration involves a greater increase in the husband’s earnings than does childbirth, the net effect is that migration contributes as much to the intrafamily earnings gap as does childbirth.

At least two important empirical issues also deserve greater attention. First, by neglecting to consider the role of migration, previous research on the gender pay gap may have overestimated the effect of childbirth on the gender earnings gap. Migration and childbirth are highly correlated life course events, and both have a negative effect on women’s earnings (Clark and Withers 2008). By neglecting to include migration in empirical analyses of the effects of childbirth on women’s earnings, the effect of natality could be overestimated. Second, the effects of divorce may amplify these effects. This research demonstrates that the wife’s loss attributable to migration is compensated by increases in total family income (even though it increases the gender earnings gap). However, the high rate of divorce suggests that many women may not be able to recoup their family migration losses after their marriage ends in divorce.5 Indeed, Boyle et al. (2008) have recently linked family migration to an increased incidence of divorce.

Finally, the implications of these results for pay inequality research are significant. Although the literature has accepted that childbirth influences the gender pay gap, the role of the family in shaping labor market outcomes has not been fully embraced. With this research, it is even more clear that what happens within the family is determining what happens in the labor market. Indeed, it is not only that childbirth or migration increases the gender pay gap but that these events are relatively frequent and occur repeatedly, such that cumulative effects are probably quite significant. Any understanding of labor market inequality must give greater weight to the family as an object of analysis.