Bayesian Estimation of Hispanic Fertility Hazards from Survey and Population Data

Abstract

Previous studies have demonstrated both large gains in efficiency and reductions in bias by incorporating population information in regression estimation with sample survey data. These studies, however, assumed that the population values are exact. This assumption is relaxed here through a Bayesian extension of constrained maximum likelihood estimation applied to U.S. Hispanic fertility. The Bayesian approach allows for the use of both auxiliary survey data and expert judgment in making adjustments to published Hispanic Population fertility rates, and for the estimation of uncertainty about these adjustments. Compared with estimation from sample survey data only, the Bayesian constrained estimator results in much greater precision in the age pattern of the baseline fertility hazard and therefore of the predicted values for any given combination of socioeconomic variables. The use of population data in combination with survey data may therefore be highly advantageous even when the population data are known to have significant levels of nonsampling error.

Regression with sample survey data is the standard method for modeling the determinants of individual demographic events. Population data are typically not considered useful for these analyses due to their lack of covariates. Building on a tradition of statistical work dating back at least as far as Deming and Stephan (1942), however, methods for obtaining large gains in efficiency and reduction in bias by additionally incorporating population information in the regression estimation have been developed in diverse social science applications. Imbens and Lancaster (1994) proposed a generalized method of moments (GMM) estimator, and Handcock, Huovilainen, and Rendall (2000) proposed a constrained maximum likelihood estimator (MLE), to incorporate population information on the overall expected value (marginal expectation) of the dependent variable. In subsequent extensions using population information on conditional expectations of the dependent variable, Hellerstein and Imbens (1999) and Handcock, Rendall, and Cheadle (2005) demonstrated further gains in efficiency and also substantial reductions in bias.

These studies assumed that the population values are exact, or that they are at least unbiased. In practice, population information relevant to many estimation problems is available only in data sources with incomplete coverage, as with census under enumeration, misreported information, an inexact match between the universes of the population data and of the survey. These are all potential sources of bias in the population data with respect to the target population of the analysis. When demographers adjust for these biases, a combination of auxiliary data and expert judgment about the magnitude of adjustment is typically used. The use of expert judgment introduces a source of uncertainty that cannot be addressed within the classical (“frequentist”) statistical paradigm. The alternatives are either to ignore this source of uncertainty or to conduct sensitivity analyses based on discrete alternative assumptions for the adjustments. Ignoring judgment-based sources of uncertainty is frequently criticized by Bayesian statisticians (e.g., Hoeting et al. 1999), while the sensitivity analysis approach has the same major disadvantage as scenario-based population projections (Lee and Tuljapurkar 1994): it provides no quantitative estimate of the probability that the outcome of interest will lie outside the range given by a low variant and a high variant, and indeed no quantitative indication of the probability that the outcome will be within any given distance from the medium variant.

The present study applies a Bayesian approach to the problem of incorporating sources of uncertainty involving demographic judgment into regression estimates that combine survey and population data. Compared with the sensitivity analysis approach, the Bayesian analysis provides a way of (1) formally assigning probabilities to alternative values that might be chosen in a sensitivity analysis; (2) replacing discrete sensitivity analysis points with a continuous distribution of alternative values; and (3) systematically combining uncertainty from expert knowledge with uncertainty from other sources, including from sampling error. The Bayesian approach allows for a formal statistical treatment of the following principal research question of the present study: how much added value from using population data in a demographic hazard model can be retained when the population data deviate substantially from the assumption that they are exact?

Bayesian methods have as yet been infrequently applied in demography. The statistical case for doing so, however, is strong. Smith (1991:322) discussed the case of using population data to poststratify a survey if the population data are not from exactly the same year as the survey. He argued that a Bayesian approach is needed to incorporate the additional uncertainty introduced through judgment about how close in time is close enough to make the population data still appropriate for use in poststratifying the survey data. An analogy to combining data from close time periods is Assuncao et al.’s (2005) use of an “empirical Bayes” approach (Carlin and Louis 2000) to combine data from neighboring locations, incorporating both spatial and socioeconomic distance. Elliott and Little (2000) applied a fully Bayesian approach to adjusting census counts of the total U.S. population by age, sex, and race/ethnicity, incorporating both objective auxiliary data and subjective, expert-based judgment into the Bayesian “priors.” These are the standard elements used by demographers in the adjustment of population data. The empirical Bayes approach, in contrast, has the disadvantage of forming the priors in a way that admits no data except those in the likelihood function and that usurps the potentially positive roles of expert judgment and auxiliary data.

Our application of Bayesian methods to the combining of survey and population data focuses on uncertainty in population-level data on Hispanic fertility. This uncertainty is introduced primarily through the census-based Hispanic population estimates that form the denominator of those fertility rates. The large contribution of immigration to the contemporary U.S. Hispanic population leads to major challenges for the accurate estimation of that denominator and for developing an accurate and up-to-date understanding of Hispanic fertility levels, patterns, and determinants from either survey or population data. We argue that these challenges both increase the need for combining data sources to arrive at “best” estimates and increase the importance of developing statistically rigorous methods for estimating the degree of uncertainty about these combined-data estimates.

DATA AND METHOD

In this section, we first describe the three data sources that provide information about Hispanic women’s fertility. We then describe the Bayesian model that allows for the incorporation of information from the three data sources in a regression model.

Data Sources

The Panel Study of Income Dynamics (PSID; Institute for Social Research 2007) allows us to estimate an annual fertility hazard for Hispanic women aged 25 to 34 in any of the years between 1991 and 1995. A restricted age range is used in part because variables including employment status are not available in the PSID for women who were not either the head of the household or partnered to the head, and in part to allow for a more parsimonious specification of the hazard in a regression model. The five-year period is chosen to incorporate data from a large Hispanic supplement sample (the “Latino sample”). The standard PSID survey instruments were applied to this subsample annually from 1990 through 1995 (Survey Research Center 1993). The Latino sample included 7,453 Mexican, Puerto Rican, and Cuban individuals in 2,043 households that were originally sampled in the 1989 Latino National Political Survey (LNPS). Central American, South American, and “other” Hispanics were not included in this LNPS sample. These omitted groups made up a relatively small proportion of the overall Hispanic population at the time the Latino sample was drawn (the late 1980s) but experienced very large increases over the 1990s. We combine this Latino subsample with the 1991–1995 person-years of Hispanic women (of all country origins) in the core sample of 1968 PSID household members and their descendant family members. Throughout the analysis, we use the core PSID weights that are designed for the use of the subsample components together. Weighted or unweighted, however, this combined sample will be only an approximation to a random sample of the rapidly changing U.S. Hispanic population over the 1991–1995 period. The sample design leads to much larger sampling error than would a sample of the same size drawn using equal probability methods. In bootstrapped estimates for a related analysis of Hispanic women’s family transitions in the PSID, we found that standard errors were, on average, 1.9 times as high as those estimated under the assumption of independent observations (results not shown). We use this 1.9 ratio when comparing the PSID with the Current Population Survey (CPS) and population data immediately below. We ignore this design effect, however, when comparing the different models that are all estimated with the PSID data. The characteristics of the PSID sample and variables used in estimating the Hispanic fertility hazard are shown in Table 1. A birth is defined as occurring or not between the previous panel year t – 1 and the current panel year t. Age is defined at t, and the remaining variables are defined at t – 1.

Table 1.

Hispanic Women’s Person-Years at Ages 25 to 34: Panel Study of Income Dynamics 1991–1995 (percentages, unless otherwise indicated)

Variable	Weighted	Unweighted
Proportion Giving Birth in Year	10.0	9.8
Union Status
Single	30.6	34.3
Cohabiting	8.2	8.5
Married	61.2	57.2
Education
Less than high school graduate	27.1	34.2
High school graduate	36.2	35.9
Some college or college graduate	36.8	29.9
Employment Status
Full-time employed	45.4	41.9
Full-time employed and less than high school graduate	8.7	8.8
Mean Age (years)	29.5	29.7
Percentage in Latino Sample	64.1	89.0
Sample Size (person-years)	1,851

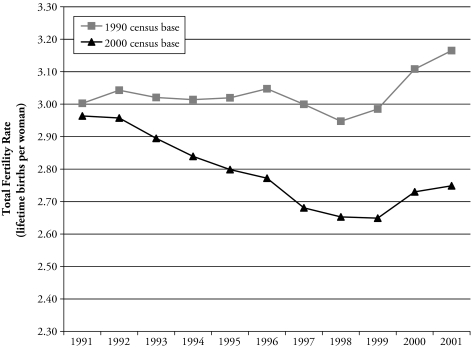
For this same 1991–1995 period, population-level data were available for births to Hispanic women by single-year age from the birth registration system (National Center for Health Statistics 2001) and for the number of Hispanic women by single-year age in the annual population estimates series extending from the 1990 census (U.S. Census Bureau 2001). Annual single-year age-specific Hispanic fertility rates (ASFRs) were calculated using these population data series, with births to Hispanic women as the numerator and number of Hispanic women as the denominator (Hamilton, Sutton, and Ventura 2003). We refer to these ASFRs as “the 1990-based NCHS rates.” The birth registration system provides a complete enumeration of births in the United States, leaving only misclassification as a source of bias in the ASFR numerator of births to Hispanic women of any given age. The Hispanic population denominator, however, is subject to potentially much larger non sampling biases. These are primarily from two sources: uncorrected 1990 census undercount, and error in estimates of net immigration by age and sex after 1990. It became clear after the 2000 census that the combined effect of these biases on the Census Bureau’s Hispanic population estimates had been large (Guzmán and McConnell 2002). The subsequent upward revisions reduced the NCHS’s estimate of the Hispanic total fertility rate in 2000 from 3.10 children per woman using the 1990-based population estimates to only 2.73 children per woman using the 2000-based population estimates (Hamilton et al. 2003). The amount of downward correction of the fertility rates increased over the decade as the 1990-based population estimates became more and more dependent on the intercensal components of population change, especially that of immigration (see Figure 1). The estimated upward bias in the 1990s-based NCHS rates was greatest for 25- to 29-year-olds, at 18% higher in 2000 and already 9% higher in 1995. For 30- to 34-year-olds, the 1990-based fertility rates were 11% higher in 2000 and 6% higher in 1995 (see Hamilton et al. 2003: Table 4).

Figure 1.

Hispanic Total Fertility Rate Using 1990-Based and 2000-Based Population Estimates

Source: Hamilton, Sutton, and Ventura (2003).

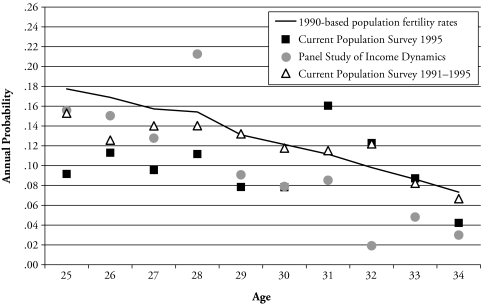
Although it was the 2000 census that clearly revealed that the Hispanic population estimates had been downwardly biased, this information was not available to researchers of Hispanic fertility in the 1990s. Information from sample surveys, however, already provided reasons to suspect that the NCHS estimates were too high before the 2000 census results.1 Chief among these were the substantially lower estimates of Hispanic fertility produced at the time from the CPS (see, e.g., Smith and Edmonston 1997). The CPS weights incorporate poststratification to census-based population estimates that are themselves closely related to the population denominators of the NCHS fertility rates (Bureau of Labor Statistics 2002). The CPS’s survey-derived birth numerators, however, make the CPS an independent source of fertility rate information from a current sampling frame. The CPS data provide both a major indicator that the NCHS data are biased and, together with expert judgment, a means for correcting this bias. In 1995, the CPS included a fertility history in its June supplement. In Figure 2, we alternatively compare the CPS in the year ended June 1995 (“CPS 1995”) and of the five years 1991–1995 to June 1995 (“CPS 1991–1995”) with both the PSID annual birth probabilities that are estimated over the period 1991–1995 and the NCHS annual fertility rate that is estimated for the calendar years 1991–1995. We do not present the NCHS estimates for the single calendar year 1995 because they differed little from the NCHS 1991–1995 average. Using the CPS sample for the year ended June 1995 avoids sample-selection biases due to migration that might be present when retrospectively estimating Hispanic fertility rates over the entire 1991–1995 period. The costs of ignoring CPS respondents’ reports of births more than a year before the survey, however, are that only bias in the NCHS or PSID data for the year ended June 1995 may be evaluated and that the CPS Hispanic sample size is then relatively small. When only this “1995” person-year of fertility exposure is used for each woman, there are 1,039 cases aged 25 to 34.

Figure 2.

Survey and Population Estimates of Hispanic Fertility, 1991–1995

Comparing the estimates in the three data sources, the main features are as follows. First, the fertility level in the 1990-based NCHS series is higher than that in either the CPS or PSID. The overall 25- to 34-year-old fertility rate is, respectively, 0.1281 in the NCHS, 0.1196 in the 1991–1995 CPS, 0.9821 in the 1995 CPS, and 0.0999 in the PSID. Both the 1995 CPS and 1991–1995 PSID rates are significantly lower than the NCHS rate at the p < .05 level, while the 1991–1995 CPS rate is significantly lower than the NCHS rate at the p < .10 level. Although a discrepancy between the population and survey data sources would normally be considered as evidence of bias in the survey data sources, here we consider it as evidence of potential bias in the population data source. Compared with the 1990-based NCHS estimates, the overall fertility rate among women aged 25–34 is 7% lower in the 1995 CPS, 23% lower in the 1991–1995 CPS, and 22% lower in the 1991–1995 PSID. With the hindsight of the 2000-based revisions, these differences are seen to be greater than the downward adjustments made by NCHS: respectively, 5.3% and 3.3% lower for 25- to 29-year-olds and 30- to 34-year-olds in 1993 (the midpoint of 1991–1995) and 8.7% and 5.6% lower in 1995. Simply shifting from using the population-level (NCHS) data to using an alternative auxiliary data source such as the CPS to provide a single best estimate of the overall Hispanic fertility hazard, then, would likely result in overcorrection of the upward bias of the NCHS fertility rate.

The NCHS estimates display a smooth age pattern, in contrast to the substantial sampling error apparent in the CPS and PSID estimates. Only in the NCHS data is it clear that the fertility rate falls monotonically with age from 25 to 34 years old. Visual inspection of the PSID line reveals a generally downward sloping function similar to the NCHS. Visual inspection of the two CPS series, however, suggests a flatter or possibly curvilinear function. While the 2000-based revisions to the NCHS age-group-specific fertility rates indicated a greater downward adjustment for 25- to 29-year-olds than for 30- to 34-year-olds, we assume below that information is not available to the researcher at the time of the construction of the Bayesian prior around the population ASFRs. The conflicting evidence between the CPS and PSID patterns, however, does not provide information with which to impose any age structure on a demographic adjustment to the 1990-based NCHS data. We therefore we use those data sources only for their information about the overall level of the fertility rates.

A Bayesian Approach to Combining Data

The fundamental characteristic of a Bayesian analysis is its combination of a likelihood function for sample data with outside information on the model’s parameters (Gelman et al. 2003). Information about the regression parameter β that is available to the researcher before the estimation using the sample is expressed as a prior probability distribution, or simply a “prior.” Bayesian statistical inference about β is made in terms of probability statements that are based on the combined information from the estimation sample and the priors. These are derived from the “posterior distribution” p(β) generated by the estimation process:

$$p\left(\beta |y,x\right)=\alpha \left(y,x\right)q\left(\beta \right)L\left(\beta |y,x\right).$$ (1)

The first term, α(y,x), is a normalizing constant to ensure the expression on the right side of the equality integrates to unity. It does not depend on β, so interest focuses on the prior distribution q(β) and the likelihood L(β | y,x). We omit reference to α(y,x) in further development of the Bayesian model below. The likelihood term expresses the information in the survey sample data about β. The posterior distribution for β represents our complete knowledge of it based both on the sample survey data and prior knowledge about the value of this parameter represented by q(β).

The likelihood function in this expression is as for standard (“frequentist”) regression estimation. In our case, the likelihood is for a discrete fertility hazard using data from the PSID only. Let β be the unknown p-dimensional parameter of interest describing the relationship between the dependent variable Y and a vector of explanatory variables X. The dependent variable Y has two levels: 0 denotes no birth, and 1 denotes a birth, during the year [t – 1, t). The regressor vector X is specified from the limited set of PSID variables described in Table 1, recognizing that more variables might be included in a model that takes full advantage of the rich information available in a panel survey data set such as the PSID. The regressors are indicator variables for union status, education, and employment status, plus nine indicator variables for single-year ages 26 to 34. The intercept represents the reference group of 25-year-old, married women who are high school graduates and were not full-time employed in the previous year. We use a binary logistic regression model for the birth probability P(Y = 1 | X = x, β):

$$\text{logit}\left[P\left(Y=1\left|X\right|x,\beta \right)\right]=x^{\prime }\beta ,$$ (2)

where the regression parameter β and regressors x are vectors. The PSID survey data, including the PSID sample weights w_i, are denoted by D = (y_i, x_i, w_i), i = 1, . . . n. The log-likelihood expression that is maximized is

$$logL(\widetilde{\mathbf{\text{β}}}|y,\hspace{0.17em}\mathbf{\text{x}})\hspace{0.17em}=\hspace{0.17em}\sum _{i=1}^n{w}_{i}log\hspace{0.17em}P(Y\hspace{0.17em}=\hspace{0.17em}{y}_i\hspace{0.17em}|\hspace{0.17em}\mathbf{\text{X}}\hspace{0.17em}=\hspace{0.17em}{\mathbf{\text{x}}}_i,\hspace{0.17em}\widetilde{\mathbf{\text{β}}}).$$ (3)

The disadvantage in estimating the parameter vector β using the sample likelihood alone is that we forgo the opportunity to allow additional information, including that from the NCHS and CPS data described above, to improve the estimation of β.

To use this additional information, we implement a specific form of the general Bayesian model (1) that is an extension of the constrained maximum likelihood (ML) approach to combining population and survey data. Instead of using a prior distribution of the parameter values themselves, this model uses a prior distribution consisting of quantities that are functions of the parameter values. These quantities are the single-year age-specific fertility rates, denoted by the vector ϕ. The function describes the relationship of the parameters of a fully specified fertility hazard model to the age-specific fertility rates. We denote this “constraint” function by C(β) = ϕ, and provide details of its nature and relationship to the likelihood below.

Let q(β,ϕ) be the prior distribution for β and ϕ in model given by the logistic regression Eq. (2) and the constraint function. This prior distribution represents what we know about β and ϕ from other sources, before the PSID survey data are formally taken into account. In its most general formulation, the prior q(β,ϕ) is a multivariate distribution representing our knowledge about the regression parameter β and the population value ϕ. Where prior information is available about both ϕ and β, additional steps need to be taken to avoid logical inconsistencies between the separate priors for ϕ and β (e.g., the Bayesian melding approach of Poole and Raftery 2000). Our application simplifies the specification of q(β,ϕ) such that prior information is available only about ϕ. In Bayesian terminology, we specify an “informative” prior distribution for ϕ and a “noninformative” distribution for β. The prior distribution is then given by

$$q\left(\beta ,\varphi \right)=q\left(\varphi \right)I\left(C\left(\beta \right)=\varphi \right),$$ (4)

where q(ϕ) is our expression of prior knowledge about the population value of the constraint. We represent our lack of prior knowledge about β as prior independence between β and ϕ and as β being diffuse over its range. Note that the constraint function implies that once a given value of ϕ is realized from its prior distribution q(ϕ), β becomes (a posteriori) dependent on that realized value and on the sampling distribution of β. Prior independence simply means that the distribution of ϕ and the sampling distribution of β are independent.

Applying Bayes theorem to this distribution, the constraint function, and the logistic regression model (2) produces the “posterior” distribution that we can interpret as representing what we know about β and ϕ after combining our prior knowledge with the survey data. This distribution has density

$$p\left(\beta ,\varphi |y,x\right)\propto \hspace{0.17em}q\left(\varphi \right)I\left(C\left(\beta \right)=\varphi \right)L\left(\beta |y,x\right),$$ (5)

omitting now the normalizing constant and replacing the equal sign with the proportionality symbol, ∝. The posterior distribution is proportional to the product of three factors: the prior distribution q(ϕ), the indicator function for constraint function C(β) = ϕ, and the likelihood L(β | y,x). Under the Bayesian paradigm, this posterior distribution represents our complete knowledge of β and ϕ based both on the sample survey data and on prior knowledge from a combination of the NCHS and CPS data and expert judgment about those data sources. We show below that this posterior density is multivariate normal in β and orthogonal between β and ϕ, and therefore that the expectation and (co)variances of β are sufficient to describe the posterior parameter of interest.

In our application, there are 10 constraint constants corresponding to each of the 10 ages in our sample, c_a, a = 25,26, . . . ,34. The constraint functions express the population values of the age-specific fertility rates (ASFRs) as weighted averages of the probabilities of birth by each combination of the socioeconomic covariates for that single-year age. The weights are the proportions of all women of the single-year age that have a given combination of the socioeconomic covariates. Formally, each of the age a constraints is given by

$$c_a\hspace{0.17em}=\hspace{0.17em}{C}_a(\mathbf{\text{β}})\hspace{0.17em}=\hspace{0.17em}\sum _{\text{x}}P(Y\hspace{0.17em}=\hspace{0.17em}y|\mathbf{\text{X}}\hspace{0.17em}=\hspace{0.17em}\mathbf{\text{x}},\hspace{0.17em}A\hspace{0.17em}=\hspace{0.17em}a,\hspace{0.17em}\mathbf{\text{β}})\hspace{0.17em}\cdot \hspace{0.17em}P(\mathbf{\text{X}}\hspace{0.17em}=\hspace{0.17em}\mathbf{\text{x}}|A\hspace{0.17em}=\hspace{0.17em}a).$$ (6)

This specification is equivalent to that of Handcock et al. (2005), where it was assumed that the values c_a were known exactly from the population data. We relax this assumption here and instead denote the 10 single-year age constraints as prior distributions of the true vector of age-specific fertility rates, ϕ = ϕ₂₅, . . . ,ϕ₃₄. Formally, these fall in the category of “elicited priors” (see, e.g., Carlin and Louis 2000:23–25; Kadane et al. 1980). Gill (2002: chap. 5) discusses different types of priors that may be used specifically in social science applications, noting that while “…an overwhelming proportion of the studies employing elicited priors are in the medical and biological sciences, the methodology is ideal for a wide range of social science applications” (p. 129). With an elicited prior, experts in the field of the substantive analysis are asked their opinions about the most likely value and how likely is the true value to exceed or be less than 1 or more-specific, meaningful quantities. The prior distribution is generated by imposing a continuous probability distribution about these points. A common choice for the form of the prior distribution, and that chosen here, is the normal. Its advantages include giving higher weights to values that are nearer the most-likely value and that deviations from this most-likely value are equally likely to be positive or negative. The elicited most-likely value then becomes the mean (μ) of the distribution. The standard deviation (σ) parameter can be derived from the elicited probability that the true value exceeds (or, conversely, is less than) a substantively meaningful point. This elicited probability is interpreted as a cumulative probability in a normal distribution with mean μ.

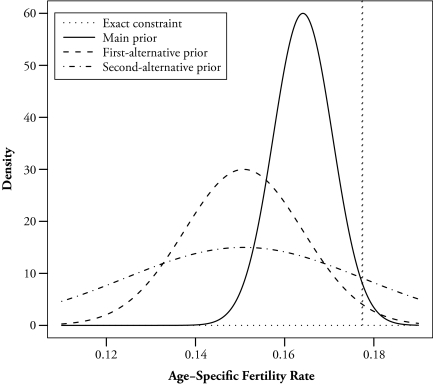
We do not conduct a formal elicitation in the present study but instead present the Bayesian priors under a likely range of the opinions of demographers working in this area, given the results from the comparisons between the 1990-based NCHS estimates and the lower CPS estimates as presented earlier. To encompass a plausible range of demographic opinion, we follow good Bayesian practice by conducting tests of the sensitivity of the posterior (the final estimates) to changes in the prior. We construct a main prior and two alternative priors. For our main prior, we adjust the population values by assuming that the true age-specific fertility rates are all 7.5% lower than of the 1990-based NCHS rates. This is very close to the 7% difference between the 25- to 34-year-old fertility rate based on the 1990 NCHS and that based on the 1991–1995 CPS. For our two alternative priors, we assume that the true age-specific fertility rates are as much as 15% lower than the 1990-based NCHS rates and therefore closer to 23% difference between the 1990-based NCHS rate and the 1995 CPS rate. We refer to the first alternative prior as the “high-bias” prior. In both the main prior and the high-bias prior, the 1990-based NCHS value is taken to be 2 standard deviations above the mean: the point at which the chance is only 1 in 20 that the true value is at least this high. The greater distance of the mean of the first alternative prior from the 1990-based NCHS value, however, implies a higher variance than for the main prior. We add further variance in a second alternative prior, referred to as the “high-bias, high-variance” prior. Its mean is again 15% lower than the 1990-based NCHS value, but now there is a 1 in 6 chance that the true value is at least as high as the 1990-based NCHS value, implying that the 1990-based NCHS value is only 1 standard deviation above the mean of these two alternative priors. Due to the symmetry of the normal distribution, it also implies a 1 in 6 chance that the true population ASFR was as much as 30% lower than the NCHS value. As such, it reflects extremely low confidence in the reliability of the population-level Hispanic fertility rates; it is therefore presented as an upper bound on the plausible degree of uncertainty of the true population value given the 1990-based NCHS data and our knowledge from other sources. The shapes and locations of the three different priors are illustrated for age 25 in Figure 3.

Figure 3.

Main and Alternative Bayesian Prior Distributions About the Population Fertility Rate at Age 25

Estimation

If the survey data are all the information we have, under standard regularity conditions, the estimated value β̂ that maximizes the likelihood (3) is an asymptotically efficient estimator of β. The estimator is also asymptotically unbiased, and normal with asymptotic variance V_s, where V_s is the inverse of the expected information matrix for the parameter β, whose elements are given by $-E_{\beta }\left[\frac{{\partial }^2\text{log}\left[L\left(\beta |y,\text{x}\right)\right]}{\partial {\beta }_i\partial {\beta }_j}\right]$ (Casella and Berger 2002). We refer to these as the unconstrained model estimates.

If we maximize the likelihood of Eq. (2) subject to the exact constraint function (6), the estimator β̂_c is asymptotically efficient, unbiased, and normal, just as is the unconstrained MLE for the situation in which the population data are ignored. However, while the asymptotic variance in the unconstrained version is given by the expected information matrix V_S, in the constrained version, the asymptotic variance is

$$V_C=V_S-V_S{H}^T{\left[H{V}_S{H}^T\right]}^{-1}H{V}_S,$$ (7)

where $H{\left[\frac{\partial C_i\left(\tilde{\beta }\right)}{\partial {\tilde{\beta }}_j}\right]}_{p\times c}$ is the gradient matrix of C(β) with respect to β. Since the second term in this expression is positive definite, the inclusion of the population information always leads to an improvement in the estimation of β. The variance formula given in (7) shows that the constrained estimator β̂_c is, on average, closer to β than is the unconstrained estimator β̂_u. In particular, the standard error of the estimator in the version using the population information will always be less than the unconstrained estimator that ignores it. This is the key result of the constrained ML model (Handcock et al. 2005).

The standard approach to maximization in a Bayesian model is to use numerical integration to compute the posterior density in (5), using numerical approximations to integrate out the normalizing constant. Because of the prior independence assumed between the constraints and the regression parameters, we are able to use instead a computationally simpler, sequential approximation based on Monte Carlo sampling. We draw 1,000 normal variates corresponding to 1,000 realizations of the prior. Consistent with our assumption that uncertainty in the population denominator has an equal effect across all ages, a single normal variate draw is sufficient for all 10 ages, with an affine transformation of it taken to form the 10 age-specific rates ϕ = ϕ_{25, . . . ,}ϕ₃₄. For each realization of the prior, the regression estimation is then conducted as for constrained MLE with exact population values. That is, Eq. (2) is maximized subject to Eq. (6), but with the random draw ϕ_a substituting for fixed constraint value c_a. Each draw of ϕ produces a different set of parameter point estimates β̂_ϕ with (co)variances Var(β̂_ϕ). Given the univariate normality of the prior about each of the constraint values and the approximate (asymptotic) multivariate normality of the parameter estimates from the logistic regression for any given value of the prior (Handcock et al. 2005), the posterior distribution of the parameter estimates will also be closely approximated by a multivariate normal distribution.

The posterior distribution of the parameters is then generated directly from the Monte Carlo simulation results. The Monte Carlo approximations to the posterior means of the regression parameters are just the means of the 1,000 estimated regression parameter values, E_ϕ[β̂_ϕ]. Using the conditional variance identity (Casella and Berger 2002), estimates of the posterior (co)variances of the parameters are derived as the sum of two sources: (1) the Bayesian analogue of the (co)variance of the sampling distribution of the (exactly) constrained parameter estimates, E_ϕ[Var(β̂_ϕ)]; and (2) variability due to the uncertainty in the value of the population constraints, Var_ϕ(β̂_ϕ).

RESULTS

The results of estimating alternative versions of a logistic regression model of the annual probability of a birth among Hispanic women aged 25 to 34 are shown in Table 2. We compare parameter estimates and standard errors (SEs) under the unconstrained and exact constraints models, and compare these to parameter estimates and standard deviations about the posterior distribution of the parameters (SDPs) for the Bayesian constraints models. The SDPs are higher than the SEs due to the additional variability of allowing for uncertainty in the value of the population constraints Var_ϕ(E[β̂_ϕ]), as seen in the expression Var_ϕ(β̂_ϕ) = E_ϕ[Var(β̂_ϕ)] + Var_ϕ(E[β̂_ϕ]), where SDP(β̂_ϕ) is just the square root of Var_ϕ(β̂_ϕ). The term Var_ϕ(E[β̂_ϕ]) increases as the standard deviation of the prior distribution of ϕ increases. Therefore SDP(β̂_ϕ) will tend to increase when moving from the main prior to the first-alternative and then second-alternative priors.

Table 2.

Logistic Regression Model Estimates of the Annual Probability of Giving Birth Among Hispanic Women Aged 25 to 34, 1991–1995

Variable	Unconstrained		Exact Constraints		Bayesian Constraintsa
					Main Prior (fertility 7.5% and 2 SD lower)		High-Bias Prior (fertility 15% and 2 SD lower)		High-Bias, High-Variance Prior (fertility 15% and 1 SD lower)
	Parameter	SE	Parameter	SE	Posterior Parameter	SDP	Posterior Parameter	SDP	Posterior Parameter	SDP
Intercept	−1.707	0.242	−1.559	0.148	−1.642	0.157	−1.749	0.183	−1.761	0.264
Age (ref. = 25)
Age 26	−0.092	0.282	−0.112	0.022	−0.109	0.022	−0.108	0.022	−0.108	0.023
Age 27	−0.271	0.292	−0.186	0.028	−0.182	0.029	−0.179	0.029	−0.179	0.029
Age 28	0.257	0.267	−0.306	0.036	−0.299	0.036	−0.296	0.036	−0.295	0.037
Age 29	−0.687	0.330	−0.434	0.030	−0.422	0.030	−0.416	0.030	−0.416	0.032
Age 30	−0.814	0.366	−0.496	0.024	−0.482	0.024	−0.476	0.025	−0.476	0.027
Age 31	−0.790	0.339	−0.654	0.028	−0.638	0.028	−0.630	0.029	−0.630	0.032
Age 32	−2.404	0.567	−0.834	0.046	−0.816	0.046	−0.807	0.046	−0.806	0.049
Age 33	−1.446	0.379	−0.982	0.038	−0.961	0.038	−0.951	0.038	−0.951	0.042
Age 34	−1.931	0.460	−1.153	0.053	−1.130	0.053	−1.118	0.054	−1.118	0.057
Single	−0.814	0.207	−0.800	0.206	−0.802	0.206	−0.803	0.206	−0.800	0.206
Cohabiting	0.155	0.265	0.148	0.261	0.149	0.261	0.150	0.261	0.150	0.261
Education (ref. = high school graduate)
Not a high school graduate	0.619	0.241	0.604	0.238	0.606	0.239	0.607	0.239	0.604	0.238
Some college or college graduate	0.072	0.191	0.071	0.189	0.071	0.189	0.071	0.190	0.071	0.189
Employment (ref. = part-time or not employed)
Full-time employed	0.323	0.192	0.318	0.191	0.319	0.191	0.319	0.191	0.318	0.191
Full-time and not a high school graduate	−0.801	0.395	−0.782	0.390	−0.784	0.391	−0.786	0.392	−0.783	0.391
−2 Log-Likelihood	1,100.3		1,143.1		––		––		––
Sample Size (person-years)	1,851		1,851		1,851		1,851		1,851

Notes: SE = standard error about the parameter estimate. SDP = standard deviation about the posterior distribution of the parameter.

^aBayesian constrained model parameter estimates and standard errors are averages of 1,000 simulations.

The regressor variables are age, marital status, education, and employment status, as described in Table 1. The parameters and standard errors for the socioeconomic variables are little changed by constraining to population values, in either the exact constraints or the Bayesian constraints models. This is consistent with previous results (Handcock et al. 2005) showing that only the intercept and the directly constrained regressor variables have their parameter values or standard errors altered substantially by the introduction of population constraints. In the present application, only age is directly constrained. The standard errors for the age coefficients are reduced by a factor of approximately 10 by constraining to the population data. This reduction is almost as large in the Bayesian constraints models as in the exact constraints model. These results reflect the large amount of information about the single-year age pattern of U.S. Hispanic fertility conveyed by the observed, 1990-based ASFRs, together with the assumption that bias in those rates is of equal magnitude across the 10 single-year ages. This assumption accounts for the lack of change in the parameter estimates and standard errors for the age coefficients when moving from the exact constraints to the Bayesian constraints model.

The magnitude of reduction about the intercept standard error is sensitive to the specification of the prior. The reduction in the standard error about the intercept SE(β₀) ranges from 0.242 for the unconstrained model to 0.148 for the exact constraints model. When the assumption of exactly known population values in our main prior is relaxed, the standard deviation of the posterior, SDP(β₀) = 0.157, is not much higher than the exact constraints SE(β₀) of 0.148. When, under the first alternative, high-bias prior, the mean of the distribution is moved twice the distance from the 1990-based series (15% lower instead of 7.5% lower), SDP(β₀) increases to 0.183, still closer to the exact constraints value than to that of the unconstrained model. Thus, even when using constraints formed from population data that encompass unusually large magnitudes of error, statistical precision is increased not only in the estimation of the age pattern but also in the estimation of the overall fertility level.

Under the high-bias, high-variance prior, however, SDP(β₀) increases to 0.264, higher even than SE(β₀) for the unconstrained model (0.242). One interpretation of this is that it shows how extreme the variability assumption is for this prior. A second valid (and complementary) interpretation, however, is that this comparison implies an overestimation of the precision of the estimate of the intercept parameter in the unconstrained model. Precision is overestimated (uncertainty is underestimated) due to the implicit assumption that the sample is exactly representative of the population. Instead, we expect that the PSID’s sample is not fully representative of the changing U.S. Hispanic population and that indeed no panel survey will be without a very frequently refreshed sample and sampling frame. The Bayesian framework allows us to incorporate this as a source of uncertainty even in the unconstrained version.

Variance and Bias Compared Between the Three Models

In this subsection, we use the Bayesian posterior mean squared deviation (MSD; see Rendall, Handcock, and Jonsson [2007] for details) as a unified framework to compare the variance and bias of the estimates under the three model types: the unconstrained, exact constraints, and Bayesian constraints models. This is the Bayesian analogue of the frequentist mean squared error (MSE). The MSE sums two sources of error, the sampling variance and the mean squared bias. The MSD admits a third source of error that we refer to as constraint variance. It represents the variation in the parameter estimate β̂_ϕ attributable to our uncertain knowledge of the true constraint value. In Table 3, we present empirical estimates of the three components of the MSD for the intercept parameter. This is the key parameter for understanding the role of different levels of uncertainty assumed in the prior constructed to represent knowledge about the true population values, and for understanding the costs of estimating the model with no adjustment to the 1990-based NCHS values (in the exact constraints model).

Table 3.

Mean Squared Deviation (MSD)^a of the Intercept Parameter: Unconstrained, Exact Constraints, and Bayesian Constraints Models

Assumed Prior	Model Type
	Unconstrained	Exact Constraints	Bayesian Constraints
Main Prior
(1) Mean squared bias	0.0042	0.0070	0.0000
(2) Sampling variance	0.0587	0.0219	0.0220
(3) Constraint variance	0.0025	0.0025	0.0025
MSD	0.0654	0.0315	0.0245
High-Bias Prior
(1) Mean squared bias	0.0017	0.0361	0.0000
(2) Sampling variance	0.0587	0.0219	0.0221
(3) Constraint variance	0.0114	0.0114	0.0114
MSD	0.0719	0.0694	0.0335
High-Bias, High-Variance Prior
(1) Mean squared bias	0.0029	0.0408	0.0000
(2) Sampling variance	0.0587	0.0219	0.0220
(3) Constraint variance	0.0479	0.0479	0.0479
MSD	0.1094	0.1106	0.0699

^aMean squared deviation (MSD) = sum of rows (1), (2), and (3). Row (1) = point estimate of β₀ under Bayesian prior. Row (2) = asymptotic variance for the each regression estimate of β₀, given by [SE(β₀)]². Row (3) = variance in β₀ due to uncertainty about the true population constraint value.

The first new insights provided by the Bayesian approach are in comparing the exact constraints estimator with the unconstrained estimator. When the population data are biased, the exact constraints estimator is no longer unambiguously superior to the unconstrained estimator. While the sampling variance term is still unambiguously lower for the exact constraints model, this can be offset by a higher mean squared bias. An almost exact off-setting of variance by bias is indeed seen to occur empirically when either the high-bias or high-bias, high-variance prior for ϕ is used. While the sampling variance about β₀ is 0.0587 for the unconstrained estimator compared with only 0.0219 for the exact constraints estimator, this difference is offset by a much higher mean squared bias for the exact constraints estimator (0.0361 and 0.0408, respectively, for the two alternative priors) than for the unconstrained estimator (respectively, 0.0017 and 0.0029).

For the main prior, however, the mean of the constraint distribution is constructed to be only half as far from the observed population value, and the mean squared bias for the exact constraints model is accordingly greatly reduced compared with that for the high-bias and high-bias, high-variance priors. The greater sampling variance of the unconstrained estimator then dominates, and the MSD for the exact constraints model (0.0315) is only half that of the MSD for unconstrained model (0.0654). That is, under our best estimate of the true population values of the Hispanic ASFRs, the estimation of the intercept parameter using the 1990-based NCHS data as if it were unbiased (the exact constraints model) still results in estimates that are substantially better than those from the (unconstrained) model that ignores those data.

The differences in the MSDs of the exact constraints and Bayesian constraints models are due almost entirely to the mean squared bias term. The Bayesian constraints model will have a lower MSD than the exact constraints model for every prior distribution of ϕ that is not centered exactly on the 1990-based ASFR values used in the exact constraints model. In the case of the main prior, the mean squared bias for the exact constraints model (0.0070) is low relative to sampling variance (0.0219). The MSD for the Bayesian constraints model (0.0245) is therefore not much lower than it is for the exact constraints model (0.0315). Under the high-bias and high-bias, high-variance priors, however, the constraint distribution is centered twice as far from the observed population values, and so the mean squared bias of the exact constraints model is high and the consequent increase in MSD over that for the Bayesian constraints model is large: 0.0694 versus 0.0335 for the high-bias prior, and 0.1106 versus 0.0699 for the high-bias, high-variance prior.

Note that the “constraint variance” component of the MSD is identical across the unconstrained, exact constraints, and Bayesian constraints models. This result may be counterintuitive for the unconstrained model because it is specified and estimated without explicit reference to population values. Implicitly, however, the sample data used in the unconstrained model are assumed to be drawn from the population for which the constraint prior is specified. Under the Bayesian interpretation represented in the calculation of the MSD for all three models, we begin from the assumption that the PSID may not be exactly representative of the population, and we use the prior for the population values to represent our knowledge of the PSID’s departures from perfect representativeness. This knowledge, when carried through to the posterior distribution of the regression parameters, allows us to evaluate the potential impact of bias in the PSID on the parameter estimates of the PSID’s departures from perfect representativeness. Not only the location but also the variance of the prior matters when evaluating the unconstrained model. The greater the variance in the prior, the less we know about the extent to which the PSID is potentially unrepresentative. This, too, increases our uncertainty about the unconstrained model estimates.

Empirically, the constraint variance is remarkably small for the main prior: 0.0025. This is only 1/20 of the variance contributed by the PSID survey data (sampling variance) in the unconstrained case (0.0587), and 1/10 of the sampling variance when constrained estimation is used (0.0219 and 0.220 respectively, in the exact constraints and Bayesian constraints cases). The contribution of constraint variance increases to a substantial level under the high-bias prior (0.0114), though this is still only half as high as the constrained models’ sampling variances. In the high-bias, high-variance model, constraint variance is twice the level of sampling variance under constrained regression, though still lower than sampling variance for unconstrained regression. The low level of constraint variance relative to sampling variance for both the main prior and the high-bias prior provides strong support for the conclusion that the use of population data may be highly advantageous for regression estimation even when the population data are believed to have substantial levels of nonsampling error.

Predicted Birth Probabilities Under the Unconstrained, Exact Constraints, and Bayesian Constraints Models

We have seen that both the intercept and the age coefficient parameters for the Hispanic fertility model are estimated with substantially less error in the Bayesian constraints model than in the unconstrained model. Together, these parameters generate the baseline fertility hazard for women aged 25 to 34 in the multivariate regression model. Improvements in the baseline fertility hazard will be important for the researcher when predicted birth probabilities are needed.2 The intercept and age parameters are included in the function to predict the birth probability for any given set of socioeconomic regressor values. Therefore, every predicted probability will be estimated with lower bias and higher efficiency in the Bayesian constraints model than in the unconstrained model and without the bias present in the exact constraints model.

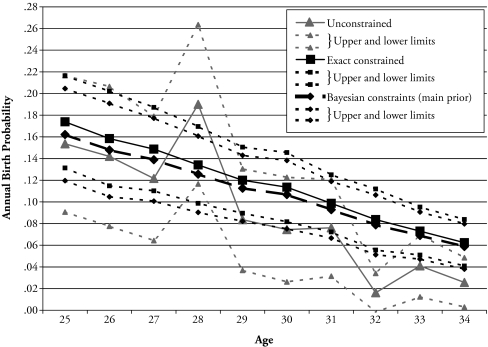
These predicted probabilities for ages 25 to 34 are presented for the three models in Figure 4 for the reference category of married women who are high school graduates and were not full-time employed in the previous year. The main prior is used in the estimation of the Bayesian constraints model. Because there were no significant age interactions, all sets of predicted probabilities for different combinations of socioeconomic variables will be represented by uniformly raised or lowered versions of these lines, according to the sign and magnitude of the coefficients for those variables in Table 2. Because the posterior distributions of the predicted probabilities are well approximated by normal distributions, it is sufficient to describe the central tendency and dispersion using the mean and the Bayesian analogue to the 95% confidence interval, referred to as the “95% credible interval” (Gill 2002). The upper and lower limits of the credible interval are also presented in Figure 4. While these are not strictly comparable to the frequentist confidence interval, the latter is also presented in Figure 4 for the unconstrained and exact constraints models. When comparing the width of a 95% confidence interval to the width of the 95% credible interval presented here, the reader should bear in mind that the latter more fully accounts for the sources of uncertainty about the point estimates, including uncertainty due to constraint variance.

Figure 4.

Predicted Birth Probabilities for College-Educated Married Women, Part-Time or Not Employed: Unconstrained, Exact Constraints, and Bayesian Constraints

The efficiency gains from including population data in both the exact constraints and Bayesian constraints models versus ignoring these data in the unconstrained model are apparent when comparing the lines and their surrounding intervals in Figure 4. Much greater uncertainty due to sampling variability in the unconstrained model is evident both from the fluctuations in the shape of the age schedule and from the much broader 95% confidence interval around the point estimates of that age schedule. This would not, moreover, be solved by a simple parameterization of the age relationship. This is apparent from the much greater difference of the PSID from the predicted values of the Bayesian constraints line at older than younger ages in the 25- to 34-year-old interval. Either a linear or smoothed curvilinear exact parameterization would result in a line that slopes too sharply downward into Hispanic women’s 30s. Thus, parameterization would decrease the variance about the estimates but would do so in a biased way.

The overall level of the predicted birth probabilities is lower for the Bayesian than for the exact constraints model, corresponding to the 7.5% lower mean in the population prior for any given age-specific fertility rate. However, compared with the highly fluctuating predicted probabilities of the unconstrained model, the exact constraints and Bayesian constraints models appear remarkably close to each other. This provides a visual representation of the dominance of the contribution of sampling error to the MSD difference between the exact constraints and unconstrained model estimates. Recall, moreover, that the MSDs we calculated above were only for the intercept term at age 25. At this age, the distance of the predicted probability of the unconstrained model (0.154) from that of the Bayesian constraints model (0.162) is less than the distance for the exact constraints model (0.174). At subsequent ages, however, the unconstrained model’s predicted probabilities drift much further away from those of the Bayesian constraints model than do the predicted probabilities of the exact constraints model. The estimates using the 1990-based NCHS values as if they were exact are therefore not only more efficient but also generally less biased than the estimates using the PSID sample data alone. The problems with using the exact constraints model, however, are that some degree of upward bias is very probably introduced and that the standard errors and confidence intervals overstate the accuracy of its regression parameter estimates.

DISCUSSION

Previous applications of constrained MLE have shown that population information may reduce both bias and variance about regression estimates from sample data. These studies, however, assume that the population data are unbiased. The present study relaxes this assumption, using a Bayesian method for incorporating a combination of auxiliary data and expert judgment. Faced with biased population data, the non-Bayesian options would be to (1) adjust the population data and assume that the amount of uncertainty due to this adjustment can either be ignored or evaluated satisfactorily through a sensitivity analysis; (2) use the population data without adjustment, noting the possible biases in a qualitative caution to the reader; or (3) not use the population data at all.

The Bayesian approach employed here improves on all three of these options. In spirit, it is closest to a combination of adjustment combined with sensitivity analysis about discrete alternative adjustments that could have been made (option (1)). In this way, our approach is consistent with the more rigorous of standard demographic approaches to handling population data. The Bayesian estimator, however, provides a fuller and more principled approach than sensitivity analysis to evaluating the additional uncertainty introduced by adjustment. As noted earlier in the article, the sensitivity analysis approach does not tell us how likely any given alternative value is, but rather only what that alternative value would be.

Option (2)—using population data without adjustment—is equivalent to the exact constraints approach to combining population and survey data as proposed by Handcock et al. (2000, 2005). Option (3)—not using population data at all—is equivalent to an unconstrained estimator, meaning standard regression estimation from survey data only. Under the first specification of the distribution of true population values (referred to as our main prior), the exact constraints estimator still outperforms the unconstrained estimator. Under the two plausible alternative assumptions, however, one incorporating a larger mean adjustment to the population data and the other incorporating a greater variance, the exact constraints estimator performed no better than the unconstrained estimator. In contrast, for the Bayesian estimator, all values in our range of plausible levels of error in the population data resulted in a greatly improved precision of the underlying age-specific fertility hazard as compared with unconstrained estimation. Therefore, to ignore the population data would be a poor choice unless the underlying age-specific hazard is of no importance for the substantive purposes of the research.

We used the Hispanic fertility application as an example of the estimation problems when both population and survey data have substantial and only partially known biases. In other applications, survey data may be clearly less biased than population data. This may occur, for example, when more sensitive survey methods are used to capture behavior that is poorly captured by population data. Abortions are one example (in Lara et al. 2006), and the underreporting of income in government administrative sources is another (Kapteyn and Ypma 2007). In these cases, constrained estimation will still bring large gains in efficiency (through reduced sampling variability) but possibly at a cost in terms of constraint bias and variance that is too great to justify the additional computational burden of using the population sources. The Bayesian model provides a sound framework for making decisions about these trade-offs.

Finally, a major issue for the acceptance of Bayesian methods in demography is the subjectivity of the priors. For this reason, we first discussed their construction as being a formalization of procedures involving subjective judgment that demographers routinely use to adjust population data. Following good practice in demographic adjustment, we used the best available auxiliary data source, the CPS, to bring as much objective knowledge as possible into the construction of the prior. Further, we argued that unconstrained estimation itself incorporates subjectivity in the researcher’s judgment that these data are sufficiently representative of the population to be useful in a regression analysis that attempts to generalize to the female Hispanic population of reproductive age. We therefore argue that the methods used here do not introduce new elements of subjectivity, but instead that they quantify the effects of traditional elements of subjectivity that implicitly enter a non-Bayesian demographic analysis.