Dynamics of the base of ribosomal A-site finger revealed by molecular dynamics simulations and Cryo-EM

Abstract

Helix 38 (H38) of the large ribosomal subunit, with a length of 110 Å, reaches the small subunit through intersubunit bridge B1a. Previous cryo-EM studies revealed that the tip of H38 moves by more than 10 Å from the non-ratcheted to the ratcheted state of the ribosome while mutational studies implicated a key role of flexible H38 in attenuation of translocation and in dynamical signaling between ribosomal functional centers. We investigate a region including the elbow-shaped kink-turn (Kt-38) in the Haloarcula marismortui archaeal ribosome, and equivalently positioned elbows in three eubacterial species, located at the H38 base. We performed explicit solvent molecular dynamics simulations on the H38 elbows in all four species. They are formed by at first sight unrelated sequences resulting in diverse base interactions but built with the same overall topology, as shown by X-ray crystallography. The elbows display similar fluctuations and intrinsic flexibilities in simulations indicating that the eubacterial H38 elbows are structural and dynamical analogs of archaeal Kt-38. We suggest that this structural element plays a pivotal role in the large motions of H38 and may act as fulcrum for the abovementioned tip motion. The directional flexibility inferred from simulations correlates well with the cryo-EM results.

INTRODUCTION

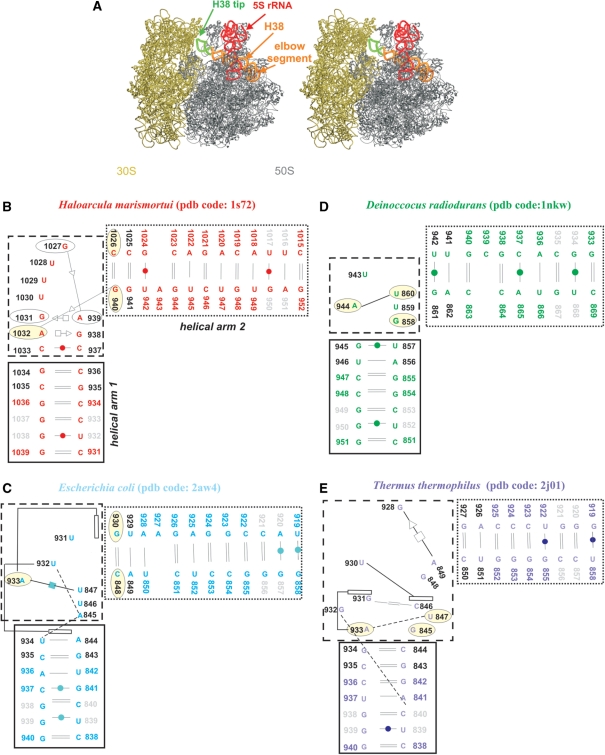
Helix 38 of the 23S rRNA, which includes ∼100 nucleotides, is known as the A-site finger (ASF) due to its unusual length, distinct bend, and direct interaction with the A-site tRNA (1). The tip of the ASF forms part of the intersubunit bridge B1a (1), which changes dynamically during the elongation cycle of protein synthesis (1). These changes go hand in hand with the ‘ratchet motion’ (2), an intersubunit rotation during mRNA–tRNA translocation that changes the ribosome conformation, in particular the constellation of subunit components lying at its periphery. In the pre-translocational complex, the tip of the ASF is in contact with ribosomal protein S13 from the small subunit, while after the ratchet motion it interacts with protein S19 (3). The loop E in the 5S rRNA forms a contact with the ‘middle’ part of H38 (Figure 1A) via a symmetric A-patch composed of A-minor interactions (4).

Figure 1.

(A) Stereo view of E.c. 70S ribosome (50S is in grey; PDB code 2aw4 and 30S is in tan; PDB code 2avy) with highlighted 5S rRNA (red ribbon). The H38 (orange ribbon) was taken from E.c. 50S subunit (PDB code: 1pny) (68) where its complete structure is present, including its tip (green ribbon). The tip is missing in the atomic resolution structures. Positioning of H38 from 1pny structure into 2aw4 structure was carried out based on superposition of the 1pny and 2aw4 structures. (B–E) Secondary structures of the studied crystal H38 segments with base pairs marked according to the classification by Leontis and Westhof (62). The black and dotted boxes specify helical arms 1 and 2 while the dashed box indicates the central hinge segment which is defined as the area with the sharp bend of the backbone and the adjacent non-WC base pairs. The light yellow ellipses mark bases forming base triples in simulations (H.m. and T.t. structures have triples present already in the crystal structures). Dashed lines represent single H-bonds and empty rectangles mark stacking. Black residue numbers indicate fragments defining the α interhelical angle while grey residue numbers indicate fragments defining the β interhelical angle (the centers of mass of the two angles coincide in the central hinge segment; see Materials and Methods for the exact numbering). Note that the local interactions in the T.t. elbow segments are not identical in different X-ray structures (25,26) underscoring some uncertainties in the available experimental structures. The pairing suggested by the X-ray T.t. structure with PDB code 1vsp is shown in Supplementary Figure S2 and is actually more ordered and more consistent with the base pair classification by Leontis and Westhof. See the legend of Table 1 for explanation of the discontinuity of nucleotide numbering in the T.t. structure.

The role of H38 in protein synthesis was investigated in several biochemical studies (5–10). Dontsonova et al. (10) observed a less efficient subunit association but basically normal functional activities of the ribosome after truncation of the ASF aimed to disrupt the intersubunit bridge B1a. Komoda et al. (8) demonstrated that the Escherichia coli (E.c.) strain with ASF-shortened ribosomes had a normal growth rate but enhanced +1 frameshift activity, suggesting that ASF is a functional attenuator for translocation helping to maintain the reading frame. Thus, while the ASF is perhaps not essential in the basic steps of translation, it appears to perform complex fine-tuning of the ribosomal activity. Mutations affecting the H38 B1a bridge and A-site tRNA interactions caused increased ribosomal affinity for the A-site tRNA (9). Such substitutions had very variable influence on the effect of A-site-specific drugs and on the suppression of nonsense codons. The study pointed out that the mutations induce structural changes that propagate into distant rRNA regions and highlighted the roles of flexible and rigid RNA segments in this process. The authors suggested the presence of an arc of unpaired ‘hinge bases’ facilitating information exchange among functional centers of the ribosome (9). It was also shown that depletion of pseuduridines of H38 of eukaryotic (yeast) ribosomes results in a wide range of adverse effects including substantially reduced cell growth and translational activity (6). Another mutational study provided evidence that H38 may play an important role in the process of assembling of the large ribosomal subunit (7). A comparison of cryo-electron microscopy (cryo-EM) maps of the ribosome determined at different stages of translation provides unique information about conformational substates and, by inference, ribosome dynamics (3,11). Among positional changes of functionally significant ribosomal segments uncovered were those of H38.

Structurally, H38 includes an elbow segment at the base of H38 which sharply changes the direction of H38 toward the small subunit (Figure 1). The largest changes of H38 so far observed are associated with the ratcheting motion (2), characterized by a rotation of the small relative to the large subunit, which has been observed in a number of ribosomal complexes bound with various factors, including elongation factor G (EF-G), release factor, and recycling factor (12). We use the terms macrostate I and II to denote the two conformational states of the ribosome. In the macrostate I → II transition, numerous ribosomal elements undergo local conformational changes. Helix 38 of the 23S rRNA is one of these dynamically changing sub-components, showing a quite noticeably different position when going from macrostate I to II (2,13,14). The displacement is most obvious at the tip of H38, which slides along with the head of the 30S subunit as the subunit rotates. The high mobility of the tip segment renders the tip invisible in structure determination of the 70S ribosome by X-ray studies.

The elbow segment in the ribosome of Haloarcula marismortui (H.m.) (15), an archaebacterium, is known as a kink-turn (Kt-38), a motif recurrently found in the ribosomal RNAs (16,17). Previously we have investigated kink-turns using explicit solvent molecular dynamics (MD) simulations (18–22). The simulations revealed that the kink-turns behave as flexible and directional molecular elbows and it was therefore suggested that Kt-38 can bestow the functionally required flexibility to the ASF (19). However, Kt-38 is present only in the ribosome of archaea. The elbow segments of H38 in eubacterial 50S subunits of E.c. (23), Deinoccocus radiodurans (D.r.) (24), and Thermus thermophilus (T.t.) (25,26) are formed with different nucleotides, with diverse base pairing and stacking (Figure 1C–E), resulting nevertheless in a Kt-38-like overall topology. When considering sequence and secondary structures, the four H38 elbow segments appear entirely unrelated. In contrast, the C-loop, another motif in H38, is conserved across all three kingdoms (16).

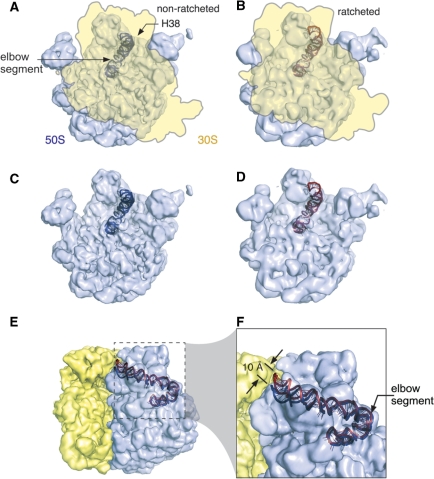
In the present study we utilize MD simulations to analyze the intrinsic dynamics and flexibility of the elbow segments of the H38 in eubacterial 50S subunits of E.c., T.t. and D.r. along with Kt-38 of H.m. (Figure 1). The dynamics of the elbow segments are simulated in the context of extended helical arms of H38 predominantly composed of canonical base pairs (Figure 1B–E). The aim was to characterize their intrinsic stochastic fluctuations that may be important for the function of the ribosome (27–31) and can be studied by explicit solvent MD simulations (32). Despite being limited by force field approximations and the short (∼10–100+ ns) simulation timescale, MD simulations are instrumental in structural studies of RNAs (19,33–43). The dynamical information conveniently complements the structural picture provided by experiments (32,44,45). We also have reanalyzed the earlier cryo-EM maps of the E.c. ribosome (14) by deriving atomic models via flexible fitting of cryo-EM maps using real-space refinement (see below), to better visualize the H38 dynamics (Figure 2). The results show a movement of 10 Å between the positions of the H38’s tip (Figure 2F). Due to the considerable length of the helix, this movement is consistent with a relatively small motion at the H38 base [see also discussion in (19)], despite that such motion is obviously far below the experimental resolution.

Figure 2.

Illustration of the motion of H38 as the E.c. 70S ribosome undergoes a ratcheting movement, as observed by the cryo-EM studies. (A) The density map of the 70S ribosome in a non-ratcheted state (3,64) (EMDB Access Code: 1056), with the fitting model of H38. The density map of 30S subunit (yellow) is outlined. (B) The density map of the 70S ribosome in a ratcheted state (3) (EMDB Access Code: 1363), with the fitting model of H38. (C) The 50S subunit in the non-ratcheted state. (D) The 50S subunit in the ratcheted state. (E) The 70S density map is re-oriented from the position shown in A, and the H38 model in the ratcheted state is added at the ratcheted position (red). (F) A zoom-in view of the boxed region shown in E. All cryo-EM density maps are shown as transparency.

The simulations reveal large thermal fluctuations while the simulated structures do not systematically deviate from the X-ray structures (i.e. they keep vast majority of those molecular interactions that are present in the starting structures; see specific analysis for the individual systems below). As expected, the range of instantaneous geometries seen in unrestrained simulations of the isolated H38 elbow segments is considerably larger than the range of substates seen in (or suggested by) experimental structures, which occur in a fully assembled ribosome. In addition, all experimental structures represent averages. However, the preferred direction of thermal fluctuations in simulations, which reflects the intrinsic flexibility of the studied RNA segment, is consistent with the direction inferred by comparison of experimental maps. Despite the apparent lack of any sequence and secondary structure conservation, all four studied H38 elbow segments show qualitatively similar hinge-like (open versus closed) dynamics resembling those of the kink-turn. Therefore, within the assembled ribosome, all these four very diverse sequences form structures that show a substantial degree of topological and dynamical (flexibility) equivalence, which may be of functional importance (46).

MATERIALS AND METHODS

All simulations were carried out using the Sander module of AMBER-8.0 (47,48) with the parm99 (49) version of the Cornell et al. force field (50). The total length of the simulations performed was ∼0.5 µs (Table 1). The production simulations were extended to 65 ns while the basic results of the study could be inferred already from ∼20 ns simulations. The RNA molecules were solvated in a periodic TIP3P water box extending 10–15 Å away from the solute in all directions, which allows the solute molecules to freely move and rotate. The simulated molecules were neutralized by standard AMBER Na⁺ monovalent cations (radius 1.868 Å and well depth 0.00277 kcal/mol) (51), initially placed using the Xleap module of AMBER at the most negative sites around the solute. Control simulations were carried out in KCl with ∼0.2 M excess salt (Table 1) using parameters for K⁺ (radius 1.705 Å and well depth 0.1936829 kcal/mol) and Cl⁻ (radius 2.513 Å and well depth 0.0355910 kcal/mol) preventing salt crystallization at low to medium salt concentrations (52).

Table 1.

Survey of the simulations

Organism	Simulated segment	Simulation name	Resolution (Å); PDB code	Simulation length (ns)	RMSD (Å)a	Ions used in the simulation
Escherichia coli	838–858, 919–940 E.c. numbering	MD_Ec	3.5, 2aw4b	65	4.3 ± 0.8	41 Na+
Deinoccocus radiodurans	851–869,c 933–951 D.r. numbering	MD_Dr	3.1, 1nkw	65	5.4 ± 1.0	37 Na+
Thermus thermophilus	838–858, 919–940d E.c. numbering	MD_Tt_1	2.8, 2j01	65	5.2 ± 0.9	40 Na+
Thermus thermophilus	838–858, 919–940d E.c. numbering	MD_Tt_2	3.8, 1vsp	65	5.0 ± 1.1	40 Na+
Haloarcula marismortui	931–952, 1015–1039 H.m. numbering	MD_Hm	2.4, 1s72	65	5.4 ± 1.2	45 Na+
Haloarcula marismortui	931–952, 1015–1039 H.m. numbering	MD_Hm_KCl	2.4, 1s72	65	4.5 ± 1.0	77 K+ and 32 Cl−
Escherichia coli	838–858, 919–940 E.c. numbering	MD_Ec_KCl	3.5, 2aw4b	30	4.8 ± 0.8	88 K+ and 45 Cl−
Deinoccocus radiodurans	851–869,c 933–951 D.r. numbering	MD_Dr_KCl	3.1, 1nkw	30	3.2 ± 0.9	67 K+ and 30 Cl−
Thermus thermophilus	838–858, 919–940d E.c. numbering	MD_Tt_1_KCl	2.8, 2j01	30	4.3 ± 1.0	82 K+ and 40 Cl−

^aRMSD values are calculated along the trajectory for the individual snapshots with respect to the starting crystal structure.

^bRibosomal segment 837–858, 919–941 has identical geometry in E.c. crystals of 70S with PDB codes 2aw4 and 2awb. Hence MD simulation was carried out only for the 2aw4 structure.

^cAdenine 865 is protonated at N1 position (Figure S1). Control simulation with canonical adenine revealed visible instabilities (data not shown).

^dThe 2j01 and 1vsp T.t. structures do not contain 929 and 927 residuum, respectively. This discontinuity of the nucleotide numbering is due the utilization of E.c. numbering. The ‘missing’ nucleotide number has been assigned differently by the authors of the two independent T.t. crystal structures while we keep this numbering in our study.

The A865/C937 base pair in the D.r. structure is a cis WC/WC base pair (Supplementary Figure S1), which requires an adenine protonated at the N1 position which was prepared using the Antechamber module of AMBER. The simulations were carried out using the particle mesh Ewald technique (53) with a non-bonded cutoff of 9 Å and 2 fs integration time step. The equilibration and production phases were carried using standard protocols (38). Trajectories were analyzed using the Ptraj module of AMBER and structures were visualized using the VMD, http://www.ks.uiuc.edu/Research/vmd/ (54). The figures were prepared using VMD and Pymol (http://www.pymol.org) (55).

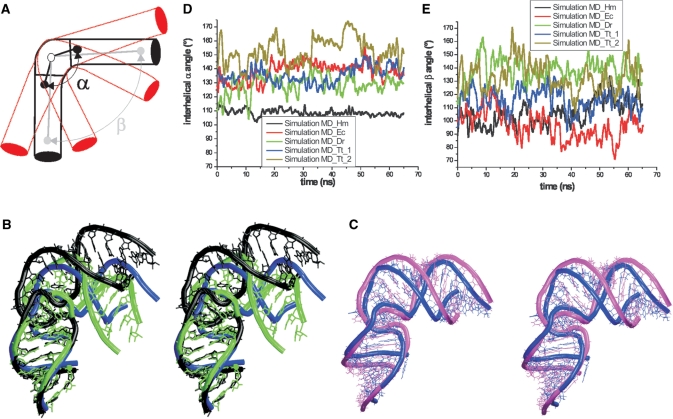
Motions stemming from the dynamics of the central (elbow) RNA segment are characterized by the interhelical α angle, while the interhelical β angle describes the dynamics of the whole system. Both angles are defined by three centers of mass located in the central part of the simulated segment and in the attached helical arms 1 and 2 (Figures 1B–E and 3A). The α angle was calculated using the following nucleotide segments: for H.m. 935–936/1034–1035; 937–939 and 1027–1033; and 940–941/1025–1026; for E.c. 843–844/934–935; 845–847 and 931–933; and 848–849/929–930; for T.t. 843–844/934–935; 845–849 and 928–933; and 850–851/926–927; and for D.r. 856–857/945–946; 858–860 and 943–944; and 861–862/941–942 (Figure 1B–E). The β angle was defined using the following segments: for H.m., 932–933/1037–1038; 937–939, and 1027–1033; and 950–951/1016–1017; for E.c. 839–840/938–939; 845–847 and 931–933; and 856–857/920–921; for T.t. 839–840/938–939; 845–849 and 928–933; and 856–857/920–921; and for D.r. 852–853/949–950; 858–860 and 943–944; and 867–868/934–935 (Figure 1B–E). The α and β angles provide only rough description of the full dynamics as they approximately reflect 1D projections of the fluctuations along the main dynamics mode. Due to the substantial diversity of the local variations in the individual systems the numerical values of the angles calculated for different species vary significantly despite that the overall topologies of the elbow segments are similar (Figure 3).

Figure 3.

(A) Scheme of the studied H38 segments with depicted interhelical α and β angles. The red helices schematically show the hinge-like dynamics. (B) Stereo superposition of the starting E.c. crystal structure (blue) and two MD snapshots representing open (black) and closed (green) conformations (Table 2). The simulated molecule does not move away the X-ray structure but shows considerable stochastic fluctuations. (C) Stereo superposition of average structure of the simulated E.c. segment (magenta) and the starting crystal structure (blue). See Supplementary Figure S8 for superposition over different trajectory portions. (D and E) Developments of interhelical α and β angles in performed Na⁺ simulations (the plots are averaged over 1 ps windows to make the curves smoother). Note that due to the profound local structural diversity of the structures the reference experimental (and also equilibrium) values of the α and β angles differ for different structures.

The essential dynamics analysis (EDA) was done using the Ptraj module of AMBER-8.0 program considering all atoms of RNA. Control calculations were carried out using the GROMACS program (56) where only phosphorus atoms (P) were included. EDA highlights the leading correlated dynamical modes of the dynamics and filters out unessential fluctuations considered noise. EDA decomposes the overall motion of molecule in the course of the simulation into individual (essential) modes represented by eigenvectors with associated eigenvalues (57). EDA thus extracts the dominant modes in the motion of the molecule from the MD trajectory. Projections were visualized using Interactive Essential Dynamics (58) in the VMD program. The eigenvalues were calculated taking into account the leading 100 EDA modes. The first two modes calculated by Ptraj are discussed in the main text while further information including comparison of the Ptraj and GROMACS data is given in the Supplementary Data.

Clustering analysis (59) was carried out utilizing the Ptraj module of AMBER and the kclust program of the MMTools (60), as described in detail in new version of the AMBER package (61). The clustering analysis was carried out for 50000 snapshots (a limit of the kclust method). After testing of different radii (from 3 Å to 6 Å), the clustering was carried out with cluster radius set to 4 Å. Smaller cluster radii produced a number of insignificant (less populated) clusters while larger cluster radii did not lead to a satisfactory separation of the structures.

RESULTS

Starting structures

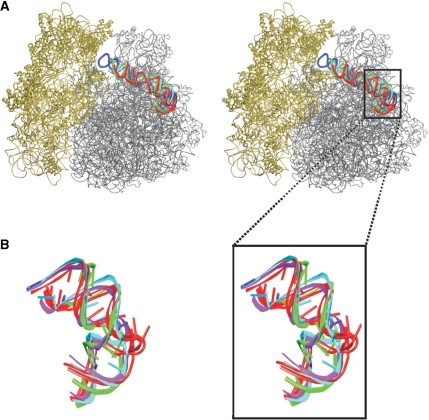
The starting geometries were taken from the crystal structures of E.c. (23), D.r. (24), T.t. (25,26) and H.m. (15) 50S subunits (Table 1). Each H38 elbow segment was divided into three parts. The sharply bent region and the adjacent non-canonical base pairs will be termed central hinge, the flanking helical arm pointing toward the center of the 50S subunit helical arm 1 and the arm pointing toward the 30S subunit helical arm 2 (Figure 1). The overall fold of all four systems is strikingly similar (Figure 4). However, while the H.m. central hinge contains recurrent RNA motif known as kink-turn (Kt-38), different and entirely diverse RNA segments are seen in the three eubacterial species.

Figure 4.

(A) Stereo view of superposition of the 50S subunits of E.c. (grey), H.m., T.t. (PDB code: 2j01), and D.r. (the later three subunits are not shown explicitly to keep clarity) with highlighted H38s colored identically as the corresponding secondary structures in the Figure 1B–E. The 30S subunit of E.c. (PDB code: 2avy) is in tan. (B) Superposition of studied H38 segments colored identically as in Figures 1B–E and 4A. The black box marks the simulated segments of H38.

The Kt-38 is structured with trans Sugar Edge (SE)/SE G1027/A939 and G940/A1032 base pairs, corresponding to the consensus signature interactions between canonical and non-canonical stems of the kink-turn (16,17). The latter SE/SE interaction participates in the A-minor type I interaction (Figure 1B). There are trans Hoogsteen (H)/SE ‘sheared’ A939/G1031 and A1032/G938 base pairs and a cis bifurcated C937/C1033 base pair forming the non-canonical stem of Kt-38; the first two are again consensus interactions of the kink-turn. The equivalent regions in the other X-ray structures consist of less ordered interactions (Figure 1B–E and Supplementary Figure S2). However, all structures are V-shaped with a close to identical mutual orientation of helical arms 1 and 2 (Figure 4). Thus we can consider the eubacterial central hinges kink-turn analogs.

The two T.t. X-ray structures show several differences in the local interactions of their central hinges (see Supplementary Data). The 1vsp structure appears to be more consistent with the RNA base pairing classification (62). We assume that the differences probably stem from the rather low resolution of the X-ray experiments. This illustrates that the local X-ray geometries in all the studied RNA segments may be to a certain extent affected by data and refinement errors and the uncertainty in the starting structures may influence the subsequent simulations (63).

H38 elbow segment of the E.c. ribosome shows spontaneous hinge-like fluctuations

RMS deviations (RMSDs) of instantaneous fluctuations calculated along the MD_Ec trajectory (see Table 1 for simulation names) with respect to the starting crystal structure oscillate around 4 Å (Table 1 and Supplementary Figure S3). The RMSD with respect to the averaged MD structure is 2.9 ± 0.7 Å. The simulation is basically sampling the space around the starting geometry and does not result in any systematic deviation from the starting structure.

The simulation shows spontaneous anisotropic (directional) hinge-like fluctuations coming from the central hinge and propagating to the attached helical arms (Figure 3B). The fluctuations of these arms substantially enhance the range of the motions. Thus the range of mutual positional fluctuations of the ends of arms 1 and 2 is larger than it would be in case of attaching entirely rigid helices to the central hinge. Despite the large-scale hinge-like or ‘open vs. closed’ dynamics the structure averaged over the trajectory is very similar to the X-ray structure (Figure 3C, see below for further discussion).

There is a modest rearrangement (second substate) in the central hinge segment at ∼19 ns. It had no qualitative effect on the direction and magnitude of the overall fluctuations, albeit it affects the calculated values of the interhelical angles. This is because the local rearrangement, albeit subtle, changes the position of the bases defining the center of mass used to calculate the interhelical angles. In the crystal structure the central hinge is stabilized by just a single cis H/H A933/U847 base pair (Figure 1C) complemented by U932(O2)-A845(N6) and U934(O2)-A845(N6) H-bonds. The cis H/H A/U base pair is not consistent with RNA base pair classification (62). It is therefore not surprising that it causes some local instability in the simulation. The A/U base pair fluctuated for 19 ns and then it was disrupted. At 20 ns the A933, originally stacked onto G930 (Figure 1C), formed a new base triple with the G930 = C848 base pair, which is a characteristic of the second substate of the simulated system (Supplementary Figure S4). The triple was stabilized by the trans H/SE A933/G930 base pair and by the A933(O2’)-C848(O2’) contact oscillating between direct and water-mediated H-bonding. This base triple, including its flexible A/C contact, resembles the A-minor I interactions of kink-turns. The second substate can be considered as a variant of the original geometry. The rearrangement may be due to the absence of ribosomal contacts in the simulation, the sparse internal H38 interactions, and also some imperfectness in the initial structure (see Supplementary Data for further details).

In the course of the simulation, the instantaneous values of interhelical α angle (calculated for all the individual snapshots) fluctuated between 110°–165° (see Figure 3D for the smoothed time course of the α angle, Supplementary Figure S5A for its distribution, and Supplementary Figure S6 for non-smoothed time development). The distribution of the α angle (Figure S5) two peaks for this particular simulation. This is because the local rearrangement occurring at 19 ns somewhat affected the equilibrium value of the calculated α angle. The first peak corresponds to the initial substate (1–19 ns) and the second one to the second substate (20–65 ns).

The hinge-like dynamics was identified mainly in the first EDA essential mode, representing 36% of the total motion (Supplementary Table S1 and Figure S7). This mode also includes the rearrangement in the central hinge segment and considerable breathing of grooves of both helical arms. The second essential mode (13%) reflects the rearrangement of the central region, breathing of the helical arm 2 and changes of A927 bulge region in helical arm 2 unrelated to the hinge-like motions (see Supplementary Data for more details). Unfortunately, while EDA shows the main motions seen in the simulation, it does not provide their clear separation. We have also calculated the EDA modes separately for periods 1–19 and 20–65 ns which did not bring much new insight.

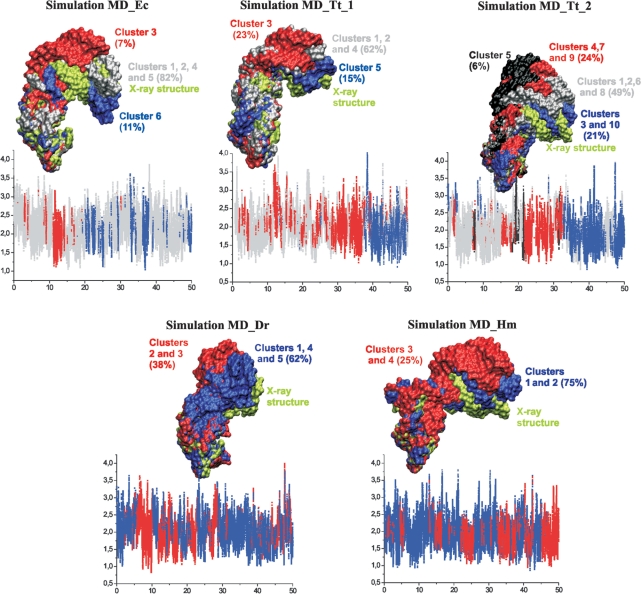
Clustering of the MD_Ec simulation provided six clusters. Superposition of best members of these clusters over helical arm 1 (Figure 5) shows the range of hinge-like fluctuations described above. Clusters 1, 2, 4 and 5 represent geometries that are close to the starting X-ray structure and also close to the cryo-EM structures discussed below. Their total population is 82% (Supplementary Table S2). Cluster 3 (7%) represents the most ‘open’ geometries while cluster 6 (11%) represents the most ‘closed’ geometries. This wide range of structures is sampled essentially without any significant rearrangements of the local molecular interactions. When comparing the MD clustering results with experimental structures one should not overlook the fact that we compare MD simulation of isolated rRNA building block with experimental structures of the helix which are constrained by the context of the ribosome and which represent averages. The ribosomal context obviously affects the populations of individual states substantially.

Figure 5.

3D structures of best members of individual clusters in simulations. The structures are superimposed over helical arm 1 and highlighted in surface representation. Clusters adopting similar conformations are visualized using identical colors to keep clarity of the figure. Corresponding plots indicating population of individual clusters along the trajectory are shown below. The x-axis stands for time (ns) while y-axis stands for ‘Distance to center of cluster’ (Å).

Comparison of MD and experimental structures

The interhelical β angle that includes motion of the extended arms sampled a range of 80°–135° during the first 19 ns and a range of 65°–126° since 20 ns till the end of the simulation, i.e., after the second substate was established (Figure 3E and Supplementary Figure S5B). The structure averaged over the first 19 ns has an interhelical β angle of 106° while after the rearrangement it drops to an averaged value of 92°. By comparison, the experimental value is 96°. The Supplementary Figure S8 shows an overlay of 1–19 ns and 19–65 ns averaged structures over the X-ray structure, with the second substate being closer to the X-ray structure. Thus it is possible (albeit not guaranteed) that the simulation locally improved the interactions in the elbow region compared to the starting X-ray structure, which may be imperfect due to the lower ∼3.5 Å resolution. The X-ray structure is, nevertheless, clearly within the low-energy region identified by the simulation.

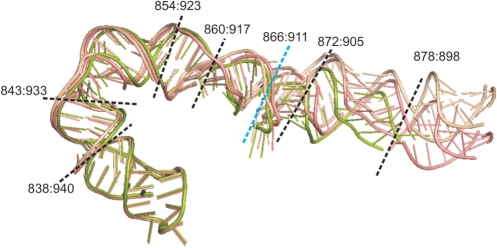
The ∼10-Å resolution cryo-EM data do not allow an unambiguous determination of structural details that would be needed to derive the corresponding α and β angles. Cryo-EM maps representing the 70S ribosome in either the post-translocational state (non-ratcheted; EMDB Access Code: 1056) or the EF-G-GDPNP-bound state (ratcheting; EMDB Access Code: 1363) were obtained previously using the single-particle cryo-electron microscopy method (3,64). These two cryo-EM maps, with resolutions of 9 Å and 12 Å, respectively, were used as targeted electron-density functions for building atomic models of the two ribosomal states using the real-space refinement method (65). Following this method, rigid pieces of an X-ray structure were optimally fitted into the EM density map under observance of stereochemical restraints. Previous modeling efforts (66,67) used more than 100 rigid pieces for the entire ribosome but represented H38 by only two pieces (dividing blue line in Figure 6), omitting the tip segment, a representation which failed to do justice to the dynamic aspects of the helix. Another distinction between the two models is in the source of the X-ray structures used for the refinement: Gao et al., 2003 (67) combined the 50S structure from H.m. (PDB code 1ffk) with the 30S structure from T.t. (PDB code 1ibl), while Gao et al., 2009 (66) used the recent (2005) 70S X-ray structure from E.c. [PDB code: 30S: 2avy/50S: 2aw4 (23)].

Figure 6.

Illustration of different observed conformations of H38: the X-ray structure (PDB: 2aw4, green, the tip of H38 is not resolved), the RSRef fitting structures for the non-ratcheted state (this work, pink) and the ratcheted state (this work, wheat). In the fitted structures, the tip of H38 has original coordinates from the low resolution X-ray 50S structure (1pny). The dashed lines are demarcations defining the rigid-bodies for RSRef fitting. Blue line: demarcation of the division into two segments used earlier by Gao et al. (66,67). Black lines: demarcations used in the present study, defining eight rigid pieces which include the tip. Note that the ∼10 Å resolution of the experiment does not allow to visualize any local movements, even upon the improved fitting. So we cannot asses the changes occurring in the elbow area. Nevertheless, the EM maps give an impression that the movement may start to build up close to the elbow region. The overall movement of H38 may stem from the H38 elbow region and propagate towards the tip. In fact, a change of the elbow angle as small as 6° would result in ∼10 Å movement of the tip, if it propagates from the elbow to the tip.

In the present study, the new division (see black lines in Figure 6) keeps Gao et al.'s rRNA segmentation except that it now represents H38 by eight pieces, which include the structure of the tip as an added segment [1pny, from Vila-Sanjurjo et al., (68)] that is missing from the E.c. atomic X-ray structure. The X-ray structure of elongation factor G (EF-G) from T.t. (PDB code: 1fnm) was divided into five rigid pieces, for the five domains. The atomic models that were generated for H38 are currently been deposited in the PDB database while the other parts of the ribosomal complexes retain their previously deposited PDB coordinates (PDB codes: 3dg2 and 3dg0).

The assessment of the cryo-EM maps as well as the fittings indicate that although the movement of the tip of ASF is the most visible, it evidently does not originate in structural changes localized at the tip. Rather, the displacement appears to propagate along the whole H38 structure. As could be inferred from Figure 6, a change of the β angle in the H38 elbow region by 6° would be entirely sufficient to give the experimentally observed relocation of the tip of the ASF. The cryo-EM data do not allow changes of the β angle at the elbow itself to be directly monitored, since substates in the elbow region are far below the resolution of the method. However, the analysis of the MD data, including visual inspection of the trajectories, EDA, and clustering show a match between the preferred direction of intrinsic thermal fluctuations seen in the simulations and the direction of the overall H38 movement inferred from cryo-EM data.

Other eubacterial species—simulations for the D.r. and T.t. H38 segments confirm the flexibility of E.c. H38 elbow segment

The MD_Dr, MD_Tt_1 and MD_Tt_2 simulations (see Table 1) revealed hinge-like fluctuations resembling those observed for E.c. H38 elbow segment. The direction of the fluctuations is conserved. The α angle in the MD_Dr and MD_Tt_1 simulations fluctuated around the X-ray values from 95° to 155° and from 110° to 160°, respectively. The ranges of α angle fluctuations are comparable with the MD_Ec simulation (Figure 3D and Supplementary Figure S5A). The MD_Tt_2 simulation resulted in mean value of the α angle shifted by about 15° from the X-ray value, with the range 120°–180° (Supplementary Figure S5A) (see above and Supplementary Data for the explanation of the difference between the two experimental X-ray T.t. structures). The shift is related to local structural changes in the MD_Tt_2 simulation (see Supplementary Data).

In contrast to the MD_Ec simulation, mean values of β angles in the MD_Dr, MD_Tt_1 and MD_Tt_2 simulations deviated from the X-ray values towards larger values (Supplementary Figure S5B). Note that these differences arise basically outside the central hinge region. In the MD_Tt_1 simulation the shift was 17° (range of the β angle was 80°–150°) while in the MD_Dr and MD_Tt_2 simulations the mean β values shifted by about 30° and 35°, respectively. The ranges of the β angles in these simulations were 95°–180° and 90°–175° (Supplementary Figure S5B). In the MD_Tt_2 and MD_Dr simulations the whole elbow segment could even reach basically straight conformations (Supplementary Figure S9) but then the structures bounced back to the starting structures without a loss of local interactions. Full details are given in Supplementary Data.

Clustering of the simulations confirmed hinge-like dynamics of the elbow segments. There are five clusters in the MD_Dr and in the MD_Tt_1 simulations (Supplementary Table S2). Clustering of the MD_Tt_2 simulation, which showed the largest range of fluctuations, revealed ten significant clusters (Supplementary Table S2). All clusters obtained in the MD_Dr, MD_Tt_1 and MD_Tt_2 simulations represent more open geometries than the corresponding X-ray structures (Figure 5 and Supplementary Table S2). Population of more open structures (which could lift the H38 from the body of the large subunit) in the simulations of isolated H38 elbow region is perhaps not surprising, since 5S rRNA pins down the H38 in assembled ribosome.

Dynamics of the elbow segment of the H.m. ribosome is dominated by hinge-like fluctuations of Kt-38

The intrinsic fluctuations of the MD_Hm trajectory are dominated by the genuine anisotropic (directional) hinge-like dynamics of Kt-38, in line with simulations for truncated Kt-38 (18–20). The α angle fluctuated between 90° and 125°, a motion virtually identical to that found in simulations of Kt-38 without the helical arms (19), while the β angle that captures the motion of the extended arms fluctuated in a wider range of 75° to 140° (Figure 3 and Supplementary Figure S5). Clustering provided four clusters visualizing the hinge-like dynamics (Figure 5 and Supplementary Table S2). Further details are given in Supplementary Data.

Analysis of the twisting component of the flexibility

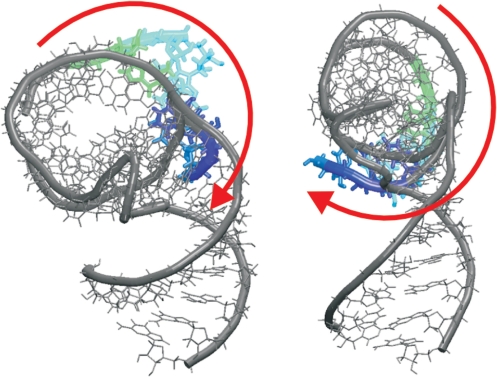
Besides the dominant hinge-like dynamics, we have also tried to identify eventual twisting components of the dynamics. Not surprisingly, the studied systems, due to their overall flexibility, show also visible and fast twisting fluctuations (Figure 7). It would be very unusual to have an RNA segment possessing large non-harmonic hinge-like flexibility while being simultaneously stiff with respect to twisting fluctuations. The twisting flexibility is typically reflected by the second or third EDA modes. More details of the twisting flexibility (including its visualization, Supplementary Figure S10) are given in Supplementary Data. We reiterate that the hinge-like fluctuations are clearly the dominant ones.

Figure 7.

Twisting flexibility of the simulated H.m. H38 elbow segment (the upper part of arm 2 is colored; the figure shows structures with approximately maximal and minimal twisting). The red arrows indicate the motion. See Supplementary Figure S10 for more details.

Simulations in the presence of KCl are similar to net-neutralizing Na⁺ simulations

The 65 ns KCl simulation of the H.m. H38 elbow segment revealed very similar behavior as the corresponding 65 ns Na⁺ simulation (see Supplementary Data). All local interactions in the hinge region remained stable and the overall dynamics of the Kt-38 was close to identical in both simulations, with typical dynamical water insertion into the A-minor I interaction between the stems of the kink-turn (19). There is a modestly larger propensity for more closed structures with smaller β angle in the KCl simulation (Supplementary Figure S11 and Table S2). However, considering the size of the simulated system, its unusual flexibility and the simulation time scale this subtle apparent ∼5° preference should not be interpreted as any systematic effect.

Simulations of eubacterial H38 elbow segments for 30 ns in the presence of KCl (Table 1) revealed also very similar behavior as the corresponding 65 ns Na⁺ simulations. Clustering of these KCl simulations led to virtually identical clusters as those obtained for Na⁺ simulations (Figure 5, and Supplementary Figure S11 and Table S2). Furthermore, also the inspection of local dynamics confirms that the solute behavior is similar in presence of net-neutralizing Na⁺ and excess salt KCl ion atmospheres (see Supplementary Data). The local rearrangement at the central hinge segment of the E.c. elbow detected in Na⁺ simulation at ∼19 ns (see above) was seen in the KCl simulation at ∼1ns.

In principle, higher salt strength could improve the screening of the RNA electrostatic repulsion and consequently lead to population of structures with smaller β angles compared with Na⁺ simulations. However, the effect was very subtle, if any. For β angles averaged over equivalent portions of trajectories, KCl simulations reduced the averaged β angle for the E.c., D.r. and H.m. systems by 5° while the angle increased by 2° for T.t. Thus, Na⁺ net-neutralizing and 0.2 M excess salt KCl ionic conditions lead to comparable behavior of the simulated RNAs. While the Na⁺ net-neutralizing salt condition is not perfect, increase in salt strength or inclusion of divalents might also have adverse effects due to force field approximations. In reality, the RNA molecule anyway redistributes the cloud of ions in its neighborhood to achieve local ion atmosphere with excess of cations exactly neutralizing its negative charge, which resembles the condition achieved by the net-neutralizing monovalent ion atmosphere in simulations quite well (69,70), considering also the fact that net-neutralization for the present systems correspond to ∼0.2 M concentration of cations.

DISCUSSION

Helix 38 (H38) of the large ribosomal subunit (the ASF) is a long helical structure that extends across the large ribosomal subunit from the subunit’s back side to its front side. The tip of H38 participates in the B1a intersubunit bridge and is changing its interacting partners (protein S13 versus S19) depending on the state the ribosome is in during the translocation process. H38 modulates many ribosomal functions and is dynamic (5–10,71). The ASF may serve as a functional attenuator for translocation (8) or a pike regulating access of tRNA from the A-site to the P-site (19). The ubiquitous occurrence of the ratchet motion during initiation, elongation, termination, and recycling (12) implicates H38 as an element involved in these processes, as well.

The bottom part of H38 contains an elbow RNA segment that is bent (Figures 1 and 2). The long helix then continues toward the small ribosomal subunit. The X-ray structure of the large ribosomal subunit of H.m. reveals that the elbow segment contains a recurrent ribosomal RNA motif, the kink-turn. Kink-turns are flexible hinge-like RNA building blocks that can passively mediate large-scale RNA motions (18,19,21). Thus, flexibility conferred by Kt-38 may contribute to the overall dynamics of H38. However, while Kt-38 occurs in Archaea it is not conserved in Eubacteria and Eucarya (16). X-ray structures of eubacterial large ribosomal subunits [E.c. (23), D.r. (24) and T.t. (25,26)] show, at the position equivalent to Kt-38 of H.m., similarly bent RNA structures with very diverse sequences and local interactions (Figure 1). Despite this, Kt-38 and the equivalent eubacterial regions are V-shaped molecules with very similar fold resulting in similar positioning of the attached arms (Figure 4). We have carried out unrestrained explicit solvent MD simulations of the H38 elbow segments from all organisms where X-ray structures are available. The main aim of our investigation was to compare the basic structural-dynamics properties of these systems.

Proper interpretation of the results requires consideration of several points. 1) We simulate rRNA segments starting from their experimental ribosomal structures affected by surrounding ribosomal elements. 2) As exemplified by the differences between the two T.t. experimental structures, the lower resolution of the ribosomal X-ray structures causes uncertainties in the local arrangements in the starting structures. These affect the development of subsequent simulations and, e.g. 65 ns simulation time scale was not sufficient to resolve the local differences of the two starting T.t. structures. 3) The H38 elbow segments would adopt different secondary (2D) and tertiary (3D) structures outside the context of the folded ribosome. Actually, comparative analysis of T.t. 23S rRNA (72) carried out prior to the X-ray structure studies proposed an entirely different 2D model of the H38 elbow segment where all bases were well paired. Isolated kink-turns unfold in solution (73–77). However, the time-scale of the simulations is too short to investigate any such unfolding. The simulations, on the other hand, give extensive insights into the intrinsic stochastic fluctuations and flexibility associated with the functional geometry occurring in the ribosome, irrespective of whether the system is in the global or just a local minimum. The E.c. and H.m. systems did not show any sign of unfolding. The D.r. and one of the T.t. simulations revealed more substantial opening oscillations. The MD_Tt_2 trajectory is capable of temporarily reaching basically straight geometries, however, the simulated molecule then returns back quite close to the initial structure. Thus, the bent H38 elbow segment geometries correspond to rather robust local minima separated by energy barriers from potential other conformations. RNA segments that are just trivially compressed or bent like a spring would relax in simulations within ∼1–5 ns (21,39). In summary, the simulations qualitatively describe the intrinsic flexibility of the H38 elbow segments relevant to their folded functional geometries.

The simulations were carried out in presence of a net-neutralizing set of Na⁺ ions as well as with ∼0.2 M excess KCl salt. Both ionic conditions lead to very similar simulation behavior on the present time scale. Net neutralization by monovalent ions (mostly Na⁺) is the most common treatment of ionic effects in MD simulations of nucleic acids, which provides fairly sufficient concentration of cations of ∼0.15–0.2 M. Basic correctness of this approach at the presently affordable simulation time scale (10 ns – 1 µs) has been verified in many long reference simulations of nucleic acids (18–21,32,36,39,78–84). The net-neutralizing monovalent ion atmosphere achieves satisfactory sampling in 20–50+ ns scale simulations. Main ion binding sites are localized usually within ∼1–2 ns even when not been occupied initially while the ions smoothly exchange between the ion binding sites and the bulk solvent. Details of ion dynamics are documented in the literature for a broad set of ion binding sites around folded RNAs (see also Supplementary Data in these studies) (20,33,85–88). Despite the basic equivalence of the Na⁺ and KCl simulation results we do not suggest that the Na⁺ and KCl environments are identical when considering specific local cation–solute interactions. As well, we do not suggest that the simulation description is perfect, as there are limitations imposed by the simulation protocol, such as periodicity and finite box size. However, in our particular study we are looking at the overall salient direction of the movements rather than details of specific conformations. Such studies are considerably less sensitive to the limitations imposed by the force field and starting structures than analyses of small structural details. The flexibilities of RNA segments stem from the intrinsic mechanics of the solute; therefore, their insensitivity to the choice of ion atmosphere is not surprising. Note also that, in simulations, the accuracy of ion treatment is for all currently available ion parameter sets primarily affected by the common pair-additive force field approximation, which neglects polarization effects. This leads to some discrepancies in the ion–solvent–solute balance, such as an underestimation of the cation–solute direct interaction energy and excessive short-range repulsion between the cations and solute atoms (32,89). The Aqvist’s cation parameters (51) that we used in net-neutralization Na⁺ simulations were recently criticized as producing salt-crystalization artifacts in excess-salt simulations (specifically for KCl) (90). However, this problem is rather caused by imbalance of adapted Aqvist’s cation parameters combined with inconsistent anion parameters and does not indicate any substantial bias in net-neutralizing simulations. Thus the Na⁺ Aqvist’s parameters remain a valid option for net-neutralizing simulations and may actually have a subtly better balance for cation–solute inner-shell interactions than some other parametrizations (91). For excess salt KCl simulations we used one of the recent parameter sets that does not lead to salt clustering (52). The presented results do not depend on the choice of the ion atmosphere, at least within the range of available force fields.

All simulated rRNA segments are characterized by surprisingly similar stochastic fluctuations and thus internal flexibility. The kink-turn shows substantial hinge-like fluctuation dynamics (19,20). Very similar overall hinge-like dynamics was detected in simulations of the equivalent regions of the three eubacterial species, which thus can be considered as dynamical equivalents of Kt-38. In other words, while Kt-38 is not conserved, it is in all three cases replaced by RNA building blocks possessing qualitatively the same directional flexibility. This flexibility signature is thus conserved during the evolution. If Kt-38 is involved in large-scale dynamical movements of H38, as suggested earlier (19), then all three Kt-38 replacements would be equally fit to support similar motion. Obviously, the oscillations seen in different simulations are not identical. As explained above, the present study faces several limitations which do not allow us to achieve a quantitative accuracy. However, taking into account the entire diversity of the sequences forming the H38 elbow regions, it is justified to conclude that all simulated systems show surprisingly similar thermal fluctuations, especially regarding the preferred direction of motions.

The movement was roughly visualized by α and β angles describing fluctuations of the central hinge segment and of the whole system including the extended helical arms, respectively. The β angle sampled larger range of values than the α angle. Thus, the arms add additional flexibility (due to bending and groove breathing) which enhances the hinge-like dynamics stemming from the flexibility of the central hinge segment. The dynamics was also captured using essential dynamics analysis and clustering methods.

We have analyzed the internal structural dynamics of all four simulated segments at the level of individual molecular interactions (see Supplementary Data). However, each simulated segment achieves its flexibility in a different manner. For the Kt-38, we see the common dynamics of kink-turns having A-minor I interaction (18–21). In the E.c., D.r. and T.t. H38 elbow segments, the hinge-like dynamics is coupled with flexibility of H-bonds formed in the central hinge segment and with fluctuations of major groove widths. The motions are rather complex and we did not find a unifying picture of local movements in these four equivalently positioned, identically shaped, but otherwise very diverse flexible RNA segments. Despite this diversity, they have similar effects on the mutual fluctuations of the attached helical arms of H38. Perhaps, a substantial contribution to the flexibility could stem from their overall V-like topology; i.e., it could be a rather common feature of V-shaped RNAs.

We have compared the geometries of the E.c. H38 elbow segment sampled in the simulation with H38 structures seen in E.c. X-ray 70S vacant ribosome structure (23) and in cryo-EM studies (Figures 2, 3 and 6, Table 2). Specifically, we carried out a new real-space refinement fitting of the H38 positions in post-translocational state (non-ratcheted; EMDB Access Code: 1056) and the EF-G-GDPNP-bound state (ratcheting; EMDB Access Code: 1363) E.c. ribosomes, where the segmentation now divides the whole H38 into 8 rigid pieces (Figure 6). Although structural changes localized at the elbow region are entirely below the ∼10-Å resolution of the experimental method, the refinement gives the impression that the movement propagates along the ASF. Furthermore, the overall shape of the ASF and direction of preferred flexibility of the H38 elbow regions derived from the simulation mean that a change of the β angle in the H38 elbow region by 6° would be entirely sufficient to give the experimentally observed large relocation of the tip of the ASF. Obviously, the cryo-EM technique visualizes ensemble averages of structures in a finite range of conformations, so the actual range of dynamic motions may be considerably larger than what we infer from a comparison of two maps. The direction of fluctuations seen in the simulations is consistent with the experimental geometries (Figures 2 and 6). As noted above, the limitations of the theoretical and experimental data as well as the overall complexity of the ribosome do not allow us to make more quantitative comparison between theory and experiment. Nevertheless, considering all the results together leads us to suggest that the intrinsic flexibility of the H38 elbow region, as characterized by MD simulations, may indeed facilitate a substantial part of the functional movements of the ASF. The H38 elbow segment is well poised to facilitate instantaneous large-scale fluctuations of the ASF tip with no free energy penalty.

Table 2.

E.c. segments of MD and X-ray structures used for the superpositions

Molecule (segment)	PDB code or simulation	Interhelical β angle (°)
Example of open MD geometry (838–858, 919–940)	MD_Ec	112
Example of closed MD geometry (838–858, 919–940)	MD_Ec	81
Averaged MD geometry (838–858, 919–940)	MD_Ec	97
Crystal geometry (838–878, 898–940)	2aw4 (23)	96

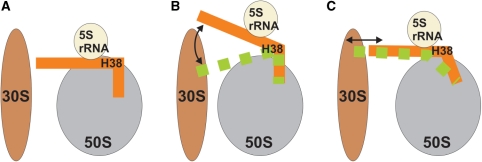
When interpreting the simulation results it is important to note that the Figure 3 illustrates solely the internal flexibility of the segment studied. It does not, without further constraints, unambiguously determine its motion with respect to the subunit. The apparent direction of fluctuations in the Figure 3 results from using the arm 1 as the fixed reference point for the structure overlay. With respect to the ribosome (represented in a standard position, with the large subunit in the crown view and the small subunit in front of it) the stochastic hinge-like fluctuations of the H38 elbow segment could support movements with an up-and-down as well as a back-and-forth components depending on additional constraints imposed by the surrounding ribosomal elements (Figure 8). This is consistent with the macrostates inferred from the cryo-EM data (Figures 2 and 6).

Figure 8.

Schematic representation of H38 with respect to the 5S rRNA and both subunits (A) illustrating two possible components of movement consistent with the hinge-like intrinsic flexibility of the H38 elbows: up-and-down motion (B) and back-and-forth motion (C).

BIOLOGICAL SIGNIFICANCE

The suggestion emerging from mutational studies, cryo-EM and our MD simulations is that the H.m. kink-turn 38 and its equivalents in eubacteria species are passive elbow-like elements that, due to their strategic position at the back of the subunit, allow smooth large-scale fluctuations and swift barrier-free repositioning of the whole ASF, particularly affecting the tip area and the 5S rRNA contact area. These movements could allow a range of back and forth dynamics, up and down dynamics, and their combination (Figure 8). For example, changing the elbow angle by 6° would result in more than 10 Å positional shifts of the ASF tip, provided the motion fully propagates along the 100-Å path of a stiff H38 (Figures 2, 6 and 8) (19). This idea is consistent with the role of the ASF in the attenuation of translocation. Attenuation probably includes slowing down the tRNA movement and—considering the alternate B1a bridging contacts of its tip with S13 and S19 (3)—participation in a molecular ruler that establishes two preferred ratchet orientations. The idea is also consistent with the proposed involvement of H38 in complex dynamical allosteric signaling between ribosomal functional centers involving the dynamics of 5S rRNA (9). The large flexibility (floppiness) of the H38 elbows suggests that they are unlikely to be spring-like elements. Spring-like elements have essentially harmonic free energy surface around the optimal geometry, so that they respond by a quadratic increase of energy to deviations from their optimal geometries. The H38 elbow regions behave as non-harmonic elements which have broad basins of iso-energetic conformations and are thus suitable to act as passive elbows with a wide range of easily accessible geometries (22).

We suggest that future biochemical and mutational studies could consider mutations and modification in the H38 elbow regions. One obvious option is to target Kt-38, which is universally conserved in archaea. Simulations show that the C1026 = G940/A1032 A-minor-I interaction between the C and NC stems, exhibiting the specific dynamical water insertion, is important for the K-turn flexibility. While A1032 is universally conserved, sequence alignments show the 1026/940 base pair to be 88% CG (presumably WC) and 12% UG (presumably near-isosteric WC ‘wobble’) (16). This A-minor-I interaction appears to not be involved in any tertiary contacts with other parts of the ribosome. Therefore, it would be tempting to test why the CG→GC substitution is not tolerated. This isosteric substitution might affect the K-turn dynamics which specifically profits from the water insertion into the A/C base pair. More disruptive could be substitutions of the A1032 nucleotide or the A1032/G938 base pair, destabilizing the K-turn signature tertiary contact between the C and NC-stems. Furthermore, it would be possible to replace the Kt-38 by another kink-turn, as kink-turns represent a rather variable RNA motif (16,17). When considering the diverse and mutually unrelated sequences present in equivalent positions in the three eubacterial species, there appears to be large latitude in the allowed choices of sequence inserted in this position. Thus, testing how the archaeal ribosome responds to modifications of its Kt-38 could shed light on the actual role of the H38 elbow region and its functional and evolutionary constraints. Such experiments could be complemented by additional simulations.

More drastic modifications (analogous to the tip deletion studies) could attempt swaps of H38 elbows between species. For example, could the (at first sight unrelated) eubacterial sequences be interchanged? Can Kt-38 be functional in eubacteria and some of the eubacterial elbows in the archaeal ribosome? For example, when considering the H.m. and E.c. X-ray structures, the segments between H.m. 1018A/949U (E.c. 922C/855G) and H.m. 1036G/934C (E.c. 937C/841G) base pairs should be exchangeable with basically no effect on the static averaged positions of the attached arms. However, the flexibility would be modestly modified, as predicted by simulations. Furthermore, all the elbows are intrinsically very flexible (see the simulation behavior) and thus can extensively structurally adapt to the surrounding elements with no energy costs. The flexibility can facilitate the H38 swaps compared to what one would guess based on superposition of the static averaged X-ray structures. Note that changes in the elbow region may affect not only the ASF tip, but also its dynamical interaction with 5S rRNA and the overall dynamical allosteric signaling between ribosomal functional centers. Therefore, modifications of the elbow region may provide interesting clues regarding the ribosome dynamics.

Finally, one could also attempt to rigidify the H38 elbow segment, simply by substituting sequences that would be prone to form standard Watson–Crick (WC) (especially GC) base pairs. However, this could not only interfere with the H38 elbow flexibility, but could perhaps ultimately disrupt folding of the large subunit, specifically the interaction between 23S rRNA and 5S rRNA of the central protuberance.

Obviously, it is also important to take into account the tertiary contacts of H38, which may impose static constraints on the ribosome components. A brief analysis of H38 elbow contacts is given in the Supplementary Data. The H38 elbows are basically free of such contacts and the elbow is rather exposed on the surface of the subunit. The proximal attached helical arms are involved in some tertiary interactions, for example helical arm 1 of E.c. H38 elbow makes contact with H36 while helical arm 2 makes contacts with ribosomal proteins L30 and L27. Similar contacts can be seen for other species. Nevertheless, it still is one of the least crowded areas of the ribosome and therefore functional fluctuations can be expected to occur in this region.

Motions of H38 should be coupled with 5S rRNA dynamics. Mutational studies indicate that 5S rRNA mediates allosteric transmission of information from the decoding center via the B1a/B1b bridges to the elongation factor binding site (92). This again agrees with the previous real-space fitting results (67) which show that 5S rRNA moves approximately in a range from 2 to 5 Å (Figure 5 on page 796 in that paper). Thus, when considering the allosteric role of 5S rRNA movements, the flexibility of the H38 elbow region must be of high functional importance.

SUPPLEMENTARY DATA

Supplementary Data are available at NAR Online.

FUNDING

Ministry of Education of the Czech Republic (grant numbers AVOZ50040507, AVOZ50040702, MSM0021622413 and LC06030); Grant Agency of the Academy of Sciences of the Czech Republic (grant numbers KJB400040901, 1QS500040581 and IAA400040802); Grant Agency of the Czech Republic (grant number 203/09/1476); Howard Hughes Medical Institute and the National Institutes of Health (grant number R01GM55440 to J.F.). Funding for open access charge: The Wellcome Trust.

Conflict of interest statement. None declared.