Income Inequality and Self-Rated Health Status: Evidence from the European Community Household Panel

Abstract

We examine the effect of income inequality on individuals’ self-rated health status in a pooled sample of 11 countries, using longitudinal data from the European Community Household Panel survey. Taking advantage of the longitudinal and cross-national nature of our data, and carefully modeling the self-reported health information, we avoid several of the pitfalls suffered by earlier studies on this topic. We calculate income inequality indices measured at two standard levels of geography (NUTS-0 and NUTS-1) and find consistent evidence that income inequality is negatively related to self-rated health status in the European Union for both men and women, particularly when measured at national level. However, despite its statistical significance, the magnitude of the impact of inequality on health is very small.

Numerous studies have reported an association between the level of income inequality in a population and aggregate health outcomes: average health among people living in high-inequality areas appears to be lower than among people living in low-inequality areas. A statistically significant relationship has been reported in studies using aggregate data both across countries (Rodgers 1979; Wilkinson 1992) and across regions within countries (Kawachi and Kennedy 1997; Lynch et al. 1998). This observation has lead researchers to argue that increasing income dispersion directly translates into poor health, thereby suggesting additional welfare gains from more progressive income redistribution policies. This argument is embodied in Wilkinson’s (1996) controversial income inequality hypothesis (IIH), which posits that the primary determinant of differences in health performance among developed countries is the extent of differences in the disparity between the incomes of the rich and the poor within countries rather than differences in income levels.

Authors have typically conjectured that inequality has an effect on health either because it is a source of psychosocial stress, which eventually leads to stress-related afflictions, or because it fosters the development of environments hazardous to public health (Daly et al. 1998). However, providing a fully convincing theory characterizing the actual direct (or indirect) pathways by which inequality affects health remains a contentious issue (for recent reviews, see Deaton 2003; Leigh, Jencks, and Smeeding 2009; and Subramanian and Kawachi 2004). Subramanian and Kawachi (2004) identified three potential pathways by which greater income inequality may translate into poorer health. First, according to a structural pathways argument, increased inequality leads to spatial concentrations (poverty, race, ethnic enclaves), and residential segregation is potentially detrimental to individual health (Wen, Browning, and Cagney 2003). Second, building on the argument that individual health is influenced by social relations, the social cohesion and collective social pathway suggests that inequality affects health by weakening social cohesion and holding back the formation of social capital beneficial to health (Kawachi et al. 1997). Third, policy pathways hypotheses posit that income inequality could affect health via an influence on the implementation of particular social and health-related policies (Neckerman and Torche 2007; Schwabish, Smeeding, and Osberg 2006). Overall, little evidence to date permits us to distinguish between these hypothesized pathways.

Furthermore, studies have cast doubt on the robustness to model specification of the empirical association found in macro-level analyses and have questioned the comparability of data sources both across countries (Gravelle 1998; Gravelle, Wildman, and Sutton 2002; Judge, Mulligan, and Benzeval 1998) and across U.S. states (Mellor and Milyo 2001). Rodgers (1979), and more recently Gravelle (1998) and Gravelle et al. (2002), cautioned that this apparent causal relationship may just be a statistical artifact if individual health is a nonlinear function of income.1 In order to identify the effect of income inequality on health, one needs to turn to individual-level data and to control for relevant confounders, particularly individual income. Recent studies have taken this approach, and the new evidence about an association between health and income inequality is mixed at best.

The majority of studies based on individual-level data have focused on the United States.2 Kennedy et al. (1998) and Mellor and Milyo (2002) found that state-level income inequality significantly affects self-reported health status even after controlling for individual incomes and other demographic variables. However, Mellor and Milyo (2002) reported that this association is no longer significant after controlling for regional fixed effects that take into account differences in, for example, diet, lifestyle, and access to medical care. In fact, the finding that state-level inequality is detrimental to self-rated health is not robust to alternative health outcomes. For instance, Daly et al. (1998) found very weak evidence that state-level income inequality translates into increased mortality. Furthermore, unlike Kawachi et al. (1997) and Lynch et al. (1998), they reported that this association is not robust to different measures of income inequality.

Considering a lower level of geography, Mellor and Milyo (2002) and Blakely, Lochner, and Kawachi (2002) did not find any significant association between metropolitan-area-level income inequality and self-rated health. Interestingly, some studies have found evidence of a statistically significant association between county-level income inequality and self-reported health status (Fiscella and Franks 2000; Soobadeer and LeClere 1999). However, the relationship is no longer significant when the health outcome is measured by mortality (Fiscella and Franks 1997). Overall, these studies present weak support for the assertion that greater income inequality is detrimental to individual health in the United States.

Few comparable micro-level studies have examined the robustness of this association outside the United States. Results from these studies generally corroborate U.S. findings. For instance, Shibuya, Hashimoto, and Yano (2002) found no significant evidence that income inequality measured at the prefectures level has a detrimental effect on self-rated health status in Japan. Likewise, Gerdtham and Johannesson (2004) found no significant effect of community-level income inequality on mortality in Sweden.3 Weich, Lewis, and Jenkins (2001, 2002) found a significant association between the Gini coefficient in Britain’s regions and mental disorders and self-reported health status, but the results were highly sensitive to the choice of inequality measure. Lorgelly and Lindley (2008) confirmed the absence of a clear association within Britain.

Distinguishing the effect by gender has been largely overlooked so far (Macintyre and Hunt 1997). This is surprising given the often-cited gender paradox in health—that is, that women experience higher rates of various measures of morbidity despite living longer than men (Rieker and Bird 2005). In a macro-level study of 13 OECD countries, McIsaac and Wilkinson (1997) did not find that the magnitude of the correlation between income inequality and mortality was significantly different across gender. Similar results were reported by Kaplan et al. (1996). On the contrary, using data from 1980, Regidor et al. (2003) found some evidence that female mortality in Spain might be more sensitive to income inequality than male mortality. However, they failed to confirm this finding using more recent data. Lorgelly and Lindley (2008) explored the association separately for men and women in Britain. While they found that men report to be in better health than women, they did not find any significant association with income inequality regardless of gender.

The objective of this article is to investigate the issue on a large entity outside the United States. We use individual-level data from 11 countries included in the European Community Household Panel (ECHP) survey data. Providing additional evidence for the European Union is of particular interest because although its level of economic development is comparable to that of the United States, it generally fosters more progressive health and social policies. At the same time, the European Union as a whole can be viewed as a fairly heterogeneous federation of independent states with pronounced regional identities. As a result, one should expect to observe nonnegligible regional variations in income and income inequality. This strongly enhances the possibility of testing whether individual health outcomes are responsive to variation in inequality. To the best of our knowledge, this analysis is the first focusing on cross-national variations in inequality using individual-level data.4 Our large sample size allows us to consider men and women separately.

Our empirical strategy follows and extends the framework of Mellor and Milyo (2002) to take advantage of the longitudinal nature of the ECHP data. The use of panel data limits the problem of omitted variable bias since it allows us to control for the potential confounding effects of unobservable fixed effects in the relationship between health, income, and income inequality. We are also able to address issues of cross-national data comparability and to mitigate the problem of differences in norms and expectations that plague cross-regional studies on self-assessed health. Unlike in many macro-level, cross-country studies, cross-national comparability of the regional data on health and income is largely guaranteed in the ECHP because they have been gathered simultaneously and with a common questionnaire and methodology in different countries. Nevertheless, there is a well-founded concern that measures of self-reported health, even when collected from surveys sharing common wording of the health question, cannot be interpreted comparably because of implicit variations in norms and health expectations between individuals (Sadana et al. 2000). An additional contribution of this article is to offer a simple approach to handle the lack of comparability of the self-rated variables in micro-level cross-country studies.

To preview our results, we find statistically significant evidence supporting the income inequality hypothesis regardless of gender, even after controlling for individual socioeconomic characteristics, income, and other unobserved fixed regional or individual characteristics. Although we observe effects that are significantly different from zero in a statistical sense, the magnitude of the effect of inequality on health turns out to be very small. Estimated differences across gender are small and insignificant.

DATA AND VARIABLE DEFINITIONS

The European Community Household Panel Survey

Our study draws on data from the public-use file of the European Community Household Panel survey (ECHP). The ECHP is a standardized multipurpose annual longitudinal survey providing comparable micro-data about living conditions in the European Union over the period 1994–2001. More than 60,000 households and 130,000 adults across the European Union were interviewed at each wave. The first wave covered all EU-15 Member States with the exception of Austria, Finland, and Sweden. Austria joined in the second wave; Finland, in the third; and Sweden, in the fourth.5 Topics covered in the survey include income, employment, housing, health, and education. A harmonized (E.U.-wide) questionnaire was designed at Eurostat, and the survey was implemented in each Member State by National Data Collection Units. The public-use database is created, maintained, and centrally distributed by Eurostat.6 The attractive feature of the ECHP for our purpose is that it provides longitudinal, individual-level data on income and demographics, including individual health, that are comparable across countries and over time.

Household Income and Regional Measures of Income Inequality

The ECHP data identify country and region of residence of respondents down to the NUTS-1 level. The NUTS (Nomenclature des Unités Territoriales Statistiques) classification is the European Union’s official regional classification system. NUTS-0 is the country level, and NUTS-1 is the first level of aggregation below the country level. The size of the regions defined by the NUTS-1 classification varies considerably. However, because the NUTS classification was precisely created to facilitate the collection, compiling, and dissemination of comparable regional statistics in the European Union and is determined on the basis of population thresholds, it is reasonable to expect that these regions delimit relatively homogeneous territorial units.7 Interestingly, NUTS-1 regions broadly correspond in population to U.S. states, which have often been used as a basis for tests of the IIH.

The ECHP Users Database contains a measure of total net household income, expressed in national currency. To make the household income data comparable across countries and over time, (1) all these data were expressed in 1995 prices using national consumer price indices, and (2) cross-national differences in currency and price levels were normalized using the purchasing power parity standards provided in the ECHP database.8 In addition, in order to take economies of scale in household consumption and differences in needs between adults and children into account, we converted all household incomes into a single-adult equivalent household income by applying the conventional modified-OECD equivalence scale (see, e.g., the recommendations in Atkinson et al. 2002:99). Hereafter, we refer to respondents’ single-adult equivalent household income as their household income.

We used these household income data to estimate five measures of regional income inequality: the Gini coefficient, two generalized entropy measures (the Theil index and the mean log deviation), the coefficient of variation, and the ratio of the 90th to the 10th inequality. They are all relative in the sense that they are insensitive to changes in scale (equiproportionate increases in everyone’s income), but their finer properties differ.9 Because there is little guidance about which measure best picks up the pathway by which inequality can affect individual health, and because some earlier studies have reported the health-inequality relationship to be sensitive to the way inequality is measured, we considered all five measures in our analysis.

Inequality indices were computed for all NUTS-0 and NUTS-1 regions and for all survey years for which we have sample data in the ECHP. Data for all individuals in each region were used regardless of age.10 All sample observations were weighted using the cross-section sample weights provided in the database. We estimated mean income at the two NUTS levels similarly. The number of households per region used for estimation at the NUTS-1 level ranges from 209 (in East Anglia, United Kingdom, in Wave 8) to 4,055 (in Finland in Wave 3). In several countries, the estimated NUTS-1 level inequality measures in the first wave of the panel (1994) appeared to be at odds with the rest of the series (frequently substantially higher). In order to limit potential measurement error, we therefore decided not to include data from Wave 1 in our models and to restrict our estimation sample to data from Waves 2 to 8.

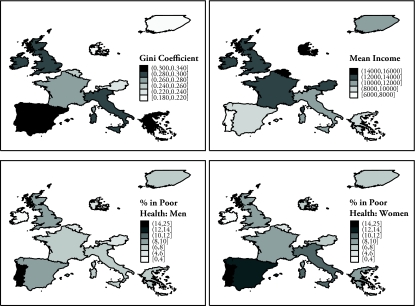
Thematic maps at the top of Figure 1 show average NUTS-0 Gini coefficients and mean household income across our sample of countries. As expected, countries exhibit substantial variation in inequality and income levels, with richer, more equal countries in the North and poorer, more unequal countries in the South. Summary statistics about the estimated indices are also presented in Appendix Table A1.11

Figure 1.

Thematic Maps for 11 European Countries: Gini Coefficient (top left), Average Household Income (top right), Percentage of Men Aged 24–75 Reporting Poor Health (bottom left), and Percentage of Women Aged 24–75 Reporting Poor Health (bottom right)

Note: Estimates are from ECHP data (1995–2001) for Austria, Belgium, Denmark, Finland, France, Greece, Ireland, Italy, Portugal, Spain, and the United Kingdom.

Notice that concerns about the quality and comparability of existing international data on income distribution is one of the most severe drawbacks suffered by a majority of (aggregate-level) cross-national studies (Judge et al. 1998; Macinko et al. 2003). Many studies relied on heterogeneous sources of income distribution data often collected at different points in time and/or failed to use an adequate measure of disposable income. Using the ECHP allows us to circumvent these limitations because we estimated our own regional income inequality measures across the European Union with fully comparable individual-level income data.

Health Indicators

The ECHP survey collects information on self-reported health status for all respondents older than 16. This subjective measure of (nonfatal) health is commonly used in the literature. It is measured on a standard 5-point scale labeled very good, good, fair, poor, and very poor. We used this variable to derive two proxy measures of individual health.

We first defined a dummy indicator of poor health equal to 1 for the bottom two modes of this self-reported health status variable, as did Fiscella and Franks (1997, 2000), Mellor and Milyo (2002), Soobadeer and LeClere (1999), and Weich et al. (2002). The increasingly popular use of this indicator in the health literature comforted by the consistent finding of a significant association between this proxy measure of poor health and mortality (see, e.g., Idler and Benyamini 1997; Idler and Kasl 1995; McCallum, Shadbolt, and Wang 1994; Strauss and Thomas 1998).

Table 1 presents the distribution of self-reported health and our proxy measure of poor health by country and gender for the countries included in our analysis. The proportions of men and women reporting poor health are also mapped in the bottom two panels of Figure 1. In all countries, a larger proportion of women report being in poor health—an observation consistent with the so-called gender paradox in health (Rieker and Bird 2005).12 Cross-country differences in the probability of reporting poor (or very poor) health are particularly striking. The prevalence of poor health among men ranges from 3% in Ireland to 18% in Portugal; among women the prevalence of poor health ranges from just below 3% in Ireland to almost 25% in Portugal. Similarly striking differences emerge with the proportion of respondents reporting very good health. Aside from genuine differences in health across countries, a plausible explanation for these cross-national differences is the sensitivity of self-reported health responses to systematic reporting biases across countries. Efforts to achieve cross-country comparability in survey data are mostly concentrated on eliminating one source of systematic bias—namely, language—by producing comparable wording of questions. The ECHP data are comparable in the sense that careful wording of questions should largely eliminate bias due to differences in survey methodologies: the questions and response items are identical in all countries. However, differences in the wording of questionnaires is not the only source of systematic bias. Sadana et al. (2000) convincingly argued that reporting biases due to regional differences in norms and health expectations among individuals may be responsible for considerable variations in self-reported health across countries, such as the one observed between Portugal and Ireland. Differences in the prevalence of poor health as assessed by survey respondents may therefore not reflect genuine differences in absolute levels of health, but instead might suggest cross-national differences in its perception. This effect could possibly bias estimates of the relationship between health and income inequality if there is correlation between the systematic cultural differences in self-rated health responses and inequality levels.

Table 1.

Distribution of Self-Reported Health Level by Country (percentages)

Country	On a 5-Point Scale					Poor or Very Poor
	Very Good	Good	Fair	Poor	Very Poor
Men
Austria	31.3	43.0	19.6	5.0	1.0	6.0
Belgium	24.3	53.8	17.9	3.3	0.7	4.0
Denmark	46.4	33.6	15.7	3.3	1.1	4.3
Finland	16.6	45.4	31.6	5.7	0.8	6.4
France	12.3	49.6	31.4	3.2	3.4	6.6
Greece	53.5	26.6	13.0	5.1	1.8	6.9
Ireland	44.1	37.9	15.1	2.2	0.6	2.9
Italy	16.5	47.4	27.8	6.9	1.4	8.4
Portugal	3.6	46.4	32.5	13.8	3.8	17.6
Spain	16.7	53.9	20.9	7.5	1.1	8.6
United Kingdom	25.4	46.6	19.9	6.4	1.8	8.2
Women
Austria	28.2	44.2	21.0	5.4	1.3	6.6
Belgium	18.7	51.8	24.3	4.4	0.8	5.2
Denmark	42.1	33.3	18.4	4.8	1.4	6.2
Finland	14.9	45.9	32.1	6.2	0.9	7.1
France	9.9	46.8	35.0	4.2	4.1	8.3
Greece	45.2	28.9	17.6	6.4	1.9	8.3
Ireland	44.5	35.9	16.3	2.8	0.5	3.3
Italy	11.4	44.1	33.3	9.5	1.7	11.2
Portugal	1.8	36.0	37.4	20.7	4.1	24.8
Spain	14.4	49.8	23.7	10.3	1.8	12.2
United Kingdom	20.2	47.8	22.0	7.7	2.4	10.0

Notes: All waves of ECHP data are pooled (except those for the United Kingdom from the BHPS Wave 6). Data include individuals aged 24–75. Sample weights are used.

To handle this problem, we considered a second health indicator for our empirical analysis. This alternative measure is a score of relative ill-health derived from the 5-point self-assessed health variable. It does not attempt to measure an individual’s absolute level of health as reported by the face-value self-assessed health response, but rather to assess her relative level of health when comparing herself to individuals sharing similar characteristics. The idea is that a person reporting fair health when all respondents with similar characteristics report good health is to be considered “unhealthy, relatively speaking.” On the contrary, if all respondents in her comparison group reported poor health, then she would be considered “healthy, relatively speaking.” To achieve this, we use as a health indicator the rank of each respondent in the conditional distribution of self-assessed health when conditioning on age, gender, education, marital status, and—crucially—country of residence. The resulting indicator is a number between 0 and 1 that can be interpreted as the proportion of people with similar characteristics in the sample that report being in better health. In order to apply standard linear regression models, we map this indicator from the [0,1] space onto an unbounded range by applying an inverse Gaussian transformation, Φ⁻¹(·). The transformation is monotonic, so it linearizes the score but leaves rank orders unaffected. Details on the construction of the indicator are provided in the appendix.

Because of the conditioning on a number of individual characteristics and on the country of residence, this second indicator is purged from systematic differences in self-reported health due to differences in response behavior and norms and health expectations across countries (as well as across age groups, gender, etc.). Results are valid provided that response behavior is homogeneous within comparison groups. Variations across comparison groups have no effect on the estimated score of relative ill-health. However, by construction, genuine differences in health levels across comparison groups are also discarded. The income inequality hypothesis, when tested against this score of relative ill-health, is therefore identified either by variations over time in inequality (if inequality is measured at the country level [NUTS-0]) or by both variations over time and across regions within countries (if inequality is measured at the regional level [NUTS-1]).

Sample Selection

In principle, the design of the ECHP allows us to cover all EU-15 Member States. However, because of exceptions to the general ECHP design rules and missing information, we had to restrict our analysis to a subset of 11 countries: Austria, Belgium, Denmark, Finland, France, Greece, Italy, Ireland, Portugal, Spain, and the United Kingdom.13

For comparability with earlier studies, we follow Fiscella and Franks (1997) and Mellor and Milyo (2002) in limiting our sample to individuals aged 25 to 74. The resulting estimation sample contains a total of 506,598 observations, of which 261,496 are about female respondents. As in Mellor and Milyo (2002), our econometric analysis is based on unweighted data. Unweighted descriptive statistics of individual-level variables used in our analysis are presented separately for men and women in Appendix Table A2.

EMPIRICAL STRATEGY AND RESULTS

Empirical Strategy

We have argued that cross-country variations in self-reported health are likely to be contaminated by cultural differences or norms across countries. If the observed differences in health responses across countries partly originate from these non-health-related factors, evaluating the effect of income inequality on health applying standard discrete choice methods with our binary measure of poor health as the dependent variable will yield unreliable estimates.14 To handle this issue, we opt for a linear unobserved heterogeneity panel data specification, with our score of individual relative ill-health as the dependent variable:

$$s_{it}={\mathbf{\text{X}}}_{it}\beta +{\alpha }_i+e_{it},$$ (1)

where s_it is the score of relative ill-health of individual i at time t, and X_it is a vector of explanatory variables including a measure of income inequality in the region of residence (either NUTS-0 or NUTS-1) of individual i at time t.

Following Mellor and Milyo (2002), Weich et al. (2002), and Gerdtham and Johannesson (2004), we examine two versions of the IIH. The strong IIH assumes that income inequality is detrimental to all individuals in the society—poor and rich—while the weak IIH states that income inequality is detrimental to the least well-off in the society. We interpret the estimated coefficient of the regional income inequality variable as measuring the effect of inequality on health and use it to assess the strong IIH. To examine the weak IIH, we allow the effect of income inequality to vary by the income level of the household. This is done by interacting our inequality variable with a set of dummy variables for household income quintile group. Quintile groups are defined for the income distribution of each separate country and year. According to the weak IIH, we expect the coefficients on the inequality variable interacted with low-income groups to be higher than those interacted with high-income groups. A strict interpretation of the weak IIH would suggest that the latter should not be significantly different from zero.

In addition, X_it includes the mean income of the region of residence (either NUTS-0 or NUTS-1) of individual i at time t, and a quadratic function of her household income.15 The inclusion of these additional covariates allows us to also test the absolute and the relative income hypotheses as in Gerdtham and Johannesson (2004). The absolute income hypothesis posits that, ceteris paribus, higher individual income has a protective effect on individual health. By contrast, according to the relative income hypothesis, an individual’s health is not so much affected by her absolute level of income as by her level of income relative to the average income in her reference community.16 We purposely limit the number of additional control variables because the estimated scores are already relative to individual characteristics and country of residence (see the appendix).

The individual-specific error, α_i, captures unobserved individual heterogeneity in health, and e_it is an independent error term. To the extent that respondents live in the same region (NUTS-0 or NUTS-1) at each of the survey waves, α_i picks up simultaneously unobserved, time-invariant individual and regional attributes.17 When estimated with a fixed-effects (within) estimator, this specification has the crucial advantage of controlling reliably for unobserved time-invariant covariates that are correlated with both health outcomes and regional inequality. This includes, in particular, fixed regional characteristics, such as differences in the public provision of health care, which have often been pointed out as causes of a (spurious) association between inequality and health (see, e.g., Mellor and Milyo 2002).

It is important to note that because the score of relative ill-health is specific to the country of residence, the effect of inequality on health is identified through variations of inequality over time as well as through variations across regions within countries (when looking at the NUTS-1 level of geography). In other words, we test whether individuals rank lower in the (conditional) distribution of health in years when inequality is high or when they live in regions with inequality above national standards. The conditions for observing the IIH are therefore very strict in this model. Our standard error estimates take into account the correlation of repeated observations from the same individual as well as the stratification of the data into a fixed set of regions.

Most of the earlier studies about the IIH report estimated marginal effects (or simply coefficient estimates) and discuss signs and significance levels. However, the ultimate question is not so much about statistical significance of the effect as it is about its magnitude. Standard marginal effects (or coefficient estimates) do not provide intuitively interpretable indications on the order of magnitude of the effect of inequality on individual health, and they are difficult to compare across measures of inequality because of differences in their range of variation. For this reason, in addition to coefficient estimates, we report the change in the predicted rank order of individuals in the (conditional) distribution of ill-health implied by a discrete change in the explanatory variables (i.e., regional inequality, regional income, or household income), according to our model coefficient estimates. Remember that the rank order is the probability that an individual with the same age, education, marital status, and country of residence reports being in better health than the respondent.18 We predict, for all respondents, their rank in the (conditional) health distribution given by the estimated coefficients and by the value of their covariates, but we set one key covariate (e.g., the income inequality index) to either a fixed high value (Z^H) or a fixed low value (Z^L). We then compute the difference between the two predictions and average over all sample observations:

$$D(Z^H,Z^L)=\frac{1}{N}\sum _{i=1t}^n\sum _{\in {\Omega }_i}\Phi ({\mathbf{\text{W}}}_{it}\widehat{\beta }+\widehat{\gamma }{Z}^H)-\Phi ({\mathbf{\text{W}}}_{it}\widehat{\beta }+\widehat{\gamma }{Z}^L),$$ (2)

where N is the overall sample size, n is the number of distinct respondents, Ω_i is the set of time periods at which i is observed in the data, W_it are the explanatory variables except the covariate of interest Z, and β̂ and γ̂ are the estimated coefficients of Eq. (1). The value of D(Z^H,Z^L) informs us about the (counterfactual) health effect that would be observed if all respondents had their covariate Z moved from a low value to a high value, given the estimated coefficients. We set Z^H and Z^L at the 80th quantile and 20th quantile of the distribution of Z. In the sequel, we refer to the D(Z^H,Z^L) statistic as the predicted discrete effect of Z. This statistic makes it easy to capture the magnitude of the estimated effects, and not just their statistical significance.

Results

Tables 2 and 3 report coefficient estimates and predicted discrete effects for all estimated models when inequality is measured by the Gini coefficient. Results are reported in columns for model specifications with and without household income included as a regressor. Results from Table 2 provide tests of the strong IIH, while results from Table 3 provide tests of the weak IIH.

Table 2.

Fixed-Effects Linear Models of the Relative Ill-Health Score With the Gini Coefficient as the Regional Inequality Measure: Coefficient Estimates and Predicted Discrete Effects

Variable	Men				Women
	NUTS-0		NUTS-1		NUTS-0		NUTS-1
Coefficient Estimates
Mean regional income	1.47** (4.80)	1.55** (5.02)	0.81** (3.12)	0.88** (3.35)	−0.60* (2.00)	−0.54 (1.80)	−0.56* (2.22)	−0.51* (1.99)
Gini coefficient	1.18** (5.87)	1.18** (5.90)	0.55** (4.25)	0.55** (4.27)	0.68** (3.46)	0.69** (3.49)	0.38** (3.01)	0.39** (3.03)
Household income		−0.07* (2.14)		−0.07* (2.04)		−0.06* (1.99)		−0.07*(2.09)
Household income squared		0.00 (0.14)		0.00 (0.05)		0.01** (3.88)		0.01** (3.92)
Predicted Discrete Effects
Mean income effect	0.029	0.031	0.017	0.018	−0.012	−0.011	−0.012	−0.011
Inequality effect	0.043	0.043	0.013	0.013	0.025	0.025	0.009	0.009
Household income effect		−0.003		−0.003		−0.003		−0.003

Notes: Coefficients on mean regional income and household income are multiplied by 100,000. The coefficient on squared household income is multiplied by 10e¹⁰. Absolute z values are in parentheses. See the text for an explanation on the construction of predicted discrete effects.

^*p < .05;

^**p < .01

Table 3.

Fixed-Effects Linear Models of the Relative Ill-Health Score With the Gini Coefficient as the Regional Inequality Measure and Interaction Effects With Income Quintile Groups: Coefficient Estimates and Predicted Discrete Effects

Variable	Men				Women
	NUTS-0		NUTS-1		NUTS-0		NUTS-1
Coefficient Estimates
Mean regional income	1.46** (4.76)	1.42** (4.60)	0.81** (3.11)	0.77** (2.96)	−0.60* (2.03)	−0.57 (1.91)	−0.57* (2.23)	−0.53* (2.09)
Gini coefficient × Lowest fifth	1.28** (6.36)	1.28** (6.39)	0.64** (4.94)	0.65** (4.99)	0.72** (3.65)	0.72** (3.63)	0.42** (3.27)	0.41** (3.21)
Gini coefficient × Second fifth	1.21** (6.02)	1.21** (6.04)	0.57** (4.43)	0.58** (4.46)	0.69** (3.47)	0.68** (3.46)	0.39** (3.01)	0.38** (2.98)
Gini coefficient × Third fifth	1.19** (5.93)	1.19** (5.92)	0.55** (4.28)	0.55** (4.29)	0.70** (3.54)	0.70** (3.54)	0.40** (3.10)	0.40** (3.09)
Gini coefficient × Fourth fifth	1.14** (5.68)	1.14** (5.66)	0.50** (3.88)	0.50** (3.86)	0.66** (3.36)	0.67** (3.38)	0.36** (2.84)	0.37** (2.86)
Gini coefficient × Highest fifth	1.13** (5.62)	1.12** (5.56)	0.49** (3.82)	0.48** (3.73)	0.66** (3.35)	0.67** (3.40)	0.36** (2.82)	0.37** (2.89)
Household income		0.04 (1.02)		0.04 (1.00)		−0.04 (0.91)		−0.04 (1.08)
Household income squared		−0.01** (2.60)		−0.01* (2.57)		0.01** (3.15)		0.01** (3.26)
Predicted Discrete Effect
Mean income effect	0.029	0.028	0.017	0.016	−0.012	−0.011	−0.012	−0.011
Inequality effect (lower quintile)	0.046	0.047	0.016	0.016	0.026	0.026	0.010	0.010
Inequality effect (upper quintile)	0.041	0.041	0.012	0.012	0.024	0.024	0.009	0.009
Household income effect		0.001		0.001		−0.001		−0.002

Notes: Coefficients on mean regional income and household income are multiplied by 100,000. The coefficient on squared household income is multiplied by 10e¹⁰. Absolute z values are in parentheses. See the text for an explanation of the construction of predicted discrete effects.

^*p < .05;

^**p < .01

Coefficients on the Gini index in Table 2 are positive and significantly different from zero. This is evidence in support of the strong IIH that an increase in income inequality is detrimental to all members of society. This finding is robust to the level of geography and across gender. Predicted discrete effects are very small in magnitude, however. They range between 0.01 for women at the NUTS-1 level and 0.04 for men at the NUTS-0 level. This suggests that a substantial change in the inequality in a person’s environment (as used to construct the discrete effects) would lead to a change in her relative rank of between only 1 and 4 positions out of 100, on average.

Regardless of gender, when income inequality is measured at the NUTS-1 level, the impact of inequality on health is reduced, but coefficient estimates remain significantly different from zero. This finding is in line with a number of U.S. micro-level studies that found that the magnitude and significance of the detrimental effect of income inequality tends to disappear when it is measured at a lower level of aggregation than U.S. states. It would be useful to investigate whether we would lose statistical significance when income inequality is measured at a lower level of geographical aggregation (such as NUTS-2). However, respondent’s residence information at this level of geography is not available in the ECHP.

We do not find evidence in Table 3 supporting a strict interpretation of the weak IIH: all the interaction coefficients between income inequality and household income quintiles are significant. Coefficient estimates are smaller when the Gini is interacted with higher-income quintile groups, but the impact on differences in predicted discrete effects between high-income and low-income groups is negligible.

European men appear to be more adversely affected by inequality than are women. However, the observed difference is small and generally not statistically different from zero, particularly when income inequality is measured at the NUTS-1 level.19 The gender paradox in health therefore cannot be explained by a higher sensitivity to inequality among women.

Coefficients on the household income variables in Tables 2 and 3 do not provide support for the absolute income hypothesis that higher household income directly leads to better health outcomes. Controlling for individual unobserved heterogeneity and regional income, the impact of household income is small (Table 2) or not significant (Table 3). On the contrary, our results provide partial support for the relative income hypothesis. If it is household income relative to the regional mean that matters to people’s health, we should observe positive coefficients on the mean regional income variable: higher mean regional income implies a higher reference income and therefore a lower health outcome for a given (absolute) income level.20 Consistent with this hypothesis, the coefficient estimates reported in Tables 2 and 3 are positive and significant among men. However, we fail to find any significant association among women. This finding is robust regardless of the level of geography considered. The magnitude of the predicted effects of mean regional income is similar to those of inequality.

In sum, our fixed-effects specification provides evidence of a statistically significant association between income inequality and individual health. However, the predicted discrete effects reveal that the magnitude of this association is very small. This result is robust to model specifications, as well as across geographic levels and gender. The impact is greater among men and when inequality is measured at the country level.

ROBUSTNESS CHECKS

For clarity, we have restricted our discussion to models with the Gini coefficient. However, the Gini coefficient is only one of many measures that have been used to capture the inequality-health relationship (De Maio 2007). To ensure that our results are not sensitive to the choice of inequality index, we estimated all models with four additional measures: the ratio of the 90th to the 10th percentile (hereafter, the P90/P10 ratio), the Theil index, the mean log deviation, and the coefficient of variation. Coefficients on the inequality index and predicted discrete effects for the different models are summarized in Tables 4 and 5. It is reassuring that the observation of a small, positive effect of inequality on health prevails regardless of the inequality index chosen.

Table 4.

Fixed-Effects Linear Models of the Relative Ill-Health Score: Coefficient Estimates and Predicted Effects for Alternative Inequality Indices

Index	Men				Women
	NUTS-0		NUTS-1		NUTS-0		NUTS-1
Coefficient Estimates
Gini coefficient	1.18**	1.18**	0.55**	0.55**	0.68**	0.69**	0.38**	0.39**
P90/P10 ratio	0.04**	0.04**	0.02**	0.02**	0.02*	0.02*	0.02**	0.02**
Theil index	0.95**	0.95**	0.44**	0.44**	0.66**	0.66**	0.32**	0.32**
Mean log deviation	0.77**	0.77**	0.36**	0.36**	0.52**	0.53**	0.31**	0.32**
Coefficient of variation	0.25**	0.25**	0.12**	0.12**	0.20**	0.20**	0.09*	0.09*
Predicted Discrete Effects
Gini coefficient	0.043	0.043	0.013	0.013	0.025	0.025	0.009	0.009
P90/P10 ratio	0.027	0.027	0.009	0.009	0.017	0.017	0.010	0.010
Theil index	0.032	0.032	0.011	0.011	0.022	0.022	0.008	0.008
Mean log deviation	0.031	0.031	0.010	0.010	0.021	0.021	0.009	0.009
Coefficient of variation	0.017	0.017	0.007	0.007	0.013	0.014	0.005	0.005

Note: See the text for an explanation of the construction of predicted discrete effects.

^*p < .05;

^**p < .01

Table 5.

Fixed-Effects Linear Models of the Relative Ill-Health Score: Coefficient Estimates and Predicted Effects for Alternative Inequality Indices Interacted With Top and Bottom Income Quintile Groups

Index	Men				Women
	NUTS-0		NUTS-1		NUTS-0		NUTS-1
Coefficient Estimates
Gini coefficient (lower quintile)	1.28**	1.28**	0.64**	0.65**	0.72**	0.72**	0.42**	0.41**
Gini coefficient (upper quintile)	1.13**	1.12**	0.49**	0.48**	0.66**	0.67**	0.36**	0.37**
P90/P10 ratio (lower quintile)	0.04**	0.05**	0.02**	0.02**	0.03**	0.03**	0.02**	0.02**
P90/P10 ratio (upper quintile)	0.03**	0.03**	0.01*	0.01*	0.02*	0.02*	0.02**	0.02**
Theil index (lower quintile)	1.14**	1.15**	0.62**	0.63**	0.73**	0.72**	0.39**	0.38**
Theil index (upper quintile)	0.85**	0.83**	0.34**	0.32**	0.61**	0.62**	0.26*	0.28*
Mean log deviation (lower quintile)	0.95**	0.96**	0.51**	0.52**	0.59**	0.59**	0.38**	0.37**
Mean log deviation (upper quintile)	0.67**	0.65**	0.26**	0.24*	0.47**	0.48**	0.26**	0.27**
Coefficient of variation (lower quintile)	0.30**	0.31**	0.17**	0.17**	0.22**	0.22**	0.11**	0.10**
Coefficient of variation (upper quintile)	0.23**	0.22**	0.09*	0.09*	0.19**	0.19**	0.08*	0.08*
Predicted Discrete Effects
Gini coefficient (lower quintile)	0.046	0.047	0.016	0.016	0.026	0.026	0.010	0.010
Gini coefficient (upper quintile)	0.041	0.041	0.012	0.012	0.024	0.024	0.009	0.009
P90/P10 ratio (lower quintile)	0.032	0.032	0.012	0.012	0.019	0.019	0.011	0.011
P90/P10 ratio (upper quintile)	0.024	0.023	0.006	0.006	0.016	0.016	0.009	0.009
Theil index (lower quintile)	0.039	0.039	0.016	0.016	0.025	0.025	0.010	0.009
Theil index (upper quintile)	0.029	0.028	0.009	0.008	0.021	0.021	0.007	0.007
Mean log deviation (lower quintile)	0.038	0.038	0.015	0.015	0.024	0.024	0.011	0.011
Mean log deviation (upper quintile)	0.027	0.026	0.007	0.007	0.019	0.019	0.007	0.008
Coefficient of variation (lower quintile)	0.020	0.020	0.009	0.009	0.015	0.015	0.006	0.006
Coefficient of variation (upper quintile)	0.015	0.015	0.005	0.005	0.013	0.013	0.004	0.005

Note: See the text for an explanation of the construction of predicted discrete effects.

^*p < .05;

^**p < .01

The evidence supporting the IIH reported in this article was obtained from the sample of ECHP countries that could not be dropped on the grounds of missing information or lack of genuine comparability. However, given the large discrepancy in the distribution of self-reported health between Portugal, Ireland, and the remaining countries included in our estimation sample (see Table 1), these two countries could be considered potential outliers. We examined the sensitivity of our results to the exclusion of these two countries.21 We first excluded Portuguese respondents from our final estimation sample. This exclusion was motivated by the high incidence of respondents reporting being in poor health in this high-inequality country. Thus, its exclusion allows us to examine the potential risk of biasing our results in favor of the income inequality hypothesis by the impact of a single idiosyncratic country with high inequality and very poor health. Overall, we found that dropping Portugal from our estimation sample did not affect our main finding of a small negative and significant association between individual health and income inequality.

Arguably, Ireland is also a potential outlier in the distribution of self-assessed health in comparison with the rest of the E.U. countries. Because Ireland combines good aggregate health indicators and high inequality, we expected that its exclusion would strengthen the significance of the association between income inequality and health. We found that our main finding is robust to the exclusion of Ireland from our estimation sample.

CONCLUSION

This is the first study that has formally explored, separately for men and women, the robustness of the income inequality hypothesis using individual-level multicountry data of Member States of the European Union. By carefully modeling the self-assessed health variable and taking advantage of both the large geographical coverage and the longitudinal nature of the European Community Household Panel survey, this article avoids several pitfalls suffered by earlier studies on the association between health and income inequality. In particular, the common design of the ECHP for all countries minimizes data comparability problems (of health outcomes and of income). The large coverage permits the observation of heterogeneous regions with substantial variation in inequality levels, and the longitudinal nature of the data allows us to control for the confounding effect of time-invariant omitted variables (such as access to health care facilities, social protection provision, lifestyle, and diet). Furthermore, we offer a simple solution to a major concern that is specific to individual-level multicountry studies using the self-reported health variable as proxy measure of health—namely, that individuals’ responses to self-reported health could be contaminated by systematic cross-country reporting biases due to differences in norms and expectations across countries.

Controlling for potential reporting bias, we generally find statistically significant support in favor of the strong version of the income inequality hypothesis for both men and women in our pooled sample of 11 E.U. countries. This finding is seemingly at odds with comparable recent within-country studies in the United States (Mellor and Milyo 2002), Sweden (Gerdtham and Johannesson 2004), and Great Britain (Lorgelly and Lindley 2008; McIsaac and Wilkinson 1997). However, our results corroborate the emerging pattern arising from the large bulk of existing literature. Evidence supporting a significant association between income inequality and health in the United States is found overwhelmingly in state-level studies. Support for this association is extremely weak at lower levels of geography. This observation led Subramanian and Kawachi (2004) to posit the importance of political mechanisms in identifying a meaningful pathway explaining the association between inequality and health, because many health care and social programs in the United States are fully or partly funded by state tax dollars and implemented at the state level. Similarly, we observe stronger effects at the NUTS-0 aggregation-level, which is the level that best captures the differences in political behavior and implementation of policies in our sample of countries. Our finding of a significant association at NUTS-0 is therefore consistent with the existence of a policy pathway linking income inequality to health. As Subramanian and Kawachi (2004) pointed out, it is also consistent with the finding of no association in single-country studies of Europe. Pronounced regional variations in policy making, such as those observed across U.S. states, are unlikely within the regions of a single European country, even in European states with very decentralized health care systems. In any case, when we control for the confounding effect of time-invariant unobserved individual and regional characteristics, the magnitude of the detrimental effect of inequality on health appears to be modest, despite its statistical significance. Our results therefore suggest that the potential welfare gains from lower inequality in the form of improved health outcomes are likely to be of limited magnitude.

For the reasons mentioned in the article, we are confident that many of the usual problems of similar studies have been avoided. Still, we are able to assess only the impact of inequality on relative health, not on absolute levels of health (such as indicated by mortality or morbidity indicators). Also, our panel data models do not fully control for potential omitted variables that are volatile over time. However, we cannot think of potential confounding regional variables that would vary substantially in the short time dimension of our panel (seven years). Possible extensions of this article could also examine the sensitivity of our results to objective measures of health or to mortality. However, objective health variables available in the ECHP data are too limited, and a rigorous mortality study would require a much longer panel, such as that used in Gerdtham and Johannesson (2004).

APPENDIX

Construction of the Score of Relative Ill-Health

The score of relative ill-health is a monotone function of the rank of each respondent in the conditional distribution of self-assessed health when conditioning on a number of individual characteristics, gender, and country of residence.

Let g_i, c_i, and X_it denote, respectively, the gender of respondent i, her country of residence, and a set of other individual characteristics measured at interview year t (the ECHP being a longitudinal survey, respondents are interviewed up to seven times in our data set).22 The variable r_it is the self-assessed health status of respondent i at time t, where the values are ordered such that r_it = 1 corresponds to very poor health, and so on up to r_it = 5 for very good health. We model the probability that r_it = k for any k ∈ {1,…,5} given g_i, c_i, and X_it by using the standard ordered probit assumption (for a recent review, see, e.g., Boes and Winkelmann 2006; or Long 1997):

$$\begin{array}{ll}{p}_{it}(k)& \equiv Pr(r_{it}=k | {\mathbf{\text{X}}}_{it},c_i=c,g_i=g)\\ & =\Phi ({\kappa }_k^{c,g}-{\mathbf{\text{X}}}_{it}{\beta }^{c,g})-\Phi ({\kappa }_{k-1}^{c,g}-{\mathbf{\text{X}}}_{it}{\beta }^{c,g}),\end{array}$$ (A1)

where Φ is the cumulative Gaussian distribution, and β^c,g and $-\infty ={\kappa }_0^{c,g}<{\kappa }_1^{c,g}<\dots {\kappa }_5^{c,g}=+\infty$ are parameters that vary across country and gender. Parameter estimates β̂^c,g and ${\widehat{\kappa }}_k^{c,g}$ are obtained by estimating this ordered probit model separately by country and gender with X_it containing a cubic function of age and sets of dummy variables for marital status (single, married, divorced, separated, or widowed) and education (less than second stage of secondary level education, second stage of secondary level education, or higher education), as well as with additional controls for the month of interview to control for potential seasonal effects.

The set (p̂_it (1),p̂_it (2), ..., p̂_it (5)) obtained by plugging parameter estimates into (A1) gives the estimated conditional probability distribution of self-assessed health for individuals with identical covariates X_it, g_i, and c_i. The proportion of individuals expected to report a better self-assessed health than respondent i at time t after conditioning on these covariates can therefore be computed as

$${\pi }_{it}=\sum _{k=r_{it}+1}^5{\widehat{p}}_{it}(k)+0.5{\widehat{p}}_{it}(r_{it}).$$

The variable π_it reflects how badly the respondent fares compared with individuals from the same country and sharing the same gender, education, etc. The score is therefore a relative indicator of health purged from systematic differences in self-reported health due to country of residence, age, gender, education, marital status, and month of interview. Note that π_it can also be understood as a residual from the ordered probit model.

Finally, an inverse Gaussian transformation is applied to linearize the health indicator and map it to an unbound range. Our second measure of health—the score of relative ill-health—is therefore given by:

$$s_{it}={\Phi }^{-1}({\pi }_{it}).$$

Appendix Table A1.

Summary Statistics on Estimated Regional Measures of Mean Income and Inequality

Index	Mean	P25	P75	Minimum	Maximum
NUTS-0 Level Data  (11 countries, 7 time periods)
Mean income	11,479	9,241	13,632	7,582	15,295
Gini coefficient	0.30	0.27	0.33	0.20	0.37
P90/P10 ratio	4.06	3.44	4.67	2.47	5.65
Mean log deviation	0.17	0.13	0.21	0.07	0.25
Theil index	0.16	0.13	0.19	0.07	0.23
Coefficient of variation	0.61	0.56	0.67	0.41	0.78
NUTS-1 Level Data  (52 regions, 7 time periods)
Mean income	11,286	8,380	13,328	5,513	17,986
Gini coefficient	0.29	0.26	0.32	0.20	0.41
P90/P10 ratio	3.91	3.16	4.53	2.47	7.16
Mean log deviation	0.16	0.12	0.19	0.07	0.34
Theil index	0.15	0.12	0.18	0.07	0.29
Coefficient of variation	0.60	0.52	0.66	0.41	0.89

Appendix Table A2.

Summary Statistics on Individual-Level Variables

Variable	Mean	P25	P75	Minimum	Maximum
Men (sample size = 245,102)
Poor health binary indicator	0.08			0.00	1.00
Score of relative ill-health (raw)	0.50	0.30	0.71	0.00	1.00
Score of relative ill-health (normalized)	0.02	−0.53	0.54	−3.52	3.94
Household income (in 000s of single-adult equivalent units)	12.3	7.1	15.4	1.5	1,292.9
Age	47	35	58	25	74
Higher education	0.20			0.00	1.00
Upper secondary education	0.29			0.00	1.00
Less than upper secondary education	0.51			0.00	1.00
Married	0.73			0.00	1.00
Separated	0.01			0.00	1.00
Divorced	0.03			0.00	1.00
Widowed	0.02			0.00	1.00
Never married	0.21			0.00	1.00
Women (sample size = 261,496)
Poor health binary indicator	0.10			0.00	1.00
Score of relative ill-health (raw)	0.50	0.29	0.71	0.00	1.00
Score of relative ill-health (normalized)	0.02	−0.54	0.56	−3.88	4.02
Household income (in 000s of single-adult equivalent units)	11.9	6.9	14.9	1.5	1,292.9
Age	47	35	59	25	74
Higher education	0.18			0.00	1.00
Upper secondary education	0.26			0.00	1.00
Less than upper secondary education	0.56			0.00	1.00
Married	0.70			0.00	1.00
Separated	0.02			0.00	1.00
Divorced	0.05			0.00	1.00
Widowed	0.09			0.00	1.00
Never married	0.14			0.00	1.00