What Explains the Rural-Urban Gap in Infant Mortality: Household or Community Characteristics?

Abstract

The rural-urban gap in infant mortality rates is explained by using a new decomposition method that permits identification of the contribution of unobserved heterogeneity at the household and the community level. Using Demographic and Health Survey data for six Francophone countries in Central and West sub-Saharan Africa, we find that differences in the distributions of factors that determine mortality—not differences in their effects—explain almost the entire gap. Higher infant mortality rates in rural areas mainly derive from the rural disadvantage in household characteristics, both observed and unobserved, which explain two-thirds of the gap. Among the observed characteristics, environmental factors—a safe source of drinking water, electricity, and quality of housing materials—are the most important contributors. Community characteristics explain less than one-quarter of the gap, with about two-thirds of this coming from community unobserved heterogeneity and one-third from the existence of a health facility within the community. The effect of disadvantageous environmental conditions—such as limited electricity and water supply—derives both from a lack of community-level infrastructure and from the inability of some households to exploit it when available. Policy needs to operate at both the community and household levels to correct such deficiencies.

Rural children face higher mortality rates than their urban counterparts (Brockerhoff 1995; Cai and Chongsuvivatwong 2006; Cleland, Bicego, and Fegan 1992; Gould 1998; Heaton and Forste 2003; Knobel, Yang, and Ho 1994; Lalou and LeGrand 1997; Sastry 1997b; Wang 2003). Although the rural disadvantage in average child survival in developing countries is firmly established, its explanation is less clear. In this article, we seek to redress the paucity of information on the causes of the rural-urban gap in infant mortality rates by using a new decomposition method that permits quantification of the contribution of unobserved heterogeneity at the household and the community level. Because of the limited availability of community-level data, few studies of child survival have been able to focus on the relative roles of community and household characteristics (Sastry 1996). The distinction is nonetheless important because it helps determine the most appropriate level for policy intervention. We exploit community-level data on health facilities and public infrastructure but also identify the contribution of unobservable community-level characteristics. The decomposition is applied to data from six Francophone countries in Central and West sub-Saharan Africa, a region that is relatively understudied despite having infant mortality rates that are among the highest in the world (World Bank 2006).

Household-level factors appear to be important in explaining rural-urban differences in child mortality. Van de Poel, O’Donnell, and Van Doorslaer (2007) found that controlling for differences in household wealth reduces the median rural-urban risk ratio in under-five mortality in a set of 47 developing countries by 59%. After controlling for a broad range of household socioeconomic and demographic factors, the urban advantage in child mortality remains significant in about one-third of the countries. However, this study does not exploit any information on community characteristics, such as availability of health care services, which are integral to the differential conditions experienced in urban and rural locations and are potentially important contributors to the rural-urban disparity in infant mortality. Sastry (1996, 1997b) highlighted the importance of community-level factors in explaining the rural-urban infant mortality differential in Brazil. Lalou and LeGrand (1997) and Heaton and Forste (2003) provided evidence suggesting that the limited availability of health care is partly responsible for the lower survival chances of children born in the rural Sahel and rural Bolivia, respectively.

In this article, we use Demographic and Health Survey data for sub-Saharan African countries for which the latest round also had a community survey providing information on the availability of health care services and other community infrastructure. We explicitly distinguish between characteristics that vary at the community and household levels and further categorize the latter into proximate and socioeconomic determinants of child mortality (Mosley and Chen 1984). Besides these observed determinants of child survival, many household and community factors might affect infant mortality but are not measured in the data. At the household level, these include biological and genetic factors, as well as cross-infection rates and health-related behavior. At the community level, infant mortality might be influenced by specific cultures and customs; by geographical aspects, such as climate and soil fertility; and by the quantity and quality of infrastructure. To take account of these unobservable determinants of infant mortality at both the household and the community level, we use a three-level, random intercept probit model (Bolstad and Manda 2001; Gibbons and Hedeker 1997; Sastry 1997a) extended to allow for correlation between the observable and unobservable determinants (Chamberlain 1980; Mundlak 1978). Thereafter, we explain the rural-urban gap in infant mortality by applying an Oaxaca-type decomposition for nonlinear models (as suggested by Fairlie [2005]) that we extend to take account of the unobserved-household and community-level heterogeneity.

Data are from six sub-Saharan African countries (Benin, Central African Republic, Chad, Guinea, Mali, and Niger). With an average of 96 of 1,000 children dying before the age of 1, sub-Saharan Africa has the highest infant mortality burden in the developing world (World Bank 2006). Within this region, infant mortality levels are among the highest in West (mostly Francophone) Africa (excluding Ghana) (Kuate-Defo and Diallo 2002). However, most published research on infant mortality in sub-Saharan Africa has focused on Anglophone countries.

Attention to reproductive health in Francophone Africa developed much later than in other regions. For many years after independence, most countries operated under pronatalist policies. Family planning services were not introduced into national health programs until the mid- to late-1980s, which was due in part to a 1920 French law forbidding abortion and promotion of contraceptives. The law has now been repealed in all countries studied except Benin and Mali, where it is no longer enforced. Population policies have evolved in all the countries, albeit at varying speeds (Tantchou and Wilson 2000). Rural-urban differences in infant mortality rates are marked in the region. On average, across the six countries studied, mortality in rural areas exceeds that in urban areas by 5 deaths per 100 births. If infant mortality rates in rural areas were reduced to those in urban areas, about 80,000 fewer children would die each year in these countries.1

The remainder of this article is organized as follows: we first discuss the conceptual framework and data. We then present the methodology we used to model infant mortality allowing for unobservable heterogeneity at the household and community levels and to decompose its difference across rural and urban locations. Thereafter, results are presented and discussed. The final section concludes with an interpretation of the implications of the study and acknowledgement of its limitations.

CONCEPTUAL FRAMEWORK

Our conceptual framework for modeling infant mortality derives from Mosley and Chen (1984), who distinguished between proximate and socioeconomic determinants. The former are mostly biological risk factors with a direct aetiological impact on child mortality. Of the five categories of proximate determinants identified by Mosley and Chen, the one covering maternal factors—such as the mother’s age at birth and birth interval—has been confirmed quite extensively in the literature as of primary importance (see, e.g., Bhargava 2003; Curtis, Diamond, and McDonald 1993; Folasada 2000; Manda 1999; Ronsmans 1996; Sastry 1997b).

In the Mosley and Chen framework, socioeconomic factors affect child health and survival through the proximate determinants. In the absence of data that perfectly capture all proximate determinants, socioeconomic factors should explain some of the residual variation in child survival. Mosley and Chen distinguished between socioeconomic determinants at the individual, household, and community levels. At the individual level, maternal education has been considered an important determinant of child mortality since the work of Caldwell (1979), and this has subsequently been reaffirmed (see, e.g., Cleland and van Ginneken 1988; Hobcraft 1993). Education may affect child survival chances through knowledge of health production (Grossman 1972) but also through the empowerment of women within the household and the consequent priority given to child health in household resource allocation (Caldwell 1979; Hobcraft 1993).

At the household level, income and wealth can raise survival chances through the purchase of food, medicines, and access to health care, but may also operate through exposure to environmental contamination, which Mosley and Chen identified as one of the five proximate determinants of mortality. The health effects of such environmental determinants were highlighted in the World Health Organization’s 2002 World Health Report (World Health Organization 2002), which showed that unsafe water, poor sanitation, and hygiene are the cause of 4%–8% of the overall burden of diseases in developing countries and nine-tenths of diarrheal diseases, which is a major contributor to infant mortality. There is also evidence of a strong association between sanitation and child survival (Esrey et al. 1991; Hertz, Herbert, and Landon 1994). Of course, these environmental effects are determined not only at the household level but also at the community level through the extent and quality of the public hygiene infrastructure to which a household with sufficient means can connect.

At the community level, Mosley and Chen discussed factors related to the ecological setting, political economy, and health system. However, because community-level data are seldom available, few empirical studies have assessed the relative roles of these factors (Sastry 1996). To the extent that community-level determinants are important, there should be cross-community variation in the prevalence of infant mortality, which, in the absence of sufficient data on relevant community characteristics, could be captured in a model by community-specific intercepts.

Socioeconomic determinants also include traditions, social norms, and attitudes that may operate through the social status of women, health-related behavior, and child-rearing practices. For example, a tradition of dowry payment may result in differential investments in the health of boys and girls (Rosenzweig and Schultz 1982; Tambiah et al. 1989). Traditions and social norms are largely determined at the community level, but conformity with them varies across households. To a large extent, norms and conformity are not observable and are a potentially important source of unobservable heterogeneity at both the community and household levels. However, some individual- and household-level characteristics, such as the mother’s age at first marriage and use of contraception, can proxy for attitudes that may influence behavior related to child health.

In Table 1, we present the individual, household, and community characteristics categorized according to the Mosley and Chen framework that we use to explain rural-urban differences in infant mortality. The precise variables are described in the next section. This empirical specification is largely consistent with many other studies of the determinants of infant mortality (see, e.g., Bhargava 2003; Boldstad and Manda 2001; Curtis et al. 1993; Folasada 2000; Lalou and LeGrand 1997; Manda 1999; Ronsmans 1996). The reasons for not including variables such as immunization and food intake (breast-feeding) are twofold. First, these data are available only for children born in the five years preceding the survey, which would drastically reduce sample size and impede the estimation of household-level heterogeneity. Second (and perhaps most importantly), there is an endogeneity problem with using immunization and breast-feeding because these are also determined by survival.

Table 1.

Covariate Definitions and Their Classifications According to the Mosley and Chen (1984) Framework

Mosley and Chen Category	Variable	Definition
Proximate Determinants
Maternal factors	Firstborn	1 if child is mother’s firstborn, 0 otherwise
	Birth order > 4	1 if child’s birth order is higher than four, 0 otherwise
	Mother’s age at birth	3 categories: ≤ 20, 21–35 (reference), > 35
	Short birth interval	1 if less than 24 months after preceding birth, 0 otherwise
Socioeconomic Determinants
Education	Mother did not complete primary education	1 if mother has not completed primary education, 0 otherwise
Traditions/social norms/attitudes	Contraception	1 if mother has ever used modern contraception, 0 otherwise
	Mother’s age 1st marriage	Mother’s age at her first marriage (in years)
	Male child	1 if child is male, 0 otherwise
	Age of household head	Age in years
	Male household head	1 if head is male, 0 otherwise
Environmental	Toilet	1 if household has any toilet facility, 0 otherwise
	Water	1 if water coming from tap, protected well, bottle, or vendor, 0 otherwise
	Electricity	1 if household has electricity, 0 otherwise
	No finished floor	1 if household has no finished floor (sand or mud), 0 otherwise
Economic status	Assets index	3 categories: poorest third, middle third, richest third (reference)
Community Determinants
Service and infrastructure	Health facilities	1 if health facility is within community, 0 otherwise
	Public transportation	1 if community is connected by some form of public transportation, 0 otherwise

The model estimated also incorporates unobservable heterogeneity at both the household and community levels to allow for the effects of correlated proximate and socioeconomic determinants that are not observable in the data.

DATA

Infant Mortality

The most recent round of the Demographic Health Surveys (DHS) of sub-Saharan African countries includes a survey on community characteristics in six countries: Benin (2001), Central African Republic (CAR; 1995), Chad (2004), Guinea (1999), Mali (2001), and Niger (1998).2 Children born 1–10 years before the survey are included in the sample. The first two rows of Table 2 show estimates of the urban/rural infant mortality rates (expressed as the proportion of all live-born children that die before reaching age 1) and the urban/rural population proportions.

Table 2.

Infant Mortality Rates and Means of Covariates Split by Urban/Rural Areas

Variable	Pooled		Benin		CAR		Chad		Guinea		Mali		Niger
	Urban	Rural	Urban	Rural	Urban	Rural	Urban	Rural	Urban	Rural	Urban	Rural	Urban	Rural
Infant Mortality	0.0959	0.1414	0.0780	0.1122	0.0781	0.1075	0.1037	0.1239	0.0901	0.1393	0.1232	0.1588	0.0936	0.1604
% of Population	21.67	78.33	28.87	71.13	38.03	61.97	18.06	81.94	23.67	76.33	20.32	79.68	15.15	84.85
Proximate Determinants
Firstborn	0.21	0.18	0.26	0.19	0.22	0.21	0.21	0.19	0.22	0.18	0.20	0.16	0.19	0.17
Birth order > 4	0.32	0.38	0.28	0.35	0.30	0.29	0.35	0.36	0.28	0.35	0.35	0.41	0.38	0.41
Mother’s age at birth ≤ 20	0.22	0.22	0.15	0.18	0.25	0.21	0.25	0.25	0.22	0.22	0.22	0.22	0.21	0.25
Mother’s age at birth 21–35	0.70	0.67	0.74	0.71	0.69	0.71	0.68	0.66	0.69	0.68	0.69	0.66	0.73	0.67
Mother’s age at birth > 35	0.08	0.10	0.11	0.11	0.06	0.08	0.07	0.08	0.09	0.10	0.09	0.12	0.06	0.08
Short birth interval	0.21	0.25	0.14	0.19	0.22	0.28	0.27	0.27	0.16	0.19	0.23	0.28	0.23	0.25
Socioeconomic Determinants
Mother did not complete primary education	0.81	0.97	0.82	0.97	0.74	0.95	0.81	0.99	0.80	0.97	0.84	0.98	0.77	0.96
Contraception	0.31	0.11	0.30	0.18	0.26	0.06	0.14	0.03	0.22	0.07	0.41	0.18	0.43	0.08
Mother’s age at first marriage	16.78	15.98	18.71	17.50	16.33	16.90	15.76	15.70	16.90	15.98	16.71	16.14	15.73	14.68
Male child	0.51	0.51	0.50	0.50	0.50	0.51	0.52	0.51	0.52	0.51	0.52	0.50	0.51	0.51
Age of household head	42.74	42.61	41.59	42.75	40.40	38.32	42.78	39.59	46.39	46.96	42.32	42.85	43.39	42.77
Male household head	0.87	0.92	0.85	0.91	0.83	0.92	0.85	0.90	0.85	0.93	0.91	0.93	0.94	0.93
Toilet	0.85	0.40	0.52	0.12	0.95	0.61	0.81	0.14	0.94	0.50	0.98	0.72	0.78	0.06
Water	0.71	0.26	0.65	0.33	0.85	0.45	0.70	0.31	0.57	0.05	0.66	0.34	0.92	0.12
Electricity	0.31	0.02	0.41	0.04	0.09	0.01	0.18	0.00	0.48	0.02	0.32	0.02	0.33	0.00
No finished floor	0.41	0.88	0.25	0.56	0.67	0.94	0.79	0.99	0.10	0.75	0.42	0.94	0.32	0.97
Poorest third	0.16	0.34	0.19	0.33	0.18	0.30	0.12	0.43	0.19	0.36	0.13	0.29	0.17	0.35
Middle third	0.26	0.36	0.32	0.36	0.31	0.33	0.28	0.38	0.24	0.36	0.23	0.36	0.26	0.37
Richest third	0.58	0.30	0.49	0.31	0.51	0.37	0.61	0.19	0.57	0.28	0.64	0.35	0.58	0.28
Community Determinants
Health facilities	0.71	0.23	0.57	0.35	0.57	0.18	0.77	0.11	0.53	0.28	0.91	0.28	0.74	0.12
Public transportation	0.55	0.27	0.36	0.16	0.60	0.50	0.53	0.09	0.12	0.23	0.70	0.20	0.97	0.58
Number of Observations	16,396	46,077	2,204	5,920	2,039	3,397	3,728	5,010	2,410	6,993	3,535	16,641	2,480	8,116

Source: Authors’ calculations based on Demographic and Health Surveys, Benin (2001), CAR(1995), Chad (2004), Guinea (1999), Mali (2001), and Niger (1998).

Note: Rates in boldface type indicate a significant difference between the urban and rural models at the 10% level. Infant mortality rates are the proportion of infant deaths per 100 live births. Sample weights are applied, and in the pooled estimates, observations are further weighted to take account of the different population sizes of countries.

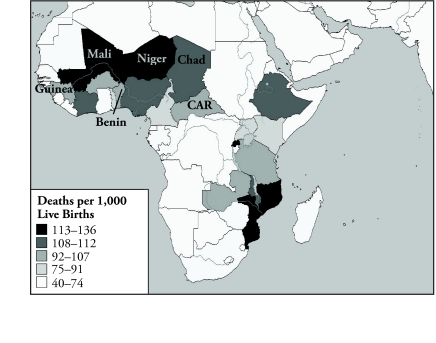
In the DHS, localities are defined as urban or rural on the same basis as in the respective country census, which is predominantly according to population size.3 Although this may result in some rather crude designations, the figures presented in Table 2 confirm significant and large differences in the characteristics of urban and rural areas. Use of the census definitions of urban-rural will generate some cross-country inconsistency in the classifications, but given the geographic proximity of the countries and the similarity of their institutions inherited from a common colonial history, this is likely to be limited. In any case, in addition to the pooled cross-country analysis presented later, all results have been produced separately for each country, and they show a high degree of consistency. In all countries, the great majority of the population—a little less than four-fifths, on average—is located in rural areas and suffers from significantly higher infant mortality than the urban population. The rural-urban gap is by far the largest in Niger. As can be seen from Figure 1, even relative to the rest of sub-Saharan Africa, infant mortality rates are high in the countries included in this study.

Figure 1.

Infant Mortality in Study Countries Compared With Others in Sub-Saharan Africa

Note: For countries in the lightest shade, no data were available.

Source: Demographic and Health Survey StatMapper.

Preliminary analysis of the data revealed clear evidence of clustering of deaths within households. For example, in urban areas, 4% of households with more than one death account for 40% of all deaths. In rural areas, 48% of deaths are concentrated in the 7% of households with more than one death. This clustering indicates the presence of household-specific, correlated risk factors and suggests that it may be important to allow for household-level heterogeneity in modeling infant mortality.

The primary sampling unit (PSU) in the DHS is the community. Generally, a rural community spans one village or settlement, whereas an urban community is a part of a town or city. The average number of children per community is considerably larger within rural than within urban areas (57 versus 33, respectively), reflecting both the larger number of women interviewed within rural PSUs (30–40, rather than 20–25) and the slightly larger household sizes in rural areas. Within urban areas, 7% of deaths occur in the 1% of communities with 10 or more deaths; comparatively, within rural areas, 49% of deaths are concentrated in the 22% of communities with 10 or more deaths. These numbers suggest that although there is clustering of infant deaths within communities, deriving from correlated risk factors at this level, the degree of concentration is less pronounced than that within households, and is even less so within urban areas.

Explanatory Variables

With respect to the proximate determinants, the DHS, like many other nationally representative data sets, provide only direct measures of what Mosley and Chen (1984) referred to as “maternal factors.” We include mother’s age at birth, birth order, and an indicator of a short birth interval (< 24 months). The effect of birth order is captured by a dummy variable for first-born children and another for children with a birth order higher than four (Rutstein 2000; Sastry 1997b).

Maternal education is represented by a dummy variable indicating no or incomplete primary education. We further control for the social status and empowerment of the mother through her age at first marriage (Bhargava 2003; Folasada 2000), the sex of the household head (Canagarajah 2001; Lloyd and Blanc 1996), and the mother’s use of contraception (Birdsall and Chester 1987). Attitudes, traditions, and social norms that may affect investments in child health are further proxied by the sex of the child (to allow for the effect of discriminatory traditions) and the age of the head of household. Molbak et al. (1997) found that children in households with a younger head are associated with higher prevalence of diarrhea, which is a major contributor to infant mortality.

Exposure to environmental contamination is proxied by a dummy variable for household access to water from a safe source and another for availability of a toilet (see Table 1 for definitions) (Victora et al. 2005). Further, we include information on the floor material of the household dwelling and whether the household has an electricity supply (Smith, Ruel, and Ndiaye 2005). Housing materials may act as a proxy for the quality of housing, exposure to vermin, and overcrowding, all of which raise the risk of respiratory disease. Electricity facilitates more hygienic preparation of food, as well as sterilization. Although these indicators of environmental conditions are defined at the household level, they are clearly not independent from community-level infrastructure (Sastry 1996). In fact, the between-community variation in source of water and in electricity supply is larger than the within-community variation, though the latter is still considerable. In communities where at least one household has safe water or electricity, only one-half or one-third of all households, respectively, have a supply. On the other hand, when at least one household does not have a safe source of water or electricity, more than two-thirds or nine-tenths, respectively, of all households in the community are without a supply. Community-level investments in infrastructure are necessary but not sufficient for households to have a safe supply of water or an electricity supply. Constraints and preferences at the household level also seem to be important.

To obtain a proxy for wealth—beyond that indicated by access to drinking water, sanitation, electricity, and housing materials—we construct an index by using principal components analysis on possession of assets, such as a car, motor, bicycle, radio, television, and refrigerator (Filmer and Pritchett 2001; Hong 2006). The first principal component is used to divide households into the poorest, middle, and richest thirds.4

At the community level, we approximate the availability of health care services and public transport with dummy variables to indicate the presence of a health facility and any public transport, respectively.5 Brenneman (2002) found evidence reported in various studies that better transportation contributes to easier access to health care as well as easier staffing and operation of clinics. Moreover, improved transportation policy can reduce air pollution in urban areas and increase the supply of food in rural ones.

Table 2 shows the means of all covariates across urban and rural areas. Children born in rural areas are at a disadvantage across virtually all health determinants. This is true for the pooled cross-country sample as well as within each country.6

Although the data allow us to measure many of the important determinants of infant mortality, one might expect to observe considerable variation in survival chances across households and communities that is not captured by these covariates. In the next section, we present a model of infant mortality that allows for household- and community-level effects, and then we show how the contribution of these effects to the rural-urban gap, as well as those of the observable factors, can be quantified.

METHODS

Three-Level, Random Intercept Probit Model

We model the probability of infant mortality using a three-level probit model with random intercepts representing unobservable heterogeneity at both the household and the community level (Gibbons and Hedeker 1997). Compared with a standard probit, this model has the advantage of estimating the correlation in survival probabilities among children belonging to the same family and that among those residing in the same community that persists after controlling for observed characteristics (Bolstad and Manda 2001; Sastry 1997a). Failure to account for this unobserved heterogeneity would lead to inconsistent coefficients.7 An important assumption of any random-effects model is that the unobservable components at each level are uncorrelated with the observable covariates. This can be overly restrictive. For example, it rules out the possibility that high birth order and short birth interval reflect previous infant deaths resulting from the same unobservable factors that condition the survival chances of all children in a household (Bhargava 2003). To allow for correlation between unobserved heterogeneity and observable characteristics, while still identifying the contribution of the latter, we adopt the Mundlak-Chamberlain approach (Mundlak 1978; Chamberlain 1980) of parameterizing the unobservable effects as functions of the means of the regressors at the next lowest level. The three-level, random component probit model can then be written as

$$\begin{array}{l}{y}_{ihc}=1 \text{if} y_{ihc}^{*}>0\\ y_{ihc}^{*}={\mathbf{\text{x}}}_{ihc}\beta +{\alpha }_{hc}+{\alpha }_c+{\epsilon }_{ihc}\end{array}$$ (1)

with

$$\begin{array}{l}{\alpha }_{hc}={\overline{\mathbf{\text{x}}}}_{hc}\delta +{\eta }_{hc}\\ {\alpha }_c={\overline{\mathbf{\text{x}}}}_c\gamma +{\eta }_c\end{array}$$

where $y_{ihc}^{*}$ is a latent index, the sign of which determines observation of an infant death (y_ihc = 1); and the indices i, h, and c refer to infants, households, and communities, respectively. To simplify the notation, we use x_ihc to represent the entire vector of covariates, but covariates can vary on child, household, or community level. The unobservable household (α_hc) and community-level intercepts (α_c) are assumed to be a function of the within-household means of the child-level covariates (x̄_hc) and the within-community means of the household-level covariates (x̄_c), respectively. Conditional on these means, the residual unobservable heterogeneity at each level (η_hc and η_c) is assumed to be independent of the covariates. This exogeneity assumption is weaker than that in the standard three-level, random-effects probit model because the within-household means, for example, should absorb the effects of unobservable factors that affect both infant mortality and covariates across all individuals within the same household. The within-community means serve a similar purpose in absorbing effects common to infant mortality and covariates across all households in the same community.

The idiosyncratic error term (ε_ihc) is assumed to follow a standard normal distribution. The random components at each level are assumed to be multivariate normal, mutually independent, and independent of the idiosyncratic error (ε_ihc). The assumption of multivariate normality is standard in multilevel models.

The likelihood of the model can be written as

$$\prod _{c=1}^n\int \left\{\prod _{h=1}^{n_c}\int f(y_{ihc}|{\mathbf{\text{x}}}_{ihc},{\overline{\mathbf{\text{x}}}}_{hc},{\overline{\mathbf{\text{x}}}}_c,{\eta }_{hc},{\eta }_c)\phi ({\eta }_{hc}|{\mathbf{\text{x}}}_{ihc},{\overline{\mathbf{\text{x}}}}_{hc},{\overline{\mathbf{\text{x}}}}_c)d{\eta }_{hc}\right\}\phi ({\eta }_c|{\mathbf{\text{x}}}_{ihc},{\overline{\mathbf{\text{x}}}}_{hc},{\overline{\mathbf{\text{x}}}}_c)d{\eta }_c,$$ (2)

where

$$\begin{array}{ll}f(y_{ihc}|{\mathbf{\text{x}}}_{ihc},{\overline{\mathbf{\text{x}}}}_{hc},{\overline{\mathbf{\text{x}}}}_c,{\eta }_{hc},{\eta }_c)& =\prod _{i=1}^{n_{hc}}\Phi {(x_{ihc}\beta +{\overline{\mathbf{\text{x}}}}_{hc}\delta +{\overline{\mathbf{\text{x}}}}_c\gamma +{\eta }_{hc}+{\eta }_c)}^{y_{ihc}}\\ & \times (1-\Phi {({\mathbf{\text{x}}}_{ihc}\beta +{\overline{\mathbf{\text{x}}}}_{hc}\delta +{\overline{\mathbf{\text{x}}}}_c\gamma +{\eta }_{hc}+{\eta }_c))}^{1-y_{ihc}}\end{array}$$

is the joint density of the dependent variable for all infants within a given household, conditional on the household and community effects as well as the observable explanatory variables and their within-household and within-community means. Φ() is the normal cumulative density function, φ() represents the normal density function of the random disturbances with variances standardized to unity, n indicates the number of communities, n_c denotes the number of households within any given community, and n_hc is the number of infants within a given household.

The posterior (conditional) density function of the random components can be calculated by using Bayes’ Theorem. For the household component, this gives

$$\begin{array}{ll}p({\eta }_{hc}|y_{ihc},{\mathbf{\text{x}}}_{ihc},{\eta }_c)& =\frac{f(y_{ihc}|{\mathbf{\text{x}}}_{ihc},{\overline{\mathbf{\text{x}}}}_{hc},{\overline{\mathbf{\text{x}}}}_c,{\eta }_{hc},{\eta }_c)\phi ({\eta }_{hc})}{f(y_{ihc}|{\mathbf{\text{x}}}_{ihc},{\overline{\mathbf{\text{x}}}}_{hc},{\overline{\mathbf{\text{x}}}}_c,{\eta }_c)}\\ & =\frac{f(y_{ihc}|{\mathbf{\text{x}}}_{ihc},{\overline{\mathbf{\text{x}}}}_{hc},{\overline{\mathbf{\text{x}}}}_c,{\eta }_{hc},{\eta }_c)\phi ({\eta }_{hc})}{\int f(y_{ihc}|{\mathbf{\text{x}}}_{ihc},{\overline{\mathbf{\text{x}}}}_{hc},{\overline{\mathbf{\text{x}}}}_c,{\eta }_{hc},{\eta }_c)\phi ({\eta }_{hc})d{\eta }_{hc}},\end{array}$$ (3)

where p() denotes the posterior density. Because of the assumed independence between the household- and community-level random components and of each with the covariates, φ(η_hc |x_ihc,x̄_hc,x̄_c,η_c) = φ(η_hc), and the marginal distribution of η_c appears in both the numerator and denominator and so cancels out. Following from this, the posterior means of the random household components are given by

$${\widehat{\eta }}_{hc}=\frac{\int {\eta }_{hc}f(y_{ihc}|{\mathbf{\text{x}}}_{ihc},{\overline{\mathbf{\text{x}}}}_{hc},{\overline{\mathbf{\text{x}}}}_c,{\eta }_{hc},{\eta }_c)\phi ({\eta }_{hc})d{\eta }_{hc}}{\int f(y_{ihc}|{\mathbf{\text{x}}}_{ihc},{\overline{\mathbf{\text{x}}}}_{hc},{\overline{\mathbf{\text{x}}}}_c,{\eta }_{hc},{\eta }_c)\phi ({\eta }_{hc})d{\eta }_{hc}}.$$ (4)

Similarly, the posterior means of the community component are given by

$${\widehat{\eta }}_c=\frac{\int {\eta }_c\left\{\prod _{h=1}^{n_c}\int f(y_{ihc}|{\mathbf{\text{x}}}_{ihc},{\overline{\mathbf{\text{x}}}}_{hc},{\overline{\mathbf{\text{x}}}}_c,{\eta }_{hc},{\eta }_c)\phi ({\eta }_{hc})d{\eta }_{hc}\right\}\phi ({\eta }_c)d{\eta }_c}{\int \left\{\prod _{h=1}^{n_c}\int f(y_{ihc}|{\mathbf{\text{x}}}_{ihc},{\overline{\mathbf{\text{x}}}}_{hc},{\overline{\mathbf{\text{x}}}}_c,{\eta }_{hc},{\eta }_c)\phi ({\eta }_{hc})d{\eta }_{hc}\right\}\phi ({\eta }_c)d{\eta }_c}.$$ (5)

The likelihood is maximized and the posterior means of the random components are computed by adaptive quadrature, using the GLLAMM program in Stata (Rabe-Hesketh, Skrondal, and Pickles 2002, 2005).

Decomposition

Rural-urban disparity in infant mortality rates can arise from differences in: (a) the distributions of observable determinants of infant mortality; (b) the effects of those determinants; and (c) the distributions of unobservable determinants. A Blinder-Oaxaca–type decomposition can be used to quantify the relative importance of these three explanations (Blinder 1973; Oaxaca 1973). In a standard decomposition, the difference in the mean effects of unobservable factors is reflected in the difference in the intercepts of urban- and rural-specific regressions. However, these intercept differences are not particularly helpful in pinpointing the source of rural-urban disparities in infant mortality because they provide no information on the level at which unobservable factors operate. We provide a more detailed explanation of the rural-urban disparity by quantifying the contribution of unobservable determinants of infant mortality at both the household and community levels. This is achieved by extending the nonlinear decomposition of the group difference in a binary indicator proposed by Fairlie (2005) to a three-level, random intercept probit model.

The rural-urban gap in average infant mortality can be decomposed as follows:

$$\begin{array}{ll}{\overline{Y}}^r-{\overline{Y}}^u& =\left[\sum _{i=1}^{N^r}\frac{\Phi ({\mathbf{\text{x}}}_{ihc}^r\stackrel{⌢}{\beta }+{\overline{\mathbf{\text{x}}}}_{hc}^r\stackrel{⌢}{\delta }+{\overline{\mathbf{\text{x}}}}_c^r\stackrel{⌢}{\gamma }+{\stackrel{⌢}{\eta }}_{hc}^r+{\stackrel{⌢}{\eta }}_c^r)}{N^r}-\sum _{i=1}^{N^u}\frac{\Phi ({\mathbf{\text{x}}}_{ihc}^u\stackrel{⌢}{\beta }+{\overline{\mathbf{\text{x}}}}_{hc}^u\stackrel{⌢}{\delta }+{\overline{\mathbf{\text{x}}}}_c^u\stackrel{⌢}{\gamma }+{\stackrel{⌢}{\eta }}_{hc}^u+{\stackrel{⌢}{\eta }}_c^u)}{N^u}\right]\\ & +\left[\sum _{i=1}^{N^u}\frac{\Phi ({\mathbf{\text{x}}}_{ihc}^u{\stackrel{⌢}{\beta }}^r+{\overline{\mathbf{\text{x}}}}_{hc}^u{\stackrel{⌢}{\delta }}^r+{\overline{\mathbf{\text{x}}}}_c^u{\stackrel{⌢}{\gamma }}^r+{\stackrel{⌢}{\eta }}_{hc}^u+{\stackrel{⌢}{\eta }}_c^u)}{N^u}-\sum _{i=1}^{N^u}\frac{\Phi ({\mathbf{\text{x}}}_{ihc}^u{\stackrel{⌢}{\beta }}^u+{\overline{\mathbf{\text{x}}}}_{hc}^u{\stackrel{⌢}{\delta }}^u+{\overline{\mathbf{\text{x}}}}_c^u{\stackrel{⌢}{\gamma }}^u+{\eta }_{hc}^u+{\eta }_c^u)}{N^u}\right],\end{array}$$ (6)

where superscripts r and u indicate values of covariates/estimates obtained from the rural and urban samples of children respectively, N^r and N^u indicate the number of infants located in rural and urban areas respectively, $\stackrel{⌢}{\beta }$ refer to the coefficients from the pooled (urban and rural) model, and ${\stackrel{⌢}{\eta }}_j^k$ j = hc,c and k = r,u are the household- and community-specific posterior means of the random disturbances that are estimated from Eqs. (4) and (5). The term in the first set of brackets represents the part of the rural-urban gap that is due to differences in the distributions of the observable determinants of infant mortality as well as the differences in the unobservable household- and community-level determinants. The term in the second brackets gives the gap due to differences in the effects of the observable determinants.8 The coefficients from the pooled (urban and rural) model are used to weight the differences in the x’s in the first term, and the urban distribution of x’s is used to weight differences in the coefficients in the second term.9

The gap can then be decomposed further into the contributions of each covariate, both through its distribution and its effect. However, we will focus on the contributions of differences in the distributions of covariates and random household and community effects because, as will become apparent, differences in coefficients contribute only marginally to explanation of the rural-urban gap in infant mortality. To illustrate how the contributions of differences in the distributions of particular covariates are identified, consider a simple case in which infant mortality is explained by two determinants: x₁ and x₂, and N^r = N^u. The contribution of the difference in the distributions of x₁ to the rural-urban gap is then equal to (Fairlie 2005):

$$\begin{array}{l}\frac{1}{N^r}{\sum }_{i=1}^{N^r}\Phi ({\stackrel{⌢}{\beta }}_0+x_{1ihc}^r{\stackrel{⌢}{\beta }}_1+x_{2ihc}^r{\stackrel{⌢}{\beta }}_2+{\overline{\mathbf{\text{x}}}}_{hc}^r\stackrel{⌢}{\delta }+{\overline{\mathbf{\text{x}}}}_c^r\stackrel{⌢}{\gamma }+{\stackrel{⌢}{\eta }}_{hc}^r+{\stackrel{⌢}{\eta }}_c^r)\\ -\Phi ({\stackrel{⌢}{\beta }}_0+x_{1ihc}^u{\stackrel{⌢}{\beta }}_1+x_{2ihc}^r{\stackrel{⌢}{\beta }}_2+{\overline{\mathbf{\text{x}}}}_{hc}^r\stackrel{⌢}{\delta }+{\overline{\mathbf{\text{x}}}}_{hc}^r\stackrel{⌢}{\gamma }+{\stackrel{⌢}{\eta }}_{hc}^r+{\stackrel{⌢}{\eta }}_c^r).\end{array}$$ (7)

Similarly, the contribution of x₂ can be expressed as

$$\begin{array}{l}\frac{1}{N^r}{\sum }_{i=1}^{N^r}\Phi ({\stackrel{⌢}{\beta }}_0+x_{1ihc}^u{\stackrel{⌢}{\beta }}_1+x_{2ihc}^r{\stackrel{⌢}{\beta }}_2+{\overline{\mathbf{\text{x}}}}_{hc}^r\stackrel{⌢}{\delta }+{\overline{\mathbf{\text{x}}}}_c^r\stackrel{⌢}{\gamma }+{\stackrel{⌢}{\eta }}_{hc}^r+{\stackrel{⌢}{\eta }}_c^r)\\ -\Phi ({\stackrel{⌢}{\beta }}_0+x_{1ihc}^u{\stackrel{⌢}{\beta }}_1+x_{2ihc}^u{\stackrel{⌢}{\beta }}_2+{\overline{\mathbf{\text{x}}}}_{hc}^r\stackrel{⌢}{\delta }+{\overline{\mathbf{\text{x}}}}_c^r\stackrel{⌢}{\gamma }+{\stackrel{⌢}{\eta }}_{hc}^r+{\stackrel{⌢}{\eta }}_c^r).\end{array}$$ (8)

Basically, the contribution of each variable to the gap equals the change in the average predicted probability of dying from replacing the rural distribution with the urban distribution of that variable while holding the distributions of the other variables constant.10

To quantify the contribution of the difference between rural and urban areas in the means of the unobservable household-level heterogeneity, we have to take into account that according to specification (1), this heterogeneity is a function of the means of the child-level covariates x̄_hc. It can be estimated by11

$$\begin{array}{l}\frac{1}{N^r}{\sum }_{i=1}^{N^r}\Phi ({\stackrel{⌢}{\beta }}_0+x_{1ihc}^u{\stackrel{⌢}{\beta }}_1+x_{2ihc}^u{\stackrel{⌢}{\beta }}_2+{\overline{\mathbf{\text{x}}}}_{hc}^r\stackrel{⌢}{\delta }+{\overline{\mathbf{\text{x}}}}_c^r\stackrel{⌢}{\gamma }+{\stackrel{⌢}{\eta }}_{hc}^r+{\stackrel{⌢}{\eta }}_c^r)\\ -\Phi ({\stackrel{⌢}{\beta }}_0+x_{1ihc}^u{\stackrel{⌢}{\beta }}_1+x_{2ihc}^u{\stackrel{⌢}{\beta }}_2+{\overline{\mathbf{\text{x}}}}_{hc}^u\stackrel{⌢}{\delta }+{\overline{\mathbf{\text{x}}}}_c^r\stackrel{⌢}{\gamma }+{\stackrel{⌢}{\eta }}_{hc}^u+{\stackrel{⌢}{\eta }}_c^r).\end{array}$$ (9)

This contribution depends both on rural-urban differences in the means of random household-level determinants ( ${\widehat{\eta }}_{hc}^r-{\widehat{\eta }}_{hc}^u$) and on differences in determinants at this level that are correlated with the covariates ( ${\overline{\mathbf{\text{x}}}}_{hc}^r\widehat{\delta }-{\overline{\mathbf{\text{x}}}}_{hc}^u\widehat{\delta }$). Finally, the contribution of the difference in community-level heterogeneity is estimated in a similar way by

$$\begin{array}{l}\frac{1}{N^r}{\sum }_{i=1}^{N^r}\Phi ({\stackrel{⌢}{\beta }}_0+x_{1ihc}^u{\stackrel{⌢}{\beta }}_1+x_{2ihc}^u{\stackrel{⌢}{\beta }}_2+{\overline{\mathbf{\text{x}}}}_{hc}^u\stackrel{⌢}{\delta }+{\overline{\mathbf{\text{x}}}}_c^r\stackrel{⌢}{\gamma }+{\stackrel{⌢}{\eta }}_{hc}^u+{\stackrel{⌢}{\eta }}_c^r)\\ -\Phi ({\stackrel{⌢}{\beta }}_0+x_{1ihc}^u{\stackrel{⌢}{\beta }}_1+x_{2ihc}^u{\stackrel{⌢}{\beta }}_2+{\overline{\mathbf{\text{x}}}}_{hc}^u\stackrel{⌢}{\delta }+{\overline{\mathbf{\text{x}}}}_c^u\stackrel{⌢}{\gamma }+{\stackrel{⌢}{\eta }}_{hc}^u+{\stackrel{⌢}{\eta }}_c^u).\end{array}$$ (10)

Because in our case, the urban sample is smaller than the rural, a random rural subsample is drawn and matched with the urban sample on the basis of predicted probabilities of dying (Fairlie 2005).12 Because the results depend on the specific subsample that is drawn, the process is repeated 100 times, and average results are reported.13

Regression estimates as well as the random drawing of the rural sub-sample take into account the sample weights that come with DHS data. Although the analysis has been conducted for each country separately, here we present results only from a pooled analysis across countries. In this, weights are adjusted for differences in population size (World Bank 2006) such that countries with larger populations have relatively more influence, and the results can be interpreted as being representative for the region.14

RESULTS

Regression Results

The first column of Table 3 shows regression coefficients estimated from the pooled cross-country sample of the Mundlak-Chamberlain specification (1). The second and third columns show similar coefficients for the urban and rural subsamples. Because the dependent variable indicates whether the child died within its first year, a positive coefficient indicates an increased risk of death. All coefficients have intuitive signs. We find that all proximate determinants are very strongly related to infants’ survival. Firstborn children have a higher probability of dying within their first year, and the opposite holds for children of a higher birth order (above four). The latter finding contradicts earlier results of, for example, Sastry (1997a) and Rutstein (2000), and appears to be attributable to taking account of correlated, unobservable household-level heterogeneity, which we will return to shortly. Children born to women younger than age 20 have worse survival chances than those born to women between ages 20 and 35. A short interval between succeeding births is correlated with an increased likelihood of infant death.

Table 3.

Coefficients of Probit Models With Random Household and Community Effects

Variables	Model (1)			Without Community Means
	Pooled	Urban	Rural	Pooled	Urban	Rural
Firstborn	0.222**	0.152**	0.239**	0.222**	0.154**	0.222**
Birth Order > 4	−0.049†	−0.025	−0.054†	−0.049†	−0.025	−0.049†
Mother’s Age at Birth ≤ 20	0.116**	0.125*	0.114**	0.116**	0.124*	0.116**
Mother’s Age at Birth > 35	−0.018	0.026	−0.027	−0.018	0.027	−0.017
Short Birth Interval	0.0975**	0.086*	0.100**	0.098**	0.086*	0.098**
Mother Did Not Complete Primary Education	0.1267**	0.059	0.167*	0.117**	0.059	0.117**
Contraception	−0.124**	−0.148**	−0.112**	−0.122**	−0.152**	−0.122**
Mother’s Age at First Marriage	0.0038	−0.000	0.005	0.004	0.002	0.004
Male Child	0.079**	0.057†	0.085**	0.079**	0.055†	0.079**
Age of Household Head	0.001	0.001	0.001	0.001†	0.001	0.001†
Male Household Head	0.047	−0.013	0.075†	0.057†	−0.029	0.058†
Toilet	−0.028	−0.024	−0.026	−0.017	0.098†	−0.017
Water	−0.081**	−0.124*	−0.069*	−0.085**	−0.096*	−0.085**
Electricity	−0.109*	−0.021	−0.171†	−0.130**	−0.036	−0.131**
No Finished Floor	0.030	0.128*	−0.023	0.066*	0.128**	0.066*
Poorest Third	0.000	0.107*	−0.022	0.019	0.119*	0.019
Middle Third	0.001	0.052	−0.016	0.0120	0.095*	0.012
Health Facilities	− 0.042†	−0.109**	−0.033	−0.048*	−0.098**	−0.048*
Public Transportation	−0.020	0.027	−0.044	−0.023	0.026	−0.023
Benin	0.168**	0.246*	0.134*	0.122**	0.172*	0.122**
Chad	0.036	0.162*	−0.023	0.025	0.112†	0.025
Guinea	0.243**	0.238**	0.231**	0.221**	0.206**	0.221**
Mali	0.270**	0.345**	0.248**	0.275**	0.324**	0.275**
Niger	0.221**	0.247**	0.204**	0.202**	0.177**	0.202**
Household Means
Birth order > 4	0.236**	0.220**	0.239**	0.235**	0.220*	0.235**
Mother’s age at birth < 20	0.236**	0.197*	0.244**	0.236**	0.198*	0.236**
Mother’s age at birth > 35	−0.069	0.008	−0.088	−0.068	0.006	−0.068
Short birth interval	0.990**	0.946**	0.997**	0.991**	0.951**	0.991**
Community Means
Poorest third	0.143*	0.060	0.183*
Middle third	0.082	0.257*	0.033
No finished floor	0.125*	0.016	0.161†
Mother did not complete primary education	−0.098	0.019	−0.132
Contraception	0.047	0.009	0.132
Mother’s age at first marriage	0.001	0.017	−0.001
Age of household head	0.001	0.000	0.000
Sex of household head	0.066	−0.056	0.135
Toilet	0.058	0.314**	0.008
Water	0.005	0.064	−0.007
Electricity	−0.008	−0.059	−0.108
Constant	−2.413**	−2.656**	−2.443**	−2.216**	−2.136**	−2.216**
Variance of Household Effect	0.221**	0.088**	0.249**	0.222**	0.091**	0.222**
Variance of Community Effect	0.020**	0.000	0.023**	0.021**	0.000	0.021**
Joint Test Household Means (p value)	0.000	0.0000	0.000	0.000	0.000	0.000
Joint Test Community Means (p value)	0.324	0.0805	0.197

Notes: The dependent variable is 1 if the child died before his or her first birthday. The analysis is based on data pooled across all countries and split by urban/rural areas. Coefficients in boldface type indicate a significant difference between the urban and rural models at the 10% level.

^†p < .10;

^*p < .05;

^**p < .01

Regarding the socioeconomic determinants, we find that maternal primary education reduces the risk of infant mortality. The point estimate is larger in rural areas, but the difference between urban and rural areas is not significant. Among the proxies for traditions, social norms, and attitudes, only familiarity with contraception and the sex of the child are significantly correlated with infant mortality. Children of women who have ever used contraception are more likely to survive, as are girls.

Environmental conditions—in particular, a safe source of drinking water—appear to be important determinants of infant mortality risks in both urban and rural locations. In the latter, the very few households with an electricity supply have a greatly reduced probability of infant death. In urban areas, the mortality risk is substantially higher among households living in premises with no finished floor. It seems likely that this characteristic identifies slum dwellings and the poor public health conditions found there. In rural areas, the majority of dwellings have no finished floor, and this is not significantly correlated with mortality risk. Surprisingly, having a toilet is not significantly correlated with mortality risk in either urban or rural areas. Children in households with fewer assets face a greater risk of death in urban but not in rural areas. This is consistent with a greater socio economic gradient in child health in urban areas that has been found in other studies (Fotso 2006; Van de Poel et al. 2007). Note that with controls for the community means of these environmental and socioeconomic variables, the effects under discussion are identified from within-community variation alone and are unlikely to be biased by correlated community-level unobservable variables.

The existence of a health facility is correlated with a reduced risk of death, but the effect is strongly significant only in urban areas. The lack of significance in rural areas may reflect the low quality of health services, with frequent absences of staff and medicines, or the lower probability of seeking health care in rural areas because of high opportunity costs and/or cultural sensitivity (Lalou and LeGrand 1997; Lavy et al. 1996; Lindelouw and Serneels 2006; Say and Raine 2007). The availability of public transportation is negatively correlated with infant mortality in rural areas, where presumably it is more crucial, but the effect is not significant in either sample.

The coefficients on household and community means of the child- and household-level covariates should be interpreted as reflecting the degree to which these variables are correlated with the unobserved household- and community-level heterogeneity, respectively. Jointly, the household-level means are highly significant, and all are individually significant except for the indicator of the mother being older than 35 at the time of birth. The inclusion of these household-level means reduces the coefficient on the indicator of short birth interval and reverses the sign on birth order higher than four.15 As we discuss in the Methods section, it is likely that short birth interval and high birth order reflect previous infant deaths, and therefore not only have a direct effect on survival chances but also are correlated with unobservable mortality risks that threaten all children born within a household. However, after this unobserved mortality risk is controlled for, having more siblings within the household can be beneficial for infant survival if, for example, these siblings can take up some child care responsibilities (Bhargava 2003).

The community means of the household-level variables are not jointly significant in the pooled and rural samples and are only weakly significant in the urban sample. Only the proportion of households with few assets and with no finished flooring is significantly correlated with the unobserved community mortality risk. Counterintuitively, the proportion of households with satisfactory sanitation is positively correlated with community-level mortality risk in urban areas. The joint insignificance of the community means indicates that household-level covariates are not strongly correlated with unobservable community-level risks and, consequently, that our model might be overparameterized. To check whether the decomposition results are overly influenced by many insignificant variables, we also conduct the analysis omitting the community-level means. The regression results are generally very robust to this exclusion—as illustration, compare the first and last three columns of Table 3—except for the expected increase in the magnitude of the coefficients on the few variables for which the community means are significant.

Conditional on the covariates and their household/community means, household-level heterogeneity accounts for 18% of the remaining variance in infant mortality; community-level heterogeneity, while significant, accounts for less than 2%. These results are robust to exclusion of the community means of household characteristics, which is a further indication that the community heterogeneity is uncorrelated with these covariates. The relative importance of the household-level variance could be anticipated from the strong clustering of deaths by household discussed in the Data section. Curtis et al. (1993) also found household heterogeneity explaining about 23% of the random variance in infant mortality in Brazil. However, another study of child survival (to age 5 rather than 1) in Brazil that allowed for both household and community random effects found the latter to be more important (Sastry 1997a). The only other study of child survival that has allowed for both effects was a study of Malawi, which—like the present study—found household-level heterogeneity to be more important (Bolstad and Manda 2001). Both household- and community-level heterogeneity are greater within rural areas. The community component is even absent within urban areas.

When using under-5 instead of infant mortality, which almost doubled the number of deaths, we still found a very small estimate of community-level variance. This suggests that the low community-level variance is not due just to the smaller number of deaths in urban communities.16 Further, the community-level variance did not increase much by omitting the household random effect, suggesting that there is not a problem of separately identifying the two effects. Finally, when we reestimated the model, omitting community-level covariates, the community-level variance did not increase by much, suggesting that it is not the case that there is a large community-level effect that is adequately captured by observable characteristics.

Decomposition Results

The decomposition method (6) reveals that very close to 100% of the rural-urban gap in infant mortality can be explained by differences in the distributions of the covariates and the random effects; and so, in aggregate, differences in the coefficients do not explain any of the gap. This does not mean that there are no differences in the effects of determinants of infant mortality across rural and urban areas. Rather, there are no systematic differences. Some determinants, such as electricity supply, have a stronger effect in rural areas; other determinants, such as wealth, as indicated by possession of assets, have a stronger effect in urban areas. Given the limited evidence of significant rural-urban differences in coefficients and their zero net effect in aggregate, in the remainder of the analysis, we focus on the contributions of differences in the distributions of observable and unobservable determinants of infant mortality.

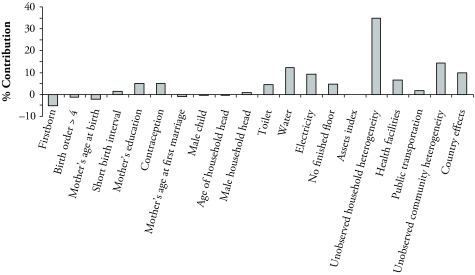
In Table 4, we present the contribution of each covariate, computed analogously to (7) and (8), and that of the unobservable household and community heterogeneity, estimated as in (9) and (10), respectively. Relative contributions are presented in Figure 2.17 We first discuss results generated from Model (1), which includes both the household- and community-level means to capture correlated unobservable effects, and thereafter discuss robustness of the results when the community means are omitted. Keep in mind that the contribution of a covariate reflects both the difference between the rural and urban distributions of that variable and the magnitude of its association with infant mortality, as given in Table 3.

Table 4.

Detailed Decomposition of the Rural-Urban Gap in Infant Mortality

Variables	Model (1)		Without Community Means
	Contributiona	%b	Contributiona	%b
Proximate Determinants
Firstborn	−0.25	−5.25	−0.25	−5.21
Birth order > 4	−0.07	−1.38	−0.07	−1.38
Mother’s age at birth	−0.11	−2.24	−0.11	−2.28
Short birth interval	0.07	1.39	0.07	1.38
Socioeconomic Determinants
Mother did not complete primary education	0.24	5.02	0.21	4.50
Contraception	0.25	5.13	0.23	4.93
Mother’s age at first marriage	−0.04	−0.90	−0.04	−0.85
Male child	−0.02	−0.38	−0.02	−0.37
Age of household head	−0.01	−0.24	−0.01	−0.26
Male household head	0.05	0.93	0.05	1.14
Toilet	0.21	4.32	0.13	2.72
Water	0.60	12.26	0.61	12.82
Electricity	0.45	9.18	0.50	10.58
No finished floor	0.22	4.61	0.48	10.11
Assets index	0.00	0.04	0.05	1.06
Unobserved household heterogeneity	1.70	34.93	1.74	36.43
Total household	3.27	67.43	3.59	75.33
Community
Health facilities	0.32	6.68	0.36	7.52
Public transportation	0.08	1.74	0.09	1.95
Unobserved community heterogeneity	0.70	14.34	0.24	5.03
Total community	1.11	22.77	0.69	14.50
Country
Country effects	0.48	9.80	0.48	10.17
Total explained	4.86	100.00	4.77	100.00
Gap in infant mortality rate	4.54		4.54

^aThe absolute percentage-point contribution to the rural-urban gap in the infant mortality rate.

^bThe contribution as a percentage of the total explained gap.

Figure 2.

Percentage Contribution of Each Covariate to the Rural-Urban Gap in Infant Mortality in the Pooled Sample

The major part of the rural-urban gap in infant mortality is attributed to household-level characteristics (67%). Proximate determinants actually reduce the rural-urban gap by about 7%. This negative contribution derives mainly from the lower proportion of firstborn children in urban areas (−5%)—a consequence of the lower fertility rate—which face a higher mortality risk. Socioeconomic determinants account for 40% of the gap. Among the socioeconomic characteristics, the most important contribution comes from environmental conditions, with water supply, electricity, and finished flooring, respectively, accounting for 12%, 9%, and 5% of the gap. Maternal education also accounts for about 5% of the gap. Except for familiarity with contraception, which contributes 5%, all other proxies for traditions, social norms, and attitudes do not contribute much.

Differences in household-level unobserved heterogeneity contribute a substantial 35% to the gap. This is attributable to differences in the means of both uncorrelated and correlated unobservable household-level determinants, with the contribution of the latter being identified from across household variation in individual-level determinants.

Community characteristics contribute 23% to the gap, the most important contribution coming from the unobserved community heterogeneity (14%). The contribution of this heterogeneity includes that of correlated effects identified through the across-community variation in the means of household-level variables. As discussed above, these means are jointly insignificant, and their inclusion in the decomposition could result in an overestimate of the contribution of unobserved community-level heterogeneity. To check this, we repeat the analysis, omitting the community means of covariates from the model and decomposition. The contribution of community-level heterogeneity is indeed reduced, falling by almost two-thirds to 5% of the gap. Otherwise, the results are quite robust to this restriction. The contribution of finished flooring doubles to reach 10% in relative terms, and that of asset ownership increases to 1%. Because it is only the means of these variables that are significant in the unrestricted model, there is evidence that they are correlated with unobservable community effects and that their contributions are biased upward when there is no control for this correlation. After we take account of the impact on the contributions of these two variables, the estimated contribution of unobserved community heterogeneity does not appear to be greatly inflated by the inclusion of many insignificant community means. To avoid overstating the contribution of any single variable, we suggest that greater weight be placed on the results from the more general model, in which the contributions of household-level covariates are identified from their within-community variation alone and that of their across-community variation is attributed to correlated, unobservable community-level determinants.

The existence of a health facility in the community accounts for 7% of the gap, and public transportation contributes a further 2%. Note that interpretation of these effects as causal relies on the assumption that conditional on the other covariates, including the community-level means, the existence of a health facility and of public transportation is uncorrelated with the residual community-level heterogeneity. Even if this assumption does not hold, the two characteristics provide proxies for community-level determinants, and we still have an estimate of the rural-urban gap in infant mortality that is explained by differences at the community level, as opposed to the household level.

The contribution of the country effects amounts to 10% and is caused by two factors. First, there are differences across countries in the urban-rural population split (Table 2); therefore, the proportion of infants from any one country in the pooled sample differs across urban and rural areas. Second, infant mortality differs across countries even after we control for all covariates (Table 3).

Country-Specific Analysis

The relative importance of household- versus community-level determinants in explaining the rural-urban gap in infant mortality could differ across countries. To check this, we carried out the analysis for each country separately. In fact, there is a high degree of consistency in the results across countries, so we comment on them briefly.18

As would be expected, and has been found elsewhere (Kuate-Defo and Diallo 2002), there is greater cross-country consistency in the effects of maternal characteristics than in those of socioeconomic factors. Notwithstanding the variation in the latter, the country-specific results generally confirm those from the pooled analysis. Unobserved household heterogeneity explains a substantial part of the random variance in infant mortality, ranging from 32% in Chad to 7% in Mali. The proportion of the random variance explained by the community component is again very small, being highest in Niger (2%) and insignificant in Benin, CAR, Guinea, and Mali. In all countries, the decomposition shows that the major part of the rural-urban gap is caused by differences in the distributions of household determinants, with the major contributions coming from household environmental characteristics (ranging from 48% in Chad to 15% in Guinea) and household-level heterogeneity (ranging from 102% in Chad to 26% in CAR).

CONCLUSION

Our decomposition analysis has demonstrated that the rural-urban gap in infant mortality in six Central and West sub-Saharan African countries is explained by differences in the distributions of factors that determine mortality and not by differences in the effects of those determinants between rural and urban locations. Rural-urban differences in household-level determinants, which explain two-thirds of the gap, are much more important than those in community-level determinants, which explain less than one-quarter.

At the household level, within the Mosley and Chen (1984) framework, proximate determinants of infant mortality—which, in this article, mainly consist of maternal factors, such as a short birth interval and birth order—are strongly and consistently related to infant survival. This is very much in line with previous research (e.g., Manda 1999; Sastry 1996). However, because these determinants are very equally distributed across urban and rural areas (and because their effects are so consistent), they are not important in explaining the rural-urban infant mortality gap.

Our results confirm the previously established relationship between infant mortality and socioeconomic characteristics, such as maternal education, familiarity with contraception, and access to a safe water source. Because rural-urban differences in the distributions of these determinants are much larger than for the proximate ones, they are far more important in explaining the gap, accounting for around one-half of the household-level contribution. Housing conditions and access to utilities play a particularly strong role. We have identified the causal effects of these environmental factors only from their within community variation across households. This does not imply that the large contribution of environmental factors can be influenced only through policies that operate on household constraints and behavior. Access to sanitation, safe water, and electricity is constrained first by the community-level infrastructure and only second by the household’s means to make lower-level investments in connecting to this infrastructure. The large contributions of water and electricity supply, together with the relatively large between-community variation they exhibit, suggest that investments in community infrastructure could potentially play an important role in narrowing differences in infant mortality. Still, the availability of a water or electricity supply by itself does not ensure that all households are connected to it. Investments in the community infrastructure need to be combined with initiatives that help households take advantage of it.

Unobservable household-level factors are as important as observable determinants in explaining the rural-urban disparity in infant mortality, accounting for 35% of the gap. Although the absolute contribution of unobservable heterogeneity at the community level is less (14%), it is larger relative to that of observable community-level determinants. Allowing for unobserved heterogeneity in the decomposition is important not only because it reveals the contribution of unobservable household- and community-level determinants but also because accounting for them provides better estimates of the contribution of the observed characteristics. We use household- and community-level means of observable variables to proxy the unobserved household- and community-level mortality risk, respectively, and so make the exogeneity assumption of the three-level, random-effects probit model more plausible. The results do indeed reveal dependencies between fertility-related variables, such as a short birth interval and high birth order, and the unobserved household mortality risk. There is less evidence of correlation between the household-level covariates and the unobservable community-level mortality risks. However, to reduce the risk of overstating the importance of household relative to community-level factors in explaining the rural-urban gap, we have continued to use the between-community variation in household characteristics to represent unobservable community-level heterogeneity. This increases the robustness of our main result: that rural-urban differences in household characteristics are more responsible for the gap in infant mortality than those in community characteristics.

Most of the contribution of observed community-level factors is due to the lower proximity to health facilities in rural areas. The interpretation of this effect as causal relies on the assumption that the within-community means of household-level factors are sufficient to absorb any effects common to infant mortality and access to health facility, as well as other covariates across all households in the same community. Although if the assumption were not to hold the interpretation of the health facility effect would change, in the decomposition, its contribution would remain at the community level, only now being counted as a proxy for unobservable heterogeneity. So, either way, the decomposition quantifies the total contribution of community-level determinants relative to household-level determinants of the rural-urban gap in infant mortality rates.

In sum, we have shown that child survival in these countries depends first and foremost on the living conditions that constrain the ability of households to care for their children. Rural households do not behave so differently from their urban counterparts, but they live under conditions that are far more detrimental to their infants’ health. The decomposition reveals that the larger part of the rural-urban gap in infant mortality is caused by differences in household rather than community characteristics. This suggests that policies aiming to reduce the excess rural infant mortality need to operate not only through investments in community infrastructure and health programs but also by targeting the material needs of disadvantaged households within rural communities. Disadvantageous environmental conditions—such as limited electricity and water supply—contribute greatly to the rural-urban gap and derive both from a lack of community-level infrastructure and from the inability of some households to exploit the infrastructure when it is available. In this respect, policy needs to operate at both the community and household levels to correct such deficiencies.