Trends in U.S. Adult Chronic Disease Mortality, 1960–1999: Age, Period, and Cohort Variations

Abstract

In this paper, I examine temporal changes in U.S. adult mortality by chronic disease cause of death and by sex over a 40-year period in the second half of the twentieth century. I apply age-period-cohort (APC) analyses that combine conventional approaches and a new method of model estimation to simultaneously account for age, period, and cohort variations in mortality rates for four leading causes of deaths, including heart disease, stroke, lung cancer, and breast cancer. The results show that large reductions in mortality since the late 1960s continued well into the late 1990s and that these reductions were predominately contributed by cohort effects. Cohort effects are found to differ by specific causes of death examined, but they generally show substantial survival improvements. Implications of these results are discussed with regard to demographic theories of mortality reductions, differential cohort accumulation of health capital and lifetime exposures to socioeconomic and behavioral risk factors, and period changes in diagnostic techniques and medical treatment.

Substantial mortality declines in the United States for a large part of the past 100 years have been widely documented. However, trends of recent mortality change and sources of the demographic variations in U.S. adult mortality are not well understood. Relatively little is known about the evolution of mortality experiences attributable to distinct impacts of age, period, and cohort. Empirical investigations of sources of recent mortality reductions are typically confined to changes in one or two of these demographic components. The cohort effect is less frequently tested, but its presence implies that certain assumptions currently used by demographers and other social scientists to analyze factors contributing to mortality declines can be misleading. For instance, it is frequently assumed that rates of mortality declines over time are equal across birth cohorts. It is also assumed that these declines depend on rates of changes in period-specific conditions, such as economic advance and health care technology, that are independent of the birth year. These assumptions neglect cohort effects, and greatly simplify estimations, but are increasingly inconsistent with accumulating evidence of cohort changes in a variety of health outcomes that predict mortality (Fogel 2004).

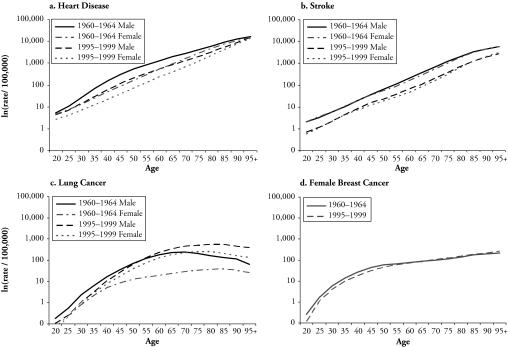
Age-period-cohort (APC) analysis plays a critical role in the search for particular agents of or risk factors for disease and mortality by depicting the whole complex of social and environmental factors that create these risk factors. Identifying the age-period-cohort patterns of adult mortality by cause can contribute in important ways to an understanding of the recent decline of mortality. First, the composition of deaths by cause bears directly on the age patterns of mortality because the incidence of cause-specific mortality varies substantially with age. For instance, Figure 1 shows that much higher rates of deaths attributable to degenerative diseases and cancer occur in older ages than in young adulthood. Second, the ebbs and flows of cause-specific mortality rates over time are the product of period and cohort factors (Manton, Stallard, and Corder 1997). U.S. adult mortality changes may be affected by public health and medical care changes from 1950 to 1990. Changes in deaths attributable to chronic diseases also reflect longterm health effects of the processes of differential accumulation of lifetime exposure to risk factors that suggest clues to the pathways responsible for cohort mortality differences. Third, temporal trend analyses of disease-specific mortality rates are frequently used in etiological investigations to provide clues to the diseases themselves (Holford 1991). When such analyses are conducted on a comparative basis between different diseases and populations—such as between sexes—the results can be used to identify populations with significantly higher or lower incidence of disease, so that the search for risk factors associated with the disease may be more selective and specific.

Figure 1.

Age-Specific Death Rates (logarithmic scale) for U.S. Adults, by Sex and by Four Causes of Death: 1960–1999

Findings from previous studies using APC analysis of mortality change are tentative because of limitations in data and in analytic methods. And evidence regarding the relative importance of period and cohort effects in recent U.S. adult mortality change is particularly scant. Three interesting questions remain. First, to what extent did the large mortality declines since the 1960s continue into the 1990s? Second, what are the patterns of mortality risks that are uniquely attributable to age, period, and cohort factors? Third, what are the age-period-cohort patterns of mortality attributable to the leading causes of death from degenerative diseases and cancer? This study aims to address these questions and to test hypotheses about the roles of period and cohort effects in recent mortality decline with upto-date population level mortality data and a rigorous modeling effort. With data from men and women aged 20–95 and older over a 40-year period (from 1960–1999) in the United States, I analyze temporal patterns of adult mortality attributable to heart disease, stroke, lung cancer, and breast cancer. I conduct an APC analysis based on a combination of informal descriptive devices and formal modeling techniques. A recently developed method of estimation—the Intrinsic Estimator (IE) for log-linear APC accounting models (Yang, Fu, and Land 2004)—provides a model-based summary of temporal effects of mortality that can be delineated into changes across ages, over time, and among birth cohorts.

TEMPORAL CHANGES OF U.S. ADULT MORTALITY

Evident declines for adult, total-cause mortality are noted in recent decades. First, increases in life expectancies at birth and for advanced ages have been substantial. Second, after showing only small declines from 1954 to 1968, death rates declined steadily from the late 1960s to the early 1990s (Crimmins 1981). The examination of mortality patterns by cause links total mortality with underlying chronic diseases. The United States is among several industrialized societies that have entered the age of delayed degenerative diseases—the final health state depicted by the epidemiologic transition theory (Olshansky and Ault 1986). And temporal changes in adult mortality vary by degenerative causes of deaths and sex (Manton 2000). Figure 1 shows large reductions in those age-specific mortality rates between 1960 and 1999 that are attributable to cardiovascular disease (heart disease and stroke) across all adult ages for both sexes, sizable increases in rates of lung cancer mortality in adults (especially women) aged 40 and older, and no evident declines in rates of female breast cancer mortality.1

Age, Period, and Cohort Distinctions

The conceptual distinctions of age, period, and cohort effects are important to the identification of different demographic components in the temporal changes in mortality. Age is undoubtedly the most important source of variation in vital rates. Mortality risks increase with the biological process of aging, and the age patterns of mortality change exhibit considerable regularities across nations and historical time (Hobcraft, Menken, and Preston 1982). Of central focus in the APC analyses of mortality change is the distinction of the other two components of temporal effects—namely, period and cohort differences—through the use of APC models.

Period effects relate to variations in mortality, by time at which the death is recorded, that influences all age groups. Period effects subsume a complex set of historical events and environmental factors—such as world wars, economic crisis, famine, and pandemics of infectious diseases—which influence mortality of all society members (Omran 1982). Period effects may also arise with public health efforts and medical technology break-throughs that lead to reductions in mortality rates of all ages (Frost 1939; Mason and Smith 1985). In addition to these direct effects, changes in disease classification or diagnostic techniques might affect the mortality outcomes of certain diseases (Tarone, Chu, and Gaudette 1997).

Cohort effects represent variations in mortality across groups of individuals born in the same year or years. Cohort effects may arise when each succeeding cohort carries with it the imprint of physical and social exposures from gestation to old age that bear upon its morbidity and mortality risks in a specific way. Chronic disease epidemiology has long noted the importance of early life exposures in explaining the susceptibility to disease and mortality later in the adulthood. For example, malnutrition (Barker 1998; Kuh and Ben-Shlomo 2004) and inflammatory infection (Finch and Crimmins 2004) in utero and during infancy adversely affect intrauterine growth and postnatal development and have been hypothesized to increase risk of cardiovascular and respiratory diseases, cancer, non–insulin-dependent diabetes, metabolism syndromes, and mortality. Cohort effects may also reflect the impacts of lifelong accumulation of exposures to risk factors (Ryder 1965). This is particularly relevant in the examination of chronic diseases and cancer, wherein long-term exposure to a carcinogen is the major cause of the disease (Jemal, Chu, and Tarone 2001).

To the extent that period and cohort effects are aggregates and proxies of different sets of structural correlates of mortality, such distinctions are especially valuable for better identification and understanding of underlying social and environmental factors that are amenable for modifications or reversions.

Hypotheses of Period and Cohort Effects

Mortality decline in recent history followed major advancement in economic development, standard of living, and medical measures (McKeown 1976). It has been argued that improved nutrition and reduced exposure to diseases that are associated with economic development are likely to produce cohort effects in a population, while the introduction of medical techniques is likely to produce period effects. Some studies suggested that the overall contribution of medical measures is small for period effects but large for cohort effects. For example, specific birth cohorts in Italy and England/Wales benefited substantially from these measures (Collins 1982). Other studies of mortality reductions in developed countries emphasized strong period effects, especially for older ages after the 1950s in some European countries (Barbi and Vaupel 2005; Kannisto et al. 1994). The vast majority of previous studies, however, have merely documented the temporal declines in mortality based on descriptive plots of changes in death rates by time period and did not explicitly nor effectively distinguish period and cohort effects. (See the upcoming methods section for details.) Studies using formal APC modeling of mortality mostly suggested the existence of independent cohort effects (Hobcraft et al. 1982; Mason and Smith 1985). Distinct period and cohort patterns in overall mortality have been found in studies of several industrialized countries, including France (Wilmoth 1990), Italy (Caselli and Capocaccia 1989), and the United Kingdom (Robertson and Ecob 1999), based on different APC modeling techniques. As discussed later in this paper, statistical APC analyses have been largely hampered by lack of improvement in methodology and have yielded inconsistent findings. Nevertheless, they provided preliminary or indirect information regarding these effects.

Although few studies tested the distinct role of period versus cohort effects in recent changes in U.S. adult mortality by using multivariate APC analyses, the weight of the evidence points to the possibility that period and cohort factors contribute jointly to survival improvements in the U.S. population. Findings, however, are not clear on the shapes and relative importance of period and cohort effects as driving forces of mortality reduction. In addition, previous findings were restricted to data for older ages or to the time period before the 1960s, or to mortality in European populations. Less is known regarding period-specific and cohort-specific influences that operate on adult mortality in the United States in the latter half of the twentieth century.

I hypothesize that period effects continued to contribute to recent mortality change, but the potency of such effects may have decreased relative to those in the first half of the last century. Although there were continuous mortality reductions during most periods in the past 100 years, evidence also exists that the decline was much more dramatic early during the twentieth century than during periods after 1960 (White and Preston 1996). This indicates that social forces that contributed to mortality decline in previous periods (such as the nation’s level of economic development, improved standard of living, or advancement in medical measures) may have become less responsible for improvement in survival during this period. This is largely due to reductions in or the elimination of many infectious diseases as causes of death (Finch and Crimmins 2004; Omran 1982). Because period effects result from variations in forces that affect the mortality rates of all age groups simultaneously, large period effects are more likely to occur if diseases being considered are more acute or infectious in nature and kill individuals of a wide age-range alike. The advent and diffusion of new medical technology may effectively prevent the spread of such diseases and also elevate survival chances of all affected individuals in a relatively short time. As the United States has reached the fourth stage of the epidemiological transition—that is, the age of delayed degenerative diseases—the leading causes of death have shifted to chronic diseases that disproportionately affect older adults, who have higher risks of mortality (Olshansky and Ault 1986). Also, the effects of medical measures may take longer to translate into widespread improvement in survival detectable to the same extent as those for acute diseases.

Meanwhile, I hypothesize that cohort effects contributed to recent mortality change independently of period effects. Whereas period-specific conditions affect death rates at all ages, cohort-specific conditions tend to take effect at early ages and depend upon subsequent length of exposure to risk factors. This has important implications for chronic diseases as causes of death that span longer time intervals since the age of onset. In a study of English death rates the nineteenth century, Kermack, McKendrick, and McKinlay (1934) attributed the regularity in cohort mortality patterns to a cohort’s health risk as determined by environmental conditions in its first 15 years of life. The well-known study of tuberculosis mortality conducted by Frost (1939) also pointed to the importance of early life influences on cohort experiences rather than on current conditions in the case of a disease that has long latency. The study of Finch and Crimmins (2004) further discovered that decreased inflammation during early life in more recent Swedish cohorts may have made an important contribution to the historical decline in old-age mortality.

The theory of technophysio evolution also provides alternative explanations to a period effects hypothesis that attributes the mortality decline between 1970 and 1990 to health interventions during that period (Fogel 2004; Fogel and Costa 1997). The theory implies that during the twentieth century, individuals’ health capital changed with the year of birth. More recent cohorts fared substantially better in the initial endowment of health capital at birth and also enjoy lower rates of health capital depreciation. These improvements led to increased physiological capacities in later cohorts that also bode well for effectiveness of medical treatments. This is consistent with mounting evidence in recent literature in demography of aging that successive birth cohorts experience later onset of chronic diseases and disabilities (Crimmins, Reynolds, and Saito 1999; Freedman and Martin 1998). Fogel (2004) argued that improvements in life expectancy may not exclusively be due to medical advancements during those years but may also reflect improved physiologies by later cohorts as a result of exposures, long before 1970, to improvements in health care technologies, nutrition, and personal and public health practices. In addition, cohorts with more years of schooling have substantial survival advantages (Kitagawa and Hauser 1973; Lauderdale 2001). The increasing educational attainment in successive birth cohorts (Hughes and O’Rand 2004) suggests increases in the amount of health capital available to later birth cohorts from better lifestyle choices and health behaviors as well as access to medical care that may lead to reductions in cohort mortality levels.

Trends in Mortality by Four Leading Causes

Cardiovascular disease (CVD) and cancer cause more than two-thirds of all deaths in the United States.2 As both direct and indirect indicators of the influences of a myriad of social and behavioral, economic, and environmental factors on population health, CVD and cancer mortality rates are crucial for understanding the longevity of men and women. Four causes of mortality that represent leading chronic conditions—namely, heart disease, stroke, lung cancer, and female breast cancer—are of interest to the current analysis because their temporal variations have distinct public health and clinical characteristics and different implications for socioeconomic changes during the past 40 years.

As with total mortality rates, declines in CVD mortality rates in the United States have been projected to continue in the post-1990 period through 2000 (Crimmins 1981). Previous studies of changes in CVD mortality were mainly descriptive (e.g., Manton 2000; Peltonen and Asplund 1996) and are, therefore, of limited use to generate informed hypotheses about the net period and cohort effects. Since the launch of the Framingham Heart Study in 1948, several major risk factors for CVD have been established. These include hypertension, high low-density lipoprotein (LDL; “bad” cholesterol) levels, diabetes, low socioeconomic status, cigarette smoking, lack of physical activity, and obesity (Barrett-Connor 1997). On the one hand, increasing knowledge about prevention, diagnosis, and treatment of hypertension—together with diffusion of current medical techniques—should largely decrease CVD mortality (CDC 1999). On the other hand, the obesity epidemic in recent years may reduce the rate of decline (Mokdad et al. 1999; Rogers, Hummer, and Krueger 2003). Period and cohort changes in distributions of specific risk factors may lead to corresponding rise and fall of period and cohort effects of CVD mortality.

Lung cancer and female breast cancer mortality have received more attention in temporal analyses that use APC regression models. Both have been shown to have characteristic period and cohort patterns. Inconsistencies in these patterns, however, preclude conclusive inferences of the role of period and cohort effects.

Results concerning period effects of lung cancer mortality are ambiguous. For example, Gardner and Osmond (1984) found virtually no period effect when cohort effects are considered in APC models of lung cancer mortality in England and Wales from 1950 to 1980. The authors concluded that the period of time did not appear to be the major influence and offered a “much modified interpretation,” emphasizing birth-cohort experiences that accorded with known changes in smoking behavior in women. Others found monotonically increasing period effects in Belgian female lung cancer mortality that suggests a log-linear trend (Clayton and Schifflers 1987a) and inverse U-shaped period effects in the United States (Jemal et al. 2001). Still others found large fluctuations in numerical estimates of the effect coefficients using different model identifying constraints (Kupper et al. 1985). Compared with cohort effects, the absolute magnitudes of the period effects are generally small.

In contrast, findings of cohort patterns of lung cancer mortality have been consistent and show inverse U-shaped curves across developed countries, with varying peaks among cohorts (Gardner and Osmond 1984; Jemal et al. 2001; Lee and Lin 1996; Tarone and Chu 2000a). Such effects suggest the influence of gender-specific risk factor exposure and behavioral differences, especially cigarette smoking, in the life experience of specific birth cohorts. Studies have found diverse patterns of smoking across cohorts and the presence of sex differences, with recent increases in smoking in later cohorts of females (Harris 1983; Zang and Wynder 1996). Male cohorts adopted smoking cigarettes in large numbers earlier than did females, and this pattern preceded that of females by a decade or two (Lopez 1995). The gender gap in lung cancer mortality that first increased and then decreased reflected this lag in the diffusion of smoking (Pampel 2005). Therefore, it can be expected that the peak of the inverse U-shaped male cohort mortality curve precedes that of the females, and the mortality decline in male cohorts started earlier than that in females.

Period effects of breast cancer mortality differ, depending on analytic methods used and the specific populations examined. Studies reported continuous declines in mortality rates from the 1950s to the 1970s in the United States, Japan, and Canada, slight increases in the 1980s, and decreases in recent years (1990–1995) in the United States and Canada (Clayton and Schifflers 1987b; Tarone and Chu 2000b; Tarone et al. 1997). Several period factors can be hypothesized to be responsible for the temporal trends in female breast cancer mortality. First, the increase in mortality the 1980s coincided with a rise in diagnosis via mammography (Breen and Kessler 1994). Second, medical interventions, such as increased use of tamoxifen therapy and early detection, can temper the increases and even lead to decreases in deaths from breast cancer (Tarone et al. 1997). Third, the link between weight gain during adult life and the increased risk of breast cancer (Eliassen et al. 2006) suggests possible increases in mortality due to the large increases in obesity rates after 1980s.

There is evidence of large cohort effects in U.S. breast cancer mortality that show steep increases until the peak in 1925, followed by moderations until the mid-1940s, and decreases for cohorts born after 1950 (Tarone and Chu 2000b; Tarone et al. 1997). The exposure of breast tissue to endogenous estrogens is a known risk factor for breast cancer (MacMahon, Cole, and Brown 1973). Fertility-related behaviors, such as reductions in completed pregnancies and delaying of childbearing to later ages, are socially and culturally regulated and determine the length of hormonal exposure. Recent fertility changes in women—including declines in the proportion ever marrying and increases in the mean age at marriage (Schoen et al. 1985), accelerated labor force attachment among baby boomers that reduced lifetime births (Schoen et al. 1997), and delayed births to progressively later ages (Yang and Morgan 2003)—may be consequential for cohort changes in the exposure to this risk factor. It is, therefore, possible that changes in female cohort fertility patterns lead to cohort variations in breast cancer mortality (Tarone et al. 1997). However, this hypothesis found limited support in previous studies. Manton (2000) found only small cohort differences in age-specific death rates from breast cancer. Tarone and colleagues (Tarone and Chu 2000b; Tarone et al. 1997) found stable or decreasing rates of mortality for baby boomers who experienced decreased fertility because of increased female labor force participation and uses of oral contraceptives.

Extensive methodological discussions of APC model specifications and identification problems are available elsewhere (see, e.g., Mason and Wolfinger 2002; Robertson, Gandini, and Boyle 1999), but the empirical studies cited earlier give examples of both the power of such models in delineating cohort effects from the age and period effects as well as the problems associated with inconsistencies of findings owing to different model assumptions used. This study combines conventional methods of APC analyses with a new statistical approach to provide new evidence on the age, period, and cohort effects of U.S. adult mortality.

DATA

Data on numbers of deaths used in this study are from the Multiple Cause of Death public use files of all U.S. death certificates reported to the Centers for Disease Control and Prevention, National Center for Health Statistics (NCHS) for adults aged 20 and older from 1960 to 1999. The underlying cause of death is reported on the death certificate by the physician or other certifier. The medical condition for each cause of death is numerically coded, according to the manual of the International Classification of Diseases (ICD), which changed during the 40-year period. The ICD codes changed from the 7th through the 10th revision for the four causes of deaths examined in this study: namely, heart disease, stroke, lung cancer, and female breast cancer. However, recent studies found that ICD revisions have little effect on the temporal trends for the four causes in that these cause-of-death categories represent catastrophic health events and are much less subject to major diagnostic errors over time than other causes (CDC 1999).

Data on population exposure to risk by age and sex from 1960 to 1999 were taken from U.S. Census Bureau estimates provided by the Human Mortality Database (HMD) of the University of California, Berkeley (available online at http://www.mortality.org). For most of the age range, the HMD used either linear interpolation of population estimates or intercensal survival methods. At ages 80 and older, the HMD used population estimates that were computed using the methods of extinct cohorts and survivor ratios.

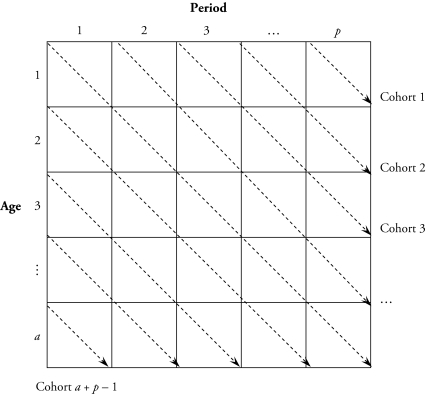
Death rates are then calculated as the ratio of reported number of deaths to population exposure. The tabular rate data structure is shown in a diagram in Figure 2. In this rectangular age by period array, age-specific death rates are summarized in an a × p table for a age groups and p time periods of equal interval lengths. The diagonal elements of the matrix connected by the dashed arrows correspond to (a + p – 1) birth cohorts. In the following analysis, I use 16 five-year age groups, ranging from ages 20–24 to 95 and older; and eight five-year time periods, from 1960–1964 to 1995–1999.3 This yields 23 successive, 10-year birth cohorts labeled by their central birth years. The oldest cohort (born before 1865) corresponds to the bottom-left cell in the diagram, and the youngest cohort (born between 1970 and 1980; the 1975 cohort) corresponds to the top-right cell in the diagram.

Figure 2.

Tabular Rate Data Structure

ANALYTIC METHODS

Descriptive Analysis

The majority of previous studies have relied on two analytic approaches to depict the time trends by age, period, and birth cohort. One common practice is to use summary measures that are independent of age composition, such as standardized indices (age-standardized death rates) arrayed by time periods. The other device more relevant to APC analyses is a graphical display of the table of age- and period-specific rates or age- and cohort-specific rates. An example of age- and period-specific rates is given in Figure 1. This figure illustrates that both sexes experienced declines in age-specific death rates from heart disease and stroke over time for all adult ages. Unlike the continuous declines in total mortality at older ages in European countries (Kannisto et al. 1994), in the United States, the declines decreased in older ages for heart disease mortality but increased in lung cancer mortality after age 55 for men and after early adulthood for women over the 40-year period. The period changes in age-specific female breast cancer death rates show a modest crossover that indicates improvement of survival that was restricted to ages 20–65 and a slight increase in postmenopausal breast cancer mortality. Consistent with previous results on cohort trends in death rates cause, the data (not presented) show continuous cohort declines in heart disease and stroke mortality, large increases in lung cancer mortality, and small cohort differences in breast cancer mortality.

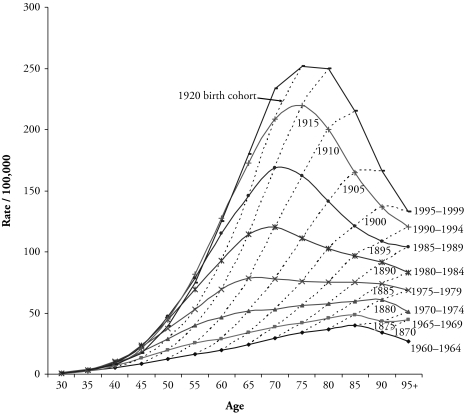
The preceding two approaches do not explicitly consider an age-period-cohort modeling framework. Both are descriptive and share two disadvantages. First, they describe only variation in the rates attributable to factors associated with either period of death or birth cohort. Second, neither summarizes the rate table satisfactorily. Standardization ignores trends at different ages; and graphical methods represent all available rates, thus providing no summary at all (Osmond 1985). In addition, they each have their own limitations. Standardized rates depend on the selection of an appropriate standard population-age composition and give more weight to the older ages (Schoen 1970). Substantial population aging across the decades makes the choice even more difficult. Graphs of rates from two-way age-by-period tables are helpful for qualitative impressions about temporal patterns, but they provide no quantitative assessment of the source of mortality change (Kupper et al. 1985). For example, in Figure 3, the curve of age-specific lung cancer death rates for females in any given time period—say, 1995–1999—cuts across a number of birth cohort curves, such as 1900, 1905, 1910, and 1920. Therefore, the shape of the period curve is affected by both varying age effects and cohort effects. The question of how these effects operate simultaneously to shift the period curve motivates the use of statistical regression modeling.

Figure 3.

U.S. Female Lung Cancer Mortality Rates per 100,000, by Age at Death, Period of Death, and Birth Cohort

APC Accounting Models

APC multiple classification/accounting models (Mason et al. 1973) have been a popular tool for separately estimating the effects of these three variables and have received considerable attention in statistical demography (Fienberg and Mason 1985). Although previous demographic studies sought to determine whether there are distinct contributions of age, period, and cohort variation to mortality changes, few of them succeeded in taking all three dimensions of temporal trends into account simultaneously in multivariate analysis. One problem in the early age models was that the cohort effects were not explicitly controlled. Studies that attempted to identify period and cohort effects did so only loosely because the linear dependence among age, period, and cohort components creates a model identification problem for three-factor analysis. The methods on which previous studies of period and cohort effects are based may not be statistically rigorous and powerful (Hobcraft et al. 1982). It follows that the findings are not complete and accurate and, consequently, are difficult to interpret.

In order to specify the models to be estimated, it will be useful to review briefly the APC accounting model outlined in Mason et al. (1973). The model for tabular mortality data can be written in log-linear regression form as

$$\text{log}(r_{ijk})=\text{log}(d_{ijk}/n_{ijk})=\square +{\alpha }_i+{\beta }_j+{\gamma }_k,$$ (1)

where r_ijk denotes the expected death rate in age-period-cohort cell (i, j, k); d_ijk denotes the expected number of deaths and is assumed to be distributed as a Poisson variate; n_ijk is the population or exposure-at-risk, the log of which is also termed as the offset or adjustment for the log-linear contingency table model; □ denotes the intercept or adjusted mean rate; α_i denotes the ith row age effect for i = 1, . . ., a age groups; β_j denotes the jth column period effect for j = 1, . . ., p periods; and γ_k denotes the kth diagonal cohort effect for k = 1, . . ., (a + p – 1) cohorts, with k = a – i + j. In conventional practice, one of each of the α_i, β_j, and γ_k coefficients is set to zero as a “reference” age, period, or cohort category against which the estimated coefficients for the other categories can be compared. An alternative parameterization is to center the parameters so that they sum to zero: Σ_iα_i = Σ_jβ_j = Σ_kγ_k = 0.

The key problem in APC analysis using Eq. (1) is the “identification problem.” Rewriting Eq. (1) in matrix form, we have

$$\mathbf{\text{Y}}=\mathbf{\text{Xb}},$$ (2)

where Y is a vector of logged death rates, and X is the regression design matrix that contains dummy variable column vectors for the model parameter b of dimension m = 1 + (a – 1) + (p – 1) + (a + p – 2), and b = (□, α₁, . . ., α_{a – 1}, β₁, . . ., β_{p – 1}, γ₁, . . ., γ_{a + p – 2})^T. Assuming for now that the vector b is to be estimated by ordinary least squares, the normal equations to be solved takes the form X^TXb = X^TY. The linear relationship between the age, period, and cohort variables (period = age + birth year) translates to a design matrix, X, that is one less than full column rank. This implies that X^TX is singular: the inverse of X^TX does not exist. It follows that solution to normal equations is not unique. Therefore, it is not feasible to estimate the three effects separately without assigning certain additional identifying constraints.4

One possible solution is to estimate a reduced age and period, two-factor model that contains no cohort effects and can be written as

$$\text{log}(r_{ij})=\text{log}(d_{ij}/n_{ij})=\square +{\alpha }_i={\beta }_j.$$ (3)

Because cohort effects can be interpreted as a special form of interaction effect between the categorical age and period variables, Eq. (3) rests on the assumption of no interaction effect (Fienberg and Mason 1985). In particular, the expected rate in age by period cell (i, j) is modeled as a function of the marginal or gross effects of age i and period j only, and not also of the cell-specific effect—such as γ_{a – i + j}—which is a function of both i and j. Violation of this assumption can be detected by plots of age-specific death rates by time period, and a lack of parallelism among these curves suggests birth cohort effects that are operating (Kupper et al. 1985). The same applies to period effect as a particular type of age-cohort interaction (Holford 1991). The present study finds nonparallelism among age curves by period in rates of mortality from all causes (see, e.g., Figure 3), confirming the inadequacy of age-period effects model. Age curves by cohort also show nonparallelism only in plots of lung cancer and breast cancer mortality, but not in those of heart disease and stroke mortality. Therefore, period effects are likely more important in some causes of deaths than others. Thus, these preliminary graphical analyses argue against the plausibility of reduced two-factor models.

The most widely used approach to estimating the full APC models is to place at least one equality constraint on two or more of the age, period, or cohort coefficients (e.g., Fienberg and Mason 1985; Mason et al. 1973). This has been referred to as the constrained generalized linear models (CGLIM) approach (Yang et al. 2004). For example, one can constrain the effect coefficients of two adjacent age groups, periods, or cohorts to be equal to identify the model (see, e.g., Mason and Smith 1985; Yang et al. 2004). The main criticisms of this approach and its variants are that different equality constraints yield different effect coefficient estimates but identical model fit; and that the model estimates are sensitive to the choice of the identifying constraints that depends on strong prior or external information that rarely exists or can be well verified (Mason and Wolfinger 2002; Robertson et al. 1999).5 Therefore, analysts have been advised that any statistical modeling of APC data should be carried out in conjunction with a detailed descriptive analysis (Kupper et al. 1985; Mason and Smith 1985).

Intrinsic Estimator Analysis

Recently, a promising alternative modeling approach was described and evaluated by Yang and colleagues (2004). Incorporating recent methodological developments using estimable functions in biostatistics, a new method of estimation—termed the intrinsic estimator (IE)—yields a unique solution to Eq. (1) that is determined by the Moore-Penrose generalized inverse and removes the arbitrariness of linear constraints on parameters. This solution is the only estimable function of the parameter vector, and it estimates both linear and nonlinear components (Fu 2008). It also achieves model identification with minimum assumption imposed to data. To illustrate this comparative advantage of the IE, I briefly review the nature and properties of this estimator.

First, the exact linear dependency between age, period, and cohort variables in Eq. (2) is mathematically equivalent to

$$\mathbf{\text{X}}{\mathbf{\text{B}}}_{\mathbf{\text{0}}}=0.$$ (4)

This equation states the property that X is singular and that the product of X and some nonzero vector B₀ is 0 (see also Christensen 2002). Kupper et al. (1985) showed that B₀ has the specific form that is a function of the design matrix. Specifically, $\begin{array}{l}{\mathbf{\text{B}}}_{\mathbf{0}}=\frac{{\widetilde{\mathbf{\text{B}}}}_{\mathbf{\text{0}}}}{||{\widetilde{\mathbf{\text{B}}}}_{\mathbf{0}}||}\\ \end{array}$, or a normalized vector of B̃₀:

$$\begin{array}{l}{\widetilde{\mathbf{\text{B}}}}_{\mathbf{\text{0}}}=(0,\mathbf{\text{A}},\mathbf{\text{P}},\mathbf{\text{C}}{)}^T,\\ \end{array}$$ (5)

where

$$\mathbf{\text{A}}=\left(1-\frac{a+1}{2},\dots ,(a-1)-\frac{a+1}{2}\right),$$

$$\mathbf{\text{P}}=\left(\frac{p+1}{2}-1,\dots ,\frac{p+1}{2}-(p-1)\right),$$

and

$$\begin{array}{l}\mathbf{\text{C}}=\left(1-\frac{a+p}{2},\dots ,(a+p-2)-\frac{a+p}{2}\right).\\ \end{array}$$

It is important to note that the vector B₀ is fixed or nonrandom because it is a function solely of the number of age groups (a) and periods (p). The fact that the fixed vector B₀ is independent of the response variable Y suggests that it should not play any role in the estimation of effect coefficients. However, this principle may be violated in the conventional CGLIM approach, as illustrated below.

Second, the parameter space of the APC regression Eq. (2), P, can be decomposed into the direct sum of two linear subspaces that are orthogonal (independent) to each other: P = N □ Θ, where one subspace (N) denotes the null space of X defined by the vector B₀, corresponding to the unique zero eigenvalue of the matrix X^TX, and the other subspace (Θ) denotes the complement non-null space orthogonal to N. Note further that B₀ represents a special direction in the parameter space with Euclidean norm or length 1. This special direction in the parameter space is defined by the difference between two arbitrary CGLIM estimators b̂₁ − b̂₂:

$$\begin{array}{l}\mathbf{\text{X}}({\widehat{\mathbf{\text{b}}}}_{\mathbf{\text{1}}}-{\widehat{\mathbf{\text{b}}}}_{\mathbf{2}})=\mathbf{\text{X}}(t{\mathbf{\text{B}}}_{\mathbf{0}})=0,\\ \end{array}$$ (6)

where t is an arbitrary real number, and tB₀ represents arbitrary linear trends. Thus, the difference of any two arbitrary CGLIM estimators must be in the null space of X: the space defined by B₀. Different equality constraints of the CGLIM estimators assign different values to t. And the arbitrary term in these parameter vectors, tB₀, leads to different estimates.

The structure of the vector B₀ (as shown in Eq. (5)) and the nature of CGLIM estimator (as shown in Eq. (6)) suggest that the influence of null vector B₀ that varies only with the number of age and period groups and is independent of death rates should be removed from the estimation. And using a vector-space projection approach, this can be realized. Corresponding to the parameter space decomposition is the decomposition of the parameter vector:

$$\mathbf{\text{b}}={\mathbf{\text{b}}}_{\mathbf{\text{0}}}+t{\mathbf{\text{B}}}_{\mathbf{\text{0}}},$$ (7)

where b₀ = P_projb is a special parameter vector that is the projection of the parameter vector b to the non-null space Θ. The geometric projection implies that because the vector b₀ is orthogonal to—and, therefore, independent of the arbitrary component tB₀—b₀ is an estimable function and is invariable to the choice of linear constraints. No other constrained functions of b, with t not equal 0, are estimable (for details see Yang et al. 2004: figure 1).

It follows that each of the infinite number of possible estimators of parameter vector of Eq. (2), denoted as b̂, can be written as a linear combination of two parts that are orthogonal or independent to each other in the parameter space:

$$\widehat{\mathbf{\text{b}}}=\mathbf{\text{B}}+t{\mathbf{\text{B}}}_{\mathbf{\text{0}}},$$ (8)

where B is the special estimator—the intrinsic estimator (IE)—that estimates the special parameter vector b₀ defined in Eq. (7), corresponding to t = 0, that satisfies the projection. The projection of the estimator onto the non-null space yields the IE: $\mathbf{\text{B}}=(I-{\mathbf{\text{B}}}_{\mathbf{0}}{\mathbf{\text{B}}}_{\mathbf{0}}^{\mathbf{\text{T}}})\widehat{\mathbf{\text{b}}}$.6 Alternatively, the IE can be obtained using the principal component regression algorithm exemplified in the Appendix.

The geometrical projection shows that the IE may also be viewed as a constrained estimator. However, in contrast to the equality constraints on coefficients that are imposed in conventional approaches, the constraint imposed by the IE to identify Eq. (2) is a constraint on the geometric orientation of the parameter vector b in parameter space. Specifically, the IE imposes the constraint that the direction in parameter space defined by the unique eigenvector B₀ in the null space of the design matrix X have zero influence on the parameter vector to be estimated. This constraint is reasonable in that B₀ is fixed and solely a function of the dimension of the age by period data matrix and therefore does not relate to the observed mortality rates or frequencies being analyzed. Removing this component of B₀ from the estimates reduces the subjectivity associated with conventional constraints.

To summarize, the new approach of using the IE to estimating the APC accounting model yields unique solutions and identifies the model by imposing minimum assumptions of prior information. Yang et al. (2004) further showed that the IE possesses the desirable statistical properties in finite-time-period APC analyses of tabulated rates for a fixed number of time periods. Note that identifying constraints obtained by the CGLIM methods or any linear combination of IE estimates of the coefficient vector will also identify the model and yield an identical model fit to the data. Still, any substantial departure from the IE estimates, which incorporates a large nonzero t, will not yield an estimable function and thus will induce bias in the estimates. In contrast, for a finite number of time periods of data, the IE produces an unbiased estimate of the coefficient vector. Also, the IE has a variance smaller than that of any CGLIM estimators—unless, again, the CGLIM constraints result in t = 0. Therefore, it also has relative statistical efficiency. In addition, Yang and colleagues noted that as the number of time periods in the analysis increases, the bias in CGLIM estimators decreases, and the CGLIM estimators converge to the IE.7 Yang and colleagues also described the statistical consistency of the IE: namely, that under suitable regularity conditions on the error term process and a fixed set of age categories, the IE will converge asymptotically to the “true” parameters that generate the sequence of APC rates.8

The empirical analysis of U.S. female total mortality rates conducted by Yang et al. (2004) further suggested that the IE yields results that are similar to those of the CGLIM estimators under sensible equality constraints, but the IE produces point and interval estimates in a direct way, without the necessity of choosing from among many possible constraints on coefficients that may not be immediately verifiable in the data. The consistency of the results achieved using the IE and certain CGLIM estimators thus provides an empirical validation of the IE constraint.9

The remainder of this paper employs the Poisson log-linear model to analyze temporal trends of cause-specific mortality. In combination with descriptive analyses, I use multiple model specifications as a means of model validation, including the two-factor models, the CGLIM estimators, and the IE method of estimation for the full APC accounting models. The log-linear Poisson regression coefficients, standard errors, and model fit are computed using Stata 9.2.10

RESULTS

Model Comparison

Following the example of Yang et al. (2004), I conducted comparisons of conventional constrained-coefficients and the IE analyses. I first estimated six reduced log linear models: three gross-effects models—namely, model A for age effects, model P for period effects, and model C for cohort effects—and three, two-factor models—namely, AP, AC, and PC effects models. I then estimated the full APC model wherein all three factors are simultaneously controlled. Goodness-of-fit statistics were calculated and used to select the best-fitting models for male and female mortality data. Because likelihood ratio tests tend to favor models with a larger number of parameters, I calculated the two most commonly used, penalized-likelihood model selection criteria: Akaike’s information criterion (AIC) and Bayesian information criterion (BIC), which adjust the impact of model dimensions on model deviances.11 Table 1 presents the comparisons of the goodness-of-fit statistics from the preceding models using the AIC and the BIC. Because age is the most important source of variation in mortality, models with no age effects (P, C, and PC) have shown to be significantly lack of fit and are thus omitted from Table 1. For both male and female data and all causes of mortality, the AIC and BIC statistics imply that the full APC models fit the data significantly better than any of the reduced models.

Table 1.

Goodness-of-Fit Statistics for Age-Period-Cohort Log Linear Models of U.S. Adult Mortality

Cause of Death	Male				Female
	A	AP	AC	APCa	A	AP	AC	APCa
Total
Deviance	978,783	108,289	45,427	25,828	695,527	40,443	72,089	18,903
AIC	979,007	108,499	45,607	25,996	695,751	40,653	72,269	19,071
BIC	979,019	108,510	45,617	26,005	695,763	40,664	72,279	19,080
Heart Disease
Deviance	1,110,502	63,080	14,811	5,533	782,210	52,225	18,638	9,243
AIC	1,110,726	63,290	14,991	5,701	782,434	52,435	18,818	9,411
BIC	1,110,738	63,301	15,000	5,711	782,446	52,446	18,827	9,420
Stroke
Deviance	543,470	7,260	17,947	1,027	655,622	12,660	25,967	1,480
AIC	543,694	7,470	18,127	1,195	655,846	12,870	26,147	1,648
BIC	543,706	7,482	18,137	1,204	655,858	12,881	26,157	1,657
Lung Cancer
Deviance	115,651	51,520	7,073	611	320,050	42,126	5,296	245
AIC	115,875	51,730	7,253	779	320,274	42,336	5,476	413
BIC	115,887	51,741	7,262	788	320,286	42,347	5,486	422
Breast Cancer
Deviance					9,748	7,403	1,553	512
AIC					9,972	7,613	1,733	680
BIC					9,984	7,625	1,743	689
df	112	105	90	84	112	105	90	84

Notes: AIC = deviance + 2df; BIC = deviance + log(N) × df, where df is the degrees of freedom used by model parameters. The smaller the AIC and BIC, the better the model fit.

^aThe full APC models, using the intrinsic estimator and conventional equality coefficient constraints, yield the same model fit.

For all of the causes of death in the analyses, I then estimated APC models for males and females with different identifying constraints using the CGLIM approach. I tested three possible types of equality constraints: one on two adjacent age coefficients (e.g., 20 = 25), one on period coefficients (e.g., 1960 = 1965), and the other on cohort coefficients (e.g., 1865 = 1870). In the interest of space, these model coefficients are not presented. As expected, because all of these models incorporate all three of the age, period, and cohort factors, they fit the data equally well (see Table 1). However, they differ in the coefficient estimates. Both the exploratory graphical analyses described earlier and the results from the gross-effects models suggest that the mortality risks attributable to all four causes considered—that is, two types of cardiovascular disease and two types of cancer— vary substantially across five-year age groups. Therefore, the age effect constraints may be less reasonable than the latter two. For heart disease and stroke mortality, the early two periods and two earliest cohorts born long before 1900 did not exhibit large changes and may both be deemed as having equal effects. The results show that the CGLIM estimates under these two constraints have similar trends and that both are highly consistent with the IE results. For lung cancer and breast cancer mortality, the period changes were more pronounced and continuous, and were less likely to give credence to the equality constraint. The cohort equality constraints, on the other hand, produced remarkably similar results to those of the IE.12 In addition, the results on period and cohort effects are also highly consistent with a prior epidemiological study that used earlier data and APC models to project lung cancer mortality rates to year 2000 (Osmond 1985).

Intrinsic Estimates of Age, Period, and Cohort Effects

The results from the estimation of the full APC models using the IE method for females are displayed in Table 2. This table summarizes the model coefficients, their standard errors, model deviance, and overdispersion coefficient.13 To facilitate the comparisons of the temporal effects of mortality by cause and sex, Figures 4–6 plot the point estimates of selected effect coefficients from each model. These plots compare the coefficients of successive categories within period and cohort classifications and show the net period and cohort trends of mortality. The results largely accord with the observed patterns from descriptive displays of the data, but they also offer additional insights of distinct sources of mortality change.14

Table 2.

Intrinsic Estimates for the U.S. Female Adult Mortality Rates by Cause

	All Causes	Heart Disease	Stroke	Lung Cancer	Breast Cancer
Intercept	−4.571 (0.007)	−6.064 (0.018)	−7.223 (0.014)	−8.922 (0.022)	−8.007 (0.017)
Age
20–24	−2.032 (0.032)	−3.344 (0.101)	−3.082 (0.059)	−4.148 (0.102)	−4.495 (0.094)
25–29	−1.995 (0.029)	−2.964 (0.079)	−2.681 (0.046)	−3.357 (0.061)	−2.564 (0.036)
30–34	−1.819 (0.026)	−2.504 (0.063)	−2.228 (0.037)	−2.252 (0.037)	−1.362 (0.023)
35–39	−1.555 (0.023)	−1.977 (0.049)	−1.766 (0.029)	−1.253 (0.026)	−0.639 (0.018)
40–44	−1.245 (0.020)	−1.436 (0.039)	−1.342 (0.024)	−0.495 (0.021)	−0.137 (0.016)
45–49	−0.915 (0.017)	−0.970 (0.032)	−0.972 (0.020)	0.088 (0.017)	0.245 (0.013)
50–54	−0.596 (0.015)	−0.521 (0.026)	−0.671 (0.017)	0.507 (0.014)	0.505 (0.012)
55–59	−0.295 (0.013)	−0.101 (0.022)	−0.400 (0.015)	0.826 (0.012)	0.631 (0.011)
60–64	0.026 (0.011)	0.323 (0.018)	−0.018 (0.012)	1.074 (0.010)	0.702 (0.010)
65–69	0.349 (0.010)	0.708 (0.015)	0.429 (0.010)	1.262 (0.010)	0.754 (0.009)
70–74	0.701 (0.009)	1.107 (0.013)	0.942 (0.009)	1.389 (0.011)	0.821 (0.009)
75–79	1.072 (0.008)	1.504 (0.012)	1.472 (0.008)	1.422 (0.012)	0.891 (0.010)
80–84	1.484 (0.008)	1.932 (0.012)	1.996 (0.009)	1.397 (0.015)	0.989 (0.011)
85–89	1.896 (0.009)	2.352 (0.014)	2.454 (0.010)	1.320 (0.018)	1.111 (0.013)
90–94	2.273 (0.011)	2.746 (0.017)	2.802 (0.012)	1.187 (0.022)	1.199 (0.017)
95+	2.652 (0.014)	3.144 (0.021)	3.064 (0.016)	1.031 (0.031)	1.348 (0.024)
Period
1960–1964	−0.115 (0.009)	−0.119 (0.015)	0.123 (0.010)	−1.100 (0.014)	−0.283 (0.009)
1965–1969	−0.064 (0.008)	−0.075 (0.012)	0.136 (0.008)	−0.757 (0.011)	−0.193 (0.008)
1970–1974	−0.042 (0.007)	−0.051 (0.009)	0.146 (0.006)	−0.391 (0.008)	−0.114 (0.007)
1975–1979	−0.081 (0.007)	−0.079 (0.008)	−0.001 (0.006)	−0.076 (0.005)	−0.051 (0.006)
1980–1984	−0.034 (0.007)	0.006 (0.008)	−0.118 (0.006)	0.231 (0.005)	0.045 (0.006)
1985–1989	0.044 (0.007)	0.065 (0.009)	−0.156 (0.007)	0.489 (0.006)	0.155 (0.006)
1990–1994	0.094 (0.007)	0.084 (0.011)	−0.141 (0.008)	0.719 (0.009)	0.221 (0.007)
1995–1999	0.197 (0.008)	0.169 (0.014)	0.011 (0.009)	0.886 (0.012)	0.220 (0.008)
Cohort
1865	0.939 (0.060)	1.185 (0.065)	1.213 (0.043)	0.756 (0.235)	0.820 (0.120)
1870	0.937 (0.031)	1.222 (0.037)	1.203 (0.024)	0.872 (0.092)	0.809 (0.057)
1875	0.900 (0.021)	1.209 (0.027)	1.177 (0.019)	0.820 (0.056)	0.774 (0.037)
1880	0.834 (0.016)	1.149 (0.022)	1.125 (0.016)	0.721 (0.044)	0.685 (0.029)
1885	0.748 (0.014)	1.062 (0.019)	1.041 (0.014)	0.593 (0.038)	0.603 (0.025)
1890	0.653 (0.012)	0.956 (0.018)	0.937 (0.014)	0.482 (0.034)	0.538 (0.023)
1895	0.556 (0.011)	0.837 (0.017)	0.820 (0.013)	0.422 (0.031)	0.474 (0.022)
1900	0.449 (0.011)	0.695 (0.017)	0.673 (0.014)	0.402 (0.029)	0.404 (0.021)
1905	0.331 (0.011)	0.523 (0.018)	0.494 (0.014)	0.465 (0.027)	0.372 (0.020)
1910	0.243 (0.011)	0.364 (0.020)	0.330 (0.016)	0.580 (0.025)	0.342 (0.019)
1915	0.148 (0.012)	0.179 (0.023)	0.159 (0.017)	0.653 (0.024)	0.294(0.019)
1920	0.060 (0.013)	0.005 (0.026)	0.003 (0.019)	0.635 (0.024)	0.209 (0.020)
1925	−0.018 (0.015)	−0.151 (0.029)	−0.136 (0.022)	0.587 (0.024)	0.130 (0.020)
1930	−0.124 (0.017)	−0.304 (0.033)	−0.250 (0.025)	0.461 (0.024)	−0.015 (0.021)
1935	−0.249 (0.019)	−0.452 (0.039)	−0.358 (0.028)	0.275 (0.025)	−0.165 (0.022)
1940	−0.416 (0.022)	−0.651 (0.045)	−0.506 (0.032)	−0.008 (0.027)	−0.284 (0.023)
1945	−0.567 (0.024)	−0.856 (0.051)	−0.672 (0.035)	−0.344 (0.029)	−0.394 (0.024)
1950	−0.678 (0.026)	−1.021 (0.060)	−0.832 (0.040)	−0.759 (0.032)	−0.518 (0.026)
1955	−0.732 (0.030)	−1.108 (0.071)	−0.933 (0.047)	−0.972 (0.037)	−0.696 (0.029)
1960	−0.805 (0.035)	−1.129 (0.087)	−1.028 (0.058)	−1.149 (0.045)	−0.851 (0.035)
1965	−0.918 (0.044)	−1.188 (0.119)	−1.223 (0.083)	−1.446 (0.072)	−1.010 (0.050)
1970	−1.063 (0.060)	−1.246 (0.172)	−1.474 (0.129)	−1.728 (0.139)	−1.160 (0.098)
1975	−1.230 (0.103)	−1.280 (0.307)	−1.766 (0.258)	−2.318 (0.362)	−1.361 (0.340)
Deviance (df = 84)	18,903.2	9,243.4	1,479.8	245.3	611.0
Overdispersion	224.3	109.7	17.5	2.9	7.3

Note: Numbers in parentheses are standard errors.

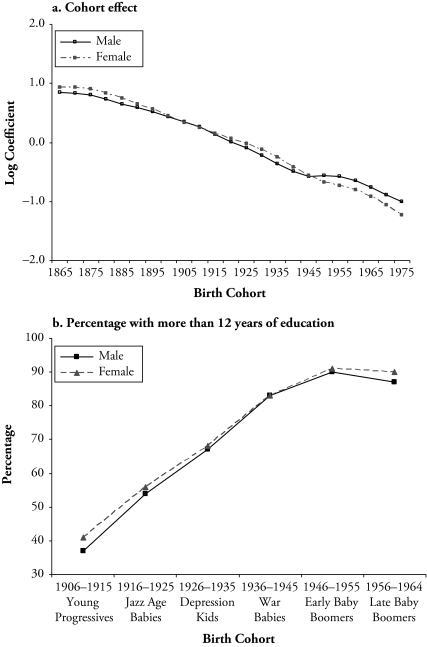
Figure 4.

Cohort Effects of Mortality for All Causes, by Sex

Note: The top panel shows the intrinsic estimates of the cohort effects of U.S. mortality for all causes for men and women that are reported in Table 2. The bottom panel shows the percentage of people with 12 years of education or more, including high school graduate, some college, and college degree or more. This figure reproduces the table on educational attainment by gender and cohort using the Integrated Public Use Microdata Series (IPUMS 2003) that was published in Hughes and O’Rand (2004: table 2).

Figure 6.

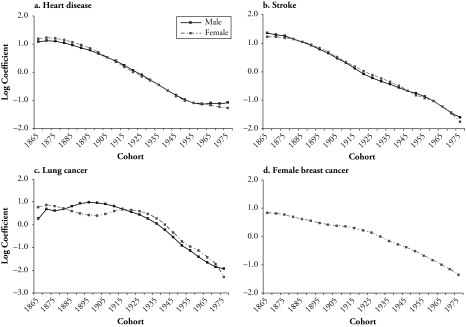
Intrinsic Estimates of Cohort Effects of Mortality, by Cause and Sex

The IE analysis of the total mortality change shows the dominance of age and cohort effects over period effects. When all three factors are considered in the APC models, there seem to be only modest period effects but substantial cohort effects. The finding of mortality declines by cohort largely supports the contention that nutrition, reduced exposure to disease, and improved medical measures all contributed to increasing health capital in more recent cohorts that improved cohort survival. And cohort trends in educational attainment may be one important mechanism through which these influences were realized.

Figure 4 shows that cohort differences in total mortality mirror cohort changes in education levels for cohorts born from the mid-1900s through the mid-1960s. Cohort effects on mortality show persistent declines from early cohorts until that of the early baby boomers (1946–1955) and decreases in the rates of declines for males. The data on cohort educational attainment show that succeeding cohorts from the Young Progressives (1906–1915) to the early baby boomers have increasingly higher proportions of high school graduates and those with some college education. Although the baby boomers (1946–1964) had higher levels of education than their parents born in the Jazz Age (1916–1925) and the Depression Era (1926–1935), the educational achievement leveled off across the baby boomer cohorts. The gender-specific attainments show a slight drop of education level among late–baby boomer men and an educational advantage for late–baby boomer women (Hughes and O’Rand 2004). Furthermore, there is evidence that this trend has continued among cohorts younger than the baby boomers (Gamoran 2001). These patterns correspond well with the slowdown in recent cohort mortality decline among males and the relatively smoother progressive decline among females.

Age effects of mortality attributable to heart disease generally exhibit exponential increases, and this is consistent with previous findings. There is also a notable sex difference in the rates of changes in mortality risks with age. Although women’s mortality risks show log-linear increases with age, those for men show a faster increase before age 55 but a slower increase afterward. The decrease of the acceleration rate occurring in middle-aged men is intriguing. A conventional view relates this change in sex difference to hormonal effects that may protect premenopausal women against higher cholesterol levels, a benefit lost in postmenopausal women. However, a review of recent studies indicated that menopause has no discernible effect on the age pattern of coronary heart disease and that male midlife mortality change is more compatible with a change in male hormones than with menopause (Barrett-Connor 1997).

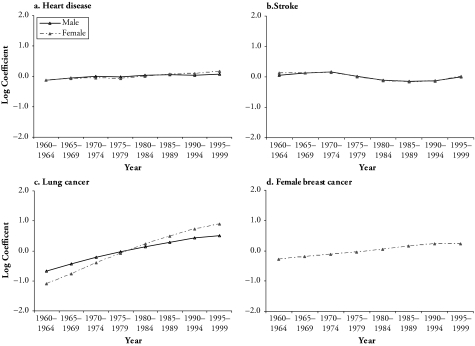
Similar to the period trends in total mortality, period effects of heart disease mortality are small when simultaneously estimated with the age and cohort effects, as shown in Figure 6. In contrast, cohort effects shown in Figure 5 suggest that both males and females had large monotonic declines in heart disease deaths for most of the pre–baby boomer cohorts. The declines slowed considerably for female cohorts, starting with the late baby boomers, and leveled off for the same male cohorts. These mortality changes for late baby boomers and more recent cohorts are similar to those found in the analysis of total mortality and, therefore, also reflect the cohort differences in socioeconomic attainment. The modest increase in heart disease mortality rates for the most-recent male cohorts also suggests the effects of changes in other major heart disease risk factors that are associated with nutritional and lifestyle choices.

Figure 5.

Intrinsic Estimates of Period Effects of Mortality, by Cause and Sex

Age effects of stroke mortality are similar to those of heart disease mortality. Gender differences in the growth rates differ across the adult ages. It has been suggested that estrogen has both neuroprotective and neurodeleterious effects, which may contribute to the variable sex mortality differences at different ages (Fullerton et al. 2002).

Period effects of stroke mortality are modest and comparable to those of heart disease mortality. Different from cohort effects of heart disease mortality, declines in stroke mortality are largely continuous from the earliest to the most recent cohorts, with no evident decrease in the rate of decline. This result is surprising in that heart disease and stroke mortality share several medical and social risk factors and should demonstrate similar patterns of mortality rates. Among the classic risk factors for heart disease, only LDL cholesterol has not been proven to be a strong risk factor for stroke (Barrett-Connor 1997). It can thus be inferred that cohort differences in LDL cholesterol levels play a role in the different cohort effects for the two causes of deaths. Possibly, late baby boomers and recent cohorts, especially males, have been disproportionately affected by behavioral changes, such as a diet high in animal fat that can lead to higher levels of LDL cholesterol.

Age effects of lung cancer death rates are concave: the risk of mortality increased rapidly from early adulthood to peaks near ages 80–85 and then leveled off. Compared with the relatively flat period effects of heart disease and stroke mortality, the period effects of lung cancer mortality show monotonic increases similar to those found in Belgium female population. Females had a steeper increase than males throughout the 40-year period. There were signs of reductions in tar and nicotine yield per cigarette in the United States from 1950 to 1995 (Hoffman, Djordjevic, and Brunnemann 1996), which should decrease the harmful effects of smoking. It is, therefore, possible that changes in cigarette composition do not affect lung cancer death rates until after a sufficiently long latency. It is also possible that changes in mortality reflect more accurate diagnoses of lung cancer. However, no evidence shows dramatic increases in diagnosis of lung cancers during this period. Other factors need to be considered and are discussed in the subsequent section.

Cohort effects of lung cancer mortality are consistent with the expectation: mortality curves increased first and decreased for more recent cohorts, following an inverse U-shape. The decrease in the male cohort mortality that started after the turn of the twentieth century correlates with reduced initiation of cigarette smoking in young men during the Great Depression (1929–1933), as suggested by Tarone and Chu (2000a). However, the argument relating economic deprivation to reduced smoking does not seem to explain increased initiation of smoking and lung cancer deaths for the same female birth cohorts. Men and women also differ in birth cohorts that experienced the highest levels of lung cancer mortality: 1895–1900 for men and 1920–1925 for women. The lag of 25 years between the peaking male and female birth cohorts can be attributed to the sex differences in stages of cigarette diffusion. The subsequent decreases in mortality for more recent males and females may reflect the long-term benefits of increases in smoking cessation.

Age effects of female breast cancer mortality are large and fit the general description of the age variations of breast cancer risks that are described as the “Clemensen’s hook” (Clayton and Schifflers 1987b). Such an age pattern is indicative of the etiology of the disease: early (premenopausal) disease risk is more strongly genetically determined, and the increases in risk slow at menopause. The period effects are fairly small and indicate a similar upward trend with those of lung cancer mortality.

Cohort effects show a steady downward trend, suggesting continuous improvement in cohort survival from breast cancer. Such monotonic declines in mortality cannot be entirely related to changes in female fertility behaviors. Fertility rates dropped for the Depression and World War II cohorts; increased afterward until 1964, which produced the baby boomer cohorts; and decreased again since then (Easterlin 1987: figure 1.1). However, mothers of the baby boomer cohorts who had historically high fertility rates did not have lower mortality rates than their daughters or more recent cohorts of women who had lower fertility rates. Delaying childbearing and bearing fewer children affect the exposure of breast tissue to endogenous estrogen levels and may elevate the risks for breast cancer. Still, recent female cohorts had progressively lower breast cancer mortality rates, which is a cohort trend consistent with those in mortality from other causes. The combination of increased female education and labor force participation may delay or reduce childbearing, yet also enhance socioeconomic status in more recent female cohorts. Too, greater access to resources such as health insurance and medical care reduces risks of morbidity and mortality. The result may well imply that early exposures to, and accumulation of, these resources have substantial positive effects for survival from breast cancer.

DISCUSSION

I employed a new approach to APC analysis to examine the temporal change in the U.S. adult mortality from leading degenerative diseases and cancer during the second half of the twentieth century. The study improved previous estimates in several regards. First, the new modeling approach yields results that can serve as objective criteria for selecting the best among alternative summaries of data on mortality and provide a test of whether the observed pattern revealed in descriptive analysis is real or random. Second, delineation of different sources of variations in death rates brings clarity to the specific components of mortality dynamics in recent historical period and highlights important period- and cohort-specific factors that are operational in the declines in the population risks of chronic diseases and improvement in general health conditions. Third, the empirical assessment of mortality trends from the most recent data available may help to generate theoretical insights into continuing mortality reductions in the United States and reveal previously unknown forces affecting health and mortality conditions in this country that likely will continue.

The analyses show that the large mortality reductions from the 1960s to the 1970s continued well into the late 1990s. The analyses also relate these temporal patterns of mortality to specific demographic components by delineating age, period, and cohort effects. Related to each of these components are epidemiologic conditions determined by a host of biological, socioeconomic, and behavioral factors as well as public health and personal medical services. Whereas differences associated with age may primarily indicate different etiological factors underlying specific degenerative diseases, period and cohort variations reflect the effects of social change. There are three major findings.

First, these analyses provide new evidence on persistent cohort differences in mortality rates of all causes of deaths examined. The most striking finding is the dominance of cohort effects in explaining recent trends of mortality reductions. The results largely support the theory of technophysio evolution, which implies large cohort improvements in health capital and physiological capacities. The effects associated with birth cohorts reflect processes of differential cohort accumulation of health effects of lifetime exposures to risk factors: education, diet and nutrition, physical activity, and smoking. If the finding on cohort effects is valid, the assumption that the declines in death rates are fixed for different birth cohorts is violated, and standard models of period changes in death rates (such as those shown in descriptive analyses in and Eq. (3)) are misspecified. The role of cohort effects in mortality decline undeniably has serious implications for measurement and analysis.

Cohort effects for the four causes of death studied are generally consistent with the cohort patterns for total mortality and show substantial survival improvements across most birth cohorts. The cause-specific effects, however, differ from those of total mortality in more recent cohorts. For three causes of death examined, including stroke, lung cancer, and breast cancer, recent cohort declines were largely continuous. However, declines in total mortality slowed, starting from the baby boomer cohorts. This trend may be due to the stagnation in cohort declines of heart disease mortality, which is the leading cause of adult mortality in recent decades. It may also relate to other causes of death not included in this study. Further studies are needed to fully understand this difference.

Second, sex differences in the cohort effects are most evident for heart disease and lung cancer mortality. Cohort trends in heart disease mortality have shown similar de clines for earlier male and female cohorts but diverged for recent male and female cohorts since the later-born baby boomers (1960–1964), with men experiencing a small increase and women continuing to decline at a slower rate. Although this pattern corresponds well with the differential cohort changes in educational attainments by sex, it may also be attributable to cohort differences in exposures to risk factors that are specific for heart disease, such as LDL cholesterol. Sex differences are largest for lung cancer mortality. The differential timing of initiations of cohort declines in lung cancer mortality by sex are consistent with the recent demographic finding of a lag of reduction in lung cancer deaths between men and women. This finding, therefore, sheds light on remote sources of gender differences in lung cancer mortality, such as stages of diffusion of cigarette consumption.

Third, period effects are generally small or modest when birth cohort and age effects are simultaneously controlled. Specifically, there is virtually no period effect for heart disease mortality and a very moderate decrease in stroke mortality since 1975. Lung cancer and breast cancer mortality show monotonically increasing, albeit small, period effects that suggest log-linear trends. This result is comprehensible in light of the hypotheses of independent period and cohort effects. Because successive cohorts experienced more favorable historical and social conditions, they not only had lower exposure levels to socioeconomic, behavioral, and environmental risk factors, but they also benefited from reduction in the exposure earlier in life course than previous cohorts. In this sense, mortality reductions as a consequence of advancements in medical measures—namely, those measures that tend to persist after they are introduced and are found to be effective—manifest as cohort declines because the cumulative effects are more pronounced in successive cohorts compared with periods.

The finding of weak period effects relative to the cohort effects is surprising in light of strong period changes shown in previous and present descriptive analyses (e.g., Kannisto et al. 1994)15 but largely consistent with previous findings from epidemiologic studies using APC modeling (see, e.g., Osmond 1985). It suggests that the anticipated mortality declines have been mostly captured by cohort effects rather than by period effects. The insights from descriptive analysis further suggest that this is not likely to be an artifact of the modeling. As discussed earlier, nonparallelism among age curves across time periods suggests differential period changes in mortality by age groups or a special form of age by period interaction related to cohort effects. However, evidence for nonparallelism among age curves across cohorts, which relates to period effects, is restricted to cancer-related mortality; the degree of nonparallelism is smaller, suggesting smaller magnitudes of these effects.

The increasing period effects of cancer related mortality is intriguing. Whereas increases in breast cancer mortality may be related to marked increases in breast cancer incidence rates due to expanded use of effective diagnostic techniques, such as mammography, and the increasing obesity epidemic among adult women, increases in lung cancer mortality are not likely to be affected by such changes. Future research should further investigate the role of period changes in drug use and air pollution in explaining this trend.

An alternative explanation to the increasing period effects is that they represent a special age-cohort interaction implied by the APC modeling framework. Recent cohorts, exposed to new favorable epidemiologic conditions for earlier in life, may experience greater delays of deaths to more advanced ages than cohorts who are already old at the time of exposure to these conditions (Guillot 2006). The postponement of proportions of deaths in succeeding cohorts to older ages may create a seemingly increasing period trend. Such a trend may actually result from the beneficial effects of early cancer detection and treatment of cancer patients. Supplementary analyses suggest evidence in the changing composition of death distributions by cause. The years between 1960 and 1999 saw an approximate 50% increase in proportions of lung cancer deaths and a 42% increase in proportions of breast cancer deaths within the elderly population (65 and older) in the United States. The increases were much smaller for heart disease (12% for females and 18% for males) and stroke (10% for females and 6% for males), consistent with their smaller period effects. Combining the estimated period and cohort effects, one can infer not only marked decreases in the level of mortality across cohorts but also postponement in the timing of deaths across cohorts between 1960 and 1999, especially for cancer-related deaths.

In conclusion, this study focused on adult, cause-specific mortality in the United States for a relatively short period in the late twentieth century. One should not infer that birth cohort declines in mortality are always dominant in other cases. Period effects likely are more prominent in times of wars or other major events that have massive social impacts, as is the case for French male mortality during World War II (Wilmoth 1990). Additional studies are needed to systematically examine the temporal components of mortality attributable to other causes and other demographic outcomes such as fertility. Comparison of results across societal contexts in different historical periods may shed light on a more general demographic theory of period and cohort dependence of changes in vital rates.

The study of sources of variations in mortality can be used as a triage for a refined analysis of explanatory factors underlying period and cohort processes of change. Knowledge gained from such combined analysis can provide specific clues to improve the prospect of future mortality reductions. For instance, period increases in lung cancer mortality and stagnation of recent cohort declines in heart disease mortality may be closely related to contemporaneous social patterns of health behaviors, such as cigarette smoking, drug use, a high-fat and high-cholesterol diet, and a sedentary life style. Even without major biomedical advances (e.g., in stem cell and genomic therapies), if greater social and public health efforts are directed toward modifications of these debilitative behaviors and other unfavorable environmental factors, then the mortality reductions will continue into the twenty-first century.

APPENDIX: THE COMPUTATIONAL ALGORITHM OF THE INTRINSIC ESTIMATOR (IE)

1. Compute the eigenvectors u₁, . . ., u_r of matrix X^TX, where X denotes the design matrix of model (1). Normalize them with ||u_m|| = 1, . . ., r, and denote the orthonormal matrix as U = (u₁, . . ., u_r)^T.

2. Identify the special eigenvector B₀ corresponding to eigenvalue 0. Denote u₁ = B₀ without loss of generality.

3. Select the principal components to be the remaining eigenvectors u₂, . . ., u_r with nonzero eigenvalues.

4. Fit a principal components regression (PCR) model with the outcome variable of interest (e.g., logged death rates) as the response using a design matrix V whose column vectors are the principal components u₂, . . ., u_r—that is, V = (u₂, . . ., u_r)—to obtain the coefficients (w₂, . . ., w_r).

5. Set coefficient w₁ equal to 0 and transform the coefficients vector w = (w₁, . . ., w_r)^T by the orthonormal matrix U = (u₁, . . ., u_r)^T to obtain the intrinsic estimator B = Uw.

Note that instead of using reference categories, the IE uses the “usual ANOVA-type constraints” that the sums of the respective age, period, and cohort coefficients equal zero. The computational algorithm used by the IE estimates effect coefficients for each of the a – 1, p – 1, and a + p – 2 age, period, and cohort categories, respectively, which is consistent with the definition of the parameter vector in Eq. (1). Then the IE uses the zero-sum constraints to obtain the numerical values of the deleted age, period, and cohort categories. See also Footnote 5, which explains the applicability of the IE to other forms of linear models.