Retrospective Information on Health Status and its Application for Population Health Measures

Abstract

Healthy life expectancies are almost always calculated by using health data from cross-sectional surveys. This type of calculation is done partly because data from longitudinal surveys are not always available, and when they are available, they are collected at intervals that are longer than one year. In such cases, collecting health information retrospectively for the years skipped by the survey is useful. The main purpose of this paper is to show how retrospective health information can be used to estimate life expectancies in different health states. Healthy life expectancies are estimated with and without using data on retrospective health information, and the corresponding estimates are compared. The two sets of estimates are similar. We conclude that retrospectively assessed health information based on a one-year recall period can be used to estimate years of life in various health states and that estimates based on such information will closely approximate estimates based on concurrent health information.

A recent report prepared for the World Health Organization (WHO) noted that as of 1998, healthy life expectancies were being calculated in 49 countries, 20 of which were developed market-economy countries. The report further pointed out that in almost all cases, healthy life expectancies were calculated based on health data from cross-sectional surveys (Robine and Romieu 2000). Although it is preferable to calculate healthy life expectancies based on health data from longitudinal surveys, such data are rarely available. Even in the United States, most of the health data that are being collected are based on cross-sectional surveys (Sondik 2002), partly because longitudinal surveys are more difficult to conduct, time consuming, and expensive (Freedman et al. 1988).1

Even when such data are available, they may be collected at intervals longer than considered suitable for assessing change in health with reasonable confidence. For example, in the first Longitudinal Study of Aging of the U.S. population aged 70 and older, the mean delays between interviews for the periods 1984–1986, 1986–1988, and 1988–1990 were 2.2, 2.1, and 1.9 years, respectively (Lièvre, Brouard, and Heathcote 2003). A possible way to overcome the problem of a long duration between rounds of a longitudinal survey is to collect retrospective information on health and to use such data to estimate health transitions over a shorter period.

Retrospective information has been collected in cross-sectional and longitudinal surveys, and retrospective histories have been used to study demographic processes, such as marriage and divorce, fertility, mortality, and migration (United Nations Population Fund 1993). Such information has also been employed to analyze life-cycle events (Peters 1988), to determine treatment outcomes (Aseltine et al. 1995), and to analyze prenatal and perinatal events (Buka et al. 2004). Data with retrospective information are analyzed by using the same statistical techniques used for analyzing data with current information. For example, Allison (1995) showed that survival analysis applicable with current information could be equally applicable with retrospective information.

The main purpose of this paper is to show how retrospective health information can be used to estimate life expectancies in different health states. Life expectancies in various health states are estimated by using a multistate (increment-decrement) life-table model and longitudinal survey data. We use a respondent’s assessment of his health one year ago together with his assessment at the time of the survey (which we call “concurrent”) to estimate life expectancies in various health states. We then compare these estimates with corresponding life expectancies estimated by using concurrent information from three successive interviews.

DATA AND METHODS

Model Specification

Health measures that integrate mortality and morbidity are usually estimated by using the life-table approach. The two models that are most frequently used for estimating healthy life expectancy are (1) the Sullivan method or the prevalence-rate table (Rogers, Rogers, and Belanger 1990) and (2) the multistate life-table model. The models differ both in the type of life table and in the health data that they use for calculating healthy life expectancies. The Sullivan method uses a single-decrement life-table and health data from a single cross-sectional survey (Molla, Wagener, and Madans 2001, 2004), whereas the multistate life-table model uses an increment-decrement life-table and health data from at least two interviews of a longitudinal survey (Rogers, Rogers, and Belanger 1989). The multistate life-table model has the advantage of generating life expectancies in different health states while accounting for the probability of recovery (Crimmins, Hayward, and Saito 1996; Hayward, Friedman, and Chen 1996; Land, Guralnik, and Blazer 1994; Schoen 1988).

In this study, healthy life expectancies are estimated based on a multistate life-table model with four health states. Health State 1 stands for excellent/very good health, Health State 2 represents good health, and fair/poor health is defined as Health State 3. Death, which is an absorbing state, is State 4. Because the first three health states are transient, individuals may move from one health state to another from one year to the next.

Expected years in each health state are calculated by using the IMaCh computer program. IMaCh is a maximum-likelihood program that makes use of the Markov Chains and is developed by the Institute d’Etudes Démographiques (INED Paris). It calculates probabilities of transition from one health state to another, total life expectancy, and life expectancies in different health states. It also uses sample survey weights and covariates through a multinomial logistic regression. The program outputs both population- and status-based life-table estimates. The program calculates expected life in various health states based on health transition probabilities (Lièvre et al. 2003) from longitudinal data and incorporates a statistical method developed by Laditka and Wolf (1998) for estimating health transition probabilities for intervals of varying lengths.

The multistate life-table model defines a one-step health transition probability as Eq. (1):

$$P_{ij}=\text{pr}(STATU{S}_{t+1}=j|STATU{S}_t=i).$$ (1)

That is, the probability of occupying any health state at any given age in year (t + 1) depends on the health state occupied in year (t). In this study, STATUS stands for excellent/very good, good, or fair/poor health.

The annual health transition probabilities for the model can be arranged in a four by four matrix and given by Eq. (2):

$${}_n{P}_x=\left[\begin{array}{cccc}{}_n{p}_x^{11}& {}_n{p}_x^{12}& {}_n{p}_x^{13}& {}_n{p}_x^{14}\\ {}_n{p}_x^{21}& {}_n{p}_x^{22}& {}_n{p}_x^{23}& {}_n{p}_x^{24}\\ {}_n{p}_x^{31}& {}_n{p}_x^{32}& {}_n{p}_x^{33}& {}_n{p}_x^{34}\\ 0& 0& 0& 1\end{array}\right],$$ (2)

where P = health transition probability, x = age, n = number of years, 1 = excellent/very good health, 2 = good health, 3 = fair/poor health, and 4 = death. Because transition from death to any other health state is impossible, in the fourth row of the matrix, P₄₁ = P₄₂ = P₄₃ = 0 and P₄₄ = 1; death is an absorbing state.

The probability of a person being in a health state at a given time (t + 1), given the person’s health state at a prior time (t), is calculated for the total study sample as well as separately for each of the four subsamples (men and women, and those with and without college education). The health transition probabilities for each of the four population subgroups are estimated based on parameters of a multinomial logistic regression (Cox 1972), stated as follows in Eq. (3):

$$\text{ln}\left[\frac{{}_n{P}_x^{ij}}{{}_n{P}_x^{ii}}\right]={\beta }_{ij0}+{\beta }_{ij1}{\text{Age}}_x+{\beta }_{ij2}\text{Sex}+{\beta }_{ij3}\text{Education},$$ (3)

where age is measured in single years; sex is coded as 1 for female and 0 for male; and education is coded as 1 for at least one year of college education and as 0 for high school education or less.

For each population subgroup, a synthetic cohort of 100,000 individuals exactly 65 years old is created and used to generate life expectancies in the various health states. The health transition probabilities are calculated as explained in Appendix A. The method assumes that the underlying process is Markovian.

The mutually exclusive pathways of health transitions for a person who was in Health State 1 (excellent/very good health) at age (x) and in Health State 3 (fair/poor health) at age (x + 2), for example, are 113, 123, or 133 with corresponding transition probabilities of (P₁₁ × P₁₃), (P₁₂ × P₂₃), and (P₁₃ × P₃₃). The probability of being in Health State 1 at age (x) and in Health State 3 subsequently and dying before age (x + 2) is simply P₁₃. The overall probability of ending up in a fair/poor state of health, given that the person was in an excellent/very good health state at baseline, and assuming a baseline interview and two subsequent interviews at an interval of one year each is given by Eq. (4):

$$[P_{13}+(P_{11}\times P_{13})+(P_{12}\times P_{23})+(P_{13}\times P_{33})].$$ (4)

Source of Data and the Study Sample

The data used to illustrate the application of the method are from the 1999, 2000, and 2001 Medicare Concurrent Beneficiary Surveys (MCBS). The MCBS is a longitudinal panel survey, which surveys Medicare beneficiaries aged 65 and older as well as disabled Medicare beneficiaries younger than age 65. Three survey rounds are conducted each year. The annual sample size is about 12,000 completed interviews and includes community dwellers as well as the institutionalized population. The survey follows a rotating panel design with one-third of the sample replaced each year. The survey collects data on demographic characteristics as well as health and functioning status in the September–December round every year (Adler 1994; Centers for Medicare and Medicaid Services 2000). The study sample consists of 4,446 non-Hispanic white males and females aged 70 and older who were interviewed in the September to December round in 1999, and survivors were interviewed in 2000 and 2001. The number of persons in other race groups was too small to analyze separately.2

Imputed Health Status Data

To illustrate the use of retrospective information on health, we estimated life expectancies by health state twice. Life expectancies by health states were estimated first, using concurrent health status information for 1999, 2000, and 2001; again, assuming that the 2000 interview year was skipped; and then using concurrent health status information for 1999 and 2001 as well as imputed retrospective health status information for 2000.

Retrospective health status information for 2000 was inferred by using two questions on health status at the time of the 2001 interview. Data were inferred both for those who were still alive at the time of the 2001 interview and for those who died in the 12 months prior to the 2001 interview. Respondents who were still alive during the 2001 interview were asked first to assess their general health at the time of the interview—compared with the health of other persons of the same age—as excellent, very good, good, fair, or poor. They were then asked to compare their health status at the time of the interview with their health status one year earlier. The response items were (a) much better now than one year ago, (b) somewhat better now than one year ago, (c) about the same, (d) somewhat worse now than one year ago, and (e) much worse now than one year ago. Based on the responses to these questions, we impute the 2000 health status data for those alive at the time of the 2001 interview based on the assumptions given in Appendix B.

At baseline in 1999, 4,446 individuals were included in this study. By the end of the September–December 2001 interview, 772 members of the study sample were dead (Table 1). Of these, 335 died after the 2000 interview but prior to the 2001 interview. Even if the 2000 interview year was skipped, these deaths would still be reported at the time of the 2001 interview, and date of death would be known. However, unless health status data were collected via proxy in 2001, there would be no data on their 2000 health status.

Table 1.

Health Status by Data Type and Sex: Non-Hispanic White Persons Aged 70 Years and Older, 1999–2001

Health Status	1999		2000 Concurrent		2000 Retrospective		2001
	Number	%	Number	%	Number	%	Number	%
Total	4,446	100.0	4,446	100.0	4,446	100.0	4,446	100.0
Excellent/Very Good	1,826	41.1	1,706	38.4	1,803	40.6	1,508	33.9
Good	1,456	32.7	1,332	30.0	1,386	31.2	1,222	27.5
Fair/Poor	1,164	26.2	971	21.8	820	18.4	944	21.2
Dead	0	0.0	437	9.8	437	9.8	772	17.4

Source: The Medicare Current Beneficiary Survey, Center for Medicare and Medicaid Services, U.S. Department of Health and Human Services.

Based on their 1999 health status, we consider three assumptions about the 2000 health status of these individuals. First, their health status at the time of the 2000 interview was the same as their health status at the time of the 1999 interview. Second, for persons in Health Status 1 or 2 at the time of the 2000 interview, their health status was assumed to be one step lower than their health at the 1999 interview. Third, for persons in Health Status 1 at the time of the 2000 interview, their health status was assumed to be two steps lower than in 1999. Life expectancies were estimated under each assumption and compared. As expected, healthy life expectancy estimates based on the second assumption were consistently smaller than estimates based on the first assumption yet slightly larger than estimates based on the third. To avoid possible over- or underestimation bias, the estimates based on the second assumption were chosen for the overall analysis.

RESULTS

Health Transition States, 2000–2001

At the time of the 2000 interview, based on reported (concurrent information) health status (Table 1), 1,706 respondents (38%) were in excellent/very good health; 1,332 (30%) were in good health; and 971 (22%) were in fair/poor health. The retrospectively inferred health status information indicated that at the time of the 2000 interview, 1,803 (41%) of the 4,009 survivors would be in excellent/very good health; 1,386 (31%) would be in good health; and 820 (18%) would be in fair/poor health.

Health status at the time of the 2001 interview was compared with both the concurrent and retrospectively inferred health status at the time of the 2000 health interview, and changes in health status were noted. The retrospective information implied a seven-percentage-point drop in excellent/very good health, a four-percentage-point drop in good health, and a three-percentage-point rise in fair/poor health. The concurrent information, on the other hand, showed a five-percentage-point drop in excellent/very good health, almost a three-percentage-point drop in the percentage of good health, and no change in fair/poor health. The percentage who were deceased rose by about eight percentage points. Overall, the retrospective information implied a relatively larger change in health status between 2000 and 2001.

Health Transition Probabilities

Table 2 and Table 3 present a set of one-step health transition probabilities, by sex, at selected ages, for the interval 1999 to 2000. Table 2 shows probabilities of a health status decline by sex and age, and Table 3 presents probabilities of a health status improvement by sex and age. The probabilities of moving from one health state to another for the total sample shows the expected gradients by age both for worsening health and recovery. The health transition probabilities also confirm the positive correlation between aging and poor health. That is, as age advances, the probability of transition from good to poor health rises, while the probability of transition from poor to good health declines. However, some variations are observed between corresponding health transition probabilities estimated by using the two types of data. Compared with the probabilities estimated by using concurrent health status information, probability estimates based on retrospective health information indicate a smaller chance of transition from good to excellent/very good health as well as a larger chance of transition from good to fair/poor health.

Table 2.

Probabilities of a Health Status Decline by Estimation Method, Age and Sex: Non-Hispanic White Persons, 1999–2000

Age	Transition Probabilities						Concurrent – Retrospective
	Excellent/Very Good to Good		Good to Fair/Poor		Excellent/Very Good to Fair/Poor		Excellent/Very Good to Good	Good to Fair/Poor	Excellent Very Good to Fair/Poor
	Concurrent	Retrospective	Concurrent	Retrospective	Concurrent	Retrospective
Male
70	0.193 (0.013)	0.166 (0.012)	0.180 (0.014)	0.207 (0.015)	0.034 (0.004)	0.036 (0.006)	0.027*	–0.027*	0.002
75	0.210 (0.011)	0.188 (0.010)	0.205 (0.010)	0.237 (0.011)	0.046 (0.005)	0.042 (0.005)	0.021*	–0.031*	0.004
80	0.225 (0.012)	0.211 (0.011)	0.232 (0.012)	0.268 (0.013)	0.061 (0.007)	0.048 (0.006)	0.014*	–0.036*	0.013*
85	0.235 (0.014)	0.232 (0.014)	0.256 (0.015)	0.298 (0.016)	0.079 (0.009)	0.054 (0.007)	0.003	–0.042*	0.025*
90	0.236 (0.018)	0.247 (0.019)	0.277 (0.022)	0.324 (0.023)	0.099 (0.014)	0.059 (0.010)	–0.011	–0.047*	0.039*
Female
70	0.216 (0.014)	0.180 (0.012)	0.172 (0.014)	0.212 (0.015)	0.036 (0.005)	0.035 (0.012)	0.036*	–0.040*	0.000
75	0.235 (0.010)	0.205 (0.010)	0.198 (0.010)	0.243 (0.011)	0.048 (0.005)	0.041 (0.012)	0.031*	–0.045*	0.007
80	0.253 (0.009)	0.230 (0.009)	0.225 (0.009)	0.276 (0.009)	0.064 (0.005)	0.047 (0.012)	0.023*	–0.051*	0.016*
85	0.267 (0.011)	0.256 (0.011)	0.251 (0.012)	0.308 (0.012)	0.083 (0.005)	0.054 (0.012)	0.012*	–0.057*	0.029*
90	0.275 (0.017)	0.280 (0.017)	0.275 (0.017)	0.338 (0.018)	0.106 (0.011)	0.061 (0.012)	–0.005	–0.063*	0.045

Notes: Sample persons entered the Medicare Current Beneficiary Survey in 1998 and 1999 and were interviewed in 1999, 2000, and 2001. Retrospective = estimates based on data that included retrospective health information. Concurrent = estimates based on data with concurrent health information only.

^*p < .05

Table 3.

Probabilities of a Health Status Improvement by Estimation Method, Age and Sex: Non-Hispanic White Persons, 1999–2000

Age	Transition Probabilities						Concurrent – Retrospective
	Good to Excellent/Very Good		Fair/Poor to Good		Fair/Poor to Excellent/Very Good		Good to Excellent/Very Good	Fair/Poor to Good	Fair/Poor to Excellent/Very Good
	Concurrent	Retrospective	Concurrent	Retrospective	Concurrent	Retrospective
Male
70	0.285 (0.019)	0.237 (0.018)	0.297 (0.024)	0.291 (0.026)	0.055 (0.011)	0.096 (0.017)	0.048*	0.006	–0.040*
75	0.273 (0.015)	0.223 (0.014)	0.279 (0.018)	0.253 (0.018)	0.059 (0.010)	0.091 (0.013)	0.050*	0.026*	–0.032*
80	0.258 (0.014)	0.207 (0.013)	0.256 (0.016)	0.214 (0.015)	0.062 (0.009)	0.084 (0.011)	0.051*	0.042*	–0.022*
85	0.240 (0.014)	0.190 (0.013)	0.229 (0.018)	0.174 (0.015)	0.063 (0.011)	0.075 (0.012)	0.051*	0.055*	–0.011
90	0.217 (0.018)	0.169 (0.016)	0.199 (0.021)	0.136 (0.016)	0.063 (0.013)	0.064 (0.013)	0.048*	0.063*	–0.001
Female
70	0.288 (0.019)	0.234 (0.018)	0.265 (0.018)	0.365 (0.028)	0.061 (0.012)	0.083 (0.015)	0.054*	–0.100*	–0.022*
75	0.277 (0.014)	0.221 (0.018)	0.253 (0.018)	0.328 (0.018)	0.066 (0.009)	0.081 (0.011)	0.057*	–0.075*	–0.015
80	0.264 (0.010)	0.206 (0.013)	0.239 (0.018)	0.289 (0.013)	0.071 (0.008)	0.078 (0.008)	0.058*	–0.050*	–0.006
85	0.248 (0.012)	0.189 (0.009)	0.222 (0.018)	0.248 (0.014)	0.076 (0.008)	0.073 (0.009)	0.059*	–0.025*	0.003
90	0.228 (0.016)	0.170 (0.010)	0.203 (0.018)	0.206 (0.017)	0.079 (0.012)	0.066 (0.011)	0.058*	–0.003	0.013

Notes: Sample persons entered the Medicare Current Beneficiary Survey in 1998 and 1999 and were interviewed in 1999, 2000, and 2001. Retrospective = estimates based on data that included retrospective health information. Concurrent = based on data with concurrent information only.

^*p < .05

Also compared with probability estimates based on data with concurrent health information, probability estimates based on data with retrospective information show a larger chance of transition from fair/poor to good health or even from fair/poor to excellent/very good health at younger ages. On the other hand, at older ages, the probability estimates based on data with concurrent health information show a larger chance of transition from fair/poor to good as well as from fair/poor to excellent/very good health.

Life Expectancies in Various Health States

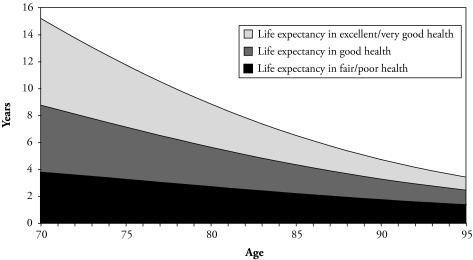
Life expectancies were estimated for the total sample using data that includes retrospective information on health (Figure 1). The expected years in each of the three health states fall with age. On average, a 70-year-old person would expect to spend 6.4 years of his/her remaining life in excellent/very good health, 5.0 years in good health, and only 3.8 years in fair/poor health. On the other hand, a 95-year-old person would expect to spend only 1.0 year of his/her remaining life in excellent/very good health, 1.1 years in good health, and 1.3 years in fair/poor health. As would be expected, the proportion of life spent in excellent/very good health is higher at younger ages, and the proportion of life spent in fair/poor health is higher at older ages.

Figure 1.

Life Expectancy in Each of the Three Health States Estimated Using Data With Retrospective Information on Health Status: Non-Hispanic White Persons, 1999–2001

We estimate life expectancies in each of the three health states separately for males and females, using data with and without retrospective information on health (Table 4). Life expectancies in each health state, estimated on retrospective information, are very close to corresponding estimates based on concurrent health status information. This is true for almost all ages for males and females. We also estimate life expectancy in the various health states for those with at least one year of college education and those with no college education (data not shown in the table). Again, corresponding estimates from the two data sets do not differ by large amounts. As would be expected, these tables also show that the share of life expectancy to be spent in excellent/very good health declines with age for each group and that the share of life expectancy expected to be spent in fair/poor health increases with age.

Table 4.

Life Expectancy in Years (and standard errors) in Different Health States, Estimated Using Retrospectively Inferred and Concurrent Health Status Information: Non-Hispanic White Males and Females, 1999–2001

Age	Life Expectancy in Each Health State						Difference in Years
	Excellent/Very Good		Good		Fair/Poor		Excellent/Very Good	Good	Fair/Poor
	Concurrent	Retrospective	Concurrent	Retrospective	Concurrent	Retrospective
Male
70	5.94 (0.19)	6.05 (0.21)	4.37 (0.17)	4.11 (0.17)	3.04 (0.18)	3.14 (0.17)	–0.11*	0.25*	–0.09*
75	4.26 (0.15)	4.23 (0.17)	3.34 (0.14)	3.18 (0.14)	2.54 (0.15)	2.64 (0.14)	0.02	0.17*	–0.10*
80	2.94 (0.14)	2.87 (0.15)	2.47 (0.12)	2.37 (0.12)	2.06 (0.13)	2.14 (0.12)	0.07	0.10	–0.09*
85	1.97 (0.14)	1.90 (0.15)	1.77 (0.11)	1.72 (0.11)	1.62 (0.12)	1.70 (0.11)	0.06	0.04	–0.08*
90	1.28 (0.13)	1.25 (0.14)	1.23 (0.10)	1.23 (0.10)	1.26 (0.12)	1.32 (0.11)	0.03	0.00	–0.06
Female
70	6.64 (0.15)	6.87 (0.17)	5.57 (0.16)	5.64 (0.16)	4.53 (0.22)	4.25 (0.18)	–0.23*	–0.07	0.28*
75	4.89 (0.12)	4.90 (0.14)	4.37 (0.13)	4.45 (0.13)	3.88 (0.18)	3.67 (0.15)	–0.01	–0.08	0.21*
80	3.49 (0.13)	3.37 (0.13)	3.31 (0.12)	3.38 (0.12)	3.22 (0.17)	3.05 (0.14)	0.12*	–0.07*	0.17*
85	2.41 (0.13)	2.25 (0.14)	2.42 (0.12)	2.48 (0.12)	2.59 (0.16)	2.46 (0.13)	0.16*	–0.05	0.13*
90	1.61 (0.13)	1.47 (0.13)	1.72 (0.12)	1.77 (0.12)	2.04 (0.16)	1.93 (0.14)	0.14*	–0.04	0.11*

Notes: Based on transition probabilities for those entering sample in 1998 and 1999 and interviewed in 1999, 2000, and 2001 in the Medicare Current Beneficiary Survey.

^*p < .05

The comparison also shows that corresponding life expectancy estimates (Table 4) are much closer than corresponding health transition probabilities (Tables 2 and 3). This is expected for a number of reasons. First, although each health transition probability is based on a one-step health transition, the corresponding life expectancy represents the net result of the transitions from healthy to unhealthy state and the transition from unhealthy to healthy state. Second, although Tables 2 and 3 present a set of health transition probabilities over a single one-year interval, the life expectancies were estimated based on the combination of transition probabilities of two single-year intervals.

CONCLUSION

Ever since WHO defined health as “a state of complete physical, mental and social well-being” and recommended that “person-years of life in health” be calculated and be compared with the total person-years of life (WHO 1974), health measures that integrate mortality and morbidity have become the preferred tools of assessing the overall health of populations in most developed and many developing countries. In the United States, for example, the importance of accounting for both mortality and morbidity in measuring population health has been recognized since the late 1960s (Sanders 1964; Sullivan 1969, 1971a, 1971b; U.S. Department of Health, Education, and Welfare 1969). In Europe, the Organization for Economic Cooperation and Development (OECD) started producing a report on healthy life in 1973 (OECD 1973). Also, more recently, the report of the Institute of Medicine of the U.S. National Academy of Sciences reaffirmed the increasing relevance of summary measures of population health that integrate mortality and morbidity for both public health and medical decision-making (Field and Gold 1998). One aspect of health measurement on which little research has been done is the usefulness and quality of information on health status collected between two or more consecutive waves through retrospective questions, especially when follow-up is conducted at intervals that are more than one year apart. Hence, the focus of this study is on this particular data-related issue.

This study compares estimates of health transitions and life expectancies based on retrospective reports to estimates-based concurrent data. The findings show that retrospectively assessed health information based on a one-year recall period can be used to estimate years of life in various health states and that estimates based on such information will closely approximate estimates based on concurrent health information. Several points emerge for future studies. First, although we use retrospectively inferred health status to illustrate the application of the method, retrospective information can be collected in all areas of health, including activity and functional status. Second, we use inferred retrospective health status based on assumptions necessitated by the nature of the available health data. However, the method may be applicable without using those assumptions if survey respondents were asked about their health with direct questions, such as, “Would you say your health in general was excellent, very good, good, fair/poor last year this time?”

Third, in collecting retrospective information on health, one also needs to be aware of the issue of post hoc rationalization about prior health. Researchers who compared progressive and retrospective measurements of change in health status found that responses to transition items were positively skewed. That is, in a one-year interval, more people reported an improvement in health than deterioration (Perneger, Etter, and Rougemont 1997). However, in another similar study, no such difference was found in a 12-week interval (Middel et al. 2006). Researchers have also shown that such biases in response may be minimized, and the accuracy and reliability of information collected retrospectively may be improved if survey questionnaires include retrospectively collected, data quality–enhancing techniques, such as a life history calendar (Freedman et al. 1988). Fourth, collecting information on retrospective health status could be considered both for those who are alive at the time of the second and all subsequent interviews as well as those who die between interviews. Collecting retrospective information on the health of both survivors as well as those who die between interviews (through a proxy, or next of kin) could prove to be both parsimonious and cost effective.

APPENDIX A. MODEL SPECIFICATION OF HEALTH TRANSITION PROBABILITIES

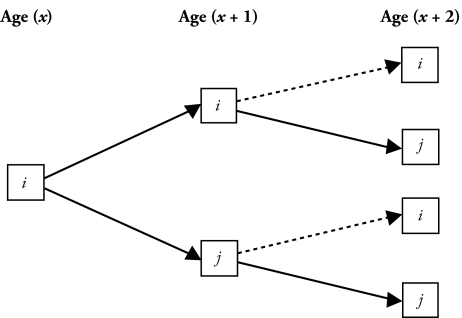
The mechanism through which the model transition probabilities are calculated can be explained by differentiating two distinct possibilities of survival. The first possibility is a person who was in state j at age (x + 1) and (x + 2), given that the person was in state i at

Appendix Figure A1.

Mutually Exclusive Paths of the Health Transitions

age (x) and alive at age (x + 2) or in state i at age (x + 1) and state j at age (x + 2), given that the person was in state i at age (x) and was alive at age (x + 2). The second possibility is that the person who was in health state j at age (x + 1), given that he (she) was in health state i at age (x) dies before reaching age (x + 2). For the first possibility, the mutually exclusive paths of the health transitions can be schematically presented as in Appendix Figure A1. For this possibility, the transition paths and the associated probabilities are presented as in Appendix Table A1.

The combined probabilities represent the two-year transition obtained by combining the two possible paths (solid lines) that are mutually exclusive. It may also be alternatively stated as

$$\begin{array}{l}\{[\text{Prob}(\text{state}(x+1)=i|\text{state}(x)=i)\times \text{Prob}(\text{state}(x+2)=j|\text{state}(x+1)=i]\hfill \\ \hspace{1em}+[\text{Prob}(\text{state}(x+1)=j|\text{state}(x)=i)\times \text{Prob}(\text{state}(x+2)=j|\text{state}(x+1)=j]\}.\hfill \end{array}$$

For the second possibility—that is, in which the person dies before age (x + 2)—the probability of being in state j at age (x + 1), given that the person was in state i at age (x), is stated with a probability P_ij; this probability can also be presented as [Prob state (x + 1) = j | state (x) = i].

The overall transition probability is then given by

$$(P_{ij}+P_{ii}\times P_{ij}+P_{ij}\times P_{jj}),$$

which reduces to the P_ij element of the matrix P² (Laditka and Wolf 1998). Another way of presenting the same probability is

$$\begin{array}{l}\{[\text{Prob}(\text{state}(x+1)=j|\text{state}(x)=i]\hfill \\ \hspace{1em}+[\text{Prob}(\text{state}(x+1)=i|\text{state}(x)=i)\times \text{Prob}(\text{state}(x+2)=j|\text{state}(x+1)=i]\hfill \\ \hspace{1em}+[\text{Prob}(\text{state}(x+1)=j|\text{state}(x)=i)\times \text{Prob}(\text{state}(x+2)=j|\text{state}(x+1)=j]\}.\hfill \end{array}$$

Appendix Table A1.

Transition Paths and Probabilities

Path	Probabilities by Path	Combined Probabilities
(1) iij (2) ijj	$\begin{array}{l}{P}_{ii}\times P_{ij}\\ P_{ij}\times P_{jj}\end{array}\}$	(Pii× Pij+ Pij× Pjj)

APPENDIX B. ASSUMPTIONS MADE TO CREATE THE 2000 HEALTH STATUS OF SURVIVORS RETROSPECTIVELY

The assumptions we made to create the 2000 health status of survivors retrospectively were as follows:

1. Individuals who responded to the question on their health one year ago, with the response “about the same,” were assigned the same health status for 2000 as their health status at the time of the 2001 interview.

2. Individuals who reported their 2001 health status as “somewhat better now than one year ago” were assigned health status for 2000 that is one step lower than reported during the interview.

3. Individuals who reported their 2001 health status as “much better now than one year ago” were assigned health status for 2000 that is two steps lower than reported during the interview.

4. Individuals who reported their 2001 health status as “somewhat worse now than one year ago” were assigned health status for 2000 that is one step higher than reported in the interview.

5. Individuals who reported their 2001 health status as “much worse now than one year ago” were assigned a health status for 2000 that is two steps higher than the health status reported in the interview.3

It is important to note that a question on self-reported health at the time of the survey and another question on health one year prior to the survey were used in the study because their format allows us to test our approach. However, it should also be noted that the method could have been illustrated with questions on activities of daily living (ADL) or instrumental activities of daily living (IADL) if retrospective questions on ADL or IADL were available.