The Exceptionally High Life Expectancy of Costa Rican Nonagenarians

Abstract

Robust data from a voter registry show that Costa Rican nonagenarians have an exceptionally high live expectancy. Mortality at age 90 in Costa Rica is at least 14% lower than an average of 13 high-income countries. This advantage increases with age by 1% per year. Males have an additional 12% advantage. Age-90 life expectancy for males is 4.4 years, one-half year more than any other country in the world. These estimates do not use problematic data on reported ages, but ages are computed from birth dates in the Costa Rican birth-registration ledgers. Census data confirm the exceptionally high survival of elderly Costa Ricans, especially males. Comparisons with the United States and Sweden show that the Costa Rican advantage comes mostly from reduced incidence of cardiovascular diseases, coupled with a low prevalence of obesity, as the only available explanatory risk factor. Costa Rican nonagenarians are survivors of cohorts that underwent extremely harsh health conditions when young, and their advantage might be just a heterogeneity in frailty effect that might disappear in more recent cohorts. The availability of reliable estimates for the oldest-old in low-income populations is extremely rare. These results may enlighten the debate over how harsh early-life health conditions affect older-age mortality.

Two key findings have emerged from recent studies of old-age mortality in humans (Vaupel et al. 1998): (1) mortality rates are declining substantially, and (2) the increase of death rates with age decelerates among the oldest-old. In the words of Vaupel et al. (1998), these findings are perplexing and hard to reconcile: according to evolutionary biology, there is no possible selection against mutations occurring after reproduction and nurturing have ceased. A possible explanation of the old-age deceleration is heterogeneity in frailty; that is, as the frail die at early ages, the old tend to be a select subpopulation of the fit-test (Barbi, Caselli, and Vallin 2003; Horiuchi and Wilmoth 1998; Vaupel et al. 1998). In turn, a possible explanation of the mortality decline at old ages is a cohort effect of past improvements in health conditions at early ages; that is, recent improvements in health status among the elderly would echo events that happened decades ago when cohorts were young. These two explanations are somehow contradictory: does high, early-life mortality make a cohort stronger by eliminating the frail, or does the cohort become weaker because of accumulated injuries? An important scientific debate is taking place in this regard (Barbi and Vaupel 2005; Finch and Crimmins 2004, 2005).

The heterogeneity in frailty argument has been mostly supported by mathematical and simulation models (Vaupel, Manton, and Stallard 1979); by indirect evidence from genetic homogeneous populations such as twins (Yashin and Iachine 1997); and by observations in other species, such as the Mediterranean fruit fly (Vaupel and Carey 1993). Indirect methods have been developed to determine the existence of heterogeneity from cohort mortality patterns (Manton, Stallard, and Vaupel 1981). Data showing low death rates at old ages in low-income populations that saw harsh health conditions at young ages might support the heterogeneity in frailty argument, given the prejudice that the poor cannot be healthy nor live longer. Coale and Kisker (1986) offered two possible explanations of the observed mortality crossover at old ages among some socioeconomically disadvantaged populations: selection in heterogeneity or bad data. They concluded that bad data was the probable cause of these crossovers given the positive association between mortality in childhood and at young adult ages, and mortality in old age that was observed in cohorts with good data. A social selection argument, which has been used to explain good health in low-income populations (especially immigrants), parallels the heterogeneity in frailty argument. A well-known example of this is the “Hispanic paradox” (i.e., that Hispanics have lower mortality than whites) in the United States, which some researchers explain by several types of selection biases (Khlat and Darmon 2003; Palloni and Morenoff 2001).

Genetic makeup as well as nutrition, well-being, access to health care, lifestyles, and environmental conditions (contemporary and past) are, of course, determinants of old-age mortality above and beyond selection effects. The relative importance of these factors is, however, unknown. In addition, determinants of mortality might act differently at old ages than at young ages, challenging conventional wisdom that extrapolates to old ages what has been observed for younger ages. For example, Okinawa displays exceptional longevity even though it is one of the least developed regions in Japan (Cockerham and Yamori 2001). Another challenging example is that of Hispanics in the United States, who have lower adult mortality than whites in spite of Hispanics’ lower socioeconomic status and limited access to health care (Elo et al. 2004). And there is also the case of exceptional longevity in Sardinia, Italy, where old-age life expectancy is higher than in the much richer northern region of the country (Caselli and Lipsi 2006). Are elderly Okinawans, U.S. Hispanics, and Sardinians really exceptions to the rule of a socioeconomic gradient in mortality? Might it be that at old ages, the rules of survival are different than at young ages? To what extent do poor health conditions early in life strengthen or weaken a cohort at old ages? If dietary caloric restriction slows aging in other species (Roth et al. 2002), could certain human populations that were undernourished when young have an advantage for survival at old age?

An obstacle to answering these questions is the absence of sufficiently accurate data about old-age mortality in low-income populations. Costa Rica may be an exception. Since 1961, the United Nations has graded the Costa Rican vital statistics system—which was established in 1883––as “complete” (United Nations 1961). The country also has a carefully kept population registry used for voting purposes. Costa Rica is one of 11 developing countries whose vital registration statistics in 1995 are characterized by Hill et al. as both complete (recording at least 90% of births and deaths) and accurate (producing mortality estimates similar to those based on census and survey data) (Hill et al. 1999).

With its 4.5 million inhabitants, Costa Rica is the second most-densely populated country in the Continental Americas. (El Salvador ranks first.) Located in the Central American Isthmus, Costa Rica somehow escaped the wars and turbulences of the region in the 1980s and has enjoyed political stability for many decades. In economic terms, Costa Rica does not differ from the Latin American average. According to the World Bank (2006), its per capita income is about $4,600 per year, compared with the $3,600 annual average for Latin America. In terms of equity in income distribution, social security coverage, access to public health services and sanitation, labor laws, and protection of the environment, Costa Rica ranks among the highest in the Americas. Costa Rica has both a mixed economy with open markets and government control of key areas, such as health, education, banking, energy, communications, and insurance (Mesa-Lago 2000). The Human Development Index of the United Nations ranks Costa Rica as 48th in the world and 4th in Latin America (after Chile, Argentina, and Uruguay).

The country has essentially completed its demographic transition (World Bank 2006). Its life expectancy is the second highest in the Americas (Canada is first), which is higher than in the United States. The total fertility rate of 2.00 in 2005 is lower than in the United States (2.04 births), and it is the second lowest in Latin America after Cuba. Costa Rica is also one of the few Latin American countries with a substantial stock of international immigrants. Ten percent of the total population is foreign-born, a figure not that different from the 12% foreign-born population of the United States (United Nations Population Division 2006). Because the demographic transition was so quick and recent, a population aging process has not yet occurred: only 5.6% of Costa Ricans are aged 65 and older, although this will change very quickly in the next few decades, surpassing 20% by the year 2050 (INEC and CCP 2002).

Official life tables for 1995–2000 (Rosero-Bixby, Brenes-Camacho, and Collado-Chaves 2004) suggest exceptionally high old-age longevity in Costa Rica. Comparing the age-80 life expectancy in those tables with 13 high-income countries in exactly the same period in a database kept at the Max Plank Institute (Kannisto et al. 1994),1 Costa Rican males are the leaders with 8.2 years, followed by Japan with 7.6 years, and Iceland with 7.4 years. Costa Rican females, with 9.0 years of age-80 life expectancy, are in the middle of this elite pack: for example, Japan has 10.0 years, and Iceland has 8.7 years.

Costa Rica is well known as a country with outstanding health indicators. For example, it was included as one of the four study cases in the Rockefeller Foundation report on “Good Health at Low Cost” (Halstead, Walsh, and Warren 1985). However, there is a huge difference between having good health indicators and being the world-champion in longevity, leaving clear grounds for skepticism. Past claims of exceptional longevity in communities in the Andes and in the Caucasus have not resisted scientific scrutiny (Garson 1991). Demographers know well that age exaggeration among the elderly in censuses leads to substantial inflation of old-age populations and, consequently, underestimated mortality rates (Coale and Kisker 1986; Preston, Elo, and Stewart 1999). With these antecedents, academic circles may disregard this Costa Rican claim as just another case of “bad data.” This article relies on new data of very high quality to validate the patterns observed in the life tables and to obtain a more refined estimate of late-life longevity.

DATA AND METHODS

In an attempt to avoid data errors that have hampered studies of mortality of the oldest-old in other populations (Garson 1991; Kannisto 1988), the estimates in this article do not use conventional data sources. In particular, this article avoids using information on reported age from censuses or vital statistics but instead uses the Costa Rican national population voter registry, from which a database was created to study 24,400 Costa Rican nonagenarians in 1983–2004. This database includes, essentially, extinct birth cohorts born in 1878–1903 and quasi-extinct cohorts born in 1904–1913.

The Supreme Electoral Tribunal (Tribunal Supremo de Elecciones) provided the voter registry, which includes databases of births, naturalizations, and deaths as well as the voting lists (the padrón) for the 1990, 1994, 1998, and 2002 elections. The computerized birth registry, which is supposed to include all ever-living Costa Ricans, includes individuals who contacted the civil registration system since its computerization in 1970. Individuals contacted the registry because of registration (or certification requests) of vital events such as births, deaths, or marriages as well as to obtain (or renew every 10 years) an identification card, or cédula. The databases of the registry are linked by the unique identification (ID) number that each Costa Rican is given as of birth registration or naturalization. Given that this ID number also appears on the cédula, it is known in Costa Rica as the cédula number. A “survival time” data set was created using STATA (Statacorp 2005) with information on sex as well as dates of birth, death, and likely place of residence in each election year for all Costa Rican nonagenarians ever living in 1983–2004; the entry date is January 1, 1983 or the 90th birthday date, and the exit date is the date of death or October 30, 2004. Note that ages (at death or at any time of observation) in this data set do not come from reports but rather from computations based on dates documented in the registry.

Data Quality

The quality of the database of nonagenarians is crucial for this article. Three potential biases may occur and need to be validated: (1) selection bias, if the registry does not include all individuals and if those excluded have differential mortality; (2) underregistration of deaths, which would result in an underestimation of death rates, as well as an overcount of individuals still alive, especially toward the end of the observation period; and (3) age-misreporting biases, which, in other studies, underestimate mortality as result of age exaggerations.

How complete is the Costa Rican registry? It is almost impossible that a Costa Rican adult lived in the country since 1970 without ever having his/her cédula and, thus, never appearing in the registry. The cédula is required everywhere for all kinds of transactions, public or private. Besides, no deceased can be buried (keep in mind that the great majority of the studied nonagenarians have died) without a death certificate issued by either the Civil Register offices or, in remote locations, by the Rural Guard. Thus, all the dead are in the database, and a selection bias by exclusion of individuals from the registry is unlikely. A cross section from the nonagenarian database revealed 5,900 people alive and aged 90 or older at the time of the 2000 census. The census count was 7,000, or about 20% more; the percentage is similar by sex. This discrepancy does not come from deficiency in the registry but from overcounting in the census that is likely due to age exaggeration, as it was reported in the evaluation of the 2000 census (INEC and CCP 2002). Moreover, a study of the 1984 census estimated about a 50% overcount of population aged 80 and older, which is also due to age exaggeration (MIDEPLAN, CELADE, and DGEC 1988).

The second potential bias, the inflation in the count of people alive if the registry failed to exclude some of the dead, is addressed by looking at cohorts that should be extinct. Cohorts born in 1880–1895 were indeed extinct by 2004 in the registry. The maximum age reached by any of the 24,400 nonagenarians was 109; three died at this age. If under-registration of deaths occurred, one would see individuals still alive at age 120 or so, which is not the case. Therefore, estimates for extinct cohorts are, by definition, free of error from death underregistration. In addition, if the analysis showed that mortality in nonextinct cohorts is not significantly different from mortality in extinct cohorts, it would suggest that there are not missing deaths in the two groups.

Regarding the third potential bias, as mentioned earlier, this article’s information about age (at death or at any time during survival) does not come from reports but is instead computed from the dates in birth and death certificates, avoiding the most problematic data error in studies of mortality of the oldest old: age exaggeration that translates to underestimated mortality. In addition, information within the ID number (cédula) that each Costa Rican receives at birth allows for a second check of possible birth-date errors. This number is given to each individual at birth registration (or naturalization) and includes the number of the ledger and page where the person is registered. Because the ledgers are uniquely and sequentially numbered since the beginning of the civil registration system in 1880, looking at the ID number can establish the year when each individual was actually registered. Those with timely registration—say, within a year of their stated birth date—cannot have their age exaggerated. A person who appears timely registered could make consistent the two years (birth and registration) only by moving ahead the birth year, never by moving it back (which would cause the problematic age-exaggeration error). In contrast, those who registered late (some of them as adults, including foreigners who are citizens by naturalization) may have reporting errors in their birth date that produce age exaggeration. For example, somebody born in 1920 and registered in 1960 can have a wrong birth year of, say, 1900, which will result in 20-year age exaggeration. The analysis in this article tests for significant mortality differences by registration timing.

About 1,100 individuals (or 5%) in the database are centenarians: that is, they were alive at their 100th birthday. Although this is a small figure, it is worth exploring its validity by checking the reliability criteria used by Kannisto (1988) in his article on centenarians. Two indicators of data reliability in centenarians are applicable to the data in this article (Kannisto 1988: table 1). First, deaths of those aged 105 and older as a percentage of deaths at ages 100 or older are expected to be less than 5% and to be lower for men than for women. In the Costa Rican database, this indicator is 5.2% for men and 5.9% for women after excluding late registration births. These figures are borderline acceptable and much better than in (for example) the United States (7% and 8% among whites, and 30% among nonwhites), Spain (10% and 11%), and Portugal (16%) (Kannisto 1988: table 1). Second, the probability of dying is expected to be higher at age 101 than at age 100, and the ratio between them (q₁₀₀ / q₁₀₁) should be below unity. In the Costa Rican database, this ratio was 0.94 for men and 0.79 for women, far lower than most populations in the Kannisto article. For example, the ratio is 1.19 and 0.99 in Japan, 1.16 and 1.31 in Spain, 1.02 and 0.97 for whites in the United States, and 1.25 and 1.38 for nonwhites in the United States (Kannisto 1988: table 1).

Table 1.

Selected Data on Costa Rican Nonagenarians, 1983–2004

	Total	Birth Cohort
		1878–1893	1894–1903	1904–1913
Number of Individuals	24,438	2,150	7,692	14,596
Number of Observed Years
Total	101,439	8,778	38,981	53,680
In 1983–1993	33,409	8,611	24,798	0
In 1994–2004	68,030	167	14,183	53,680
Mean Number of Observed Years	4.15	4.08	5.07	3.68
Deceased (%)	73	100	97	57
Mean Age at Death	93.8	96.1	94.4	92.9
Mean Observed Age	92.7	94.9	93.2	92.0
Female Ratio	1.28	1.20	1.24	1.33
Late Birth Registry (%)	17	36	17	13
Central Region (%)	71	76	71	69

Source: National Registry of the Tribunal Supremo de Elecciones.

Characteristics of the Nonagenarians in the Database

The database of nonagenarians rendered about 101,000 person-years for 24,400 individuals born from 1878 to 1913 (Table 1). More than two-thirds of the observation segments correspond to the 1994–2004 period. Almost all individuals born before 1904 are deceased; these individuals were dubbed “extinct cohorts.” Mean age at death is 93.8 years, ranging from 96.1 in the oldest cohorts to 92.9 in the youngest one. These figures and trends are, however, severely biased by censoring effects: left-censoring for oldest cohorts because observation starts in 1983, and right-censoring for the youngest because observation stops in 2004. They are not good indicators of life expectancy. From those born in 1904–1913, 43% were still alive at closing date in 2004. Each individual was observed a little more than four years on average. The mean observed age is about 93 years. The female to male ratio is 1.28, with an increasing trend in more recent cohorts, which indicates that the sex gap in mortality is widening. The proportion of late-registered births is 17% overall and substantially higher (36%) in the cohorts born before 1893. Almost three-fourths of the observations correspond to the Central region.

Estimates of Mortality and Life Expectancy

This article estimates the mortality rates of Costa Rican nonagenarians using the “extinct cohort” method, which was developed for European countries by Vincent (1951) and was used in the United States by (among others) Rosenwaike (1981). The denominators for the rates in this article based on microdata are exact counts of person-years lived in each age.2 Survival-time routines in the STATA software facilitated these computations (Statacorp 2005).

The observed age-sex rates are summarized and smoothed out using a three-parameter relational model of mortality adapted from the Coale’s model for marital fertility (Coale 1977). The death rate m at age x and sex d (dummy variable equal to 1 for males) is modeled as a function of an old-age standard mortality schedule V of high-income countries; I refer to this as the Kannisto-Thatcher standard.3 The modeled death rate is a product of the standard V and the parameters M, denoting the relative level of mortality of females at age 90; A, representing the effect of aging above and beyond the standard schedule; and S, representing the effect of sex above and beyond the standard schedule. Values of 1 for the parameters indicate a behavior identical to the standard schedule. In symbols,

$$m_{xd}=V_{xd}M{A}^{(x-90)}{S}^d.$$

This model is preferable to a parametric hazard regression model for two reasons: (1) parameters are meaningful in substantive terms and not just in mathematical terms; and (2) death rates are not forced to follow a mathematical function, such as Gompertz or Weibull, but are allowed to adjust to patterns observed in other populations; this is an analytic strategy with a long tradition in demographic modeling that includes the Louis Henry model of natural fertility, the Ansley Coale models for fertility and nuptiality, and the William Brass models for survival (Brass 1971; Coale 1977; Henry 1972).

This article estimates model parameters using Poisson regression, following to Rodríguez and Cleland (1988), who estimated the analogous Coale/Page model for fertility using this log-linear regression model. Given that the mortality rate m is the ratio of the count of deaths Y and the number of person-years of exposure N, the Poisson regression models expected number of deaths E[Y] as the dependent variable:

$$E[Y_{xd}]=[N_{xd}{V}_{xd}]\text{exp}[b_0+b_1(x-90)+b_{2}d],$$

where the product NV is an offset term (McCullagh and Nelder 1989), and b_i are the estimated regression coefficients, which when exponentiated, render the M, A, and S parameters, respectively. The model’s parameters b_i were estimated using STATA (Statacorp 2005).4

To investigate mortality covariates, the three parameters of the model are also estimated for subgroups defined by variables of interest. Those variables are included as additional terms in the Poisson regression model as well as their interactions with x and d. The only additional variables available in the database of nonagenarians are the calendar year of observation (1983–2004); whether the individual was registered in a timely manner at birth (an indication that age is error-free); the place of residence, which is a time-varying variable (for each age-segment, the most recent voting place listed on the padrón), and the month of birth (a proxy to assess the effect of early life-health conditions). Preliminary analyses showed that most geographic variations are captured by the dummy variable “residence in the Central region,” which includes the capital city.

Causes of Death

Six broad groups of causes of death, plus a residual category, are defined as follows, with the codes from the 9th International Classification of Diseases (ICD-9) listed in parentheses after each cause: (1) communicable diseases (1–139, 460–490); (2) cancer (140–239); (3) cardiovascular diseases (390–459); (4) Chronic respiratory diseases (491–519); (5) diabetes (250); and (6) accidents and violence (800–999). The information on causes of death comes from the vital statistics system because the voter registry does not have these data. Age-specific mortality rates were computed for the six groups of causes of death for the period 1990–1999. For comparative purposes, standardized death rates were also computed for the United States (white population only) and Sweden for the period 1994–1996. Data disaggregated by age and causes of death were not readily available for ages 85 or older in these or other countries. The comparison thus refers to the group aged 85 or older and uses the “indirect” procedure of standardization (Shryock and Siegel 1976), with the Costa Rican rates as the standard.5

RESULTS

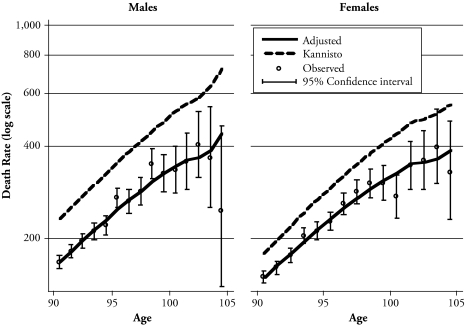
The age-specific death rates from the Costa Rican database are substantially lower than the average of 13 high-income countries (listed in footnote 1)—the Kannisto-Thatcher standard (see Figure 1). The Costa Rican advantage is larger for males, which means a narrower sex gap in Costa Rica, analogous to one observed in Sardinia, Italy (Robine et al. 2006). The rates increase with age, with a slope resembling that of the standard. In populations with bad data at these ages, one usually observes flat curves. There is some deceleration in the increases at advanced ages—a phenomenon observed in other populations and species as well, which is the subject of intense scrutiny (Horiuchi and Wilmoth 1998).

Figure 1.

Observed and Adjusted Age-Specific Death Rates: Costa Rica (1983–2004) and Kannisto-Thatcher Average (1990–1999)

The three-parameter model provides a reasonable adjustment of the Costa Rican rates in Figure 1. Smoothing the rates with the model seems necessary to eliminate large, random fluctuations. The 95% confidence intervals (CI) illustrate that the observed rates become highly unreliable by age 98 and beyond because of random errors originated in small numbers of observations. The relational model in this article corrects these probably random fluctuations and purposely imposes a monotonic pattern of increasing rates with age, as observed in 13 developed populations.

Table 2 shows the three parameters of the mortality model estimated for Costa Rican nonagenarians and used to smooth the rates in Figure 1. The M parameter is estimated at 0.829; that is, Costa Rica has 17% lower mortality at age 90 than the Kannisto-Thatcher standard for high-income countries. The A parameter is estimated at 0.989; aging occurs more slowly in Costa Rica than in the standard, at a rate 1.1% slower for each extra year of age. The S parameter came out as 0.878; Costa Rican males have an additional advantage of 12% lower-than-expected death rates.

Table 2.

Three Models Describing Mortality of Costa Rican Nonagenarians Estimated With Poisson Regression, Robust Estimates: Models Differ by the Explanatory Variables Included

	Model 1		Model 2		Model 3
	Parameter	95% Confidence Interval	Parameter	95% Confidence Interval	Parameter	95% Confidence Interval
M Level	0.829	0.808–0.851	0.847	0.814–0.882	0.859	0.833–0.886
S Male = 1	0.878	0.853–0.905	0.888	0.862–0.915	0.874	0.848–0.904
A Age (90 = 0)	0.989	0.984–0.994	0.991	0.985–0.997	0.990	0.984–0.997
Effects on M
Late registry			0.985	0.947–1.026	0.937	0.887–0.990
Year (1995 = 0)			0.991	0.987–0.996	0.996	0.992–1.000
Non-Central region			0.892	0.863–0.922	0.851	0.809–0.894
Non-extinct cohort			1.005	0.955–1.058
Born in March or April			1.036	0.996–1.078	1.070	1.009–1.133
Effects on S
Late registry					1.088	1.006–1.177
Effects on A
Year (1995 = 0)					0.998	0.997–0.999
Non-Central region					1.013	1.001–1.024
Born in March or April					0.990	0.977–1.004
Effects on Year
Non-Central region					1.007	1.001–1.013

Notes: The effects on sex, age and year were estimated by including the respective interaction variable in the model. See the text for an explanation of the parameters.

Table 2 shows estimates for two additional models. The second model allows for variation in mortality levels (the M parameter) with five additional variables. It is useful just to show that there is no significant difference in mortality of extinct and non-extinct cohorts, which is an assurance that there are no death underregistration errors. By including statistical interactions,6 the third model also allows variation in the sex and age effects. Being a late-birth registry (a proxy for potential age errors) reduces mortality by 6%, but this effect occurs only among women, as shown by the interaction effect with sex. There is also a significant trend of mortality reduction over time of 0.4% per year, but this trend occurs only in the Central region (as shown by the region-year interaction) and dissipates at older ages (age-year interaction). The non-Central regions have 15% lower mortality by 1995. Given that those regions are the most remote and least developed, one wonders whether this apparent advantage may come from data errors. The advantage of non-Central regions, however, disappears at older ages and more recent times, as shown by the corresponding interactions. Finally, those born in March or April have a 7% higher mortality at age 90, a disadvantage that diminishes with age. Analogous effects of month of birth observed in other populations have been taken as indication of the direct correlation between early-life conditions (in utero and neonatal) and old-age health, linked to the shortage of food during winter.7 Costa Rica does not see that kind of food shortage, but seasonality does occur for other factors, particularly those linked to the dry season that goes from January to April. In particular, conceptions and diarrhea used to peak in January and February, months in which people also used to be very busy harvesting coffee and celebrating the extra income from this and other harvests and the dry season. It may be that infections in the final months of pregnancy that hampered in utero development affect the health of these newborn babies even when they reach very old ages.

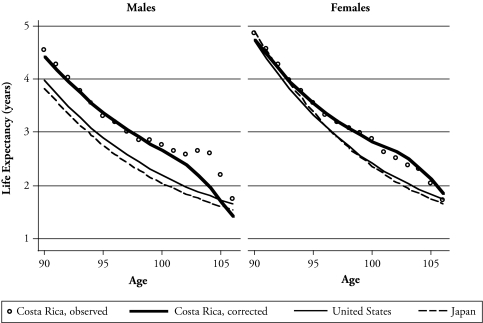
Restricting the analysis only to the Central region and timely registered births assures high-quality estimates, although these may be conservative. With these two restrictions, the parameters for aging (A) and sex (S) are about the same as in the simple model presented earlier. The parameter for mortality level (M) is a bit higher, and the advantage for Costa Rica declines from 17% to 14%. The exceptional longevity of Costa Ricans does not seem sensitive to this refinement. Figure 2 shows life expectancy by age originally estimated with the observed death rates, as well as that estimated with the rates from the model and restricted to timely registered births and the Central region. No important differences are seen between the two series up to age 102. The figure also shows that while Costa Rican females differ little from those in Japan and the United States, Costa Rican nonagenarian males have a one-half year advantage in life expectancy at all ages. By age 100, Costa Rican males have 2.7 years of life expectancy, and females have 2.8 years; in the United States (whites only), males have 2.2 years, and females have 2.4 years. However, after about age 100, comparisons must be taken cautiously because of uncertainties originated in the small number of observations in Costa Rica and the sensitivity of the estimates to small variations in computation methods or in data errors.

Figure 2.

Life Expectancy, by Age and Sex: Costa Rica (1983–2004), the United States (whites only, 1990–1995), and Japan (1990–1995)

Note: “Costa Rica, corrected” refers to Costa Rican estimates based on death rates smoothed with the regression model and restricted to timely registered births and residence in Central region.

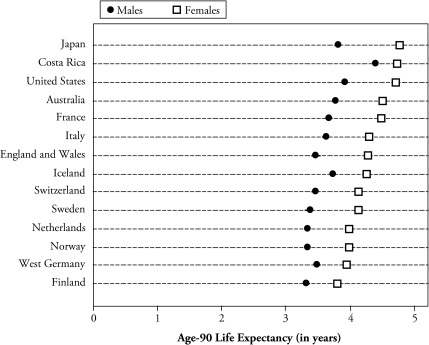
Age-90 life expectancy—a summary of the mortality of nonagenarians—in this new data set resulted in 4.7 and 4.4 years for women and men, respectively—figures almost identical to those in the official life tables for 1995–2000. Figure 3 compares my estimate for Costa Rica for the period 1983–2004 (central year 1994) with high-income countries in the aforementioned Kannisto-Thatcher database for the period 1992–1998 (with 1995 as the central year). The estimates in the figure are thus contemporary to the same period. Costa Rican males have the highest life expectancy, which is one-half year more than the United States, Japan, Australia, and Iceland. Costa Rican females are essentially tied in first place with Japan and the United States. The sex gap in life expectancy is notoriously smaller in Costa Rica: 0.3 years at age 90 compared with 1.1 year for France or the United States (see Figure 3).

Figure 3.

Age-90 Life Expectancy, by Sex, for Selected Countries Ordered by Female Life Expectancy: Costa Rica (1983–2004) and Other Countries (1990–1995)

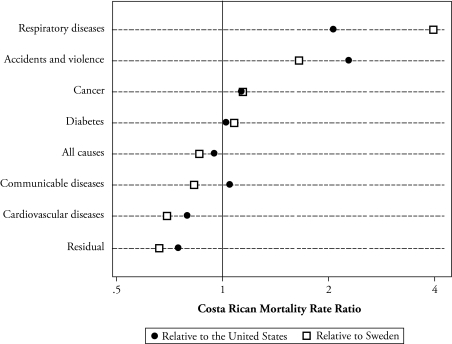
Data on causes of death may help to understand the Costa Rican advantage. Cardiovascular diseases (CVDs) are, by far, the leading cause of death, accounting for nearly 50% of all deaths of nonagenarians. Chronic respiratory diseases (mostly “other chronic airway obstructive diseases”), communicable diseases (mostly bronchopneumonia and pneumonia), and cancer have similar importance, each accounting about 12% of old-age deaths. A comparison with the United States and Sweden in Figure 4 points out that the Costa Rican advantage is mostly due to its lower CVD mortality. The age-adjusted rate of mortality from CVD, at ages 85 and older, is 20% lower in Costa Rica than in the United States and 30% lower than in Sweden. In turn, mortality by communicable diseases is similar to that in the United States and lower than in Sweden. By contrast, Costa Rican elders have substantially higher mortality from chronic respiratory diseases and accidents (huge rate ratios on the order of 200%–400%). Cancer is another pathology from which Costa Ricans have slightly higher mortality rates than do U.S. and Swedish citizens (about 15% higher), mostly attributable to stomach cancer.

Figure 4.

Mortality Rate Ratio by Cause of Death in Costa Rica Relative to the United States and Sweden for Those Aged 85 and Older in the 1990s: Indirect Standardization by Age and Sex

DISCUSSION

Fresh data from a population registry kept in Costa Rica for voting purposes confirms early estimates of exceptional longevity of its elders. Life expectancy for nonagenarian males is one-half year more in Costa Rica than in any other country, with reliable statistics. Although this life expectancy is still less than that for females, the difference is only 0.3 years, which is the smallest recorded by national populations at these mortality levels.

Are these figures valid or just a product of “bad data”? How could they be valid, considering that well-being and health services in Costa Rica are far behind those in high-income countries?

This article is mostly concerned with the validity of the estimates. By not basing the estimates on self-reported age data, it avoids age exaggeration, which is the most problematic and pervasive data error at old ages. By double-checking birth dates and excluding individuals whose birth dates are fully documented but whose registration did not occur close to birth, almost no possibility of age errors exists. The only possibility of error would come from massive identity suplantation of older and deceased individuals by younger ones. Such a massive fraud does not seem plausible.

Estimates in this article for extinct cohorts are free from death underregistration errors: cohorts were not extinct if there was a failure to register some deaths. Independent census data, which are also free of missing-death errors, confirm that survival of Costa Rican nonagenarians may be exceptional. Table 3 shows that although the percentage of nonagenarians in the total population is not impressive (0.2%) because of very rapid population growth in the past, the nonagenarian rate is exceptionally high for Costa Rican males: more than twofold those of France, Italy, Sweden, or the United States, and four times higher than in Russia. Following common practice in demographic analyses of centenarians (see, e.g., Robine and Paccaud 2005), the nonagenarian rate was defined as the ratio of the population aged 90 and older in 2000 to the population 60 and older in 1970: that is, a 30-year cohort survival proportion among the elderly and assuming null migration. A problem with these census data is age exaggeration that might inflate the nonagenarian rate. An independent evaluation of the 2000 census found that age exaggeration did indeed exist, especially among the oldest-old.8 Correction of the age-reporting errors reduces the Costa Rican nonagenarian rate from 6.9% to 5.6% for males (Table 3, second row), but this figure continues to be more than twice as large as in France, Italy, and Sweden. The nonagenarian sex ratio in Table 3 is also exceptional in Costa Rica: there are only 30% or 40% more women than men, compared with the 200% or 300% excess of women in the other countries in the table. This result corroborates this article’s finding that the mortality sex gap among Costa Rican nonagenarians is substantially smaller than in other countries. It is reassuring to reach the same result with two independent data sources. This Costa Rican peculiarity has also been observed in the island of Sardinia of Italy (Robine et al. 2006).

Table 3.

Nonagenarians in the Population, Cohort Nonagenarian Rate,^a and Female to Male Ratio in Nonagenarians: Costa Rica and Selected Countries, Circa 2000

Country	In Population (%)		Cohort Rate (%)		Female Ratio
	Female	Male	Female	Male
Costa Rica, Observed	0.22	0.17	9.2	6.9	1.4
Costa Rica, Corrected	0.19	0.14	7.4	5.6	1.3
France	1.09	0.33	6.1	2.5	3.5
Italy	0.90	0.31	5.4	2.3	3.0
Japan	0.77	0.26	8.3	3.3	3.0
Russia	0.39	0.10	2.8	1.6	4.2
Sweden	1.05	0.37	5.6	2.2	2.9
United States	0.78	0.26	6.9	2.9	3.1

Sources: Data for Costa Rica are from the country’s 2000 census, observed and corrected figures, correction in (INEC and CCP 2002). Data for other countries are from the Human Mortality Database (http://www.mortality.org).

^aNonagenarian rate = the population aged 90 and older in 2000 / Population aged 60 and older in 1970.

According to the World Bank (2006), by 2004, Costa Rica had a per capita gross national income of about US$4,700 and a health expenditure of $310. These figures are about one-tenth those in high-income countries. In the United States, these amounts were $41,400 and $5,700, respectively. Indicators of health services, such as per capita physicians and hospital beds, are also substantially lower in Costa Rica: they equate to only one-third the number of U.S. physicians and one-tenth the number of Japanese beds. It is perplexing that a country with these modest levels of well-being, health investments, and infrastructure may be the one with the highest life expectancy among the elderly.

Broad explanations of Costa Rica’s health achievements in the literature include the orientation of the government toward equity and social development, with large social investments being possible, in part, because of the absence of military expenditures (Rosero-Bixby 1991). The 1949 constitution abolished the armed forces. Investments in education and the very high coverage of health insurance are often mentioned as key factors (Caldwell 1986). Health insurance covers 82% of the population, including the 9% population deemed destitute, whose insurance is paid by the government (Rosero-Bixby 2004). Provision of primary health care, particularly to remote or poor populations, has a quantifiable impact on death rates, especially among children (Rosero-Bixby 1986). A 17-year follow-up of a group of Costa Rican elderly has shown no meaningful differences in survival by socio economic condition (education or wealth) nor by being covered by the national health insurance9 (Rosero-Bixby, Dow, and Lacle 2005); this suggests that the Costa Rican advantage at old ages may be present across the entire society, with no clear-cut health interventions or classic socioeconomic gradients as explanation.

Data on causes of death suggested that the Costa Rican advantage comes mostly from CVDs. However, the comparison with Sweden and the United States must be taken cautiously because differences may be an artifact from variations in how causes of death are registered in each country, as well as from age misreporting errors or possibly under-registration of deaths. The data for this comparison are regular data from vital statistics, which are good albeit not perfect in Costa Rica. However, it is worth noting that an early study (Rosero-Bixby 1996) among young adults found similar patterns. For example, it found that mortality by heart disease among males aged 25–74 is 42% lower in Costa Rica than in the United States. The CVD advantage of Costa Rican males does not seem to occur only among the oldest old, and this advantage is so large that its being the result of bad data is hard to believe.

In Sardinia, another place with exceptional old-age longevity among males and a small sex gap, Caselli and Lipsi (2006) also found that low CVD mortality explains the survival advantage of elderly Sardinians compared with other Italians.

Another suggestive result regarding causes of death is that old-age mortality by communicable diseases is similar to that in the United States and is lower than in Sweden. This result somehow confirms the high level of development of the current Costa Rican primary health care system, which other studies have identified as an important factor for the low mortality at earlier ages in Costa Rica (Rosero-Bixby 1986, 2004).

One can safely assume that the lower CVD mortality of elderly Costa Rican males does not come from access to superb health care. Costa Rica has a good health care system, especially at the primary level, with almost universal coverage. However, the Costa Rican health care system is not comparable with the health infrastructure of Sweden and the United States, especially considering the access to health care that Medicare provides to the elderly in the United States. So what are the preventive, genetic, or behavioral factors that protect Costa Ricans from high CVD rates? Table 4 provides some hints by comparing selected markers from National Health and Nutrition Examination Survey (NHANES) 2001–2002 in the United States and results from an ongoing study, Costa Rica: Estudio de Longevidad y Envejecimiento Saludable (Costa Rican Study of Longevity and Healthy Aging; CRELES). Smoking, past and present, is not a factor among males, nor is high blood pressure or elevated cholesterol or triglycerides levels. It does not seem that Costa Ricans have the genes or a diet that reduce these risk factors. The only lowered risk factor for which Costa Rican males have a clear advantage is a lesser prevalence of obesity. Prevalence of obesity in Costa Rican males is two-thirds that found in the United States. This probably results in the significantly lower prevalence of uncontrolled diabetes in males as measured by the glycohemoglobin level, the only other factor in Table 4 that shows a Costa Rican advantage. Other factors that may be worth investigating are levels of stress, support networks, and the like.

Table 4.

Proportion of Those Aged 60–90 Who Suffer From Selected Risk Factors, by Sex: Costa Rica (2005) and United States (2001–2002)

Risk Factor	Males		Females
	Costa Rica	United States	Costa Rica	United States
Obese: BMI ≥ 30	.16	.22 *	.31	.27
Waist ≥ 94/80cm, Male/Female	.48	.80 *	.86	.87
Ever Smoked	.68	.66 *	.22	.42 *
Currently Smokes	.14	.07 *	.04	.06 *
High Blood Pressure, Diastolic > 90	.37	.04 *	.41	.03 *
High Blood Pressure, Systolic > 140	.67	.38 *	.69	.51 *
HDL Cholesterol ≤ 40/50 mg/dl, Male/Female	.46	.31 *	.59	.28 *
Total Cholesterol > 250	.14	.07 *	.26	.16 *
Triglycerides ≥ 150 mg/dl	.43	.44	.48	.50
Glycohemoglobin ≥ 6.5%	.12	.14 *	.20	.11 *
Average N	1,176	557	1,410	607
Mean Age	75	75	75	75

Notes: Figures are age-adjusted proportions with logistic regression to age 75. Figures in gray boxes indicate risk factors for which Costa Ricans have a significant advantage.

Sources: For the United States, data come from the Centers for Disease Control (CDC), National Health and Nutrition Examination Survey, 2001–2002 (http://www.cdc.gov/nchs/nhanes.htm). For Costa Rica, the data come from the study “Costa Rican Study of Longevity and Healthy Aging” (CRELES), Centro Americano de Población, Universidad de Costa Rica (http://ccp.ucr.ac.cr/creles).

^*Difference is significant at p < .05.

This article does not have an answer to the question of why elderly Costa Ricans do so well. It could be a genetic factor, lifestyle, social factors, or the environment. It could also be just a heterogeneity in frailty effect. Costa Rican nonagenarians are true survivors of cohorts that underwent extremely harsh health conditions when young. For example, they survived infant mortality rates in the range of 250 per thousand prevalent in Costa Rica in the early twentieth century. Malaria, tuberculosis, and diarrheic diseases decimated these cohorts when they were young. It looks like the selection-of-the-fittest effect prevailed over the weakening effect. In addition, modern health evils, such as obesity and a sedentary lifestyle, are less common among them. Finally, a reasonably good health care system is currently protecting them from dying of communicable diseases.

These explanations, however, say nothing regarding why the Costa Rican advantage occurs mostly among males, or why the sex gap in mortality is so small. The only thing known so far is that this population exhibits low cardiovascular mortality and that Costa Rican males of these ages are thin. Comparatively, Costa Rican women tend to be obese, which perhaps is due to their high fertility in the past; each extra pregnancy usually increases mother’s weight, as shown, for example, by Arroyo et al. (1995) for Mexican women.

If the high longevity of elderly Costa Ricans is mostly a result of a selection process of the less frail, this may be an ephemeral advantage that may disappear as more frail individuals reach old ages, thanks to the rapid progress that took place in the past.10 Analyses in other low-income countries with adequately robust data are needed to see whether the early harsh conditions generally faced 80–100 years ago in these countries lead to similar patterns of low mortality at old ages.

Appendix Table A1.

Age and Sex Mortality Rates per 1,000 Population

Age	Kannisto-Thatcher		Costa Rica (1983–2004)
	Males	Females	Males	Na	Females	Na
90	231	178	166	9,391	149	11,780
91	253	198	181	7,704	160	9,790
92	277	220	195	5,925	175	7,652
93	302	243	211	4,529	203	5,891
94	328	268	220	3,430	211	4,419
95	357	295	271	2,505	227	3,286
96	387	323	264	1,781	259	2,359
97	419	352	285	1,236	284	1,656
98	453	382	351	844	303	1,123
99	489	412	326	561	303	756
100	526	444	335	362	274	515
101	556	482	355	236	346	344
102	582	495	405	146	358	218
103	635	518	365	77	397	128
104	721	553	246	49	330	79
105	853	604	274	29	369	49
106	1,054	672	344	17	441	25

^aN = person-years observed.