Parametric Modeling of Localized Melanoma Prognosis and Outcome

Abstract

This investigation explored the most suitable parametric model for melanoma prognosis and compared it with the Cox model. Cox-Snell residuals and survival function plots were applied to assess the generalized gamma (GG) model was the best fit parametric model for the data. The GG model is a powerful alternative to the Cox model in prognostic modeling. The GG model offers an advantage of explicit and flexible individualized hazard functions over the Cox model, and provides a clinically useful risk assessment over time to aid clinicians in formulating patient treatment and follow-up plans and for clinical trial design and analysis.

Introduction

The introduction of the Cox proportional hazards model represents the most important methodological development in the area of survival data analysis in over three decades. In melanoma research, a large number of clinical factors (e.g., age, gender, lesion site) and pathological factors (e.g., tumor thickness, tumor ulceration, level of invasion, growth pattern) related to disease recurrence and patient survival have been studied extensively over the past 30 years. With an application of Cox regression model in almost all major multivariate prognostic factor studies of melanoma, remarkable progress has been made in the identification of key prognostic factors that characterized the natural history and prognosis of melanoma (Balch, 1970, 1978, 1981, 1982, 1983, 2000, 2001; Eldh, 1978;Van Der Esch 1981; Drzewiecki, 1982; Soong, 1984, 1998, 2003; Cascinelli 1985; Kheir 1988; Coit 1991; Garbe 1995. In addition, several useful predictive models based on Cox model for predicting individual patient’s survival and disease recurrence in melanoma were also developed from several large melanoma databases (Soong, 1992, 2003). Using the key prognostic factors identified by Cox regression analyses as stratification criteria, a major melanoma surgical trial was designed and successfully concluded with statistical analyses done primarily using Cox regression model (Balch 2000). In 2001, melanoma become the first disease site that employed a large multi-institutional database (n>17,000) to define a truly evidence-based staging system adopted by the American Joint Committee on Cancer (AJCC) and the International Union Against Cancer (UICC) (Balch, 2001). Comprehensive multivariate analyses of prognostic factors for the melanoma staging definition were again carried out by Cox regression model (Balch, 2001).

Although the Cox model has demonstrated its flexibility and usefulness in modeling survival data in melanoma, it also has inherent limitations due to its proportional hazard assumption and its inability to generate an explicit and flexible hazard function (Cox 1972, 2007). In this paper, we investigate several parametric models for melanoma prognosis and modeling and compared to the Cox model using a prospective melanoma research database established by the Melanoma Task Force of the AJCC. The objectives of the current investigation are to: (1) evaluate the applicability of parametric models to localized melanoma survival data, including prognostic factors; (2) compare the results of parametric models and the Cox model; and (3) estimate and interpret the hazard functions of melanoma death under various conditions.

Materials and methods

Data source

The dataset used in this study is abstracted from the data used for building the current AJCC melanoma staging system and for clinical management developed by the AJCC and the UICC in 2001 (Balch, 2001). This dataset consists of over 17,000 melanoma patients from 13 institutions who were prospectively followed (Balch, 2001). The current analysis incorporates data from 14,914 localized melanoma patients. Five staging subgroups were defined for localized patients: IA (n=4510), IB (n=4665), IIA (n=2675), IIB (n=2086) and IIC (n=978), as described previously (Balch, 2001). For patients with localized disease, three factors were used to define staging: tumor thickness, ulceration and Clark’s level. Tumor thickness was defined categorically for ease in clinical staging although the relationship to survival had been demonstrated in a continuous fashion (Balch, 2001). In this analysis, three additional covariates (age, gender and primary melanoma site) were also included in the modeling (Soong, 2003; Balch 2001). The coding for the covariates was: age (0 = < 60 years, 1 = ≥60 years); gender (0 =male, 1=female); site (0=extremity, 1=axial ); Clark’s level ( 0= II/III,1 = IV/V); and ulceration (0=No, 1=Yes). Tumor thickness was coded in a continuous fashion (mm). Survival time was calculated as the interval between date of onset of primary melanoma diagnosis and melanoma-specific death (for those who died) and date of last follow-up (for those alive or for those who died of other causes).

Statistical analysis

Survival models

In survival analysis, the components of primary interest are the survivor function and the hazard function. In this study, we evaluated six different parametric distributions from the general accelerated failure time (AFT) family (exponential, Weibull, log-normal, standard gamma, log-logistic and generalized gamma (GG) distributions) to find the best-fit distribution for localized melanoma survival data (Stacy, 1962; Lee, 2003; Allison, 1995). Let Ti be a random variable denoting the survival time or right-censored time under study for the ith patient in sample, and let x_il, ···, x_ip be the values of p covariates for that same individual. The AFT model, which is a parametric linear model with the log-transformation of T_i and the covariates, can be written as:

$$\begin{array}{l}log{T}_i={\mu }_i+\sigma {\epsilon }_i,i=1,2,\cdots ,n\\ {\mu }_i={\beta }_0+\sum _{j=1}^p{\beta }_j{x}_{ji},i=1,2,\cdots ,n\end{array}$$

Where β₀, β₁, ···, β_p are the regression coefficients, σ is a scale parameter and ε_i ’s the random distribution terms, usually assumed to be independent and identically distribution.

If ε_i is the log-gamma distribution with the density function g(ε) and survival function G(ε) (Lee, 2003):

$$\begin{array}{l}g({\epsilon }_i)=\{\begin{array}{ll}\frac{\mid \delta \mid {[exp(\delta {\epsilon }_i)/{\delta }^2]}^{1/{\delta }^2}exp[-exp(\delta {\epsilon }_i)/{\delta }^2]}{\mathrm{\Gamma }(1/{\delta }^2)}\hfill & \delta \ne 0\hfill \\ \frac{1}{\sqrt{2\pi }}exp(-\frac{{\epsilon }_i}{2})\hfill & \delta =0\hfill \end{array}\\ G({\epsilon }_i)=\{\begin{array}{ll}I\left[\frac{exp(\delta {\epsilon }_i)}{{\delta }^2},\frac{1}{{\delta }^2}\right]\hfill & i\text{f}\delta <0\hfill \\ 1-I\left[\frac{exp(\delta {\epsilon }_i)}{{\delta }^2},\frac{1}{{\delta }^2}\right]\hfill & i\text{f}\delta >0\hfill \\ 1-\mathrm{\Phi }({\epsilon }_i)\hfill & \text{if}\delta =0\hfill \end{array}-\infty <{\epsilon }_i<+\infty \end{array}$$

Note: When δ→0, log-gamma distribution reduces to log-normal distribution. then it can be shown that T has the GG distribution with the density function:

$$f(t_i,\alpha ,{\lambda }_i,\gamma )=\frac{\mid \alpha \mid {\gamma }^{\gamma }{\lambda }_i^{\alpha \gamma }}{\mathrm{\Gamma }(\gamma )}{t}_i^{\alpha \gamma -1}exp[-\gamma {({\lambda }_i{t}_i)}^{\alpha }]t_i>0,\gamma >0,{\lambda }_{\text{i}}>0$$

When γ → ∝ (i.e. δ=0), it becomes log-normal distribution with density function:

$$f(t_i,{\lambda }_i,\sigma )=\frac{1}{t_i\sigma \sqrt{2\pi }}exp[-\frac{1}{2{\sigma }^2}{(log{\lambda }_i{t}_i)}^2],t_i>0,\sigma >2$$

and survival function:

$$S(t_i,\alpha ,{\lambda }_i,\gamma )=\{\begin{array}{ll}1-\frac{1}{\mathrm{\Gamma }(\gamma )}{\int }_0^{\gamma {({\lambda }_i{t}_i)}^{\alpha }}{v}^{\gamma -1}{e}^{-v}dv\hfill & \text{if}\alpha >0\hfill \\ \frac{1}{\mathrm{\Gamma }(\gamma )}{\int }_0^{\gamma {({\lambda }_i{t}_i)}^{\alpha }}{v}^{\gamma -1}{e}^{-v}dv\hfill & \text{if}\alpha <0\hfill \end{array}$$

When γ → ∝ (i.e. δ=0), it becomes log-normal survival function:

$$S(t_i,{\mu }_i,\sigma )=\frac{1}{\sigma \sqrt{2\pi }}{\int }_i^{\infty }\frac{1}{x}exp[-\frac{1}{2{\sigma }^2}{(log{\lambda }_{i}x)}^2]dx=1-\mathrm{\Phi }\left(\frac{log{\lambda }_i{t}_i}{\sigma }\right)$$

And hazard function

$$h(t_i,\alpha ,{\lambda }_i,\gamma )=\{\begin{array}{ll}\frac{\mid \alpha \mid {\gamma }^{\gamma }{\lambda }_i^{\alpha \gamma }{t}_i^{\alpha \gamma -1}exp[-\gamma {({\lambda }_i{t}_i)}^{\alpha }]}{\mathrm{\Gamma }(\gamma )-{\int }_0^{\gamma {({\lambda }_i{t}_i)}^{\alpha }}{v}^{\gamma -1}{e}^{-v}dv}\hfill & \text{if}\alpha >0\hfill \\ \frac{\mid \alpha \mid {\gamma }^{\gamma }{\lambda }_i^{\alpha \gamma }{t}_i^{\alpha \gamma -1}exp[-\gamma {({\lambda }_i{t}_i)}^{\alpha }]}{{\int }_0^{\gamma {({\lambda }_i{t}_i)}^{\alpha }}{v}^{\gamma -1}{e}^{-v}dv}\hfill & \text{if}\alpha <0\hfill \end{array}$$

When γ → ∝ (i.e. δ=0), it becomes log-normal hazard function:

$$h(t_i,{\lambda }_i,\sigma )=\frac{(1/t_i\sigma \sqrt{2\pi })exp[-{(log{\lambda }_i{t}_i)}^2/2{\sigma }^2]}{1-\mathrm{\Phi }(log({\lambda }_i{t}_i/\sigma ))}$$

where:

$${\lambda }_i=exp(-{\mu }_i)\alpha =\frac{\delta }{\sigma }\gamma =\frac{1}{{\delta }^2}$$

Γ(x) is the complete gamma function defined as $\mathrm{\Gamma }(x)={\int }_0^{\infty }{v}^{x-1}{e}^{-v}dv$, I(a,x) is the incomplete gamma function defined as $I(a,x)=\frac{1}{\mathrm{\Gamma }(x)}{\int }_0^a{v}^{x-1}{e}^{-v}dv$, And δ is a shape parameter, and σ is scale parameter.

The exponential (α = γ = 1), Weibull (α > 0 and γ = 1), log-normal (δ=0), and standard gamma (α = 1, δ=σ) distributions are the special cases of the GG model. Although the log-logistic distribution is not a special case of the GG distribution, it belongs to the family of AFT models.

In contrast to parametric models, the Cox proportional hazard model (Cox, 1972) is a semi-parametric model and is currently the most widely used model in survival regression analysis. The proportional hazard means that the risk of death at any given time for an individual in one group is proportional to the risk at that time for similar individual in the other group. Whereas GG models adopt log-survival times to evaluate the relationship with covariates, Cox models use the log-hazard function as follows:

$$logh(t_i\mid Z)=log{h}_0(t_i)+Z^{\prime }\beta$$

where Z= (Z_1, ···, Z_p) is the ( p × 1) covariate vector with associated p × 1parameters vector β, and h₀ (t_i) is a baseline hazard function.

Assessment of model adequacy

Several statistical procedures are available to assess the adequacy of survival models (Lee, 2003; Allison, 1995; Nardi, 2003). In this paper, we used the widely used Cox-Snell residual method (Lee 2003; Cox 1968) to select the best fitted parametric models for predicting clinical outcome of localized melanoma. The similar method was also used to evaluate the adequacy of the Cox model. The Cox-Snell residual is defined as r_i= −log(Ŝ(t_i x_i)) where t_i is the observed survival time or censoring time for patient i, x_i is the vector of covariate values for patients i, and Ŝ(t) is the estimated survival function based on the maximum likelihood estimation of the parameters. The Cox-Snell residual r_i is actually an estimated cumulated hazard value at t_i, and if the model selected fit the data, r_i‘s follow the unit exponential distribution. Therefore, if we apply the Kaplan-Meier method to estimate r_i‘s the survival function S_r(r_i), and the plot of r_i versus −log Ŝ_r(r_i) should be close to a 45° line (unit slope and zero intercept) if the fitted survival model is adequate (Lee, 2003).

The maximized likelihood is an important statistic in survival analysis. The log likelihood, log L̂, is useful to compare different models. For a given data set, the larger the value of log likelihood, the better the agreement between the model and the observed data. All models mentioned above except the log logistic model are specific cases of GG model. Therefore, we can compute the likelihood-ratio chi-square statistics to test the fit of the nested models. If model A is nested within model B, the fit of model A can be evaluated through the likelihood-ratio statistic by taking twice the positive difference between log L̂ ( A) and log L̂ (B) for the two models. This statistic has an asymptotic chi-squared distribution. Model A is not a better fit for the observed data if P< 0.05 (Allison, 1995).

Comparisons of the best fitted parametric model with the Cox model

After selecting the best-fitted parametric model from the AFT family, the performance of the parametric model was compared with the Cox model based on: 1) the Cox-Snell residual method, 2) estimated survival functions by models and Kaplan-Meier method, and 3) regression model fitting and identification of prognostic factors. Although in the regression analyses, the estimated coefficients in both models are not directly comparable, the efficiency of coefficient estimates can be compared by Wald chi-square values (χ²) that measured the gains in precision for highly significant effects (Nardi, 2003). Larger Wald chi-square values indicate greater efficiency of the model coefficients. All the above comparisons were repeated for each substage of localized melanoma.

Hazard function estimation

The hazard function h(t) is the risk of event at time t and can be readily generated from a parametric survival model. In this investigation melanoma death is the event and the hazard function can be interpreted as risk of dying or mortality among survivors at time t. It is also referred to as time-specific mortality rate (Simes, 1985). The hazard functions are graphed as a function of time by melanoma stage and also plotted by individual patient’s risk profile. The maximum hazard is the largest value of the hazard functions for a specific patient risk factor profile or stage of disease over time. The maximum hazard and its corresponding time point for each risk factor profile can provide the valuable information regarding the peak hazard for a specific patient or stage of disease.

Results

Evaluation of parametric model fit

The analyses of parametric models were stratified by substage of localized melanoma defined as IA, IB, IIA, IIB, and IIC. We assessed the fit of the data for the six parametric distributions (exponential, Weibull, log-logistic, log-normal, standard gamma and GG) with and without including any covariates stratified by substage. The GG model without covariates is equivalent to the baseline model. Accordingly, the significance of the covariates can be determined with the likelihood-ratio (LR). The log likelihood of the GG model is the largest among all models which indicates that the GG model is the best fit model. Table 1 shows that the likelihood-ratio and their corresponding p-values. The p-values all are less than 0.05 except for standard gamma in IA group. At the same time, δ was estimated as 0.46(IA), −0.91(IB), −1.11(IIA), −0.66(IIB) and −1.36(IIC), and σ was estimated as 1.12(IA), 1.68(IB), 1.57(IIA), 1.53(IIB) and 1.22(IIC). Then δ is neither equal toσ nor equal to 1, nor close to 0. This provides additional evidence that the exponential, Weibull, log-normal and standard gamma models are not nested within the GG model and not a better fit for the melanoma survival data.

Table 1.

Likelihood-ratio chi-square statistics and P-values

Stage	GG vs GG_B* (d.f.=6)		GG vs Exponential (d.f.=2)		GG vs Weibull (d.f.=1)		GG vs log-normal (d.f.=1)		GG vs Standard gamma (d.f.=1)
	χ2	P	χ2	P	χ2	P	χ2	P	χ2	P
1A	161.84	2E-32	33.86	4E-08	5.08	0.024	4.30	0.038	2.78	0.095
1B	606.14	1E-127	132.58	2E-29	78.10	1E-18	14.94	1E-04	65.8	5E-16
11A	611.54	8E-129	129.98	6E-29	108.64	2E-25	26.72	2E-07	97.62	5E-23
11B	601.36	1E-126	118.38	2E-26	117.52	2E-27	17.82	2E-05	113.1	2E-26
11C	293.16	2E-60	170.86	8E-38	170.12	7E-39	62.88	2E-15	192.98	7E-44

^*GG_B is GG model without covariates

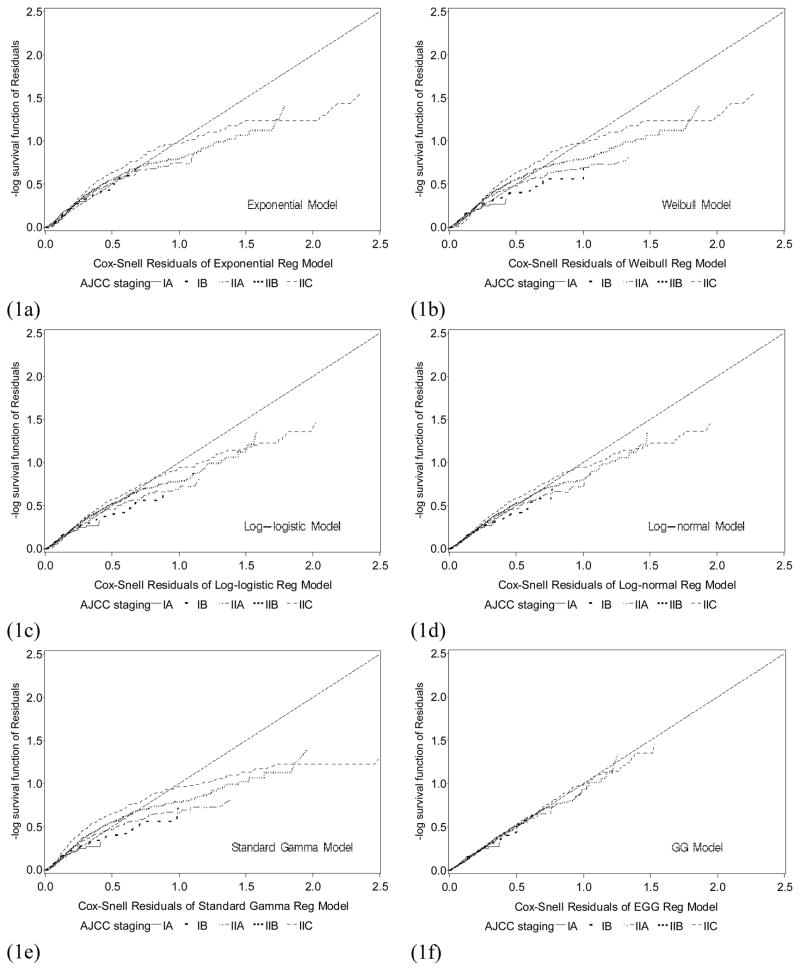
Figure 1a–1f shows the Cox-Snell residual plots for the exponential, Weibull, log-logistic, log-normal, standard gamma, and GG distributions for the survival models adjusted for the six covariates. In these plots, the larger the deviations from a straight line with slope 1 and intercept 0 indicate the poorer the model fit. Comparison of these graphs shows that the GG model (Figure 1f) is the best fitted parametric model for the localized melanoma data.

Figure 1.

Cox-Snell residual plots of staging subgroup for (1a) exponential model; (1b) Weibull model; (1c) log-logistic model; (1d) log-normal model; (1e) standard gamma; (1f) Generalized gamma model. Comparing these graphs, the straight line in the GG plot appears to provide the best fit to the melanoma data.

Comparisons of GG model with Cox model and Kaplan-Meier method

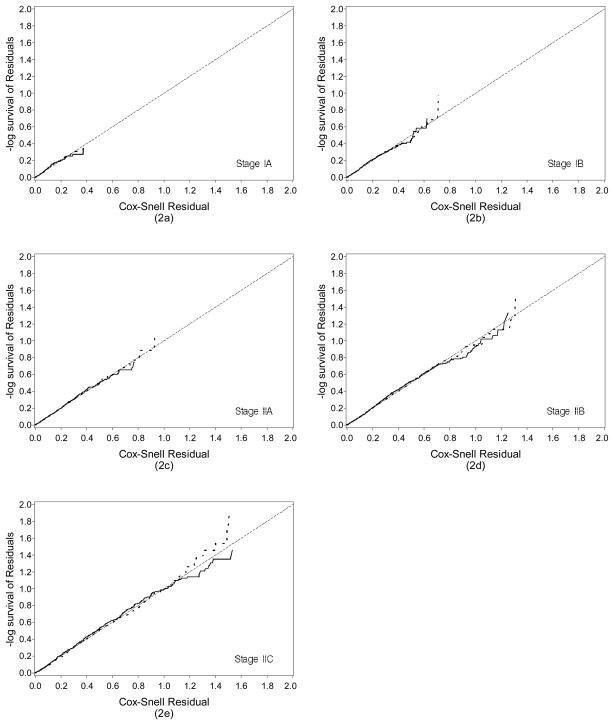
The Cox-Snell residual plots of the GG model and the Cox model are shown in Figure 2a–2e according to the substage of localized melanoma. The figures show that GG model is virtually identical to the Cox model for localized melanoma data for all staging subgroups. The departures of the residuals from the predicted are minimal for both models for all substages.

Figure 2.

Comparison of the Cox-Snell residuals for the GG and Cox model for localized melanoma by stage at diagnosis (2a) Stage IA; (2b) Stage IB; (2c) Stage IIA; (2d) Stage IIB; and (2e) Stage IIC. The solid lines represent the GG model and the dashed lines the Cox model.

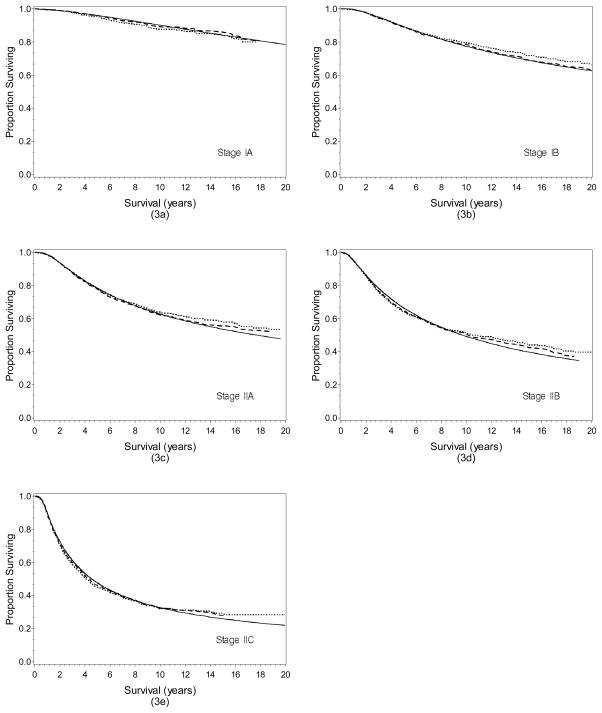
The estimated survival functions of the GG model were compared with those generated by the Cox model and the Kaplan-Meier method (Figure 3a–e). The estimated survival functions for all of these three methods are virtually identical across staging subgroups, indicating that both the GG and the Cox model produced similar estimated survival rates that are consistent with the observed survival rates calculated by the Kaplan-Meier method.

Figure 3.

Comparison of the survival functions of GG, Cox model and Kaplan-Meier method for localized melanoma by stage at diagnosis (3a) Stage IA; (3b) Stage IB; (3c) Stage IIA; (3d) Stage IIB; and (3e) Stage IIC. Solid lines represent the GG model, dashed lines the Cox model, and dotted lines the Kaplan Meier method.

The results of the survival regression analyses by the GG and the Cox model for each substage of localized melanoma are summarized in Table 2. The significant prognostic factors identified by both the GG model and the Cox model were nearly identical for each of the substages. However, in comparing the values of Waldχ₂ statistics for testing the significance of coefficients in the GG model and the Cox model, 70.4% (19/27) of the comparisons showed larger Wald χ² statistics for the GG model compared to the Cox model. Thus, the GG model in general appeared to be more efficient for coefficient estimation than the Cox model in the survival regression analyses of localized melanoma.

Table 2.

Estimated parameters of the GG and Cox models for predicting survival outcome in localized melanoma.

Stage	GG Model			Cox Model
	β (se)	Wald X2	p	β (se)	Wald X2	p
IA
Thickness	−1.34 (0.26)	27.41	<0.0001	1.83 (0.33)	30.98	<0.0001
Clark’s	*	*	*	*	*	*
Gender	0.28 (0.12)	5.60	0.018	−0.34 (0.16)	4.62	0.032
Ulceration	*	*	*	*	*	*
Site	−0.16 (0.12)	1.74	0.187	0.21 (0.16)	1.75	0.186
Age	−0.44 (0.13)	11.68	0.001	0.57 (0.17)	11.04	0.001
IB
Thickness	−0.33 (0.11)	9.92	0.002	0.40 (0.13)	9.09	0.003
Clark’s	−0.04 (0.08)	0.27	0.602	0.12 (0.11)	1.34	0.248
Gender	0.20 (0.08)	6.25	0.012	−0.26 (0.11)	5.98	0.014
Ulceration	−0.37 (0.16)	5.39	0.020	0.49 (0.20)	6.17	0.013
Site	−0.35 (0.08)	18.82	<0.0001	0.40 (0.11)	14.45	0.0001
Age	−0.26 (0.09)	9.32	0.002	0.33 (0.11)	8.98	0.003
IIA
Thickness	−0.32 (0.08)	17.04	<0.0001	0.37 (0.09)	15.83	<0.0001
Clark’s	−0.08 (0.09)	0.86	0.353	0.07 (0.11)	0.53	0.469
Gender	0.09 (0.08)	1.05	0.306	−0.003 (0.10)	0.001	0.972
Ulceration	−0.55 (0.13)	19.36	<0.0001	0.56 (0.15)	13.71	0.0002
Site	−0.30 (0.08)	12.95	0.0003	0.33 (0.10)	11.55	0.0007
Age	−0.20 (0.08)	5.99	0.014	0.33(0.10)	12.06	0.0005
IIB
Thickness	−0.10 (0.03)	11.33	0.001	0.09 (0.02)	14.12	0.0002
Clark’s	−0.20 (0.10)	3.87	0.049	0.13 (0.10)	1.68	0.194
Gender	0.25 (0.09)	7.91	0.005	−0.17 (0.09)	3.47	0.063
Ulceration	−0.53 (0.13)	15.83	<0.0001	0.47 (0.13)	12.74	0.0004
Site	−0.32 (0.09)	14.09	0.0002	0.29 (0.09)	10.75	0.001
Age	−0.26 (0.08)	9.82	0.002	0.29 (0.08)	11.73	0.0006
IIC
Thickness	−0.06 (0.01)	20.97	<0.0001	0.02 (0.01)	3.67	0.055
Clark’s	−0.12 (0.14)	0.76	0.382	0.005 (0.15)	0.001	0.974
Gender	−0.12 (0.09)	1.59	0.208	−0.081 (0.11)	0.57	0.452
Ulceration	*	*	*	*	*	*
Site	−0.17 (0.09)	3.61	0.058	0.12 (0.11)	1.35	0.245
Age	−0.20 (0.09)	5.30	0.021	0.24 (0.10)	5.66	0.017

Note: Tumor thickness measured in mm, Clark level (IV/V vs. II/III), Gender (female vs. male), ulceration (yes vs. no), Site (axial vs. extremity) and Age (≥ 60 vs. < 60). The GG model parameters are in general opposite sign of the Cox Model.

^*By definition, Stage IA includes only patients with Clark’s level II/III lesion without ulceration, therefore these two variables cannot be assessed. Similarly, stage IIC includes only patients with ulcerated lesion.

Hazard function estimation

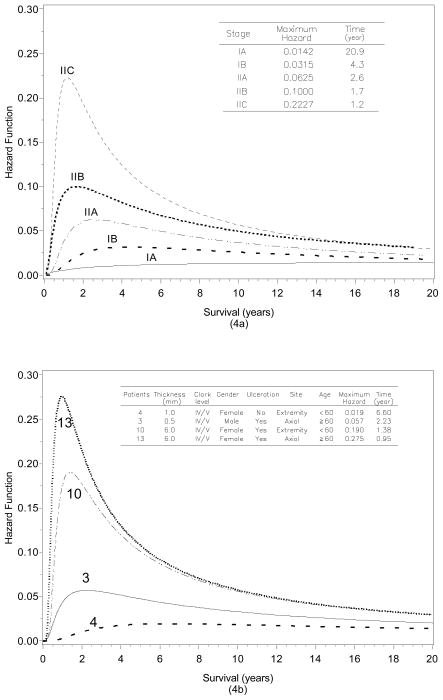
A major advantage of the parametric survival model on the Cox model is that a completed description of the hazard function over time can be obtained. The hazard function is practically useful to obtain insight into failure patterns quantitatively. The hazard function is plotted for the GG model with six covariates in Figure 4a by stage of disease at diagnosis. The maximum hazard for patients in more advanced stages is higher than patients diagnosed at earlier stages. In addition, it is immediately apparent that patients who present with later stage disease have a peak in the hazard function in the early years compared to those with earlier stage disease. In fact, the maximum hazards and their corresponding times estimated by substage at diagnosis are IA (1.4% at 20.9 years), IB (3.2% at 4.3 years), IIA, (6.3% at 2.6 years), IIB (10.0% at 1.7 years) and, IIC (22.3% at 1.2 years). This means, for example, that the mortality of stage IIA patients reach a peak in 2.6 years after diagnosis and approximately 6% of stage IIA patients survived prior to this specific time were expected to die. The hazard function increased dramatically early for stage IIC patients at that time point. The mortality of stage IIC was highest in 1.2 years after diagnosis and 22.3% of stage IIC survivors were expected to die at that time point. However, for patients who survived past 1.2 years the hazard drops off dramatically. At five years after diagnosis, the risk of mortality for stage IIC patients is only about 10% given they have survived prior to this time point.

Figure 4.

(4a) Hazard function of EEG model with six covariates for localized melanoma by stage at diagnosis. (4b) Hazard function plots by prognostic factors for individual patients. A decrease in the hazard function is a decline in the mortality, given a patient has survived to that time point.

We can also compare the risk of death at time t for different values of covariates. Thus, for an individual patient with a given set of characteristics (covariates), a specific hazard function can be generated for each patient. As shown in Table 3, we can vary the baseline presenting covariates and compute the time of the maximum hazard (mortality) and its corresponding time. For instance, for a female patient ≥60 years with a presenting non-ulcerated extremity melanoma of 0.5mm thickness the maximum risk occurs at a very long interval after diagnosis (20.5 years) and only a small proportion (1.4%) of patients were expected to die at that time. In contrast, for a ≥60 year old male patient presenting with a 3mm ulcerated melanoma of the chest, the maximum risk occurs much earlier (1.26 years) necessitating the need for close follow-up during this interval when the mortality rate at that time for patients who lived to this time point was 20.7%. Table 3 also shows the maximum hazard and its corresponding time for other combinations of patient and tumor factors. To illustrate this, the varying covariates for localized melanoma yield different hazard functions as shown in Figure 4b. The hazard function for patients 3, 4, 10, and 13 in Table 3, are plotted in Figure 4b. It is important to remember that the hazard is time-dependent in Figure 4b and the risk of mortality reflects the risk for patients surviving up until that time.

Table 3.

Maximum hazard values and survival rates for combination of prognostic factors for individual patients (examples).

Patient	Thickness (mm)	Clark level	Gender	Ulceration	Site	Age	Maximum hazard	Time Reached Maximum Hazard (years)	5-year Survival Rate	10-year Survival Rate
1	0.5	I/II/III	Female	No	Extremity	≥ 60	0.014	20.5	0.9597	0.9000
2	1.0	I/II/III	Male	No	Extremity	<60	0.024	12.3	0.9207	0.8197
3	0.5	IV/V	Male	Yes	Axial	≥ 60	0.057	2.23	0.7935	0.6520
4	1.0	IV/V	Female	No	Extremity	< 60	0.019	6.60	0.9469	0.8611
5	1.5	IV/V	Male	Yes	Axial	≥ 60	0.092	1.74	0.6998	0.5440
6	2.0	IV/V	Female	Yes	Extremity	<60	0.061	2.62	0.7894	0.6359
7	3.0	IV/V	Male	Yes	Axial	≥ 60	0.164	0.98	0.5461	0.3851
8	2.0	IV/V	Female	Yes	Extremity	<60	0.066	2.46	0.7653	0.6009
9	3.0	IV/V	Male	Yes	Axial	≥ 60	0.207	1.26	0.4940	0.3395
10	6.0	IV/V	Female	Yes	Extremity	< 60	0.190	1.38	0.5164	0.3565
11	6.0	IV/V	Female	Yes	Extremity	≥ 60	0.234	1.12	0.4637	0.3168
12	6.0	IV/V	Female	Yes	Axial	< 60	0.224	1.17	0.4752	0.3254
13	6.0	IV/V	Female	Yes	Axial	≥ 60	0.275	0.95	0.4254	0.2888

Survival rate estimation

The 5-year and 10-year survival rates as estimated for the patient profiles were calculated from the GG model (Table 3). As expected, these compare similarly to the previously published data from this cohort (Balch, 2001). Comparing the 5-year and 10-year survival rates by overall stage for both the GG model and Cox model shows that they are very similar. The calculated 5-year survival rates were 0.96(IA), 0.89(IB), 0.78(IIA), 0.67(IIB), 0.48(IIC) and 0.96(IA), 0.89(IB), 0.78(IIA), 0.65(IIB), 0.46(IIC) for the GG and Cox models, respectively. The calculated 10-year survival rates were 0.90, 0.77, 0.63, 0.49, 0.33 and 0.89, 0.78, 0.62, 0.51 and 0.32 for the GG and Cox models, respectively.

Conclusion

Results demonstrate that the GG model can serve as a powerful alternative and practically useful model to the commonly used Cox model in multivariate prognostic modeling of melanoma survival data. Moreover, the GG model offers an important advantage over the Cox model in that explicit and flexible individualized hazard functions can be estimated. The Kaplan-Meier observed survival curves and the predicted survival curves by both GG and Cox model were super imposable for each AJCC substage.

Two major clinical issues should be considered in developing models for predicting outcomes: 1) what is the patient’s chance of surviving for a given time period (e.g.: 5 or 10 years) after a diagnosis of melanoma; and, 2) if the patient has survived for a given period of time, what are the risks of death subsequently? The parametric model (GG model in this study) can effectively provide answers for both issues.

The GG model offers an evaluation of the hazard as a survival surrogate for comparing the effectiveness of a melanoma treatment under investigation. This information can also be used for patient stratification criterion for randomization in clinical trials. The “individualized hazard functions” are important clinically to be able to closely monitor the patient’s risk of dying from the melanoma over a long period of time based on this patient’s presenting clinical and pathological characteristics. Based on the pattern of hazard function over time, a patient-specific clinical treatment plan could be implemented to calibrate the intensity of follow-up with the declining risk of dying over time. The interpretation of the parameters from this model can be considered as accelerating or decelerating a patient’s biological clock (Cox, 2007). The GG model for melanoma prognosis can be an excellent alternative to Cox model since it appears to be more sensitive in identifying the majority of significant prognostic factors in melanoma. However, it should be note that it is generally expected that a parametric model, which has a specific model formulation and lower number of parameters, is more efficient than a semiparametric model, which has an infinite-dimensional nonparametric component.

Physicians are increasingly using electronic prediction tools to predict a patient’s clinical outcome, such as mortality and survival. According to the estimation by the American Cancer Society, melanoma is the fifth and seventh most common cancers in men and women, respectively, among new cases of cancer in the United States in 2007. It is estimated that 59,940 cases of invasive melanoma will be diagnosed in this country in 2007 and that 8,110 patients will die of the disease (American Cancer Society, 2007). Therefore, physicians involved in diagnosing and treating melanoma will need to be informed about prognosis and staging of this common cancer. Current staging tools do not allow outcomes predictions because they cannot accommodate multiple and continuous variables and cannot predict risk of dying after periods of survival. This parametric model can utilize all these predictive factors and thereby calculate an individual patients’ predicted outcome at the onset of their disease stage and at any timepoint thereafter. Such an electronic predictive tool will be used in the coming years by physicians for staging, treatment planning and follow-up.

In conclusion, this GG model is practically useful as a predictive model for time-specific survival rates based on individual patient’s clinical and pathological characteristics. It also provides an important capability to generate explicit and flexible individualized hazard functions for risk assessment of melanoma patients over time after diagnosis of melanoma. Using this model, individualized survival and hazard functions can be generated for a specific melanoma patient with an informative graphic display of time-specific survival and hazard rates. To our knowledge, this is the first application of this model in melanoma, and the same methodology can be applied to other oncology disciplines as well.