Abstract
Visual inspection of single-case data is the primary method of interpretation of the effects of an independent variable on a dependent variable in applied behavior analysis. The purpose of the current study was to replicate and extend the results of DeProspero and Cohen (1979) by reexamining the consistency of visual analysis across raters. We recruited members of the board of editors and associate editors for the Journal of Applied Behavior Analysis to judge graphs on a 100-point scale of experimental control and by providing a dichotomous response (i.e., “yes” or “no” for experimental control). Results showed high interrater agreement across the three types of graphs, suggesting that visual inspection can lead to consistent interpretation of single-case data among well-trained raters.
Keywords: data analysis, single-case design, visual inspection
Applied behavior analysis is characterized by the reliable measurement of observable behavior (Baer, Wolf, & Risley, 1968). Once recorded, these data are converted to a graphical display, and behavior analysts typically rely on visual inspection to summarize and interpret these data (Fahmie & Hanley, 2008; Sidman, 1960). When visually inspecting data, the data are examined to determine the extent to which a meaningful change in the behavior occurred and the extent to which this change can be attributed to the independent variable (i.e., experimental control). The following variables are taken into consideration when evaluating experimental control for intrasubject data: variability, level, and trend (Cooper, Heron, & Heward, 2007).
Although visual inspection is the primary method of analyzing single-case data, the method has been criticized for the absence of formal decision rules to guide analysis (Fisch, 1998; Ottenbacher, 1990; Wampold & Furlong, 1981). This lack of a formal set of rules reportedly may lead to subjectivity and inconsistency (Kazdin, 1982). To address this criticism, researchers have proposed the use of structured criteria (e.g., Pfadt, Cohen, Sudhalter, Romanczyk, & Wheeler, 1992) or visual aids (e.g., Fisher, Kelley, & Lomas, 2003) to standardize analysis of single-case data. Despite these alternative methods of data analysis, visual inspection continues to be the predominant method of analysis for single-case data. Several studies have empirically examined consistency of visual inspection (for reviews, see Franklin, Gorman, Beasley, & Allison, 1996; Ottenbacher, 1993). For example, DeProspero and Cohen (1979) asked members of the editorial board or guest reviewers from the Journal of Applied Behavior Analysis (JABA) and the Journal of the Experimental Analysis of Behavior (JEAB) to evaluate nine ABAB graphs for experimental control. Each graph was constructed according to various combinations of graphic features, such as pattern of mean shift (i.e., consistent, inconsistent, and irreversible), degree of mean shift, variability within a phase, and trend (Hersen & Barlow, 1976). DeProspero and Cohen asked the 108 raters who responded to evaluate how satisfactorily (on a scale of 0 [low] to 100 [high]) the graphs demonstrated experimental control. With the exception of the most obvious graphs (“ideal patterns”), interrater agreement was relatively poor (.61 mean Pearson correlation coefficient).
Other studies have evaluated the extent to which varying graphic features may affect agreement between observers. Ottenbacher (1990) evaluated six AB graphs with 61 professionals who had experience working with individuals with mental retardation (e.g., physical therapists, occupational therapists, special educators, and speech therapists). The graphs were varied according to mean shift across phases, variability across phases, change in slope across phases, change in level across phases, amount of overlap, and the degree of serial dependency. The participants indicated whether or not there was a significant change in performance from the A to B phase. Ottenbacher found poor agreement for a majority of the graphs across raters. Results also suggested that variability and slope were most associated with low agreement, and changes in the mean shift and level were associated with the highest agreement.
Research on the consistency of visual inspection as a means of data analysis generally suggests that visual inspection of graphical data may be inconsistent across raters. However, the results of these studies may be somewhat outdated (e.g., DeProspero & Cohen, 1979) due to increased and improved training opportunities in visual inspection of single-case data. The purpose of the current study was to replicate, extend, and update the study conducted by DeProspero and Cohen by instructing raters to evaluate graphs, based on a scale of 0 to 100, for experimental control (as in the DeProspero and Cohen study) in addition to a dichotomous response (“yes” or “no”) for a series of ABAB graphs.
METHOD
Stimulus Materials
The graphs were similar to those used by DeProspero and Cohen (1979). Thirty-six ABAB graphs were generated (using hypothetical data) that illustrated four different graphic features that represent characteristics that influence visual inspection: (a) pattern of mean shift across phases, (b) degree of mean shift across phases, (c) variability within a phase, and (d) trend (for additional examples, see DeProspero & Cohen).
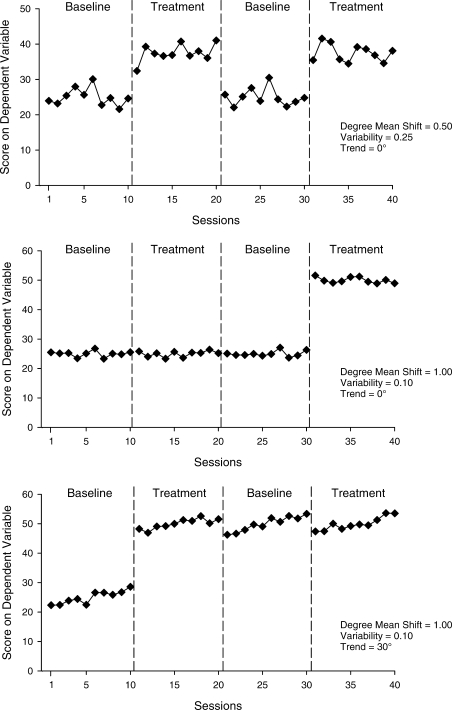
The first graphic feature, pattern of mean shift across phases, was represented using the criteria established by DeProspero and Cohen (1979). An ideal pattern depicted consistent increases in levels of responding in both B phases and consistent decreases in the return to baseline (e.g., Figure 1, top). The inconsistent treatment pattern showed no mean changes across the first three phases and an increase in the final B phase (e.g., Figure 1, middle). The irreversible effect pattern showed an increase in the first B phase, with levels of responding maintained at similar levels in the subsequent A and B phases (e.g., Figure 1, bottom).
Figure 1.
Examples of graphs sent to raters (for additional examples, see DeProspero & Cohen, 1979). The top panel shows ideal data with moderate shift in means, moderate variability, and no slope. The middle panel shows inconsistent treatment effects with low levels of variability, a high shift in means between phases, and no slope. The bottom panel shows irreversible effects with low levels of variability, a high shift in means between phases, and a slope of 30°.
Degree of mean shift across phases, the second graphic feature, was the mean percentage change from phase x to phase x + 1. For example, if the mean was 10 during the baseline phase and 15 during the treatment phase, the difference between treatment and baseline (5) was divided by the mean of the earlier phase (10) to yield a value of 0.5. The three mean-shift values evaluated were 1.0 (e.g., Figure 1, middle), 0.5 (e.g., Figure 1, top), and 0.25 (not shown).
The third graphic feature, variability within a phase, was determined by considering the relation between the mean and standard deviation. The standard deviation was divided by the mean to generate a variability coefficient. For example, if a phase had a mean of 10 and a standard deviation of 1, the variability coefficient was 0.1. Two variability coefficients, 0.1 (e.g., Figure 1, middle and bottom) and 0.25 (e.g., Figure 1, top), were evaluated.
Finally, the slope (i.e., trend) of the lines was manipulated to evaluate trend, which is defined as the extent to which data from a given phase follow a line with a particular slope. Half of the graphs had a zero slope (e.g., Figure 1, top and middle), and the other half had a linear slope of 30° (e.g., Figure 1, bottom) in an increasing direction.
Data construction included the procedures described by DeProspero and Cohen (1979) to ensure randomly distributed variability that had no effect on the pattern or degree of mean shift or the slope. A total of 144 phase means were selected, 4 for each of the 36 graphs. The means were selected such that each of the three patterns of degree of mean shift (ideal, inconsistent, and irreversible) was illustrated in the 12 pairs of phase means. A set of 1,440 standard deviation scores (one for each of the 10 points in each phase) was generated to establish variability. These had a mean of 0 and a standard deviation of 1. Each behavior data point was multiplied by the deviation score and the respective variability coefficient (0.1 or 0.25). Finally, for half the graphs, the trend was introduced by rotating the lines 30° about the middle data point of the phase.
Participants
The participants were members of the editorial board and associate editors of JABA from 2002 to 2004. The participant pool varied slightly from DeProspero and Cohen (1979) in that they surveyed members of both JABA and the JEAB. Of the 83 surveys sent, 47 surveys were returned; two of those were excluded because they were incomplete, resulting in 45 surveys used for this study (54% response rate).
Procedure
All 36 graphs (four graphs per page, each graph placed in random order on the page) were mailed to the participants with a letter stating the purpose of this study. The following instructions were provided:
Enclosed please find 36 ABAB reversal graphs depicting hypothetical data for your review. At the bottom of each graph, you will find two questions about experimental control. For the first question, we ask that you rate how satisfactory a demonstration of experimental control you consider this to be using a scale of 0 to 100 (0 represents no experimental control and 100 represents perfect experimental control). The second question will then require that you indicate whether or not the graph demonstrates experimental control (circle “yes” or “no”). Please complete both questions for each graph, or we will be unable to include your data in our analysis. Experimental control is demonstrated when there is a clear functional relation between the independent and dependent variables. That is, the dependent variable depends on or is a function of the independent variable and nothing else (Johnston & Pennypacker, 1993).
Participants were asked to return the survey within 3 weeks of the date it was sent. These procedures varied from DeProspero and Cohen (1979) in two ways. First, each rater received nine graphs in the earlier study, whereas each participant rated all 36 graphs in the current study. Second, DeProspero and Cohen did not include a definition of experimental control with their instructions.
Interobserver Agreement
Once the survey was received, graduate students in applied behavior analysis summarized the data and entered them into a Microsoft Excel spreadsheet. A second graduate student randomly selected the surveys of 15 participants (33%), summarized the data, and compared them to the first observer's data. An agreement was defined as both observers reporting the same response. Interobserver agreement was calculated by dividing the number of agreements by the number of agreements plus disagreements and converting the ratio to a percentage. For the question in which raters judged experimental control on a scale of 0 to 100, agreement was 99.9% (range, 99.7% to 100%), and for the dichotomous yes–no rating, agreement was 98% (range, 75% to 100%).
RESULTS
Interrater Agreement
The intraclass correlation coefficient (ICC; Müller & Büttner, 1994) is the appropriate measure of interrater agreement when there are a number of raters of the same phenomena; in this instance, the 45 participants' ratings of the 36 graphs for the demonstration of experimental control. The ICC is preferable to the mean Pearson correlation because the Pearson correlation can be positively biased due to the repeated use of the same set of participants. For the dichotomous yes–no question indicating experimental control, we calculated the mean kappa across 990 participant pairs. For the 100-point measure, the ICC evaluating absolute agreement was .89. We also calculated the Pearson correlation to directly compare the results of the present study to those of DeProspero and Cohen (1979). The mean Pearson correlation across the 990 participant pairs was .93, with a standard deviation of .05. The mean kappa was .84 (standard deviation of the kappa values was .21) for the dichotomous yes–no response. As with other measures of interrater agreement, values less than .70 are considered poor; from .70 to .80, adequate or acceptable; from .80 to .90, good or desired; and above .90 as very high (Müller & Büttner). Thus, both measures showed high levels of interrater agreement.
Evaluation
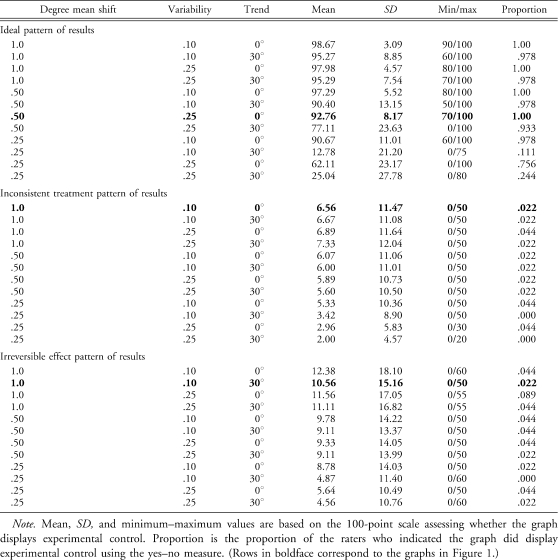
Table 1 provides both the mean and standard deviation of the 100-point scale and the proportion of respondents who indicated that the graph demonstrated experimental control for each combination of stimuli. Mean ratings were typically consistent with the proportion of participants who indicated that a given graph demonstrated experimental control. That is, when the mean rating was relatively high, the proportion of raters who indicated that the graph displayed experimental control using the yes–no measure was also high. For example, the mean rating for Figure 1 (top) was 92.76, and the proportion of raters indicating experimental control was 1.0. Similarly, when the mean rating was relatively low, the proportion was also low. For example, the mean rating for Figure 1 (middle) was 6.56, and the proportion of raters indicating experimental control was .022. Any graph that displayed either inconsistent treatment or an irreversible effect was rated pronouncedly lower than the majority of graphs displaying the ideal pattern. Within the ideal pattern, participants typically rated graphs very high, with the exception of graphs that had degree of mean shift of 0.25 and a 30° positive slope.
Table 1.
Mean, Standard Deviation, Minimum and Maximum Values, and Proportion of Graphs Indicated as Demonstrating Experimental Control at Each Combination of Stimuli
| Degree mean shift | Variability | Trend | Mean | SD | Min/max | Proportion |
| Ideal pattern of results | ||||||
| 1.0 | .10 | 0° | 98.67 | 3.09 | 90/100 | 1.00 |
| 1.0 | .10 | 30° | 95.27 | 8.85 | 60/100 | .978 |
| 1.0 | .25 | 0° | 97.98 | 4.57 | 80/100 | 1.00 |
| 1.0 | .25 | 30° | 95.29 | 7.54 | 70/100 | .978 |
| .50 | .10 | 0° | 97.29 | 5.52 | 80/100 | 1.00 |
| .50 | .10 | 30° | 90.40 | 13.15 | 50/100 | .978 |
| .50 | .25 | 0° | 92.76 | 8.17 | 70/100 | 1.00 |
| .50 | .25 | 30° | 77.11 | 23.63 | 0/100 | .933 |
| .25 | .10 | 0° | 90.67 | 11.01 | 60/100 | .978 |
| .25 | .10 | 30° | 12.78 | 21.20 | 0/75 | .111 |
| .25 | .25 | 0° | 62.11 | 23.17 | 0/100 | .756 |
| .25 | .25 | 30° | 25.04 | 27.78 | 0/80 | .244 |
| Inconsistent treatment pattern of results | ||||||
| 1.0 | .10 | 0° | 6.56 | 11.47 | 0/50 | .022 |
| 1.0 | .10 | 30° | 6.67 | 11.08 | 0/50 | .022 |
| 1.0 | .25 | 0° | 6.89 | 11.64 | 0/50 | .044 |
| 1.0 | .25 | 30° | 7.33 | 12.04 | 0/50 | .022 |
| .50 | .10 | 0° | 6.07 | 11.06 | 0/50 | .022 |
| .50 | .10 | 30° | 6.00 | 11.01 | 0/50 | .022 |
| .50 | .25 | 0° | 5.89 | 10.73 | 0/50 | .022 |
| .50 | .25 | 30° | 5.60 | 10.50 | 0/50 | .022 |
| .25 | .10 | 0° | 5.33 | 10.36 | 0/50 | .044 |
| .25 | .10 | 30° | 3.42 | 8.90 | 0/50 | .000 |
| .25 | .25 | 0° | 2.96 | 5.83 | 0/30 | .044 |
| .25 | .25 | 30° | 2.00 | 4.57 | 0/20 | .000 |
| Irreversible effect pattern of results | ||||||
| 1.0 | .10 | 0° | 12.38 | 18.10 | 0/60 | .044 |
| 1.0 | .10 | 30° | 10.56 | 15.16 | 0/50 | .022 |
| 1.0 | .25 | 0° | 11.56 | 17.05 | 0/55 | .089 |
| 1.0 | .25 | 30° | 11.11 | 16.82 | 0/55 | .044 |
| .50 | .10 | 0° | 9.78 | 14.22 | 0/50 | .044 |
| .50 | .10 | 30° | 9.11 | 13.37 | 0/50 | .044 |
| .50 | .25 | 0° | 9.33 | 14.05 | 0/50 | .044 |
| .50 | .25 | 30° | 9.11 | 13.99 | 0/50 | .022 |
| .25 | .10 | 0° | 8.78 | 14.03 | 0/50 | .022 |
| .25 | .10 | 30° | 4.87 | 11.40 | 0/60 | .000 |
| .25 | .25 | 0° | 5.64 | 10.49 | 0/50 | .044 |
| .25 | .25 | 30° | 4.56 | 10.76 | 0/60 | .022 |
Note. Mean, SD, and minimum–maximum values are based on the 100-point scale assessing whether the graph displays experimental control. Proportion is the proportion of the raters who indicated the graph did display experimental control using the yes–no measure. (Rows in boldface correspond to the graphs in Figure 1.)
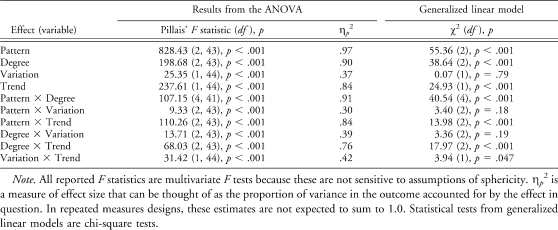
The 100-point rating data were analyzed using a 3 (Pattern) × 3 (Degree) × 2 (Variability) × 2 (Trend) four-way repeated measures analysis of variance (ANOVA). Only main effects and two-way interactions were estimated; higher order interactions were not included. The presence of an interaction between two variables (e.g., pattern and trend) suggests that the effect of one variable changes depending on the level of the other variable (e.g., the effect of the differing levels of pattern changes depending on whether the slope is 0° or 30°). Table 2 provides the summary from this analysis (columns 2 and 3). The dichotomous ratings of experimental control (yes–no ratings) were evaluated using a generalized linear model. (The generalized linear model allows evaluation of a logistic regression model, dichotomous outcomes, in which there are repeated measurements; sometimes referred to as “generalized estimating equations” when the outcome is dichotomous.) As with the ANOVA model, the estimated model included the four main effects (pattern, degree, variation, and trend) as well as the six two-way interaction effects; the results of this model are provided in the final column of Table 2.
Table 2.
Results of Analyses Used to Predict Ratings of Experimental Control (ANOVA) and Dichotomous Indication of the Presence of Experimental Control (Generalized Linear Models)
| Results from the ANOVA | Generalized linear model | ||
| Effect (variable) | Pillais' F statistic (df), p | ηp2 | χ2 (df), p |
| Pattern | 828.43 (2, 43), p < .001 | .97 | 55.36 (2), p < .001 |
| Degree | 198.68 (2, 43), p < .001 | .90 | 38.64 (2), p < .001 |
| Variation | 25.35 (1, 44), p < .001 | .37 | 0.07 (1), p = .79 |
| Trend | 237.61 (1, 44), p < .001 | .84 | 24.93 (1), p < .001 |
| Pattern × Degree | 107.15 (4, 41), p < .001 | .91 | 40.54 (4), p < .001 |
| Pattern × Variation | 9.33 (2, 43), p < .001 | .30 | 3.40 (2), p = .18 |
| Pattern × Trend | 110.26 (2, 43), p < .001 | .84 | 13.98 (2), p < .001 |
| Degree × Variation | 13.71 (2, 43), p < .001 | .39 | 3.36 (2), p = .19 |
| Degree × Trend | 68.03 (2, 43), p < .001 | .76 | 17.97 (2), p < .001 |
| Variation × Trend | 31.42 (1, 44), p < .001 | .42 | 3.94 (1), p = .047 |
Note. All reported F statistics are multivariate F tests because these are not sensitive to assumptions of sphericity. ηp2 is a measure of effect size that can be thought of as the proportion of variance in the outcome accounted for by the effect in question. In repeated measures designs, these estimates are not expected to sum to 1.0. Statistical tests from generalized linear models are chi-square tests.
Rather than relying solely on statistical significance levels, we also examined the effect size of the variables. Specifically, we focused on those effects that showed a very large effect size (ηp2 > .50) in order to focus on the variables of greatest importance. The results showed that the effects were remarkably consistent across the 100-point rating and the simple indication of whether the graph demonstrated experimental control when comparing results for the two outcomes. There were effects of pattern, degree, and trend in both analyses. More important, interaction effects between pattern and degree, pattern and trend, and degree and trend were observed in both analyses.
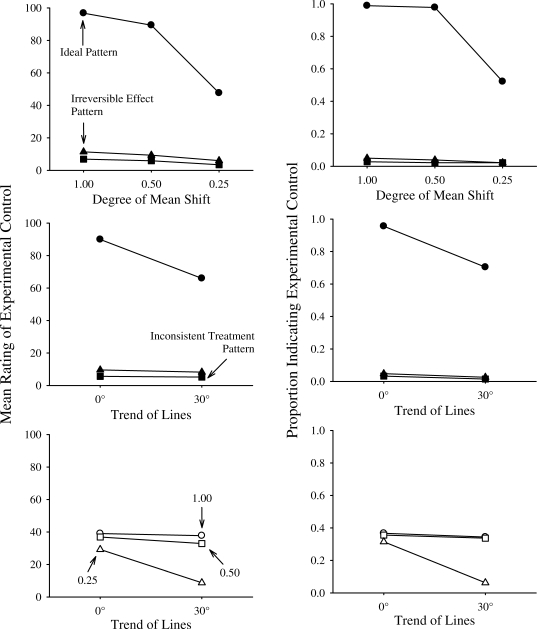
To help understand the interactive effects of pattern, degree, and trend, we generated plots for the combination of these variables for both the mean rating (100-point scale) and the dichotomous responses. Figure 2 (top) provides the mean levels of rating of experimental control for each combination of pattern with degree (top left panel) and the proportion of the sample indicating experimental control was demonstrated for each combination of pattern with degree (top right panel). Evidence of experimental control was most apparent to the reviewers under the ideal pattern. However, even when considering the ideal pattern, the effect of degree of mean shift was evident (notably when degree of mean shift was 0.25). The means for the inconsistent treatment pattern and the irreversible effect pattern, although they differed from each other based on conventional statistical significance levels, did not meet our criteria in terms of evaluating differences based on effect size. Figure 2 (middle) shows the Pattern × Trend interaction. As in the top panels, the distinguishing characteristic of this interaction is the effect of the ideal pattern and the relative impacts of a 0° trend line and a 30° trend line on ratings of experimental control for both the mean rating (Figure 2, center left panel) and proportion of sample indicating experimental control (Figure 2, center right panel). Finally, Figure 2 (bottom) illustrates the Degree × Trend interaction. This interaction was somewhat different from the prior two interactions in that it was a specific combination that resulted in low ratings of experimental control; specifically, instances in which the degree was 0.25 associated with a 30° trend line.
Figure 2.
Top panels depict the Pattern × Mean Shift interaction in the prediction of raters' assessment of experimental control. The top left panel plots means and corresponds to results from the ANOVA analyses. The top right panel plots proportions and corresponds to results from the generalized linear models. The center panels depict the Pattern × Trend interaction in the prediction of raters' assessment of experimental control. The center left panel plots means and corresponds to results from the ANOVA analyses. The center right panel plots proportions and corresponds to results from the generalized linear models. The bottom panels depict the Degree × Trend interaction in the prediction of raters' assessment of experimental control. The bottom left panel plots means and corresponds to results from the ANOVA analyses. The bottom right panel plots proportions and corresponds to results from the generalized linear models.
DISCUSSION
We evaluated the consistency of visual inspection of single-case data in this study by replicating and extending the procedures used by DeProspero and Cohen (1979). Previous research suggested that visual inspection may lead to inconsistent conclusions about judgment of experimental control across raters (e.g., Bobrovitz & Ottenbacher, 1998; DeProspero & Cohen; Fisch, 2001), despite the conventional wisdom among behavior analysts that visual inspection of intrasubject data is largely reliable and conservative (e.g., Baer, 1977; Michael, 1974; Parsonson & Baer, 1992). In the current investigation, individuals skilled in the visual inspection of graphical data judged whether graphs generated from hypothetical data demonstrated experimental control along two dimensions: a scale of 0 to 100 and a dichotomous yes–no response. The results of this study contradict previous findings by showing a generally high degree of agreement across raters for all three patterns of graphs evaluated. That is, raters were relatively consistent when asked to determine experimental control in graphs that depicted ideal patterns as well as inconsistent and irreversible treatment effects.
There are several potential reasons for these differing results. First, it has been over 30 years since the publication of some studies that examined visual inspection (e.g., DeProspero & Cohen, 1979). During this period, there has been a significant growth of behavior analysis. For example, membership in the Association for Behavior Analysis International has nearly doubled from just over 2,500 members in 1997 to nearly 5,000 members in 2006 (Malott, 2006). This membership growth parallels the development of academic training programs for behavior analysts. The Behavior Analyst Certification Board approves course sequences in applied behavior analysis. Since the inception of this program in 2000, the board has approved nearly 140 course sequences (Shook & Johnston, 2006). Thus, it is likely that more students in behavior-analytic graduate programs receive formal academic training in experimental designs and visual inspection than in years past. (For graduate students, the board requires a minimum of 20 hr of coursework in the experimental evaluation of interventions and 20 hr of coursework in the measurement of behavior and displaying and interpreting data; see the revised standards for Board-Certified Behavior Analysts at http://www.bacb.com/pages/bcba_stand.html).
Another reason for the differing results may be our dependent variables. DeProspero and Cohen (1979) asked their participants to rate the demonstration of experimental control on a scale of 0 to 100. In addition to using this ordinal scale, we asked raters to reply yes or no as to whether the graph demonstrated experimental control. In general, when raters evaluate whether intrasubject data have met criteria for demonstrating experimental control for research or clinical purposes, it is more likely that visual inspection produces a dichotomous decision (i.e., experimental control either is or is not demonstrated, rather than the degree to which experimental control has been demonstrated), which may lead to higher interrater agreement. It is interesting to note that, in the current study, both measures resulted in high levels of interrater agreement. It is unclear, however, if rating the graphs as a dichotomous yes or no affected the ratings on an ordinal scale for each participant.
Finally, it is possible that two other procedural differences may have contributed to the differing results. The instructions we provided to our participants may have also accounted for the differences between the findings in the current study and that of DeProspero and Cohen (1979). We provided a definition of experimental control, whereas DeProspero and Cohen did not. In addition, we surveyed only editorial board members and associate editors of JABA, whereas DeProspero and Cohen (1979) surveyed members of the boards for both JABA and JEAB. Thus, their broader subject pool may have led to more variability in responses. We chose to solicit only JABA editors given the greater likelihood of experience in judging single-case experimental designs on a regular basis.
Given that we relied on members of the editorial board and associate editors of JABA, the results of the current study suggest that visual inspection may be an appropriate tool for evaluation by the scientific community. However, it is important to recognize that most practitioners in applied behavior analysis also use visual inspection on a frequent basis to guide their treatment decisions. Thus, future research should examine consistency of visual inspection across practitioners.
A limitation to the current study may be the use of graphs generated from hypothetical data. One rater commented that interpretation may be affected by the context of the behavior (e.g., what the behavior is, who is engaging in the behavior). Future research could examine the consistency of visual inspection of actual data or hypothetical data with accompanying vignettes describing the context of the behavior. Also, our study focused solely on ABAB experimental designs. Although ABAB designs can provide a powerful demonstration of experimental control, there are many other single-case experimental designs (e.g., multielement design, multiple baseline design) that also can demonstrate experimental control. Future research could also examine the consistency of visual inspection using these other designs.
Finally, future research could examine the effects of rater characteristics on the consistency of visual inspection. For example, as previously discussed, the differences in raters may account for some of the differences in results between this study and those of DeProspero and Cohen (1979). Other characteristics that could be examined include (a) practitioners (e.g., Board-Certified Behavior Analysts or Board-Certified Associate Behavior Analysts) versus researchers, (b) number of years in practice, and (c) type of graduate degree (e.g., masters degree vs. doctorate).
Despite previous research demonstrating the inconsistency of visual inspection, the current study suggests that under certain circumstances, visual inspection can lead to consistent conclusions across raters. Thus, this study supports the continued reliance on visual inspection by well-trained behavior analysts.
Acknowledgments
Katharine Gutshall is now at the Center for Autism and Related Disorders, Inc. We thank Wayne Fisher for helpful comments on earlier versions of this manuscript. We also thank Jennifer Boensch and Tiffany Reid for their assistance in various phases of this study.
Contributor Information
SungWoo Kahng, KENNEDY KRIEGER INSTITUTE AND THE JOHNS HOPKINS UNIVERSITY SCHOOL OF MEDICINE.
Kyong-Mee Chung, YONSEI UNIVERSITY.
Katharine Gutshall, KENNEDY KRIEGER INSTITUTE AND UNIVERSITY OF MARYLAND, BALTIMORE COUNTY.
Steven C Pitts, UNIVERSITY OF MARYLAND, BALTIMORE COUNTY.
Kelli Girolami, KENNEDY KRIEGER INSTITUTE AND UNIVERSITY OF MARYLAND, BALTIMORE COUNTY.
REFERENCES
- Baer D.M. Perhaps it would be better not to know everything. Journal of Applied Behavior Analysis. 1977;10:167–172. doi: 10.1901/jaba.1977.10-167. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Baer D.M, Wolf M.M, Risley T.R. Some current dimensions of applied behavior analysis. Journal of Applied Behavior Analysis. 1968;1:91–97. doi: 10.1901/jaba.1968.1-91. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bobrovitz C.D, Ottenbacher K.J. Comparison of visual inspection and statistical analysis of single-subject data in rehabilitation research. American Journal of Physical Medicine & Rehabilitation. 1998;77:94–102. doi: 10.1097/00002060-199803000-00002. [DOI] [PubMed] [Google Scholar]
- Cooper J.O, Heron T.E, Heward W.L. Applied behavior analysis (2nd ed.) Upper Saddle River, NJ: Pearson Education; 2007. [Google Scholar]
- DeProspero A, Cohen S. Inconsistent visual analyses of intrasubject data. Journal of Applied Behavior Analysis. 1979;12:573–579. doi: 10.1901/jaba.1979.12-573. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fahmie T.A, Hanley G.P. Progressing toward data intimacy: A review of within-session data analysis. Journal of Applied Behavior Analysis. 2008;41:319–331. doi: 10.1901/jaba.2008.41-319. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fisch G.S. Visual inspection of data revisited: Do the eyes still have it. The Behavior Analyst. 1998;21:111–123. doi: 10.1007/BF03392786. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fisch G.S. Evaluating data from behavioral analysis: Visual inspection or statistical models. Behavioural Processes. 2001;54:137–154. doi: 10.1016/s0376-6357(01)00155-3. [DOI] [PubMed] [Google Scholar]
- Fisher W.W, Kelley M.E, Lomas J.E. Visual aids and structured criteria for improving visual inspection and interpretation of single-case designs. Journal of Applied Behavior Analysis. 2003;36:387–406. doi: 10.1901/jaba.2003.36-387. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Franklin R.D, Gorman B.S, Beasley T.M, Allison D.B. Graphical display and visual analysis. In: Franklin R.D, Allison D.B, Gorman B.S, editors. Design and analysis of single-case research. Hillsdale, NJ: Erlbaum; 1996. pp. 119–158. [Google Scholar]
- Hersen M, Barlow D.H. Single case experimental designs: Strategies for studying behavior change. New York: Pergamon; 1976. [Google Scholar]
- Johnston J.M, Pennypacker H.S. Strategies and tactics of behavioral research (2nd ed.) Hillsdale, NJ: Erlbaum; 1993. [Google Scholar]
- Kazdin A.E. Single-case research designs: Methods for clinical and applied settings. New York: Oxford University Press; 1982. [Google Scholar]
- Malott M.E. ABA financial update. The Association for Behavior Analysis International Newsletter, 29(3) 2006. Retrieved from http://www.abainternational.org//ABA/newsletter/vol293/ABAFinances__All.asp.
- Michael J. Statistical inference for individual organism research: Mixed blessing or curse. Journal of Applied Behavior Analysis. 1974;7:647–653. doi: 10.1901/jaba.1974.7-647. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Müller R, Büttner P. A critical discussion of intraclass correlation coefficients. Statistics in Medicine. 1994;13:2465–2476. doi: 10.1002/sim.4780132310. [DOI] [PubMed] [Google Scholar]
- Ottenbacher K.J. Visual inspection of single-subject data: An empirical analysis. Mental Retardation. 1990;28:283–290. [PubMed] [Google Scholar]
- Ottenbacher K.J. Interrater agreement of visual analysis in single-subject decisions: Quantitative review and analysis. American Journal on Mental Retardation. 1993;98:135–142. [PubMed] [Google Scholar]
- Parsonson B.S, Baer D.M. The visual analysis of data, and current research into the stimuli controlling it. In: Kratochwill T.R, Levin J.R, editors. Single-case research design and analysis: New directions for psychology and education. Hillsdale, NJ: Erlbaum; 1992. pp. 15–40. [Google Scholar]
- Pfadt A, Cohen I.L, Sudhalter V, Romanczyk R.G, Wheeler D.J. Applying statistical process control to clinical data: An illustration. Journal of Applied Behavior Analysis. 1992;25:551–560. doi: 10.1901/jaba.1992.25-551. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shook G.S, Johnston J. Trends in behavior analyst certification. The Association for Behavior Analysis International Newsletter, 29(3) 2006. Retrieved from http://www.abainternational.org//ABA/newsletter/vol293/Practice.Shook.asp.
- Sidman M. Tactics of scientific research. New York: Basic Books; 1960. [Google Scholar]
- Wampold B.E, Furlong M.J. The heuristics of visual inference. Behavioral Assessment. 1981;3:79–92. [Google Scholar]