Conditioned Reinforcement and Response Strength

Abstract

Stimuli associated with primary reinforcers appear themselves to acquire the capacity to strengthen behavior. This paper reviews research on the strengthening effects of conditioned reinforcers within the context of contemporary quantitative choice theories and behavioral momentum theory. Based partially on the finding that variations in parameters of conditioned reinforcement appear not to affect response strength as measured by resistance to change, long-standing assertions that conditioned reinforcers do not strengthen behavior in a reinforcement-like fashion are considered. A signposts or means-to-an-end account is explored and appears to provide a plausible alternative interpretation of the effects of stimuli associated with primary reinforcers. Related suggestions that primary reinforcers also might not have their effects via a strengthening process are explored and found to be worthy of serious consideration.

An influential review of conditioned reinforcement 15 years ago (Williams, 1994a) opened with a quote from more than 40 years ago lamenting the fact that there may be no other concept in psychology in such a state of theoretical disarray (Bolles, 1967). Unfortunately, Bolles' evaluation of conditioned reinforcement appears relevant despite 40 additional years of work on the topic. Given the reams of published material and long-running controversies surrounding the concept of conditioned reinforcement, this review will not attempt to be exhaustive. For more thorough reviews, the interested reader should consider other sources (e.g., Fantino, 1977; Hendry, 1969; Nevin, 1973; Wike, 1966; Williams, 1994a,b). Also, when considering a concept like conditioned reinforcement with such a long and storied past, it is difficult to say anything that has not been said before. Thus, much of what follows will not be new. Rather, I will briefly review the contemporary approach to studying the strengthening effects of conditioned reinforcers and then consider how recent research has led me to reexamine an old question about the nature of conditioned reinforcement: Do conditioned reinforcers actually strengthen behavior upon which they are contingent?

To begin, it may be helpful to consider a couple of definitions of conditioned reinforcement from recent textbooks.

“A previously neutral stimulus that has acquired the capacity to strengthen responses because it has been repeatedly paired with a primary reinforcer” (Mazur, 2006).

“A stimulus that has acquired the capacity to reinforce behavior through its association with a primary reinforcer” (Bouton, 2007).

As these definitions suggest, neutral stimuli seem to acquire the capacity to function as reinforcers as a result of their relationship with a primary reinforcer. This acquired capacity to strengthen responding is generally considered to be the outcome of Pavlovian conditioning (e.g., Mackintosh, 1974; Williams, 1994b). Thus, the same principles that result in a stimulus acquiring the capacity to function as a conditioned stimulus when predictive of an unconditioned stimulus seem to result in a neutral stimulus acquiring the capacity to function as a reinforcer when predictive of a primary reinforcer.

Evidence for such acquired strengthening effects traditionally came from tests to see if the stimulus could result in the acquisition of a new response or change the rate or pattern of a response under maintenance or extinction conditions (see Kelleher & Gollub, 1962 for review).

Somewhat later work showed that stimuli temporally proximate to primary reinforcement could change the rate and pattern of behavior upon which they are contingent in chain schedules of reinforcement (see Gollub, 1977, for review). In that sense, such stimuli may be considered reinforcers. But, as will be discussed later, interpreting such changes in rates or patterns of behavior in terms of a strengthening process has been controversial for a long time. Before returning to a discussion of whether conditioned reinforcers actually strengthen responding, I first examine the contemporary approach to measuring strengthening effects of conditioned reinforcers within the context of matching-law based choice theories and then discuss a more limited body of research examining the strengthening effects of conditioned reinforcers within the context of behavioral momentum theory.

Theories of Choice and Relative Strength of Conditioned Reinforcement

Herrnstein (1961) found that with concurrent sources of primary reinforcement available for two operant responses, the relative rate of responding to the options was directly related to the relative rate of reinforcement obtained from the options. Quantitatively the matching law states that:

1

where B₁ and B₂ refer to the rates of responding to the two options and R₁ and R₂ refer to the obtained reinforcement rates from those options. With the introduction of Equation 1 and its extensions (e.g., Herrnstein, 1970), relative response strength as measured by relative allocation of behavior became a major theoretical foundation of the experimental analysis of behavior.

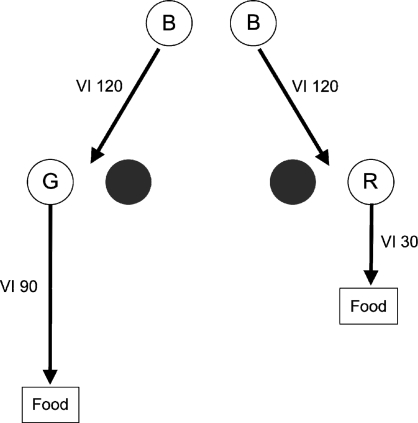
The insights provided by the matching law were extended to characterize the relative strengthening effects of conditioned reinforcers using concurrent-chains procedures. Figure 1 shows a schematic of a concurrent-chains procedure. In the typical arrangement, two concurrently available initial-link schedules produce transitions to mutually exclusive terminal-link schedules signaled by different stimuli. For example, in Figure 1, responding to the concurrently available variable-interval (VI) 120-s schedules in the presence of blue keys produces transitions to terminal links associated with different VI schedules in the presence of either red or green keys. The allocation of responding in the initial links is presumably, at least in part, a reflection of the relative conditioned reinforcing effects of the terminal-link stimuli.

Fig 1.

Schematic of a concurrent-chains procedure (B = Blue, G = Green, R = Red). Dark keys are inoperative. See text for details.

Early work with concurrent chains suggested that the relative rate of responding in the initial links matched the relative rates of primary reinforcement delivered in the terminal links as described by Equation 1 (Autor, 1969; Herrnstein, 1964). This outcome led Herrnstein to conclude that the strengthening effects of a conditioned reinforcer are a function of the rate of primary reinforcement obtained in its presence. However, Fantino (1969) soon showed that preference for a terminal link associated with a higher rate of primary reinforcement decreased as both initial links were increased. A simple application of Equation 1 does not predict this outcome because the relative rate of reinforcement in the two terminal links remains unchanged. Thus, the strengthening effects of a conditioned reinforcer are clearly not just a function of the rate of primary reinforcement obtained in its presence. To account for these findings, Fantino (1969) proposed the following extension of the matching law known as delay reduction theory (DRT):

2

where B₁ and B₂ are response rates to the two options in the initial links, T is the average delay to primary reinforcement from the onset of the initial links, and t₁ and t₂ are the average delays to primary reinforcement from the onset of each of the terminal link stimuli. DRT provides a quantitative theory of conditioned reinforcement suggesting that the value or strengthening effects of a stimulus depend upon the average reduction in expected time to reinforcement signaled by the onset of that stimulus. As noted by Williams (1988), DRT is similar to comparator theories of Pavlovian conditioning (i.e., Scalar Expectancy Theory; Gibbon & Balsam, 1981) that predict the related finding that conditioning depends on duration of a CS relative to the overall time between US presentations. Such a correspondence with findings and theorizing in Pavlovian conditioning is obviously good given the assumption noted above that the acquired strengthening capacity of conditioned reinforcers is the result of a Pavlovian conditioning process.

One well-known complication of using chain schedules to study conditioned reinforcement is that there is a dependency between responding in an initial link and ultimate access to the primary reinforcer (e.g., Branch, 1983; Dinsmoor, 1983; Williams, 1994b). Thus, responding in the initial links of chain schedules likely reflects the strengthening effects of both primary reinforcement in the terminal links and any conditioned reinforcing effects of the terminal link stimuli. This additional dependency is especially relevant when initial links of different durations are arranged in concurrent-chains schedules (i.e., when different rates of conditioned reinforcement are arranged). To accommodate the impact of changes in primary reinforcement associated with differential initial-link durations, Squires and Fantino (1971) modified DRT such that:

3

where all the terms are as in Equation 2, and R₁ and R₂ refer to the overall rates of primary reinforcement associated with the two options. In the absence of terminal links and their putative conditioned reinforcing effects, Equation 3 reduces to the strict matching law (i.e., Equation 1). DRT thus became a general theory of choice incorporating the effects of both primary and conditioned reinforcement.

The basic approach of DRT inspired a number of additional general choice theories incorporating the strengthening effects of both primary and conditioned reinforcers. Examples of such theories include incentive theory (Killeen, 1982), melioration theory (Vaughan, 1985), the contextual choice model (CCM; Grace, 1994), and the hyperbolic value-added model (HVA; Mazur, 2001). A consideration of the relative merits of all these models is beyond the scope of the present paper, but CCM and HVA will be briefly reviewed in order to explore some relevant issues about conditioned reinforcement and response strength.

Both CCM and HVA are based on the concatenated generalized matching law. The generalized matching law accounts for common deviations (i.e., bias, under- or over-matching) from the strict matching law presented in Equation 1 (Baum, 1974) and states that:

4

where the terms are as in Equation 1 and the parameters a and b reflect sensitivity to variations in reinforcement ratios and bias unrelated to relative reinforcement, respectively. The concatenated matching law (Baum & Rachlin, 1969) suggests that choice is dependent upon the value of the alternatives, and that value is determined by the multiplicative effects of any number of reinforcement parameters (e.g., rate, magnitude, immediacy etc). Generalized concatenated matching thus suggests that:

5

with added terms for reinforcement amounts (A1 and A2), reinforcement immediacies (1/D₁ and 1/D₂), and their respective sensitivity terms a2 and a3. Davison (1983) suggested that the concatenated matching law could be used as a basis for a model of concurrent-chains performance by replacing rates of primary reinforcement (i.e., R₁ and R₂) with rates of transition to the terminal-link stimuli and the value of the terminal-link stimuli (i.e., conditioned reinforcers). A general form of such a model is:

6

where r₁ and r₂ refer to rates of terminal-link transition (i.e., rate of conditioned reinforcement) associated with the options, and V₁ and V₂ are summary terms describing the value or strengthening effects of the two terminal-link stimuli. The question then becomes how the value or strengthening effects of the conditioned reinforcers should be calculated.

According to CCM, the value of a conditioned reinforcer is a multiplicative function of the concatenated effects of the parameters of primary reinforcers obtained in the presence of a stimulus:

7

where all terms are as in Equation 5, and the added terms T_t and T_i refer to the average durations of the terminal and initial links, respectively. Thus, CCM suggests that conditioned reinforcing value is independent of the temporal context, but sensitivity to relative value of the conditioned reinforcers changes with the temporal context. This occurs because the T_t /T_i exponent decreases the other sensitivity parameters (a₂, a₃) when relatively longer initial-link schedules are arranged. In essence, CCM is a restatement of Herrnstein's (1964) original conclusion that the strengthening effects of a conditioned reinforcer are a function of primary reinforcement obtained in its presence, but modified by the fact that temporal context affects sensitivity to such strengthening effects.

Alternatively, HVA suggests that the value of a terminal-link stimulus is determined by the summed effects of the amounts and delays to primary reinforcers obtained in its presence and uses Mazur's (1984) hyperbolic decay model to calculate the value of a conditioned reinforcer such that:

8

where the terms are as above and the parameter k represents sensitivity to primary-reinforcement delay. Furthermore, HVA suggests that preference in concurrent chains is determined by the increase in value associated with a transition to a terminal link from the initial links such that:

9

where V_t1 and V_t2 represent the values of each of the terminal links, V_i represents the value of the initial links, and a₂ is a sensitivity parameter scaling initial-link values. Like DRT, HVA is similar to comparator theories of Pavlovian conditioning, but in the case of HVA this is because a terminal stimulus will only attract choice if the value of that stimulus is greater than the value of initial links.

To aid in the comparison of DRT, CCM, and HVA, consider a generalized-matching version of the DRT (cf. Mazur, 2001) with free parameters for sensitivity to relative rates of primary reinforcement a₁, sensitivity to terminal-link durations a₂, and sensitivity to relative conditioned reinforcement value k, such that:

10

Note that DRT, CCM, and HVA each propose a different way for calculating the value of conditioned reinforcers. Note also that CCM and HVA differ from DRT in that DRT includes relative rates of primary reinforcement (R₁/R₂) rather than relative rates of conditioned reinforcement (r₁/r₂). Despite these differences in approach, the theories all do about equally well accounting for the main findings from the large body of research on concurrent-chains schedules when equipped with the same number of free parameters (see Mazur, 2001).

Although the study of behavior on concurrent-chains schedules and the associated models have no doubt increased our understanding of conditioned reinforcement, the heavy reliance on concurrent chains has been limiting with respect to the questions that can be answered about conditioned reinforcement. The vast majority of research on concurrent-chains schedules has focused on how to characterize the effects of changes in primary reinforcement or the effects of temporal context on conditioned reinforcement value. These are surely interesting and important questions, but the dependency noted above between responding in the initial links and access to primary reinforcers in the terminal links has made it difficult to examine the effects of parameters of conditioned reinforcement on choice. For example, the most straightforward way to vary the rate of conditioned reinforcement is to modify the duration of an initial link. But, doing so also changes the rate of primary reinforcement, relative value of the conditioned reinforcer, or sensitivity to relative value, depending on the model. The confound between rates of primary and conditioned reinforcement is such a prominent feature of the procedure that, as noted above, DRT has formalized the effects of changes in initial link duration as resulting from the associated changes in primary reinforcement and the value of the conditioned reinforcer.

An alternative approach to study conditioned reinforcement rate in concurrent chains involves adding extra terminal-link entries associated with extinction and then vary their relative rate of production by the two initial-link options. Although this approach has produced some modest evidence for the effects of conditioned reinforcement rate on choice (e.g., Williams & Dunn, 1991), the procedure is plagued by the transitive nature of the effects and interpretive problems (Mazur, 1999; see also Shahan, Podlesnik, & Jimenez-Gomez, 2006, for discussion). If one's interest is in examining the strengthening effects of conditioned reinforcers, this state of affairs is unfortunate. The reason is that it becomes very difficult to examine the effects of variations in parameters of conditioned reinforcement independently of changes in primary reinforcement. Thus, our understanding of the putative strengthening effects of conditioned reinforcers might benefit from increased use of procedures allowing better separation of the effects of primary and conditioned reinforcers.

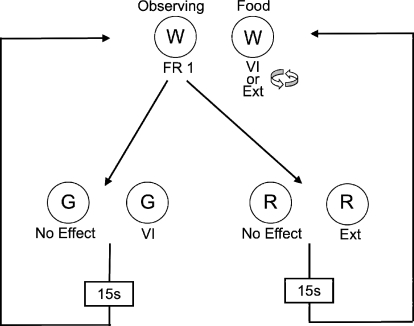
One such procedure is the observing-response procedure (Wyckoff, 1952). Figure 2 shows an example of an observing-response procedure. Unsignaled periods of food reinforcement on a VI schedule alternate irregularly with extinction on the food key (i.e., a mixed schedule). Responses on a separate observing key produce brief periods of stimuli differentially associated with the schedule of reinforcement in effect on the food key—either VI (i.e., S+) or extinction (i.e., S−). Responding on the observing key is widely believed to be maintained by the conditioned reinforcing effects of S+ presentations (e.g., Dinsmoor, 1983; Fantino, 1977). In fact, S− deliveries can be omitted from the procedure with little impact if S+ deliveries are made intermittent (e.g., Dinsmoor, Browne, & Lawrence, 1972). Importantly, responding on the observing key has no effect on the scheduling of primary reinforcers on the food key. All food-key reinforcers can be obtained in the absence of responding on the observing key. In addition, unlike chain schedules of reinforcement, parameters of conditioned reinforcement delivery (e.g., rate) can be examined across a wide range without affecting primary reinforcement rates or conditioned reinforcement value.

Fig 2.

Schematic of an observing-response procedure (W = White, G = Green, R = Red). See text for details.

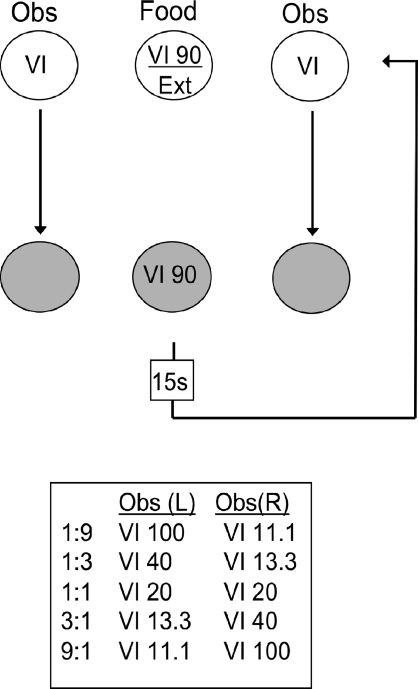
In order to study effects of relative conditioned reinforcement rate on choice in the absence of changes in rates of primary reinforcement and value of the conditioned reinforcers, Shahan et al. (2006) used a concurrent observing-response procedure (cf. Dinsmoor, Mulvaney, & Jwaideh, 1981). Figure 3 shows a schematic of the procedure used by Shahan et al. On a center key, unsignaled periods of a VI 90-s schedule of food reinforcement alternated irregularly with extinction. Responses to either the left or the right key intermittently produced 15-s S+ presentations when the VI 90 was in effect on the food key. Both observing responses produced S+ deliveries on VI schedules, and the ratio of S+ delivery rates for the two observing responses was varied by changing the VI schedules across conditions. Thus, assuming that S+ deliveries function as conditioned reinforcers, the relative rate of conditioned reinforcement was varied across conditions. Importantly, rates of primary reinforcement remained unchanged across conditions and the value of the S+ deliveries likely remained unchanged (i.e., the ratio of S+ to mixed-schedule food deliveries remained unchanged). Despite the lack of changes in primary reinforcement rate or conditioned reinforcement value, relative rates of responding on the observing keys varied as an orderly function of relative rates of S+ delivery. Furthermore, relative rates of observing were well described by the generalized matching law when relative rates of conditioned reinforcement (i.e., r₁/r₂) were used for the reinforcement ratios. Thus, the data of Shahan et al. appear to be consistent with general choice models like CCM and HVA that clearly include a role for relative conditioned reinforcement rate when the value of the conditioned reinforcers remains unchanged, and inconsistent with DRT which does not (see Fantino & Romanowich, 2007; Shahan & Podlesnik, 2008b; for further discussion).

Fig 3.

Schematic of the concurrent observing-response procedure used by Shahan et al. (2006). “Obs” refers to an observing-response key. The box at the bottom lists the different ratios of S+ presentation rates examined across the conditions of the experiment and VI schedules on the left and right observing keys to generate those ratios. See text for details.

If relative allocation of behavior as formalized in the matching law is accepted as an appropriate measure of relative response strength, the fact that choice was governed by relative rate of S+ deliveries seems consistent with the notion that conditioned reinforcers function like primary reinforcers. In short, all seems well for the notion of conditioned reinforcement. Conditioned reinforcers appear to acquire the capacity to strengthen responding as a result of their association with primary reinforcers, and they appear to impact relative response strength in a manner consistent with a hallmark quantitative theory of operant behavior. In addition, contemporary choice theories like CCM and HVA capture the effects of relative rate of conditioned reinforcement and the effects of changes in conditioned reinforcement value associated with variations in primary reinforcement and/or the temporal context. Unfortunately, all does not seem well when the relative strengthening effects of putative conditioned reinforcers are considered within the approach to response strength provided by behavioral momentum theory.

Behavioral Momentum and Response Strength

Behavioral momentum theory (e.g., Nevin & Grace, 2000) suggests that response rates and resistance to change are two separable aspects of operant behavior. The contingent relation between responses and reinforcers governs response rate in a manner consistent with the matching law (e.g., Herrnstein, 1970), but the Pavlovian relation between a discriminative stimulus and reinforcers obtained in the presence of that stimulus governs the persistence of responding under conditions of disruption (i.e., resistance to change). Furthermore, the theory suggests that resistance to change provides a better measure of response strength than response rates because response rates are susceptible to control by operations that may not necessarily impact strength (e.g., Nevin, 1974; Nevin & Grace, 2000). For example, schedules requiring paced responding (e.g., differential reinforcement of low rate behavior versus differential reinforcement of high rate behavior) may produce differential response rates, but these differences may not be attributable to differential response strength.

In the usual procedure for studying resistance to change, a multiple schedule of reinforcement is used to arrange differential conditions of primary reinforcement in the presence of two components signaled by distinctive stimuli. Some disruptor (e.g., extinction, presession feeding) is then introduced and the decrease in response rates relative to predisruption response rates provides a measure of resistance to change. Greater resistance to change (i.e., response strength) is evidenced by relatively smaller decreases from baseline. Higher rates of primary reinforcement have been found to reliably produce greater resistance to change (see Nevin, 1992). Furthermore, support for the separable roles of response rates and resistance to change comes from experiments in which the addition of response-independent reinforcers into one component of a multiple schedule decreases predisruption response rates, but increases resistance to change (e.g., Ahearn, Clark, Gardenier, Chung, & Dube, 2003; Cohen, 1996; Grimes & Shull, 2001; Harper, 1999; Igaki & Sakagami, 2004; Mace et al., 1990; Nevin, Tota, Torquato, & Shull, 1990; Shahan & Burke, 2004). This outcome is consistent with the expectations of the theory because the inclusion of the added response-independent reinforcers degrades the response–reinforcer relation, but improves the stimulus–reinforcer relation by increasing rate of reinforcement obtained in the presence of the discriminative-stimulus context.

The relation between relative resistance to change and relative primary reinforcement rate obtained in the presence of two stimuli is well described by a power function such that:

11

where m₁ and m₂ are the resistance to change of responding in stimuli 1 and 2, and R₁ and R₂ refer to the rates of primary reinforcement delivered in the presence of those stimuli (Nevin, 1992). The parameter b reflects sensitivity of ratios of resistance to change to variations in the ratio of reinforcement rates in the two stimuli, and is generally near 0.5 (Nevin, 2002). Thus, as with the matching law, relative response strength is a power function of relative reinforcement rate, but in the case of behavioral momentum theory, resistance to change provides the relevant measure of response strength.

Behavioral Momentum and Conditioned Reinforcement

Unlike the well-developed extensions of the matching law to conditioned reinforcement using concurrent-chains procedures, relatively little work has been conducted extending insights about response strength from behavioral momentum theory to conditioned reinforcement. Few experiments have examined resistance to change of responding maintained by conditioned reinforcement. Presumably if conditioned reinforcers acquire the ability to strengthen responding in a manner similar to primary reinforcers, then conditioned reinforcers should similarly increase resistance to change.

A fairly large body of early work with simple chain schedules demonstrated that responding in initial links tends to be more easily disrupted than responding in terminal links (see Nevin, Mandell, & Yarensky, 1981, for review). Assuming that responding in the initial links of chain schedules reflects the strengthening effects of the terminal-link stimuli, this result might be interpreted to suggest that responding maintained by conditioned reinforcement is less resistant to change than responding maintained by primary reinforcement. Such an outcome is not unexpected given that any capacity to reinforce shown by conditioned reinforcers should be derived from primary reinforcers, and thus is likely weaker. But, with the exception of this apparent difference in the relative strengthening effects of conditioned and primary reinforcers, this early research provided little information about the impact of conditioned reinforcement on resistance to change.

Like the vast majority of research on choice using concurrent-chains schedules, some research on resistance to change has examined how parameters of primary reinforcement occurring in the presence of a conditioned reinforcer affect resistance to change of responding maintained by that conditioned reinforcer. Nevin et al. (1981) examined resistance to change of responding in a multiple schedule of chain schedules. The two components of the multiple schedule arranged alternating periods of two-link chain random-interval (RI) schedules using different stimuli for the initial- and terminal-link stimuli in the two components. The initial links in both components of the multiple schedule were always RI 40-s schedules, but the terminal links differed either in terms of the rate or magnitude of primary reinforcement. Thus, the arrangement resembled the usual multiple schedule of reinforcement used in behavioral momentum research, but allowed comparisons of resistance to change of responding in the initial links. As a result, the effects of variations in the parameters of the primary reinforcers in the two terminal links could be examined in terms of their effects on resistance to change of responding producing those terminal links (i.e., conditioned reinforcers). As is true with preference in concurrent-chains schedules, Nevin et al. found that response rates and resistance to change of responding in an initial link were greater with higher rates or larger magnitudes of primary reinforcement in a terminal link. Nonetheless, as with the use of concurrent-chains schedules to study the effects of conditioned reinforcement on preference, the dependency between responding in the initial links and access to the primary reinforcer in the terminal links makes it difficult to know the relative contributions of conditioned and primary reinforcement to initial-link resistance to change.

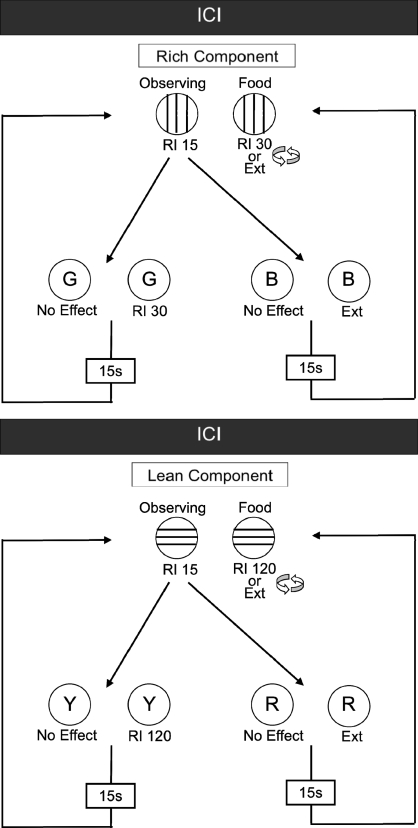
Accordingly, Shahan, Magee, and Dobberstein (2003) used an observing-response procedure to examine resistance to change of responding maintained by a conditioned reinforcer. Like Nevin et al. (1981), they examined the effects of rate of primary reinforcement obtained during a conditioned reinforcer on resistance to change of responding maintained by that conditioned reinforcer. Specifically, Shahan et al. arranged a multiple schedule of observing-response procedures in two experiments. The procedure from Experiment 2 is depicted in Figure 4. The two components of the multiple schedule each arranged an observing-response procedure using different stimuli for the mixed schedule, S+, and S−. The components were alternately presented for 5 min at a time, and were separated by an intercomponent interval. Observing responses in both components produced the schedule-correlated stimuli on an RI 15-s schedule. In the Rich component, an RI 30 schedule of food reinforcement alternated with extinction on the food key, and in the Lean component an RI 120 schedule of food reinforcement alternated with extinction. Thus, observing in the Rich component produced an S+ associated with a fourfold higher rate of primary reinforcement. Consistent with initial-link responding in the Nevin et al. (1981) multiple chain-schedule experiment, observing rates and resistance to change were greater in the Rich component than in the Lean component. Furthermore, Shahan et al. noted that even though responding on the observing key was less resistant to change than responding on the food key (also consistent with previous chain-schedule data), sensitivity parameters (i.e., b in Equation 1) for both observing and food-key responding were near the typical value in previous behavioral momentum research (i.e., 0.5). Thus, responding maintained by a conditioned reinforcer was affected by the rate of primary reinforcement obtained in its presence in a manner similar to responding maintained directly by the primary reinforcer. These data led Shahan et al. to conclude that the strengthening effects of a stimulus as a conditioned reinforcer (as measured with resistance to change) depend upon the rate of primary reinforcement obtained in the presence of that stimulus. This conclusion is obviously the same as the conclusion reached by Herrnstein (1964) based on concurrent chains data, and formalized in CCM.

Fig 4.

Schematic of the multiple schedule of observing-response procedures used by Shahan and Podlesnik (2005). ICIs refer to intercomponent interval. Other details available in the text.

At this point, there seems to be satisfying integration of findings across different domains examining the strengthening effects of stimuli associated with primary reinforcers on choice and resistance to change. Grace and Nevin (1997) noted that preference for a terminal-link stimulus and resistance to change of responding in the presence of that stimulus are correlated (see also Nevin & Grace, 2000). Thus, relatively better stimulus–reinforcer relations not only increase the strength of responding that occurs in their presence, they also generate preference for behavior that produces them. This outcome led Nevin and Grace (2000) to conclude that the relative strengthening effects of a stimulus as measured by choice and relative resistance to change of responding in the presence of that stimulus are reflections of a single central construct (Grace & Nevin, 1997; Nevin & Grace, 2000). Importantly, this underlying construct appears to be a result of the Pavlovian stimulus–reinforcer relation characterizing the relevant stimulus. The findings of Nevin et al. (1981) and Shahan et al. (2003) further support the notion of such a central construct by showing that not only do stimuli with a better Pavlovian stimulus–reinforcer relation with a primary reinforcer attract preference and increase resistance to change of responding in their presence, they also increase resistance to change of responding that produces them. Thus, we have a consistent account of the strengthening effects of conditioned reinforcers on responding measured by both preference and resistance to change of behavior that produces them, and the effects of those conditioned reinforcers on the strength of responding occurring in their presence. Interestingly, the expression used for the Pavlovian stimulus–reinforcer relation providing the basis of behavioral momentum theory (see Nevin, 1992) is the rate of reinforcement in the presence of a stimulus relative to the overall rate of reinforcement within an experimental session, or in other words, a re-expression of the cycle-to-trial ratio of Scalar Expectancy Theory (Gibbon & Balsam, 1981). Thus, it appears that we have an integrative account of various strengthening effects of food-associated stimuli that appears appropriately grounded in an influential comparator account of Pavlovian conditioning.

The integration above, however, is based entirely on differences in primary reinforcement experienced in the presence of a stimulus. The concurrent observing-response data of Shahan et al. (2006) can be considered an extension of the generality noted above by showing that the relative frequency of presentation of a food-associated stimulus also impacts choice when the rate of primary reinforcement in that stimulus remains unchanged. Thus, the relative strengthening effects of food-associated stimuli depend upon the Pavlovian relation between food and the stimuli, and variations in the relative frequency of such stimuli earned by two responses produces an outcome consistent with what we would expect if the stimuli were functioning as reinforcers. If such stimuli are conditioned reinforcers and strengthen responding that produces them, then variations in conditioned reinforcement rate should also impact resistance to change in a manner consistent with their effects on choice noted by Shahan et al. (2006). The useful properties of the observing-response procedure noted above also allow one to address this apparently straightforward question. Surprisingly though, variations in relative rate of putative conditioned reinforcers do not appear to affect response strength as measured by resistance to change.

In two experiments, Shahan and Podlesnik (2005) used a multiple schedule of observing response procedures to examine the effects of rate of conditioned reinforcement on resistance to change. The procedure was like that in Figure 4, but the food keys in the two components arranged the same rate of primary reinforcement by using the same value for the RI schedule of food delivery. Most importantly, the two components delivered different rates of conditioned reinforcement by arranging different RI schedules on the observing key. Experiment 1 arranged a 4:1 ratio of conditioned reinforcement rates by using RI 15 and RI 60 schedules for the Rich and Lean observing components, respectively. Experiment 2 arranged a 6:1 ratio of conditioned reinforcement rates by using RI 10 and RI 60 schedules for the Rich and Lean observing components, respectively. Consistent with the concurrent observing data of Shahan et al. (2006), observing rates in both experiments were higher in the component associated with a higher rate of S+ deliveries. In that sense, one might conclude that S+ deliveries served as conditioned reinforcers. However, in Experiment 1, there was no difference in resistance to presession feeding or extinction in the Rich and Lean components. In Experiment 2, resistance to change was actually somewhat greater in the component with the lower rate of S+ delivery. Thus, despite the fact that higher rates of a putative conditioned reinforcer generated higher response rates, they did not increase resistance to change of responding. This is not what one would expect if the S+ deliveries had indeed acquired the capacity to strengthen responding.

Shahan and Podlesnik (2008a) used a multiple schedule of observing-response procedures to ask a similar question about the effects of value of a conditioned reinforcer on resistance to change in three experiments. The first two experiments placed conditioned reinforcement value and primary reinforcement rate in opposition to one another and the third experiment arranged different valued conditioned reinforcers, but the same overall rate of primary reinforcement. Briefly, Experiment 1 decreased the value of S+ presentations in one component by degrading the relation between S+ and food deliveries via additional food deliveries uncorrelated with S+. Experiment 2 increased the value of S+ in one component by increasing the probability of an extinction period on the food key, thus decreasing the rate of primary reinforcement during the mixed schedule and increasing the improvement in reinforcement rate signaled by S+. Experiment 3 was similar to Experiment 2 except that the rate of primary reinforcement during S+ was increased in the higher-value component to compensate for the primary reinforcers removed during the mixed schedule and to equate overall primary reinforcement rate in the two components. The data showed that, as expected, response rates were higher in the component in which observing produced an S+ with a higher value. One might conclude based on response rates alone that higher valued S+ deliveries are more potent conditioned reinforcers than lower valued S+ deliveries. However, despite the higher baseline response rates, resistance to change was not affected by the value of S+ deliveries. Thus response strength as measured by resistance to change appears not to be affected by the value of a conditioned reinforcer.

Shahan and Podlesnik (2008b) provided a quantitative analysis of all the resistance to change of observing experiments described above in order to explore how conditioned and primary reinforcement contributed to resistance to change. When considered together, the six experiments provided a fairly wide range in variables that might contribute to resistance to change of observing. Separate analyses of relative resistance to change of observing were conducted as a function of relative rate of primary reinforcement during S+, relative rate of S+ delivery (i.e., conditioned reinforcement rate), relative value of S+ (S+ food rate/mixed-schedule food rate), relative overall rate of primary reinforcement in the component, and relative rate of primary reinforcement in the presence of the mixed-schedule stimuli. There was no meaningful relation between relative resistance to change of observing and any of the variables except for relative rate of primary reinforcement in the presence of the mixed-schedule stimuli. Interestingly, the mixed-schedule stimuli provide the context in which observing responses actually occur. Thus, relative resistance to change of observing appears to have been determined by the rates of primary reinforcement obtained in the context in which observing was occurring. Although parameters of conditioned reinforcement had systematic effects on rates of observing, they had no systematic effect on response strength of observing as measured by resistance to change. If resistance to change is accepted as a more appropriate measure of response strength than response rates, then stimuli normally considered to function as conditioned reinforcers (i.e., S+ deliveries) do not appear to impact response strength in the same way as primary reinforcers.

Is Conditioned “Reinforcement” a Misnomer?

Based only on the resistance to change of observing findings above, one could be forgiven for dismissing any suggestion that conditioned reinforcers do not acquire the capacity to strengthen behavior. The procedures are complex, the experiments have all been conducted in one laboratory, and the interpretation hinges on accepting resistance to change as the appropriate measure of response strength. Nonetheless, the findings of those experiments have led me to reconsider other long-standing assertions that conditioned reinforcers do not actually strengthen behavior.

Perhaps the most cited threat to the notion that stimuli associated with primary reinforcers themselves come to strengthen behavior is a series of experiments by Schuster (1969). In a concurrent-chains procedure with pigeons, Schuster arranged equal VI 60-s initial links that both produced VI 30-s terminal links in which a brief stimulus preceded food deliveries. In one terminal link, additional presentations of the food-paired stimulus were presented on a fixed-ratio (FR) 11 schedule. Response rates in the terminal link with the additional food-paired stimuli were higher than in the terminal link without the stimuli. Based on these higher response rates alone, one might conclude that the food-paired stimulus functioned as a conditioned reinforcer in the traditional sense. If the stimulus presentations were reinforcers, one might also expect that they would produce a preference for the terminal link in which they occurred, much like the addition of primary reinforcers would. But Schuster found that, if anything, there was a preference for the terminal link without the added stimuli. In a similar arrangement in a multiple schedule, Schuster found that added response-dependent presentations of the food-paired stimulus in one component increased response rates, but failed to produce contrast, an effect that was obtained when primary reinforcers were added. These results led Schuster and many subsequent observers (e.g., Rachlin, 1976) to conclude that response rate increases produced by the paired stimuli were a result of some process other than reinforcement. A similar interpretation may be applied to the concurrent observing data of Shahan et al. (2006) and the resistance to change data of Shahan and Podlesnik (2005, 2008a,b). The higher response rates obtained with more frequent or higher valued S+ presentations may reflect some process other than strengthening by reinforcement.

Although many interpretations have been offered as alternatives to a reinforcement-like strengthening process, a common suggestion is that stimuli predictive of primary reinforcers function as signals for primary reinforcers and thus serve to guide rather than strengthen behavior (e.g., Bolles, 1975; Davison & Baum, 2006; Longstreth, 1971; Rachlin, 1976; Staddon, 1983; Wolfe, 1936). Although many names might be used to refer to stimuli in such an account (e.g., discriminative stimuli, signals, feedback, etc.), for reasons that will be discussed later, I am partial to “signposts” or “means to an end” as suggested by Wolfe (1936), Longstreth (1971), and Bolles (1975). In what follows, I will not attempt to show how a signpost account may be applicable to the vast array of data generated under the rubric of conditioned reinforcement. What I will do is briefly discuss some examples raising the possibility that a signpost or means-to-an end account is plausible.

Consider a set of experiments by Bolles (1961). In one experiment, rats responded on two concurrently available levers that both intermittently produced food pellets and an associated click. The scheduling of pellet deliveries was such that receipt of a pellet on one lever was predictive of additional pellets on that lever. During extinction, both levers were present, but only one intermittently produced the click. As might be expected if the click were a conditioned reinforcer, the rats showed a shift in preference for the lever that produced the click during extinction. In a second experiment, however, the scheduling was such that a pellet on one lever was predictive of subsequent pellets on the other lever. During extinction with the click available for pressing one of the levers, the rats showed a shift in preference away from the lever that produced the click. Based on this outcome, Bolles concluded that the food-associated click commonly used in early experiments on conditioned reinforcement might not be a reinforcer at all, but merely a signal for how food is to be obtained.

More recently, Davison and Baum (2006) reached the same conclusion as Bolles using a related procedure with pigeons. They used a frequently changing concurrent schedules procedure in which the relative rates of primary reinforcement varied across unsignaled components arranged during the session. In the first experiment, a proportion of the food deliveries were replaced with presentation of the food-magazine light alone. The magazine light was paired with food deliveries and could reasonably be expected to function as a conditioned reinforcer. Previous work with similar frequently changing concurrent schedule procedures has shown that the delivery of primary reinforcers produces a pulse of preference to the option that produced them (Davison & Baum, 2000). In the Davison and Baum (2006) experiment, both food deliveries and magazine-light deliveries produced preference pulses at the option that produced them, but the pulses produced by magazine lights tended to be smaller. This outcome is consistent with what might be expected if the stimuli were functioning as conditioned reinforcers. However, it is important to note that because the magazine-light presentations replaced food deliveries on an option, the ratio of magazine light deliveries on the two options was perfectly predictive of the ratio of food deliveries arranged. Thus, as in Bolles (1961), the stimulus presentations were also a signal for where food was likely to be found. In a second experiment, Davison and Baum (2006) explored the role of such a signaling function by arranging for correlations of +1, 0, or −1 between stimulus presentations and food deliveries across conditions. They also examined whether the pairing of the stimulus with food deliveries was important by arranging similar relations with an unpaired keylight. They found that the pairing of the stimulus with food did not matter, but that the correlation of the stimulus with the location of food did matter. As in the Bolles experiments, if the stimulus predicted more food on an option, the preference pulse occurred on that option, but if the stimulus predicted food on the other option the pulse occurred on that other option. Based on this outcome, Davison and Baum also suggested that all conditioned reinforcement effects are really signaling effects.

The experiments of Bolles (1961) and Davison and Baum (2006) above are provided as examples of how one might view food-associated stimuli as signposts for food. Stimuli associated with primary reinforcers by definition predict when and where that primary reinforcer is available. A signpost-based account suggests that when a response produces a stimulus associated with a primary reinforcer, the stimulus serves to guide the animal to the primary reinforcer by providing feedback about how or where the reinforcer is to be obtained. Responding that produces a signpost might occur not because the signpost strengthens the response in a reinforcement-like fashion, but because production of the signpost is useful for getting to the primary reinforcer. This is the sense in which Wolfe (1936), Longstreth (1971), and Bolles (1975) suggested that signposts might also be thought of as means to an end for acquiring primary reinforcers.

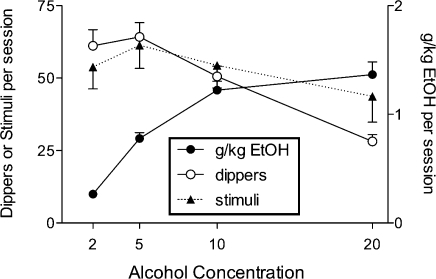
To explore the notion that stimuli associated with primary reinforcers might be thought of as means to an end, consider an experiment by Shahan and Jimenez-Gomez (2006) examining alcohol-associated stimuli with rats. An observing-response procedure arranged alternating periods of unsignaled extinction and a random ratio (RR) 25 schedule of alcohol solution delivery on one lever. Responses on a separate (i.e., observing) lever produced 15-s presentations of stimuli correlated with the RR 25 (i.e., S+) and extinction (i.e., S−) periods. Across conditions, alcohol concentrations of 2%, 5%, 10%, and 20% were examined with a fixed 0.1-ml volume of alcohol deliveries across conditions. A robust finding with a variety of self-administered drugs is that overall drug consumption increases as a function of the dose of each drug delivery, but the number of drug deliveries earned first increases and then decreases as a function of dose (see Griffiths, Bigelow, Henningfield, 1980, for review). The reason for this outcome is thought to be that lower doses are poorer reinforcers, producing fewer deliveries and lower total consumption. As the dose increases, drug deliveries become more potent reinforcers, but fewer of them are required to achieve larger total amounts of drug consumption and satiation. Thus, unlike the typical arrangement with food reinforcers, variations in the magnitude of drug reinforcers in self-administration preparations often span the range from a relatively ineffective reinforcer to one that produces satiation and fewer total reinforcer deliveries in a session.

The question addressed by Shahan and Jimenez-Gomez (2006) was how such variations in the unit dose of an alcohol reinforcer would affect responding maintained by a conditioned reinforcer associated with the availability of the alcohol deliveries. Given that alcohol is the functional reinforcer in the solutions, one might reasonably expect that an S+ associated with higher concentrations would support more observing. The reason is that the S+ is associated with a greater magnitude of primary reinforcement and higher overall consumption of the primary reinforcer. On the other hand, as a means to an end, S+ deliveries might track the number of needed dipper deliveries instead of overall alcohol consumption. Figure 5 shows the data from the relevant conditions. Clearly, the number of stimulus presentations earned tracked the number of dipper deliveries earned, rather than overall alcohol consumption. Although the number of stimulus presentations earned is depicted in the figure, because data from an FR1 schedule of observing are presented, observing-response rates showed the same pattern. A similar pattern was obtained with a range of other FR schedule values on the observing lever (data not shown here). Thus, observing maintained by the alcohol-associated stimulus presentations might be thought of as a means to acquire dippers of alcohol, rather than as being strengthened by presentations of alcohol-associated stimuli. When fewer dippers are needed, fewer stimulus presentations are also needed.

Fig 5.

Effects of concentration of an orally self-administered alcohol solution on the number of alcohol dipper and stimulus presentations (left y-axis) and g/kg ethanol delivered (right y-axis) in the observing-response procedure of Shahan and Jimenez-Gomez (2006). Data are means (± 1SEM) for 7 rats. Reprinted with permission of Behavioural Pharmacology.

Viewing stimuli associated with primary reinforcers as a means to an end highlights the relation between such stimuli and tokens. As noted by Hackenberg (2009), “A token is an object or symbol that is exchanged for goods and services.” In fact, it was research on tokens with chimpanzees that led Wolfe (1936) to suggest a means-to-an-end interpretation in the first place. Tokens are easily viewed as a means to an end for primary reinforcers, because that is precisely what they are, a medium of exchange. Obviously, things are somewhat less clear with stimuli produced by observing responses, but the data from the Shahan and Jimenez-Gomez experiment suggest that the economic aspects of the situation might play a role. The use of a drug reinforcer in Shahan and Jimenez-Gomez is important because drug reinforcers often result in fairly large changes in motivation as a result of rapid satiation, dependent upon the dose as noted above. This aspect of drug reinforcers is precisely the reason that regulation-based economic theoretical approaches have been so popular and useful in the drug self-administration literature (e.g., Bickel, DeGrandpre, & Higgins, 1993; Hursh, 1991). Such economic considerations also may help to put the role of stimuli associated with primary reinforcers into perspective—they are useful for obtaining primary reinforcers in a manner that is likely affected by the economic or regulatory circumstances of the primary reinforcer. Although tokens are often viewed as conditioned reinforcers in addition to being a medium of exchange, the evidence for response-strengthening effects of tokens above and beyond their role as a means to an end or signposts is fairly weak (see Hackenberg, 2009, for review). Unfortunately, relatively little contemporary research has been conducted on token-maintained behavior, and strangely, even less work has been conducted integrating tokens into modern regulation-based behavioral economic accounts. Work by Hackenberg and colleagues (see Hackenberg, 2009) is helping to fill this gap and could lead to a more systematic and internally consistent economic-based account of what we once called conditioned reinforcers. In short, although tokens are often viewed as conditioned reinforcers, it might be useful instead to consider viewing conditioned reinforcers as tokens (i.e., means to an end).

If the stimuli in our observing experiments are to be viewed as signposts and means to an end, one immediate concern is that unlike tokens or terminal-link stimuli in chain schedules, S+ presentations are not required to obtain primary reinforcers. This aspect of the observing-response procedure is precisely why it was used in the experiments discussed above. But, if one assumes that evolution has equipped organisms to follow predictive stimuli in order to obtain food, it is not too surprising that behavior that produces such stimuli would occur in an observing-response procedure. S+ presentations might be considered a means to an end because they are instrumental for guiding organisms to the richer than average patches of primary reinforcement they signal. Since they were first introduced, observing responses have been considered a proxy for looking at or for important environmental stimuli (Wyckoff, 1952; see also Dinsmoor, 1985). In order for behavior to be appropriately allocated to the periods of reinforcement and nonreinforcement arranged by a multiple schedule, an organism must be in contact with the relevant stimuli. When such stimuli are removed and then made contingent upon an arbitrary response (i.e., an observing response), that arbitrary response functionally becomes part of the looking or attending to the relevant stimuli. Although S+ presentations are not required to obtain primary reinforcers, such looking or attending is required for ultimate effective action with respect to the primary reinforcer. That is the sense in which one might say the organism is using observing responses and the stimuli they produce as a means to an end.

Clearly, the interpretation above focusing on the utility of S+ deliveries and the more general signposts or means-to-an-end approach being explored is related to the information or uncertainty-reduction hypothesis of conditioned reinforcement. What might be called the strong uncertainty reduction hypothesis suggests that a reduction of uncertainty per se is reinforcing (e.g., Hendry, 1969). In the observing-response procedure, observing responses reduce uncertainty by producing stimuli correlated with the conditions of primary reinforcement in effect. Importantly, both S+ and S− reduce uncertainty by the same amount (i.e., 1 bit), and should both function as reinforcers. Contrary to this suggestion, a considerable amount of research has shown that S− presentations alone are not reinforcing, at least with pigeons, thus posing a serious challenge to the strong uncertainty hypothesis (see Dinsmoor, 1983, for review). Having said that, there is some compelling evidence that S− can function as a reinforcer for adult humans under some circumstances (e.g., Perone & Kaminski, 1992).

Regardless, the fact that S− alone typically fails to function as a reinforcer misses the point of the signpost or means-to-an-end account being explored here. A signpost account need not assert that either S+ or S− function as a reinforcer. Signposts guide behavior and earning them is instrumental as a means to an end with respect to effective action related to the primary reinforcer. Such an account is not based on negative reinforcement produced by a reduction in the aversive properties of uncertainty nor the positive conditioned reinforcing effects of S+. It is not at all surprising that a response producing S− alone does not continue in most of the research examining the reinforcing effects of S−. The procedures are rather restrictive and leave no way for the subjects to better their situation. Typically, subjects have nothing to do but wait out the S− period. To use the metaphor of a signpost, imagine riding in a car and having no control over the direction it is headed. Looking out the window, you see signs revealing that you are headed in the wrong direction. How long would you continue looking for or at the signs? Clearly the signs are informative, but they are not useful. If on the other hand, you could change the direction of the car when error-revealing signs are encountered, you might be more likely to continue looking. The typical S− alone procedure used in observing experiments is more similar to the former than the latter case. A signpost that tells you that you are headed in the wrong direction is a signal to change directions. If you cannot change directions, the signpost is not useful.

It is well established that when organisms are allowed to control the duration of S+ and S−, they tend to maintain S+ and to terminate S− (see Dinsmoor, 1983, for review). Similarly, there is evidence that organisms prefer an observing response that produces S+ alone to one that produces S+ and S− (Mulvaney, Dinsmoor, Jwaideh, & Hughes, 1974). The usual interpretation of these findings is that the S− is aversive and functions as a conditioned punisher of observing. An interpretation based on a signposts approach suggests that the S− presentations serve as a signal to change course and do something else. Thus, S− might be seen as a signal to go in another direction by disengaging from an observing response that continues to lead in the wrong direction. If, on the other hand, S− is permitted to be useful by allowing a period of rest during a difficult task or providing time to do something else useful, responding that produces S− is maintained (e.g., Case, Fantino, & Wixted, 1985; Case, Ploog, & Fantino, 1990; Perone & Baron, 1980). It is worth noting that the version of the information hypothesis originally proposed by Berlyne (1956) is much more in line with this notion of the usefulness of stimuli than with the strong uncertainty hypothesis requiring that an S− must always maintain responding (see Lieberman, Cathro, Nichol, & Watson, 1997, for discussion).

At this point, I suspect many readers will not have fundamentally changed their minds about whether stimuli associated with primary reinforcers strengthen behavior that produces them. This is especially likely given that in previous reviews of the conditioned reinforcement literature, both Fantino (1977) and Williams (1994a,b) concluded that an account based on conditioned strengthening effects is to be preferred over alternative accounts (e.g., uncertainty reduction, marking, bridging). Fantino (1977) based his conclusion largely on the failures of strong uncertainty reduction noted above. But, strong uncertainty reduction has always served as something of a straw man for a more nuanced informational account (Berlyne, 1956). Hopefully the discussion above has made it clear that rejection of strong uncertainty reduction does not inexorably lead to acceptance of response strengthening by conditioned reinforcement as the only remaining alternative. Williams (1994a,b) concludes in favor of strengthening by conditioned reinforcement based largely on the effects of food-paired stimuli during delays to reinforcement in discrimination procedures (e.g., Cronin, 1980). The data from such delay-to-reinforcement procedures do appear to show that alternative concepts like marking and bridging cannot account for all putative conditioned reinforcement effects. But, ruling out marking and bridging is not the same thing as showing that the remaining effects must be due to a reinforcement-like strengthening processes. Williams (1994a,b) places considerable weight on Cronin's finding that pigeons will choose an option that immediately produces a stimulus paired with food at the end of a 1-min delay over an option that produces a stimulus normally paired with the absence of food at the end of the delay, despite the fact that doing so decreases the overall rate of food obtained. The fact that animals sometimes behave suboptimally in the long run as a result of being misguided by stimuli normally predictive of food delivery is not terribly surprising when the long-term consequences occur after considerable delays. Again, this outcome is not evidence that such immediate effects of stimuli must be due to the reinforcement-like strengthening effects of food-associated stimuli. Unfortunately, empirically differentiating between a reinforcement-like strengthening account and a signpost or means-to-an-end account is difficult under these and many other conditions. My intention here is not to assert that the available data force acceptance of a signposts account and rejection of a conditioned reinforcement account. Rather, the point is that a signposts account is worth considering, and there is ample room for differences in perspective to guide interpretation of the existing data.

Regardless, in considering whether stimuli associated with primary reinforcers strengthen responding that produces them, it is not unreasonable to ask the related question of whether primary reinforcers themselves strengthen behavior that produces them. Certainly if primary reinforcers do not strengthen behavior, any discussion of whether conditioned reinforcers strengthen behavior would be pointless. As discussed below, the possibility that primary reinforcers also might not strengthen behavior appears to be worthy of consideration.

Do Primary Reinforcers Strengthen Behavior?

In their influential treatment of Pavlovian and operant conditioning, Gallistel and Gibbon (2002) argue that strengthening by a US or primary reinforcer is not the process underlying conditioning. As an alternative, they suggest organisms learn what, where, and that events occur in the environment and that they compare events, durations, and rates to make threshold-based choices. Thus, their alternative to strengthening is a comparator approach based largely on Scalar Expectancy Theory augmented by a host of more specific models for calculating the relevant quantities to be compared. Although one might quibble with the cognitive flavor of the statistical-decision-theory-based modeling approach, it does not change the fact that organisms might learn about the environment and make comparisons rather than having responses strengthened by reinforcers via back propagation. Gallistel and Gibbon present and reinterpret a wealth of data to support the feasibility of their general approach. A set of experiments by Cole, Barnet, and Miller (1995) provide an example that is particularly challenging for a response-strengthening account of conditioning.

Cole et al. (1995) examined the role of temporal-map learning in Pavlovian conditioning. In the relevant portions of the experiments, fear conditioning was compared for two groups of rats. The first group received a 5-s tone followed immediately by a shock presentation (i.e., standard delay conditioning). The second group received a 5-s tone followed by a 5-s trace interval without the tone present and then the shock (i.e., standard trace conditioning). Not surprisingly, when a subset of control rats from each group was tested with the tone alone, the tone was a less effective fear-CS for the group with the trace interval. The standard interpretation of such an effect of a trace interval is that the lack of contiguity between the CS and US has disrupted the strengthening effects of the CS–US bond or the transfer of value from the US to the CS. In the important comparison, the remaining rats from the delay and trace conditioning groups were exposed to a backward second-order conditioning phase. Specifically, the original 5-s tone CS was then followed by a 5-s clicking stimulus and the US was not presented. This is second-order conditioning because the original CS was being paired with the novel clicking stimulus. It is backward second-order conditioning because the original CS preceded rather than followed the novel stimulus, as is usually the case in second-order conditioning. The results showed relatively little conditioning to the novel clicking stimulus for the delay-conditioning animals, but strong conditioning for the trace-conditioning animals. This result is surprising from a traditional strengthening account for a couple of reasons. First, the original tone CS for the trace conditioning group should have been strengthened less than for the delay-conditioning group. Thus, it should have had less value or ability to strengthen the novel CS in the second-order phase of the experiment. Second, the second-order phase of the experiment involved a backward conditioning procedure in which one would traditionally expect little strengthening to occur because the order of events is in the wrong direction.

Even more problematic for a strengthening-based account of conditioning, Cole et al. (1995) conducted another version of the experiment in which they reversed the order of the conditions. Thus, the rats experienced a sensory preconditioning phase in which a neutral tone was followed by the clicking stimulus without the US and then exposed to the delay- or trace-conditioning phases involving the US. This reversal of the order of phases did not affect the results. Again, a traditional transfer-of-value or strengthening account is strained, to say the least, by the effectiveness of the backward sensory preconditioning for the group subsequently exposed to trace conditioning. Although Cole et al. note that a more traditional strengthening-based account of the results of their experiments is not impossible, such an account is fairly convoluted and raises concerns about plausibility and parsimony. Nonetheless, as Gallistel and Gibbon (2002) explain, the result does make sense if one assumes that the animals learned about the temporal structure of the sequence of events across the conditions.

Interestingly, even in the absence of the Cole et al. (1995) data, Gallistel and Gibbon (2002) note that the simple phenomenon of sensory preconditioning is damaging enough in its own right to the traditional approach. If reinforcement-like strengthening is required for conditioning, then learning should not occur when two neutral stimuli are paired in the absence of a US (i.e., sensory preconditioning should not occur). They argue that the phenomenon has been largely ignored in terms of its implication for conditioning theory and has instead been given a name to suggest that it is somehow different from “real” conditioning (i.e., “sensory” and “pre” conditioning). From their perspective, sensory preconditioning is just another instance of organisms learning about the structure of the environment and what events predict about where and when other events occur. From such a timing-based comparator perspective, reinforcement is important for performance, not learning.

Although the most challenging examples presented by Gallistel and Gibbon (2002) come from Pavlovian preparations, they argue that the processes are fundamentally the same for Pavlovian and operant conditioning. In addition, their argument makes use of a large amount of data from operant timing procedures that also seem to challenge the notion that reinforcers strengthen behavior. Although the challenges raised by Gallistel and Gibbon have largely been ignored by those of us who study operant conditioning, Davison and Baum (2006) have nevertheless similarly suggested that primary reinforcers may not strengthen behavior. Davison and Baum made this suggestion based upon the signaling effects of conditioned reinforcers discussed above, and upon related findings with primary reinforcers obtained by Krageloh, Davison, and Elliffe (2005). Thus, Davison and Baum suggest that:

“The most general principle, rather than a strengthening and weakening by consequences, may be that whatever events predict phylogenetically important (i.e., fitness-enhancing or fitness-reducing) events, such as food and pain, will guide behavior into activities that produce fitness-enhancing events and into activities that prevent the fitness-reducing events.”

Although I suspect that Gallistel and Gibbon and Davison and Baum would disagree about the details of how to construct such a framework, I hope that the basic similarity in their approaches is obvious—organisms learn the predictive relations between events in the environment and are guided by what is learned. Davison and Baum suggested that such guidance of behavior by what are traditionally thought of as reinforcers and punishers might result from such events serving as discriminative stimuli for future occurrences of those events. In my view, the traditional notion of a discriminative stimulus as a stimulus that sets the occasion for a reinforced response retains little utility if a “reinforcer” is considered only to be discriminative for future occurrences of itself. Above, I noted that many names including “discriminative stimulus” might be used for stimuli usually referred to as conditioned reinforcers when they are instead considered to guide rather than to strengthen behavior. My preference for the terms “signpost” and “means-to-an-end” is based on this more general viewpoint that the term “discriminative stimulus” makes little sense if both primary and conditioned reinforcers serve to guide rather than to strengthen behavior.

Terminological issues notwithstanding, the available data also leave ample room for one's general perspective to determine how the effects of primary reinforcers are to be interpreted. Nonetheless, the challenges raised by Gallistel and Gibbon (2002) and Davison and Baum (2006) about how primary reinforcers have their effects are certainly worthy of serious consideration. However, even if one dismisses such suggestions and continues to believe that primary reinforcers strengthen operant behavior, the challenges raised by the data from Pavlovian procedures reviewed by Gallistel and Gibbon would continue to pose problems for the notion that the strengthening effects of primary reinforcers are transferred to conditioned reinforcers. The reason is that such a transfer of the ability to strengthen behavior would continue to require Pavlovian conditioning. Although we are pleased to have the effects of stimuli on operant behavior grounded in widely accepted models of Pavlovian conditioning, in reality, relatively little serious attention has been paid to the potential implications of recent developments in the Pavlovian literature.

Implications for Choice Theories and Behavioral Momentum Theory

If one were to accept that primary and/or conditioned reinforcers do not strengthen behavior that produces them, what would be the implications for the general choice theories discussed earlier? Obviously, choice theories like CCM and HVA are based upon the value or strengthening effects of conditioned reinforcers. However, discarding the notion that conditioned and primary reinforcers strengthen behavior would likely have little real impact on the theories. The reason is that each of the theories quantitatively describes systematic changes in behavior with changes in the structure of the environment. The notion of value rests in the conceptual interpretation of the relations captured by the quantitative machinery of the models, and value need not carry any connotation of reinforcement-like response strengthening for the models to be useful. Such an approach would be consistent with the more general response-strength free behavioral economic/regulatory or consumption-based approaches within which the models might be subsumed (e.g., Rachlin, Green, Kagel, & Battalio, 1976; Rachlin, Battalio, Kagel, & Green, 1981). Further development of choice theories like CCM and HVA based on conditioned reinforcers as signposts or means to an end might be helpful for further incorporating both tokens and stimulus-based guidance of behavior into a broader economic or regulatory framework.

The implications of dropping the notion of response strength are somewhat more complicated when considering behavioral momentum theory. If reinforcers do not strengthen behavior, then what is it that behavioral momentum theory captures? Baum (2002) has suggested that the effects of different rates of reinforcement in different stimulus contexts might be thought of as the stimuli enjoining (i.e., instructing, directing, urging) different allocations of behavior during baseline conditions. During disruption, a stimulus associated with a higher rate of reinforcement might be thought of as enjoining that allocation of behavior more persistently. Although this enjoining approach resembles a signposts account on its surface, Baum's suggestion that enjoining itself might be strengthened by reinforcement appears to be similar enough to the Pavlovian-strengthening account of behavioral momentum theory as to be difficult to tell the difference between the two, until it is further developed. Nonetheless, Baum's general approach of focusing on the guiding or directive effects of stimuli signaling different rates of primary reinforcers, rather than on the putative strengthening effects of reinforcers in a stimulus context, seems like a reasonable way to proceed. There is no reason in principle that an enjoining function of stimuli be based on strengthened by reinforcement.

Alternatively, Gallistel and Gibbon (2002) suggested a timing-based account of resistance to extinction based on a comparison of the time since the occurrence of the last reinforcer in the presence of a stimulus to the overall average time between reinforcers in the stimulus (i.e., rate estimation theory). Although rate estimation theory apparently does a good job with many findings in the Pavlovian literature, an explicit test of its predictions in a typical behavioral-momentum type experiment with multiple schedules of reinforcement has questioned its applicability to behavioral momentum theory (Nevin & Grace, 2005). In addition, at present, rate estimation theory appears to be limited to disruption by extinction and does not provide a broader framework within which to understand the effects of differential reinforcement rate on resistance to other types of disruption (e.g., satiation). Nonetheless, the failures of the particular version of a timing-based account of resistance to extinction provided by rate estimation theory do not mean that another such account based on different assumptions cannot provide a viable alternative to the reinforcement-strengthening account of behavioral momentum theory. Regardless, any such account would still need to address the fact that variations in parameters of primary reinforcement impact resistance to change, but parameters of conditioned reinforcement appear not to.

In conclusion, perhaps it goes without saying that considerably more research needs to be conducted on the effects of parameters of conditioned reinforcement on choice and resistance to change. Ideally, such work would come from a variety of procedures to study conditioned reinforcement. Given the relation between the signpost or means-to-an end account and token reinforcement, examinations of how variations in parameters of token reinforcement affect choice and resistance to change might be especially helpful. Another potentially fruitful question would be whether preparations like those in Cole et al. (1995) discussed above could be extended from fear conditioning to the generation of positive conditioned reinforcers for operant behavior. If they could, the results might pose a serious challenge to the notion that conditioned reinforcers have their effects via an acquired capacity to strengthen behavior that produces them. Hopefully, such research would also be accompanied by further exploration of whether primary reinforcers themselves impact behavior via a response-strengthening process.