Exploration of the potential of liquid scintillators for real-time 3D dosimetry of intensity modulated proton beams

Abstract

In this study, the authors investigated the feasibility of using a 3D liquid scintillator (LS) detector system for the verification and characterization of proton beams in real time for intensity and energy-modulated proton therapy. A plastic tank filled with liquid scintillator was irradiated with pristine proton Bragg peaks. Scintillation light produced during the irradiation was measured with a CCD camera. Acquisition rates of 20 and 10 frames per second (fps) were used to image consecutive frame sequences. These measurements were then compared to ion chamber measurements and Monte Carlo simulations. The light distribution measured from the images acquired at rates of 20 and 10 fps have standard deviations of 1.1% and 0.7%, respectively, in the plateau region of the Bragg curve. Differences were seen between the raw LS signal and the ion chamber due to the quenching effects of the LS and due to the optical properties of the imaging system. The authors showed that this effect can be accounted for and corrected by Monte Carlo simulations. The liquid scintillator detector system has a good potential for performing fast proton beam verification and characterization.

INTRODUCTION

In scanning beam proton therapy (and more generally, particle therapy), fast, accurate, and efficient characterization of intensity and energy-modulated proton therapy (IMPT) beams and patient-specific quality assurance of such beams is a considerable challenge. Each IMPT beam in a treatment may employ thousands of individual pencil beams (or “spots”) of variable intensities, energies, and positions to produce highly inhomogeneous dose distributions within the target. The sum of contributions of all such beams is the desired dose distribution in the target. For this emerging technology of IMPT, continuous profile scanning with a conventional ion chamber (or diode) is not feasible because the pencil beam sweeps continuously over a certain line in a given time, and any profile acquired with a moving detector would not be a representative of a true dose profile. The alternative approach of integrating dose at each of a sequence of points would be extremely time consuming and impractical because complete scan pattern would have to be delivered for each point.

Previously, different stationary detector systems have been used to measure two-dimensional (2D) proton dose distributions perpendicular to the beam direction. For example, Lomax et al.¹ obtained orthogonal profiles with 25 ion chambers arranged in a cross, while Boon et al.² used a 2D scintillation screen located distally behind a slab of water equivalent material in combination with a mirror and CCD camera, and Nohtomi et al.³ employed an obliquely oriented photoluminescence detector plate inside a water phantom. However, the 2D method requires multiple layers of material with different thicknesses to obtain the three-dimensional (3D) dose, which would require multiple beam deliveries. This problem was approached by Cirio et al.,⁴ who built a very complex detector system based on a layout from high energy particle physics experiments. It consisted of 12 large-area parallel plate ionization chambers, each further divided into pixel ion chambers. The clinically utilized detector system by Karger et al.,⁵ which comprised an array of up to 24 pin-point ion chambers inside a water tank, provided fast and instant read-out capabilities for patient-specific dosimetry.

Although the ion chamber detectors are the gold standard in radiation therapy dosimetry, an array of ion chambers lacks the spatial resolution because the detectors tend to be separated by distances of the order of 1 cm. In contrast, dosimetric gels exhibit better spatial resolution and are an alternative for 3D dosimetry; however, they exhibit linear energy transfer (LET) dependence⁶ and require time consuming processing. Another promising method suggested by Kirov et al.,⁷ used a liquid scintillator (LS) for 2D dosimetry. This technique was extended to 3D for application to brachytherapy.⁸ Such a system has the potential for fast, accurate, and high-resolution dosimetry for quality assurance in 3D. The authors stated that further investigations are required for proton or heavy ion particle irradiation.

We investigated the feasibility of using the light signal produced by a proton beam incident on a three dimensional volume of liquid scintillator to perform characterization and verification of that proton beam. More specifically our goals were (1) to evaluate the scintillation signal intensity produced in a LS detector system from a theoretical and an experimental point of view, (2) to assess the feasibility of real-time or near real-time data acquisition, and (3) to study the potential of the system for proton beam characterization and verification. It must be stressed that even if the amount of scintillation light produced in the LS is related to the dose deposited, we do not aim to measure a complete 3D dose distribution because this would necessitate measurement of scintillation light distribution from a large number of perspectives in a manner somewhat similar to a cone-beam CT. Our long-term goal with this LS detector system is to use it for verification of spot scanning IMPT treatments where the 3D coordinates and the range of proton spots could be determined from a pair of orthogonal images of the LS light distribution.

MATERIALS AND METHODS

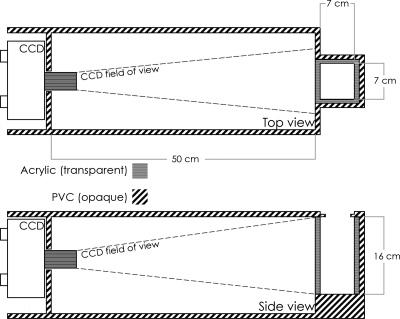
The detector system was developed in-house and consisted of a rectangular light-tight gray PVC phantom containing an acrylic tank filled with LS and a CCD camera, as shown in Fig. 1. The organic LS material used in this study was BC-531 (Saint Gobain Crystals, Newbury, OH). The physical characteristics of this material are shown in Table 1. The BC-531 LS light yield emission is compared to anthracene, an organic crystal commonly used as the standard for scintillators. Comparison of the LS with water, polystyrene, and the most standard plastic scintillator (BC-400) illustrates its near water equivalence. The water equivalent thickness of the LS was measured to be 0.87, which means that its water equivalent thickness scales linearly with its specific gravity. When irradiated with particles with low LET, a liquid scintillator will emit light in proportion to the dose delivered. For particles with higher LET such as protons, the scintillation process can be quenched, which results in an under-response of the scintillator. For a proton beam, the LET is a function of the proton energy distribution, which varies with depth. Therefore, the quenching will be more visible in the vicinity of the Bragg peak where the LET is at the highest. In general, we can assume that the LET is uniform in a plane perpendicular to the beam direction at any given depth. It is also known that for either low or high LET particles, the light output produced through the scintillation process is proportional to the beam intensity.

Figure 1.

The detector system consisting of a light-tight gray PVC phantom, a transparent acrylic inner tank filled with liquid scintillator, and a CCD camera. The dashed lines represent the camera’s field of view.

Table 1.

Physical characteristics of the liquid scintillator BC-531 compared to the BC-400 plastic scintillator, polystyrene, and water.

	BC-531	BC-400	Polystyrene	Water
Emission (% of anthracene)	59	65	N∕A	N∕A
Peak wavelength (nm)	425	423	N∕A	N∕A
Electron density (1023 e∕g)	2.930	3.272	3.238	3.343
Specific gravity (g∕cm3)	0.870	1.032	1.060	1
Composition	1:11.98	1:8.470	1:7.740	1:11.19
[Z: fraction by weight (%)]	6:88.02	6:91.53	6:92.26	8:88.81

The volume of the LS tank was 7×7 cm² and its depth was 16 cm. The CCD camera was a high sensitivity CCD (Luca EM CCD, Andor Technologies, South Windsor, CT) with 658×496 pixels. Although this camera model is capable of amplification through electron multiplication, this feature was not used in the current work and the camera was operated as a normal CCD. The pixels were digitized at 14 bits, thus providing 16 383 gray scale levels that allowed for a large dynamic range for image processing. An objective lens (JML Optical Industries, Rochester, NY) was mounted on the camera to produce the image. The distance between the center LS and the CCD was 53.5 cm. At this distance the field of view of the system was 12.5×9.4 cm². We used acquisition times of 100 and 50 ms per image. To minimize the time between image acquisitions, the camera was operated in frame transfer acquisition mode. During a frame transfer acquisition, an image is acquired in the light sensitive area of the CCD, then rapidly transferred to a storage area shielded from light. Then a second image is acquired in the light sensitive area, while, at the same time, the data in the storage area are read. Therefore, the time gap between two consecutive images is equal to the time required to transfer an image from the light sensitive area to the storage area. This time gap is equal to 0.3 ms and therefore required no correction.

Image processing is required before extracting quantitative information from images acquired during the irradiation. First, a series of the dark images acquired before the irradiation is averaged and is subsequently subtracted from the images acquired during the irradiation. This step is important to make sure that the background on all data images is zeroed. Typically, every pixel has an offset of about 500 gray scale levels. Furthermore, subtracting the dark images also corrects for stray light that may have entered the phantom, but only if that stray light is also present at the time of irradiation. Subtracting background images cannot correct for background contribution from scattered scintillation light (see Sec. 5B for a discussion on the impact of scattered light). Further image processing is necessary if the amount of radiation induced noise on the CCD chip is large. Stray radiation, mostly photons and neutrons, directly incident on the CCD chip may produce noise in the form of sharp spikes. With our current setup, we have found this noise to be of a relatively low level (less than 100 events per image frame). Therefore, data presented for a single image frame were not processed to remove those spikes because it was always possible to find a line of pixels free from radiation spike noise. For data acquired over a longer period (e.g., 100 MU), a median based filter was used as is often done in such cases.⁹ Images were combined with the median operation as suggested from our recent work on the impact of stray radiation from linac on CCD cameras.¹⁰

The proton irradiation experiments were conducted at the M. D. Anderson Cancer Center’s Proton Therapy Center to assess the feasibility of using a LS detector system for scanning proton beam dosimetry. Proton measurements of dose distributions produced by a 120 MeV passively scattered proton beam with a field size of 2×2 cm² (to approximate a pencil beam from a passive scattering system, although a real pencil beam will be much smaller) were produced inside the LS detector. The nominal beam penetration in water was 5 cm.

Measurements were also performed in water with ion chambers for the same proton beam as the one used on the LS system. The depth of measurements with the ion chamber was corrected to account for the different densities between the LS and water. Depth dose curves were measured with an Advanced Markus® plane parallel ion chamber model N34045 (PTW, Freiburg, Germany) with a sensitive volume radius of 2.5 mm, a thickness of 1 mm, and a total volume of 0.02 cm³. Lateral profiles were measured with a 0.015 cm³ PTW 31006 Pinpoint ionization chamber (an inner radius of 1 mm, a length of 5 mm, and a total sensitive volume of 0.015 cm³).

GEANT 4.9.1 Monte Carlo toolkit was used to verify the feasibility of using Monte Carlo techniques to model the response of the LS system irradiated by proton beams. A simple proton beam was directed toward a cubic volume of liquid scintillator. The beam-energy spectrum was Gaussian and its mean and standard deviation were adjusted to reproduce depth dose curves measured with ion chamber. We have shown in an earlier work that quenching can be accounted for in Monte Carlo simulations by including the two-parameter Birks function.¹¹ The same quenching model was used in these simulations. Moreover, GEANT4 can produce and track scintillation photons. By combining the quenching with the tracking of scintillation photon, it was possible to simulate the light distribution seen by the CCD camera.

THEORETICAL EVALUATION OF LIGHT COLLECTION

The purpose of the objective lens is to collect scintillation light produced in the 3D liquid scintillator volume and to form an image on the CCD chip. The overall performance of the LSD system will depend on the properties of the lens and the sensitivity of the CCD. In this section, we perform a theoretical evaluation of the system parameters.

One of the main differences in imaging a three-dimensional volume instead of a two-dimensional plane is that the image focus must be preserved over the entire width of the irradiated volume in order to produce a sharp image. The region, or depth, over which the image is on focus, is called depth of field (DOF). If an object placed in front of a lens at a distance d_o produces an image on focus at a distance d_i behind the lens, then any displacement of the object (d_o±Δx) will results in a blurred image at position d_i. Blurring means that a point in the object will be spread and will become a disk on the image. This disk of diameter c is sometimes referred to as the circle of confusion. The value of c is zero at the focal plane and increases with increasing distance from that plane. Most imaging system can tolerate certain nonzero values of c without noticeable effect. The value of c will have an impact on the spatial resolution of the imaging system. The distance over which c is within tolerable limits defines the depth of field. With geometric optics, it is possible to describe the proximal d_p and distal d_d distances of the DOF (for example, see Ref. 12)

$$d_p=\frac{d_o\cdot f^2}{f^2+F\cdot c\cdot \left(d_o-f\right)},d_d=\frac{d_o\cdot f^2}{f^2-F\cdot c\cdot \left(d_o-f\right)},$$ (1)

where F is the f-number of the objective lens (i.e., the ratio of the focal length f and the lens diameter). In the setup used, the object distance was 53.5 cm (i.e., the middle of the liquid scintillator tank) and the focal length was 2.5 cm. For a digital, pixilated imager such as a CCD camera it is common practice to set the value of c as the size of one CCD pixel (10×10 μm²). Then, we can determine the length of the DOF for different values of F. The f-number can be adjusted experimentally by opening or closing an iris. In our setup, an f-number of 1.4 was used which resulted in a DOF length of 1.7 cm.

The signal magnitude of a pixel depends on three factors: (1) The number of scintillation photon produced, (2) the optical coupling efficiency of the optical system (i.e., the probability that a scintillation photon will reach the photosensitive CCD), and (3) the conversion of that scintillation photon into a gray scale level. Before evaluating the signal magnitude in the 3D case, let us first consider a 2D system such as described by Boon et al.² Let us assume that all the scintillation light is produced in a given plane of thickness Δx at a fixed distance x from the objective lens. The number of scintillation photons N_Y produced in that plane in a region corresponding to one pixel of the CCD after receiving a dose D is defined as

$$N_{\gamma }\left(\lambda \right)=A_p\cdot \Delta x\cdot \rho \cdot D\cdot S\left(\lambda \right)\cdot Q,$$ (2)

where A_p is the surface area of the pixel and ρ is the mass density. The first product (A_p×Δx×ρ) is the mass of the emitting volume. The scintillation efficiency S(λ) is described in terms of the number of scintillation photons emitted at a wavelength λ per unit of energy deposited and can be obtained from the scintillator manufacturer. The quenching term Q represents the under-response of the liquid scintillator and is function of the stopping power of the proton beam. Only a small fraction of N_γ will reach the CCD camera. Assuming that every irradiated point in the liquid scintillator acts as an isotropic light source, the optical coupling efficiency ε can be described with a well known equation¹³

$$\epsilon =\frac{T{m}^2}{16F^2{\left(1+m\right)}^2{n}_s^2},$$ (3)

where T is the transmission of the lens, m is the magnification factor, and n_s is the refractive index of the scintillator. Equation 3 neglects the loss of scintillation photons due to absorption, Rayleigh scattering, or vignetting for pixels far from the central axis. Finally, the resulting pixel value, I(x), in gray scale levels is given by

$$I\left(x\right)=\frac{N_{\gamma }\left(\lambda \right)\cdot \epsilon \cdot \eta \left(\lambda \right)}{N_{e-}},$$ (4)

where η(λ) is the CCD quantum efficiency and N_e− is the number of photoelectron per gray scale level. If the depth of field covers the whole radiation beam, the entire irradiated volume of the liquid scintillator will be on focus. In that case, one can approximate the 3D case as a sum of 2D planes with different distances x from the objective lens. However, varying x affects the pixel size (A_p) and the magnification (m) and Eqs. 2, 3 must be rewritten accordingly

$$I={\int }_{x_1}^{x_2}{\left(\frac{x\cdot h_i}{d_i}\right)}^2\cdot dx\cdot \rho \cdot D\cdot S\left(\lambda \right)\cdot Q\cdot \frac{T\cdot {\left(d_i∕x\right)}^2}{16\cdot F^2\cdot {\left(1+d_i∕x\right)}^2\cdot n_s^2}\cdot \frac{\eta \left(\lambda \right)}{N_{e-}},$$ (5)

where h_i is the image height. With a CCD camera, d_i is the fixed distance between the objective lens and the CCD chip and h_i is the size of the CCD chip. If the DOF is not sufficient to cover the whole irradiated volume, the light that is out of focus will also contribute to I. However, we aim at using a DOF larger than the irradiated volume.

EXPERIMENTAL RESULTS

Figure 2 shows a 35 image series obtained from a continuous CCD acquisition of multiple frames acquired during one single continuous proton irradiation. Each frame corresponds to a 100 ms time acquisition interval. A total of 100 MU where delivered at a dose rate of 150 MU∕min for this series of data acquisition. 1 MU corresponds to 2.7 cGy for this setup. This means that each image received 0.25 MU. Two consecutive proton pulses (first pulse: frames 2–6; second pulse: frames 28–32) can be seen in Fig. 2, separated by 20 frames of dark images (frames 7–27). This corresponds exactly to the programed proton pulse from the Hitachi synchrocyclotron (0.5 s pulse, with a 2 s repetition time). The dose deposition that is characteristic of the proton beam Bragg Peak can be clearly seen in frames 3–5 in the first pulse.

Figure 2.

A consecutive series of images of the LS detector system exposed to a 120 MeV proton beam. Each image represents the total light output seen within a 100 ms time interval.

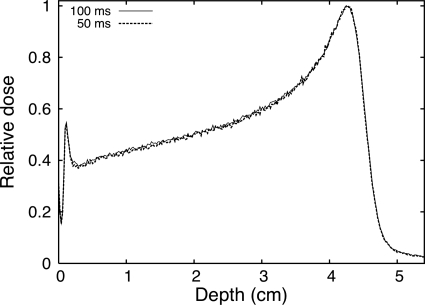
Analysis of the measured light distribution can be performed either by combining all images acquired over a given number of MU or on an image-per-image basis. Figure 3 shows a depth profile of the measured light profile for single images acquired over 100 and 50 ms. The instantaneous dose rate during each proton pulse is approximately equal to 800 cGy∕min, corresponding to maximum doses per frame of 1.3 and 0.67 cGy for acquisition times of 100 and 50 ms, respectively. From Fig. 3, we can see that the signal obtained from an integration time of 50 ms (0.67 cGy) is more than sufficient for these measurements. The standard deviations of the measurements at the depth of 2 cm at the center of the field are 0.7% and 1.1% for the 100 and 50 ms, respectively. Smoother curves could be obtained at the expense of spatial resolution by averaging the signal over consecutive pixels. It is possible to compare pixel values measured in this experiment with the predictions from Eq. 5. For a dose of 0.67 cGy (50 ms integration time) with the experimental conditions described above, we measured an average pixel value of 6.1×10³ gray scale levels at the Bragg peak after subtracting the background image. For the same experimental setup, assuming a quenching factor of 0.77 (as predicted from the simulations) and assuming that all scintillation photons are emitted at the peak wavelength for which the CCD camera has a quantum efficiency of 50%, Eq. 5 predicts 5.3×10³ gray scale levels. This agreement is excellent considering that Eq. 5 was derived from first principles. In addition to the approximation made while deriving Eq. 5, other factors may explain the difference between the measured and theoretical values: (1) Eq. 5 was integrated over the 2 cm nominal field size therefore neglecting the penumbra of the beam; (2) light scattering on the walls of the phantom may artificially raise the measured pixel value (see Sec. 5B); and (3) uncertainty in the data provided by the various manufacturers.

Figure 3.

Depth scintillation light profile measured from single images with acquisition times of 100 and 50 ms.

The pixel value at the Bragg peak for integration times of 50 ms (0.67 cGy) and 100 ms (1.3 cGy) were 6.1×10³ and 1.2×10⁴ gray scale levels, respectively. Both are well within the dynamic range of the camera, but the image acquired with 1.3 cGy takes full advantage of the dynamic range with some room for higher doses. With this setup a dose variation of 1% would cover 610 or 1220 gray scale levels for the short and long acquisition time, respectively. In both cases, a 1% dose variation would be detectable.

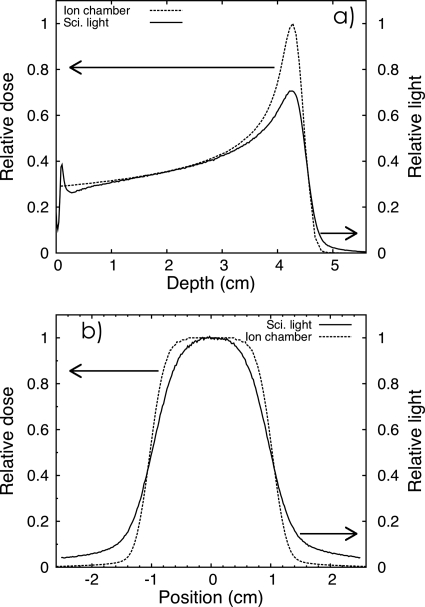
The scintillation light distribution profile as a function of depth, as shown in Fig. 3, has a shape roughly similar to the shape of the dose distribution of a Bragg peak. However there are some important differences between the light distribution and the dose distribution that need to be noted. To better illustrate these differences, Fig. 4a shows a depth profile of the light distribution integrated over 100 MU compared to the depth dose as measured with the Markus chamber. Figure 4b shows a lateral profile of the light distribution integrated over 100 MU compared to the pinpoint ion chamber lateral dose profile measured at a depth of 2 cm. Both curves were normalized at that depth (2 cm depth). There are several reasons for the differences between the dose and light profiles: (1) The ion chamber measured dose in a relatively small area of integration (i.e., the chamber sensitive volume) while the light distribution measured with CCD camera is the sum of all the light produced along the depth of field [see Eq. 5]. (2) The light distribution is blurred because of scattering and other optical phenomena such as total internal reflection, which produce the artifacts at the surface of the liquid. (3) The quenching of the scintillator near the Bragg peak.

Figure 4.

(a) Scintillation light profile measured with the LS detector system along the depth of the beam and compared to ion chamber depth dose curve measurements (Advance Markus chamber perpendicular to the beam direction). (b) Lateral profiles taken at 2 cm depth with the LS detector system and compared to ion chamber measurements (Pinpoint ionization chamber). All measurements were averaged over an acquisition period of 100 MU.

As mentioned in Sec. 1, scintillation detectors are sensitive to the stopping power of the incident particle. While this is not sufficient to affect scintillators linearity for photon and electron beams^{14, 15, 16, 17} it can cause an underestimation of the dose in the vicinity of a proton Bragg peak.¹¹ This quenching effect due to the changing LET of the incoming particle beam also needs to be corrected. In theory, to determine the exact quenching correction factor, one would need to know the exact energy spectrum of the proton beam at any given point. However, some assumption can be made to simplify the process. As mentioned previously, we can assume the stopping power to be constant in a plane perpendicular to the beam direction. It is also possible to take advantage of the fact that, with the LS system, we are always using the same geometry. The proton beam leaving the nozzle is always incident on the same uniform and homogeneous tank of liquid scintillator. Consequently, with the LS system, the quenching correction should always be the same for a given beam energy and beam-energy spread at a given depth. This would not be the case if there were heterogeneities in the beam path because phenomena such as distal edge degradation would change the proton energy spectrum. Therefore, quenching corrections can be performed by computing tables of correction factors that would depend on the depth and on the nominal energy of the beam.

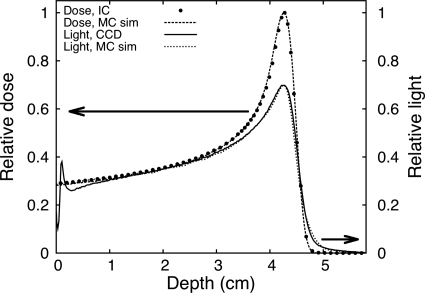
Comparison of the ion chamber dose distribution, the measured light distribution, and the Monte Carlo simulation of both light and dose distribution is shown in Fig. 5. Even with a simple beam model, there is good agreement between simulations and measurements. This indicates that Monte Carlo simulations could be used to define quenching correction factors. We plan to refine the model in future work by expanding our simulations and measurements to a large number of clinical beam energies.

Figure 5.

Scintillation light profile measured with the LS detector system compared to depth dose measurement with an ion chamber and Monte Carlo simulations (all the curves were normalized at 2.0 cm).

DISCUSSION

Spatial resolution

The spatial resolution of the LS detector system is determined by two factors: The blurring of the image due to light diffusion and the discrete nature of the pixels. As Fig. 4b shows, the light profile is blurred compared to the actual dose profile. Even if the images were to contain no blurring, the spatial resolution would still be limited by the pixel size. The smaller the pixel size is, the better the spatial resolution would be. Interpolating between pixel values can result in a better spatial resolution than the pixel size. The field of view and the spatial resolution are both linearly dependent on the distance between the CCD and the LS detector. Increasing the distance between the camera and the LS detector can increase the field of view, but will increase the pixel size. With our current setup with a distance of 50 cm between the scintillator and the CCD, each pixel covers an area of 0.19×0.19 mm² of the LS, thus resulting in a field of view of 12.5×9.4 cm². Increasing the LS-CCD distance to 100 cm would result in a field of view of 25×19 cm² and a pixel size of 0.38 mm in both directions, which would be adequate for the energies and field sizes encountered in proton therapy.

Theoretical calculations performed in Sec. 3 showed that the depth of field for our setup was 1.7 cm, which is slightly shorter than the size of the radiation beam (2×2 cm²). This explains in part the amount of blurring seen in Fig. 4. However, even with a larger DOF, blurring would still be present because of light scattering (see Sec. 5B). There are two possible ways to account for blurring in our setup. The first technique to account for the blurring would be to perform a deconvolution of the blurred image. This could be performed in order to convert the light profile into the real dose distribution. The second technique to account for the blurring is to make a forward projection of the dose distribution to predict what the light distribution should look like. The deconvolution approach is interesting because it would allow direct comparison with the dose distributions such as the ones provided by a treatment planning system. However, the deconvolution process is a delicate procedure requiring a fine adjustment of several parameters to minimize the risk of systematic errors. Both the deconvolution approach and the forward projection will be tested in our future work.

Image artifacts and corrections

Light propagation (scattering and absorption)

Even though the liquid scintillator is transparent to the light it produces, some absorption might occur and diffusion by Rayleigh scattering results in a light distribution that is blurred. In addition to this, some light is reflected on the walls of the LS tank and causes the background level to be nonzero. This effect is especially strong with the current prototype because of its narrow cross section (i.e., only 7×7 cm² wide) and the color of its wall material (i.e., gray). The walls of the tank should be black in color and grainy in texture to reduce this source of artifact to negligible levels. Blurring is most visible in the tail of the depth dose curve [see Fig. 4a] and in the wide penumbral width [see Fig. 4b]. The band of light seen at the surface of the LS is due to total internal reflection at the LS-air interface and is heightened by the meniscus at the surface of the LS [see Fig. 4a].

Vignetting

Vignetting is characterized by a reduction in light intensity in the periphery of an image caused by geometrical factors ranging from the inverse square law to mechanical blocking of incident light rays by the frame enclosing the lenses. Obliquely incident light “sees” a smaller lens opening than does light approaching perpendicularly to the lens. In our current setup, the small proton field only occupied the middle of the image and was therefore only slightly affected by vignetting (less than 2% on the field edges). However, because of the relatively short distance between the objective lens and the LS tank, we can expect vignetting to have an effect on the LSD system if a large LS tank and larger field size are used. With our CCD camera and objective lens, vignetting can reach up to 10% in the periphery of the image. If necessary, we can correct vignetting by acquiring a uniform image (e.g., a white screen) and then using this image to correct subsequent images.

Parallax

A 3D object projected on a 2D plane can cause parallax artifacts because of the perspective view. Because of this, sizes of objects seen on the image depend on their distances from the objective lens. This effect was partially taken into account in equation (D) by having m and Ap vary as a function of the distance to the objective lens. However to fully correct for parallax, it is necessary to use a second point of view (i.e., we need to image the phantom with two cameras).

Several steps are required to convert the light distribution into dose distribution. Our next prototype will be larger and would have walls made of a darker and grainier (nonreflecting) material in order to reduce the intensity of the background signal. The surface effect can be corrected by placing a thin (<1 mm) light-absorbing sheet on top of the surface of the LS. In addition to an improved prototype design, we will measure or estimate the point spread function of our imaging system in order to deconvolve the blurred light distribution and restore the sharpness of the dose distribution. Although the LS detector system shows a good potential for fast evaluation of proton plan delivery, there is still work to be done before such a system can be used in the clinic.

Toward 3D QA of IMPT

For an active pencil beam delivery, the dose is delivered through a large number (e.g., thousands) of a few millimeter-sized discrete proton spots of varying energies and intensities, which sum up to the desired dose distribution. In IMPT, a single spot from our scanning beam system can be delivered with doses of as low as 0.005 MU to doses as of high as 0.04 MU. However the definition of a monitor unit with this scanning beam system is different from the usual convention used in photon therapy (1 MU corresponds to 1 cGy at d_max). For our scanning beam at our facility, 1 MU is defined as the dose in the middle of a 10 cm spread-out Bragg peak for a field of 10×10 cm² with a maximum range of 30.6 cm in water. We measured that the dose at the Bragg peak for a single proton spot can vary from 1.5 to 10 cGy. This means that even if the number of monitor units per spot seems low, the dose delivered in a single spot is of the same magnitude as the dose that was measured in a single frame with our passive scattering experiment. Therefore the signal intensity will be sufficiently high to be measured by our system.

For the QA of IMPT fields, a second CCD camera orthogonal to the first one will be used to acquire images simultaneously. Both cameras should also be synchronized with the beam delivery system. Using such a method, images of every proton pencil beam can be viewed at two different angles, which can be used to determine the exact three-dimensional position of the pencil beam and its depth in a single irradiation beam delivery. This spatial information will complement the dose information obtained by the quantitative assessment of the amount of scintillation light produced by the beam. For the QA of IMPT beams, it is expected that the LS detector system will determine the position, integrated intensity at each position, and range (energy) of each pencil beam incident on the LS detector phantom.

Because an IMPT treatment is the sum of a series of nearly monoenergetic beams, quenching could be corrected by applying a depth dependent correction factor specific to the beam nominal energy. These correction factors can be determined either by measurements or by Monte Carlo simulations.

CONCLUSION

We have demonstrated the feasibility of using a LS detector system to measure the dose distribution produced by a proton beam in 2D. The system is capable of acquiring multiple images within a single proton pulse with good signal-to-noise ratio and submillimeter image resolution. The advantages of using this method over other methods, such as ion chamber arrays, include high spatial resolution and the ability to perform real-time measurements. We have also proposed a method for acquiring 3D measurements in real time without the need for multiple beam deliveries. Further investigations are warranted to bring this new detector system to its fullest potential in the detection and dose characterization of therapeutic proton beams.