Computer-aided diagnosis of pulmonary nodules on CT scans: Improvement of classification performance with nodule surface features

Abstract

The purpose of this work is to develop a computer-aided diagnosis (CAD) system to differentiate malignant and benign lung nodules on CT scans. A fully automated system was designed to segment the nodule from its surrounding structured background in a local volume of interest (VOI) and to extract image features for classification. Image segmentation was performed with a 3D active contour method. The initial contour was obtained as the boundary of a binary object generated by k-means clustering within the VOI and smoothed by morphological opening. A data set of 256 lung nodules (124 malignant and 132 benign) from 152 patients was used in this study. In addition to morphological and texture features, the authors designed new nodule surface features to characterize the lung nodule surface smoothness and shape irregularity. The effects of two demographic features, age and gender, as adjunct to the image features were also investigated. A linear discriminant analysis (LDA) classifier built with features from stepwise feature selection was trained using simplex optimization to select the most effective features. A two-loop leave-one-out resampling scheme was developed to reduce the optimistic bias in estimating the test performance of the CAD system. The area under the receiver operating characteristic curve, A_z, for the test cases improved significantly (p<0.05) from 0.821±0.026 to 0.857±0.023 when the newly developed image features were included with the original morphological and texture features. A similar experiment performed on the data set restricted to primary cancers and benign nodules, excluding the metastatic cancers, also resulted in an improved test A_z, though the improvement did not reach statistical significance (p=0.07). The two demographic features did not significantly affect the performance of the CAD system (p>0.05) when they were added to the feature space containing the morphological, texture, and new gradient field and radius features. To investigate if a support vector machine (SVM) classifier can achieve improved performance over the LDA classifier, we compared the performance of the LDA and SVMs with various kernels and parameters. Principal component analysis was used to reduce the dimensionality of the feature space for both the LDA and the SVM classifiers. When the number of selected principal components was varied, the highest test A_z among the SVMs of various kernels and parameters was slightly higher than that of the LDA in one-loop leave-one-case-out resampling. However, no SVM with fixed architecture consistently performed better than the LDA in the range of principal components selected. This study demonstrated that the authors’ proposed segmentation and feature extraction techniques are promising for classifying lung nodules on CT images.

INTRODUCTION

Lung cancer is the leading cause of cancer death in the United States, causing an estimated 160 400 deaths in 2007. At the time of diagnosis, most patients already present advanced disease. Despite advances in treatment and diagnosis, the 5 year overall survival rate is only 15%.¹ As for earlier detection, the “serendipitous discovery of lung cancer in asymptomatic people is currently the principal way in which stage I lung cancer is detected.”² Thus, there is great interest in determining whether earlier detection can reduce the mortality rate. Previous trials in the 1970s for screening of lung cancer with chest x-ray and sputum analysis did not result in a significant reduction in mortality.³

Computed tomography (CT) has been shown to have higher sensitivity in detecting small lung nodules compared to chest x ray.^{4, 5, 6, 7, 8, 9, 10} This suggests that CT screening has a strong potential for improving the likelihood of detecting lung cancer at an earlier and potentially more curable stage.^{11, 12} A 30-site randomized controlled study [National Lung Screening Trial (NLST)], sponsored by the National Cancer Institute (NCI), has enrolled about 50 000 participants to compare the effect of screening using helical CT or chest x rays on the mortality rate of lung cancer patients. If CT screening is recommended, however, it would also exacerbate already mounting challenges for detection and diagnosis of lung nodules with CT, namely, interpretation of an ever increasing number of slices and management of a large number of nodules. Despite the increasing spatial resolution of CT, the assessment of the likelihood of malignancy of nodules by visual inspection is difficult. It has been reported that as many as 50% of nodules resected at surgery are benign,¹⁰ emphasizing the need to provide radiologists with additional information to improve the accuracy for characterization of nodules and to handle large data sets.

Much work has been reported for the development of automated nodule detection methods in CT for computer-aided detection. In this study, we focus on the classification between malignant and benign nodules using features automatically extracted from the image data. Gurney and Swensen¹³ conducted a characterization study with a data set of 318 nodules (153 benign and 163 malignant) with features that were subjectively assessed by radiologists. They trained and tested a neural network in a feature space containing morphological features of the nodule, such as diameter (mm) and appearance of the edge, and demographic features such as age in years and smoking history in pack years provided by radiologists. They found that the neural network achieved an area under the receiver operator characteristic (ROC) curve, A_z, of 0.871 but concluded that Bayesian analysis was a better predictor of malignancy with an A_z of 0.894 (p<0.05).

Although data sets were smaller for other preliminary studies, the results were encouraging. The features were extracted from the image data, with the goal of quantifying the visual features radiologists typically use to discriminate malignant from benign nodules. Kawata et al.¹⁴ used surface curvatures and ridge lines as features for characterization of 62 nodules (47 malignant and 15 benign) and showed good evidence of separation between malignant and benign classes in feature maps; no A_z value was reported. McNitt-Gray et al.¹⁵ obtained 90.3% correct classification accuracy between 17 malignant and 14 benign cases. Shah et al.¹⁶ achieved A_z values between 0.68 and 0.92 with 48 malignant and 33 benign nodules using four different types of classifiers in a leave-one-out method. The features were extracted from contours manually drawn on a single representative slice of each nodule. Way et al.¹⁷ developed an automated 3D active contour (AC) segmentation method and extracted morphological and texture features from the segmented nodule. A leave-one-out test A_z of 0.83±0.04 was achieved in a data set of 44 malignant and 52 benign nodules.

Several classification studies were performed with a larger data set, although the number of malignant nodules was still below 100. Armato et al.¹⁸ used an automated detection scheme then manually separated nodules from non-nodules before the classification step. They achieved an A_z value of 0.79 for 59 malignant and 276 benign nodules using features such as the radius of a sphere of equivalent volume, minimum and maximum compactness, gray-level threshold, effective diameter, and location in the lungs. Li et al.¹⁹ reported an A_z of 0.937 for differentiation between 61 malignant and 183 benign nodules in a leave-one-out method and an A_z of 0.831 for a randomly selected subset consisting of 28 primary lung cancers and 28 benign nodules. The features used included the diameter and contrast of the segmented nodule and those extracted from the gray-level histograms of pixels inside and outside the segmented nodule. Aoyama et al.²⁰ reported an A_z of 0.846 for classifying 76 primary lung cancers and 413 benign nodules using multiple thick slices (10 mm collimation and 10 mm reconstruction interval), which was a statistically significant improvement over an A_z of 0.828 when using only single slices. Suzuki et al.²¹ obtained an A_z of 0.882 by use of a massive training artificial neural network (MTANN) on a data set of 76 malignant and 413 benign nodules.

We are developing a computer-aided diagnosis (CAD) system to assist radiologists in the classification task. Our CAD system automatically segments a nodule from a volume of interest (VOI) on CT images and provides a malignancy rating based on features extracted from the images. Our preliminary results have been reported previously.¹⁷ In this study, we have designed new image features that characterize the nodule boundary and improved the classifier training with an enlarged data set. In addition we investigated the effect of age at the time of the CT exam and gender as demographic features. Finally, we compared the performance between the linear discriminant analysis (LDA) and support vector machine (SVM) classifiers.

METHODS AND MATERIALS

CT scan collection

We retrospectively collected CT scans from the patient files in the Department of Radiology at the University of Michigan with the Institutional Review Board (IRB) approval. The CT scans were acquired with a variety of GE (GE, Waukesha, WI) Genesis HiSpeed and the GE LightSpeed series scanners, including Plus, Power, Pro 16, QX∕i, Ultra, and LightSpeed16. Each CT slice was 512×512 pixels, with pixel sizes ranging from 0.448 to 0.859 mm and corresponding fields of view of 25–44 cm. The slice thickness averaged 2.3±1.44 mm (range: 1–7.5 mm), and the slice interval averaged 2.0±1.6 mm (range: 0.6–7.5 mm). All but two scans were reconstructed with a GE standard kernel. The remaining two were reconstructed with a bone kernel. The average values for the scanning parameters were 120 kVp for tube voltage (range: 120–140 kVp) and 214±141 mA s (range: 40–570 mA s) for tube current-time product. In terms of the extremes, there were 13 cases scanned at 40–45 mA s and reconstructed at 1.25 mm slice thickness and interval. There was one case scanned at 570 mA s, but it was also reconstructed at 1.25 mm slice thickness and interval. The thicker-sliced scans (5–7 mm) were scanned at an average of 240±71 mA s.

Lung nodule data set

For this study, 256 lung nodules (124 malignant and 132 benign) were identified by radiologists from 152 patients. A nodule was included in the data set only if it could be seen in at least three consecutive slices. Because of the invasiveness of the lung biopsy procedure, clinicians generally do not perform biopsy for every lung nodule in clinical practice. The cases were determined to be benign, primary cancer, or metastatic cancer by clinicians using all available diagnostic information during the patients’ clinical care. The original diagnosis in the clinical reports and any additional follow-up information available by the time of our data collection were used as reference to determine whether a nonbiopsied nodule in our data set should be labeled as benign, primary, or metastatic cancer. Of the 124 malignant nodules, 64 were biopsy proven and 60 were determined to be malignant as described above. Seventy-two were primary and 52 were metastatic cancers. Of the 132 benign nodules, 15 were biopsy proven and 117 were determined to be benign with at least 2 year follow-up stability on CT.

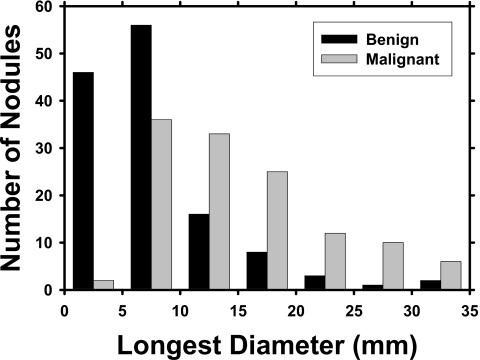
Four experienced chest radiologists with 35, 13, 3, and 3 years of post-fellowship experience in interpreting chest CT scans read mutually exclusive subsets of the data set. They indicated the location, measured their longest diameters, and assessed their characteristics such as malignancy, margin, calcification, and cavitation using a graphic-user interface (GUI). No clinical information about the case was provided to these radiologists during the assessments. These nodule characteristics from the radiologists’ subjective assessment were obtained only for the purpose of characterizing the data set used in this study. All the image features input to the CAD system were automatically extracted by the computer from the CT images, as discussed in Sec. 2D. Of the 256 nodules, 53 were juxtapleural and 19 were juxtavascular. A distribution of the longest diameters of the nodules is shown in Fig. 1. The nodules had an average longest diameter of 11.7±7.7 mm (range: 3.0–37.5 mm).

Figure 1.

Histograms of the longest diameters of the benign and malignant nodules as measured by experienced chest radiologists.

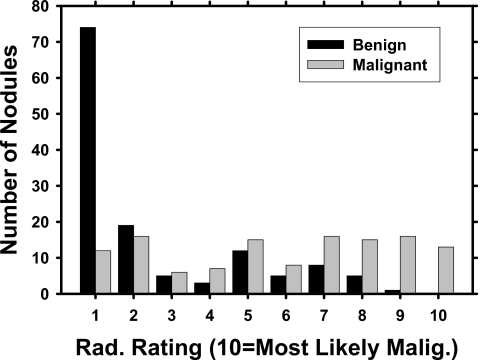
An experienced radiologist, different from the radiologists who helped collect the data set, provided malignancy ratings for each nodule on a scale of 1 to 10, with 10 indicating most likely malignant. This radiologist read the nodules separately without providing the other nodule characteristics. His malignancy ratings depended solely on the image information, just as what the computer classifier did. The area A_z under the ROC curve fitted to this radiologist’s malignancy ratings was 0.827±0.027 (Fig. 2).

Figure 2.

Malignancy ratings, provided by a radiologist who did not help collect the data set, on a scale of 1 to 10, with 10 being most likely malignant. The radiologist estimated the malignancy of a nodule solely based on the image information. The radiologist’s classification performance was evaluated relative to the clinically determined diagnosis of the nodules by ROC analysis. The area A_z under the ROC curve fitted to the radiologists malignancy ratings is 0.827±0.027.

CAD system overview

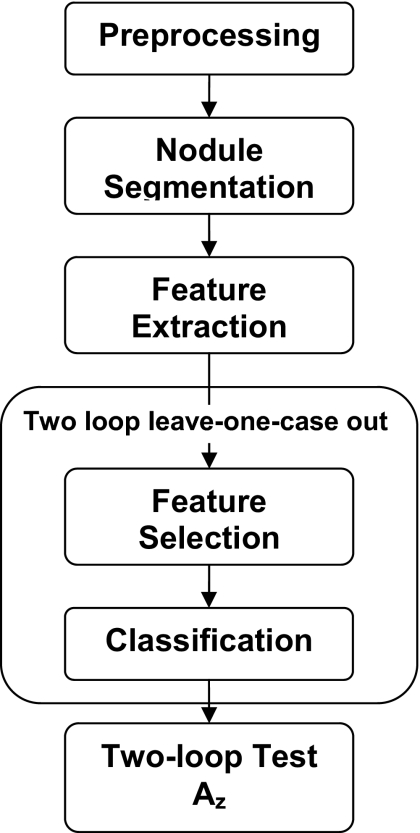
A detailed description of our CAD system can be found in the literature.¹⁷ A short summary is provided here, and the flowchart is shown in Fig. 3. First, the radiologist-identified VOI containing nodule was extracted from the CT scan. We obtained isotropic voxels for each scan by performing linear interpolation in the z direction if the slice interval was greater than the pixel size or bilinear interpolation in the axial plane otherwise. The purpose of interpolation is to facilitate initial contour generation and segmentation. The interpolation would not improve spatial resolution. To generate the initial contour, k-means clustering assigned voxels that were not part of the mediastinum or chest wall in the VOI to either the object or the background class. The mediastinal or pleural voxels were excluded from this and subsequent feature extraction processing by using a lung mask as described previously.¹⁷ Morphological opening was performed with a spherical structuring element that had an automatically calculated size based on the size of the clustered object. The morphological opening may remove attachments such as blood vessels from the object. A 3D AC model was then used to segment the nodule in the VOI. We estimated the weights for the 3D AC based on the optimization method with classification performance as the figure of merit described in our previous study.¹⁷ The segmentation was optimized separately using the feature space with and without the new image features for the performance comparison described below. After optimization, the same set of weights was used to segment all the nodules for the given feature space.

Figure 3.

A schematic showing the major image processing steps of the CAD system. The two-loop resampling scheme is described in Fig. 4.

We have conducted fairly extensive work in evaluating the segmentation performance of our 3D AC algorithm. In our previous study, we compared the segmentation results with experienced radiologists’ segmentation on the 23 nodules from the LIDC first data set.¹⁷ In addition to lung nodules, we also evaluated segmentation performance on spherical phantom nodules of three different known sizes and varying CT scanning parameters.²²

From the nodule contour, 2D and 3D morphological features were extracted. A few examples and descriptions of morphological features are given here, and the rest are described in the literature.¹⁷ The volume was found by multiplying the number of voxels within the contours by the size of one voxel. The longest diameter was the longest distance between two points on a contour. Statistics such as the average, standard deviation, skewness, minimum, and maximum of the CT values (Hounsfeld units) of the nodule voxels were calculated.

To quantify texture around the nodule, texture features were extracted first from the individual 2D image slices that intersect the nodule, and then the corresponding features were averaged over the nodule slices. For a given slice, the rubber band straightening transform²³ converted the 15-pixel-wide band of pixels surrounding the nodule into a rectangular image. The nodule boundary was mapped to the horizontal dimension of the rectangle while the spiculations emanating radially from the nodule became mapped to an approximately vertical direction. The transformed image was enhanced with Sobel filtering in the vertical and horizontal directions, from which the run-length statistics (RLS) features^{24, 25} were calculated.

In this study, we included new features in the feature space, as described in Sec. 2D. A feature selection method was then applied to the multidimensional feature space to select the most effective features for the classification task. A feature classifier was trained with the selected features. The performance of the trained classifier was evaluated with test cases and the classification accuracy was quantified by ROC analysis.

Gradient field and radius features

In addition to the morphological and texture features, we designed three sets of new features to characterize the nodule surface smoothness and shape irregularity. The first two sets were gradient magnitude and profile features, which were based on the gradient field, and the last set contained statistics of the nodule radii. The gradient vector and its magnitude M_v were computed at each voxel v using a filter-based method as described by Ge et al.,²⁶ which was a generalization of the 2D isotropic kernel proposed by Jain.²⁷

Gradient magnitude features

The gradient magnitude features described the sharpness of the nodule boundary. Let F be the set of gradient magnitude values for all voxels on the surface of the nodule segmented by the 3D AC method. We found the mean, standard deviation, variance, minimum, maximum, skewness, kurtosis, and coefficient of variation (standard deviation∕mean) for all values in set F. A nodule with well-defined boundary would have a higher mean than a nodule with less distinct boundary.

Profile features

Profile features described the smoothness of the gradient magnitudes in a shell of voxels just inside and outside the nodule surface. The weighted centroid C of the segmented nodule was calculated with the weights based on voxel intensity. The vector from the centroid to a surface voxel v is referred to as the radius r_v, where v=1,…,n and n denotes the number of surface voxels. The length of the radius ∣r_v∣ for each surface voxel was stored. The average radius rad_av of the nodule was defined as the average of all ∣r_v∣, v=1,…,n. Along this radial vector and centered at surface voxel v, gradient magnitude values were sampled at one pixel intervals to a distance of (1∕2rad_av) on the two sides of the surface voxel. Let P_v be the set of sampled gradient magnitude values along r_v, M_v,i be the ith sample, and ∣P_v∣ be the cardinality of P_v. Then the average gradient magnitude along one vector is

$$A_{\text{av},v}=\left(\frac{1}{\mid P_v\mid }\sum _{i=1}^{\mid P_v\mid }{M}_{v,i}\right).$$ (1)

The features we calculated are listed below, and mathematical formulas for some of the features are given.

• PF1 (profile feature 1): Mean of the average gradient magnitudes over all surface voxels,

  $$\text{PF}1=\frac{1}{n}\sum _{v=1}^n\left(A_{\text{av},v}\right).$$ (2)
• PF2: Standard deviation of the average gradient magnitudes over all surface voxels,

  $$\text{PF}2=\sqrt{\frac{1}{n-1}\sum _{v=1}^n{\left(A_{\text{av},v}-\text{PF}1\right)}^2}.$$ (3)

• PF3: Variance of average gradient magnitudes over all surface voxels.

• PF4: Mean of maxima,

  $$\text{PF}4=\frac{1}{n}\sum _{v=1}^n\left(\text{max}\left\{P_v\right\}\right).$$ (4)

• PF5: standard deviation of maxima.

• PF6: Variance of maxima.

• PF7: Mean of minima,

  $$\text{PF}7=\frac{1}{n}\sum _{v=1}^n\left(\text{min}\left\{P_v\right\}\right).$$ (5)

• PF8: Standard deviation of minima.

• PF9: Variance of minima.

It can be expected that high contrast nodules would have high values of PF1 and PF4. Nodules with mixed ground glass opacity (GGO) might have high values of PF2. However, if the nodule is attached to blood vessels, that would have an effect on these features compared to a solitary nodule surrounded by lung parenchyma voxels with lower CT numbers.

Radius features

The radius features were calculated based on ∣r_v∣, the magnitude of the radial vector from the weighted centroid C to surface voxel v:

• RA1: The average of all radii,

  $$\text{RA}1=\frac{1}{n}\sum _{v=1}^n\mid r_v\mid .$$ (6)

• RA2: The standard deviation of all radii.

• RA3: The variance of all radii.

• RA4: The skewness of all radii.

• RA5: The kurtosis of all radii.

It can be expected that a spherical nodule with a smooth surface would have very low values of RA2, RA3, and RA4 and high values of RA5 since all the radii would be similar. The radius segments of an irregularly shaped nodule would have varying lengths, with expected high values of RA2 and RA3. These features may therefore be useful in quantifying a nodule’s surface smoothness. RA1 is another feature that described the size of the nodule.

Demographic features

We investigated the effect of patient characteristics including age at the time of the scan and gender as adjunct information for the CAD system. The age was an integer value and gender was represented as 1 for male and 0 for female. Although most CAD systems only utilize image features, the use of demographic information has been found beneficial.^{13, 28} For our data set, we did not obtain smoking history consistently in the patient files so that this potentially useful information cannot be included.

Two-loop leave-one-case-out resampling

A feature classifier was trained to differentiate the malignant and benign nodules in the multidimensional feature space described above. We designed a “two-loop” leave-one-case-out resampling scheme to estimate the test performance of the CAD system. In comparison to the commonly used one-loop leave-one-case-out resampling, this method introduces another level of independence and reduces the bias in test A_z. In our data set, the 256 nodules were extracted from 152 patients so that the number of independent cases, N, was equal to 152. When a case was left out as a test case in the leave-one-case-out scheme, all nodules from that case are taken out and reserved for testing.

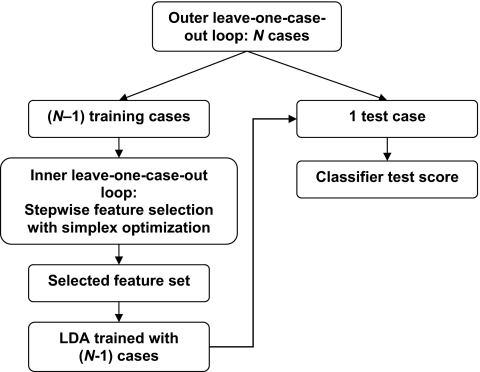
In the two-loop leave-one-case-out resampling scheme (Fig. 4), an inner leave-one-case-out loop was nested within the outer leave-one-case-out loop. For a data set with N available cases, there were N cycles in the outer loop. In each cycle, one case was excluded as the independent test case. The remaining (N−1) training cases were used to build the classifier in an inner leave-one-case-out loop that included feature selection and classifier weight determination. Stepwise feature selection (SFS) with LDA was used to select a subset of effective features. In each cycle of this inner loop for feature selection, (N−2) cases were used for training while one case was left out as the test case. The best parameters for SFS, namely, the F_in and F_out for determining whether a feature should be included or removed from the feature space, respectively, and the tol threshold for the tolerance on how correlated the selected features can be, were searched by simplex optimization using the test A_z from the (N−1) left-out cases in the inner loop as a guide. After the best SFS parameters were determined, they were applied to the (N−1) training cases of the outer loop to select a subset of features from the available feature space, and an LDA classifier using the selected features as the input predictor variables was formulated using the (N−1) training cases. This classifier was then applied to the independent left-out case in the outer loop and a test score for each nodule in that case was obtained. The procedure was cycled through the N cases of the entire data set, so that each case was left out in turn, resulting in independent test scores for all the nodules in the data set. These 256 test scores were then evaluated by ROC analysis to obtain the two-loop test A_z. Since the test case was kept out of the SFS parameter estimation, feature selection, and classifier weight training processes, the estimated performance using the two-loop resampling scheme was less optimistically biased than the one-loop scheme.

Figure 4.

In the outer leave-one-case-out loop, the data set is divided into (N−1) training cases and 1 test case. For each (N−1) case cycle, an LDA classifier is designed from a set of selected features as a result of an inner leave-one-case-out training and testing scheme. After each case is left out in turn, the two-loop test A_z is calculated from the malignancy scores of N test cases.

Evaluation of CAD System on the entire data set and on primary and metastatic nodules

The CAD system without and with the newly developed features described in Sec. 2D in addition to the demographic information was evaluated on the entire data set. Furthermore, nodules from primary cancers and metastases have distinctive characteristics. The former are more likely to be irregularly shaped or spiculated whereas the latter are often round and smooth. We therefore also evaluated the performance of the CAD system using two subsets of the data set, one containing primary cancers and benign nodules and the other metastatic cancers and benign nodules. For each of the two subsets, a new set of weights for the 3D AC segmentation was determined using the procedure described previously.¹⁷ The two-loop test A_z and features selected were compared.

Comparison between LDA and SVM

We compared the classification performance of LDA with that of SVMs. Since the SFS method described above used the LDA classification result as a guide, the selected feature set may be biased toward LDA. We therefore used principal component analysis (PCA), which is a well-known method for dimensionality reduction and is independent of the choice of the classifier, to obtain a reduced set of features as input to both classifiers for this comparison. PCA transforms a number of correlated variables into a number of uncorrelated variables, i.e., the principal components. It performs eigenvalue decomposition of the covariance matrix of the features, projecting the multivariate feature vectors onto the space spanned by the eigenvectors. The order of a principal component represents its importance in accounting for the variance in the data set. The dimensionality of the feature space is reduced by retaining the lower-order (higher-magnitude) principal components that are most important while ignoring the higher-order ones. Retaining only the lower-order principal components is essentially equivalent to approximating the data by a linear subspace using the mean squared error criterion.²⁹

The SVM works similarly to the LDA by constructing a decision hyperplane to separate classes using training data. A brief overview of the SVM is given below, with more details in the literature.³⁰ Geometrically, the SVM maps the original data to a higher-dimensional Euclidean space H, via a kernel K. A decision hyperplane is constructed in this higher-dimensional space such that the distance between the training samples of both classes and the hyperplane is maximized. This distance between a training sample and the hyperplane is called the margin, and the SVM calculates the hyperplane with the largest margin.

Suppose we have labeled training data {x_i,y_i}, i=1,…,t, y_i∊{−1,1}, and x_i∊R^u, where t is the number of samples, u is the dimensionality (number of features), and y_i is the class label of the ith sample that can assume a value of −1 (class 1) or +1 (class 2). The design of the SVM can be shown to consist of a quadratic programming optimization problem. In the dual of the quadratic program, the data appear in the form of dot products, x_i⋅x_j. The SVM algorithm uses a mapping Φ to a higher-dimensional Euclidean space H, Φ:R^u↦H. Because of the mapping, the algorithm depends only on data through the dot products in H of the form Φ(x_i)⋅Φ(x_j). There exist kernel functions K so that K(x_i,x_j)=Φ(x_i)⋅Φ(x_j), and the training algorithm uses only the kernel K and operations in the lower-dimensional space R^u instead of computationally expensive operations in H. A number of different kernels have been proposed in the literature, and we chose commonly used ones for this study. The dot kernel is the inner product: K(x_i,x_j)=x_i⋅x_j. The polynomial kernel has the parameter degree z: K(x_i,x_j)=(x_i⋅x_j+1)^z. The neural kernel has parameters a and b: K(x_i,x_j)=tanh(ax_i⋅x_j+b). The radial kernel is defined as

$$K\left({\mathbf{x}}_i,{\mathbf{x}}_j\right)=\text{exp}\left(-\gamma {\Vert {\mathbf{x}}_i-{\mathbf{x}}_j\Vert }^2\right),$$ (7)

with parameter γ. A capacity parameter cap is common to all kernels. We implemented the SVM with the freely available software mySVM.³¹

From the PCA, we selected the r largest eigenvalues and transformed the data with their corresponding eigenvectors. Since it was not known how many principal components were optimal for this classification task, we varied r from 1 to 15. For the LDA and SVM, we performed leave-one-case-out training and testing for each r to arrive at the test A_z. Because we varied r from 1 to 15 and did not have to choose features, a one-loop leave-one-case-out resampling process was used for classification. In addition, we varied the four kernels and their associated parameters of the SVM to investigate the effect of the kernel and parameters on test performance. A total of 120 (16 polynomial kernels of various degrees, 4 dot kernels of various parameters, 36 radial kernels of various γ, and 64 neural kernels of various coefficients) separate leave-one-case-out training and testing processes were performed for each r.

RESULTS

There were four groups of features used in this study: Morphological features (M), texture features extracted from the RBST images (T), newly developed image features based on the gradient field and radius features (G), and demographic features (D). In the following results, the subscript denotes which groups of features were included in the feature space, e.g., feat_MTG is the feature space containing the morphological, texture, and newly developed image features.

Effect of gradient field and demographic features on classification

The training and test A_z were calculated from the two-loop procedure described in Sec. II.F. When feat_MT was used as the feature space, the CAD system achieved an average training A_z of 0.858±0.023 and two-loop test A_z of 0.821±0.026. An average of 5.80 features was selected. The six most consistently selected features were surface area, maximum CT value, variance of nodule gray-level values, and three RLS texture features. When the newly developed image features were combined with the previous features, i.e., the feat_MTG feature space, the average training A_z was 0.881±0.021, and the two-loop test A_z increased significantly (p<0.05) to 0.857±0.023. An average of 6.62 features was selected. The most consistently selected features were the perimeter, a profile feature (PF2), the skewness of the gradient magnitude values of the surface voxels, two radius features (RA3 and RA4), and two RLS texture features. Four of these features were from the new space. These results are summarized in Table 1, and the features that were selected the most times are listed with the total number of times they were selected in the inner leave-one-case-out loop.

Table 1.

Two-loop test A_z for (a) entire data set, (b) primary and benign subset, and (c) metastatic and benign subset. The average number of features selected over all inner loop leave-one-case-out cycles and most frequently selected features and their frequency being selected are also shown for the different data subsets and feature spaces. The features that were consistently selected can be considered the effective features for this classification task. For the RLS texture features, SR is for short range, LR is for range, GL is for gray level, horiz is for the axial plane, obl is for the oblique plane, x and y specify which direction Sobel filtering was performed, and 0 or 90 indicates the direction the run-length statistics features were acquired. More details on these features were described in our previous study (Ref. ¹⁷).

	(a) Entire data set
	featMT	featMTG	featMTGD
Two-loop training Az	0.858±0.023	0.881±0.021	0.892±0.020
Two-loop test Az	0.821±0.026	0.857±0.023	0.863±0.022
Av. No. of features selected	5.80	6.62	7.50
Feature name	No. of times feature was selected
Surface area	122
Max CT	51
Variance of gray levels	100
LR low GL, obl, x, 90	151
LR high GL, obl, x, 90	138	86	73
LR high GL, obl, y, 90	144	152	152
Perimeter		152	152
PF2		151	152
Skewness of gradient magnitude		152	152
RA3		150	152
RA4		152	152
Age			152
	(b) Primary cancers and benign nodules
	featMT	featMTG	featMTGD
Two-loop training Az	0.895±0.022	0.902±0.021	0.921±0.019
Two-loop test Az	0.857±0.026	0.892±0.022	0.900±0.022
Av. No. of features selected	5.92	4.04	5.01
Feature name	No. of times feature was selected
LR low GL, y, 0	118
LR low GL, y, 90	112
LR, horiz, y, 0	126
SR, obl, y, 90	105	126	123
GL nonuniformity, x, 0	124
Min. CT	125
Run-length nonuniformity		126	124
RA4		126	126
PF4		125	125
Age			126
	(c) Metastatic cancers and benign nodules
	featMT	featMTG	featMTGD
Two-loop training Az	0.855±0.027	0.890±0.024	0.890±0.024
Two-loop test Az	0.822±0.031	0.803±0.034	0.803±0.034
Av. No. of features selected	2.96	6.69	6.69
Feature name	No. of times feature was selected
Perimeter	100
LR high GL, horiz, x, 90	104	67	67
LR high GL, obl, x, 90	99	83	83
RA1		104	104
RA5		104	104
RA3		103	103
Mean of all surface voxel gradients		96	96
PF2		58	58

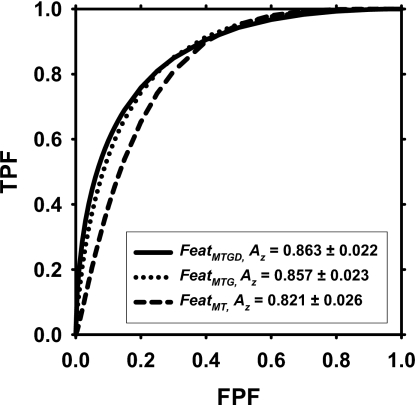
When the feat_MTGD space that included the demographic information was used, the average training A_z was 0.892±0.020, and the two-loop test A_z was 0.863±0.022, with an average of 7.50 features selected. The consistently selected features were the same as those when the feature space was feat_MTG, with the addition of the patient age. However, the improvement compared to the feat_MTG feature space did not achieve statistical significance (p=0.585). The ROC curves are compared in Fig. 5.

Figure 5.

ROC curves for the performance of the CAD system based on the two-loop test scores. The two-loop test A_z using features selected from the feat_MTG space was 0.857±0.023, which was significantly higher (p<0.05) than the two-loop test A_z of 0.821±0.026 when features were selected only from the feat_MT space. The addition of demographic information improved the two-loop test A_z to 0.863±0.022, but the difference did not achieve statistical significance (p=0.585).

Figure 6 shows examples of nodules in which the CAD system performed poorly. The benign nodules that obtained higher malignancy scores were generally larger and not spherical in shape. Some of the nodules were juxtavascular, emphasizing the need for a more effective vessel-removal method than that used in this study. The malignant nodules that had low malignancy scores were mostly metastatic, with round shapes and smooth, distinct edges. The texture around these nodules was also more homogeneous.

Figure 6.

Examples of nodules for which the CAD system performed poorly. (a) A large benign nodule that was unchanged over 2 years, (b) biopsy-proven non-necrotizing benign granuloma, (c) adenocarcinoma that may have been too small for the extraction of useful texture information, and (d) metastatic adenoid cystic carcinoma with features that may overlap with many benign nodules, e.g., round shape and distinct boundaries.

Classification performance on primary and metastatic nodules

Primary cancers

For classification of primary cancers and benign nodules, the CAD system achieved an average training A_z of 0.895±0.022 and a two-loop test A_z of 0.857±0.026 in the feat_MT feature space. An average of 5.92 features was selected. The six most consistently selected features were minimum CT number and five RLS texture features. When feature selection was performed in the feat_MTG feature space, the average training A_z was 0.902±0.021, and the two-loop test A_z increased to 0.892±0.022, although the improvement fell short of statistical significance (p=0.07). An average of 4.04 features was selected. The most consistently selected features included one gradient profile feature (PF4), one radius feature (RA4), and two RLS texture features. Of the most consistently selected features, two were from the new space. When the demographic information was added, the average training A_z was 0.921±0.019, and the two-loop test A_z was 0.900±0.022 for feat_MTGD. The improvement compared to feat_MTG feature space again did not achieve statistical significance (p=0.7). An average of 5.01 features was selected. The most consistently selected features were the same as those when the feature space was feat_MTG, with the addition of the patient age. These results are summarized in Table 1.

Metastatic cancers

On the subset containing metastatic cancers and benign nodules, the CAD system achieved an average training A_z of 0.855±0.027 and two-loop test A_z of 0.822±0.031 when feat_MT was used as the feature space. An average of 2.96 features was selected, with the largest perimeter and two RLS texture features as the three most consistently selected features. When feat_MTG was used as the feature space, the average training A_z was 0.890±0.024, and the two-loop test A_z decreased to 0.803±0.034, though the decrease was not significant (p=0.45). An average of 6.69 features was selected. Among the features most consistently selected were two texture features and five from the new feature space including three radius features (RA1, RA3, and RA5), the average gradient magnitude of surface voxels, and one gradient profile feature (PF2). In the feat_MTGD feature space, no demographic features were selected, and the performance was the same as that in the feat_MTG feature space. These results are summarized in Table 1.

LDA and SVM comparison

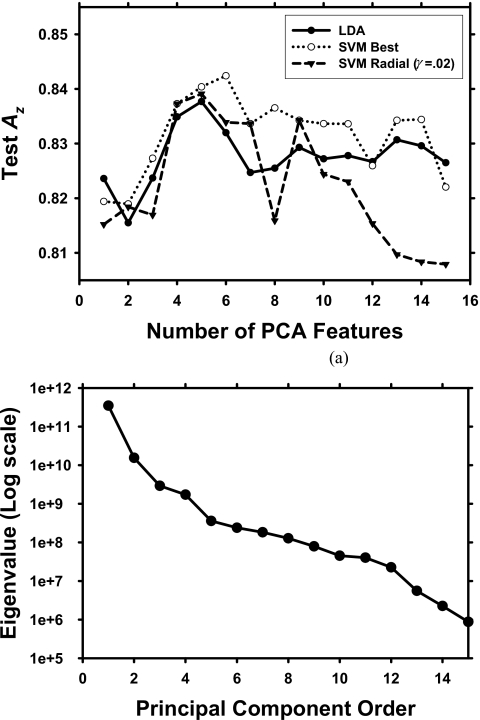
The performance comparison between the test A_z values of the LDA and the SVM classifiers is shown in Fig. 7. PCA was applied to the feat_MTG feature space, and the same number of features from PCA was input into each classifier. For a given number of chosen features, a set of 120 different combinations of kernels and parameters for the SVM was studied. The highest test A_z for the SVM for a given number of selected features is shown. The SVM performance using the radial kernel with γ=0.02 [Eq. 7] and cap=1 is also shown in Fig. 7 to demonstrate SVM performance with a fixed kernel and fixed parameters. This SVM was chosen as an example because it provided the best performance among the SVMs the most times for the values of r investigated. The classification performance of this SVM was slightly higher or lower than that of the LDA when the number of PCA features was less than 10 and was consistently lower when the number of PCA features increased to greater than 10. The highest test A_z among all SVMs studied was generally higher than the test A_z from LDA except at r=1, but it was still within one standard deviation of the test A_z from LDA. None of the SVM architectures used in our study provided a consistently better performance than the LDA over the range of the number of PCA features investigated (r=1–15).

Figure 7.

(a) Comparison of test A_z between LDA and SVM. For a given number of selected features, 120 combinations of parameters and kernels were evaluated for the SVM, and the best test A_z is shown. The standard deviations of the test A_z ranged from 0.024 to 0.026 for both classifiers. The test A_z using the radial kernel is also shown as an example of the performance when the kernel and parameters are fixed. (b) The sorted eigenvalues of the covariance matrix of the feat_MTG feature space obtained from PCA.

DISCUSSION

The newly designed features utilized the gradient field to determine whether the nodule edge is distinct or fuzzy. We also designed features that analyzed statistics of the radius segments of a nodule to quantify surface irregularities and size. The profile features examine a shell of voxels on either side of the segmented boundary, and these features are robust to contours that may be close to but not on the nodule boundary. Nevertheless, the segmented boundaries using the 3D AC are reasonable, as evaluated in our previous study.¹⁷

Previous simulation studies using LDA with SFS performed by our group found that increasing the dimensionality of the feature space resulted in more pessimistic holdout performance estimate.³² Based on these results, we would expect that adding features that have only small incremental discriminatory power would degrade the classification performance. However, a few of the new gradient field and radius features were selected, and their inclusion significantly (p<0.05) improved the test A_z for the entire data set. This demonstrates that the newly designed features are beneficial in discriminating between malignant and benign nodules when used in conjunction with the other types of features used in this study.

Effective features are important due to the inherent variability in lung nodule appearance. Previous studies that investigated the performance of CAD systems in classifying nodules show that no single feature can perfectly distinguish malignant from benign nodules.^{14, 15, 16, 17, 18, 20, 21} Nodule shape, size, margin, and presence of calcifications or fat are major features that are useful but far from being perfectly accurate in lung nodule characterization. There is substantial overlap in the appearance of malignant and benign nodules,^{33, 34, 35} which may be one reason that as many as 50% of nodules resected at surgery are benign.¹⁰

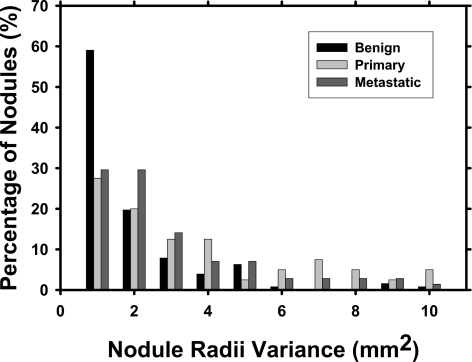
The classifier designed to distinguish primary cancers from benign nodules had a higher performance, whereas the one designed to distinguish metastatic cancers from benign nodules had a lower performance compared to the classifier designed to distinguish all cancers (primary and metastatic) from benign nodules. This may be due to the different characteristics that are unique to primary and metastatic cancers. Primary lung cancers tend to be more spiculated and irregular whereas metastatic cancers tend to be rounder with well-defined borders, which are more similar to benign nodules. It is therefore difficult to design features that can distinguish both primary and metastatic cancers from benign nodules. These differences were also reflected in the computer-extracted features. One example is the radius feature RA3, which is the variance of the radial lengths from the centroid to each surface voxel of a nodule. The histograms of the variance values for the three groups of nodules are compared in Fig. 8, and the means and medians are listed in Table 2. As expected, most of the benign nodules had small variance values. A large fraction of the metastatic nodules also had small variance values although they were less dominant than those of the benign nodules, signifying that they tended to be spherical. The primary nodules, however, showed relatively higher variance values, indicating irregular shapes. Table 2 shows that the mean and median of the benign nodules were smaller than those of the metastatic cancers, which, in turn, were smaller than that of the primary cancers. RA3 was selected as one of the effective features for differentiation of malignant and benign nodules in the entire data set [Table 1(a)] and for differentiation of the metastatic cancer from benign nodules [Table 1(c)].

Figure 8.

Variance of radial lengths from nodule centroid to each surface voxel (feature RA3). Note that the percentage of nodules for each class does not add up to 100% because a small number of nodules had variance >10 mm².

Table 2.

The estimated mean and median values of the three groups of nodules for feature RA3, which is the variance of the radial lengths from the centroid to each surface voxel. A lower mean signifies that the radial lengths are more similar, suggesting that the nodule tended to be more spherical.

	Primary	Metastatic	Benign
Mean	4.601	3.417	2.033
Median	2.322	1.775	0.851

Furthermore, it is interesting to note that the most frequently selected features from the feat_MTGD feature space for the two classification tasks, primary cancer vs benign [Table 1(b)] and metastatic cancer vs benign [Table 1(c)], were completely different when the two classifiers were separately trained. This confirmed that the features that could most effectively distinguish benign nodules from primary cancers were very different from those that could distinguish the same benign nodules from metastatic cancers. When the two cancer groups were combined as one class, the most frequently selected features [see Table 1(a)] included two of the best features from the primary cancer classifier and three from the metastatic cancer classifier, indicating a compromise in the selected features to accommodate both groups. From a screening perspective, radiologists may be more interested in using CAD to detect and classify primary cancers, since they may already be alerted to the possibility of metastatic cancer if the patient has a history of cancer elsewhere in the body. The performance of the CAD system on primary lung cancers may be a more informative indicator of its potential usefulness.

Radiologists use a variety of factors in arriving at a diagnosis, including a patient’s gender, age, and smoking history. We investigated the effect of two demographic features, gender and age, at the time of the scan. Other features such as smoking history or presence of other diseases were either incomplete from the patient records or difficult to quantify. Gender was never selected as a feature, but age as a feature improved the accuracy of the CAD system for the entire data set and for the subset of primary cancers and benign nodules, although the improvement did not achieve statistical significance. Demographic and clinical information may not always be available or reported accurately, especially if large-scale screening with CT is performed. Using the objective image data to design a CAD system is more flexible in that the radiologist can use the assessment by the CAD system as a complement to the other clinical information, if available, in the decision-making process. This study showed that although some demographic information is beneficial in diagnosis, the CAD system would perform similarly without the nonimage features we investigated.

Currently, researchers are not able to compare the performance of their CAD systems because of the lack of a common test set. If a large test data set with proven diagnoses is available, it will be a useful resource to compare the effectiveness of different approaches to classification of malignant and benign nodules. A publicly available data set would also increase the number of training samples that CAD developers may use for design of their CAD systems.

Because of the relatively small data sets available, we designed the two-loop leave-one-case-out scheme for feature selection and training of the classifier weights. A one-loop leave-one-case-out resampling method is sometimes used for the design of an LDA classifier with SFS. In each cycle of the one-loop leave-one-case-out, SFS and LDA classifier weights are determined using (N−1) cases and tested on the left-out case. The SFS parameters F_in, F_out, and tol may be fixed based on previous experience or may be chosen based on the test A_z from the N test cases. If one attempts to optimize the classifier with respect to SFS parameters, the use of the test A_z from the N test cases for this optimization will introduce an optimistic bias because the test cases are being used in the classifier design process. In other words, in such an optimization scheme, the test A_z is not independent of training. In the two-loop leave-one-case-out resampling process, optimization of the SFS parameters is performed only within the (N−1) training cases in the inner leave-one-case-out cycle. The left-out case in the outer loop is not used either to design the stepwise LDA or to guide the selection of the SFS parameters, so that the test A_z may not be as optimistically biased. However, since we used the same data set to iteratively improve the CAD system, our CAD system may still have been overtrained to suit the characteristics of the nodule samples in this small data set. Further evaluation of its generalizability is needed when an independent test set is available in the future.

We compared the performance between the LDA and SVM classifiers. Because we were only interested in the relative performance between the two, we performed PCA on the extracted feat_MTG features of the entire data set first and then varied the selected number of features as input to the classifiers based on the highest eigenvalues of the covariance matrix of the features. PCA was used because it is a filter feature selection method such that it does not select features based on the performance of a specific classifier. This is opposed to a wrapper method such as SFS, which selects features guided by the performance of a classifier using those features. The SVM performed slightly better than the LDA when the highest performance was chosen among a large number of combinations of kernels and set of parameters for a given set of input PCA features. This indicated that, for our data set, if the SVM was tuned for a specific set of input features, it could achieve better performance than the LDA. However, none of the SVMs with a fixed kernel and fixed parameters performed consistently better than the LDA for the combinations of kernels and parameters that we investigated.

A CAD system will only be considered useful if radiologists show improvement in diagnostic accuracy when they use the system as a second reader. The effect of our CAD system on radiologists’ classification of lung nodules will be investigated in an observer study. To that end, it is important to continually improve the CAD system to provide radiologists with accurate diagnostic information. Future work will also include analyzing interval change information for classification of malignant and benign nodules^{36, 37} and building on our previous work^{32, 38} in investigating the effect of sample size on feature selection and classification.

This study has several limitations. First, a heterogeneous data set with a wide range of scan parameters including slice thickness, slice interval, and dose was used. The scan parameters affected the image quality such as the resolution, noise, and partial volume effect of the CT scans which, in turn, would affect the quality of the extracted features. The increased variance in a feature may decrease the separation of the malignant and benign classes in the feature space, and hence reduce its effectiveness. We did not choose a more homogeneous data set because of the limited availability of cases with known diagnosis and similar scan parameters. It is also a fact that there are inter- and intrainstitution variations in CT scan protocols. If our method and features are tailored to suit only a data set of homogeneous imaging parameters or thin-slice scans, the estimated performance will likely be overly optimistic compared to what will be achieved if our method and features are applied to data sets acquired with different parameters. The use of a mixed data set as in our study may provide a more realistic estimate of an average performance when the CT scan is not ideal given the large variability in scan parameters and image quality in a clinical environment.

Second, there were 12 malignant and 7 benign juxtavascular nodules in the data set. We used morphological filtering to trim off potential blood vessels attached to a nodule for extraction of morphological features. However, the voxels that might be part of a vessel were not excluded when the surface features were extracted because we have not developed a robust automated blood vessel tracking method to label vascular voxels attached to nodules. Vascular voxels surrounding the nodule may distort the gradient magnitude, profile, and radius features calculated at the nodule surface. Although these features might be suboptimal for juxtavascular nodules, they improved the classification accuracy when combined with other features. This indicates that they still provided useful information complementary to the other features, probably because the surface voxels belonging to a vessel were typically only a small fraction of the entire surface. The effectiveness of these features may potentially be improved when the vascular voxels can be reliably excluded.

Third, in the current study, we focused on the characteristics of the individual nodules and did not examine the lungs as a whole. Some potentially useful features were not included in the feature space. For example, the presence of multiple benign-looking nodules in a patient may be indicative of metastatic disease, and the patient’s cancer history may play a role in differentiating benign lesions and metastases. The usefulness of these features will be investigated in future studies.

CONCLUSION

In this study we designed new image features by analysis of the gradient field and the surface smoothness of the nodules. We have demonstrated that the new features could improve the performance of our CAD system. The test A_z for the entire data set was improved significantly (p<0.05) when feature selection was performed in the entire feature space that included the new features in addition to the morphological and texture features. The discrimination of the CAD system between primary lung cancers and benign nodules was higher than that between metastatic cancers and benign nodules likely because there is a larger overlap between the appearance of benign nodules and metastatic cancers. When the LDA and SVM classifiers used the same feature set obtained by PCA, and the number of features was varied between 1 and 15 by changing the number of selected principal components, our comparison indicated that no single SVM classifier resulted in a consistently higher performance than the LDA in our classification task. Further work is underway to evaluate the usefulness of the CAD system in assisting radiologists in the classification of malignant and benign lung nodules.