Neuromechanical tuning of nonlinear postural control dynamics

Abstract

Postural control may be an ideal physiological motor task for elucidating general questions about the organization, diversity, flexibility, and variability of biological motor behaviors using nonlinear dynamical analysis techniques. Rather than presenting “problems” to the nervous system, the redundancy of biological systems and variability in their behaviors may actually be exploited to allow for the flexible achievement of multiple and concurrent task-level goals associated with movement. Such variability may reflect the constant “tuning” of neuromechanical elements and their interactions for movement control. The problem faced by researchers is that there is no one-to-one mapping between the task goal and the coordination of the underlying elements. We review recent and ongoing research in postural control with the goal of identifying common mechanisms underlying variability in postural control, coordination of multiple postural strategies, and transitions between them. We present a delayed-feedback model used to characterize the variability observed in muscle coordination patterns during postural responses to perturbation. We emphasize the significance of delays in physiological postural systems, requiring the modulation and coordination of both the instantaneous, “passive” response to perturbations as well as the delayed, “active” responses to perturbations. The challenge for future research lies in understanding the mechanisms and principles underlying neuromechanical tuning of and transitions between the diversity of postural behaviors. Here we describe some of our recent and ongoing studies aimed at understanding variability in postural control using physical robotic systems, human experiments, dimensional analysis, and computational models that could be enhanced from a nonlinear dynamics approach.

Successful postural control is both a precursor to and an integral component of locomotion in humans and other animals. Babies can only walk once they are able to stand, and constant postural corrections are necessary during locomotion to negotiate real environments. The ability to maintain standing balance in itself is a challenging problem that may provide a framework for addressing fundamental questions regarding the organization, diversity, and flexibility of biological motor behaviors in general. Evidence suggests that postural control dynamics are constantly being modified or “tuned” by the nervous system in response to prior and anticipated postural challenges. Moreover, a range of postural strategies contributes to our ability to maintain balance: swaying, stepping, or reaching. Therefore, the true postural capacity of an organism may not be captured by models assuming invariant parameter values or experiments examining only averaged postural responses. Here, we present a possible dynamical system framework for interpreting—and eventually understanding—the physiological mechanisms underlying postural stability. An important physiological property to consider is the long conduction delays present in transmitting the sensory and motor commands between the muscles and the nervous system. This property ensures that there are always at least two different mechanisms involved in maintaining posture in response to a perturbation. The initial movement and joint torques in response to perturbations are due to the intrinsic mechanical properties of the body. These properties are determined by feedforward activation levels of muscles prior to the perturbation. The latter movement and joint torques include the effects of sensory feedback that change the muscle activity after a delay. Because of the overlap in the effects of these two mechanisms, they must be carefully unraveled and explicitly accounted for in order to understand the flexible control of posture observed in physiological systems.

INTRODUCTION

To maintain standing balance, the nervous system must confront the classic “degrees of freedom” problem in motor control posed by Bernstein (1967) that arises from the vast redundancy in the musculoskeletal system. This redundancy requires not only a large number of elements to be coordinated in performing a task but also a method for selecting one possible solution amongst many. In balance control, the muscles and joints across the limbs, trunk, and neck must be coordinated to maintain the body’s center of mass (CoM) over the feet that form the base of support. These many degrees of freedom at the actuation or execution level are generally thought to pose a problem to the nervous system because the task requirements are not sufficient to uniquely specify how each muscle and joint must be controlled. However, as neural systems are both adaptive and must perform tasks in parallel, this redundancy may be necessary to allow flexibility in motor tasks such as posture and balance control. Therefore, seemingly simple behaviors may not be definable in terms of one-to-one mappings between the task goal and the coordination of the underlying elements.

Whereas the term “postural control” often refers to the restoration of a particular body configuration, in the context of standing balance in a gravity environment we define postural control as the suite of dynamic neuromechanical processes that maintain the body’s CoM over the base of support. In certain types of motor tasks, such as controlling the location of the hand when reaching to an object, it may be sufficient to maintain a particular kinematic configuration or body scheme (see Massion, 1994). However, in standing balance, returning the posture of the body to the original configuration following a perturbation may or may not be sufficient to avoid falling down. For example, when balance is disturbed or disrupted, various postural control strategies can be used, such as maintaining balance with the feet in place, taking a step, or grabbing a handhold. Even with a particular motor strategy, the execution of the task can be highly variable at many levels, including body motion (Bernstein, 1967), muscle activation (Gottlieb, 1998), and activity of neural circuits (Churchland et al., 2006; Horn et al., 2004) both within and across subjects. Moreover, postural responses to identical perturbations can vary significantly within an individual and are influenced by the condition of the previous trials, habituation, anticipation, cognitive load, and emotion (Carpenter et al., 2006; Woollacott and Shumway-Cook, 2002).

Recent evidence suggests that movement variability is not random but organized to allow the organism to flexibly reconfigure execution-level elements to achieve task-level goals. Variability in muscle activity or joint angles during postural and other motor tasks may be organized to minimize variability in task-level variables such as CoM movement or target attainment (Krishnamoorthy et al., 2004; Scholz et al., 2002; Scholz and Schoner, 1999; Torres-Oviedo and Ting, 2007; d’Avella et al., 2003; Ting and Macpherson, 2005; Tresch et al., 1999; Welch and Ting, 2008). Thus, in their normal functioning, biological systems may use the multiple “correct” solutions defined by manifolds appropriate for any given task (Latash et al., 2007; Ting and McKay, 2007). While important stochastic variations also exist in sensation and actuation (Hamilton et al., 2004; Harris and Wolpert, 1998), motor variability may be more attributable to optimal feedback processes that balance the opposing demands of achieving a task-level performance goal versus minimizing energy expenditure (Kording, 2007; Lockhart and Ting, 2007; Shadmehr and Krakauer, 2008; Ting and McKay, 2007; Todorov and Jordan, 2002). Open questions remain as to (1) how and why global, task-level goals of regulating endpoint trajectory, CoM movement, or energetic efficiency vary across different contexts and (2) how such task-level goals are flexibly achieved by redundant execution-level commands at the level of neurons, muscles, and joints.

In this communication we present our perspective of important physiological postural control mechanisms as well as some experimental results that must be taken into consideration when formulating models of postural control. First, we review important aspects of the balance control literature with respect to nonlinear dynamical system analysis. Significant advances in understanding postural control may be achievable though nonlinear dynamical analyses of postural control models that reflect an appropriate level of complexity of the physiological systems involved. Then, with the goal of identifying common neural mechanisms, we review the current postural control literature addressing different experimental conditions: quiet standing, and postural responses to both continuous and discrete perturbations. We present a delayed linear feedback model that may be useful in unifying these different postural behaviors. Finally, we present our recent and current work from robotic, human, animal, and computational studies that demonstrate how neural and mechanical (neuromechanical) tuning can alter postural performance and induce transitions across postural strategies. It is our hope that this review will stimulate future research to develop experimental, computational, and analytical techniques that will help understand how the global goal of balance control is achieved through the flexible integration and coordination of multiple neuromechanical elements.

BALANCE CONTROL AS A NONLINEAR DYNAMICAL SYSTEM

A nonlinear dynamical system perspective may be useful for understanding how variability and diversity in the coordination of execution-level elements contribute biological postural control. To understand postural variability requires studying the precise tuning of the underlying neuromechanical elements and not just reproducing the task-level functions of the postural control system. While single parameter variations are useful and necessary for investigating relevant nonlinear behaviors in biological systems, it is important to maintain the perspective that the nervous system is perhaps capable of simultaneously tuning all parameters that may contribute to task-level goals. From a physiological perspective, we present several important execution-level neuromechanical elements that contribute to postural control dynamics and their relevant features and characteristics. Next, a conceptual framework is given that may help illustrate how nonlinear dynamic analyses might contribute to our understanding of how these elements are coordinated during postural control.

Feedforward and feedback execution-level neuromechanical mechanisms are necessary to navigate the long delays associated with neural pathways that mediate sensory input and motor output (Fig. 1). We define feedforward neuromechanical elements to be those that adjust the intrinsic mechanical stability of the musculoskeletal system, requiring an anticipation of a postural perturbation. We define feedback neuromechanical elements to be those that activate muscles reactively following postural perturbations. Muscles are the actuators of the physiological system and contribute to both feedforward and feedback postural stability. Muscle activity is measured as an electrical signal called an electromyogram (EMG) and reflects the level of excitation of a muscle by the nervous system. In humans, the minimum time before a change in EMG activity following a postural perturbation is roughly 100 ms (Horak and Macpherson, 1996). Additional electromechanical delays of about 50 ms are required for force production to build within the muscle and to be transmitted through the musculoskeletal system. Since motion of the body depends upon the initial position and velocity as well as the integrated effects of applied forces, actual changes in the displacement of the body due to the feedback response may not be observed for as long as 500 ms after perturbation.

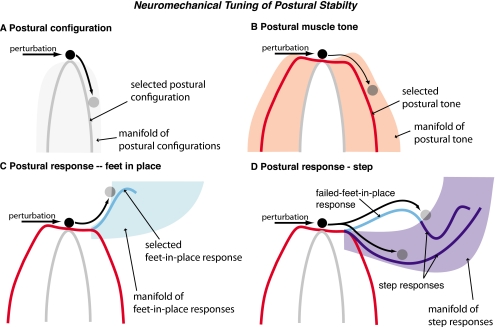
Figure 1.

Conceptual framework for understanding tuning and coordination of neuromechanical elements contributing to postural stability. The intrinsic dynamics of the musculoskeletal system at the time of a perturbation depends upon the feedforward contributions of postural configuration and postural muscle tone, which are selected in advance by the nervous system. (a) The chosen postural configuration determines the basic skeletal mechanics of the body, which in standing balance control is unstable due to the divergence of the gravitational force field. Because of the redundancy of joints and limbs, there are many possible postural configurations that can be chosen during standing. (b) The selection of postural muscle tone during standing can also alter the stability of the body, as the instantaneous stiffness and viscosity of muscles vary as a function of their level of activation. Due to the redundancy of muscles across each joint, a large manifold of muscle activation patterns satisfies the static equilibrium requirements for maintaining the selected postural configuration and differs in the stability afforded to the body. Postural muscle tone may increase the time constant of instability of the body or provide a degree of local stability to very small perturbations. (c) When a perturbation to the body is sensed, directionally specific feedback postural responses are elicited, which alter muscle activity after a long delay. During the initial 150 ms following the onset of a perturbation, the dynamics of the body are determined by the intrinsic dynamics set by the feedforward neuromechanical elements in (a) and (b). Postural responses that allow the feet to remain in place have differential stabilizing capacities, which will depend upon the pattern and magnitude of muscle activation elicited. Generally, postural strategies that use primarily hip torques can generate larger restoring forces than those that rely on ankle torques due to limitations in maximum muscle force generation. (d) If the feet-in-place strategy is insufficient to stabilize the body, a step response that expands the base of support and generates a different fixed-point location can occur. Steps can vary in size and can also be elicited as the primary feedback response following a perturbation.

Delays are an important aspect of physiological postural control processes that may present a “problem” for the neural control system but provide a convenient feature for decoupling the contributions of feedforward and feedback neuromechanical stability. In control theory, feedback time delays are typically destabilizing because the system continues to change during the time it takes for delayed-feedback response to be generated, often rendering the resulting response inappropriate and destabilizing (e.g., Milton et al., 2009). Therefore, the dynamics of the system need to be tuned via feedforward mechanisms to ensure that the time constant of the system is matched to that of the feedback delay. Although feedforward intrinsic stability is typically insufficient by itself to prevent an organism from falling in the face of a perturbation, a sufficient degree of intrinsic stability is necessary to allow for the delayed-feedback response to take effect. Neural delays are similarly problematic in locomotion and other movements; however, it is difficult to distinguish whether changes in muscle activity and performance are due to feedforward or feedback mechanisms during periodic behaviors. Moreover, very different muscle activation patterns can produce similar kinetic and kinematic outputs (Gottlieb et al., 1995; Lockhart and Ting, 2007). Therefore, explicit examination of muscle activity during postural control can provide insight about the information and computations of the nervous system.

Feedforward neuromechanical stability

The instantaneous response of the body to a perturbation is determined by the tuning of feedforward neuromechanical elements. Postural configuration refers to the strategic arrangement of limb segments in space and determines the basic mechanical dynamics of the skeletal system. Due to the gravitational field and joint mobility, standing postural configurations are typically unstable when considering skeletal dynamics alone [Fig. 1a]. Postural muscle tone refers to the baseline or “background” activity of muscles during quiet standing. The nominal function of postural muscle tone is to supply sufficient joint torques to maintain static equilibrium against gravity. However, a more important function of postural muscle tone may be to modulate the instantaneous stiffness and viscosity of the joints [Fig. 1b]. The dynamics of the system in response to a perturbation depend upon the postural configuration, which sets the length of muscle, tendons, and soft tissues, which all have nonlinear stiffness properties (Gasser and Hill, 1924; Gordon et al., 1966; Rack and Westbury, 1974). Within a given postural configuration, the dynamics are further modulated by the postural muscle tone (Crago et al., 1976; Hoffer and Andreassen, 1981; Nichols and Houk, 1976).

In both normal and clinical populations, postural configuration and postural muscle tone are commonly modulated to affect the intrinsic stability of the musculoskeletal system. The particular combination of postural configuration and postural muscle tone adopted by a particular individual at any time may reflect a variety of factors—for example, high tonic muscle tone may be metabolically unsustainable over long periods of time, and particular postural configurations may reduce the maneuverability and agility of the body. However, the mechanisms governing the modulation of these feedforward neural mechanisms are poorly understood—we do not know the extent to which such changes are symptomatic versus adaptive (e.g., Amiridis et al., 2003). Postural configuration is commonly modified in healthy individuals to increase postural stability, such as placing the feet wider apart or crouching conditions where balance control is challenging (e.g., Dietz and Sinkjaer, 2007^; Jang et al., 2008). Similarly, subjects alter arm configuration to increase stability in unstable manipulation tasks (Perreault et al., 2004). Changes in postural tone are commonly observed when subjects learn new tasks or move in unpredictable environments (Osu et al., 2002), and increased postural muscle tone is symptomatic of a number of neurological movement disorders (Dietz and Sinkjaer, 2007).

Feedback neuromechanical stability

A postural response refers to the coordinated activation of muscles that stabilize the body following a perturbation. Postural responses are evoked at a minimum of 80–100 ms following the onset of a perturbation in humans and activate multiple muscles as a function of the direction of destabilization as well as the postural strategy chosen (Horak and Macpherson, 1996). Restoring forces due to postural responses do not act until ∼150 ms after the onset of perturbation. For example, postural responses to a perturbation can maintain the original base of support by keeping the feet in place [Fig. 1c] or by taking a step [Fig. 1d]—each strategy activates different muscular patterns but provides postural stability in the appropriate direction. A continuum of feet-in-place postural responses of varying efficacy is observed in humans. The stereotypical responses at the ends of the continuum are referred to as the “ankle” and “hip” strategies because those joint angles exhibit the largest changes (Horak and Macpherson, 1996; Kuo, 1995). A feet-in-place postural response can be sufficient to return the body to the original fixed-point location [Fig. 1c]. However, it is possible for a perturbation to be large enough that the initial postural response is insufficient to stabilize the body, resulting in a change in strategy to a stepping response that essentially moves the fixed point to a different location by expanding the base of support. Stepping responses can also be evoked in the initial response to perturbation [Fig. 1d]. Postural systems are flexibly tuned to overall task goals—this has been previously referred to as changes in the “central set” or state of preparedness of the individual, modifying postural responses in an adaptive or predictive manner (Horak and Diener, 1994; Horak et al., 1989; Horak and Nashner, 1986; Timmann and Horak, 1997). The central set may predetermine the postural response parameters related to the expectation of the individual. Variations in the central set may be responsible for the differences in magnitude of postural response as a function of habituation, expectation, fear, or cognitive load (Carpenter et al., 2006; Woollacott and Shumway-Cook, 2002).

UNDERSTANDING COMMON MECHANISMS ACROSS DIVERSE POSTURAL BEHAVIORS

Although experimental and computational postural control studies typically focus on specific regimes of postural behaviors, similarities in modeling studies across the postural behaviors suggest the existence of common underlying neural mechanisms. These studies generally provide information about postural control well within the bounds of postural stability for a particular strategy. Here we briefly summarize the three primary postural regimes of continuous movement, discrete perturbations, and postural sway, with an emphasis on possible evidence for shared neural mechanisms.

Postural control during continuous movement

Studies on the regulation of posture during continuously induced postural movements have helped reveal the flexible modulation of sensory information in regulating balance. A simple model of the body as an inverted pendulum controlled by delayed position and velocity feedback can describe the modulation of different sensory contributions during continuous movement (Peterka, 2000, 2002). While the visual and vestibular systems encode the motion of the head relative to the environment, the somatosensory system encodes the motion of the body relative to the ground. Low amplitude and frequency motion of the support surface affects somatosensory information about joint positions and velocities, allowing subjects to maintain their postural configuration with respect to the surface even as it tilts (Peterka, 2002). Conversely, subjects orient to a perceived vertical in the environment as frequency and amplitude of the surface increase because the vestibular and visual systems preferentially encode high frequency information (Peterka, 2002). Although motion of the visual surroundings alone can elicit movement responses, this effect is attenuated by the degree of incongruence with somatosensory information from the muscles, skin, and joints (Buchanan and Horak, 1999; Creath et al., 2005; Keshner et al., 2004).

One of the challenges in interpreting postural orientation with respect to a continuous motion is that the effects of anticipatory feedforward and reactive feedback postural control are confounded. When subjects first stand on a sinusoidally moving surface in the horizontal plane, they tend to maintain their orientation to the surface, moving with the displacement of the floor beneath. However, as platform frequency increases, subjects transition gradually from in-phase to out-of-phase motion (Buchanan and Horak, 1999; Ko et al., 2003) and can switch their phase relationship voluntarily. Similarly, during oscillations of the body when visually tracking a moving target, transitions between in-phase and antiphase postural coordination modes are found as movement frequency increases, but the transition frequencies can be modified by the subject (Bardy et al., 2002; Ferry et al., 2007; Martin et al., 2006). The transition in-phase relationship with frequency suggests a nonlinear model of the postural system with a bifurcation (Verdaasdonk et al., 2004), but models must also reconcile the evidence indicating that subjects tune neuromechanical elements to avoid instabilities in the transition between regimes.

The current methodologies used to study postural control produce insufficient information to examine the underlying neural mechanisms governing the tuning of postural control. Studies of continuous postural control rely primarily on kinematic measures of postural orientation; muscle activity during continuous postural movements is typically not recorded. Although studying continuous motions allows frequency-domain system identification techniques to be used, interpreting the resulting transfer functions and frequency spectra is challenging from the point of view of understanding underlying neuromechanical mechanisms. As in locomotion, perturbations can have effects that last for several subsequent cycles, so it is difficult to distinguish the modulation of muscle activity or postural configuration due to feedforward versus feedback mechanisms in periodic movements.

Postural responses to discrete perturbations

Postural responses to discrete perturbation events have provided the most detail about the underlying neural mechanisms producing postural responses through the analysis of muscle activity, ground-reaction forces, and kinematics of body segments in healthy and neurologically impaired individuals. Typically, a subject stands on a support surface that is displaced in either a horizontal translation that simulates a slip or a pitch and roll rotation that simulates an unstable surface (Carpenter et al., 2004; Nashner, 1977; Ting and Macpherson, 2004; Torres-Oviedo et al., 2006). As discussed above, the delay before the postural response is elicited allows feedforward and feedback contributions of balance control to be dissociated, although little is known about their interactions. While postural responses can also evoke stepping and upper-body postural strategies, prior research has focused primarily on feet-in-place postural responses.

Postural responses can be attributed directly to the occurrence of a perturbation, so that the timing, amplitude, and organization of the evoked muscle activity reflect the sensorimotor feedback processes contributing to postural stability. For example, loss of vestibular information or closing the eyes does not alter the delay or the directional specificity of postural responses but causes the magnitude of the evoked muscle activity to increase (Horak and Macpherson, 1996; Inglis and Macpherson, 1995). This suggests that vestibular and visual information help establish a stable reference point for interpreting changes in body motion arising from somatosensory receptors throughout the body (Horak and Macpherson, 1996; Macpherson et al., 2007). Loss of somatosensory neurons that provide kinesthetic information about the body segments, however, can cause gross postural deficits and can greatly increase the postural response delay (Inglis et al., 1994; Stapley et al., 2002). Loss of somatosensory acuity could be responsible for degradation of postural control with aging, peripheral neuropathy, multiple scelerosis, and a host of neurological disorders (Horak et al., 1997). Examining the deficits in individuals with neurological disorders also highlights the importance of neuromechanical tuning to fluid and functional movement. Postural response studies have revealed deficits in the ability to appropriately modulate both feedforward and feedback postural mechanisms with respect to changing environmental contexts in Parkinson’s disease. Deficits in feedforward tuning are evident in the inappropriate changes in ground-reaction force when the distance between the feet (postural configuration) is altered during the period before the onset of a perturbation (Dimitrova et al., 2004; Jacobs et al., 2005). Deficits in feedback tuning is evident in the inappropriate activation of leg muscle activity when Parkinson’s subjects respond to seated perturbation immediately following postural perturbation during standing (Dimitrova et al., 2004; Horak and Macpherson, 1996). It has also been demonstrated in cerebellar dysfunction that the ability to adjust postural response muscle activity to an anticipated postural disturbance is impaired (Horak and Macpherson, 1996).

Postural response studies also demonstrate that muscle activity is organized to provide global stability rather than simply restore the original postural configuration. Muscle activity is consistently evoked in response to CoM destabilization rather than local joint angle changes (Ting, 2007; Ting and Macpherson, 2004). The direction of CoM motion is the critical task-level biomechanical variable defining the motion of the body and reliably predicts the directional tuning of muscles across postural perturbation conditions where any single sensory signal would fail to predict the appropriate muscle response. These studies demonstrate that local proprioceptive signals, as well as vestibular and visual information, are insufficient to robustly predict the ensuing muscle activity for the full suite of postural responses. Rotations (pitch and roll) versus translations (horizontal plane) of the support surface that elicit similar patterns of muscle activation induce opposite changes in joint angles but similar changes in CoM displacement in both humans and cats (Carpenter et al., 1999; Diener et al., 1983; Gollhofer et al., 1989; Nardone et al., 1990; Nashner, 1977; Ting and Macpherson, 2004). These results reinforce the finding that early (∼50 ms after perturbation onset) and very weak stretch-reflex activation of muscles related to joint angle changes is incapable of providing global postural stability (Carpenter et al., 1999).

The flexibility and variety in muscle activity observed during feet-in-place postural responses can be robustly modeled by an inverted pendulum model with delayed feedback on CoM kinematics. We modified the model used by Peterka (2002) to describe postural control during continuous movements, which is discussed in more detail in a later section (Lockhart and Ting, 2007; Welch and Ting, 2008). Although the body can act explicitly like an inverted pendulum during ankle-strategy responses, we were able to reproduce muscle activity evoked during both ankle- and hip-strategy postural responses using the model (Welch and Ting, 2009). Variations in muscle activity across a wide range of perturbation amplitudes as well as across individual subjects can be predicted by taking the measured CoM position, velocity, and acceleration trajectories, delaying them by 100 ms, multiplying each by a weight or feedback gain, and summing them (Welch and Ting, 2008, 2009). Thus the variations in temporal patterns of muscle activity appear to reflect modulation of just three feedback gain variables. This idea is further supported in studies of well-trained animals in which feedback gains reproducing temporal patterns of muscle activity can be predicted by an optimal trade-off between CoM stabilization and energetic expenditure. This model is also relevant for degraded postural control in these animals when large somatosensory neurons are damaged, but the animals are still able to maintain balance. The resulting muscle activation pattern is qualitatively different from intact animals but is nonetheless predicted by the model using the same optimal trade-off with no acceleration feedback (Lockhart and Ting, 2007). Together these studies help delineate the important global variables regulating postural responses as well as the relatively low-dimensional manifolds within which variability in postural responses is constrained.

Postural sway

Postural sway refers to the constant motion of the body when standing “still” in the absence of obvious external perturbations. Advantages of studying this phenomenon are that there is no need for perturbation devices that impose motion on the body, and it only requires subjects to stand on a force platform. Postural sway is rather low in frequency (<2 Hz) and can be considered to be quasistatic. Additionally, the CoM motion is commonly estimated from the motion of the center of pressure (CoP), the point of net force application on the ground. Postural sway therefore minimizes the experimental manipulation of the body and reflects characteristics of the underlying dynamic neuromechanical processes.

Differences in postural sway measures have been observed across different populations and may be attributable to variations in both feedforward and feedback contributions to postural stability. Athletic subjects tend to exhibit less sway (Schmit et al., 2005), whereas older adults tend to exhibit more sway with higher postural muscle tone (Amiridis et al., 2003). Postural sway is also modulated with fear of falling (Adkin et al., 2002, 2000) and attention to other tasks (Woollacott and Shumway-Cook, 2002). The magnitude of postural sway is also affected by both feedforward changes in postural configuration by manipulating feedback sensory information, such as when closing and opening the eyes (Amiridis et al., 2003; Day et al., 1993). However, CoM is typically the only measure of motion taken, making it difficult to extract information about the neural mechanisms underlying the tuning of postural sway. Studies with more precise measurement of the individual joint motions during postural sway reveal that multiple concurrent movement modes corresponding to hip and ankle postural response strategies contribute to postural sway (Creath et al., 2005).

By examining kinetics, kinematics, and muscle activity during postural sway, the mechanisms of postural sway have been attributed to a number of different concepts including intermittent feedforward control, positive feedback control, and delayed-feedback control. Based on the analysis of CoP movement, postural sway has also been described as a correlated random walk. Time series analysis suggests that postural sway arises as an open-loop mechanism allowing the body to drift at short time intervals and a closed-loop feedback mechanism that acts at delay of about 1 s to restore the displacement of the CoP (Collins and De Luca, 1994). Peaks in muscle activity tend to precede peaks in CoM motion by about 100–250 ms during postural sway (Fitzpatrick et al., 1992). This observation has been used to argue that postural sway is in fact a feedforward mechanism that moves the body in a predictable way to counteract the long sensory delays (Loram et al., 2005), yet postural sway is altered when sensory information from the feet is enhanced (Priplata et al., 2002). The results clearly show that the muscle activity during postural sway cannot be explained solely by feedback of CoM displacement. However, considering that somatosensory receptors can encode velocity and possibly acceleration, it is possible that the relative timing of muscle activity and CoM motion during postural sway can still be explained by neural feedback mechanisms. For example, during postural responses to perturbation, muscle activity follows peak CoM acceleration by 100 ms but precedes peak CoM displacement by about 135 ms (Welch and Ting, 2008). Therefore it is possible that the same delayed-feedback mechanisms act during both postural sway and postural responses to perturbations. Consistent with this idea, the same inverted pendulum model used to describe postural control during continuous movement can also reproduce postural sway when noise is added to the sensory channel. Moreover, the structure of the simulated postural sway using the inverted pendulum model exhibits similar characteristics of a correlated random walk when compared to subjects (Peterka, 2000).

A DELAYED-FEEDBACK MODEL FOR UNDERSTANDING NEURAL CONTROL OF POSTURE

As outlined above, delayed-feedback models of postural control can be used to explain results from divergent postural control experiments. In our work, we have focused on characterizing the feedback modulation of muscles during postural responses to perturbation. This model could be extended by incorporating mechanical properties affected by postural configuration and postural tone into the model. Here we present the model described by Lockhart and Ting (2007) to describe postural control in cats and the adaptation of feedback gains after sensory loss, and subsequently used to describe variations in postural responses in humans across individuals (Welch and Ting, 2008) and perturbation conditions (Welch and Ting, 2009).

We developed an inverted pendulum model that utilized a lumped mass to represent the movement of the CoM rather than modeling the movement of particular body segments and allowed for a simple encapsulating description of body motion with respect to gravity and external forces. Our motivation for using delayed feedback in the inverted pendulum model was to explain the time course of muscle activity following postural responses to perturbations. In humans, the first burst of muscle activity occurs 100 ms (40 ms in cats) after the initial onset of a ramp-and-hold perturbation to the support surface (Horak and Macpherson, 1996). This lag is due primarily to the transmission delays associated with neural conduction and processing. In cats, we observed that the initial burst of delayed muscle activity contained many similar features to the perturbation acceleration that occurred 40 ms prior [Figs. 2a, 2b]. Further observation showed that when perturbation acceleration was varied the characteristics of the delayed initial burst of muscle activity varied accordingly (Lockhart and Ting, 2007). This suggested that the initial burst of muscle activity is modulated as a function of body acceleration. This has been corroborated by results showing that perturbation acceleration is encoded by muscle spindle receptors that exist throughout the body (Schafer, 1967; Jansen and Matthews, 1962; Lennerstrand and Thoden, 1968).

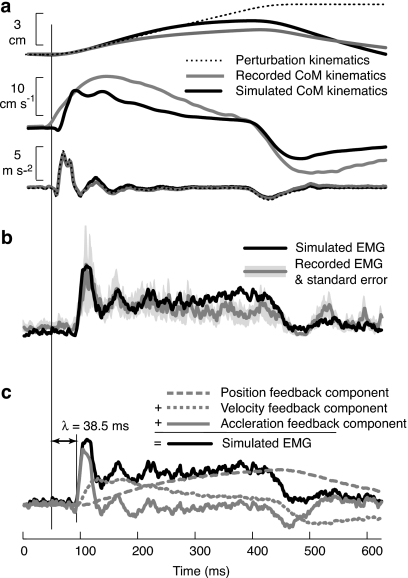
Figure 2.

Recorded and simulated CoM kinematics and muscle activation patterns in cats. (a) Recorded (gray lines) and simulated (black lines) CoM displacement, velocity, and acceleration. (b) Recorded (gray line) muscle activity in a calf muscle occurs about 40 ms after the onset of the perturbation. The initial burst of muscle activity resembles the temporal features of the CoM acceleration. The simulated (black line) muscle activity is derived by identifying the feedback gains and delay that minimize the squared error between recorded and simulated EMGs. (c) Decomposition of simulated muscle activity (black line) into components arising from CoM position feedback (gray dashed line), CoM velocity feedback (gray dotted line), and CoM acceleration feedback (gray solid line). Note that the initial burst is due primarily to delayed acceleration feedback, whereas later muscle activity is primarily from delayed velocity and position feedback.

Based on the observations of muscle activity and perturbation acceleration, we modified an existing model of joint kinetics for analyzing postural stability that used only delayed position and velocity feedback (Peterka, 2002) by adding a delayed acceleration term to the feedback loop (Fig. 3). The model was further modified by feeding the output of the feedback through a first-order muscle model to account for the dynamics of muscle force production. It is worth noting that the inclusion of delayed acceleration feedback in this model applies a force that is dependent on the acceleration at a prior time point rather than the current time point and furthermore is filtered through the low-pass muscle dynamics before affecting the model dynamics.

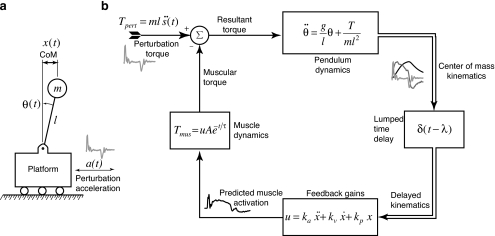
Figure 3.

Simple feedback model of postural control used to predict muscle activity during balance responses. (a) The mechanics of the CoM during the balance task is approximated as an inverted pendulum on a moving cart. Experimentally measured accelerations of the platform were applied to the cart so that realistic acceleration, velocity, and displacement trajectories of the platform were modeled. (b) The perturbation acceleration generates a disturbance torque at the base of the pendulum. Kinematics of the horizontal CoM were controlled with a delayed-feedback law that generated model muscle activation patterns, which were compared to those measured experimentally. The model muscle activation was passed through a first-order muscle model to generate a stabilizing torque about the representative joint.

This simple model gave a method for analyzing the interaction of muscle activity, torque produced by the muscle, and external perturbations by reproducing measured muscle activity and CoM kinematics recorded in both cats [Figs. 2b, 2c, Lockhart and Ting, 2007] and humans (Welch and Ting, 2008, 2009). The analysis of this model showed that the contribution of acceleration feedback greatly increased the amount of initial muscle activity compared to velocity and position feedback, especially when considering neural delays. However, the small total displacement of the perturbation and resulting body motion at the time of the initial muscle activity has led to debates over whether this muscle activity is due to feedforward or positive feedback mechanisms (e.g., Loram et al., 2005). This model could be further developed to reflect the true nonlinear elements of the components and to explore both feedforward and feedback mechanisms of postural control. These improvements may include the addition of greater physiological detail in skeletal structures for understanding changes in postural configuration, as well as the inclusion of stiffness and viscosity elements for examining changes in postural tone.

DISCUSSION

Now that the various strategies and regimes of postural control have been described, the challenge for future research lies in understanding the mechanisms and principles underlying neuromechanical tuning of and transitions between the diversity of postural behaviors. Contributions from theoretical, computational, physiological, and robotic studies can all be valuable in understanding transitions in postural behaviors as well as the modulation of neuromechanical elements to flexibly achieve the same goal of stabilizing the CoM. Here we describe some of our recent and ongoing studies that only begin to address such questions. We use a simple physical robotic model of postural control to demonstrate the modulation of postural stability tuning the interactions between feedforward and feedback mechanisms for postural stability, as well as the emergence of stepping postural responses. We demonstrate trial-by-trial modification of postural dynamics that capture the transition between stepping and feet-in-place postural responses. Musculoskeletal modeling studies are used to demonstrate the range of tuning and muscular redundancy in the modulation of feedforward postural stability. This redundancy is consistent with the individual variations in the low-dimensional manifolds to which trial-by-trial variations in muscle activation patterns are constrained. For each study we propose some possible avenues of study that could be enhanced using nonlinear dynamics analysis.

Tuning and variability of postural stability in a robotic model

To study the nonlinear interactions between postural configuration, postural tone, and delayed-feedback control, we developed a simple robotic model of medial-lateral postural control in response to perturbations (Scrivens et al., 2008). The robot consisted of two stiff legs connected by a horizontal segment and was controlled by a feedback controller based on our delayed-feedback model (Lockhart and Ting, 2007). The resistance due to the inertia and friction of the motors was canceled out so that the passive dynamics were compliant. We demonstrated that close comodulation of feedforward and feedback neuromechanical dynamics is required for maintaining balance in the face of physiological delays. When delays are present, an entire spectrum of overly compliant or overly stiff responses can be produced by varying the stance width or distance between the feet without modifying feedback gains (Scrivens et al., 2008). Therefore, the feedforward postural configuration and the delayed-feedback gains provide redundancy in the modulation of overall CoM dynamics. Due to the delays, we also found that it was impossible to keep the robot upright in the face of perturbations using the same set of feedback gains across multiple postural configurations. In fact, in the absence of postural tone, as modeled by a small amount of stiffness and viscosity in the joints, the feedback gains were very precisely constrained by stance width [Fig. 4a, lightest gray areas]. Any small variation in the delayed-feedback gain would cause the robot to fall over. However, adding postural tone that by itself was insufficient to stabilize the robot in response to the perturbation greatly increased the range of feedback gains that allowed the robot to remain standing [Fig. 4a]. Even using a lax stability criterion—the robot merely had to remain standing without returning to its original configuration—the range of feasible feedback gains for narrow and wide stance width did not overlap. These results are consistent with observations of increased postural tone and stance width in neurologically impaired individuals that may have degraded precision in neural feedback mechanisms.

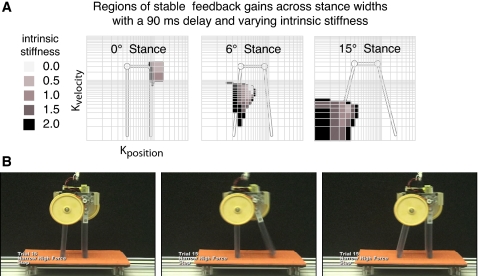
Figure 4.

A robotic model of postural control allows the neuromechanical tuning of postural stability to be studied. The robot is essentially a three-link chain that can be arranged to stand on a moving platform. When the support surface is perturbed in the horizontal plane, a delayed linear feedback loop (90 ms) generated torques at the “hip” joint based on the position and velocity of the joints. (a) A model of the robot feedback demonstrates that successful feet-in-place responses depend upon interactions between postural configuration and postural muscle tone. The set of feedback gains that allows the robot to remain standing without losing ground contact varies as the stance width changes. At a narrow stance width, high position and velocity feedback gains are necessary to maintain stability. As the stance width increases, the region of successful feedback gains shifts to lower nonoverlapping values. Postural muscle tone is simulated by adding intrinsic stiffness that simulates a spring at the joints. With no intrinsic stiffness, the tolerance to variation in feedback gains is low (lightest gray area). As intrinsic stiffness is increased, the regions of gain that allow the system to remain standing is increased as shading gets darker. Note that for the largest value of intrinsic stiffness, the system was still unable to recover balance without the delayed-feedback mechanism. (b) Emergent stepping can occur and be modulated by varying the feedback gain values, as well as the set point of the joint position. Here, the limbs generate a constant outward force while standing quietly, similar to that observed in humans in animals. Under this condition, the robot spontaneously steps upon perturbation, whereas if the outward force decreases, the step would not occur.

A surprising result of our physical robotic model was the emergence of step responses in response to perturbations [Fig. 4b] due to nonlinear ground-contact interactions. Although the robot was not explicitly programmed or designed to do so, it spontaneously takes steps when the neuromechanical elements are tuned properly. The emergence of steps can be manipulated by varying either feedforward or feedback neuromechanical elements contributing to postural stability. The addition of an outward force during quiet standing, similar to that found in healthy humans and animals, increases the likelihood of a step. This unexpected result highlights the advantages of physical modeling when studying computationally intractable or unknown interactions important to strategy transitions in movement. Intermittent and nonlinear ground-contact interactions have already been shown to be critical to self-stabilization in locomotion (Holmes et al., 2006; Seipel and Holmes, 2005). Physical models have also been useful for demonstrating gait transitions arising from interactions between both the neural control and environmental interactions in a multisegmented robotic model of the salamander (Ijspeert et al., 2007) and a legged model of insect walking (Altendorfer et al., 2001). The inclusion of nonidealized ground contacts, friction, or fluid dynamics may be required for the emergence of movement patterns (Seipel and Holmes, 2005), so physical models serve as a good validation of whether adequate complexity has been incorporated in a computational model to explain the emergent dynamics (Holmes et al., 2006).

Tuning and variability of postural stability in human subjects

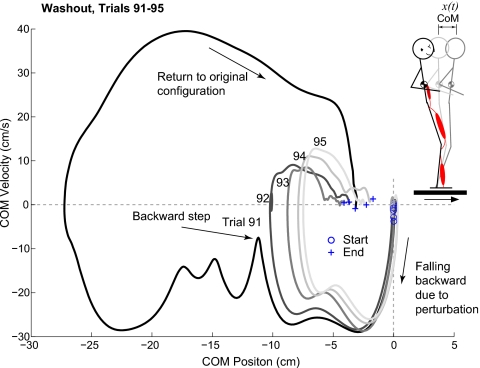
We have also begun to explicitly examine the goal-directed tuning of postural responses within and across postural strategies and the resulting changes in the postural dynamics. We found that subjects who were habituated to a series of identical perturbations of the support surface performed extremely poorly when the serially presented perturbations unexpectedly reversed direction. On the first trial after the change in perturbation direction, subjects invariably took a step to maintain balance. On the next one or two identical perturbations, subjects were able to rapidly adjust their postural stability and recovered their balance without stepping trials (Fig. 5). The tuning of postural stability can be visualized using a phase-plane representation of the CoM trajectories during this series of perturbations. The peak CoM displacement and velocity decreases during the presentation of five identical perturbations (Fig. 5), but it is not yet known whether feedforward or feedback mechanisms are tuned to result in global postural stability. Likely both are involved, but much further physiological studies of the interaction between postural configuration, postural muscle tone, and multiple delayed-feedback postural response strategies are required.

Figure 5.

Phase-plane CoM trajectories during postural responses to identical forward perturbations of the support surface. At the beginning of the experiment, subjects were able to maintain balance with feet in place to a 12 cm, 35 m/s forward perturbation. Subjects were then adapted to a series of backward perturbations, and without warning in trial 91, the original forward perturbation was presented. Subjects now had to take a step to maintain balance. The horizontal CoM dynamics also change dramatically with subsequent presentations of the same forward perturbation. In trial 91, the CoM falls backward during the perturbation. Although the CoM velocity begins to return toward zero, an abrupt change in the phase-plane trajectory indicates that a step was taken, which shifts the trajectory to a different orbit that eventually returns near the original state. Note, however, that subjects do not return to the original positions; this is common in postural control. On trial 92, the subject was able to maintain balance with the feet in place, although the reversal in the phase-plane trajectory suggests an aborted step response. On subsequent trials, the subjects are able to decrease both peak CoM displacement and velocity and return the CoM closer to the original position. These changes probably depend upon the modulation of both feedforward and feedback neuromechanical elements that modify postural stability dynamics.

At a more detailed level, we have also investigated the constraints on the variations in the spatial patterns of muscle activity as they are varied to produce postural stability. A number of recent investigations have demonstrated that neural control mechanisms tend to reduce the number of degrees of freedom used in sensing and controlling complex musculoskeletal systems (Flash and Hochner, 2005; Latash et al., 2007; Olshausen and Field, 2004; Ting, 2007; Ting and McKay, 2007). Specifically, the structure of the trial-by-trial variability in the coordination of muscles and joints during locomotion and balance control has been shown to be limited to low-dimensional manifolds (Ivanenko et al., 2007; Krishnamoorthy et al., 2004; Torres-Oviedo and Ting, 2007). We have shown in postural control that the spatial activation of muscles across a limb is arranged in motor modules that we call muscle synergies. Each muscle synergy defines an independent (but not orthogonal) pattern of muscle activation used preferentially by an individual. Muscle synergies can be considered to be basis vectors defining a preferred subspace within a larger set of possible solutions. Moreover, we have shown that each muscle synergy produces a force in the limb with a consistent global biomechanical function; this function is consistent across a range of postural configurations (Torres-Oviedo et al., 2006). In human postural control, we have also demonstrated muscle synergies that correspond to the ankle and hip postural response strategies. The trial-by-trial variations in patterns of muscle activity reflect variations in the relative contributions of each muscle synergy to a particular postural response. These results suggest that muscle synergies can map the low-dimensional task goals into a high-dimensional execution level required to simulate balance control in anchored, anatomical models of balance control (McKay et al., 2007; Ting, 2007).

Tuning and variability of postural stability in musculoskeletal models

Anatomically realistic musculoskeletal models provide a way to study the neuromechanical tuning and redundancy in postural control. Using a three-dimensional musculoskeletal model of the cat hind limb, we demonstrated that intrinsic musculoskeletal dynamics during standing can be tuned by modulating the pattern and amplitude of postural muscle tone. Consistent with the high intersubject variability in patterns of postural muscle tone observed across healthy animals (Torres-Oviedo et al., 2006), variations in postural muscle tone patterns produced physiologically realistic stability in the limb, allowing the perturbation doubling or halving time to be modulated over an order of magnitude (Bunderson et al., 2008). It is of note that the postural muscle tone patterns predicted by the prevalent algorithms used to resolve musculoskeletal redundancy in biomechanical models (Crowninshield and Brand, 1981; Harris and Wolpert, 1998) were highly unstable (Bunderson et al., unpublished results), suggesting that the patterns are not physiologically relevant. We also identified four classes of “eigenmodes” that describe coordinated patterns of movement across the hip, knee, and ankle joints. The eigenmodes associated with medial-lateral limb movements were always Lyapunov stable (Bunderson et al., 2008) suggesting that they require less neural feedback control. However, the eigenmodes associated with anterior-posterior limb movements could be either stable or unstable, consistent with the need for increased maneuverability during locomotion. Interestingly, this arrangement of stable and unstable manifolds may form a saddle node, which could have nonlinear neural control implications. Not only could those manifolds be tuned by altering the postural configuration and the postural tone, but using feedback response mechanisms to chaperone the system to various stable or unstable orbits (Ott et al., 1990) could greatly reduce the energy required to recover balance. Such principles from nonlinear dynamics have been previously demonstrated in biological systems (Garfinkel et al., 1992; Weiss et al., 1994) and may provide a useful framework for understanding postural stability.

Future research directions

Can the tools of nonlinear dynamics help us understand the rich variations in postural control that we observe? The challenges in understanding postural control are addressed by experimentalists and theorists alike and can be extended to encompass the limitations in our current knowledge and understanding about locomotion and motor behavior in general. However, we believe that postural control provides a general and perhaps more tractable paradigm for new explorations of the adaptability and reconfigurability of neuromechanical systems for biological movement control. New methodologies to understand how global stability is achieved by the tuning of various feedforward and delayed-feedback strategies that may be locally stable or unstable are required. It is our hope that nonlinear dynamical analysis applied to physiologically relevant models will help answer important questions in posture and movement: How does strategy switching emerge from the nonlinearities of the neuromechanical system? Does the nervous system tune feedforward and feedback planes in order to move the switching points? Can the differential contributions of feedforward and feedback neuromechanical elements to global postural stability be useful in understanding the effects of and compensations for various balance deficits? Ultimately, collaborations between physiologists, computational modelers, and theorists alike will be necessary to tackle these important questions.