Refining the weighted stochastic simulation algorithm

Abstract

The weighted stochastic simulation algorithm (wSSA) recently introduced by Kuwahara and Mura [J. Chem. Phys. 129, 165101 (2008)] is an innovative variation on the stochastic simulation algorithm (SSA). It enables one to estimate, with much less computational effort than was previously thought possible using a Monte Carlo simulation procedure, the probability that a specified event will occur in a chemically reacting system within a specified time when that probability is very small. This paper presents some procedural extensions to the wSSA that enhance its effectiveness in practical applications. The paper also attempts to clarify some theoretical issues connected with the wSSA, including its connection to first passage time theory and its relation to the SSA.

INTRODUCTION

The weighted stochastic simulation algorithm (wSSA) recently introduced by Kuwahara and Mura¹ is an innovative variation on the standard stochastic simulation algorithm (SSA) which enables one to efficiently estimate the probability that a specified event will occur in a chemically reacting system within a specified time when that probability is very small, and the event is therefore “rare.” The difficulty of doing this with the standard SSA has long been recognized as a limitation of the Monte Carlo simulation approach, so the wSSA is a welcomed development.

The implementation of the wSSA described in Ref. 1 does not, however, offer a convenient way to assess the accuracy of its probability estimate. In this paper we show how a simple refinement of the original wSSA procedure allows estimating a confidence interval for its estimate of the probability. This in turn, as we will also show, makes it possible to improve the efficiency of the wSSA by adjusting its parameters so as to reduce the estimated confidence interval. As yet, though, a fully automated procedure for optimizing the wSSA is not in hand.

We begin in Sec. 2 by giving a derivation and discussion of the wSSA that we think will help clarify why the procedure is correct. In Sec. 3 we present our proposed modifications to the original wSSA recipe of Ref. 1, and in Sec. 4 we show how these modifications allow easy estimation of the gain in computational efficiency over the SSA. In Sec. 5 we give some numerical examples that illustrate the benefits of our proposed procedural refinements. In Sec. 6 we discuss the relationship between the wSSA and the problem of estimating mean first passage times using as an example the problem of spontaneous transitions between the stable states of a bistable system. In Sec. 7 we summarize our findings and make an observation on the relationship between the wSSA and the SSA.

THEORETICAL UNDERPINNINGS OF THE wSSA

We consider a well-stirred chemical system whose molecular population state at the current time t is x. The next firing of one of the system’s M reaction channels R₁,…,R_M will carry the system from state x to one of the M statesx+ν_j (j=1,…,M), where ν_j is (by definition) the state change caused by the firing of one R_j reaction. The fundamental premise of stochastic chemical kinetics, which underlies both the chemical master equation and the SSA, is that the probability that an R_j event will occur in the next infinitesimal time interval dt is a_j(x)dt, where a_j is called the propensity function of reaction R_j. It follows from this premise that (a) the probability that the system will jump away from state x between times t+τ and t+τ+dτ is a₀(x)e^−a₀(x)τdτ, where $a_0\left(\mathbf{x}\right)\equiv {\sum }_{i=1}^M{a}_i\left(\mathbf{x}\right)$, and (b) the probability that the system, upon jumping away from state x, will jump to state x+ν_j, is a_j(x)∕a₀(x). Applying the multiplication law of probability theory, we conclude that the probability that the next reaction will carry the system’s state tox+ν_j between times t+τ and t+τ+dτ is

$$\text{Prob}\left\{\mathbf{x}\to \mathbf{x}+{\mathbf{\nu }}_j\text{in}\left(t+\tau ,t+\tau +d\tau \right)\right\}=a_0\left(\mathbf{x}\right)e^{-a_0\left(\mathbf{x}\right)\tau }d\tau \times \frac{a_j\left(\mathbf{x}\right)}{a_0\left(\mathbf{x}\right)}.$$ (1)

In the usual “direct method” implementation of the SSA, the time τ to the next reaction event is chosen by sampling the exponential random variable with mean 1∕a₀(x), in consonance with the first factor in Eq. 1, and the index j of the next reaction is chosen with probability a_j(x)∕a₀(x), in consonance with the second factor in Eq. 1. But now let us suppose, with Kuwahara and Mura,¹ that we modify the direct method SSA procedure so that, while it continues to choose the time τ to the next jump in the same way, it chooses the index j, which determines the destination x+ν_j of that jump, with probability b_j(x)∕b₀(x), where {b₁,…,b_M} is a possibly different set of functions from {a₁,…,a_M}, and $b_0\left(\mathbf{x}\right)\equiv {\sum }_{i=1}^M{b}_i\left(\mathbf{x}\right)$. If we made that modification, then the probability on the left hand side of Eq. 1 would be a₀(x)e^−a₀(x)τdτ×(b_j(x)∕b₀(x)). But we observe that this “incorrect” value can be converted to the “correct” value, on the right hand side of Eq. 1, simply by multiplying by the factor

$$w_j\left(\mathbf{x}\right)=\frac{a_j\left(\mathbf{x}\right)∕a_0\left(\mathbf{x}\right)}{b_j\left(\mathbf{x}\right)∕b_0\left(\mathbf{x}\right)}.$$ (2)

So in some sense, we can say that an x→x+ν_j jump generated using this modified procedure, and accorded a statistical weight of w_j(x) in Eq. 2, is “equivalent” to an x→x+ν_j jump generated using the standard SSA.

This statistical weighting of a single-reaction jump can be extended to an entire trajectory of the system’s state by reasoning as follows: A state trajectory is composed of a succession of single-reaction jumps. Each jump has a probability (1) that depends on the jump’s starting state but not on the history of the trajectory that leads up to that starting state. Therefore, the probability of the trajectory as a whole is just the product of the probabilities of all the individual jumps (1) that make up the trajectory. Since in the modified SSA scheme the probability of each individual jump requires a correction factor of the form 2, then the correction factor for the entire trajectory—i.e., the statistical weight w of the trajectory–will be the product w=w_j1w_j2w_j3⋯, where w_jk is the statistical weight 2 for the kth jump in that trajectory.

One situation where this statistical weighting logic can be applied is in the Monte Carlo averaging method of estimating the value of

$$p\left({\mathbf{x}}_0,\mathcal{E};t\right)\equiv \begin{array}{c}\\ \\ \\ \\ \text{the}\text{probability}\text{that}\text{the}\text{system}\text{starting}\hfill \\ \text{at}\text{time}0\text{in}\text{state}{\mathbf{x}}_0\text{will}\text{first}\text{reach}\hfill \\ \text{any}\text{state}\text{in}\text{the}\text{set}\mathcal{E}\text{at}\text{some}\text{time}\le t.\hfill \end{array}$$ (3)

[Note that p(x₀,E;t) is not the probability that the system will be in the set E at time t.] An obvious Monte Carlo way to estimate this probability would be to make a very large number n of regular SSA runs, with each run starting at time 0 in state x₀ and terminating either when some state x^′∊E is first reached or when the system time reaches t. If m_n is the number of those n runs that terminate for the first reason, then the probability p(x₀,E;t) could be estimated as the fraction m_n∕n, and this estimate would become exact in the limit n→∞. But m_n here could also be defined as the sum of the “weights” of the runs, where each run is given a weight of 1 if it ends because some state in the set E is reached before time t and a weight of 0 otherwise. This way of defining m_n is useful because it allows us to score runs in the modified SSA scheme, with each run that reaches some state x^′∊E before time t then being scored with its trajectory weightw as defined above. Kuwahara and Mura¹ recognized that this tactic could be used to advantage in the case p(x₀,E;t)⪡1, where using the standard SSA will inevitably require an impractically large number of trajectories to obtain an accurate estimate of p(x₀,E;t). As we shall elaborate in the next two sections, by using this wSSA method with the b_j functions carefully chosen so that they increase the likelihood of the system reaching E, it is often possible to obtain a more accurate estimate of p(x₀,E;t) with far fewer runs.

The wSSA procedure given in Ref. 1 for computing p(x₀,E;T) in this way goes as follows:

1°	mn←0.
2°	fork=1 to n, do
3°	s←0, x←x0, w←1.
4°	evaluate all ai(x) and bi(x); calculate a0(x) and  b0(x).
5°	whiles≤t, do
6°	ifx∊E, then
7°	mn←mn+w.
8°	break out of the while loop.
9°	end if
10°	generate two unit-interval uniform random   numbers r1 and r2.
11°	$\tau \leftarrow a_0^{-1}\left(\mathbf{x}\right)\text{ln}\left({1∕r}_1\right)$.
12°	j←smallest integer satisfying   ${\sum }_{i=1}^j{b}_i\left(\mathbf{x}\right)\ge r_2{b}_0\left(\mathbf{x}\right)$.
13°	w←w×(aj(x)∕bj(x))×(b0(x)∕a0(x)).
14°	s←s+τ, x←x+νj.
15°	update ai(x) and bi(x); recalculate a0(x) and   b0(x).
16°	end while
17°	end for
18°	report p(x0,E;t)=mn∕n.

Assumed given for the above procedure are the reaction propensity functions a_j and the associated state-change vectors ν_j, the target set of states E and the time t by which the system should reach that set, the total number of runs n that will be made to obtain the estimate, and the step-biasing functions b_j (which Kuwahara and Mura called predilection functions). The variable m_n in the above procedure is the sum of the statistical weights w of the n run trajectories. The value of w for each trajectory is constructed in step 13°, as the product of the weights w_j in Eq. 2 of all the reaction jumps making up that trajectory; however, if a trajectory ends because in the given time t the set E has not been reached, the weight of that trajectory is summarily set to zero. Note that the use of a₀ instead of b₀ to compute the jump time τ in step 11° follows from the analysis leading from Eqs. 1, 2: the wSSA introduces an artificial bias in choosing j, but it always chooses τ “properly” according to the true propensity functions. This strategy of using the correct τ is vital for allotting to each trajectory the proper amount of time t to reach the target set of states E.

If the b_j functions are chosen to be the same as the a_j functions, then the above procedure evidently reduces to the standard SSA. Thus, the key to making the wSSA more efficient than the SSA is to choose the b_j functions “appropriately.” It is seen from step 13°, though, that b_j must not have a harder zero at any accessible state point than a_j, for otherwise the weight at that state point would be infinite. To keep that from happening, Kuwahara and Mura proposed the simple procedure of setting

$$b_j\left(\mathbf{x}\right)={\gamma }_j{a}_j\left(\mathbf{x}\right)\left(j=1,\dots ,M\right),$$ (4)

where each proportionality constant γ_j>0, which we shall call the importance sampling factor for reaction R_j, is chosen to be ≥1 if the occurrence of reaction R_jincreases the chances of the system reaching the set E and ≤1 otherwise. This way of choosing the b functions seems quite reasonable, although a minor subtlety not mentioned in Ref. 1 is that, since the wSSA works by altering the relative sizes of the propensity functions for state selection, only M−1 of the γ_j matter; in particular, in a system with only one reaction, weighting that reaction by any factor γ will produce a single step weight 2 that is always unity, and the wSSA therefore reduces to the SSA. But of course, single-reaction systems are not very interesting in this context. A more important question in connection with Eq. 4 is: Are there optimal values for the γ_j? And if so, how might we identify them?

THE VARIANCE AND ITS BENEFITS

The statistical weighting strategy described in connection with Eq. 4 evidently has the effect of increasing the firing rates of those “important reactions” that move the system toward the target states E, thus producing more “important trajectories” that reach that target. Equation 2 shows that boosting the likelihoods of those successful trajectories in this way will cause them to have statistical weights w<1. As was noted and discussed at some length in Ref. 1, this procedure is an example of a general Monte Carlo technique called importance sampling. However, the description of the importance sampling strategy given in Ref. 1 is incomplete because it makes no mention of something called the “sample variance.”

In the Appendix0, we give a brief review of the general theory underlying Monte Carlo averaging and the allied technique of importance sampling which explains the vital connecting role played by the sample variance. The bottom line for the wSSA procedure described in Sec. 2 is this: The computation of the sample meanm_n∕n of the weights of the n wSSA trajectories should be accompanied by a computation of the sample variance of those trajectory weights. Doing that not only provides us with a quantitative estimate of the uncertainty in the approximation p(x₀,E;t)≈m_n∕n but also helps us find the values of the parameters γ_j in Eq. 4 that minimize that uncertainty. More specifically (see the Appendix0 for details), in addition to computing the sample first moment (or sample mean) of the weights of the wSSA-generated trajectories,

$$\frac{m_n}{n}\equiv \frac{m_n^{\left(1\right)}}{n}\equiv \frac{1}{n}\sum _{k=1}^n{w}_k,$$ (5)

where w_k is the statistical weight of run k [equal to the product of the weights 2 of each reaction that occurs in run k if that run reaches E before t and zero otherwise], we should also compute the sample second moment of those weights,

$$\frac{m_n^{\left(2\right)}}{n}\equiv \frac{1}{n}\sum _{k=1}^n{w}_k^2.$$ (6)

The sample variance of the weights is then given by the difference between the sample second moment and the square of the sample first moment:²

$${\sigma }^2=\left(m_n^{\left(2\right)}∕n\right)-{\left(m_n^{\left(1\right)}∕n\right)}^2.$$ (7)

The final estimate $p\left({\mathbf{x}}_0,\mathcal{E};t\right)\approx m_n^{\left(1\right)}∕n$ can then be assigned a “one-standard-deviation normal confidence interval” of

$$\text{uncertainty}=\pm \frac{\sigma }{\sqrt{n}}.$$ (8)

This means that the probability that the true value of p(x₀,E;t) will lie within $\sigma ∕\sqrt{n}$ of the estimate $m_n^{\left(1\right)}∕n$ is 68%. Doubling the uncertainty interval 8 raises the confidence level to 95%, and tripling it gives us a confidence level of 99.7%. Furthermore, by performing multiple runs that vary the b_j functions, which in practice means systematically varying the parameters γ_j in Eq. 4, we can, at least in principle, find the values of γ_j that give the smallest σ², and hence according to Eq. 8 the most accurate estimate of p(x₀,E;t) for a given value of n.

All of the foregoing is premised on the assumption that n has been taken “sufficiently large.” That is because there is some “bootstrapping logic” used in the classical Monte Carlo averaging method (independently of importance sampling): The values for $m_n^{\left(1\right)}$ and $m_n^{\left(2\right)}$ computed in Eqs. 5, 6 will vary from one set of n runs to the next, so the computed value of σ² in Eqs. 7, 8 will also vary. Therefore, as discussed more fully in the Appendix0 at Eqs. A9, A10, the computed uncertainty in the estimate of the mean is itself only an estimate. And, like the estimate of the mean, the estimate of the uncertainty will be reasonably accurate only if a sufficiently large number n of runs have been used. In practice, this means that only when several repetitions of an n-run calculation are found to produce approximately the same estimates for $m_n^{\left(1\right)}$ and $m_n^{\left(2\right)}$ can we be sure that n has been taken large enough to draw reliable conclusions.

When the original wSSA recipe in Sec. 2 is modified to include the changes described above, we obtain the recipe given below: 

1°	$m_n^{\left(1\right)}\leftarrow 0,m_n^{\left(2\right)}\leftarrow 0$
2°	fork=1 to n, do
3°	s←0, x←x0, w←1
4°	evaluate all ai(x) and bi(x); calculate a0(x) and  b0(x).
5°	whiles≤t, do
6°	ifx∊E, then
7°	$m_n^{\left(1\right)}\leftarrow m_n^{\left(1\right)}+w$, $m_n^{\left(2\right)}\leftarrow m_n^{\left(2\right)}+w^2$.
8°	break out of the while loop.
9°	end if
10°	generate two unit-interval uniform random   numbers r1 and r2.
11°	$\tau \leftarrow a_0^{-1}\left(\mathbf{x}\right)\text{ln}\left(1∕r_1\right)$
12°	j←smallest integer satisfying   ${\sum }_{i=1}^j{b}_i\left(\mathbf{x}\right)\ge r_2{b}_0\left(\mathbf{x}\right)$.
13°	w←w×(aj(x)∕bj(x))×(b0(x)∕a0(x)).
14°	s←s+τ, x←x+νj.
15°	update ai(x) and bi(x); recalculate a0(x) and   b0(x).
16°	end while
17°	end for
18°	${\sigma }^2=\left(m_n^{\left(2\right)}∕n\right)-{\left(m_n^{\left(1\right)}∕n\right)}^2$
19°	repeat from 1° using different b functions to minimize σ2.
20°	estimate $p\left({\mathbf{x}}_0,\mathcal{E};t\right)=m_n^{\left(1\right)}∕n$, with a 68% uncertainty of $\pm \sigma ∕\sqrt{n}$.

Steps 1°–17° are identical to those in the earlier procedure in Sec. 2, except for the additional computations involving the new variable $m_n^{\left(2\right)}$ in steps 1° and 7°. The new step 18° computes the variance. Step 19° tunes the importance sampling parameters γ_j in Eq. 4 to minimize that variance. And step 20° uses the optimal set of γ_j values thus found to compute the best estimate of p(x₀,E;t), along with its associated confidence interval. In practice, step 19° usually has to be done manually, external to the computer program, since the search over γ_j space requires some intuitive guessing; this is typical in most applications of importance sampling.³ An overall check on the validity of the computation can be made by repeating it a few times with different random number seeds to verify that the estimates obtained for p(x₀,E;t) and its confidence interval are reproducible and consistent. If they are not, then n has probably not been chosen large enough.

GAIN IN COMPUTATIONAL EFFICIENCY

The problem with using unweighted SSA trajectories to estimate p(x₀,E;t) when that probability is ⪡1 is that we are then trying to estimate the average of a set of numbers (the trajectory weights) which are all either 0 or 1 when that average is much closer to 0 than to 1. The sporadic occurrence of a few 1’s among a multitude of 0’s makes this estimate subject to very large statistical fluctuations for any reasonable number of trajectories n. How does importance sampling overcome this problem? If the reaction biasing is done properly, most of the “successful” trajectories that reach the target set E within the allotted time t will have weights that are much less than 1, and hence closer to the average. Most of the “unsuccessful” trajectories will rack up weights in step 13° that are much greater than 1, but when the simulated time reaches the limit t without the set E having been reached, those large weights are summarily reset to zero (they never get accumulated in $m_n^{\left(1\right)}$ and $m_n^{\left(2\right)}$ in step 7°). The result is that the bulk of the contribution to the sample average comes from weights that are much closer to the average than are the unit weights of the successful SSA trajectories. This produces a smaller scatter in the weights of wSSA trajectories about their average, as measured by their standard deviation σ, and hence a more accurate estimate of that average. Note, however, that if the event in question is not rare, i.e., if p(x₀,E;t) is not ⪡1, then the unit trajectory weights of the SSA do not pose a statistical problem. In that case there is little to be gained by importance sampling, and the ordinary SSA should be adequate. Note also that the rarity of the event is always connected to the size of t. Since p(x₀,E;t)→1 as t→∞, it is always possible to convert a rare event into a likely event simply by taking t sufficiently large.

To better understand how variance reduction through importance sampling helps when p(x₀,E;t)⪡1, let us consider what happens when no importance sampling is done, i.e., when b_j=a_j for all j and every successful trajectory gets assigned a weight w=1. Letting m_n denote the number of successful runs obtained out of n total, it follows from definitions 5, 6 that

$$m_n^{\left(1\right)}=m_n\times 1=m_n,m_n^{\left(2\right)}=m_n\times 1^2=m_n.$$

Equation 7 then gives for the sample variance

$${\sigma }^2=\left(m_n∕n\right)-{\left(m_n∕n\right)}^2=\left(m_n∕n\right)\left(1-\left(m_n∕n\right)\right).$$

The uncertainty 8 is therefore⁴

$$\text{uncertainty}=\pm \sqrt{\frac{\left(m_n∕n\right)\left(1-\left(m_n∕n\right)\right)}{n}},$$ (9a)

and this implies a relative uncertainty of

$$\text{relative}\text{uncertainty}\equiv \frac{\text{uncertainty}}{m_n∕n}=\pm \sqrt{\frac{1-\left(m_n∕n\right)}{m_n}}.$$ (9b)

When p(x₀,E;t)≈m_n∕n⪡1, Eq. 9b simplifies to

$$\text{relative}\text{uncertainty}\approx \pm \sqrt{\frac{1}{m_n}}\left(\text{if}{m}_n∕n⪡1\right).$$ (10)

This shows that if only one successful run is encountered in the n SSA runs, then the relative uncertainty in the estimate of p(x₀,E;t) will be 100%, and if four successful runs are encountered, the relative uncertainty will be 50%. To reduce the relative uncertainty to a respectably accurate 1% would, according to Eq. 10, require 10 000 successful SSA runs, and that would be practically impossible for a truly rare event.

These considerations allow us to estimate the number of unweighted SSA runs, n^SSA, that would be needed to yield an estimate of p(x₀,E;t) that has the same relative accuracy as the estimate obtained in a wSSA calculation. Thus, suppose a wSSA calculation with n^wSSA runs has produced the estimate $\widehat{p}$$\left(=m_n^{\left(1\right)}∕n^{\text{wSSA}}\right)$ with a one-standard-deviation uncertainty u^wSSA$\left(={\sigma }^{\text{wSSA}}∕\sqrt{n^{\text{wSSA}}}\right)$. The relative uncertainty is $u^{\text{wSSA}}∕\widehat{p}$. According to Eq. 10, to get that same relative uncertainty using the unweighted SSA, we would need m^SSA successful SSA runs such that

$$\sqrt{\frac{1}{m^{\text{SSA}}}}=\frac{u^{\text{wSSA}}}{\widehat{p}}.$$

But to get m^SSA successful runs with the SSA, we would need to make n^SSA total runs, where

$$m^{\text{SSA}}∕n^{\text{SSA}}=\widehat{p}.$$

Solving this last equation for m^SSA, substituting the result into the preceding equation, and then solving it for n^SSA, we obtain

$$n^{\text{SSA}}=\frac{\widehat{p}}{{\left(u^{\text{wSSA}}\right)}^2}\left(\text{if}\widehat{p}⪡1\right).$$ (11)

A rough measure of the gain in computational efficiency of the wSSA over the SSA is provided by the ratio of n^SSA to n^wSSA:

$$g\equiv \frac{n^{\text{SSA}}}{n^{\text{wSSA}}}=\frac{\widehat{p}}{n^{\text{wSSA}}{\left(u^{\text{wSSA}}\right)}^2}.$$

Since $u^{\text{wSSA}}={\sigma }^{\text{wSSA}}∕\sqrt{n^{\text{wSSA}}}$, this simplifies to

$$g=\frac{\widehat{p}}{{\left({\sigma }^{\text{wSSA}}\right)}^2}\left(\text{if}\widehat{p}⪡1\right).$$ (12)

The result 12 shows why the wSSA’s strategy of minimizing the variance when p(x₀,E;t)⪡1 is the key to obtaining a large gain in computational efficiency over the unweighted SSA: If we can contrive to halve the variance, we will double the efficiency.

NUMERICAL EXAMPLES

Reference ¹ illustrated the wSSA by applying it to two simple systems. In this section we repeat those applications in order to illustrate the benefits of the refinements introduced in Sec. 3.

The first example in Ref. 1 concerns the simple system

$$S_1\stackrel{k_1}{\to }{S}_1+S_2,S_2\stackrel{k_2}{\to }\varnothing ,$$ (13)

with k₁=1 and k₂=0.025. Since the S₁ population x₁ remains constant in these reactions, Eq. 13 is mathematically the same as the reaction set $\varnothing \underset{k_2}{\overset{k_1{x}_1}{\rightleftarrows }}{S}_2$. This reaction set has been well studied,⁵ and the steady-state (equilibrium) population of species S₂ is known to be the Poisson random variable with mean and variance k₁x₁∕k₂. Reference ¹ takes x₁=1, so at equilibrium the S₂ population in Eq. 13 will be fluctuating about a mean of k₁∕k₂=40 with a standard deviation of $\sqrt{40}=6.3$. For this system, Ref. 1 sought to estimate, for several values of ε₂ between 65 and 80, the probability p(40,ε₂;100) that with x₁=1, the S₂ population, starting at the value 40, will reach the value ε₂ before time t=100. Since the S₂ populations 65 and 80 are, respectively, about four and six standard deviations above the equilibrium value 40, then the biasing strategy for the wSSA must be to encourage reaction R₁, which increases the S₂ population, and∕or discourage reaction R₂, which decreases the S₂ population. Of the several ways in which that might be done, Ref. 1 adopted scheme 4, taking γ₁=α and γ₂=1∕α with α=1.2.

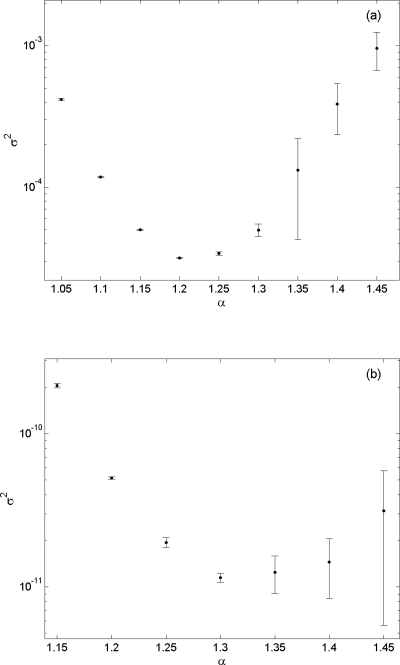
Addressing first the case ε₂=65, we show in Fig. 1a a plot of σ² versus α for a range of α values near 1.2. In this plot, the center dot on each vertical bar is the average of the σ² results found in four runs of the wSSA procedure in Sec. 3 (or more specifically, steps 1°–18° of that procedure), with each run containing n=10⁶ trajectories. The span of each vertical bar indicates the one-standard-deviation envelope of the four σ² values. It is seen from this plot that the value of α that minimizes σ² for ε₂=65 is approximately 1.20, which is just the value used in Ref. 1. But Fig. 1a assures us that this value in fact gives the optimal importance sampling, at least for this value of ε₂ and this way of parametrizing γ₁ and γ₂. Using this optimal α value in a longer run of the wSSA, now taking n=10⁷ as was done in Ref. 1, we obtained

$$p\left(40,65;100\right)=2.307\times {10}^{-3}\pm 0.003\times {10}^{-3}\left(95\%\text{confidence}\right).$$ (14)

In this final result, we have been conservative and given the two-standard-deviation uncertainty interval. To estimate the gain in efficiency provided by the wSSA over the SSA, we substitute $\widehat{p}=2.3\times {10}^{-3}$ and u^wSSA=0.0015×10⁻³ into Eq. 11, and we get n^SSA=1.025×10⁹. Since result 14 was obtained with n^wSSA=10⁷ wSSA runs, then the efficiency gain here over the SSA is g=103, i.e., the computer running time to get result 14 using the unweighted SSA would be about a hundred times longer.

Figure 1.

(a) A plot of σ² vs α obtained in wSSA runs of reactions 13 that were designed to determine p(40,ε₂;100) for ε₂=65 using the biasing scheme γ₁=α and γ₂=1∕α. Each vertical bar shows the estimated mean and one standard deviation of σ² at that α value as found in four n=10⁶ runs of the modified wSSA procedure in Sec. 3. The optimal α value, defined as that which produces the smallest σ², is seen to be 1.20. (b) A similar plot for ε₂=80, except that here each σ² estimate was computed from four n=10⁷ runs. The optimal α value here is evidently 1.30, which gives a stronger bias than was optimal for the case in (a).

For the case ε₂=80, the plot of σ² versus α is shown in Fig. 1b. In this case, obtaining a reasonably accurate estimate of σ² at each α value required using four runs with n=10⁷. But even then, as we move farther above α=1.3, it evidently becomes very difficult to estimate σ² accurately in a run with only n=10⁷ trajectories, as is indicated by the vertical bars showing the scatter (standard deviation) observed in four such runs. But each dot represents the combined estimate of σ² for n=4×10⁷ runs, and they allow us to see that the minimum σ² is obtained at about α=1.3. That value, being further from 1 than the α value 1.20 which Ref. 1 used for ε₂=80 as well as for ε₂=65, represents a stronger bias than α=1.2, which is reasonable. The four runs for α=1.3 were finally combined into one run, an operation made easy by outputting at the end of each run the values of the cumulative sums $m_n^{\left(1\right)}$ and $m_n^{\left(2\right)}$: The four sums for $m_n^{\left(1\right)}$ were added together to get $m_{4n}^{\left(1\right)}$, and the four sums for $m_n^{\left(2\right)}$ similarly gave $m_{4n}^{\left(2\right)}$. This yielded the n=4×10⁻⁷ estimate

$$p\left(40,80;100\right)=3.014\times {10}^{-7}\pm 0.011\times {10}^{-7}\left(95\%\text{confidence}\right),$$ (15)

where again we have given a conservative two-standard-deviation uncertainty interval. To estimate the gain in efficiency provided by the wSSA over the SSA, we substitute $\widehat{p}=3\times {10}^{-7}$ and u^wSSA=0.0055×10⁻⁷ into Eq. 11, and we find n^SSA=9.96×10¹¹. Since result 13 was obtained with n^wSSA=4×10⁷ wSSA runs, the efficiency gain over the SSA is g=2.5×10⁴, which is truly substantial.

The second system considered in Ref. 1 is the six-reaction set

$$S_1+S_2\underset{k_2}{\overset{k_1}{\rightleftarrows }}{S}_3\stackrel{k_3}{\to }{S}_1+S_5,$$ (16)

$$S_4+S_5\underset{k_5}{\overset{k_4}{\rightleftarrows }}{S}_6\stackrel{k_6}{\to }{S}_4+S_2,$$

with the rate constants k₁=k₂=k₄=k₅=1 and k₃=k₆=0.1. These reactions are essentially a forward-reverse pair of enzyme-substrate reactions, with the first three reactions describing the S₁-catalyzed conversion of S₂ to S₅ and the last three reactions describing the S₄-catalyzed conversion of S₅ back to S₂. As was noted in Ref. 1, for the initial condition x₀=(1,50,0,1,50,0), each of the S₂ and S₅ populations tends to equilibrate about its initial value 50. Reference ¹ sought to estimate, for several values of ε₅ between 40 and 25, the probability p(x₀,ε₅;100) that the S₅ population, initially at 50 molecules, will reach the value ε₅ before time t=100. Since those target S₅ populations are smaller than the x₀ value 50, the wSSA biasing strategy should suppress the creation of S₅ molecules. One way to do that would be to discourage reaction R₃, which creates S₅ molecules, and encourage reaction R₆, which by creating S₄ molecules encourages the consumption of S₅ molecules via reaction R₄. The specific procedure adopted in Ref. 1 for doing that was to implement biasing scheme 4 with all the biasing parameters γ_j set to 1, except γ₃=α and γ₆=1∕α with α=0.5.

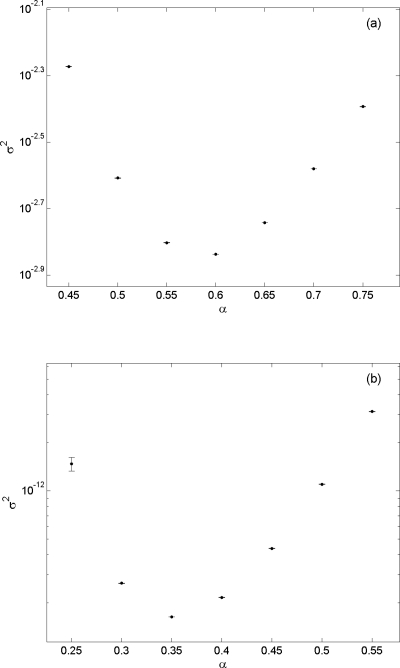
For the case ε₅=40, we first made some preliminary wSSA runs in order to estimate σ² for several values of α in the neighborhood of 0.5. The results are shown in Fig. 2a. Here the center dot on each vertical bar shows the average of the σ² values found in four wSSA runs at that α, with each run containing n=10⁵ trajectories. As before, the span of each vertical bar indicates the associated one-standard-deviation envelope. It is seen from this plot that the value of α that minimizes σ² for ε₅=40 is approximately 0.60, which is less biased (closer to 1) than the value 0.5 used in Ref. 1. Taking 0.60 as the optimal α value, we then made a longer n=10⁷ run and got

$$p\left({\mathbf{x}}_0,40;100\right)=0.04221\pm 0.00002\left(95\%\text{confidence}\right).$$ (17)

For this value of $\widehat{p}$ and a one-standard uncertainty of u^wSSA=0.000 01, formula 11 yields n^SSA=4.22×10⁸. This implies a gain in computational efficiency over the unweighted SSA of g=42.

Figure 2.

(a) A plot of σ² vs α obtained in wSSA runs of reactions 16 that were designed to determine p(x₀,ε₅;100) for ε₅=40 using the biasing scheme γ₃=α and γ₆=1∕α. Each vertical bar shows the estimated mean and one standard deviation of σ² at that α value as found in four n=10⁵ runs of the modified wSSA procedure in Sec. 3. The optimal α value here is seen to be 0.60. (b) A similar plot for ε₅=25. The optimal α value now is 0.35, which gives a stronger bias than was optimal for the case in (a).

For the case ε₅=25, the σ² versus α plot is shown in Fig. 2b. As in Fig. 2a, each vertical bar shows the result of four wSSA runs with n=10⁵. This plot shows that the optimal α value is now 0.35, which is more biased (i.e., further from 1) than the optimal α value 0.60 for the case ε₅=40 and also more biased than the value 0.50 that was used in Ref. 1. A final longer wSSA run with α=0.35 and n=10⁷ yielded

$$p\left({\mathbf{x}}_0,25;100\right)=1.747\times {10}^{-7}\pm 0.003\times {10}^{-7}\left(95\%\text{confidence}\right).$$ (18)

For this value of $\widehat{p}$ and a one-standard uncertainty of u^wSSA=0.0015×10⁻⁷, formula 11 yields n^SSA=7.76×10¹², which implies a gain in computational efficiency for the wSSA of g=7.76×10⁵.

All the results obtained here are consistent with the values reported in Ref. 1. The added value here is the confidence intervals, which were absent in Ref. 1, and also the assurance that these results were obtained in a computationally efficient way. We should note that the results obtained here are probably more accurate than would be required in practice, e.g., if we were willing to give up one decimal of accuracy in result 18, then the value of n used to get that result could be reduced from 10⁷ to 10⁵, which would translate into a 100-fold reduction in the wSSA’s computing time.

FIRST PASSAGE TIME THEORY: STABLE STATE TRANSITIONS

Rare events in a stochastic context have traditionally been studied in terms of mean first passage times. The time T(x₀,E) required for the system, starting in state x₀, to first reach some state in the set E is a random variable, and its mean ⟨T(x₀,E)⟩ is often of interest. Since the cumulative distribution function F(t;x₀,E) of T(x₀,E) is, by definition, the probability that T(x₀,E) will be less than or equal to t, it follows from Eq. 3 that

$$F(t;{\mathbf{x}}_0,\mathcal{E})=p({\mathbf{x}}_0,\mathcal{E};t).$$ (19)

Therefore, since the derivative of F(t;x₀,E) with respect to t is the probability density function of T(x₀,E), the mean of the first passage time T(x₀,E) is given by

$$⟨T({\mathbf{x}}_0,\mathcal{E})⟩={\int }_0^{\infty }t\left(\frac{dp({\mathbf{x}}_0,\mathcal{E};t)}{dt}\right)dt={\int }_0^{\infty }\left(1-p({\mathbf{x}}_0,\mathcal{E};t)\right)dt,$$ (20)

where the last step follows from an integration by parts.

In light of this close connection between the mean first passage time ⟨T(x₀,E)⟩ and the probability p(x₀,E;t) that the wSSA aims to estimate, it might be thought that the wSSA also provides an efficient way to estimate ⟨T(x₀,E)⟩. But that turns out not to be so. The reason is that, in order to compute ⟨T(x₀,E)⟩ from Eq. 20, we must compute p(x₀,E;t) for times t that are on the order of ⟨T(x₀,E)⟩. But for a truly rare event that time will be very large, and since the wSSA does not shorten the elapsed time t, it will not be feasible to make runs with the wSSA for that long a time.

From a practical point of view though, it seems likely that a knowledge of the very small value of p(x₀,E;t) for reasonable values of t might be just as useful as a knowledge of the very large value of ⟨T(x₀,E)⟩. In other words, in practice it may be just as helpful to know how likely it is for the rare event x₀→E to happen within a time frame t of practical interest as to know how long a time on average we would have to wait in order to see the event occur. To the extent that that is true, the inability of the wSSA to accurately estimate ⟨T(x₀,E)⟩ will not be a practical drawback.

An illustration of these points is provided by the phenomenon of spontaneous transitions between the stable states of a bistable system. A well known simple model of a bistable system is the Schlögl reaction set

$$B_1+2S\underset{c_2}{\overset{c_1}{\rightleftarrows }}3S,$$ (21)

$$B_2\underset{c_4}{\overset{c_3}{\rightleftarrows }}S,$$

where species B₁ and B₂ are assumed to be buffered so that their molecular populations N₁ and N₂ remain constant. For the parameter values

$$c_1=3\times {10}^{-7},c_2={10}^{-4},c_3={10}^{-3},c_4=3.5,$$ (22)

$$N_1={10}^5,N_2=2\times {10}^5,$$

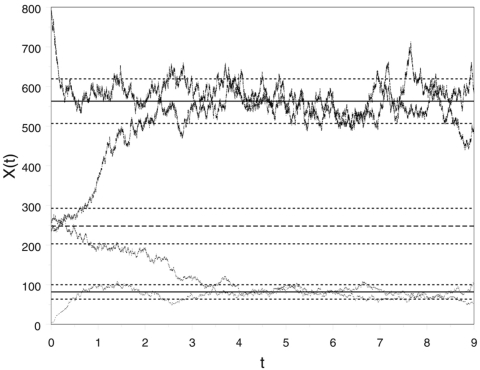
the molecular population X of species S can be shown⁶ to have two stable states, x₁=82 and x₂=563. Figure 3 shows four exact SSA simulations for these parameter values with four different initial states. In each of these simulation runs, X has been plotted after every five reaction events. The solid horizontal lines locate the stable states x₁ and x₂, and the adjacent dotted lines show the theoretically predicted “widths” of those stable states. The other three horizontal lines in the figure locate the “barrier region” that separates the two stable states. (See Ref. 6 for details.) Using first passage time theory, it can be shown that the mean time for a transition from x₁ to x₂ is⁶

$$⟨T(x_1,x_2\phantom{)}⟩=5.031\times {10}^4$$ (23)

and further that the associated standard deviation has practically the same value. This implies that we would usually have to run the simulations in Fig. 3 for times of order 10⁴ before witnessing a spontaneous transition from x₁ to x₂, and that is a very long time on the scale of Fig. 3. But it might also be interesting to know the probability of seeing an x₁-to-x₂ transition occur within a time span that is comparable to that of Fig. 3, say, in time t=5.

Figure 3.

Four SSA runs of the Schlögl reaction set 21 using the parameter values 22 and the initial states indicated. (From Ref. 6.) The S population X(t) is plotted out here after every fifth reaction event. Starting values below the barrier region between x=200 and x=300 tend to wind up fluctuating about the lower stable state x₁=82, while starting values above the barrier region tend to wind up fluctuating about the upper stable state x₂=563. The dotted lines around the two stable states show their theoretically predicted widths, which are evidently consistent with these simulations. Spontaneous transitions between the two states will inevitably occur if the system is allowed to run long enough.

Finding an effective importance sampling strategy to compute p(82,563;5) turned out to be more difficult than we anticipated. We suspect the reason for this is the extreme sensitivity of the Schlögl reactions 21 to the values of its reaction parameters in the vicinity of the bistable configuration. For example, a 5% reduction in the value of c₃ from the value given in 22 will cause the upper steady state x₂ to disappear, while a 5% increase will cause the lower steady state x₁ to disappear. This means that in the importance sampling strategy of Eq. 4, small changes in the γ_j values can result in major changes in the dynamical structure of the system. This made finding a good biasing strategy more difficult than in the two examples considered in Sec. 5. Nevertheless, we found that taking γ₃=α and γ₄=1∕α with α=1.05 produced the following estimate with n=4×10⁷ runs:

$$p(82,563;5)=4.56\times {10}^{-7}\pm 0.25\times {10}^{-7}\left(95\%\text{confidence}\right).$$ (24)

For this value of $\widehat{p}$ and a one-standard uncertainty of u^wSSA=0.125×10⁻⁷, formula 11 yields n^SSA=2.9×10⁹. Dividing that by n^wSSA=4×10⁷ gives a gain in computational efficiency of g=73.

Results 23, 24 refer to the same transition x₁→x₂, and both results are informative but in different ways. However, there does not appear to be a reliable procedure for inferring either of these results from the other; in particular, the wSSA result 24 is a new result, not withstanding the known result 23. We hope to explore more fully the problem of finding optimal wSSA weighting strategies for bistable systems in a future publication.

CONCLUSIONS

The numerical results reported in Secs. 5, 6 support our expectation that the refinements to the original wSSA¹ made possible by the variance computation significantly improve the algorithm: The benefit of being able to quantify the uncertainty in the wSSA’s estimate of p(x₀,E;t) is obvious. And having an unambiguous measure of the optimality of a given set of values of the importance sampling parameters {γ₁,…,γ_M} makes possible the task of minimizing that uncertainty. But much work remains to be done in order to develop a practical, systematic strategy for deciding how best to parametrize the set {γ₁,…,γ_M} in terms of a smaller number of parameters, and, more generally, for deciding which reaction channels in a large network of reactions should be encouraged and which should be discouraged through importance sampling. More enlightenment on these matters will clearly be needed if the wSSA is to become easily applicable to more complicated chemical reaction networks.

We described in Sec. 6 the relationship between the probability p(x₀,E;t) computed by the wSSA and the mean first passage time ⟨T(x₀,E)⟩, which is the traditional way of analyzing rare events. We showed that in spite of the closeness of this relationship, if the former is very “small” and the latter is very “large,” then neither can easily be inferred from the other. But in practice, knowing p(x₀,E;t) will often be just as useful, if not more useful, than knowing ⟨T(x₀,E)⟩.

We conclude by commenting that, in spite of the demonstration in Sec. 5 of how much more efficiently the wSSA computes the probability p(x₀,E;t) than the SSA when p(x₀,E;t)⪡1, it would be inaccurate and misleading to view the wSSA and the SSA as “competing” procedures which aim to do the same thing. This becomes clear when we recognize two pronounced differences between those two procedures: First, whereas the wSSA always requires the user to exercise insight and judgment in choosing an importance sampling strategy, the SSA never imposes such demands on the user. Second, whereas the SSA usually plots out the state trajectories of its runs, since those trajectories reveal how the system typically behaves in time, the trajectories of the wSSA are of no physical interest because they are artificially biased. The SSA and the wSSA really have different, but nicely complementary, goals: The SSA is concerned with revealing the typical behavior of the system, showing how the molecular populations of all the species usually evolve with time. In contrast, the wSSA is concerned with the atypical behavior of the system, and more particularly with estimating the value of a single scalar quantity: the probability that a specified event will occur within a specified limited time when that probability is very small.

APPENDIX: MONTE CARLO AVERAGING AND IMPORTANCE SAMPLING

If X is a random variable with probability density function P and f is any integrable function, then the “average of f with respect to X,” or equivalently the “average of the random variable f(X),” can be computed as either

$$⟨f\left(X\right)⟩={\int }_{-\infty }^{\infty }f\left(x\right)P\left(x\right)dx$$ (A1)

or

$$⟨f\left(X\right)⟩=\underset{n\to \infty }{\text{lim}}\frac{1}{n}\sum _{i=1}^{n}f\left(x^{\left(i\right)}\right),$$ (A2)

where the x⁽ⁱ⁾ in Eq. A2 are statistically independent samples of X. Monte Carlo averaging is a numerical procedure for computing ⟨f(X)⟩ from Eq. A2 but using a finite value for n. But using a finite n renders the computation inexact:

$$⟨f\left(X\right)⟩\approx \frac{1}{n}\sum _{i=1}^{n}f\left(x^{\left(i\right)}\right)(n<\infty ).$$ (A3)

To estimate the uncertainty associated with this approximation, we reason as follows.

Let Y be any random variable with a well-defined mean and variance, and let Y₁,…,Y_n be n statistically independent copies of Y. Define the random variable Z_n by

$$Z_n\equiv \frac{1}{n}\sum _{i=1}^n{Y}_i.$$ (A4)

This means, by definition, that a sample z_n of Z_n can be obtained by generating n samples y⁽¹⁾,…,y⁽ⁿ⁾ of Y and then taking

$$z_n=\frac{1}{n}\sum _{i=1}^n{y}^{\left(i\right)}.$$ (A5)

Now take n large enough so that, by the central limit theorem, Z_n is approximately normal. In general, the normal random variable N(m,σ²) with mean m and variance σ² has the property that a random sample s of N(m,σ²) will fall within ±γσ of m with probability 68% if γ=1, 95% if γ=2, and 99.7% if γ=3. (For more on normal confidence interval theory, see the article by Welch.⁷) This implies that s will “estimate the mean” of N(m,σ²) to within ±γσ with those respective probabilities, a statement that we can write more compactly as m≈s±γσ. In particular, since Z_n is approximately normal, we may estimate its mean as

$$⟨Z_n⟩\approx z_n\pm \gamma \sqrt{\text{var}\left\{Z_n\right\}}.$$ (A6)

It is not difficult to prove that the mean and variance of Z_n as defined in Eq. A4 can be computed in terms of the mean and variance of Y by

$$⟨Z_n⟩=⟨Y⟩\text{and}\text{var}\left\{Z_n\right\}=\frac{\text{var}\left\{Y\right\}}{n}.$$ (A7)

With Eqs. A7, A5, we can rewrite the estimation formula A6 as

$$⟨Y⟩\approx \frac{1}{n}\sum _{i=1}^n{y}^{\left(i\right)}\pm \gamma \sqrt{\frac{\text{var}\left\{Y\right\}}{n}}.$$ (A8)

This formula is valid for any random variable Y with a well-defined mean and variance provided n is sufficiently large (so that normality is approximately achieved).

Setting Y=f(X) in Eq. A8, we obtain

$$⟨f\left(X\right)⟩\approx \frac{1}{n}\sum _{i=1}^{n}f\left(x^{\left(i\right)}\right)\pm \gamma \sqrt{\frac{\text{var}\left\{f\left(X\right)\right\}}{n}}.$$ (A9)

This formula evidently quantifies the uncertainty in the estimate A3. Again, the values γ=1,2,3 correspond to respective “confidence intervals” of 68%, 95%, and 99.7%. But formula A9 as it stands is not useful in practice because we do not know var{f(X)}. It is here that we indulge in a bit of bootstrapping logic: We estimate

$$\text{var}\left\{f\left(X\right)\right\}\approx \frac{1}{n}\sum _{i=1}^n{\left(f\left(x^{\left(i\right)}\right)\right)}^2-{(\frac{1}{n}\sum _{i=1}^{n}f\left(x^{\left(i\right)}\right))}^2.$$ (A10)

This estimate evidently makes the assumption that n is already large enough that the n-sample first and second moments of f provide reasonably accurate estimates of ⟨f⟩ and ⟨f²⟩. In practice, we need to test this assumption by demanding “reasonable closeness” among several n-run computations of the right hand side of Eq. A10. Only when n is large enough for that to be so can we reliably invoke formulas A9, A10 to infer an estimate of ⟨f(X)⟩ and an estimate of the uncertainty in that estimate from the two sums ${\sum }_{i=1}^{n}f\left(x^{\left(i\right)}\right)$ and ${\sum }_{i=1}^n{\left(f\left(x^{\left(i\right)}\right)\right)}^2$.

The most obvious way to decrease the size of the uncertainty term in Eq. A9 is to increase n; indeed, in the limit n→∞, Eq. A9 reduces to the exact formula A2. But the time available for computation usually imposes a practical upper limit on n. However, we could also make the uncertainty term in Eq. A9 smaller if we could somehow decrease the variance. Several “variance-reducing” strategies with that goal have been developed, and one that has proved to be effective in many scientific applications is called importance sampling.

Importance sampling arises from the fact that we can write Eq. A1 as

$$⟨f\left(X\right)⟩={\int }_{-\infty }^{\infty }f\left(x\right)P\left(x\right)\left(\frac{Q\left(x\right)}{Q\left(x\right)}\right)dx={\int }_{-\infty }^{\infty }\left(\frac{f\left(v\right)P\left(v\right)}{Q\left(v\right)}\right)Q\left(v\right)dv,$$ (A11)

where Q is the probability density function of some new random variable V. Defining still another random variable g(V) by

$$g\left(V\right)\equiv \frac{f\left(V\right)P\left(V\right)}{Q\left(V\right)},$$ (A12)

it follows from Eq. A11 that

$$⟨g\left(V\right)⟩=⟨f\left(X\right)⟩.$$ (A13)

But although the two random variables f(X) and g(V) have the same mean, they will not generally have the same variance. In fact, if we choose the functionQ(v) so that it varies withvin roughly the same way thatf(v)P(v) does, then the sample values of g(V) will not show as much variation as the sample values of f(X). That would imply that

$$\text{var}\left\{g\left(V\right)\right\}<\text{var}\left\{f\left(X\right)\right\}.$$ (A14)

In that case, we will get a more accurate estimate of ⟨f(X)⟩ if we use, instead of Eq. A9,

$$⟨f\left(X\right)⟩=⟨g\left(V\right)⟩\approx \frac{1}{n}\sum _{i=1}^{n}g\left(v^{\left(i\right)}\right)\pm \gamma \sqrt{\frac{\text{var}\left\{g\left(V\right)\right\}}{n}},$$ (A15)

where

$$\text{var}\left\{g\left(V\right)\right\}\approx \frac{1}{n}\sum _{i=1}^n{\left(g\left(v^{\left(i\right)}\right)\right)}^2-{(\frac{1}{n}\sum _{i=1}^{n}g\left(v^{\left(i\right)}\right))}^2.$$ (A16)

Of course, if one is not careful in selecting the function Q, the inequality in Eq. A14 could go the other way, and Eq. A15 would then show a larger uncertainty than Eq. A9. The key to having Eq. A14 hold is to choose the function Q(v) so that it tends to be large (small) where f(v)P(v) is large (small). When that is so, generating samples v⁽ⁱ⁾ according to Q will sample the real axis most heavily in those “important” regions where the integrand in Eq. A1 is large. But at the same time, Q must be simple enough that it is not too difficult to generate those samples.

In practice, once a functional form for Q has been chosen, one or more parameters in Q are varied in a series of test runs to find the values that minimize variance A16. Then a final run is made using the minimizing parameter values and as large a value of n as time will allow to get the most accurate possible estimate of ⟨f(X)⟩.

The connection of the foregoing general theory to the application considered in the main text can be roughly summarized by the following correspondences:

$$X\leftrightarrow \text{an}\text{unbiased}\left(\text{SSA}\right)\text{state}\text{trajectory},$$

$$f\left(X\right)\leftrightarrow \text{statistical}\text{weight}\text{of}\text{an}\text{unbiased}\text{trajectory},$$

$$V\leftrightarrow \text{a}\text{biased}\left(\text{wSSA}\right)\text{state}\text{trajectory},$$

$$g\left(V\right)\leftrightarrow \text{statistical}\text{weight}\text{of}\text{a}\text{biased}\text{trajectory},$$

$$⟨f\left(X\right)⟩=⟨g\left(V\right)⟩\leftrightarrow p({\mathbf{x}}_0,\mathcal{E};T),$$

$$\frac{P\left(v\right)}{Q\left(v\right)}\leftrightarrow w_k=\prod _{\begin{array}{c}\text{all}\text{reaction}\text{events}\\ \text{comprising}\text{trajectory}k\end{array}}\frac{a_j∕a_0}{b_j∕b_0},$$

$$\sum _{k=1}^{n}g\left(v^{\left(k\right)}\right)\leftrightarrow m_n^{\left(1\right)},\sum _{k=1}^n{\left(g\left(v^{\left(k\right)}\right)\right)}^2\leftrightarrow m_n^{\left(2\right)}.$$