Lindblad equations for strongly coupled populations and coherences in photosynthetic complexes

Abstract

Recent experimental observations of time-resolved multidimensional signals in the light-harvesting antennae Fenna–Mathews–Olson [G. S. Engel et al., Nature (London) 446, 782 (2007)] show large oscillations of exciton populations coupled to the long-lived coherences. These effects may not be reproduced by the standard Redfield theory which assumes weak coupling to a bath. A more general relaxation superoperator which holds for all system-bath coupling parameter regimes is constructed by taking into account the statistics (covariances) of Lindblad equation parameters. Simulations for a model dimer reproduce all observed strong coupling effects.

INTRODUCTION

Photosynthetic complexes in plants and bacteria are responsible for the absorption of solar energy and its funneling toward a reaction center where a chain of electron transfer reaction converts it to chemical free energy.^{1, 2, 3, 4} The light-harvesting efficiency is typically very high, above 98%. Numerous experimental and theoretical studies have investigated the factors leading to this remarkably high efficiency.^{5, 6, 7, 8, 9, 10, 11}

The standard description of exciton dynamics in chlorophyll aggregates is based on the Redfield equations for the density matrix written in the secular approximation.^{10, 12, 13, 14, 15, 16} At this level, exciton populations are decoupled from coherences and satisfy an ordinary Pauli Master equation. Two important consequences are (i) population dynamics are typically slower (several picoseconds) than the dephasing of excitonic coherences (≈100 fs) and (ii) time profiles of populations are given by sums of exponential functions, while coherences are oscillatory. The wavelike energy transfer recently observed in the Fenna–Mathews–Olson (FMO) seven bacteriochlorophyll (BChl) complex indicates that populations and quantum coherences are strongly coupled.¹⁷ Diagonal peaks show that populations are oscillatory while the coherences acquire long-lived contributions related to nonequilibrium populations. These effects, which could be important for energy transfer efficiency in photosynthesis,¹⁸ may not be described by the Redfield equation.

Describing the coupled quantum dissipative dynamics of coherences and populations is a long-standing issue. The complete Redfield equation without invoking the secular approximation is derived microscopically by second order perturbative expansion with respect to the system-bath coupling.^{14, 16} However, using the full Redfield theory with strong coupling as required to couple populations and coherences usually results in unphysical density matrices with negative or diverging populations.^{14, 19, 20} One possible approach that overcomes these difficulties is to include explicitly collective bath coordinates using generalized Fokker–Planck equations.^{21, 22, 23} However, this complicates the simulations for large aggregates.

A higher-level quantum master equations (QMEs) treatment is possible by using equations of the Lindblad type for the dynamics of the reduced density matrix.^{14, 19} These equations were first derived by Gorini et al.²⁴ and by Lindblad.²⁵ A relationship between the Lindblad equation and the stochastic Schrödinger equation (SSE), which is the quantum mechanical analog of the classical Langevin equations of motion for open systems, was subsequently established.¹⁹ Because of that relation, these QMEs guarantee to yield physically acceptable density matrix for all parameter regimes including strong coupling between populations and coherences. The parameters of the SSE have been mapped into the relaxation rates obtained from the Redfield theory in the secular approximation^{14, 16} which decouples populations and coherences. The Lindblad relaxation parameters must be fitted when population and coherences are coupled.

Lindblad equations have been widely applied to the study of excitation dynamics in photosynthetic complexes. Energy transfer efficiency was studied by Rebentrost et al.²⁶ and Mohseni et al.¹⁸ using a Lindblad equation corresponding to the Redfield theory in the secular approximation. Other authors used the Lindblad equation to include pure dephasing phenomenologically and observed the enhancement of the energy transfer efficiency.^{27, 28, 29}

In this paper, we develop a practical approach that starts with the Redfield equation in the secular approximation which is calculated microscopically. The entire relaxation superoperator is then constructed by a statistical analysis based on the Lindblad equations. This leaves only few free parameters that can be obtained from a fit to experiment. Strong coupling between populations and coherences poses no difficulty. Simulations on a simple model system show population oscillations before thermal equilibrium is reached. The coherences decay along with the equilibration of the populations and thus survive for much longer times than in the secular Redfield theory. The key observables of recent experiments in FMO are thus reproduced by this level of theory.

LINDBLAD VERSUS THE REDFIELD EQUATIONS

We consider a system whose Hamiltonian is partitioned into three parts: a system (e.g., the chlorophyll aggregate in a photosynthetic complex), a bath (e.g., phonons), and their interaction. In the Redfield approach the equations for the reduced system density matrix evolution are obtained by projection operator techniques.^{23, 30, 31, 32} The Redfield equations read

$$\dot{\rho }=-\frac{i}{\hslash }\left[H,\rho \right]-\kappa \rho ,$$ (2.1)

where H is the system Hamiltonian and κ is a relaxation superoperator (a complex matrix) calculated to second order in the system-bath couplings, by averaging over the bath degrees of freedom and invoking the Markovian approximation. κ is proportional to the amplitude square of the system-bath coupling strength, and the integrated bath spectral density.¹⁶

Expanded in the basis of system eigenstates, Eq. 2.1 reads

$${\dot{\rho }}_{ij}=-\frac{i}{\hslash }\left({ϵ}_i-{ϵ}_j\right){\rho }_{ij}-\sum _{kl}{\kappa }_{ij,kl}{\rho }_{kl},$$ (2.2)

where ϵ_i is the ith state energy. ρ_ij elements with i=j and i≠j are known as populations and coherences, respectively. The density matrix is normalized, 0≤ρ_i,i≤1 and Tr[ρ]=1.

The density matrix dynamics calculated from the Redfield theory may become diverging. When the secular approximation is invoked, the relaxation superoperator reads

$${\kappa }_{ij,kl}^{\left(S\right)}=\left[{\delta }_{ij}{\delta }_{kl}+{\delta }_{ik}{\delta }_{jl}\left(1-{\delta }_{ij}{\delta }_{kl}\right)\right]{\kappa }_{ij,kl}.$$ (2.3)

In this limit the system populations are decoupled from the coherences and satisfy an ordinary Pauli Master equation with the population rate matrix κ_ii,kk, which guarantees conservation of populations and yields the correct thermal equilibrium at long times. The proper physical behavior of the density matrix is guaranteed. The population rate matrix is real so the populations relax exponentially. The coherences are completely decoupled and are damped by the dephasing rates κ_ij,ij. κ_ij,ij are complex: their imaginary part accounts for bath-induced energy shifts.

An alternative approach to quantum dissipative dynamics is provided by the Lindblad QME, which attains the form

$$\dot{\rho }=-\frac{i}{\hslash }\left[H,\rho \right]+\sum _{\alpha }\left(V_{\alpha }\rho V_{\alpha }^{†}-\frac{1}{2}\rho V_{\alpha }^{†}{V}_{\alpha }-\frac{1}{2}{V}_{\alpha }^{†}{V}_{\alpha }\rho \right),$$ (2.4)

where V_α is an arbitrary set of system operators represented by complex matrices (“†” indicates a Hermitian conjugate). The index α represents various elementary forces.

Equation 2.4 may be brought into the superoperator form of Eq. 2.2. The Lindblad equation defines a subspace of possible Redfield relaxation tensors, which lead to physically acceptable density matrix dynamics. The V_α matrices are of the same rank as the system density matrix, and appear in the stochastic Schrodinger equation used for the derivation of Eq. 2.4. They can be determined microscopically from the Redfield theory within the secular approximation.¹⁶ Applications of these equations to systems where populations and coherences are coupled require a huge parameter set which is usually guessed phenomenologically.

We shall demonstrate our approach for parametrizing the Lindblad equations using a model system of two level chromophores interacting with a bath. This system has a single ground state, two singly excited states and one doubly excited state.³ We assume that the system is prepared in its singly excited manifold by an optical pulse and then evolves freely. By neglecting relaxation into the ground state, the relevant system subspace consists of two exciton levels [i,j=1,2 in Eq. 2.2]. The most general form of V matrices in the Lindblad Eq. 2.4 is then

$$V_{\alpha }=\left(\begin{array}{cc}{a}_{\alpha }& b_{\alpha }\\ c_{\alpha }& d_{\alpha }\end{array}\right),$$ (2.5)

where a, b, c, and d are complex numbers. Combining this with Eqs. 2.2, 2.4 we can express the elements of the tetradic matrix κ in terms of the Lindblad parameters. The secular Redfield equations are recovered by the following parameters representing population transfer:

$${\kappa }_{11,11}=-{\kappa }_{22,11}=\sum _{\alpha }{\mid c_{\alpha }\mid }^2,$$ (2.6)

$${\kappa }_{22,22}=-{\kappa }_{11,22}=\sum _{\alpha }{\mid b_{\alpha }\mid }^2,$$

and the coherence-dephasing rates

$${\kappa }_{12,12}={\kappa }_{21,21}^{\ast }=\frac{1}{2}\sum _{\alpha }\left({\mid a_{\alpha }\mid }^2+{\mid b_{\alpha }\mid }^2+{\mid c_{\alpha }\mid }^2+{\mid d_{\alpha }\mid }^2-2a_{\alpha }{d}_{\alpha }^{\ast }\right).$$ (2.7)

The remaining parameters represent couplings between populations and coherences

$${\kappa }_{11,12}=-{\kappa }_{22,12}={\kappa }_{11,21}^{\ast }=-{\kappa }_{22,21}^{\ast }=-\frac{1}{2}\sum _{\alpha }{a}_{\alpha }{b}_{\alpha }^{\ast }-c_{\alpha }{d}_{\alpha }^{\ast },$$ (2.8)

$${\kappa }_{12,11}={\kappa }_{21,11}^{\ast }=-\frac{1}{2}\sum _{\alpha }2a_{\alpha }{c}_{\alpha }^{\ast }-d_{\alpha }{c}_{\alpha }^{\ast }-b_{\alpha }{a}_{\alpha }^{\ast },$$

$${\kappa }_{12,22}={\kappa }_{21,22}^{\ast }=-\frac{1}{2}\sum _{\alpha }2b_{\alpha }{d}_{\alpha }^{\ast }-d_{\alpha }{c}_{\alpha }^{\ast }-b_{\alpha }{a}_{\alpha }^{\ast },$$

$${\kappa }_{12,21}={\kappa }_{21,12}^{\ast }=-\sum _{\alpha }{b}_{\alpha }{c}_{\alpha }^{\ast }.$$

The QME, Eq. 2.2, with κ’s elements defined by Eqs. 2.6, 2.7, 2.8 is guaranteed to yield a physical density matrix at all times for an arbitrary choices of a, b, c, and d.

The form of Eq. 2.8 shows that the rates of the relaxation matrix can be interpreted as correlation coefficients of the matrix elements of V_α. We define

$$⟨\nu {\nu }^{\prime }⟩=\sum _{\alpha }{\nu }_{\alpha }{\nu }_{\alpha }^{\prime }$$ (2.9)

for ν=a,b,c,d. Since ρ₁₁+ρ₂₂=1, we can further eliminate one of the population variables and define the population difference variable $\tilde{\rho }={\rho }_{11}-{\rho }_{22}$. Equation 2.2 is then recast as

$$\left(\begin{array}{c}\dot{\tilde{\rho }}\\ {\dot{\rho }}_{12}\\ {\dot{\rho }}_{21}\end{array}\right)=-i\left(\begin{array}{ccc}-iK& 0& 0\\ 0& -\Delta -i\gamma & 0\\ 0& 0& \Delta -i{\gamma }^{\ast }\end{array}\right)\left(\begin{array}{c}\tilde{\rho }\\ {\rho }_{12}\\ {\rho }_{21}\end{array}\right)+\left(\begin{array}{c}⟨b{b}^{\ast }⟩-⟨c{c}^{\ast }⟩\\ 0\\ 0\end{array}\right)+\left(\begin{array}{ccc}0& \left(⟨a{b}^{\ast }⟩-⟨c{d}^{\ast }⟩\right)& \left(⟨a^{\ast }b⟩-⟨c^{\ast }d⟩\right)\\ \frac{1}{2}\left(⟨a{c}^{\ast }⟩-⟨b{d}^{\ast }⟩\right)& 0& ⟨b{c}^{\ast }⟩\\ \frac{1}{2}\left(⟨a^{\ast }c⟩-⟨b^{\ast }d⟩\right)& ⟨b^{\ast }c⟩& 0\end{array}\right)\left(\begin{array}{c}\tilde{\rho }\\ {\rho }_{12}\\ {\rho }_{21}\end{array}\right)+\left(\begin{array}{c}0\\ \frac{1}{2}\left(⟨a{c}^{\ast }⟩+⟨b{d}^{\ast }⟩-⟨c^{\ast }d⟩-⟨a^{\ast }b⟩\right)\\ \frac{1}{2}\left(⟨a^{\ast }c⟩+⟨b^{\ast }d⟩-⟨c{d}^{\ast }⟩-⟨a{b}^{\ast }⟩\right)\end{array}\right),$$ (2.10)

where we have introduced the total population relaxation rate constant

$$K=⟨b{b}^{\ast }⟩+⟨c{c}^{\ast }⟩,$$ (2.11)

the energy-level splitting

$$\Delta ={ϵ}_2-{ϵ}_1,$$ (2.12)

and the coherence-dephasing rate

$$\gamma =\frac{1}{2}K+\widehat{\gamma }.$$ (2.13)

Here, $\widehat{\gamma }$ is the pure dephasing rate given by

$$\widehat{\gamma }=\frac{1}{2}\left(⟨a{a}^{\ast }⟩+⟨d{d}^{\ast }⟩-2⟨a{d}^{\ast }⟩\right).$$ (2.14)

The inhomogeneous terms on the right side of Eq. 2.10 leads to the correct thermal equilibrium. The first two terms of Eq. 2.10 give the secular Redfield equation expressed in terms of the Lindblad parameters. The remaining terms are Lindblad extensions which induce couplings between the populations and coherences. The relaxation superoperator κ for a N-site system is given in Appendix A.

Unlike Eq. 2.4, Eq. 2.10 contains a finite number of parameters. The full set contains 4(4+1)∕2=10 correlation coefficients. Not all of them are independent due to other constraints such as invariance of the trace and the thermal equilibrium at long times. This will be demonstrated in Sec. 3.

By assuming that all variables are uncorrelated and only retaining ⟨aa^∗⟩, ⟨bb^∗⟩, ⟨cc^∗⟩, and ⟨dd^∗⟩ in Eq. 2.10 we recover the secular approximation with the real pure dephasing rate $\widehat{\gamma }=\frac{1}{2}\left(⟨a{a}^{\ast }⟩+⟨d{d}^{\ast }⟩\right)$. The nonsecular terms in Eq. 2.10 vanish. These parameters may be calculated using the Refield theory. The correlations between different Lindblad parameters represented by the third term in the right hand side of Eq. 2.10 thus allow to go beyond the secular approximation.

LINDBLAD EQUATIONS IN THE WEAK SYSTEM-BATH COUPLING REGIME

In the weak coupling limit, the thermal equilibrium of the system is not perturbed by the bath. Hence, at long times, the density matrix should be diagonal with zero coherences, ρ₁₂=ρ₂₁=0, and the populations satisfy the detailed balance condition: ρ₁₁∕ρ₂₂=e^{−β(ϵ₁−ϵ₂)}, where β=(k_BT)⁻¹ (k_B is Boltzmann’s constant and T is the temperature). These conditions imply that the relaxation superoperator, κ in Eq. 2.2, has a zero-value eigenvalue whose eigenvector is (e^−βϵ₁,e^−βϵ₂,0,0)^T. This condition may be achieved when¹⁹

$$-\frac{{\kappa }_{ij,22}}{{\kappa }_{ij,11}}=e^{\beta \Delta }\left(i,j=1,2\right).$$ (3.1)

For Eq. 2.10 at equilibrium, we get

$${\tilde{\rho }}_{\text{eq}}=K^{-1}\left(⟨b{b}^{\ast }⟩-⟨c{c}^{\ast }⟩\right)$$ (3.2)

and

$$\left(⟨b{d}^{\ast }⟩-⟨a{c}^{\ast }⟩\right){\tilde{\rho }}_{\text{eq}}=⟨b{d}^{\ast }⟩+⟨a{c}^{\ast }⟩-⟨c^{\ast }d⟩-⟨a^{\ast }b⟩,$$ (3.3)

as can be seen combining Eqs. 3.1, 2.8.

We can further simplify the form of the density matrix by noting that it can be written in terms of correlation functions of (a−d) and not of a and d separately. We then have

$$⟨a{a}^{\ast }⟩+⟨d{d}^{\ast }⟩-2⟨a{d}^{\ast }⟩=⟨\left(a-d\right){\left(a-d\right)}^{\ast }⟩+2i\text{Im}⟨a^{\ast }d⟩,$$ (3.4)

where Im stands for the imaginary part,

$$⟨a{c}^{\ast }⟩-⟨b{d}^{\ast }⟩=\left(⟨{\left(a-d\right)}^{\ast }b⟩-⟨\left(a-d\right)c^{\ast }⟩\right)∕{\tilde{\rho }}_{\text{eq}},$$ (3.5)

and

$$⟨a{b}^{\ast }⟩-⟨c{d}^{\ast }⟩=⟨\left(a-d\right)b^{\ast }⟩\frac{{\tilde{\rho }}_{\text{eq}}-1}{{\tilde{\rho }}_{\text{eq}}}+⟨{\left(a-d\right)}^{\ast }c⟩\frac{{\tilde{\rho }}_{\text{eq}}+1}{{\tilde{\rho }}_{\text{eq}}}.$$ (3.6)

Only the first of these three equations contains terms where a and d stand alone, ⟨a^∗d⟩, but this frequency shift term is strictly imaginary and may be absorbed in the ϵ_1,2’s. We thus drop it. Making these simplifications we obtain

$$\left(\begin{array}{c}\dot{\tilde{\rho }}\\ {\dot{\rho }}_{12}\\ {\dot{\rho }}_{21}\end{array}\right)=-i\left(\begin{array}{ccc}-iK& 0& 0\\ 0& -\Delta -i\gamma & 0\\ 0& 0& \Delta -i{\gamma }^{\ast }\end{array}\right)\left(\begin{array}{c}\tilde{\rho }-{\tilde{\rho }}_{\text{eq}}\\ {\rho }_{12}\\ {\rho }_{21}\end{array}\right)+\left(\begin{array}{ccc}0& ⟨\tilde{a}{b}^{\ast }⟩\frac{{\tilde{\rho }}_{\text{eq}}-1}{{\tilde{\rho }}_{\text{eq}}}+⟨{\tilde{a}}^{\ast }c⟩\frac{{\tilde{\rho }}_{\text{eq}}+1}{{\tilde{\rho }}_{\text{eq}}}& ⟨{\tilde{a}}^{\ast }b⟩\frac{{\tilde{\rho }}_{\text{eq}}-1}{{\tilde{\rho }}_{\text{eq}}}+⟨\tilde{a}{c}^{\ast }⟩\frac{{\tilde{\rho }}_{\text{eq}}+1}{{\tilde{\rho }}_{\text{eq}}}\\ \frac{1}{2{\tilde{\rho }}_{\text{eq}}}\left(⟨{\tilde{a}}^{\ast }b⟩-⟨\tilde{a}{c}^{\ast }⟩\right)& 0& ⟨b{c}^{\ast }⟩\\ \frac{1}{2{\tilde{\rho }}_{\text{eq}}}\left(⟨\tilde{a}{b}^{\ast }⟩-⟨{\tilde{a}}^{\ast }c⟩\right)& ⟨b^{\ast }c⟩& 0\end{array}\right)\left(\begin{array}{c}\tilde{\rho }-{\tilde{\rho }}_{\text{eq}}\\ {\rho }_{12}\\ {\rho }_{21}\end{array}\right),$$ (3.7)

where we have denoted $\tilde{a}\equiv \left(a-d\right)$. The dephasing rate may be taken as real by modifying the eigenvalues and is given by

$$\gamma =\left(K+⟨\tilde{a}{\tilde{a}}^{\ast }⟩\right)∕2.$$ (3.8)

Equation 3.7 now has only three unknown parameters, $⟨{\tilde{a}}^{\ast }b⟩$, $⟨{\tilde{a}}^{\ast }c⟩$, and $⟨{\tilde{b}}^{\ast }c⟩$, provided the secular part of the relaxation superoperator can be calculated microscopically from the Redfield theory.

NUMERICAL RESULTS

Population-coherence transfer

Equation 3.7 allows a qualitative analysis of population-coherence transfer. These variables are coupled through two types of terms,

$${\xi }_{c\to p}=⟨\tilde{a}{b}^{\ast }⟩\left({\tilde{\rho }}_{\text{eq}}-1\right)∕{\tilde{\rho }}_{\text{eq}}+⟨{\tilde{a}}^{\ast }c⟩\left({\tilde{\rho }}_{\text{eq}}+1\right)∕{\tilde{\rho }}_{\text{eq}}$$ (4.1)

represents coherence transfer to populations, while

$${\xi }_{p\to c}=\frac{1}{2{\tilde{\rho }}_{\text{eq}}}\left(⟨{\tilde{a}}^{\ast }b⟩-⟨\tilde{a}{c}^{\ast }⟩\right)$$ (4.2)

represents the reverse process; the effect of both transfer rates vanish at equilibrium when $\tilde{\rho }={\tilde{\rho }}_{\text{eq}}$ and ρ₁₂=ρ₂₁=0. Thus, the equilibrium ensures zero coherences and steady populations. ξ_c→p always vanishes when the up or down population transfer rate is zero (either b or c vanishes). ξ_p→c does not vanish in this case. The rate ξ_p→c thus enables the slow decay of coherences along with the nonequilibrium populations. The largest population-coherence coupling is obtained from Eq. 3.7 when the two correlations, $⟨\tilde{a}{b}^{\ast }⟩$ and $⟨{\tilde{a}}^{\ast }c⟩$, are out of phase so that $⟨\tilde{a}{b}^{\ast }⟩$ and $⟨{\tilde{a}}^{\ast }c⟩$ have opposite signs.

As an example we assume that all parameters are real and write, for Δ>0 (ϵ₂>ϵ₁),

$$⟨{\tilde{a}}^2⟩={\chi }_a^2,⟨b^2⟩={\chi }_b^2,⟨c^2⟩={\chi }_c^2,$$ (4.3)

where ${\chi }_b^2$ and ${\chi }_c^2$ are the population transfer rates, while the pure dephasing rate is $\gamma ={\chi }_a^2∕2$. For the correlations we use

$$⟨\tilde{a}b⟩={\chi }_a{\chi }_b\text{cos}{\theta }_{ab},⟨\tilde{a}c⟩={\chi }_a{\chi }_c\text{cos}{\theta }_{ac},$$ ()

$$⟨bc⟩={\chi }_b{\chi }_c\text{cos}{\theta }_{bc}.$$

If $\tilde{a}$, b, and c are treated as vectors in real space, the three correlation angles are related by

$$\text{cos}{\theta }_{bc}=\text{cos}{\theta }_{ab}\text{cos}{\theta }_{ac}+\text{sin}{\theta }_{ab}\text{sin}{\theta }_{ac}\text{cos}\varphi ,$$ (4.5)

where ϕ runs from −π to π. For a given θ_ab and θ_ac, not all values of θ_bc are allowed. Equation 3.7 shows that the largest transfer rates between coherences and populations occur when cos θ_ab=±1 and cos θ_ac=∓1. In both cases, it follows from Eq. 4.5 that cos θ_bc=−1.

The population-coherence transfer strongly depends on the temperature. At low temperatures (k_BT⪡∣Δ∣), the upward population transfer rate vanishes (χ_c≈0) and ${\tilde{\rho }}_{\text{eq}}=1$. In this regime, the coherence to population transfer rate, ξ_c→p, also vanishes. The population dynamics is thus not affected by the coherences; however the ${\xi }_{p\to c}=⟨{\tilde{a}}^{\ast }b⟩∕2\ne 0$ and the coherences are being regenerated as long as populations are not equilibrated. On the other hand, in the high temperature regime (k_BT⪢∣Δ∣), the up and down population transfer rates are almost equal (χ_b≈χ_c). The equilibrium population difference is

$${\tilde{\rho }}_{\text{eq}}\approx \frac{\Delta }{2k_{B}T}.$$ (4.6)

The coherence-population transfer rates are now proportional to temperature (where we set χ_b=χ_c=χ),

$${\xi }_{c\to p}=-2{\xi }_{p\to c}=-\frac{2k_{B}T}{\Delta }{\chi }_a\chi \left(\text{cos}{\theta }_{ab}-\text{cos}{\theta }_{ac}\right).$$ (4.7)

The coherence to population transfer ξ_c→p causes populations to be affected by oscillating coherences, thereby inducing oscillating dynamics of populations. To quantify this effect we notice that it may be observed only when the coherences are nonzero. This is controlled by the coherence decay rate γ. The importance of the coherence to population transfer generally can be quantified by the ratio between these rates η=ξ_c→p∕γ. At low temperature we have ${\tilde{\rho }}_{\text{eq}}\approx 1$, ${\chi }_b^2⪢{\chi }_c^2$ and the ratio is

$$\eta =4\frac{\mid {\chi }_a{\chi }_c\text{cos}{\theta }_{ac}\mid }{{\chi }_a^2+{\chi }_b^2},$$ (4.8)

the ratio is of the order of χ_c∕χ_a (we assume that the pure dephasing is larger than the population relaxation rate), and the population-coherence transfer may be ignored. However, at high temperatures,

$$\eta =\frac{4k_{B}T}{\Delta }{\chi }_a\chi \frac{\mid \text{cos}{\theta }_{ab}-\text{cos}{\theta }_{ac}\mid }{2{\chi }^2+{\chi }_a^2},$$ (4.9)

and the coupling is controlled by the temperature. When η>1, the transfer rate ξ_c→p is large compared to the population redistribution and the coherences decay rates and thus the population-coherence transfer may be observed.

Simulations based on the complete Redfield superoperator

We assume the following system Hamiltonian matrix (in cm⁻¹):

$$H_S=\left(\begin{array}{cc}0& -71.3\\ -71.3& 46.4\end{array}\right).$$ (4.10)

These are typical exciton splittings and intermolecule interactions in pigment-protein photosynthetic complexes.¹⁶ The eigenenergies are ϵ₁=−51.8 cm⁻¹ and ϵ₂=98.2 cm⁻¹. The other parts of the Hamiltonian, the bath part H_B and a system-bath coupling part, H_SB, have been described in Ref. 16. Each chromophore is coupled to its own statistically independent bath, characterized by the overdamped Brownian oscillator spectral density³³ with a relaxation time scale Λ⁻¹=106 fs. The chromophore-bath coupling strength is λ. We have used two values of λ=35 and 65 cm⁻¹, both typical in photosynthetic systems.

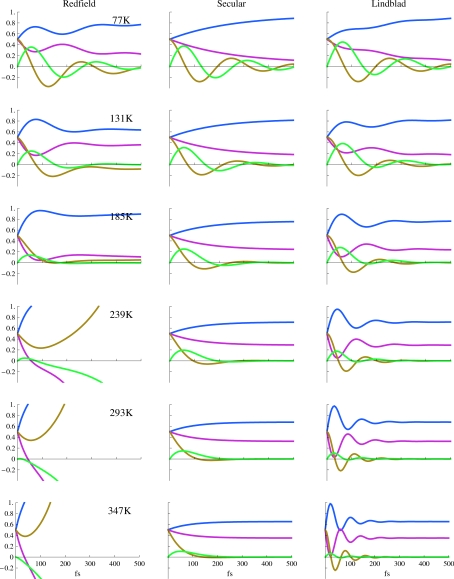
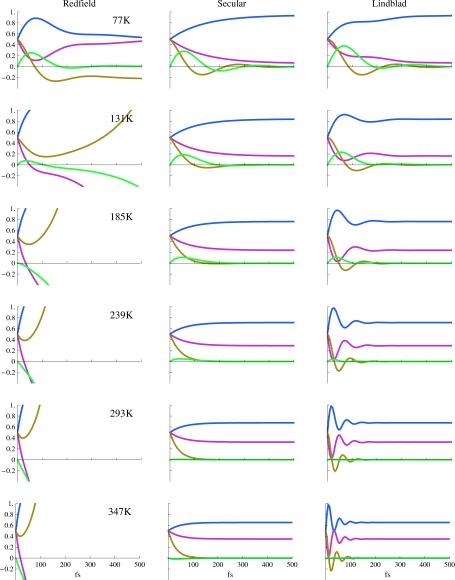
The Redfield theory can be used with these parameters to predict the time dependence of the system density matrix. The Redfield relaxation tensors, κ in Eq. 2.2, given in Appendix B, were calculated without invoking the secular approximation at six temperatures, T=77, 131, 185, 239, 293, and 347 K, where Δ∕k_BT=2.88 (low temperature) to 0.62 (high temperature). In Fig. 1 (left column), we show the time evolution of the density matrix for λ=35 cm⁻¹ at all six temperatures. In most cases, we see unphysical density matrices at long times: The positive definiteness of the density matrix breaks down quickly. At T=77, 131, and 185 K the population behavior is physical in the displayed time period, but they do not reach equilibrium at long times, while the coherences decay to nonzero values. For stronger system-bath couplings λ=65 cm⁻¹ in Fig. 2, the Redfield theory breaks down at earlier times. Only at T=77 K does the density matrix remain positive definite, but again it does not reach equilibrium.

Figure 1.

Time evolution of all elements of the density matrix for system-bath coupling λ=35 cm⁻¹ calculated with the full Redfield theory (left), the secular approximation (middle), and our Lindblad equations (right) with the system Hamiltonian described in Sec. 4: magenta (ρ₂₂), blue (ρ₁₁), brown (Re[ρ₁₂]), and green (Im[ρ₁₂]). In all cases, the initial condition is ρ₁₁(0)=ρ₂₂(0)=ρ₁₂(0)=ρ₂₁(0)=0.5. From top to bottom, the temperatures are T=77, 131, 185, 239, 293, and 347 K.

Figure 2.

Same as Fig. 1, but for stronger system-bath coupling λ=65 cm⁻¹.

Redfield equations in the secular approximation

In the secular approximation we only retain the secular elements [Eqs. 2.6, 2.7] of the Redfield relaxation superoperator; all other elements are neglected. The resulting evolution of the density matrix is shown in the middle columns of Figs. 12. Populations and coherences are now decoupled. The density matrix becomes physically acceptable (it maintains positive definiteness and the constant trace at all times), but the short time oscillations of the populations disappear. The populations redistribute and reach thermal equilibrium. The coherences decay rapidly. Both Figs. 12 show similar behavior but with different relaxation timescales, as expected.

The Lindblad equations

In the Lindblad simulations we maintain the weak coupling limit. We retain the elements of the secular Redfield relaxation tensor of Eq. 2.2. The Redfield theory thus yields the population redistribution and the pure dephasing rates (i.e., ${\chi }_a^2$, ${\chi }_b^2$, and ${\chi }_c^2$ parameters). We then construct a Lindblad relaxation tensor according to Eq. 3.7.

We assume that all parameters are real and take cos θ_ab=−1, cos θ_ac=1, and cos θ_bc=−1, where the coupling between population and coherences is maximized. The remaining parameters in Eq. 3.7 are determined by the secular Redfield rates given in Appendix B: we have χ_b=(κ_11,22)^1∕2, χ_c=(κ_22,11)^1∕2, and ${\chi }_a={\left(2\text{Re}\left({\kappa }_{12,12}\right)-{\chi }_b^2-{\chi }_c^2\right)}^{1∕2}$.

The resulting time evolution of the density matrix is shown in the right columns of Figs. 12. The Lindblad equation always yields a physical density matrix and retains transfer between populations and coherences. Population oscillations are observed at all temperatures. The oscillations are weaker at the lower temperatures, but survive for a longer time since the dephasing rates are small. At higher temperatures, strong oscillations can be accounted for, but they decay on a faster time scale. This is explained by the fact that the interactions between populations and coherences vanish at equilibrium and that thermal equilibrium is attained more rapidly at higher temperatures. The coupling between populations and coherences increases the coherence lifetime as well. This is clearly seen by comparing the Lindblad and the secular Redfield predictions at 77 and 131 K in Fig. 2. The amplitudes of the oscillations for the coherences are larger for Lindblad than for the secular Redfield. In the higher temperature regimes, the oscillations in the coherences completely vanish (overdamped limit) in the secular Redfield while the Lindblad shows coherence oscillations lasting for 100–200 fs. Clearly, in order to observe these effects in a four-wave mixing experiment, short pulses have to be used.

At 77 K, the populations (Figs. 12) for the Lindblad equations oscillate with a shifted frequency ϵ₂−ϵ₁+Im(κ_12,12). At higher temperatures, the populations oscillate at a higher frequency which does not correspond to the energy-level difference. The oscillations solely arise from the interaction between populations and coherences; the second term on the right hand side of Eq. 3.7. This is not surprising since the Lindblad relaxation matrix has the following eigenvalue structure: one zero eigenvalue (corresponding to equilibrium) and two complex conjugate eigenvalues with a negative real part that induce oscillations in the populations and coherences not at the natural frequency of the system. In the secular Redfield, these two eigenvalues are trivially obtained from the first term on the right hand side of Eq. 3.7 and the only oscillations come from the ϵ₂−ϵ₁+Im(κ_12,12) term.

DISCUSSION

We have demonstrated how the Lindblad QME can generalize the Redfield relaxation tensor in the secular approximation and couple populations and coherences. Elements of the relaxation superoperator were recast in terms of correlation coefficients of system-bath coupling variables. The secular approximation is recovered when these variables are uncorrelated. The coupling between populations and coherences is induced by correlations of the secular Redfield parameters (population relaxation and pure dephasing rates).

In the weak coupling limit, the transport from coherences to populations must vanish at zero temperature where one of the population relaxation rates is zero. Population-coherence transfer is observed at higher temperatures. Our simulations which span the low Δ∕k_BT>1 to the high Δ∕k_BT<1 temperature regime demonstrate how the population oscillations emerge. A word of caution must be made about Eq. 4.8. Even if η is large at high temperatures, it does not mean that strong signatures of the couplings will be observed for all parameter regimes. At high T, the populations and coherences rapidly decay to equilibrium and the effects of the couplings between populations and coherences may not be observable. The population oscillation frequency is not simply given by the isolated system energies and is affected by system-bath couplings.

Figures 12 were generated using the maximum coupling between population and coherences allowed by our Lindblad procedure in the weak coupling regime. The couplings can be decreased by lowering the degree of correlations between the a, b, and c variables. These correlations may be affected by temperature as well, yielding more complicated dependence of the dynamics on the temperature. The population relaxation timescales and the coherence pure dephasing rates can be obtained from Redfield theory. The remaining correlations must be obtained by fitting to experiment.

Relaxing the weak coupling condition [Eq. 3.1] introduces additional free parameters into the Lindblad equation. The coupling with the bath then modifies the original system Hamiltonian; at long times, the density matrix will evolve to a nondiagonal form in the original basis. One can always transform the system to a new eigenstate basis where coherences at equilibrium vanish. The QME in this new basis set is still in the Lindblad form. The exciton analysis and all excitons properties (transition amplitudes and frequencies) should be calculated in this new basis set which complicates the analysis. We have performed strong coupling simulations by maximizing population-coherence interaction using d_α=0 in Eq. 2.10 (not shown). This allowed us to explore further the Lindblad parameters space. The results were qualitatively similar to the weak coupling regime. Note that the full Redfield theory satisfies Eq. 3.1 only for i=j. Thus it does not retain the pure system eigenstates at equilibrium as well.

The full quantum dissipative dynamics may be simulated by including bath dynamics into simulations without invoking perturbation theory. The full Redfield theory is microscopic and guarantees realistic system dynamics under certain conditions implied in their derivation. Equation 2.1 is limited by the second order to the system-bath coupling so it holds only when the system-bath coupling is much smaller than the energy-level splitting Δ of the system eigenstates. Additionally, the bath correlation time must be much shorter than Δ⁻¹. Note that perturbation theory error may accumulate during the density matrix propagation and it may grow at long propagation times. The secular approximation cures this problem at the expense of missing some physical effects, such as population oscillations due to quantum evolution of coherences. The Redfield theory within the secular approximation leads to a particular form of the Lindblad equation. However, the Lindblad equation is not limited to the secular approximation.

Our simulations assumed an infinitely slow timescale for the irreversible decay of an excitation to the ground state. Using a finite irreversible time scale, Olaya-Castro et al.²⁷ and Mohseni et al.¹⁸ studied the efficiency of the energy transfer to the reaction center in photosynthetic complexes using a Lindblad equation corresponding to the secular Redfield theory. The time scale of such a recombination process for photosynthetic systems is in the nanosecond range and can safely be neglected in our 500 fs simulations.

We have reproduced all the qualitative features observed by Engel et al. in their study of FMO light-harvesting system. Figures 12 show that the coupling introduced between populations and coherences increases the lifetime of coherences, decreases the population equilibration time, and introduces small amplitude oscillations in the short time population dynamics unlike the secular Redfield theory. The theory yields a physically acceptable density matrix at all parameter regimes. The population oscillations and long-lived coherence oscillations predicted by the Lindblad equations do not necessarily correspond to the difference between the energy levels of the isolated system. The observed oscillations can have higher frequency component than cannot be accounted for by the Redfield frequency shift. This directly arises from the coupling between coherences and populations.

Thorwart et al.³⁴ argued that long-lived coherences can be the result of non-Markovian dynamics where the bath and system time scales are comparable. These models contain memory and go beyond the Lindblad equation. Also, note that our dimer model cannot account for coherence-coherence transfer which only occurs in systems made of three or more chromophores. This will be of interest for a future study.

APPENDIX A: GENERALIZATION TO N-SITE SYSTEM

For a system with N chromophores, Eq. 2.4 becomes

$${\dot{\rho }}_{ij}=-\frac{i}{\hslash }\left({ϵ}_i-{ϵ}_j\right){\rho }_{ij}+\sum _{\alpha }\sum _{p,q}\left(V_{ip}^{\left(\alpha \right)}{\rho }_{pq}{\left(V_{jq}^{\left(\alpha \right)}\right)}^{\ast }-\frac{1}{2}{\rho }_{ip}{\left(V_{qp}^{\left(\alpha \right)}\right)}^{\ast }{V}_{qj}^{\left(\alpha \right)}-\frac{1}{2}{\left(V_{pi}^{\left(\alpha \right)}\right)}^{\ast }{V}_{pq}^{\left(\alpha \right)}{\rho }_{qj}\right).$$ (A1)

Therefore, we can recast Eq. 2.2 with

$${\kappa }_{ij,kl}=-⟨V_{ik}{V}_{jl}^{\ast }⟩+\frac{{\delta }_{ki}}{2}\sum _q⟨V_{ql}^{\ast }{V}_{qj}⟩+\frac{{\delta }_{lj}}{2}\sum _q⟨V_{qi}^{\ast }{V}_{qk}⟩,$$ (A2)

where the correlations are defined by Eq. 2.9.

APPENDIX B: REDFIELD RELAXATION TENSORS

In this appendix, we list the Redfield relaxation tensors corresponding to the Hamiltonian described in Sec. 4 at six different temperatures calculated using Eqs. (370)–(375) of Ref. 16. When we write ρ as a column vector (ρ=(ρ₁₁,ρ₂₂,ρ₁₂,ρ₂₁)^T) in Eq. 2.2, we get for λ=35 cm⁻¹ (elements of κ are in cm⁻¹),

$$-\kappa \left(T=77\text{K}\right)=\left(\begin{array}{cccc}-1.21965& 20.115& 22.1644& 22.1644\\ 1.21965& -20.115& -22.1644& -22.1644\\ 0.39629+i2.68453& -6.53577+i15.8548& -25.0707-i20.267& 10.6673-i20.267\\ 0.39629-i2.68453& -6.53577-i15.8548& 10.6673+i20.267& -25.0707+i20.267\end{array}\right),$$ (B1)

$$-\kappa \left(T=131\text{K}\right)=\left(\begin{array}{cccc}-4.50555& 23.4009& 37.7084& 37.7084\\ 4.50555& -23.4009& -37.7084& -37.7084\\ 1.46394-i1.87351& -7.60342+i20.4129& -38.4576-i34.2952& 13.9532-i34.2952\\ 1.46394+i1.87351& -7.60342-i20.4129& 13.9532+i34.2952& -38.4576+i34.2952\end{array}\right),$$ (B2)

$$-\kappa \left(T=185\text{K}\right)=\left(\begin{array}{cccc}-8.54612& 27.4415& 53.2523& 53.2523\\ 8.54612& -27.4415& -53.2523& -53.2523\\ 2.77681-i6.51188& -8.91628+i25.0512& -52.5993-i48.5706& 17.9938-i48.5706\\ 2.77681+i6.51188& -8.91628-i25.0512& 17.9938+i48.5706& -52.5993+i48.5706\end{array}\right),$$ (B3)

$$-\kappa \left(T=239\text{K}\right)=\left(\begin{array}{cccc}-12.8804& 31.7757& 68.7962& 68.7962\\ 12.8804& -31.7757& -68.7962& -68.7962\\ 4.18509-i11.161& -10.3246+i29.7004& -67.0346-i62.8792& 22.328-i62.8792\\ 4.18509+i11.161& -10.3246-i29.7004& 22.328+i62.8792& -67.0346+i62.8792\end{array}\right),$$ (B4)

$$-\kappa \left(T=293\text{K}\right)=\left(\begin{array}{cccc}-17.3548& 36.2501& 84.3401& 84.3401\\ 17.3548& -36.2501& -84.3401& -84.3401\\ 5.63892-i15.8106& -11.7784+i34.3499& -81.6101-i77.189& 26.8024-i77.189\\ 5.63892+i15.8106& -11.7784-i34.3499& 26.8024+i77.189& -81.6101+i77.189\end{array}\right),$$ (B5)

$$-\kappa \left(T=347\text{K}\right)=\left(\begin{array}{cccc}-21.9062& 40.8016& 99.8841& 99.8841\\ 21.9062& -40.8016& -99.8841& -99.8841\\ 7.11778-i20.4587& -13.2573+i38.9981& -96.2626-i91.4945& 31.3539-i91.4945\\ 7.11778+i20.4587& -13.2573-i38.9981& 31.3539+i91.4945& -96.2626+i91.4945\end{array}\right),$$ (B6)

and the second set for λ=65 cm⁻¹,

$$-\kappa \left(T=77\text{K}\right)=\left(\begin{array}{cccc}-2.26507& 37.3564& 41.1625& 41.1625\\ 2.26507& -37.3564& -41.1625& -41.1625\\ 0.735968+i4.98555& -12.1379+i29.4447& -46.5598-i37.6387& 19.8107-i37.6387\\ 0.735968-i4.98555& -12.1379-i29.4447& 19.8107+i37.6387& -46.5598+i37.6387\end{array}\right),$$ (B7)

$$-\kappa \left(T=131\text{K}\right)=\left(\begin{array}{cccc}-8.36745& 43.4588& 70.0298& 70.0298\\ 8.36745& -43.4588& -70.0298& -70.0298\\ 2.71875-i3.47937& -14.1206+i37.9096& -71.4213-i63.691& 25.9131-i63.691\\ 2.71875+i3.47937& -14.1206-i37.9096& 25.9131+i63.691& -71.4213+i63.691\end{array}\right),$$ (B8)

$$-\kappa \left(T=185\text{K}\right)=\left(\begin{array}{cccc}-15.8714& 50.9627& 98.8971& 98.8971\\ 15.8714& -50.9627& -98.8971& -98.8971\\ 5.15693-i12.0935& -16.5588+i46.5237& -97.6844-i90.2025& 33.417-i90.2025\\ 5.15693+i12.0935& -16.5588-i46.5237& 33.417+i90.2025& -97.6844+i90.2025\end{array}\right),$$ (B9)

$$-\kappa \left(T=239\text{K}\right)=\left(\begin{array}{cccc}-23.9207& 59.012& 127.764& 127.764\\ 23.9207& -59.012& -127.764& -127.764\\ 7.77231-i20.7276& -19.1742+i55.1579& -124.493-i116.776& 41.4663-i116.776\\ 7.77231+i20.7276& -19.1742-i55.1579& 41.4663+i116.776& -124.493+i116.776\end{array}\right),$$ (B10)

$$-\kappa \left(T=293\text{K}\right)=\left(\begin{array}{cccc}-32.2303& 67.3216& 156.632& 156.632\\ 32.2303& -67.3216& -156.632& -156.632\\ 10.4723-i29.3625& -21.8742+i63.7928& -151.562-i143.351& 49.776-i143.351\\ 10.4723+i29.3625& -21.8742-i63.7928& 49.776+i143.351& -151.562+i143.351\end{array}\right),$$ (B11)

$$-\kappa \left(T=347\text{K}\right)=\left(\begin{array}{cccc}-40.683& 75.7744& 185.499& 185.499\\ 40.683& -75.7744& -185.499& -185.499\\ 13.2187-i37.9948& -24.6206+i72.4251& -178.773-i169.918& 58.2287-i169.918\\ 13.2187+i37.9948& -24.6206-i72.4251& 58.2287+i169.918& -178.773+i169.918\end{array}\right).$$ (B12)