Abstract
In this article the authors evaluate a recently proposed variable dose (VD)-digital breast tomosynthesis (DBT) acquisition technique in terms of the detection accuracy for breast masses and microcalcification (MC) clusters. With this technique, approximately half of the total dose is used for one center projection and the remaining dose is split among the other tomosynthesis projection views. This acquisition method would yield both a projection view and a reconstruction view. One of the aims of this study was to evaluate whether the center projection alone of the VD acquisition can provide equal or superior MC detection in comparison to the 3D images from uniform dose (UD)-DBT. Another aim was to compare the mass-detection capabilities of 3D reconstructions from VD-DBT and UD-DBT. In a localization receiver operating characteristic (LROC) observer study of MC detection, the authors compared the center projection of a VD acquisition scheme (at 2 mGy dose) with detector pixel size of 100 μm with the UD-DBT reconstruction (at 4 mGy dose) obtained with a voxel size of 100 μm. MCs with sizes of 150 and 180 μm were used in the study, with each cluster consisting of seven MCs distributed randomly within a small volume. Reconstructed images in UD-DBT were obtained from a projection set that had a total of 4 mGy dose. The current study shows that for MC detection, using the center projection alone of VD acquisition scheme performs worse with area under the LROC curve (AL) of 0.76 than when using the 3D reconstructed image using the UD acquisition scheme (AL=0.84). A 2D ANOVA found a statistically significant difference (p=0.038) at a significance level of 0.05. In the current study, although a reconstructed image was also available using the VD acquisition scheme, it was not used to assist the MC detection task which was done using the center projection alone. In the case of evaluation of detection accuracy of masses, the reconstruction with VD-DBT (AL=0.71) was compared to that obtained from the UD-DBT (AL=0.78). The authors found no statistically significant difference between the two (p-value=0.22), although all the observers performed better for UD-DBT.
Keywords: microcalcification, mass detection, breast tomosynthesis, dose
INTRODUCTION
Breast cancer is the most prevalent type of cancer in women, with an annual incident rate of 126.1 per 100 000 women in the US.1 Early detection with screening x-ray mammography has reduced the mortality rate, with screening (primarily x-ray mammography) lowering the rate by about 30%.2 However, mammography suffers from low sensitivity and specificity in cancer detection, predominantly due to tissue overlap. Although recent advances in detector technology have provided large-area, low-noise detectors for breast imaging, leading to increased use of digital mammography (DM), DM is still a two-dimensional (2D) imaging technique and suffers from the tissue-overlap problem. Recent years have witnessed increased research on acquisition techniques and image reconstruction algorithms3, 4, 5, 6 for digital breast tomosynthesis (DBT). With DBT, the three-dimensional (3D) breast volume is reconstructed from a series of projections acquired over a limited angular range. Although preliminary results with DBT have been encouraging, there have been anecdotal reports suggesting limitations in accurately portraying small microcalcifications (MCs) using this technique. Accurate detection of MCs in a screening environment is especially important for the detection of ductal carcinoma in situ (DCIS). DCIS is highly prevalent, and since it is thought to be a direct precursor to invasive cancer, its early detection can potentially contribute to decreased breast-cancer mortality. With conventional mammography, Feig and Shaber7 and Anderson8 reported that 89% and 95%, respectively, of DCIS were observed on the basis of mirocalcifications alone.
MC detectability in DBT can be affected by many factors including the detector type, reconstruction and acquisition parameters, blur due to source∕detector motion, and patient motion during acquisition. One of the initial clinical trial studies9 using a prototype Hologic (Bedford, MA) system concluded that “Subjectively, tomosynthesis has comparable or superior image quality to that of film-screen mammography and could decrease the recall rate when used adjunctively with digital screen mammography.” This study also reported that “tomosynthesis was inferior to diagnostic mammography in characterization of calcifications.” A more recent, small clinical study10 using a General Electric (GE) prototype system reported equal or better visibility of MC using DBT in comparison to film mammography. However this study did not assess a detection accuracy, and the MCs that were already visible using mammograms were viewed using DBT and evaluated for visibility.
X-ray imaging of the breast has the advantage of detecting both masses and MCs (unlike imaging modalities such as MRI and optical imaging, both of which do not detect MCs). One of the difficulties in optimizing DBT systems is due to the fact that the objective is to image both masses and MCs using a single 3D image for each patient. A better approach to breast-cancer screening might be to combine the separate strengths of mammography and DBT. Mammography yields very good MC detectability due to low quantum noise and the absence of source∕detector and patient motion, while DBT appears to have the edge for mass detection on account of reduced tissue overlap. One such approach suggested by Nishikawa et al.3 is a variable-dose digital breast tomosynthesis (VD-DBT) technique in which one-half of the total dose is allotted to acquiring the central projection and the other half is distributed among the other projections. It was proposed that the central projection would be primarily used to detect MCs, while the reconstructed 3D images (which can be at a lower resolution) would primarily be used to detect larger masslike lesions. Compare this to the standard uniform dose digital breast tomosynthesis (UD-DBT) approach where the total dose is equally distributed among the projection angles and the reconstructed 3D image is used to detect both masses and MCs
For any such newly proposed acquisition methodology or detection strategy, evaluation studies are required before its merits and feasibility can be determined. For this paper, we applied localization receiver operating characteristic (LROC) methodology11 with simulated breast images and human observers to evaluate the relative merits of the VD-DBT and UD-DBT strategies for MC and mass detection. Section 2 describes the simulation methods and details of the observer studies. Results and discussion are provided in Secs. 3, 4, respectively.
METHODS AND MATERIALS
A DBT computer simulation was used in evaluating the performance of the VD-DBT methodology. This simulation applied realistic models of the x-ray spectra, breast anatomy, and of the signal and noise transport through the breast and an indirect conversion flat-panel detector. Focal spot and detector blurring were also modeled. In this section, each of these components of our DBT system simulation is described as are our 3D models of malignant masses and MC clusters (MCCs).
The DBT system
Breast tomosynthesis using a rotating source and detector geometry was modeled, with 21 projection views obtained over a ±30° arc with respect to the center of rotation. The x-ray spectrum model assumed a 30 kVp molybdenum anode source,12 with x-ray fluence scaled to provide a specified mean glandular dose (MGD) to a 5 cm thick compressed breast. To perform this scaling, we determined the x-ray fluence per projection that would give the specified mean glandular dose for UD-DBT acquisition from the breast dosimetry data (DgN coefficients) generated by a Monte Carlo simulator.13 For VD-DBT the spectra were scaled to provide half of the allotted MGD for the center projection, while the spectra for the rest of the (N−1) projections was scaled to provide the other half of the allotted MGD. Focal spot blurring with a 300 micron focal spot size was modeled using a Gaussian modulation transfer function.14 Projection images were computed by modeling the x-ray transmission through breast tissue using Siddon’s ray tracing algorithm.15 Subsequent signal and noise propagation through an indirect 100-μm-thick CsI-based flat-panel detector with a 100 μmpixel size was simulated using a serial cascade model.16, 17 The scintillator blurring was modeled using an empirically measured presampling modulation transfer function (MTF).
The breast model
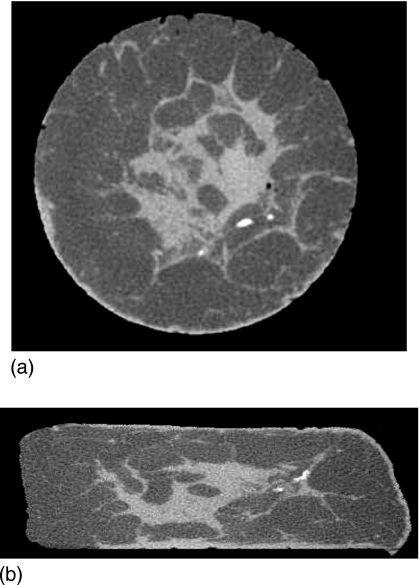
Generating a realistic object model for x-ray imaging of the breast is challenging due to the complex breast anatomy. Several mathematical models have been proposed including a power-law noise model18 and the anthropomorphic Bakic breast phantom.19 While such models have proved useful for gaining a better understanding of breast CT and tomosynthesis, they might not be adequate as the basis of a clinically realistic observer study for the assessment of mass and MC detection. In order to perform clinically realistic observer studies, one would need breast models that look as close as possible to real breast images obtained clinically. Recently we have been developing a breast model based on high-resolution, low-noise cone-beam CT images from mastectomy specimens.20 Freshly obtained mastectomy specimens were imaged (under an IRB approved protocol) in specially designed holders that provided for specimen compression to a degree appropriate for DBT. Figure 1 shows the bench-top, cone-beam CT system with rotating object holder that was used to image the specimens. The object holder rotates 360°-collecting a total of 300 projections. The average size of the breast in the compressed breast holder is 16×5×10 cm3. The maximum width and the height of each breast specimen vary slightly depending on the size of the mastectomy specimen. Figures 2a, 2b show reconstructed slices from the same mastectomy specimen imaged without and with compression respectively. The reconstruction was done with a 200 μm voxel size.
Figure 1.
Photograph of our bench-top cone-beam CT system where the mastectomy specimens are imaged by placing them in holders.
Figure 2.
(a) Cone-beam CT image of the mastectomy specimen when placed in a normal mold (uncompressed breast object). (b) Cone-beam CT image of the same mastectomy specimen when placed in a compressed breast mold.
These compressed specimen reconstructions were then used to develop breast models for tomosynthesis simulation. It was observed that cone-beam CT images of the breast show predominantly two gray levels; one representing fibroglandular tissue and the other representing adipose tissue (neglecting skin and microcalcifications). Segmentation of the mastectomy specimens was performed to classify each voxel as either fibroglandular or adipose tissue. For this study, each specimen was segmented using a threshold value in the CT image. All breast voxels above this threshold were labeled as fibroglandular tissue, and all voxels below this threshold were labeled as adipose tissue. The region outside the breast was labeled as air. With this segmentation approach, noise in the reconstructed image does not translate into noise in the breast-object model. Also, dividing the entire volume into predominantly adipose and glandular regions allows the use of energy dependent tissue attenuation coefficients as given by Johns and Yaffe.21
A total of eight 3D breast phantoms was used for the mass-detection study. Each volume provided 6 background slices, for a total of 48 slices. These slices were selected at random except that a separation of 0.6–0.8 cm was maintained between the neighboring slices. From visual inspection, this was determined to be a sufficient distance for the six slices to appear as completely different backgrounds when displayed slice by slice. For each study, 46 out of the 48 slices were used both with and without an abnormality, for a total of 92 different cases, of which 10 were training images and 82 were study images. Each abnormality was randomly placed in a given slice. As the MC study was performed later, there were more breast phantoms, leading to 24 training images and 82 study images,
The mass model
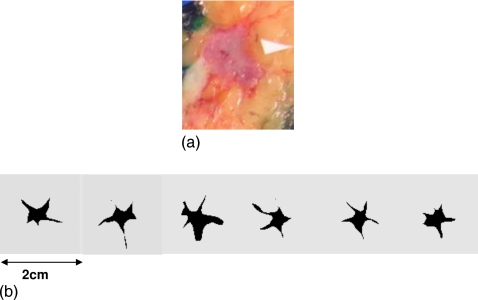
Several researchers reported observer studies with simulated mass models for 3D breast imaging system evaluation.22, 23 Many of the other existing 3D mass models use random growth model based simulations or other geometric models which might look realistic in a 2D projection, yet need improvement in order to be used in observer studies involving radiologists. Figure 3a shows a histological section that bisects a spiculated invasive ductal carcinoma. It is well known that a strong indicator for carcinoma in 2D mammography is an irregularly shaped mass with spiculated borders and several researchers have developed 2D mass models that mimic these characteristics in a mammogram.24, 25 Based on our observations of malignant masses in our CT specimen reconstructions and the corresponding histopathologic sections, most of which showed irregular or spiculated borders, it appears that the same modeling requirement applies to 3D breast imaging. Hence our aim was to generate models of 3D masses having spiculated borders. To do this, spiculated 2D objects were hand drawn, and then connected using a custom program to create a nonuniform rational B-spline (NURBS) surface. Although somewhat ad hoc, from a subjective standpoint this procedure was deemed to produce realistic 3D mass simulations.
Figure 3.
(a) Histopathology slice of a invasive ductal carcinoma. (b) Various slices of a 3D simulated lesion.
Figure 3b shows a few slices (slice numbers: 39, 47, 55, 65, 77, and 80, respectively) from a single 3D mass model containing 100 slices in total. Spiculations arise from a base volume that is, on average, smaller than 1 cm3. Eight unique mass models each one of size ∼1 cm or less of the center were developed for our study. These simulated masses were digitally embedded in the breast model (one per breast model), replacing voxels in the background tissue. Every voxel within the simulated mass was assumed to have an energy-dependent attenuation coefficient for invasive ductal carcinoma, as suggested by Johns and Yaffe.21
Microcalcifications
Although previous simulation studies have investigated MC detection with mammography and 3D imaging modalities like CT and tomosynthesis,26, 27 most of these studies used simpler breast backgrounds and∕or MCCs arranged in a regular square or rectangular array pattern. It is possible that such patterns may be easier for humans to detect, especially with simple geometrical background structures. In our study, 2D MCCs formed in irregular patterns were generated in random distributions.
Our study objective was to evaluate the detection of challenging MCCs. Eight different cluster shapes were developed for this study and each cluster consisted of seven MCs. The individual MCs had diameters of 150 or 180 μm, although all MCs in a given cluster were of the same size. The average area covered by a cluster was less than 1 cm2. To minimize sampling effects, the MCCs were generated as spheres using a finer voxel grid (about ten times smaller than the individual calcification diameters) that was subsequently resampled before projection. Within the breast phantom, each cluster was confined to a 2D plane, parallel to the detector plane. The reason for this was that our observer studies are currently done by displaying slices of reconstructed images and not the 3D image itself. X-ray attenuation properties of calcium phosphate (modeling malignant breast calcifications) were used for the entire energy range of interest.
Projection data for cases with MCCs
In the mass-detection study, the masses were embedded in the breast background volume and projections of the whole volume were generated. To simulate cases with MCCs, however, separate MCC projections were added to normal-breast projections. In this section, we describe how the projections were combined. The breast model was divided into voxels, with each voxel i represented by its percentage composition of the adipose tissue (Ci). Since it is assumed that each voxel is composed of a mixture of adipose and fibroglandular tissue, a voxel’s percentage composition of adipose tissue is given as Ci and its percentage composition of fibroglandular tissue is given as (1−Ci). If μa(E) and μg(E) represent the energy-dependent attenuation coefficient of adipose and fibroglandular tissue, respectively, then the projection at pixel j on the detector along a line Lj is given by
| (1) |
where li is the length of Lj inside voxel i.
Instead of taking projections for each energy, the equation above can be simplified to
| (2) |
Thus only two energy-independent projections [indicated by the summations in Eq. 2] are needed to express the projection data at any defined energy level.
To simulate the presence of a calcification cluster in the breast volume, we add the projection of the calcification cluster from the desired 3D location in the same imaging configuration. The attenuation values of the calcification cluster are chosen as the attenuation values of calcium phosphate. If Lc represents the length of the line through the calcification, the equation for the projection through the breast with superimposed projection of the microcalcification(s) is given by
| (3) |
where μc(E) is the energy-dependent attenuation coefficient of calcification.
For an energy range Emin to Emax, the equation for the total attenuated fluence upon propagation through the breast is
| (4) |
where I0(Ek) represents the exposure on the breast for energy Ek at a given angle. A discretized energy spectrum at 1 keV interval was used for the simulation.
To model signal and noise propagation through the CsI-based flat-panel detector, the detector is viewed as a cascaded linear system.16, 26 The interaction process of x rays in the flat-panel detector can be considered as a cascade of six stages:17 Interaction of x rays with the detector material (absorption), generation and emission of optical quanta from x-ray photons, stochastic spreading of the optical quanta towards the detector, coupling of optical quanta, integration of quanta by photodiodes, and addition of electronic noise. Thus, this simulation models images with realistic signal and noise in the detector, as well as blurring effects. The individual projections were obtained using the Siddon’s ray tracing method.15
Image reconstruction
The projections were acquired on a detector with pixel size of 100 μm. A standard filtered backprojection method28 was used to form the reconstructions with isotropic voxel size of 200 μm for the case of the mass-detection study. For the case of the calcification detection study, we reconstructed the images with isotropic voxel size of 100 μm. An example of a MC cluster projection in the VD-DBT center projection is shown in Fig. 4a. Figure 4b shows the corresponding reconstructed slice area from UD-DBT reconstructed with a pixel size of 100 μm. Slabbing was not performed since the clusters were confined to single plane and there was no three-dimensional cluster that needed to be detected. To reduce the noise in the tomosynthesis image, a post reconstruction fifth-order 3D Butterworth filter was used. For the images used for assessing mass detectability (with a reconstruction voxel size of 200 μm) the cut off frequency used was 0.25 cycles∕pixel and for the MC detectability (where the reconstructions were with a pixel size of 100 μm), the cut off frequency was 0.2 cycles∕pixel.
Figure 4.
(a) Shows the center projection (pixel-size=100 microns) of VD-DBT showing the slice with the MC cluster. (b) Shows the corresponding reconstructed slice (pixel-size=100 microns) of the UD-DBT. The area containing the MC cluster is enclosed in the circle in both the images. Dimension of each image is 1.5 cm×1.5 cm.
Acquisition methodology and LROC observer studies
As a guideline, we assumed that the MGD for screening should not exceed the total dose currently used in two-view mammography.29, 30 Hence, in this study we have used a total MGD of 4 mGy (for 5 cm thick breast models) to evaluate the VD-DBT and UD-DBT acquisition techniques. We performed separate LROC observer studies to evaluate MC and mass detectability. In the first study, we compared MC detectability using the center projection of VD-DBT and a reconstructed slice from UD-DBT. The second study compared mass detectability using reconstructed slices from VD-DBT and UD-DBT.
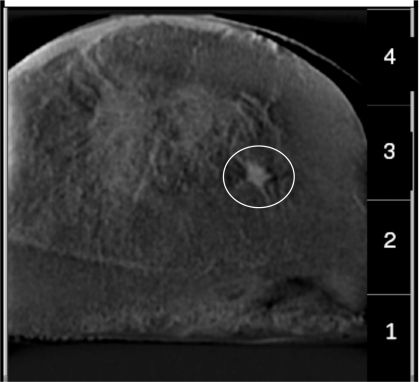
An LROC analysis was used for comparing the performance of the two acquisition techniques. The figure of merit used to assess performance was the area under the LROC curve (AL). Each LROC study consisted of the observer first reading a set of training images with feedback, followed by the study images. The observer’s task was to localize the abnormality within the displayed image and give a confidence rating for each image. An example of the LROC display that was used for the mass study is shown in Fig. 5. Four confidence ratings were used; (1) high confidence lesion present, (2) low confidence lesion present, (3) low confidence lesion absent, and (4) high confidence lesion absent. If for a given displayed image, the observer was confident that there was no abnormality present, they were instructed to click on an arbitrary location within the image and select rating 4. If the observer suspected an abnormality at a certain location, they were instructed to click on the center of the abnormality and choose one of the three ratings from 1, 2, or 3. Each of the observers read four major sets of images: (1) The VD-DBT center projection for MC detection, (2) a UD-DBT reconstructed image for MC detection, (3) a VD-DBT reconstructed image for mass detection, and (4) a UD-DBT reconstructed image for mass detection. For the case of the MC study, the projection image (detector pixel size of 100 μm) from the VD scheme was compared against the reconstructed slices (resolution of 100 μm) using FBP for UD-DBT. The display for the images was 9×9 cm2. Edges of images that exceeded this display window were chopped off. For the case of the mass study, the reconstructed slices from VD-DBT were compared to the reconstructed slices from UD-DBT. Here, the reconstruction voxel size was 200 μm, and the images displayed for the LROC study were 4.5×4.5 cm2.
Figure 5.
A typical LROC display that was used in this study. A simulated mass can be seen in this slice (in the circle). The image display size was 4.5 cm×4.5 cm and the pixel size is 200 microns.
MC detection study
Projection sets were simulated with inserted MC clusters in the breast background using both the UD-DBT and VD-DBT techniques. For UD-DBT, 21 projection views each of 0.19 mGy (i.e., 4 mGy total allotted MGD divided by 21 views) were generated and the 3D reconstructed image was formed. For VD-DBT, 21 projection views were also simulated; however, for this method, the center projection was allotted a dose of 2 mGy, and the remaining 20 projection were allotted 0.1 mGy each (i.e., 2 mGy total allotted MGD divided by 20 views).
As previously described, one of the goals of this study is to evaluate whether MC detection accuracy would be improved by reading the center projection of a VD tomosynthesis acquisition as compared to detecting MCCs from conventional UD-DBT slices. To evaluate this question, 24 training images and 82 study images were generated for both the UD-DBT and VD-DBT methods, as described above. Half of these study images contained a MCC and half did not. For the UD-DBT reconstructed data sets, the center slice bisecting the MCC was used (parallel to the detector), while for the VD-DBT study, the center projection image was used. Observer studies were conducted in a darkened room using a monitor with a perceptually linearized grayscale.31 Before conducting each reading session, each observer was required to undergo training in reading images for the method to be evaluated. This consisted of reading 24 images prepared for training, approximately half with MCC present. During this training session, feedback was provided to the reader after each selection. Immediately after the training session was completed, the comparison study was performed. Each session consisted of reading 82 images. The observers consisted of four medical physicists. Observer confidence rating and the suspected MCC location were recorded for all the images displayed. Swensson’s method11 was used to fit the data and obtain the area under the LROC curve.
LROC study for mass detection
Another goal of this study was to investigate the penalty in detecting masses by reading tomosynthesis slices obtained using a VD-DBT acquisition versus the UD-DBT method. To compare these two approaches, two tomosynthesis projection sets were generated. For UD-DBT, 21 projection views each of 0.19 mGy (i.e., 4 mGy total allotted MGD divided by 21 views) were generated and 3D reconstruction was performed. For VD-DBT, 21 projection views were also simulated; however, for this method, the center projection was allotted 2 mGy, and the remaining 20 projection views were allotted 0.1 mGy each (i.e., 2 mGy total allotted MGD divided by 20 views) and reconstructed images were obtained using this projection set. In total, 92 reconstructions from each method were generated, half of which contained a mass of 1 cm, simulated as described in Sec. 2C. Ten of these reconstructions were used for training, whereas the remaining 82 were used for the study evaluation. For each 3D reconstruction, a 2D slice was extracted for viewing. For those cases with a mass present, this slice bisected the center of the mass. Using this image set, LROC analysis was performed, as described above. Images were reconstructed with a reconstructed voxel size of 200 μm.
A two-way analysis of variance (ANOVA) (Ref. 32) study was performed to estimate the statistical significance of the differences in techniques and also to estimate the statistical significance in the performance difference between the three observers.
LROC statistical power analysis
A post-hoc assessment of the statistical power in our LROC analyses was also conducted. The Monte Carlo-based process accounted for observer variability but not case variability. For a given strategy in an LROC study, the average and standard deviation of the individual observer performances defined a normal distribution on area under the LROC curve (AL) for a population of observers. A sample from this distribution is associated with the mean and standard deviation parameters for the binormal model for LROC rating data, as shown in Eqs. (7)–(10) of Ref. 11. An equivariance assumption for the binormal model simplified these calculations. A total of 5000 sets of rating data based on four observers and 82 images (41 abnormals and 41 normals) per strategy were created and analyzed for the MC LROC study. The power analysis was carried out with an assumption of no correlation between an observer’s scores for the two strategies.
RESULTS
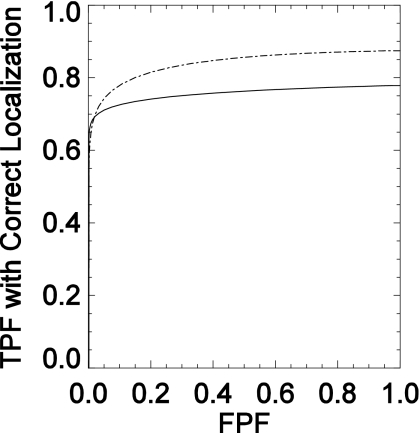
LROC study results assessing human-observer performance for MC and mass detection were obtained from the VD-DBT and UD-DBT images. Figure 6 compares the LROC curves for MC detectability averaged over the four observers. The curve for the UD-DBT reconstructions with a 100 μm pixel width is seen to be higher than the VD-DBT curve over most of the x axis. Table 1 lists the areas under the LROC curves for these two acquisition techniques for the four observers. The stated uncertainties are the standard errors reported by Swensson’s LROC fitting software.11 The average area for the VD-DBT technique was 0.76±0.04, while the UD-DBT technique had an average area of 0.84±0.01. The uncertainties represent the standard deviation in the observer performance. There is a higher interobserver agreement for the UD-DBT study in comparison to the VD-DBT study. This could be attributed to the fact that the center projection from the VD scheme is acquired with 2 mGy dose leading to a noisier projection image in comparison to the UD-DBT reconstruction image obtained from a projection set that received a total of 4 mGy dose. A two-way ANOVA found statistically significant differences (at a significance level of 0.05) in performance between the acquisition techniques (p=0.038) but not between pairs of observers (p=0.49). However, as indicated by Table 1, all four observers performed slightly better with the UD-DBT images than with the VD-DBT images.
Figure 6.
LROC curves (x-axis is the false positive fraction (FPF) and y-axis is the true positive fraction (TPF) with correct localization) for MC detectability using the central projection of VD-DBT (solid line) and using the reconstructed slice of UD-DBT (dashed line).
Table 1.
Comparison of area under the LROC curve for VD-DBT (center projection) and reconstrcucted slice of UD-DBT for the four observers (MC detection).
| AL for UD-DBT | AL for VD-DBT | |
|---|---|---|
| Observer 1 | 0.83±0.06 | 0.73±0.07 |
| Observer 2 | 0.84±0.05 | 0.80±0.06 |
| Observer 3 | 0.84±0.06 | 0.72±0.07 |
| Observer 4 | 0.84±0.04 | 0.79±0.06 |
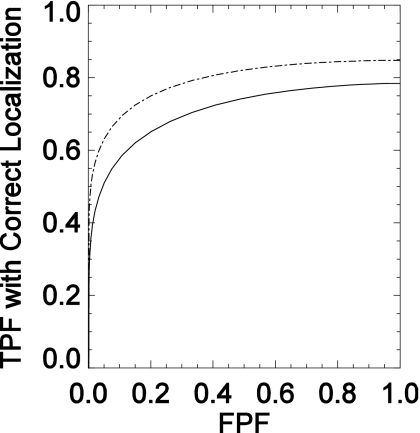
Figure 7 displays the average LROC curves for the mass-detectability study, while Table 2 gives the areas under the LROC curve and the standard errors. The average areas for the VD-DBT and UD-DBT techniques were 0.71±0.02 and 0.78±0.08, respectively. The uncertainties here represent the standard deviation in the observer performance. A two-way ANOVA did not show a statistically significant difference between the two techniques (p=0.22) or between any two observers (p=0.44) at a significance level of 0.05.
Figure 7.
LROC curves (x-axis is the false positive fraction (FPF) and y-axis is the true positive fraction (TPF) with correct localization) for UD-DBT (dotted) and VD-DBT (solid) for mass detection study.
Table 2.
Comparison of area under the LROC curve for UD-DBT and VD-DBT for the 3 observers (mass detection).
| AL for UD-DBT | AL for VD-DBT | |
|---|---|---|
| Observer 1 | 0.87±0.08 | 0.72±0.07 |
| Observer 2 | 0.71±0.07 | 0.72±0.07 |
| Observer 3 | 0.77±0.07 | 0.69±0.07 |
Since the statistical significance for MC study was borderline, a statistical power of this significance test was determined by our post-hoc analysis and was found to be 0.25. The simulation assumed there was no correlation between an observer’s scores for the two acquisition techniques. The actual correlation coefficient for these scores was 0.19 for the MC study.
DISCUSSION AND FUTURE WORK
The purpose of this investigation was to examine the possibility of combining digital mammography and breast tomosynthesis for breast-cancer detection. Radiologists are trained to detect both masses and MCs from mammograms and are thus accustomed to looking at these images. It seems reasonable to expect that any widespread clinical transition from mammography to tomosynthesis might take at least as long as the time required for digital mammography to be accepted in place of film-screen mammography. An acquisition-and-detection technique combining the benefits of both mammography and 3D imaging could help to ease this transition by yielding better cancer detection with lower radiation dose.
The VD-DBT technique is one such candidate. In this paper we evaluated two key questions: (1) How would MC detectability compare using the center view of VD-DBT alone as opposed to using the 3D reconstruction from the UD-DBT, and (2) would the accuracy of mass detection be sacrificed using 3D reconstructed images of VD-DBT over UD-DBT? In both studies, UD-DBT slightly outperformed VD-DBT. The mass-detection results do not show a statistically significant difference when using reconstructed slices from the VD-DBT and UD-DBT techniques. However, the difference in MC detection between using the center projection image (with 2 mGy dose) from the VD-DBT projection set and using a slice from the UD-DBT 3D reconstruction (100 μm pixel width) generated from a projection set with 4 mGy dose was shown to be statistically significant. For this study, observers did well with either technique at detecting MCCs with calcifications of 180 μm. The difference in performance between the two techniques resulted mainly from detection of the smaller, 150 μm calcifications. It should be noted that this MC detection study for VD-DBT did not make use of the slices from the reconstructed image that was available; the effects of doing so will be evaluated in a future study. Our study cannot be considered as a direct comparison of mammography to tomosynthesis itself for MC detection since the center projection of VD-DBT received only 2 mGy and the UD-DBT images were obtained from a projection set that received a total of 4 mGy.
These MC results differ in comparison to our previously published results.33 We believe that this is primarily due to two limitations in the previous study which have been addressed for this paper. In Ref. 33, the individual MCs in some of the clusters were very close together (less than 100 μm), causing these clusters to exhibit a brighter-than-normal overall signal. Also, the tomosynthesis reconstructions in Ref. 33 were performed using a simple backprojection method and a voxel size of 200 μm. The current simulation has more-realistic MCCs and a more-accurate filtered-backprojection reconstruction method with a voxel size of 100 μm.
Another approach to cancer detection would be to obtain the mammogram and tomosynthesis images separately. Prototype DBT systems from Hologic, Inc., now undergoing clinical testing, acquire both DM and tomosynthesis imagery in two views [mediolateral oblique (MLO) and cranio-caudal (CC)]. A downside to this approach is increased dose compared to current mammography standards. For this reason, dose allocation with the VD-DBT technique should be studied in more detail, including the possibility of two-view VD-DBT (i.e., both CC and MLO views). The impact on the detection task with change in the dose distribution in the VD-DBT should be investigated. In the current paper we have taken the total dose to be 4 mGy (for a standard 5 cm compressed breast), which is close to the accepted average dose for two-view examination in mammography. Here, the center projection view receives an average dose of 2 mGy and the remaining 2 mGy is distributed among the remaining projections. The MGD used in DM is 3.8 mGy for one examination with an average dose of 1.88 mGy for the CC view, which is lower than the average dose for MLO views.30 Higher dose does not necessarily mean better detection. With proper dose allocation, a combined acquisition technique such as VD-DBT may be sufficient to improve cancer detection.
In the current study, a dose of 2 mGy was used at the center VD-DBT projection, which was primarily used for MC detection. It would be interesting to study the effect of changing the dose allocated to this central projection. Perhaps an increase in dose at the central projection while keeping the total dose constant would improve the overall VD-DBT performances. The effect of total dose in a single projection (mammogram) for MC and mass detection has been performed by Ruschin et al.34 Figures of merit from Ref. 34 and our study cannot be directly compared due to the differences in study methodologies. However, their study shows that total dose on the mammogram can affect MC detectability. In our future studies we plan to evaluate VD-DBT with various dose distributions and total dose levels.
VD-DBT would provide an easier transition for radiologists in moving from DM to DBT. In VD-DBT, a center projection view and a 3D reconstructed image set are both available. Hence radiologists would be able to use the center projection view just as they would a mammogram and look primarily for MCs. The 3D image would be primarily for mass detection but could also aid MC detection as needed. Usually in DBT images, slabbing is performed to improve the visibility of a 3D cluster. However, VD-DBT slabbing would not be required since MCs would mostly be detected at the center projection view. Slabbing increases structural overlap and can adversely affect mass detection, which will not be an issue in VD-DBT. Another advantage of using a VD-DBT system is that the existing computer aided diagnosis (CAD) tools could be used to assist MC detection at the center projection. CAD systems for mammograms have shown to perform better on MCs than on masses.35 In a UD-DBT system, which relies entirely on the 3D reconstructed image for MC detection, the possibility of missing MCs due to blurring and motion artifacts cannot be avoided. With fast x-ray pulses, motion blur could be reduced. However patient motion or breathing can also result in blurred images, resulting in reduced detectability of tiny MCs. Thus it would be advantageous to have an acquisition technique like VD-DBT, which can yield a “mammographylike” projection image (which will have minimal effects of motion) along with the 3D reconstructed image.
The simulation study presented here has generated realistic-looking images; hence the observer study closely mimics the clinical situation. Nonetheless, many approximations are made in any simulation study. Although a clinical trial might provide more information on how these methods compare, it would be difficult to perform a similar clinical study without subjecting patients to higher dose.
In some other important respects, the LROC studies presented in this paper should be viewed as a starting point for further investigation of VD-DBT. For example, no radiologists participated in the reading. Furthermore, the study resources were quite limited, with the mass-detection study there were three observers and for the MC study there were four observers and eight breast phantoms from which to draw cases. This is reflected in the low power of our statistical analyses. Given the observer variability tested in our Monte Carlo power simulations, reasonable power (in the range of 0.7–0.8) would require actual differences of approximately 0.2 in AL (roughly 2.5 times the differences measured in our work) between the UD-DBT and VD-DBT techniques. These power estimates likely understate the actual power in our studies because (1) correlations between an observer’s scores for the two techniques were not accounted for, and (2) the sample variances in observer AL were inaccurate estimates of population variance. Nonetheless, future studies certainly will require larger case sets.
Other study limitations that should be considered for future improvements are as follows: (1) Although the VD-DBT acquisition yielded both a single projection (equivalent to mammogram) and a 3D image, we have not used the slices from the 3D image to assist MC detection. (2) The tomosynthesis image display was 2D. The accuracy of mass detection would likely improve with 3D display of images and MC detection may suffer if the observer is not presented with the actual slice that has the calcification. The 3D display of images is more realistic and better matches a clinical study. (3) The abnormality locations were chosen randomly, but these locations should have some basis in the clinical probability of a lesion being positioned in certain locations of the breast. (4) The reconstruction method used herein was filtered backprojection. Future studies will investigate other reconstruction methods. (5) The 3D Butterworth filtering applied the same cutoff frequency for VD-DBT and UD-DBT in the mass-detection study. However, since the average dose per projection was lower in VD-DBT (leading to the possibility of higher noise), a higher cutoff frequency might have been more appropriate; (6) the simulation model does not include motion artifacts that can degrade MC detectability in 3D UD-DBT images. Thus the results presented here represent the best case scenario for MC detectability in UD-DBT. Additionally, scattered x rays within the breast were not modeled, but since this was the case for both VD-DBT and UD-DBT, it might be expected that the addition of in-body scatter would not alter the relative differences between them.
CONCLUSION
This work has presented a preliminary investigation of the VD-DBT and UD-DBT acquisition techniques based on human-observer studies of MC and mass detection. In this study where we compared the center projection image from a VD scheme vs the slices of the 3D reconstructed image from a UD-DBT for MC detection, the UD-DBT yields statistically significant (p=0.038) higher performance. For mass detection where the reconstructed images from both the schemes were compared, all the observers performed better using UD-DBT although the difference was not statistically significant (p=0.22). Future studies comparing these techniques will investigate different dose distributions for VD-DBT and also make use of 3D image displays. Our study cannot be considered as a direct comparison of mammography to tomosynthesis itself for MC detection since the center projection of VD-DBT received only 2 mGy and the UD-DBT images were obtained from a projection set that received a total of 4 mGy.
ACKNOWLEDGMENTS
The authors wish to acknowledge the generous support from Dr. Ahraf Khan and Dr. Robert Quinlan at the University of Massachusetts Medical School (UMMS) for their help in obtaining the mastectomy specimens. They also acknowledge Dr. Joyeeta Mitra of the Department of Radiology at UMMS for participating in the observer study. The authors wish to thank the reviewers for improving the manuscript through their insightful comments and suggestions. This work was supported in part by the National Institutes of Health (NIH) under Grant No. R01 CA102758 from the National Cancer Institute (NCI). Its contents are solely the responsibility of the authors and do not necessarily represent the official views of the NIH or the NCI.
References
- SEER, Cancer Statistics Review, edited by Horner M. J., Ries L. A. G., Krapcho M., Neyman N., Aminou R., Howlader N., Altekruse S. F., Feuer E. J., Huang L., Mariotto A., Miller B. A., Lewis D. R., Eisner M. P., Stinchcomb D. G., and Edwards B. K., National Cancer Institute B, Bethesda, pp. 1975–2005. [Google Scholar]
- Feig S. A., “Estimation of currently attainable benefit from mammographic screening of women aged 40–49 Years,” Cancer 75, 2412–2419 (1995). [DOI] [PubMed] [Google Scholar]
- Nishikawa R. M., Reiser I., and Seifi P., “A new approach to digital breast tomosynthesis for breast cancer screening,” Proc. SPIE 6510, 65103C (2007). 10.1117/12.713677 [DOI] [Google Scholar]
- Dobbins J. T. and Godfrey D., “Digital x-ray tomosynthesis: current state of the art and clinical potential,” Phys. Med. Biol. 48, R65–R106 (2003). 10.1088/0031-9155/48/19/R01 [DOI] [PubMed] [Google Scholar]
- Wu T., Moore R. H., Rafferty E. A., and Kopans D. B., “A comparison of reconstruction algorithms for breast tomosynthesis,” Med. Phys. 31(9), 2636–2647 (2004). 10.1118/1.1786692 [DOI] [PubMed] [Google Scholar]
- Wu T. et al. , “Tomographic mammography using a limited number of low-dose cone-beam projection images,” Med. Phys. 30(3), 365–380 (2003). 10.1118/1.1543934 [DOI] [PubMed] [Google Scholar]
- Feig S. A., Shaber G. S., and Patchefsky A., “Analysis of clinically occult and mammographically occult breast tumors,” AJR, Am. J. Roentgenol. 128, 403–408 (1977). [DOI] [PubMed] [Google Scholar]
- Anderson I., “Mammographic screening for breast carcinoma,” Ph.D. thesis, Lund University, Malmo, Sweden, 1980. [Google Scholar]
- Paplack S. P. T. T. D., Kogel C. A., and Nagy H. M., “Digital breast tomosynthesis: Initial experience in 98 women with abnormal digital screening mammography,” AJR, Am. J. Roentgenol. 189, 616–623 (2007). 10.2214/AJR.07.2231 [DOI] [PubMed] [Google Scholar]
- Kopans D., Moore R., and Gavenonis S., “Calcification in digital breast tomosynthesis,” RSNA, 94th Scientific Assembly and Annual Meeting, SSJ01–SSJ02 (2008).
- Swensson R. G., “Unified measurement of observer performance in detecting and localizing target objects on images,” Med. Phys. 23(10), 1709–1725 (1996). 10.1118/1.597758 [DOI] [PubMed] [Google Scholar]
- Boone J. M., Fewell T. R., and Jennings R. J., “Molybdenum, rhodium, and tungsten anode spectral models using interpolating polynomials with application to mammography,” Med. Phys. 24(12), 1863–1874 (1997). 10.1118/1.598100 [DOI] [PubMed] [Google Scholar]
- Boone J. M., “Glandular breast dose for monoenergetic and high-energy x-ray beams: Monte Carlo assessment,” Radiology 213, 23–37 (1999). [DOI] [PubMed] [Google Scholar]
- Siewerdsen J. H. and Jaffray D. A., “Optimization of x-ray imaging geometry (with specific application to flat-panel cone-beam computed tomography),” Med. Phys. 27(8), 1903–1914 (2000). 10.1118/1.1286590 [DOI] [PubMed] [Google Scholar]
- Siddon R. L., “Fast calculation of the exact radiological path for a three-dimensional CT array,” Med. Phys. 12(2), 252–255 (1985). 10.1118/1.595715 [DOI] [PubMed] [Google Scholar]
- Vedula A. A., Glick S. J., and Gong X., “Computer simulation of CT mammography using a flat-panel imager,” Proc. SPIE 5030, 349–360 (2003). 10.1117/12.480015 [DOI] [Google Scholar]
- Siewerdsen J. H. et al. , “Empirical and theoretical investigation of the noise performance of indirect detection, active matrix flat-panel imagers (AMFPIs) for diagnostic radiology,” Med. Phys. 24(1), 71–89 (1997). 10.1118/1.597919 [DOI] [PubMed] [Google Scholar]
- Burgess A. E., “Mammographic structure: Data preparation and spatial statistics analysis,” Proc. SPIE 3661, 642–653 (1999). 10.1117/12.348620 [DOI] [Google Scholar]
- Bakic P. R. and Albert M., “Mammogram synthesis using 3D simulation. 1. Breast tissue model and image acquisition simulation,” Med. Phys. 29(9), 2131–2139 (2002). 10.1118/1.1501143 [DOI] [PubMed] [Google Scholar]
- O’Connor J. M., Das M., Didier C. S., Mah’d M., and Glick S. J., “Using mastectomy specimens to develop breast models for breast tomosynthesis and CT breast imaging,” SPIE 6913, 691315 (2008). 10.1117/12.772666 [DOI] [Google Scholar]
- Johns P. C. and Yaffe M. J., “X-ray characterisation of normal and neoplastic breast tissues,” Phys. Med. Biol. 32(6), 675–695 (1987). 10.1088/0031-9155/32/6/002 [DOI] [PubMed] [Google Scholar]
- Zhou L., Oldan J., Fisher P., and Gindi G., “Low-contrast lesion detection in tomosynthetic breast imaging using a realistic breast phantom,” SPIE 6142, 61425A (2006). 10.1117/12.652343 [DOI] [Google Scholar]
- Gong X., Thacker S., and Glick S. J., “A computer simulation study comparing lesion detection accuracy with digital mammography, breast tomosynthesis, and cone-beam CT breast imaging,” Med. Phys. 33, 1041–1052 (2006). 10.1118/1.2174127 [DOI] [PubMed] [Google Scholar]
- Burgess A. E. and Chakraborty S., “Producing lesions for hybrid mammograms: extracted tumors and simulated microcalcifications,” Proc. SPIE 3663, 316–323 (1999). 10.1117/12.349659 [DOI] [Google Scholar]
- Saunders R., Samei E., Baker J., and Delong D., “Simulation of mammographic lesions,” Acad. Radiol. 13, 860–870 (2006). 10.1016/j.acra.2006.03.015 [DOI] [PubMed] [Google Scholar]
- Gong X., Vedula A. A., and Glick S. J., “Microcalcification detection using cone-beam CT mammography with a flat-panel imager,” Phys. Med. Biol. 49(11), 2183–2195 (2004). 10.1088/0031-9155/49/11/005 [DOI] [PubMed] [Google Scholar]
- Lai C. J. et al. , “Reciever operating characteristic analysis for the detection of simulated microcalcifications on mammograms using hard copy Images,” Phys. Med. Biol. 51, 3901–3919 (2006). 10.1088/0031-9155/51/16/002 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kak A. C. and Slaney M., Principles of Computerized Tomographic Images (IEEE, New York, 1988). [Google Scholar]
- Gentry J. R. and DeWard L. A., “TLD measurements of in vivo mammographic exposures and the calculated mean glandular dose across the United States,” Med. Phys. 23(6), 899–903 (1996). 10.1118/1.597824 [DOI] [PubMed] [Google Scholar]
- Chevalier M., Moran P., Ten J. I., Soto J. M. F., Capeda T., and Vano E., “Patient dose in digital mammography,” Med. Phys. 31(9), 2471–2479 (2004). 10.1118/1.1784591 [DOI] [PubMed] [Google Scholar]
- Nawfel R., Chan K., Wagenaar G., and Judy P., “Evaluation of video gray-scale display,” Med. Phys. 19(3), 561–567 (1992). 10.1118/1.596846 [DOI] [PubMed] [Google Scholar]
- Pollard J. H., A Handbook of Numerical and Statistical Techniques (Cambridge University Press, Cambridge, 1977). [Google Scholar]
- Das M., Gifford H., O’Connor M., and Glick S., “Evaluation of a variable dose acquisition methodology for breast tomosynthesis,” SPIE 6913, 691319 (2008). 10.1117/12.773106 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ruschin M. et al. , “Dose dependence of mass and microcalcification detection in digital mammography: Free response human observer studies,” Med. Phys. 34, 400–407 (2007). 10.1118/1.2405324 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mia M., Lo J., and Floyd C., “Differences between computer-aided diagnosis of breast masses and that of calcifications,” Radiology 223, 489–493 (2002). 10.1148/radiol.2232011257 [DOI] [PubMed] [Google Scholar]