Temporal resolution improvement using PICCS in MDCT cardiac imaging

Abstract

The current paradigm for temporal resolution improvement is to add more source-detector units and∕or increase the gantry rotation speed. The purpose of this article is to present an innovative alternative method to potentially improve temporal resolution by approximately a factor of 2 for all MDCT scanners without requiring hardware modification. The central enabling technology is a most recently developed image reconstruction method: Prior image constrained compressed sensing (PICCS). Using the method, cardiac CT images can be accurately reconstructed using the projection data acquired in an angular range of about 120°, which is roughly 50% of the standard short-scan angular range (∼240° for an MDCT scanner). As a result, the temporal resolution of MDCT cardiac imaging can be universally improved by approximately a factor of 2. In order to validate the proposed method, two in vivo animal experiments were conducted using a state-of-the-art 64-slice CT scanner (GE Healthcare, Waukesha, WI) at different gantry rotation times and different heart rates. One animal was scanned at heart rate of 83 beats per minute (bpm) using 400 ms gantry rotation time and the second animal was scanned at 94 bpm using 350 ms gantry rotation time, respectively. Cardiac coronary CT imaging can be successfully performed at high heart rates using a single-source MDCT scanner and projection data from a single heart beat with gantry rotation times of 400 and 350 ms. Using the proposed PICCS method, the temporal resolution of cardiac CT imaging can be effectively improved by approximately a factor of 2 without modifying any scanner hardware. This potentially provides a new method for single-source MDCT scanners to achieve reliable coronary CT imaging for patients at higher heart rates than the current heart rate limit of 70 bpm without using the well-known multisegment FBP reconstruction algorithm. This method also enables dual-source MDCT scanner to achieve higher temporal resolution without further hardware modifications.

INTRODUCTION

Recent advances in multidetector computed tomography (MDCT) technology have enabled relatively high quality, three-dimensional coronary computed tomography angiography using intravenous contrast agents injected through a peripheral intravenous catheter. In MDCT, the temporal resolution is primarily limited by the gantry rotation speed.^{1, 2} In order to accurately reconstruct an image using current reconstruction methods, the projection data acquired within an angular range of 180° plus the fan angle is required. Since the fan angle for a typical MDCT scanner is about 60°, the minimally required data acquisition angular range is about 240°. This short-scan angular range covers about 2∕3 of a complete circle. This fact determines that the typical temporal aperture of MDCT is about 50%–70% of the gantry rotation time for a complete rotation. As a result, the best temporal resolution of a single-source MDCT scanner is about 135 ms when the rotation speed of 270 ms is used and about 175 ms for 350 ms gantry rotation speed is used. For such a high gantry rotation speed, it is highly nontrivial to maintain the stability and functionality of the components on the gantry and meet the regulatory safety requirements for a MDCT scanner. Given these design considerations, it will be extremely challenging to increase the current gantry rotation speed by a factor of 2 such that the temporal resolution can be improved by a factor of 2.

Instead of increasing the gantry rotation speed to achieve higher temporal resolution, a design concept using multiple x-ray source-detector assemblies was introduced.^{3, 4, 5, 6, 7} Due to the limited room available on a CT gantry, commercially available MDCT systems introduced thus far have used two source-detector units. The angular difference between the two x-ray source positions is about 90°(Fig. 1). Thus, when the acquired projection data from the two source-detector units are combined, each source only needs to travel slightly more than half of the short-scan angular range. As a result, a complete data set for accurate reconstruction of the heart can be acquired in a narrower cardiac window, and the temporal resolution is improved by approximately a factor of 2. For a gantry rotation speed of 330 ms, using the dual-source-detector design, the achievable temporal resolution is about 83 ms. This represents the best achievable temporal resolution among all of the state-of-the-art MDCT scanners.

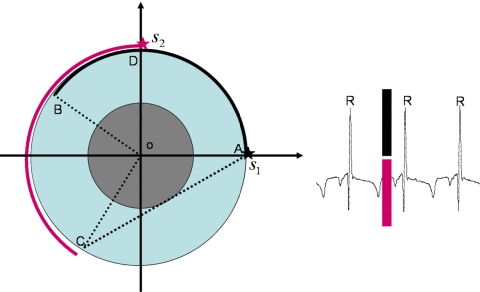
Figure 1.

Dual-source CT cardiac data acquisitions. The first source (S1) travels from A to B, while the second source (S2) travels from D to C. The short-scan angular range (ADBC) consists of the union of the angular ranges of the two sources. The data acquisition takes place within the same cardiac gating window, as shown in ECG signal sample.

In this article, instead of significant hardware modifications, we propose to use a novel image reconstruction algorithm, prior image constrained compressed sensing (PICCS),^{8, 9, 10} to achieve temporal resolution improvement for any single-source or dual-source MDCT scanner. For brevity, the method is referred to as temporal resolution improvement using PICCS (TRI-PICCS). The basic framework of the proposed TRI-PICCS method is presented in Fig. 2. The essential innovation in the proposed method is to only use half of the short-scan data and a low temporal resolution prior image for cardiac reconstruction. Note that the short-scan angular range is about 240°, which is the minimal data sufficiency condition to reconstruct the entire cross section within the scanning field of view. When the cardiac window is narrowed to half of the short-scan window, the available 120° angular range normally does not enable accurate image reconstruction, and the images are contaminated by limited-view-angle shading artifacts. In fact, without a priori information, this image reconstruction problem is the classical tomosynthetic reconstruction problem that usually does not have an algorithm to enable accurate image reconstruction. The key enabling factor in our TRI-PICCS method is the incorporation of a prior image, which is reconstructed from the short-scan angular range. Essentially, the limited-view-angle shading artifacts are eliminated by requiring that the reconstructed target image has some similarity with the prior image, which does not have limited-view-angle shading artifacts. This constraint is imposed by minimizing a cost function which will be explained in detail in the next section.

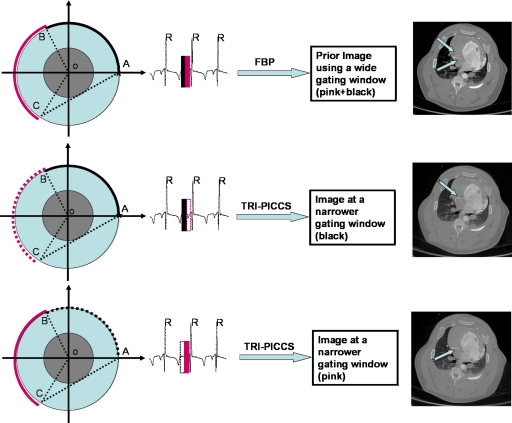
Figure 2.

Illustration of the proposed temporal resolution improvement using PICCS (TRI-PICCS) method. A standard FBP image reconstruction method is used to reconstruct a prior image from a short-scan data set acquired within a wide cardiac window (labeled by two narrow solid bars in the top panel of the figure). In the second step, only half of the short-scan data is used to reconstruct two separate cardiac images using the new TRI-PICCS algorithm. In each case, the short-scan reconstruction was used as the prior image. The resulting images (middle right and lower right) were reconstructed using cardiac windows of one-half the width. The reconstructed images clearly demonstrate how the motion artifacts in the prior image (arrows in the upper right image) are eliminated when the cardiac window is reduced by a factor of 2. This effectively improves the temporal resolution by a factor of approximately 2.

Two commonly encountered sampling problems in x-ray tomographic reconstruction are the view angle undersampling problem and the limited-view-angle problem. In the first case, the angular range of x-ray source trajectory is sufficient to provide accurate reconstruction, but sampling density is too low. In the second case, the angular range is insufficient for accurate reconstruction, as determined by the Tuy data sufficiency condition.¹¹ When a prior image of the image object is available, the PICCS algorithm may be applied to both problems in order to address the above two problems which may appear in different clinical applications.^{8, 9, 10} In this article, we will use the PICCS algorithm to address the limited-view-angle problem, which is a key in our attempt to improve temporal resolution using data from an angular range of about 120°. Given the data acquisition employed for cardiac MDCT imaging, the limited-view-angle trajectory used here will be densely sampled. The prior image will be reconstructed with a short-scan angular range (∼600–700 view angles), while the subset of the data used in the TRI-PICCS algorithm for temporal enhancement is composed of ∼300–350 view angles. Thus, the problem that TRI-PICCS must address is that of mitigating limited-view-angle induced artifacts. As a matter of fact, TRI-PICCS uses the similarity between the prior image and the target image to effectively mitigate the low frequency shading artifacts typically induced by limited-view-angle acquisitions.

METHOD AND MATERIALS

Brief review of the PICCS algorithm

In following, for completion, we introduce mathematical details of the original PICCS algorithm. When a prior image is available, it can then be utilized to significantly sparsify the target image. As shown in Fig. 3, when a subtraction of the target image (I) from the prior image (I_p) is performed, the subtracted image, I−I_p, is significantly more sparse than (I). When the total number of nonzero image pixels is counted in these three images, there are only 2700 pixels in the subtracted image, which is only about 3% of the total pixels in the target or the prior image. When an image is sparsified, it has been widely demonstrated^{12, 13, 14, 15, 16} by signal and image processing community that the image can be iteratively reconstructed using significantly fewer data samples. Sparser an image is, fewer data are needed to accurately reconstruct the image. One important condition to enable this accurate image reconstruction is that the acquired data should be well distributed in the entire frequency space, although the sampling pattern does not have to be uniform. When the frequency space is not well sampled as in our limited-view-angle problem, the shading artifacts are still inevitably present in the reconstructed image. In PICCS algorithm, we require that the gradient of the difference between the to-be-reconstructed target image, I, and the prior image without the limited-view-angle shading artifacts to be minimized (thus, dissimilarity between the target image and the prior image is minimized) to eliminate the potential limited-view-angle shading artifacts in the target image. This is achieved by minimizing the following objective function:

$$\min \left[{\mid {\nabla }_{m,n}(I-I_p)\mid }_{{\ell }_1}\right].$$

However, in coronary CTA imaging, the situation becomes more challenging due to the significant motion induced streaking artifacts present in the prior image. Without a delicate treatment, these artifacts will be present in the final image (Fig. 3, middle image, the blurred object, and the surrounding four small objects move during data acquisition), leading to degraded image quality. In PICCS algorithm, an additional term, the total variation of the to-be-reconstructed target image, was added to the above objective function to remove these potential motion streaks. The relative weight of these two terms is prescribed by a weighting factor α. As a result, the mathematics in our PICCS algorithm is to iteratively solve the following constrained minimization problem:

$$\min [\alpha {\mid {\nabla }_{m,n}(I-I_p)\mid }_{{\ell }_1}+(1-\alpha ){\mid {\nabla }_{m,n}I\mid }_{{\ell }_1}]\text{such}\text{that}PI=Y.$$ (1)

The l₁-norm in the above equation is the sum of the absolute value of each image pixel in an image. P is the system projection operator that calculates the ray sum along a given x-ray path and Y represents the measured x-ray projection values. The discrete gradient transform in Eq. 1 is defined as

$${\nabla }_{m,n}I=\sqrt{{[I(m+1,n)-I(m,n)]}^2+{[I(m,n+1)-I(m,n)]}^2}.$$ (2)

Several methods can be used to solve the constrained minimization problem in Eq. 1. In this article, it was solved in two alternating steps. In the first step, images were reconstructed using the algebraic reconstruction technique (ART) (Ref. ¹⁷) to meet the constraint PI=Y. Regarding this data constraint condition, two remarks are in order: First, the equality cannot be exactly fulfilled when data contain noise. But a relaxation factor has been introduced in the ART algorithm to account for this inexactness in data consistency constraint. Second, when the PICCS algorithm is applied to improve temporal resolution, only those projection data from the selected range of view angles corresponding to the target cardiac window (Fig. 2) are used. In the second step, the objective function α‖∇_m,n(I−I_P)‖_l1+(1−α)‖∇_m,nI‖_l1 was minimized using the gradient descent method.¹⁸ Due to the fact that the projection data set is limited in an angular range of about 120°, when the constraint PI=Y is imposed in the ART step, shading artifacts will appear in the ART image. These artifacts make it dissimilar from the prior image. When the objective function α‖∇_m,n(I−I_P)‖_l1+(1−α)‖∇_m,nI‖_l1 is minimized, motion streaks and dissimilarity relative to the prior image will be reduced in the reconstructed image. The iterative procedure was stopped when the squared difference of two successive images reached a predetermined threshold.^{12, 14, 15} In this article, the weighting factor α is chosen to be 0.5 and we find that for almost all applications, α=0.5 leads to rather robust image reconstruction.

Figure 3.

Comparison of sparsity with and without the subtraction operation. The total numbers of nonzero pixels for the target (left), prior (middle), and difference (right) images are roughly 76 000, 78 000, and 2700, respectively.

In vivo experimental data acquisitions

In order to demonstrate that, using the TRI-PICCS method, temporal resolution can be improved by a factor of approximately 2 in MDCT cardiac imaging without hardware modification on state-of-the-art MDCT scanners, we retrospectively analyzed the data acquired using a porcine model and a state-of-the-art 64-slice CT scanner (GE Healthcare, Waukesha, WI) installed in our department.

Data from two different in vivo animal experiments were analyzed. In this first animal experiment, the heart rate was approximately 83±6 bpm during the acquisition. A “cine mode” with a 0.4 s gantry rotation period was employed in data acquisitions (the acquisition speed is slower than the maximum gantry rotation speed of 350 ms to further challenge the algorithm). The animal was scanned at 120 kVp and 500 mA under ventilation. Using the ECG signal, a cardiac gating window with width of 267 ms centered at 68% R-R was used to select projection data, this cardiac window corresponds to a short-scan angular range of 235° for the GE MDCT scanner. As a result, 642 cone-beam projections were selected in this short-scan angular range.

In the second animal experiment, animal was scanned at higher heart rate and used a standard coronary CTA helical scanning protocol at gantry rotation time of 350 ms. A 181 lb swine was scanned on the same GE Lightspeed 64-slice scanner under ventilation. The imaging parameters were 120 kVp, 600 mA, a pitch of 0.24, and a gantry rotation period of 350 ms. The heart rate was around 96±5 bpm during the acquisition. Similar to the first animal experiment, short-scan data was selected from a 250 ms cardiac window centered at 68% of the R-R peak in the ECG signal. The images were reconstructed using the standard FDK cone-beam reconstruction algorithm.¹⁹

RESULTS

The first animal experiment using cine data acquisitions

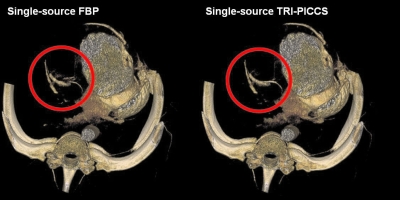
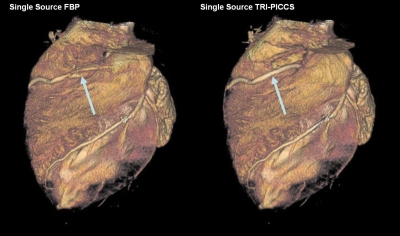
As shown in the volume rendered images in Fig. 4, residual cardiac motion caused strong motion artifacts around the right coronary (labeled by the red circle). As a result, an artifactual vessel was created in the reconstructed axial image (Fig. 5, see also Fig. 2). The TRI-PICCS method was then applied to improve temporal resolution. The left image, which was reconstructed with a low temporal resolution, was used as a prior image in TRI-PICCS reconstruction. As shown in both the volume rendered image in Fig. 4 and the single image slice in Figs. 25 after applying the TRI-PICCS method, the artifactual vessel is removed. In addition to the improvement in the reconstruction accuracy of the coronary arteries, one can also appreciate the improved delineation of the cardiac chambers (labeled by the red ellipse in Fig. 5). In the image reconstructed with the filtered back projection (FBP) algorithm, the boundary between the left atrium and the left ventricle is blurred by motion, after the TRI-PICCS method was applied, the boundary between chambers is clearly visible.

Figure 4.

Comparison of image quality with FBP (left) and with TRI-PICCS (right).

Figure 5.

Comparison of the image quality for two reconstructions: FBP reconstruction without TRI-PICCS at 200 ms temporal resolution (left) and with TRI-PICCS at 100 ms temporal.

The second animal experiment using helical data acquisitions

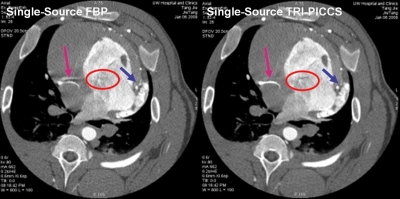
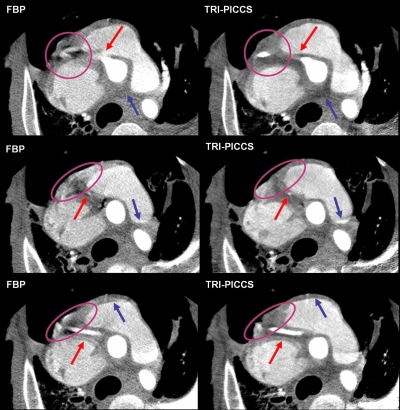
As shown in the volume rendered FBP images in Fig. 6, strong motion artifacts appeared around the RCA region. Actually, motion artifacts distorted the RCA into two disconnected vessels. The improvement in image quality can be appreciated in the volume rendered images shown in Fig. 6. One can see that a continuous segment of the RCA is visualized with TRI-PICCS reconstruction. Image quality improvement can also be appreciated in axial image slices, as shown in Fig. 7. Images in the left column were reconstructed using the conventional FBP method and images in the right column were reconstructed using the proposed TRI-PICCS method with the corresponding FBP image in the left column as the prior image. In TRI-PICCS images, the vessels were reconstructed with sharp edges and the boundaries between the cardiac chambers and myocardium are clearly visible. In contrast, strong motion artifacts are rampant in the corresponding FBP images to blur the structures.

Figure 6.

Comparison of performance between single-source FBP reconstruction (left) and TRI-PICCS reconstruction (right). Note that the motion artifacts in the RCA are removed after applying TRI-PICCS.

Figure 7.

Comparison of the image quality for a helical cardiac scan at 350 ms gantry rotation speed. The images in the left column were reconstructed using the conventional FBP method and the images in the right with the TRI-PICCS method. The arrows and elliptical circles correspond to regions where artifacts can be visualized in the FBP case but are corrected in the TRI-PICCS case.

DISCUSSION AND CONCLUSIONS

The results from the above two in vivo animal experimental studies clearly demonstrated that the proposed TRI-PICCS method enables to improve the temporal resolution by a factor of approximately 2 in single-source MDCT scanners for high heart rate up to 100 bpm in both “cine” mode at 400 ms gantry rotation time and helical scanning mode at 350 ms gantry rotation time. Motion artifacts caused by strong residual cardiac motions in the short-scan cardiac gating window are corrected using the TRI-PICCS method and projection data from one-half of the short-scan gating window. There is no limited-view- angle shading artifacts presented in the TRI-PICCS images.

We would also like to present a comparison between our TRI-PICCS method (Fig. 2), the dual- source hardware method (Fig. 1) for temporal resolution improvement. The similarity between the TRI-PICCS and dual-source methods is that image reconstruction for a given image slab only involves projection data from a single heart beat. Thus, the temporal resolution for both our TRI-PICCS method and the dual-source method are independent of the heart rate and regularity. As a result, improvement in the temporal resolution directly leads to a relaxation on heart rate limit. Similar to the dual-source method, a factor of 2 improvement in the temporal resolution using the TRI-PICCS method may potentially enable single-source CT scanner to reconstruct reliable cardiac CT images for patients with higher heart rates up to 100 bpm.

There are several potential future enhancements in our studies: The first one is that we only applied the TRI-PICCS method to a single-source 64-slice VCT scanner case, but the TRI-PICCS algorithm can equally be applied to the dual-source MDCT scanner to further improve temporal resolution. The second limitation is that we simply divided a short-scan cardiac gating window into two consecutive cardiac windows and each represents a new cardiac phase. From the current results, it is anticipated that the TRI-PICCS method may enable accurate image reconstruction for a narrower cardiac window which implies the potential to improve temporal resolution more. A more systematic research is ongoing to investigate the achievable temporal resolution improvement in MDCT cardiac imaging.

One final remark on the TRI-PICCS method is the computation time. Currently, it takes several hour CPU time to reconstruct a cardiac phase. However, when the more and more popular GPU method^{20, 21, 22, 23, 24} is used, the reconstruction time can be significantly reduced to the order of minutes to enable immediate clinical use. The GPU-based acceleration is ongoing to accelerate the PICCS reconstruction in our group. Results will be published somewhere else.

In conclusion, using in vivo animal experimental studies, a new method based on PICCS has been proposed and validated to improve the temporal resolution by approximately factor of 2 for MDCT scanners without any hardware modification on CT scanners. The proposed TRI-PICCS method may enable high quality coronary CTA imaging using single-source MDCT scanners at higher heart rates than the current upper limit of 70 bpm. Since the TRI-PICCS method only uses data from a single heart beat, it does not suffer the synchronization problem between the gantry rotation motion and cardiac motion.