Four-dimensional inverse treatment planning with inclusion of implanted fiducials in IMRT segmented fields

Abstract

The purpose of this study is to develop a 4D inverse planning strategy capable of controlling the appearance of the implanted fiducial(s) in segmented IMRT fields for cine MV or combined MV∕kV image-guided IMRT. This work is focused on enhancing the visibility of the implanted fiducial(s) in 4D IMRT inverse planning, whose goal is to derive a set of time-resolved (or phase-tagged) MLC segments to cater for the motion of the patient anatomy extracted from the emerging 4D images. The task is to optimize the shapes and weights of all the segments for each incident beam, with the fiducial(s) being forced∕encouraged to be inside the segmented fields. The system is modeled by a quadratic objective function with inclusion of a hard∕soft constraint characterizing the authors’ level of preference for the fiducial(s) to be included in the segmented fields. A simulated annealing algorithm is employed to optimize the system. The proposed technique is demonstrated using two clinical cases. A segment-based inverse planning framework for 4D radiation therapy, capable of providing tempospatially optimized IMRT plans, has been established. Furthermore, using the described 4D optimization approach, it is demonstrated that the MLC blockage of the implanted fiducial(s) during the segmented delivery is avoided without severely compromising the final dose distribution. The visibility of implanted fiducials in 4D IMRT can be improved without significantly deteriorating final dose distribution. This is a foundation for the authors to use cine MV or combined MV∕KV to effectively guide the 4D IMRT delivery.

INTRODUCTION

A critical component that is missing in current LINAC-based IMRT is the real-time monitoring of the tumor position. Furthermore, a treatment verification system capable of documenting the beam targeting and preventing geographic misses is not available, especially for modern modalities such as gated delivery^{1, 2} and therapy relying on MLC-based tumor tracking.^{3, 4, 5, 6, 7} A strategy of using combined MV treatment beam and on-board kV imaging system for real-time tracking of fiducial markers has been proposed recently.^{8, 9, 10} When the fiducials are inside both kV and MV beams, the geometric accuracy of the system is found to be on the order of 1 mm in all three spatial dimensions.⁸

In using the treatment MV beam for on-line imaging, a practical difficulty is that the fiducials may be partially or completely blocked by the MLC at a certain segment (segments) of an IMRT delivery. A potential solution to the problem is to design the IMRT plan in such a way that all or some of the implanted fiducials are inside the segmented IMRT fields provided that the final dose distribution is not compromised excessively. In this work we accomplish this by introducing a soft or hard penalty in inverse planning calculation. The penalty discourages (soft constraint) or avoids (hard constraint) the blockage of the implanted fiducials in the optimized MLC segments. In reality, “seeing” the fiducial is a general requirement whenever the fiducials need to be monitored during the beam-on time. This issue arises not only in recently available time-resolved radiation therapy, such as respiration-gated IMRT and four-dimensional (4D) IMRT, but possibly also in conventional 3D IMRT where it may be desirable to ensure that the target volume remains within a prespecified tolerance.

This paper is focused on exploring the feasibility of the above strategy for 4D IMRT inverse planning.^{7, 11, 12} 4D IMRT is a new concept that is under intense investigation.¹³ The goal of 4D IMRT inverse planning is to derive a set of time-resolved MLC segments to maximally compensate for the motion of the patient anatomy extracted from 4D images. While ideally a 4D IMRT plan yields the optimal cumulative dose distribution, a practical issue is how to ensure that the segmented IMRT dose is delivered to the target at the right position and right time. Monitoring the position of the implanted fiducial in real time represents a useful option to ensure appropriate 4D radiation therapy delivery. We find that the “visibility” of the implanted fiducials is greatly enhanced by introducing a fiducial constraint in the 4D inverse planning process. While the IMRT dose distribution with added physical constraints is degraded unsurprisingly, our results suggest that the degradation of plan quality is often not detrimental, especially when a soft constraint is employed. It is believed that the proposed functionality should be part (at least as part of the available choices) of future 4D IMRT inverse planning when cine MV imaging is involved in fiducial tracking.

METHODS AND MATERIALS

This work consists of two major but related components: (i) Incorporation of temporal variable into optimization or 4D inverse planning and (ii) enhancement of the fiducial visibility in the IMRT delivery. These two issues are addressed in different subsections below.

4D inverse planning

Recent advancement in 4D CT makes it possible to develop a patient specific 4D model for improved therapeutics and opens the possibility of 4D IMRT, in which the segments are optimized with respect to space and phase. In our study, the number of beam and their angles are specified empirically. The motion is discretized into ten phases. For convenience, each beam is composed of ten segments, each for a phase. A segment for a given gantry angle θ and a phase p is denoted by $a_{\theta ,p}\left(w_{\theta p},\left\{x_{\theta p}^l\left(A\right),x_{\theta p}^l\left(B\right)\right\}\right)$, where w_θp is the weight of the segment and $\left\{x_{\theta p}^l\left(A\right),x_{\theta p}^l\left(B\right)\right\}$ describes the coordinates of the lth MLC leaf pair of the segment.

The aim of 4D IMRT planning becomes finding the optimal shapes and weights of all segments. 4D inverse planning objective function is written as¹⁴

$$S\left(D_c\right)=\sum _{i=1}^{n_{\text{struct}}}\frac{1}{n_i^{\text{voxel}}}\left[{\sigma }_{1,i}\sum _{n=1}^{n_i^{\text{voxel}}}H\left(D_i^{\text{low}}-D_c\left(n\right)\right)+{\sigma }_{2,i}\sum _{n=1}^{n_i^{\text{voxel}}}H\left(D_c\left(n\right)-D_i^{\text{high}}\right)\right]\times {\left(D_c\left(n\right)-D_i^p\right)}^2,$$ (1)

where $D_i^p$ is the prescription dose for the ith structure, σ_i,1 and σ_i,2 are weighting factors^{15, 16} for overdosing and underdosing specific to structure i, and H(x) is the Heaviside step function (takes 1 for positive x and 0 otherwise). In this objective function, penalty goes to the voxels with dose D(n) higher than the upper bound or lower than the lower bound. The calculated dose distribution in Eq. 1 is a function of the shapes and weights of all segments. Optimization of the objective function yields the optimal segment shapes and weights subject to physical constraints imposed by system hardware.^{17, 18, 19, 20}

In segment-based 4D treatment planning, the dose to a voxel is a superposition of the doses from all phases and segments. For a given phase, the calculated dose distribution changes with segment shapes and weights and the dose is computed by summing the contribution from each segment of each beam. When multiple phases are involved, a deformable registration model is used to track the movement of each voxel. By using 4D CT images and deformable registration,^{21, 22, 23, 24, 25} the voxel displacement vector field (DVF) T_p→r is obtained. A DVF describes the displacement of a voxel in a phase (p) with respect to the reference phase (r): $\Delta {\stackrel{⃑}{x}}_{p\to r}={\stackrel{⃑}{x}}^{\left(p\right)}-{\stackrel{⃑}{x}}^{\left(r\right)}$. The cumulative dose is expressed as

$$D_c\left(n\right)=\sum _p{T}_{p\to r}\sum _{\theta }{w}_{a_{\theta p}}{K}_{a_{\theta p}}\left(n\right),$$ (2)

where K_a(n) is the dose at a voxel n from the segment depicted by a_θp with unit intensity. The DVF transforms the dose contribution computed in the pth phase into the dose in the rth (reference) phase.

Optimization

The objective function defined in Eq. 1 is optimized by using a simulated annealing (SA) technique. The segment shapes are initialized to conform to the projection of the target in the beam’s eye view (BEV) at the corresponding phase of the breathing cycle. Equal weights are assigned to all segments initially. In each iteration of SA, a trial change of the segment shape and weight is introduced. The trial change is accepted or rejected according to a probability determined by two factors. One is the conventional SA probability of rejecting a trial P, which is determined by the change of objective function ΔS and system temperature T:^{14, 26, 27, 28}

$$P=\{\begin{array}{cc}0& \text{if}\Delta S\text{<}0\\ 1-\text{exp}\left(\Delta S∕T\right)& \text{otherwise}.\end{array}\phantom{\}}$$ (3)

The other is whether the segment blocks a fiducial or not. The composite rejecting probability of a trial segment is given by

$$P^{\prime }=P+\xi \left(1-P\right),$$ (4)

where ξ is a coefficient determined by the fiducial blockage status (details are given in Sec. 2C). If the trial segment shape is not accepted, a new trial segment will be followed.

Soft and hard constraints for inclusion of implanted fiducial(s)

In this work, a built-in mechanism for avoiding MLC blockage of the fiducials in the delivery segments is introduced to the 4D inverse treatment planning strategy. The fiducials implanted in the target (Fig. 1 shows an example of three implanted fiducials in the target) can generally be blocked by the segmented fields of an IMRT plan. To discourage or prevent this from happening, a penalty scheme is introduced if any of the fiducials is blocked by a segmented field. The penalty is tuned and controlled by a coefficient ξ introduced in the composite rejecting probability [Eq. 4]. If all the fiducials fall in the segmented field, there is no penalty during optimization, that is, ξ=0 in Eq. 4 and P^′ reduces to P. Otherwise, the penalty is imposed by assigning ξ a positive value. To be specific, both hard and soft constraints are considered here. In the case of hard constraint, ξ=1 and the composite probability P^′ is equal to unity. When the hard constraint is applied, a trial segment shape that blocks a fiducial is always rejected. For soft constraint, ξ is set to be 0.5 and the probability of rejecting a trial segment shape is increased to P^′=0.5(P+1). The construction of rejecting probability for a trial segment here is somewhat empirical but serves the purpose of encouraging inclusion of implanted fiducials in the MLC segments.

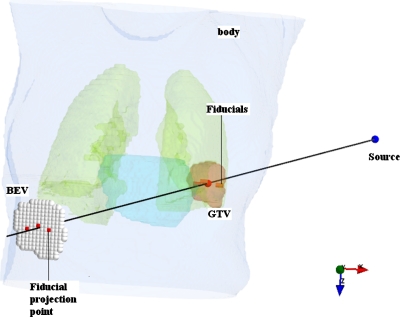
Figure 1.

A schematic of fiducial-based monitoring of tumor motion. Three fiducials are implanted in the target; the projection points of the fiducials in BEV are indicated.

Case study

Two patients’ 4D CT data, one lung cancer (Fig. 2) and one pancreas cancer (Fig. 3), are used to illustrate the performance of the proposed technique. The respiratory cycle is divided into ten phases of equal duration, with phase 10% representing the end of inhalation and phase 50% the end of exhalation. The contours of regions of interest (ROIs) are delineated on the 50% phase (reference phase). The ROI contours on the other nine phases of the 4D CT data are automatically generated using the deformation field obtained by using deformable registration.²⁹ Five 6 MV beams (80°, 150°, 250°, 300°, 350°) are used for the lung IMRT and six 6 MV beams (80°, 120°, 150°, 200°, 240°, 290°) are used for pancreas IMRT.

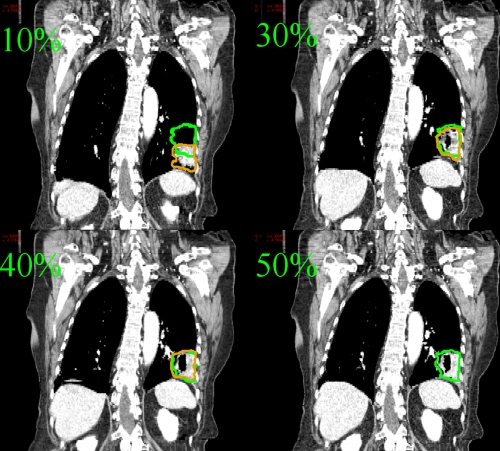
Figure 2.

Lung patient CT images at 10%, 30%, 40%, and 50% phases. The contour of the target is plotted on the CT image of the corresponding phase. The 50% phase target contour is also overlaid onto 10%, 30%, and 40% phases.

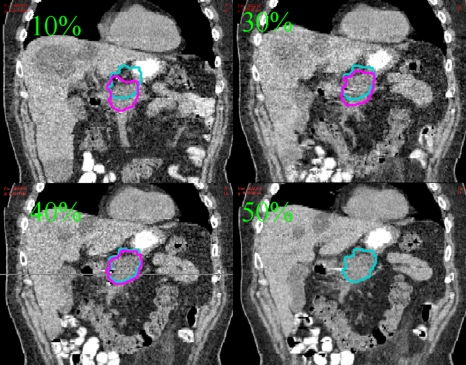
Figure 3.

Pancreas patient CT images at 10%, 30%, 40%, and 50% phases. The contour of the target is plotted on the CT image of the corresponding phase. The 50% phase target contour is also overlaid onto 10%, 30%, and 40% phases.

RESULTS AND DISCUSSIONS

Lung patient

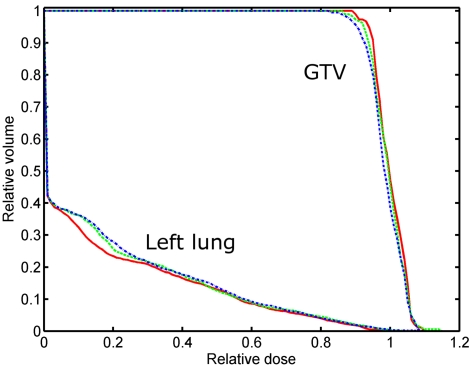
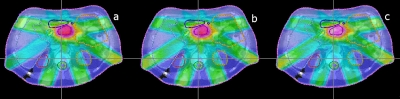
The dose-volume histograms (DVHs) and dose distributions resulting from the 4D inverse planning with or without soft∕hard fiducial constraints are shown in Figs. 45, respectively. When the fiducials are forced to be seen, slight degradation of the dose distributions are observed in both target coverage and OAR sparing. The target mean dose is lowered from 59.7 to 59.3 Gy∕58.9 Gy when the soft∕hard fiducial constraint is applied. The standard deviation (STD) of target dose is increased from 2.5 to 2.8 Gy∕2.9 Gy for the two constrained cases. Simultaneously, the target dose level covering 90% of the target volume (D90) is decreased from 95% to 94% and 93%, respectively. These results indicated that the use of fiducial constraints leads only to moderate change in the final dose distribution. Not surprisingly, the hard constraint degrades the plan more as compared to that of the soft constraint. The constraints also slightly increase the left lung dose. However, it should be noted that the lung volume receiving 25% or higher dose is essentially not changed regardless of what type of constraint is used, as is clearly seen by comparing the stomach fractional volume with 24 Gy or more dose (V24 value) for the three plans. The dose degradation mainly happens in the low dose region (<24%). The stomach fractional volumes with 10 Gy or more dose (V10 value) for the three plans are 25.3%, 28.9%, and 30.0%, respectively. Note that the parameters characterizing the plans, including the mean dose, STD, D90 for target, and V10 and V24 for the left lung, are summarized in Table 1 for the three plans.

Figure 4.

DVHs for target and left lung for the lung cancer patient. The solid, dash, and dash–dot curves represent the results obtained by the 4D IMRT plan without fiducial constraint, with soft fiducial constraint, and with hard fiducial constraint, respectively.

Figure 5.

Dose distributions in transverse plane of the lung cancer patient subject to the three different fiducial constraint conditions. The dose distributions obtained by the plans without fiducial constraint, with soft fiducial constraint and with hard fiducial constraint are shown from left to right.

Table 1.

Summary of the 4D lung IMRT plan statistics for the three different kinds of fiducial constraints.

Lung	Free	Soft	Hard
GTV mean dose (Gy)	59.7	59.3	58.9
GTV dose STD (Gy)	2.5	2.8	2.9
GTV D90 (%)	95.0	94.0	93.0
LT lung V10 (%)	25.3	28.9	30.0
LT lung V24 (%)	16.6	17.6	17.6

The optimized segment shapes of the first beam (80° gantry angle) for the three plans are shown in Fig. 6. The phase number of each segment is indicated on the top of the segmented field shape. As seen from the upper panel of Fig. 6, at least one fiducial is located in five out of ten segments when no fiducial constraint is applied. With the use of soft constraint, the number is increased to 6 for this beam. The fiducials appear in all ten segments when hard constraint is applied. Overall, for the five beams, the number of segment that blocks at least one fiducial is 52%, 32%, and 0% for plans obtained with no fiducial constraint, with soft fiducial constraint, and with hard fiducial constraint, respectively. In the present definition of fiducial constraint, ξ is a tunable parameter (0<ξ≤1) that controls the degree of the constraint. The current selection is ξ=0.5 for soft constraint.

Figure 6.

Segmented fields of the first beam (80° gantry angle) for the lung 4D IMRT plan. The top panel represents the segmented fields resulting from the 4D IMRT plan without fiducial constraint. The middle and bottom panels represent the results from the 4D IMRT plan with soft and hard fiducial constraint, respectively. The squares are the implanted fiducials. The diamonds indicates the blocked fiducials.

It is interesting that, in all three cases, the apertures for the 10% and 100% phases move down by about 2.5 cm relative to the apertures irradiating the expiration phase (50% phase). This segment shift is a direct consequence of the tumor motion. Indeed, by inspiration of the 4D CT images of the patient, it can be seen that the motion of the tumor at this phase is about 2.3 cm in superior-inferior (SI) direction (Fig. 2). In a sense, the 4D IMRT plan tracks the tumor motion by shifting the apertures.

Pancreas patient

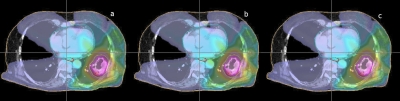
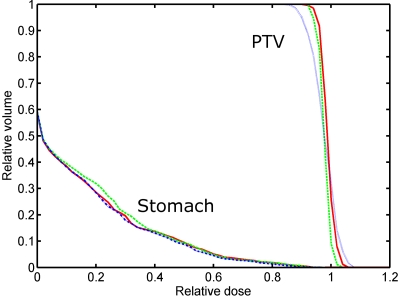
DVHs and dose distributions resulting from the 4D inverse planning with no fiducial constraint and with soft or hard fiducial constraints are shown in Figs. 78, respectively. The plan statistics for the three scenarios are summarized in Table 2. Similar to the previous case, only slight degradation in treatment plan is seen when a fiducial constraint is applied. In the dose distribution shown in Fig. 8, low dose is observed within the target in the plan with hard fiducial constraint. The target mean dose is degraded from 59.7 to 59.1 Gy∕51.1 Gy when soft∕hard fiducial constraint is applied. The STD of target dose is increased from 2.9 to 2.9 Gy∕3.3 Gy for the two constrained cases. Simultaneously, the target dose level covering 90% of the target volume (D90) is decreased from 93% to 92% and 91%, respectively. These results indicated that the use of fiducial constraints leads only to moderate change in the final dose distribution. The dose distribution in the stomach is slightly worsened by the inclusion of fiducial constraints. The degradation happens mainly in the low dose region. The V10 values are 30.3%, 31.6%, and 33.9% for plans without fiducial constraint and with soft or hard constraints, respectively. The V24 values are 11.5%, 13.1%, and 13.2% for the three plans. For the region with a dose of 40% or higher, little change is observed.

Figure 7.

DVHs for target and stomach for the pancreas cancer patient. The solid, dash, and dash–dot curves represent the results obtained by the 4D IMRT plan without fiducial constraint, with soft fiducial constraint, and with hard fiducial constraint, respectively.

Figure 8.

Dose distributions in transverse plane of the pancreas cancer patient subject to the three different fiducial constraint conditions. The dose distributions obtained by the plans without fiducial constraint, with soft fiducial constraint, and with hard fiducial constraint are shown from left to right.

Table 2.

Summary of the 4D pancreas IMRT plan statistics for the three different kinds of fiducial constraints.

Pancreas	Free	Soft	Hard
GTV mean dose (Gy)	59.7	59.1	59.1
GTV dose STD (Gy)	2.9	2.9	3.3
GTV D90 (%)	93.0	92.0	91.0
Stomach V10 (%)	30.3	31.6	33.9
Stomach V24 (%)	11.5	13.1	13.2

Figure 9 shows the optimal segment shapes of the first beam (80° gantry angle) for the three plans (constraint-free, with soft fiducial constraint, or with hard fiducial constraint). The phase number of each segment is indicated on the top of the segmented field shape. As seen from Fig. 9, five out of ten segments contain the three fiducials when no fiducial constraint is applied. With soft constraint, the number of the segmented fields blocking at least one fiducial is decreased to 4 for this beam. No fiducials show up in all the segments with the use of hard constraint. For the six beams, overall percentage of fiducial(s) blockage is 48%, 37%, and 0%, respectively, for the three scenarios.

Figure 9.

Segmented fields of the first beam (80° gantry angle) for the pancreas 4D IMRT plan. The top panel represents the segmented fields resulting from the 4D IMRT plan without fiducial constraint. The middle and bottom panels represent the results from the 4D IMRT plan with soft and hard fiducial constraint, respectively. The squares are the implanted fiducials. The diamonds indicates the blocked fiducials.

It is important to note that the inverse planning procedure described above is based on the patient’s simulation 4D CT. In reality, patient’s breathing pattern changes from time to time, which may change the relative position of the fiducials and the MLC segments and cause a problem during the actual IMRT delivery. A straightforward approach to prevent this from happening is to introduce a margin for each implanted marker so that the whole motion range of the fiducial is considered during inverse planning. The size of the margin depends on the specifics of delivery. For respiration-gated delivery, for example, the margin needs only to cover the residual motion range of the fiducial for the specific gating window.² Of course, patient setup inaccuracy should also be considered when specifying a margin to the fiducial. A more advanced approach that one can take is to include a probability model of the fiducial motion derived from 4D simulation CT. The method described in this work should be extendable to deal with the fiducial margin or probability distribution discussed here.

CONCLUSIONS

A segment-based inverse planning framework for 4D radiation therapy has been described. By extending inverse planning from 3D to 4D, a tempospatially optimized IMRT plan can be achieved. 4D IMRT allows us to fully consider the patient’s anatomical change during respiration and maximize the IMRT delivery efficiency. Furthermore, it is demonstrated that the MLC blockage of the implanted fiducial(s) during the segmented delivery can be partially or completely avoided without severely compromising the final dose distribution. 4D inverse planning with enhanced fiducial(s) visibility provides a basis for future cine MV or hybrid kV∕MV imaging guided 4D IMRT.