Scatter correction for cone-beam CT in radiation therapy

Abstract

Cone-beam CT (CBCT) is being increasingly used in modern radiation therapy for patient setup and adaptive replanning. However, due to the large volume of x-ray illumination, scatter becomes a rather serious problem and is considered as one of the fundamental limitations of CBCT image quality. Many scatter correction algorithms have been proposed in literature, while a standard practical solution still remains elusive. In radiation therapy, the same patient is scanned repetitively during a course of treatment, a natural question to ask is whether one can obtain the scatter distribution on the first day of treatment and then use the data for scatter correction in the subsequent scans on different days. To realize this scatter removal scheme, two technical pieces must be in place: (i) A strategy to obtain the scatter distribution in on-board CBCT imaging and (ii) a method to spatially match a prior scatter distribution with the on-treatment CBCT projection data for scatter subtraction. In this work, simple solutions to the two problems are provided. A partially blocked CBCT is used to extract the scatter distribution. The x-ray beam blocker has a strip pattern, such that partial volume can still be accurately reconstructed and the whole-field scatter distribution can be estimated from the detected signals in the shadow regions using interpolation∕extrapolation. In the subsequent scans, the patient transformation is determined using a rigid registration of the conventional CBCT and the prior partial CBCT. From the derived patient transformation, the measured scatter is then modified to adapt the new on-treatment patient geometry for scatter correction. The proposed method is evaluated using physical experiments on a clinical CBCT system. On the Catphan©600 phantom, the errors in Hounsfield unit (HU) in the selected regions of interest are reduced from about 350 to below 50 HU; on an anthropomorphic phantom, the error is reduced from 15.7% to 5.4%. The proposed method is attractive in applications where a high CBCT image quality is critical, for example, dose calculation in adaptive radiation therapy.

INTRODUCTION

Cone-beam CT (CBCT) is being increasingly used in modern radiation therapy for patient setup, dose verification, and adaptive replanning. However, the applications of CBCT are still limited due to its inferior image quality as compared to that of conventional CT. One major source of the poor image quality is the high scatter signals in CBCT due to the large illumination volume and complicated inhomogeneous organs.¹ Scatter causes severe shading and streak artifacts, which greatly reduce the efficacy of image-guided radiation therapy. For example, dose calculation from CBCT images is a critical step in adaptive radiation therapy.² Although some research has shown that high accuracy of dose reconstruction can be achieved using CBCT images,³ the applications of these techniques are mainly limited to imaging of small volumes, such as head and neck, where scatter signals are small. In the case of imaging on a human torso, the accuracy of dose reconstruction using CBCT images is not satisfactory for clinical applications,⁴ if no effective scatter correction method is applied. The goal of this work is to develop an effective scatter correction method for CBCT to facilitate the use of CBCT in radiation therapy.

Many scatter correction methods have been proposed in literature, and research in this field still remains very active.^{5, 6, 7, 8, 9, 10, 11} In general, these scatter correction methods can be divided into two major types. The first type performs scatter suppression during the acquisition of projection data based on the difference between the incident angles of primary photons and scatter photons. Typical examples include the antiscatter grid method¹² and the air gap method.¹³ These methods achieve instant scatter suppression, although their efficacy is usually limited. Siewerdsen et al., for example, showed that an antiscatter grid was effective only in improving the contrast-to-noise ratio of low resolution CT images.¹² An antiscatter grid attenuates primary photons as well, and the imaging dose therefore needs to be increased to maintain the image quality. Kyriakou and Kalender reported that this dose increase is very significant if the scatter is high.¹⁰ To overcome these drawbacks, much effort has been devoted to the scatter correction methods in the second category. With different strengths and drawbacks, the methods in this category correct for scatter using postprocessing techniques on scatter contaminated projection images.^{6, 7, 11, 14, 15, 16} Although improved scatter correction performances have been demonstrated, a practical implementation usually involves a combined consideration of different issues, such as correction efficacy, computation complexity, dose or scan time increase, and hardware compatibility. A standard scatter correction method for CBCT still remains elusive.

In current radiation therapy, one or two CBCT scans are performed on the same patient every day, and the whole treatment course typically lasts 4 to 6 weeks. Although the existing scatter correction methods can be implemented for CBCT in radiation therapy, they do not utilize the feature of repetitive scans and requires scatter measurement∕calculation work for each CBCT scan. The complication of scatter removal arises from the complicated dependence of the scatter on the patient geometry, imaging parameters, and relative position of the patient and the imaging system. In this work, we propose a novel scatter correction method that is particularly useful for CBCT in radiation therapy. The central idea of our approach is to obtain a patient-specific scatter database on the first day of the patient’s visit. In a subsequent scan of the same patient on a different day, the prestored scatter distributions are then used for scatter correction after an appropriate transformation based on the patient’s on-treatment geometry. During the patient setup in the first scan, a partially blocked CBCT is used to measure the scatter distributions. An x-ray beam blocker with a strip pattern is inserted between the x-ray source and the patient such that partial volume can still be accurately reconstructed and the whole-field scatter distribution can be estimated from the measured signals in the shadow regions using interpolation∕extrapolation. In the subsequent regular scans on the same patient on different days, the patient transformation is first determined using a rigid registration of the conventional CBCT and the partial CBCT from the scatter measurement scan. Based on the derived patient transformation, the measured scatter from the first scan is then modified accordingly and used for scatter correction in the regular CBCT scans. The proposed method is evaluated using physical experiments on a clinical CBCT system.

METHOD

Scatter correction scheme

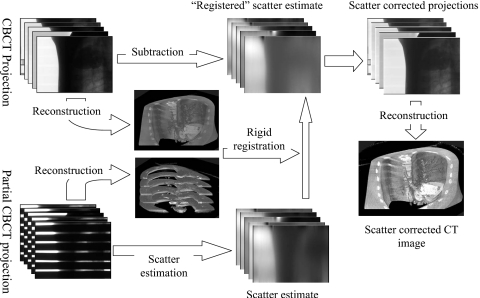
The general scatter correction scheme is shown in Fig. 1. We first estimate scatter using a partially blocked CBCT in the first CBCT scan during the treatment course of radiation therapy. The estimated scatter distributions are stored and used for scatter correction for the same patient in the subsequent scans on different days. The same imaging parameters are used in these CBCT scans. However, the scatter distributions still change for different scans due to the small transformations of the same patient. In order to estimate the scatter distributions from the premeasured data, we reconstruct the images using the partially blocked CBCT projections and the regular CBCT projections. The partially blocked CBCT and the regular CBCT images provide a precise rigid registration, as shown in our previous study.¹⁷ Based on the relative geometric information, the premeasured scatter distributions are modified accordingly to generate scatter estimates for the regular CBCT scan. These estimated scatter distributions are finally subtracted from the projection data for scatter correction. Details of these procedures are discussed below.

Figure 1.

Work flow of the scatter correction using prior scatter measurement from partially blocked CBCT.

Partially blocked CBCT and scatter measurement

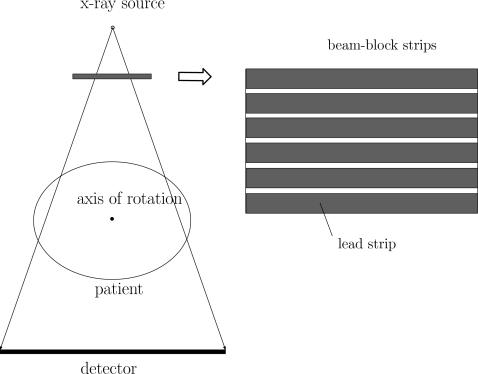
The geometry of the partially blocked CBCT system is shown in Fig. 2. The lead strips are aligned in the lateral direction and block the incident x-ray photons. When a standard filtered-backprojection reconstruction is used for the circular CBCT scan, the filtering on the projection data is applied only in the lateral direction. Based on the classic CT reconstruction theory, reconstruction of the partially blocked CBCT scan is still complete for certain axial slices. Inside the strip shadows on the detector, no primary signals are detected and the measured signals provide scatter samples. Assuming that the insertion of the lead strips does not greatly perturb the shape of the scatter distributions in the cone-beam (CB) projection and scatter contains dominant low-frequency signals,^{6, 7, 18} we can estimate the scatter distribution of the whole field in a regular CB projection using the measured scatter samples.

Figure 2.

Geometry of the partially blocked CBCT system.

To avoid the edge effect of the strips, only the measured data inside the central one-third of the strip shadows are used in the scatter measurement. The data inside the one strip shadow are first averaged in the longitudinal direction to reduce the noise in the measurement. A moving-average filtering with a width of 9 detector pixels is then applied in the lateral direction to further smooth the scatter distribution. This smoothing filter is chosen empirically based on the Monte Carlo (MC) simulation. The obtained one-dimensional (1D) profiles are the measured scatter at the centers of the strip shadows. A cubic spline interpolation∕extrapolation is then carried out in the longitudinal direction to estimate the scatter distribution of the whole detector area. Assuming that the scatter magnitude is proportional to the illuminated volume,¹ to obtain a scatter estimate in a regular CBCT projection, the scatter estimate in the partially blocked CBCT projection is finally magnified by the ratio of the total detector area to the illuminated detector area. For simplicity, hereafter, we refer to the scatter estimate from the partially blocked CBCT projections as the measured scatter.

The principle of our scatter estimation is similar to that in conventional measurement-based methods.^{7, 14, 19} However, instead of using a two-dimensional (2D) beam-block array which in general can provide more accurate scatter measurement for CB projections, we use a beam blocker with a 1D strip pattern. This design is based on two reasons. First of all, using projections of our proposed partially blocked CBCT system, the reconstructed image is still complete in certain slices in the axial direction. Therefore, an accurate registration is achievable using the partially blocked CBCT and the regular CBCT. The derived geometric information is critical to modify the premeasured scatter distribution for scatter correction of the regular CBCT. Secondly, the strip pattern downsamples the scatter distribution longitudinally and the longitudinal high-frequency scatter content cannot be estimated. Therefore, the accuracy of the proposed scatter estimation is heavily dependent on the assumption that scatter has dominant low-frequency signals in the longitudinal direction. As shown in our previous studies^{6, 20} and MC simulations in Sec. 3, the scatter in an x-ray projection of diagnostic imaging on an object with a quasicylindrical shape, such as a human torso, contains high-frequency content only in the lateral direction. Therefore, the scatter measurement using the proposed strip beam-block pattern can still achieve a high accuracy in clinical applications.

Image registration of a partial CBCT and a regular CBCT

To derive the patient transformation used in the scatter correction algorithm which will be described later, the regular CBCT data are first reconstructed without scatter correction. A rigid registration of the reconstructed volumes of the partial CBCT and the regular CBCT is then carried out. The Insight Toolkit (ITK) is used in our implementation. To improve the registration accuracy, the reconstructed images are first thresholded and only the bone structures are used for registration.²¹ The cost function chosen for minimization is the mean square pixelwise difference between the volumes. The registration uses versors and a 3D translational vector to describe the 3D rigid motion. The optimization method is a gradient descent search algorithm. Furthermore, to accelerate the registration, we generate a multiresolution image pyramid. Low resolution versions of the datasets are first registered, and then higher resolution versions are subsequently registered. The initial conditions are chosen by first placing both datasets in the same coordinate system and aligning their centers of masses. Typically, after approximately 100 steps, the step size decreases below a chosen threshold value and the registration is completed.

Scatter correction based on the registration of reconstructed volumes

Scatter distributions for the same patient change in different CBCT scans due to different patient positions. Even if the same imaging parameters are used and a rigid transformation of the patient is assumed for different scans, an accurate relationship between scatter distributions and the patient position is in general very complicated. Using a registration of the partially blocked CBCT and the regular CBCT, we propose an approximate formula to calculate the scatter distribution of a regular CB projection from the premeasured scatter distributions.

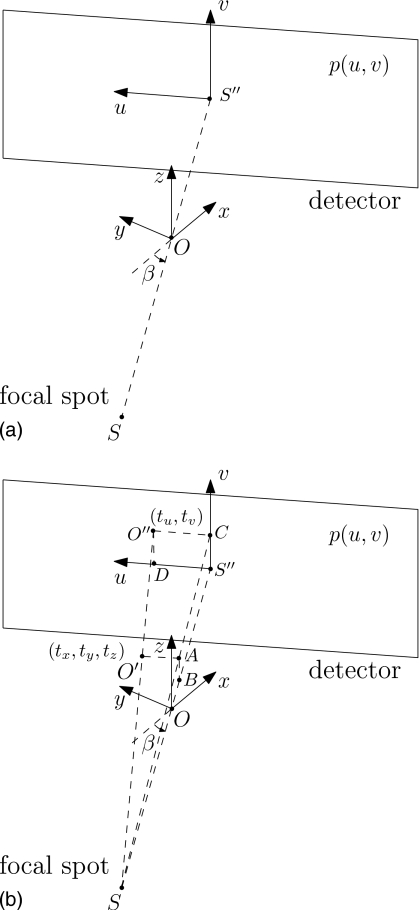
CBCT projections are functions of three arguments: The lateral and longitudinal detector coordinates u and v, and the projection view angle β. A rigid transformation on the patient can be described by six parameters: Translations in the x, y, and z directions (t_x, t_y, and t_z) and rotations around the x, y, and z axes (γ_x, γ_y, and γ_z). In our definition of transformation, the rotation is performed before the translation. The coordinate systems are shown in Fig. 3a.

Figure 3.

The cone-beam projection geometry and coordinate systems. (a) coordinate systerm before transformation; (b) coordinate system after the object translates by t_x,t_y,t_z in the directions of the x, y, and z axes, respectively.

In a parallel-beam geometry, the scatter distribution is shifted as the patient is translated. We assume that this property of shift invariance is still a good approximation in a divergent CB geometry. When the patient is translated without rotation, we approximate the scatter distributions by shifting the original scatter distributions as if in a parallel-beam geometry. Equivalently, we assume that the scatter distribution shifts together with the projection of the patient center on the detector. The distance of shifting is calculated as the patient translation in the direction parallel to the detector multiplied by a magnification factor determined by the CB geometry.

Figure 3b shows the coordinate system when the patient is shifted by t_x, t_y, and t_z in the directions of the x, y, and z axes, respectively. Correspondingly, the patient center moves from O to O^′, and O^″ is the projection of O^′ on the detector. Now the goal is to find the shifts on the detector, t_u and t_v, i.e., the position of O^″.

Denote M as the magnification factor from O^′ to the detector, SID as the source-to-imager distance (∣SS^″∣), and SAD as the source-to-axis distance (∣SO∣). Based on the geometry, M can be calculated as

$$M=\frac{\mid S{S}^{″}\mid }{\mid SB\mid }=\frac{\mid S{S}^{″}\mid }{\mid SO\mid +\mid OB\mid }=\frac{\mathrm{SID}}{\mathrm{SAD}+t_x\cos \beta +t_y\sin \beta },$$ (1)

and t_u and t_v are calculated as

$$t_u=M\mid O^{\prime }A\mid =M(-t_x\sin \beta +t_y\cos \beta ),$$ (2)

$$t_v=M\mid AB\mid =M{t}_z.$$ (3)

Denote S_m as the measured scatter obtained from the partially blocked CBCT projections and S_e as the scatter distribution in the regular CBCT projections that we need to estimate. Based on the approximation discussed earlier, we calculate S_e as

$$S_e(u,v,\beta )=S_m(u+t_u,v+t_v,\beta ).$$ (4)

Note, however, that the above approximation assumes no patient rotation. When the patient rotates during the transformation, however, Eq. 4 becomes much less accurate. Fortunately, in practice of radiation therapy, a patient rotation is typically very small (less than 2°) after the standard patient setup.²² Therefore, we can safely assume zero patient rotation about the x and y axes, i.e., γ_x≈0 and γ_y≈0. Rotation about the z axis, γ_z, can be easily included in the scatter estimation formula by shifting the rotation angle β since the axial rotation is equivalent to a change in the starting angle of the CBCT scan. The final estimation formula of S_e is expressed as

$$S_e(u,v,\beta )=S_m(u+t_u,v+t_v,\beta +{\gamma }_z),$$ (5)

where t_u and t_v are calculated using Eqs. 1, 2, 3.

Equation 5 is the main scatter estimation formula used in this article. The formula shows that the scatter can be estimated by shifting the premeasured scatter distributions in all three directions. A cubic spline extrapolation is used when the index of estimated scatter is outside the space of the premeasured scatter. Several approximations are made in the algorithm derivation. Detailed discussion on the assumptions of the imaging geometry and patient transformation will be provided in Sec. 4.

The estimated scatter is subtracted from the measured projection to generate scatter-corrected data. Note that, as generally true in scatter correction using postprocessing techniques, the scatter noise is left in the processed image.²³ A penalized weighted least-squares algorithm is implemented to suppress the image noise.^{24, 25} The data are then processed using a standard Feldkamp–David–Kress cone-beam CT reconstruction.²⁶

Evaluation

The measurement of scatter distribution using the proposed partially blocked CBCT is based on the assumption that for imaging on a human torso, the scatter distribution contains dominant low-frequency signals in the longitudinal direction. We validated this assumption using MC simulations (GEANT4) on the Zubal phantom.²⁷ The implementation details of the MC simulation can be found in Ref. 6.

A MC simulation of a complete CT scan is very time consuming, and the proposed method was further evaluated using physical experiments. The CBCT imaging system used in this work was a Varian Acuity CT simulator (Varian Medical Systems, Palo Alto, CA). A standard imaging protocol as in clinic was applied. The x-ray tube was operated at 125 kVp voltage and 80 mA with the pulse width at each projection angle of 25 ms. A bow-tie filter was placed on in order to maintain a more uniform photon statistics across the field of view (FOV). Data of a 360° scan consisted of about 680 projections with an angle interval of about 0.5°. The dimension of each acquired projection image was 397.3 mm×298.0 mm, containing 1024×768 pixels. The SAD was 1000 mm and the SID was 1500 mm. To increase the FOV, a half-fan mode was used, with the flat-panel detector shifted by approximately 160 mm.

In the partially blocked CBCT, the sheet of lead strips was mounted on the outside surface of the collimator with a distance of approximately 400 mm to the x-ray focal spot. The strips had a thickness of approximately 2 mm with an x-ray attenuation of over 99%. The strip spacing determines the sampling rate of the scatter distribution. Based on MC simulations, in our design, the strip had a width of approximately 6 mm and a gap of approximately 3 mm in between. The shadows of the strips on the detector have a width of approximately 24 mm and a gap of approximately 12 mm, resulting in a scatter sampling period of ∼36 mm on the detector. As shown in the results of experiments, this sampling period is chosen based on MC simulations and achieves a satisfactory accuracy of scatter estimation.

Two phantoms were used in the experiments. The first was the Catphan©600 phantom with a diameter of 200 mm. To increase the illumination volume such that the scatter magnitude is comparable to that in a scan on a human torso, we placed an oval body annulus in the periphery to expand the phantom to an elliptical cylinder with a major axis of 380 mm and a minor axis of 300 mm. An anthropomorphic chest phantom was used in the second study. In both experiments, we first measured the scatter using a partially blocked CBCT scan. The phantom was then transformed to simulate the patient transformation in scans on different days, and the proposed scatter correction was applied on a second regular CBCT scan.

Comparisons of the reconstructed images and 1D profiles of the regular CBCT scans are provided to illustrate the performance of the proposed method. In the experiments of the Catphan©600 phantom, to provide a benchmark image, the phantom was reconstructed using a narrow collimator, where the scatter was inherently suppressed. In this setup, the field of illumination on the detector has a width of ∼1 cm in the longitudinal direction and the geometry is equivalent to a fan-beam projection. The body annulus was also removed to further reduce the scatter. In the quantitative analysis, reconstructed values are converted to Hounsfield unit (HU) in selected regions of interest (ROI) and compared to those in the benchmark image. The error is calculated as the square root of the mean square error (RMSE), defined as

$$\mathrm{RMSE}=\sqrt{\text{mean}\left[{({\mu }_i-{\overline{\mu }}_i)}^2\right]},$$ (6)

where i is the index of the ROI, μ_i is the mean reconstructed value in HU inside the ROI, and ${\overline{\mu }}_i$ is the corresponding value measured in the benchmark image. In the experiment of the anthropomorphic phantom, the CBCT images before and after scatter correction are also compared to that using a narrow collimator. The error is quantified as the relative reconstruction error (RRE) in the ROI, defined as

$$\mathrm{RRE}=100\%\sqrt{\text{mean}\left[{\left(\frac{v(x,y)-\overline{v}(x,y)}{\overline{v}(x,y)}\right)}^2\right]},$$ (7)

$$(x,y)∊\mathrm{ROI}$$

where v is the reconstructed value in mm⁻¹ and $\overline{v}$ is the corresponding value using a narrow collimator. (x,y) are the coordinates of the reconstructed image. Since the z direction coverage is very small using a narrow collimator, only 2D slices are compared. The ROI is chosen as the nonair regions, which are determined by thresholding.

RESULTS

Monte Carlo simulation

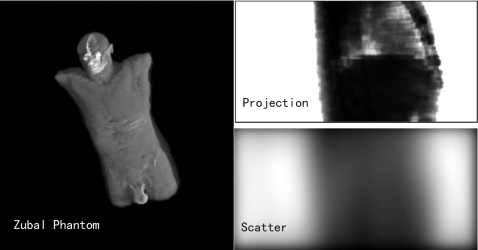
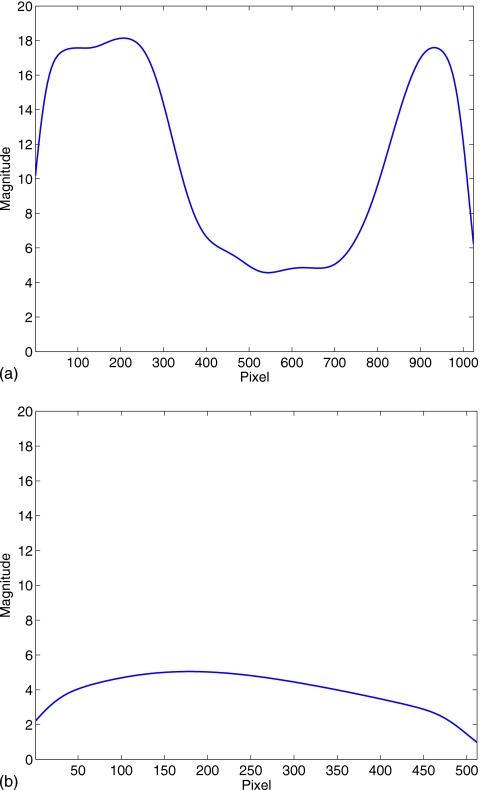
Figure 4 shows the Zubal phantom, one simulated projection of the chest region, and its corresponding scatter distribution. It is seen that the scatter distribution contains very low-frequency signals in the longitudinal direction, as also shown in Fig. 5. This reveals that the proposed partially blocked CBCT is able to provide an accurate scatter measurement.

Figure 4.

MC simulation on the Zubal phantom.

Figure 5.

1D profiles of the scatter distribution shown in Fig. 4. Note that the same scale is used in both plots. (a) Central horizontal profile; (b) Central vertical profile.

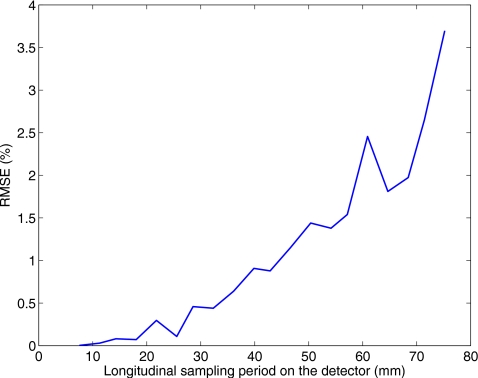
To provide a design guidance of the lead strips used in the partially blocked CBCT, we carry out scatter estimation on the simulated data using the method presented in Sec. 2A1 with different longitudinal sampling periods. The result is shown in Fig. 6. The estimation error in percentage is calculated as the error relative to the true scatter signals in a similar way as shown in Eq. 6. On the chest region of the Zubal phantom, a longitudinal sampling period on the detector not larger than 40 mm guarantees a scatter estimation accuracy of over 99%. Note that the penumbra edge effects due to the finite size of the focal spot are not included in the MC simulation. In reality, to avoid scatter estimation errors from these effects, the sampling period cannot be very small. Based on this consideration, we chose ∼36 mm as the longitudinal sampling period of the lead strip pattern.

Figure 6.

Relationship between the scatter estimation error and the sampling period based on the MC simulation.

Experiments on the Catphan©600 phantom

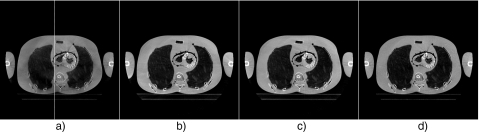
Figure 7 shows experimental results on the Catphan©600 phantom. In the regular CBCT scan after the partially blocked CBCT data acquisition, the phantom was translated laterally by 10 mm and longitudinally by 10 mm, i.e., t_y=10 mm, t_z=10 mm. Reconstructions of the regular CBCT scan are shown. As seen in Fig. 7a, shading∕cupping artifacts are severe in the reconstructed images if no scatter correction is applied. Note that the scatter artifacts have a nontypical and complicated pattern due to the use of a bow-tie filter and an offset flat-panel detector.²⁸ These artifacts are suppressed when a simple software correction scheme is used (Fig. 7b). In this scheme, we assume that the scatter is constant across the whole projection field, and its magnitude is estimated based on the volume size of x-ray illumination as described in Ref. 1. Nonetheless, new distortions are obvious around the center of the image. A superior image quality is found in Fig. 7c, where the scatter is corrected for using the proposed method. The scatter artifacts are greatly suppressed without inducing new artifacts. To illustrate the importance of estimating scatter using Eq. 5 based on the relative object geometry, we show in Fig. 7d the reconstructed image with the scatter corrected directly using the measured scatter, i.e., assuming that S_e=S_m. Distortion appears in the images, which indicates the necessity of scatter estimation using Eq. 5.

Figure 7.

Axial views of the reconstructed Catphan©600 phantom. Display window: [−500 500] HU. In the regular scan after partial CBCT, the object is translated (t_y=10 mm, t_z=10 mm): (a) No scatter correction; (b) using constant scatter correction; (c) scatter corrected using the proposed method; and (d) scatter corrected using the measured scatter from the partial CBCT, but without using the “registration” algorithm as defined in Eq. 5. The white arrow indicates the image distortion.

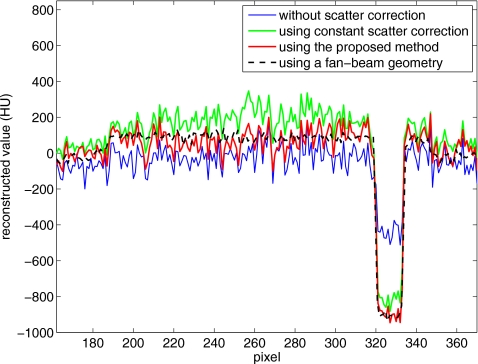
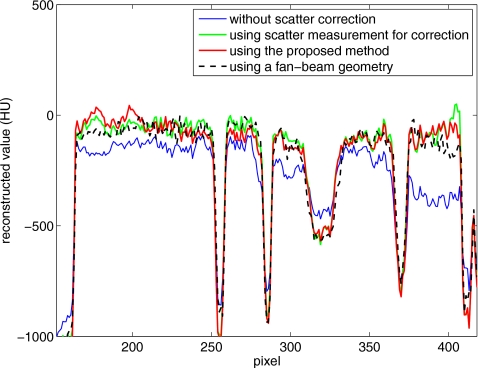
For a better comparison, we obtain a benchmark image (Fig. 8) of the Catphan©600 phantom without the body annulus and using a fan-beam geometry. The fan-beam geometry was implemented using a narrow collimator, as described in Sec. 2B. The benchmark image is registered to the images shown in Fig. 7. Figure 9 shows the comparison of 1D profiles passing through one contrast object. The benchmark image does not include the body annulus, and therefore the reconstruction data of the body annulus are excluded in the comparison. The reconstruction error due to scatter, such as signal intensity drop and contrast loss, is obvious in Fig. 9. This error is greatly suppressed using the proposed method, and the scatter correction result matches the benchmark image well.

Figure 8.

Reconstruction of the Catphan©600 phantom using a narrow collimator (a fan-beam geometry).

Figure 9.

Comparison of 1D profiles in Figs. 78 passing through one contrast rod. The data on the body annulus are excluded.

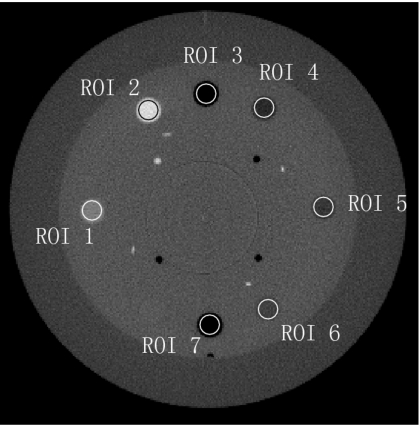
To test the stability of the proposed method, Fig. 10 shows the images with and without scatter correction when the object has different transformations in four regular CBCT scans. In the first scan, the phantom has no transformation; in the second and the third scans, the phantom is shifted laterally by 10 and 20 mm (t_y=10 mm and t_y=20 mm); in the fourth scan, the phantom is shifted laterally by 5 mm and also rotated about the x axis by 3° (t_y=5 mm, γ_x=3°). Seven contrast rods as shown in Fig. 8 are selected as the ROIs. Table 1 summarizes the reconstruction values in HU in the ROIs and the errors relative to the values obtained in a fan-beam geometry. Both the image comparison and quantitative analysis indicate that the proposed method is very effective on scatter correction even if the object has a small rotation which violates the assumption in the algorithm derivation. The reconstruction error is reduced from about 350 HU to below 50 HU. Note that the residual reconstruction error after scatter correction increases as the object transformation gets larger. However, we want to emphasize that the patient setup error in radiation therapy treatment is typically less than 10 mm in translation and less than 2° in rotation.²² Our method is expected to achieve excellent scatter correction in practice.

Figure 10.

Axial views of the reconstructed Catphan©600 phantom with different transformations in the second regular CBCT scan. Display window: [−500 500] HU. Upper row: Without scatter correction; bottom row: Using the proposed method: (a) No transformation; (b) t_y=10 mm; (c) t_y=20 mm; and (d) t_y=5 mm, γ_x=3°. The transformation parameters (t_x,y,z and γ_x,y,z) are zeros unless otherwise specified.

Table 1.

Comparison of reconstruction values (in HU) inside the contrast rods of the Catphan©600 phantom. The minimum and maximum of the errors are also shown in parentheses.

ROI	1	2	3	4	5	6	7	RMSE (min∼max)
Fan-beam	367.5	958.6	−954.7	−159.8	−66.5	−11.5	−950.9
No scatter correction
No transformation	100.5	362.8	−482.1	−160.7	−142.3	−149.5	−536.7	347.6 (−595.8∼472.6)
ty=10 mm	84.7	343.4	−502.0	−166.3	−143.9	−141.8	−526.5	351.8 (−615.2∼452.7)
ty=20 mm	119.9	353.6	−473.0	−143.9	−137.8	−166.3	−555.6	347.4 (−605.0∼481.7)
ty=10 mm, tz=10 mm	104.6	340.8	−480.6	−146.9	−134.2	−145.4	−533.7	353.0 (−617.8∼474.1)
ty=5 mm, γx=3°	69.4	363.8	−504.6	−156.1	−152.0	−152.0	−518.9	350.3 (−594.8∼450.0)
Using the proposed method
No transformation	359.7	978.6	−937.8	−156.6	−72.4	−28.6	−970.9	14.6 (−20.0∼20.0)
ty=10 mm	323.0	978.1	−957.1	−160.7	−62.2	1.0	−957.7	19.2 (−44.5∼19.5)
ty=20 mm	383.2	1035.7	−1016.8	−143.4	−72.4	−58.2	−958.7	42.4 (−62.1∼77.1)
ty=10 mm, tz=10 mm	312.8	924.5	−907.7	−134.7	−46.9	−23.0	−897.0	38.6 (−54.7∼54.0)
ty=5 mm, γx=3°	351.5	971.4	−974.0	−144.9	−73.0	−15.3	−985.2	17.9 (−34.3∼14.9)

Experiments on the anthropomorphic phantom

One partially blocked CB projection of the anthropomorphic chest phantom and its corresponding measured scatter distribution is shown in Fig. 11. In the regular CBCT scan, the phantom is slightly transformed. Using a rigid registration, the calculated transformation parameters are t_x=−4.0 mm, t_y=8.4 mm, t_z=−2.2 mm, and γ_x=2.01°, γ_y=1.99°, γ_z=0.55°. Figure 12 shows one regular CB projection and its scatter estimate using the proposed method.

Figure 11.

Projection image of partially blocked CBCT and the corresponding measured scatter distribution.

Figure 12.

CB projection image and its scatter estimate using the proposed method.

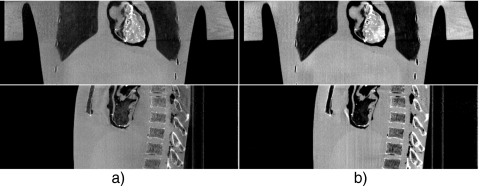
Figure 13 shows the axial views of the reconstructed volumes without and with scatter correction and using a fan-beam geometry. The image distortion and shading artifacts due to scatter are greatly suppressed by using the proposed method. The quality of the scatter corrected image is close to that using a fan-beam geometry, which is also illustrated in the 1D profile comparison as shown in Fig. 14. The sagittal and conoral views without and with scatter correction are shown in Fig. 15. It is obvious that the proposed algorithm greatly suppresses the shading artifacts mostly surrounding the bones. The proposed method reduces the RRE value as defined in Eq. 7 from 15.7% to 5.4%. To investigate the performance of the proposed scatter estimation from the scatter measurement (Eq. 5), we include a fourth image (Fig. 13b) in the comparisons of Figs. 1314. After the phantom is transformed, another scatter measurement is carried out using the partially blocked CBCT. The image is then generated using scatter correction directly based on the scatter measurement. It is seen that the measurement-based scatter correction has a similar performance as compared to the proposed method. Therefore the proposed approximation formula (Eq. 5) provides an accurate scatter estimation for this phantom scan.

Figure 13.

Axial views of the reconstructed anthropomorphic phantom. Display window: [−800 450] HU. In the regular scan after partial CBCT, the phantom is transformed by parameters of t_x=−4.0 mm, t_y=8.4 mm, t_z=−2.2 mm, and γ_x=2.01°, γ_y=1.99°, γ_z=0.55°: (a) No scatter correction; (b) measurement-based scatter correction using a partially blocked CBCT as a prescan; (c) scatter corrected using the proposed method; and (d) using a narrow collimator (a fan-beam equivalent geometry). The line in (a) indicates the location where the 1D profiles shown in Fig. 14 are taken.

Figure 14.

Comparison of 1D vertical profiles in Fig. 13.

Figure 15.

Sagittal and coronal views of the reconstructed anthropomorphic phantom. Display window: [−800 450] HU: (a) No scatter correction and (b) scatter corrected using the proposed method.

DISCUSSION AND CONCLUSIONS

An effective scatter correction method for CBCT in radiation therapy is proposed in this study. The development of this method is inspired by the fact that the same patient is scanned repetitively during the radiation treatment course. Assuming that the same imaging parameters are used, the scatter signals are closely correlated in these scans. Therefore, we can measure the scatter distributions in the first scan and perform scatter correction in the subsequent scans on the same patient on different days. A partially blocked CBCT is used to measure the scatter distributions, as well as to obtain the geometric information of the patient. An approximate formula is also proposed to estimate the scatter distributions in the subsequent regular scans based on the geometric information. The method is evaluated using experiments and shows significant suppression of scatter artifacts. On the Catphan©600 phantom, the reconstruction errors in the selected ROIs are reduced from about 350 to below 50 HU; on the anthropomorphic phantom, the reconstruction error is reduced from 15.7% to 5.4%. Note that our method is different from the existing measurement-based scatter correction methods,⁷ where an additional scan with an insertion of a beam blocker is used only for the purpose of scatter measurement and therefore the patient dose is increased. In the proposed method, the partially blocked CBCT scan not only provides an accurate scatter measurement but also can be used for precise patient setup with a much decreased patient dose.¹⁷ In the current radiation therapy where CBCT is mainly used for patient setup, the scatter measure from a partially blocked CBCT scan is “free” information. In our algorithm, several additional steps are added into the conventional data processing chain. The increased computation complexity mainly resides on the extra 3D reconstruction on the regular scan. Nonetheless, with new developments of computer technology, CT reconstruction is dramatically accelerated.^{29, 30} The proposed method can still be considered as a viable and practical solution to the scatter problem in CBCT.

The underlying philosophy of our method is to create a patient-specific scatter database and correct for scatter for different scans based on patient geometric information. In our implementation, a partially blocked CBCT scan is used to measure the scatter. In applications where partial blocking of the detector is not desired, such as in fiducial tracking using CB projections, other methods can also be used here to obtain the scatter data. For instance, since the planning CT data from the multidetector CT scanner are readily available, we can generate the scatter data using an analytical model¹⁸ or a MC simulation.¹¹

Due to the complex nature of scattering process, approximations are made to simplify the derivation of the scatter modification formula based on the measured scatter distributions and the patient geometric information. These approximations work well in the experiments. We also assume that a rigid transformation applies on the patient. In practice, the patient has deformations in different scans, and the deformation not only changes the scatter distributions but also affects the correlation of the patient geometries. However, since the point spread function of the scatter is typically smooth,¹⁸ scatter distributions are very insensitive to small patient deformations. When the patient deformation is large, a partially blocked CBCT scan can be implemented right before the regular scan to provide a more accurate scatter measurement at the price of extra patient dose. Future investigations on the accuracy of the proposed algorithm under the circumstance of patient deformation is of high interest using clinical patient studies.

The proposed method is evaluated using experiments with different transformations. The scatter estimation is expected to be less accurate as the patient transformation increases. For example, as the translation increases, due to the half-fan geometry in clinical Varian CBCT systems, the illumination volume size is more different in different scans, causing different scatter magnitudes. The use of a bow-tie filter makes the difference even larger. The overlapping projection area becomes smaller as well, resulting in scatter estimation error due to excessive signal extrapolation. The proposed algorithm also assumes that the patient has only in-plane rotation, i.e., no rotations about x and y axes. Further research will be conducted to expand the proposed method to more accurately estimate the scatter for arbitrary rigid transformations of the object. It is worth mentioning that in radiation therapy, the patient transformation is typically less than 10 mm in translation and less than 2° in rotation after the patient setup,²² and the setup error can be further reduced using in-line cone-beam CT.³¹ The object transformations used in our experiments are within or beyond the range of patient setup errors, and excellent scatter correction results are shown. Therefore, we expect our algorithm to work well in clinical applications.

The indication of the presented work is multifold. First, the proposed method greatly improves the soft-tissue contrast of CBCT, which enables clinicians to make better clinical decisions. Second, the increased HU accuracy can greatly improve the accuracy of dose reconstruction using CBCT images, which makes treatment planning using CBCT images a viable option. As such, the improved image quality using the proposed scatter correction method should be very attractive in clinical applications.