High-resolution 3D CANCA NMR experiments for complete mainchain assignments using C^α direct-detection

Abstract

The primary limitation of solution state NMR with larger, highly dynamic, or paramagnetic systems originates from signal losses due to fast transverse relaxation. This is related to the high gyromagnetic ratio γ of protons, which are usually detected. Thus, it is attractive to consider detection of nuclei with lower γ, such as ¹³C, for extending the size limits of NMR. Here, we present an approach for complete assignment of C^α and N resonances in fast relaxing proteins using a C^α detected 3D CANCA experiment for perdeuterated proteins. The CANCA experiment correlates alpha carbons with the sequentially adjacent and succeeding nitrogen and alpha carbons. This enables elongation of the chain of assigned residues simply by navigating along both nitrogen and carbon dimensions using a “stairway” assignment procedure. The simultaneous use of both C^α and N sequential connectivities makes the experiment more robust than conventional 3D experiments, which rely solely on a single ¹³C indirect dimension for sequential information. The 3D CANCA experiment, which is very useful for mainchain assignments of higher molecular weight proteins at high magnetic field, also provides an attractive alterative for smaller proteins. Two versions of the experiment are described for samples that are ¹³C labeled either uniformly or at alternate positions for removing one-bond ¹³C-¹³C couplings. In order to achieve both, high resolution and sensitivity, extensive non-uniform sampling was employed. Adding longitudinal relaxation enhancement agents can allow for shorter recycling delays, decreased measuring time, or enhanced sensitivity.

Introduction

NMR is an established technique for studying structure and dynamics of macromolecules in solution. However, its use has severe limits when studying large and/or fast relaxing systems, such as multi-protein complexes, membrane proteins, or paramagnetic proteins. In traditional proton detected triple resonance experiments, the limitations originate primarily from relaxation-induced losses of signal intensity. These affect coherences not only during evolution or detection periods but also during magnetization transfers. The large ¹H gyromagnetic ratio, which had been key to the performance of a large collection of ¹H-detected triple-resonance experiments, is actually a “double-edged sword”. While, it provides a large Zeeman polarization at the beginning of an experiment, the stronger dipolar interaction resulting from the large magnetic moment also causes fast decay during the pulse sequences and detection. Since the peak heights are proportional to the integral over the detected free induction decay (FID) and not only to the initial amplitude, a slowly decaying signal of lower initial FID amplitude may have a superior signal-to-noise ratio (S/N) over a rapidly-relaxing signal of higher FID amplitude. Moreover, conventional ¹H-detected experiments suffer from broad line widths of the detected signals leading to poor resolution. Thus, it is reasonable to consider ¹³C direct detection in these systems.

In the past, ¹³C direct detection has been demonstrated with carbonyls in uniformly ¹³C-labeled proteins^{1, 2} and was quite successful for small paramagnetic proteins. However, the carbonyl CSA becomes an efficient relaxation mechanism in large molecular weight systems, especially at high magnetic fields. In such cases, a C^α-detection experiment is expected to show better performance since C^α, which has a smaller CSA, benefits from slower transverse relaxation if the proteins are deuterated³. However, direct C^α detection is complicated due to the two strong one bond ¹³C-¹³C scalar couplings with C′ and C^β causing crowded spectra and reducing sensitivity by splitting a C^α resonance into multiplets. Spectral complexity can be avoided by computational deconvolution⁴ or by selecting a single component within the split peaks using IPAP or S³E schemes³, when conventional uniform ¹³C labeling is used. The required spin manipulation, however, cause a loss in the signal intensity. The undesirable couplings can be eliminated by alternate ¹³C carbon labeling⁵, without complicated pulse programs and/or processing, as we described before⁶. Here, we present a ¹³C^α detection 3D CANCA experiment for both alternate and uniform ¹³C labeling that is amenable for studies of large systems at high field. The resulting spectrum provides sequential correlations across all dimensions and can thus be used single-handedly to assign all C^α and N backbone resonances.

Experimental Design

The C^α-direct detected 3D CANCA experiment provides a robust way to establish complete mainchain resonance assignment with simultaneous use of both C^α and N sequential connectivities. The 3D CANCA experiment correlates a given alpha carbon (C^α_i) both with its attached nitrogen (N_i) and the nitrogen of the following residue (N_i+1). In another dimension, this alpha carbon is correlated with the C^α of both previous (C^α_i-1) and following (C^α_i+1) residues. This enables elongation of the chain of assigned residues simply by navigating along both dimensions using the so-called “stairway” assignment procedure^{7, 8}. A C^α-C^α plane at the frequency of ω (N_i) (Figure 1B (cyan shadow) and Figure 1C (cyan planes)) will have four correlations of coordinates (ω(C^α_i-1); ω(C^α_i-1)), (ω(C^α_i-1); ω(C^α_i)), (ω(C^α_i); ω(C^α_i-1)), and (co(C^α_i); ω(C^α_i)). Thus, C^α_i is directly correlated to its predecessor, C^α_i-1. The chain is easily extended by inspecting the nitrogen dimension which displays another (ω(C^α_i); ω(C^α_i)) correlation at ω(N_i+1). At this nitrogen frequency, C^α_i is correlated to its successor, C^α_i+1. Unlike the previously published 2D NCA experiment, which exclusively relies on nitrogen chemical shifts for sequential connectivities⁶, the CANCA can establish sequential assignment via both C^α and N nuclei, eliminating ambiguities in case of nitrogen chemical shift degeneracies. Thus, the CANCA experiment alone provides the information for a complete sequence specific assignment, including proline residues.

Figure 1.

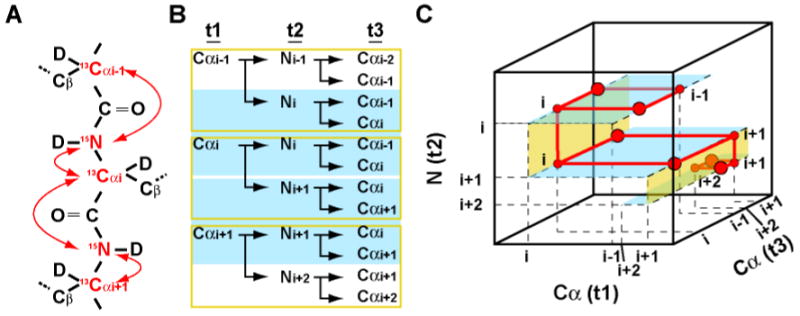
Coherences correlated by the 3D CANCA experiment. (A) Illustration of the coherences correlated with C^α_i. The nuclei involved are colored in red and their scalar couplings are indicated by red arrows. (B) Signals and correlations observed in each plane of the N (cyan shadow) or the C^α (yellow box) dimensions. (C) Schematic representation of the 3D CANCA spectrum. Each C^α-C^α plane (colored in blue) has intra-residue and sequential carbon correlations. Sequential connections are also found in nitrogen dimension (yellow plane). Thus the assignment can be easily established by navigating between C^α-C^α planes up and down the “stairway” along the nitrogen dimension

Materials and Methods

All chemicals were purchased from Sigma (St. Louis, MO) unless otherwise noted. All stable-isotope-labeled materials were acquired from Cambridge Isotope laboratories (Cambridge, MA).

Expression and purification of the B domain of protein G (GB1)

The gene for 6His-tagged GB1, consisting of 64 amino acid residues, was cloned into the pET9d vector (Novagen, San Diego, CA) as previously described⁸. GB1 was expressed in commercially available BL21 (DE3) E.coli cells (Novagen) at 37°C and protein expression was induced for 6 hours at the same temperature. For [2-¹³C-glyceol] labeled samples, the cells were cultured in ²H¹⁵N M9 media containing 8.5 g/L Na₂HPO₄, 3 g/L KH₂PO₄, 0.5 g/L NaCl, 2mM MgCl₂, 0.1 mM CaCl₂, and 1 g/L of ¹⁵NH₄Cl in D₂O, which is supplemented with 2g/L [2-¹³C] glycerol and 2g/L NaH¹³CO₃. For the uniformly ²H¹⁵N¹³C-labeled samples, the cells were cultured in ²H¹⁵N¹³C M9 media containing 1 g/L of ¹⁵NH₄Cl, 2 g/L of ²H¹³C glucose in D₂O, The protein was purified with Ni-NTA affinity chromatography as previously described⁸.

NMR Experiments

NMR spectra were recorded on a Bruker (Billerica, MA) Avance 500 spectrometer equipped with a triple-resonance carbon-cryogenic probe (TXO) designed for carbon detection experiments. All spectra were recorded at 15°C in buffer containing 10 mM sodium phosphate (pH 6.8), 100 mM NaCl and 20% w/v deuterated glycerol in D₂O to induce a tumbling corresponding to a 90kDa protein at 25°C⁶. 3D CANCA experiments were recorded with a spectral width of 3511 Hz for carbon (centered at 55 ppm) and 1519 Hz for nitrogen (centered at 117 ppm). 1024 complexed data points were recorded for direct detection. 500 points out of 128 (C^α) ×128 (N) complex point were sparsely recorded in the indirect dimensions. The data was processed with a high-fidelity forward maximum entropy reconstruction algorithm developed in our laboratory, which conserves all measured time-domain data points and predict the missing data points by an iterative procedure⁹. The reconstructed time domain data were then multiplied by a cosine window function, zero filled and Fourier transformed. The resolution in the indirect dimensions after apodization and Fourier transformation was 27 Hz for C^α and 11 Hz for N. The recycling delay was optimized to be 1.25 × T₁ (longitudinal relaxation time) = 4 sec or 1.2sec, with or without adding paramagnetic relaxation enhancement agents, respectively. All spectra were analyzed with the program Sparky¹⁰.

Pulse sequence

Figure 2 shows two alternative versions of the CANCA 3D experiment. Figure 2A displays the pulse sequence for samples with alternate ¹³C labeling (expressed by incorporating 2-¹³C glycerol or 1,3-¹³C glycerol) for removing one-bond ¹³C-¹³C scalar coupling. Figure 2B depicts the modifications that need to be implemented for uniformly ¹³C-enriched samples. The basic principle is common to both experiments and the pulse sequence of Figure 2A will first be described, and the modifications of Figure 2B will be explained later.

Figure 2.

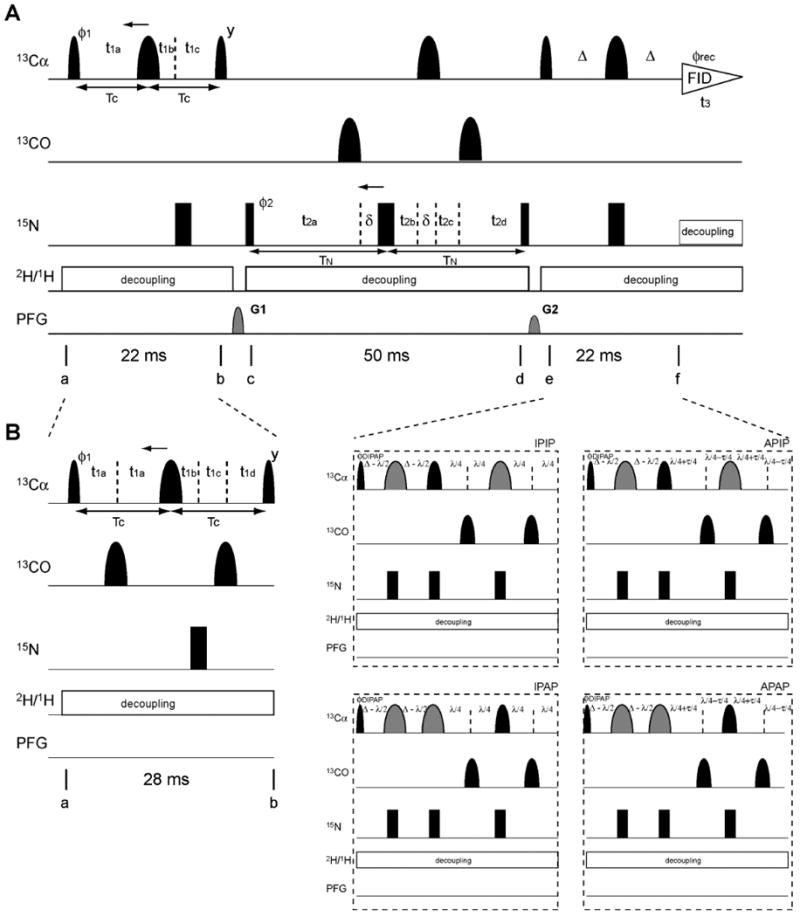
Pulse program of the 3D CANCA experiment optimized for (A) alternate and (B) uniform ¹³C-labeling. Narrow and wide black bars indicate non-selective π/2 and π pulses, respectively. Narrow and wide semi elliptical shapes on the carbon channel represent π/2 and π Gaussian cascades pulses (Q5 / 256 μs and Q3 / 205 μs, respectively)¹¹ selective for the frequencies of aliphatic carbon nuclei. Wider Gaussian shapes in gray indicate C^α selective Gaussian cascades pulses (Q3 / 1557 μs). All pulses are applied along the x-axis unless otherwise indicated. (A) The delays were T_C = Δ = 11 ms and T_N = 25 ms, which is optimal for inter-residue connectivities. The short delay δ = 205 μs compensates for a ¹³C 180° pulse. The delays and increments for the ¹³C t₁ semi-constant time (SCT) period (a-b) are: t_1a = t_1c = TC; t_1b = 5 μs; Δt_1a = -T_C/n_1max; Δt_1c = 1/(2SW_C)- T_C/n_1max; Δt_1b = 1/(2SW_C). If n_1max×Δt_1a < T_C, a constant time (CT) is used. In this case, t_1a = t_1c = T_C and t_1b = 5 μs. Δt_1a = - Δt_1c = 1/(2SW_C) and Δt_1b = 0. The delays and increments for the ¹⁵N t₂ SCT period (c-d) are: t_2a = t_2d = T_N = 25 ms; t_2b = t_2c = 5 μs; Δt_2a = -T_N/n_2max; Δt_2b = Δt_2d = 1/(2SW_N)- T_N/n_2max; Δt_2c = T_N/n_2max. If n_2max×Δt_2a < T_N, a constant time is used. t_2a = t_2d = T_N = 25 ms; t_2b = t_2c = 5 μs. Δt_2a = Δt_2b = Δt_2d = Δt_2c = 1/4(SW_N). n_1max and n_2max are the values of the maximum Nyquist grid points in each dimension. In our experiment, both C^α and N are incremented in the SCT fashion (128 (C^α) × 128 (N) complex points, SW_C = 3511 Hz, SW_N = 1518 Hz). The phase cycle employed was ϕ₁ = (x, -x), ϕ₂ = (x, x, -x, -x), ϕ_rec = (y, -y, -y, y). Phase sensitive spectra in the ¹³C(t₁) and ¹⁵N(t₂) dimensions are obtained by incrementing the phases ϕ₁ and ϕ₂, respectively, in a States-TPPI manner¹². The recycling delay is optimized based on longitudinal relaxation rates. The sine-shaped pulsed field gradients were all applied for 1.0 ms with maximum intensities of G1 = 19 G/cm (g_z) and G2 = 16 G/cm (g_z). Deuterium and proton decoupling are achieved by using WALTZ16 sequence (3.1 kHz and 1kHz, respectively). (B) The delays were T_C = 14 ms, Δ = 11 ms and T_N = 25 m, which is optimal for inter-residue connectivities. For IPAP, λ = 14.4 ms and τ = 9 ms were used. The short delay δ = 205 μs compensates for a ¹³C 180° pulse. The delays and increments for ¹³C t₁ semi-CT period are: t_1a = t_1d = Tc/2; t_1b = 3.3 ms; t_1c = 3.8 ms; Δt_1a = -Tc/n_1max; Δt_1b = 1/(2SW_C)- 2T_C/n_1max; Δt_1c = T_C/n_1max; δt_1d = 1/(2SW_C) - 2T_C/n_1max. If n_1max×δt_1a < T_C, a constant time is used. t_1a = t_1d = Tc/2; t_1b = 3.3 ms; t_1c = 3.8 ms; δt_1a = δt_1c = δt_1d = 1/4(SW_C); δt_1b = 0. The delays and increments for ¹⁵N t₂ semi-CT or CT periods are the same as in (A). The phase cycle employed was ϕ₁ = (x, -x), ϕ₂ = (x, x, -x, -x), ϕ_DIPAP = (x, x, x, x, -x, -x, -x, -x) for IPIP and APAP, (-y, -y, -y, -y, y, y, y, y) for APIP, and (y, y, y, y, -y, -y, -y, -y) for IPAP, ϕ_rec = (x, -x, -x, x, -x, x, x, -x). Phase sensitive spectra in the ¹³C(t₁) and ¹⁵N(t₂) dimensions are obtained by incrementing the phases ϕ₁ and ϕ₂, respectively, in a States-TPPI manner. The recycling delay, pulsed-field gradients, deuterium and proton decoupling were the same as in (A).

A first INEPT module between points a and b converts a carbon C^α_i single quantum coherence (SQC) into longitudinal two-spin order between this carbon and its two scalar-coupled nitrogens (N_i and N_i+1). Concomitantly, the coherence is encoded with the C^α chemical shift in either a semi-constant time (SCT) ^{13, 14} or a constant-time fashion, depending on the value of n_1max. The density operator, σ, at point b is thus:

$${\sigma }_{\text{b}}=\text{cos}\left(({\mathrm{\omega }}_{{\text{C}}_{\text{i}}^{\alpha }}){\text{t}}_1\right)\left(2{\text{N}}_{{\text{z}}_{\text{i}}}{\text{C}}_{{\text{z}}_{\text{i}}}^{\alpha }{\text{S}}_{\text{C}}{(}^1\text{J}){\text{C}}_{\text{C}}{(}^2\text{J})+2{\text{N}}_{{\text{z}}_{\text{i}+1}}{\text{C}}_{{\text{z}}_{\text{i}}}^{\alpha }{\text{S}}_{\text{C}}{(}^2\text{J}){\text{C}}_{\text{C}}{(}^1\text{J})\right)$$ (1)

where only the real component of the indirect FID is depicted. S_C(¹J) = sin(π¹J_NCa2T_C), S_C(²J) = sin(π²J_NCa2T_C), while C stands for a cos of the corresponding arguments. To maximize the amplitude of antiphase coherences, 2T_C is set to 1/4J_CαN (∼ 22 ms)^15-17. Between points c and d, nitrogen SQCs of residues i and i+1 are allowed to evolve under their respective chemical shifts, again either in a semi-constant time or in a constant-time fashion, depending on n_2max. Simultaneously, they each evolve under both one-bond and two-bonds scalar couplings with C^α carbons. The terms of the density operator that are detected are:

$$\begin{array}{l}{\sigma }_{\text{d}}=\text{cos}\left({\mathrm{\omega }}_{{\text{C}}_{\text{i}}^{\alpha }}\text{t}\right)\\ \times \left[\begin{array}{l}\text{cos}({\mathrm{\omega }}_{{\text{N}}_{\text{i}}}{\text{t}}_2)\left(2{\text{N}}_{{\text{y}}_{\text{i}}}{\text{C}}_{{\text{z}}_{\text{i}}}^{\alpha }{\text{C}}_{\text{N}}{(}^1\text{J}){\text{C}}_{\text{N}}{(}^2\text{J})-2{\text{N}}_{{\text{y}}_{\text{i}}}{\text{C}}_{{\text{z}}_{\text{i}-\text{1}}}^{\alpha }{\text{S}}_{\text{N}}{(}^1\text{J}){\text{S}}_{\text{N}}{(}^2\text{J})\right){\text{S}}_{\text{C}}{(}^1\text{J}){\text{C}}_{\text{C}}{(}^2\text{J})\\ +\text{cos}({\mathrm{\omega }}_{{\text{N}}_{\text{i}+1}}{\text{t}}_2)\left(2{\text{N}}_{{\text{y}}_{\text{i}+1}}{\text{C}}_{{\text{z}}_{\text{i}+1}}^{\alpha }{\text{C}}_{\text{N}}{(}^2\text{J}){\text{C}}_{\text{N}}{(}^1\text{J})-2{\text{N}}_{{\text{y}}_{\text{i}+\text{1}}}{\text{C}}_{{\text{z}}_{\text{i}}}^{\alpha }{\text{S}}_{\text{N}}{(}^2\text{J}){\text{S}}_{\text{N}}{(}^1\text{J})\right){\text{S}}_{\text{C}}{(}^2\text{J}){\text{C}}_{\text{C}}{(}^1\text{J})+\dots \end{array}\right]\end{array}$$ (2)

In which S_N(¹J) = sin(π¹J_NCa2T_N), S_N(²J) = sin(π²J_NCa2T_N) and C stand for a cosine of the corresponding arguments. The duration of the delay T_N is optimized by analogy to what is described for the hNcaNH experiment:¹⁸

$$2{\text{T}}_{\text{N}}\ast =0.052-4.8\cdot {10}^{-4}{\text{R}}_2.$$ (3)

Where T_N* is the optimal value of the delay T_N and R₂ is the nitrogen single-quantum relaxation rate for a deuterated amide group. Inversion pulses are applied to carbonyl carbon nuclei to refocus the evolution under ¹J_NiC'i-1. A reversed INEPT (e-f) then converts nitrogen SQCs into the detected C^α single quantum coherences:

$$\begin{array}{l}{\sigma }_{\text{e}}=\text{cos}\left({\mathrm{\omega }}_{{\text{C}}_{\text{i}}^{\alpha }}{\text{t}}_1\right)\\ \times \left[\begin{array}{l}\text{cos}({\mathrm{\omega }}_{{\text{N}}_{\text{i}}}{\text{t}}_2)\left({\text{C}}_{{\text{y}}_{\text{i}}}^{\alpha }{\text{C}}_{\text{N}}{(}^1\text{J}){\text{C}}_{\text{N}}{(}^2\text{J}){\text{e}}^{-\text{i}{\mathrm{\omega }}_{\text{i}}{\text{t}}_3}-{\text{C}}_{{\text{y}}_{\text{i}-1}}^{\alpha }{\text{S}}_{\text{N}}{(}^1\text{J}){\text{S}}_{\text{N}}{(}^2\text{J}){\text{e}}^{-\text{i}{\mathrm{\omega }}_{\text{i}-1}{\text{t}}_3}\right){\text{S}}_{\text{C}}{(}^1\text{J}){\text{C}}_{\text{C}}{(}^2\text{J})\\ +\text{cos}({\mathrm{\omega }}_{{\text{N}}_{\text{i}+\text{1}}}{\text{t}}_2)\left({\text{C}}_{{\text{y}}_{\text{i}+\text{1}}}^{\alpha }{\text{C}}_{\text{N}}{(}^2\text{J}){\text{C}}_{\text{N}}{(}^1\text{J}){\text{e}}^{-\text{i}{\mathrm{\omega }}_{\text{i}+\text{1}}{\text{t}}_3}-{\text{C}}_{{\text{y}}_{\text{i}}}^{\alpha }{\text{S}}_{\text{N}}{(}^2\text{J}){\text{S}}_{\text{N}}{(}^1\text{J}){\text{e}}^{-\text{i}{\mathrm{\omega }}_{\text{i}}{\text{t}}_3}\right){\text{S}}_{\text{C}}{(}^2\text{J}){\text{C}}_{\text{C}}{(}^1\text{J})+\dots \end{array}\right]\end{array}$$ (4)

where ${\mathrm{\omega }}_{\text{i}}={\mathrm{\omega }}_{{\text{C}}_{\text{i}}^{\alpha }}$ Thus, the C^α of a given residue is correlated to those of its following and preceding residues, as well as to its own nitrogen and the nitrogen of its successor. This results in the sets of correlations that have been described above and that allow for a straightforward stairway assignment procedure.

For uniformly ¹³C enriched proteins, the modifications of Figure 2B need to be implemented. The initial value of the semi-constant time period 2T_C is set to 1/¹J(C^αC^β) to minimize losses due to scalar couplings between alpha carbons and beta carbons. The evolution in t₁ under this coupling is scaled from 1/SW(C) (for chemical shift evolution) to 1/SW(C) -2T_C/n_max. In our implementation this results in a residual coupling of 8.1 Hz. Alternatively, a C^α selective pulse can be used for a relaxation optimized transfer, which leads to the shortening of the period “a-b” from 28 ms (1/¹J(C^αC^β) to 22 ms (1/4¹J(C^αN). The reduction of the transfer duration results in about 20% of sensitivity gain for most residues. However, the signals from Gly, Ser, and some high-field C^α resonances become weaker as a draw back (data not shown). In addition, this C^α selective pulse does not eliminate evolution under ¹J(C^αC^β) during t₁, which broadens the lines and may even split each signal into a doublet at high resolution. The C^α selective pulse can however be designed to only affect the C^β of subset of residues and obtain additional information to identify the type of amino acid residues¹⁹. It is worth emphasizing that, if alternate ¹³C labeling is used, the first (a-b) and last (e-f) INEPT transfer periods can be set to the optimal (22 ms) without having any broadening caused by the unwanted scalar coupling evolution during t₁. Thus, the highest sensitivity would be expected for those residues that are ∼100% ¹³C^α labeled in alternate sampling (Ala, Cys, Gly, His, Lys, Phe, Ser, Trp, Tyr, and Val) ⁶. Inversion pulses are applied to carbonyl carbon nuclei to refocus the evolution under ¹J(C^αC′). Multiplet patterns that would occur during detection due to ¹J(C^αC^β) and ¹J(C^αC′) are converted to single signals by using the double IPAP technique²⁰.

Because the line widths of all signals are very small, the experiment is best exploited when using non-uniform sampling²¹. In our application, 500 out of 16384 indirect data points were sampled from a Nyquist grid of 128 (C^α) × 128 (N) complex points. Thus, only 3% of the indirect time domain points were recorded. The data were reconstructed with the forward maximum entropy (FM) algorithm developed in our laboratory^{9, 22}. The final resolution in the indirect dimensions after Fourier transforms is 27 Hz for C^α and 11 Hz for N.

Results and discussion

The method was tested on a 4 mM solution of the B1 domain of protein G (GB1) uniformly enriched in ¹³C. To simulate the tumbling of a 90 kDa protein, 20% glycerol was added and the experiment was recorded at 285K (for a calibration of the correlation time, see Takeuchi et al⁶). Figure 3 shows an example of a “stairway” assignment for a small stretch of sequential residues. Each C^α-C^α plane shows the correlations between sequentially neighboring carbons at a given nitrogen frequency.

Figure 3.

Stairway sequential assignment of GB1 with the CANCA experiment recorded at conditions simulating a 90 kDa protein (20% glycerol, 285K). Red crosses indicate the correlations expected from square pattern in C^α-C^α plane. Blue arrows indicate the assignment walk in the “stairway” procedure from the C^α of residue 19 to the N of residue 23 (from top to bottom). Starting from C^α_i in a C^α-C^α plane at ω (N_i), one can find the nitrogen frequency of the preceding residue ω (N_i+1) at the C^α_i cross section in a C^α-N plane (strips on the side). The C^α-C^α plane at ω (N_i+1) gives the assignment of C^α_i+1. Slices at the position of horizontal broken lines are shown in C^α-C^α planes.

As can be seen on the 1-dimensional traces of each panel, the S/N ratio is high and the lines are narrow due to the slow transverse relaxation of C^α. A strip along the indirect nitrogen dimension (shown at the right) at a given C^α chemical shift (diagonal peaks) allows finding the C^α-C^α plane containing the signals of the succeeding (or preceding) residues. Since the delays in the pulse program were set to optimize magnetization transfers for sequential C^α_i-C^α_i+1 (or C^α_i-C^α_i-1) correlations (50 ms in our case; see description of pulse program and Figure 2), “diagonal” C^α_i-C^α_i correlations tend to be missing or weak. However, the positions of these correlations can easily be obtained from the square cross-peak patterns in the C^α-C^α planes.

For the 4 mM uniformly ²H¹⁵N¹³C-labeled GB1 sample at conditions simulating a “90 kDa” protein all sequential connectivities (C^α and N) are observed in the CANCA experiment recorded within 2 days (Figure 4A). A uniformly ¹³C-labeled sample would primary be used to perform assignments, since C^α labeling efficiency in alternate ¹³C labeling is low for certain residues resulting in the loss (or reduction in intensity) of sequential C^α–C^α correlations for some residue types⁵. This is clearly exemplified by correlations involving Leu, in which C^α positions are not labeled when using 2-¹³C glycerol (Figure 4B). However, the alternate ¹³C-labeling can be used as complement in large molecular weight system, especially for residues with faster relaxation, since the labeling allows using the scheme of Figure 1A, which has a shorter C^α-transverse period, and is not involving C^α-selective pulses or double IPAP coherence selection scheme. In addition, no resonances suffer from imperfect inversion by the C^α-selective pulses (Gly, Ser, and some high-field C^α resonances) in contrast to what may happen with the scheme of Figure 1B. For the “90 kDa” GB1 sample, the median of S/N values for the 2-¹³C glycerol labeling experiment is ∼30% higher than that for the pulse sequence designed for and applied to the uniformly labeled sample (700 for 2-¹³C glycerol labeling experiment and 540 in uniformly labeling). Thus, the sensitivity of the 2-¹³C glycerol labeling experiment is superior to uniform labeling for most of the resonances. In addition, Ile, Leu and Val can readily be identified since these residues have a ¹³C in the C^β position when using alternate ¹³C-labeling (Ile and Val with 2-¹³C glycerol labeling, and Leu with 1,3-¹³C glycerol labeling). Thus, cross peaks have opposite sign due to the C^α–C^β coupling. For the “90 kDa” GB1 sample prepared with 2-¹³C glycerol labeling, all sequential connectivities are observed except for those involving Leu as discussed above (Figure 4B). The remaining correlations should readily be observed with this experiment when using 1, 3-¹³C glycerol for labeling.

Figure 4.

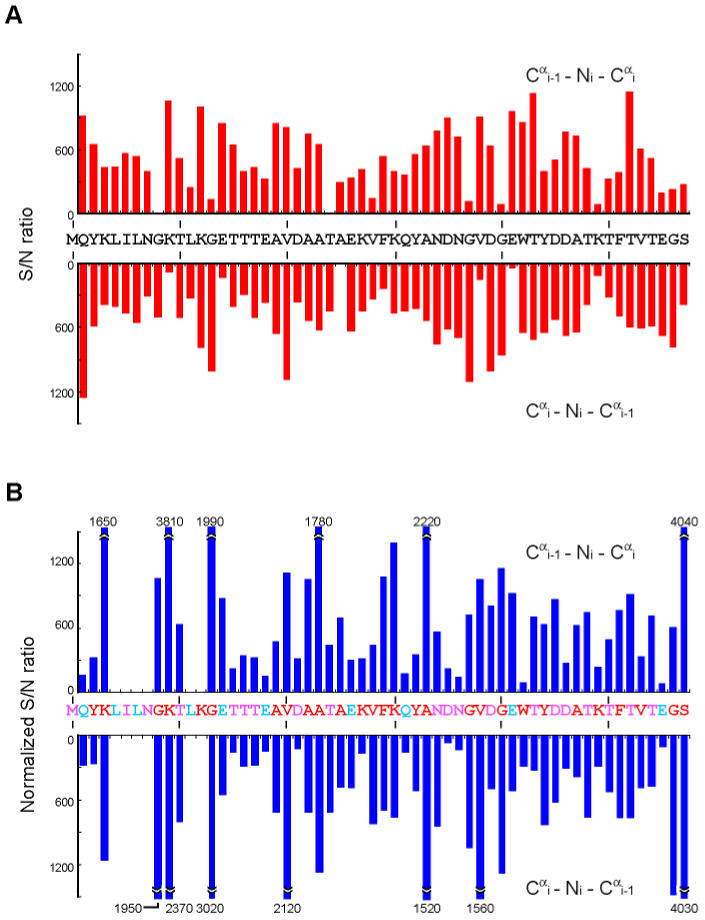
S/N ratio in CANCA experiments with (A) 4 mM uniformly ²H¹⁵N¹³C-labeled GB1 samples and (B) 5 mM 2-¹³C glycerol labeling at conditions simulating “90 kDa” proteins. Experiments were recorded for 2 days for uniformly ²H¹⁵N¹³C-labeled or 4 days for 2-¹³C glycerol labeling samples with the delays T_N optimized for sequential connectivities. The S/N ratio for (B) was normalized against (A) to account for differences in concentrations and measuring times. Upper and lower bars at positions i indicate C^α_i-1-N_i-C^α_i and C^α_i-N_i-C^α_i-1 correlations, respectively. For (B), residues that show S/N ratio of more than 1500 were clipped and the actual values are indicated. Residues colored in red are more than 80 % ¹³Cα labeled with [2-¹³C] glycerol, while cyan residues have less than 20% incorporation. Pink residues are 40-70% ¹³Cα labeled. The noise level was estimated from the median of the absolute intensity values of 10000 randomly selected points in the spectrum.

We also recorded the Cα-Cα plane of a 3D CANCA experiment for the 52 kDa dimeric GST protein. For a 1mM sample of the [ul-²H,¹⁵N,¹³C] GST dimer (2mM monomer concentration) dissolved in D₂O buffer. Without optimizing solution conditions we could observe ∼35% of the expected resonances in 5 days experiment. The observed resonances are reasonably narrow and well dispersed, indicating the applicability of the CANCA experiment to higher molecular weight protein systems (Supplement Figure 1). It is also clear that further improvements need to be introduced at the hardware level as well as in data acquisition and processing to enable a routine use of this experiment for very large proteins.

To compare the sensitivity of the CANCA experiment with other carbon detection experiments, we measured 1D traces of the CANCA and CANCO experiments. The latter was proposed previously for establishing sequential connectivities. The experiments were recorded at various temperatures in a viscous buffer using uniformly labeled GB1, and intensities of well-separated resonances from structured regions were compared (Supplement Figure 2). At conditions simulating the low molecular limit (∼6 kDa), CANCO is more sensitive than CANCA (CANCO:CANCA ∼ 1:0.6) as expected. However, the CANCA experiment shows comparable sensitivity at conditions simulating larger systems (>73 kDa) even with a 500 MHz magnet. However, it yields more useful sequential correlations than the CANCO. The CANCA experiment gives better ¹³C dispersion as well as additional sequential information in the nitrogen dimension compared to the CANCO experiment. Thus, CANCA has clear advantages for the higher molecular weight range. The advantages of CANCA would be more pronounced at higher magnetic fields. However, we would like to emphasize that the CANCA experiment is also useful for small proteins since it provides additional sequential information, and allows resolving ambiguities during the assignment process. For a system with less severe relaxation losses, the proton detected hNCAnH experiment provides sequential information in both indirect dimensions (N and CA), and is the method of choice given the increased polarization of proton nuclei.⁷ However, it is worth noting that the CANCA experiment is able to assign proline residues, which are missing in proton-detected experiments.

Since the longitudinal relaxation time (T₁) of deuterated carbon is especially long in large molecular weight systems, the repetition delay has to be carefully set to have optimal sensitivity. The sensitivity of the experiment can be further enhanced by shortening T₁ using paramagnetic reagents, such as Gd(DTPA-BMA) or Ni(DO2A) without significantly accelerating transverse relaxation rates^{23, 24}. Indeed, addition of 3 mM Gd(DTPA-BMA) to the “90 kDa” sample decreased T₁ values from 3.6 sec to 0.9 sec. This allowed faster recycling rates and acquisition of more scans per increment. It increased the sensitivity of the experiment by ∼50% (data not shown). It seemed possible that the paramagnetic relaxation enhancement would be less effective for the inaccessible core of very large proteins. We tested this with studies of the 52 kDa dimeric protein GST. We found, however, that the ¹³C^α T₁ values of GST were also significantly shortened from approximately 3.6 sec to 1.3 sec, by addition of 4mM Gd (DTPA-BMA) (data not shown). This included residues from the core of the dimeric protein.

Conclusion

In summary, the 3D CANCA C^α-direct-detection experiment provides a robust way for establishing complete main-chain resonance assignment with simultaneous detection of C^α and N sequential connectivities. Using slowly relaxing C^α nuclei is especially beneficial for assigning high molecular weight proteins. Both conventional uniform ¹³C labeling or the alternate ¹³C labeling strategy^{5, 6} are suitable for the CANCA experiment, with complementary advantages as described above. The experiments described here were recorded on a 500 MHz spectrometer. The performance will be enhanced at higher magnetic fields. This is in contrast to C′ detecting experiments, which deteriorate at higher fields due the large C′ chemical shift anisotropy. Obtaining sequential information in both C^α and N dimensions is especially beneficial for resolving degeneracies, which makes this experiment attractive even for smaller molecular weight systems. An extensive sparse sampling coupled with FM reconstitution further enhances these features by achieving high resolution in indirect dimensions.