Schooling Impacts of Conditional Cash Transfers on Young Children: Evidence from Mexico

Abstract

This paper evaluates impacts of Oportunidades, a Mexican conditional cash transfer program, on educational outcomes 5.5 years after program initiation for a group of children who were age 0 to 8 years pre-program. The oldest children within this age range received educational scholarships. The youngest children did not receive the scholarships because they had not yet started the third grade of school (the initial grade for scholarships), but were beneficiaries of the program’s health components that included nutritional supplements for children 24 months of age or younger. All of these children also may have benefitted more generally from increased household income resulting from the program. This paper investigates how the program differentially affected younger and older children within this age range and examines whether the early nutritional intervention led to improvements in subsequent educational performance. The program impact estimates are derived from a randomly assigned treatment and control group, which participated for different lengths of time in the program, and from a matched comparison group that had not participated prior to the collection of data in 2003. The empirical findings show positive program impacts on reducing ages at entering school for the younger children as well as on accumulated grades of schooling after 5.5 years of benefits for older children, with estimates implying a 1 percent reduction in the age of entry to primary and an increase in grades of schooling completed to date of about 8 to 9 percent.

1. Introduction

Oportunidades (formerly PROGRESA) has been operating since 1997 in small communities in rural areas of Mexico. Its central objective of linking monetary transfers to investments in the human capital of poor children and family members has been adopted in a number of other countries in Latin America and the Caribbean, as well as in other parts of the world. A rigorous external evaluation, with several rounds of panel data in an experimental design, as well as other approaches to analysis such as regression discontinuity design and structural modeling, was implemented at the beginning of the program (covering 1998-2000). The evaluation results demonstrate significant impacts in improving infant and child nutrition, reducing child labor, improving health outcomes, and increasing school enrollment, among other short-term effects.² Some of the initial evaluation studies also have generated estimates of longer-run effects, but they have done so conditional on assumptions such as stability in schooling transition matrices or in the structural relations underlying family behaviors (e.g., Behrman, Sengupta and Todd 2005, Parker and Skoufias 2000, Schultz 2004, Todd and Wolpin 2006). Such extrapolation of short-term effects to longer-term impacts may be misleading, for example, if there is learning-by-doing by program beneficiaries or by program providers or initial “pioneering” effects that dissipate over time (Behrman and King 2008, King and Behrman 2008).

This paper examines the educational impacts of Oportunidades on young children in the medium term in 2003, about five and a half years after households in the original treatment group began receiving benefits. We consider the group of children aged 0 to 8 in 1997, just prior to the program intervention, or those aged 6 to 14 in 2003. In particular, we study the program’s impacts on the age of starting school, on grade progression, and on the number of completed school grades.

The education of children aged 0 to 8 in 1997 just prior to the intervention, or those aged 6 to 14 in the 2003 survey, might have generally benefited some from the income resource effect of transfers to families, particularly if capital markets for human capital investments are imperfect. In addition, the distinctive components of the program affected children in this age range differentially depending on the children’s ages in 1997. The oldest children in this age range had the potential to benefit by 2003 from a number of years of the Oportunidades scholarships that started with enrollment in the third grade. For these children it would seem likely that the scholarship program would be the most important component of the Oportunidades intervention. These children also were old enough for the most part to face by 2003 a critical juncture in schooling attainment in poor communities in rural Mexico, whether primary school graduates continue into secondary school, which occurred for most individuals when they were in their early teenage years.³

The youngest children in the 0-8 year-old age range in 1997, in contrast, did not directly receive any educational scholarships by 2003, although these children’s education may have been affected by their parent’s anticipation of receiving future scholarships. Most significantly, however, the youngest group benefited from the nutritional supplements for infants,⁴ which may have improved their educational gains from attending school once they became of school age. One of the original rationales for Oportunidades was to exploit interactions among various investments in human resources in hopes that the “whole might be more than the sum of the parts.”⁵ Although there is a presumption that effects of early nutrition on child education are likely to be important and a number of studies that report associations in data that are consistent with such effects (e.g., see Behrman 1996, Pollitt 1990, Victora et al. 2008), there is a relatively small literature for developing countries that has persuasively examined the causal effects.⁶ We aim in this paper to provide suggestive evidence of a link, although the package nature of benefits complicates the isolation of the impact of each component of the program.

The information that we use to evaluate the Oportunidades medium-term impact on education of children aged 0-8 in 1997 is that provided in the ENCEL (the Oportunidades Evaluation Survey) from 2003, linked with earlier data, particularly the 1997 pre-program Survey of Household Socio-economic Characteristics (ENCASEH97) data. The strategy of analysis includes direct assessment of the impacts using two different approaches:

• Difference and difference-in-difference treatment effect estimates using the original treatment starting in 1998 group (T1998) and the original control group with treatment starting in 2000 (T1999) for children in different age ranges in 1997 to investigate the impact of the differential program exposure of about 1.5 years for these two groups.

• Difference and difference-in-difference matching estimates between those who obtained treatment in 1998 (T1998) and the 2003 matched comparison group that was incorporated into the program in 2004 (C2003) to investigate the impact of exposure to the program for five and a half years versus no exposure.

We use these methods to provide new estimates on the medium-term increase in education for children age 0-8 in 1997 due to the program. These estimates enable us to begin to explore some of the fundamental assumptions of the design of the program about the impact of scholarships on education of children and about interactions over time between components of the program package, particularly nutrition for infants and pre-school children and subsequent educational outcomes when those children are of school age.

We organize our study as follows. Section 2 provides some program background. Section 3 introduces the basic data, considers the program impact on sample attrition and some aspects of the sample used for the matching estimates. Section 4 considers the estimated program impacts using the approaches indicated above. Section 5 concludes.

2. Program Background

Oportunidades began operating in small rural communities in 1997 and has gradually expanded to urban areas. It now covers 5 million families, about one quarter of all families in Mexico. The program has a number of dimensions that might have affected the educational achievement of children aged 6-14 in 2003, who were aged 0-8 at the time the program was initiated in 1997:⁷, ⁸

(1) Cash transfers to the mothers in the treatment households

Conditional on the whole family (including pre-schoolers) regularly visiting health clinics and school-aged children attending school, Oportunidades beneficiaries receive bi-monthly cash transfers, equivalent on average to about 20% of household consumption (Behrman and Hoddinott 2005). These cash transfers may have several income effects. First, they may have induced increased education for all the children in the treatment group through intrahousehold allocations, even though very few of the children who were 0-8 years of age in 1997 were directly eligible for the schooling related transfers (see point 5 below). Second, the increased income is likely to result in greater use of health services, which may increase children’s health and thereby also impact education (see Strauss and Thomas 1995, 1998). Third, the income transfers may be used for increased nutrient consumption that also may impact children’s education. There has been considerable controversy over the extent to which increased income translates into increased nutrient consumption (see Behrman and Deolalikar 1987, 1988, Behrman, Foster and Rosenzweig 1997, Bouis and Haddad 1992, Subramanian and Deaton 1996), but estimates for the Oportunidades rural sample indicate that a 10% increase in income translates into a 3 to 4.5% increase in caloric availability, with much of this increase going to foods richer in micro nutrients (Hoddinott and Skoufias 2004). Finally, the income transfers, which go to the mother of the household, may have household bargaining effects. Although there is not much direct evidence on the intrahousehold distribution of nutrients in the Oportunidades population, studies on other poor populations have concluded that larger shares of resources that go to mothers are directed toward child health and nutrition than of resources directed to fathers and, in part for this reason, Oportunidades directs resources to mothers (Alderman et al. 1995; Behrman 1997; Haddad and Hoddinott 1994; Haddad, Hoddinott and Alderman 1996; Strauss and Thomas 1995; Rubalcava, Teruel and Thomas 2002; Thomas 1990, 1994).⁹ For all these reasons related to household income, we expect children in the treatment group to have better health and nutrition, which may translate into better schooling performance even for children who do not receive the schooling scholarship.

(2) Participation in the pláticas

Oportunidades participants are required to attend regular meetings (pláticas) at which, inter alia, health and nutritional issues and practices are discussed. These sessions are conducted by physicians and nurses trained in these specific topics (see Rivera et al 2000). If these meetings improve knowledge and practices related to child nutrition and health, they may improve child nutrition and health, again with indirect effects on improving educational performance. While the beneficiaries might be children (and adults) of any age, given that infants and very young children are most at risk of health and nutritional insults, these children would seem to be the most likely beneficiaries.

(3) Nutritional supplement or “papilla”

The nutritional component of Oportunidades includes the provision of nutritional supplements to pregnant and lactating women and to children between the ages of four months and two years and to children between two and four years (up to 59 months) if signs of malnutrition are detected by the clinic personnel.¹⁰ Mothers visit the clinic at least once a month to pick up six packets of supplements per eligible child per month with each pack containing five doses, enough for one dose per day. The supplements constitute 20% of calorie requirements and 100% of all necessary micronutrients and have presentational and flavor characteristics that result in high levels of acceptability and intake (see Rosado 1999, Rosado et al. 2000). Children in the treatment sample who were less than 24 months of age at the start of treatment (and 6-8 in 2003) should have been the primary beneficiaries of these supplements, with hypothesized benefits on their cognitive development and school performance.¹¹ As noted, children between the age of 2 and 4 were also given the supplements if they showed evidence of malnutrition. In addition, children in the treatment sample who were not direct beneficiaries, but who had younger siblings who were direct beneficiaries, may have benefited indirectly from the increased household income in kind, akin to the cash transfer discussed in (1) above.

(4) Growth monitoring

A prerequisite for receiving nutritional supplements is ongoing growth monitoring of preschool children. Conventional wisdom holds that there may be a high payoff to growth monitoring through increasing the probability that parents or other caregivers become aware of nutritional problems before longer-run damage occurs, although we are unable to locate rigorous evaluations of growth monitoring programs in Latin America. The direct beneficiaries, once again, are likely to have been primarily the children under two years of age (because they are most vulnerable to nutritional insults) when the program started — and therefore under eight years of age in 2003.

(5) Direct educational components of the program

A final major component of the program that is obviously germane to our interests in this paper is the conditionality (beyond the income effect noted in point 1) of the cash transfers to mothers for children attending school (or scholarships). Regular school attendance (at least 85% of the time) is required to continue receiving the bi-monthly grant payments. With respect to successfully completing the school year, program rules allow students to fail each grade once, but students are not allowed to repeat a grade twice (at that point educational benefits are discontinued permanently for the child). This allows a student theoretically to receive two years of grants for the same grade for each grade. Table 1 shows the monthly grant levels available for children between the third grade and the twelfth grade in the second semester of 2003 (in addition there are grants for school supplies). Until 2001, the program provided grants only for children between the third and ninth grade. The secondary and high-school grants provide higher amounts (by about 13%) for girls than boys. The extent to which children in our treatment sample benefited between 1997 and 2003 from the direct inducements for schooling provided by these conditional transfers depends on how much schooling they had had prior to the program initiation. In the group that received treatment in 1998, many of the children who were 7 or 8 years old in 1997 were ready to enter the third grade at the time of program initiation and thus had potentially five and a half years of direct benefits by 2003. For younger children in 1997, there generally was a lag before they were ready to enter third grade and thus they had potentially fewer than five and a half years of direct scholarship benefits by 2003. In addition to the direct benefits, of course, even for younger children the initiation of the program may have created increased incentives for schooling if there is forward-looking behavior regarding future benefits. Also, as noted in point (1) above, there may be income and intrahousehold allocation effects for children who live in households with older siblings who were beneficiaries.

Table 1.

Monthly amount of Oportunidades educational grant (pesos) in second semester of 2003

Grade	Boys	Girls
Primary
3rd year	105	105
4th year	120	120
5th year	155	155
6th year	210	210
Secondary
1st year	305	320
2nd year	320	355
3rd year	335	390
Upper Secondary (High School)
1st year	510	585
2nd year	545	625
3rd year	580	660

NB. The exchange rate was about 10 pesos per United States’ dollar.

Table 2 summarizes program benefits that each age group and treatment group would be expected to receive and is useful for illustrating the degree to which we can isolate the effects of the nutritional component of the program.¹² Children aged 0 to 2 years pre-program in T1998 receive nutritional supplements whereas T1999 children do not. However, the families of children aged 0 to 2 years in T1998 also receive the fixed monetary transfer for a longer period of time than T1999 families. Comparing these two groups then will provide impact estimates of the entire health/nutritional component including the fixed monetary transfer; however it will not provide the impact of the nutritional supplements separately. We can to some extent isolate the impact of the nutritional supplements by comparing the impact of the 0 to 2 year olds to the program impact of the 3 to 5 year olds. The main difference between T1998 3-5 year olds and T1999 3-5 year olds is the time of receipt of the fixed nutrition grant¹³. Thus, comparing impacts between these two age groups can largely isolate the particular impact of the nutritional supplements over time. We use this approach to study the effect of the nutritional supplements on age of entrance into primary school and on grades of schooling attainment. Given that children age 0 to 2 years pre-program are only beginning their school participation, this strategy will be more fruitful with later rounds of data than were available for this study.

Table 2.

Benefits received in Progresa/Oportunidades program between 1998 and 2003: By treatment group

Treatment group	Age in 1997	Nutritional supplements	Fixed cash transfer*	Educ. grants** for child	Educ. grants ** for older children
T1998	0 to 2	Yes	5.5 years	No	5.5 years
T1999	0 to 2	No	4 years	No	4 years
C2003	0 to 2	No	0 years	No	0 years
T1998	3 to 5	No	5.5 years	1 to 2 years	5.5 years
T1999	3 to 5	No	4 years	1 to2 years	4 years
C2003	3 to 5	No	0 years	No	0 years
T1998	6 to 8	No	5.5 years	3 to 4 years	5.5 years
T1999	6 to 8	No	4 years	3 to 4 years	4 years
C2003	6 to 8	No	0 years	No	0 years

^*linked to regular clinic attendance including growth monitoring and monthly health talks

^**linked to regular school attendance

3. Evaluation Design and Data

The 2003 Rural Evaluation Survey continues the original treatment and control experimental design begun in 1997. The original sample design involved selecting 506 communities with 320 randomly assigned to receive benefits immediately and the other 186 to receive benefits later.¹⁴ Only those households that were identified to be poor through discriminant analysis (with some modifications due to community feedback) were deemed eligible for the program (see Behrman and Skoufias 2005, Skoufias 2005). The eligible households in the original treatment localities (T1998) began receiving benefits in the spring of 1998, whereas the eligible households in the original control group (T1999) began receiving benefits about 18 months later at the end of 1999. Between 1997 and 2000, evaluation surveys with detailed information on many evaluation indicators, including education, health, income and expenditures were applied to households in both groups every six months.

In the year 2003, a new follow-up round of the rural evaluation survey (ENCEL2003) was carried out. The sample includes eligible and ineligible households in the original treatment (T1998) and original control (or delayed treatment, T1999) groups and a new sample of households from comparison communities that were selected through matching on observed community characteristics from a larger set of communities that had not had the program by 2003 (C2003).¹⁵ The C2003 sample respondents answered questions concerning their characteristics and behaviors in 2003 as well as retrospective questions about their characteristics and behaviors in 1997, used in part to determine whether they would have been eligible for the program at that time. We link the T1998 and T1999 data from 2003 to the pre-program 1997 ENCASEH data, to have longitudinal data on individual children who were 0 to 8 years of age in 1997 and 6 to 14 years of age in 2003. As in the previous ENCEL surveys, the ENCEL2003 contains data on a myriad of program outcomes, including several indicators of educational performance.

The comparison of T1998 and T1999 (what we term differential exposure estimates) continues to be based on the original randomized experimental design of the program. Given that T1999 households also began to receive benefits late in the year 1999, comparing the two groups provides information on the effect of differential lengths of participation in the program, in this case 5.5 years versus almost 4 years. The differential exposure estimates are likely to be most informative for those impact indicators that would be expected to accumulate with additional time in the program, such as child height and grades of completed schooling

Estimates based on an experimental design are generally more convincing than those based on non-experimental designs because they are less susceptible to selectivity bias. However, social experiments are usually short-lived, lasting only a year or two, and therefore do not usually speak to the long-term effects of exposure to a program. For this reason, studies of long-term effects often rely on non-experimental estimates. In this paper, we exploit the experimental data to study the effects of 5.5 years of exposure verses 4 years, and also use nonexperimental data and a matching methodology to study the effects of 5.5 years of exposure verses no exposure.

The difference-in-difference estimates we report rely on the assumption that in the absence of the program, trends in the outcome indicators would be similar in the treatment and control communities. To get an idea of potential differential trends in the communities over time, we examine pre-program Census information on community characteristics between 1995 and 2000. Table 3 provides changes over time between 1995 and 2000 for the three groups of communities as well as t-tests comparing the two treatment groups with the C2003 group. Given that the T1998 communities began receiving benefits in 1998 (before the 2000 Census), the most appropriate comparison is T1999 versus C2003 communities. For the available educational variables, Table 3 shows that those measuring schooling attainment show no significant differences between changes over time in the T1999 and C2003 groups. There are, however, significant differences in population changes with the C2003 communities showing a larger population growth over time than the treatment communities and a significantly smaller change in the proportion of households with electricity overtime in C2003. Overall, however, given our focus on educational impacts, the lack of differences in educational trends is encouraging.

Table 3.

Trends in population and housing characteristics pre-program: by treatment group.

	C2003		T1998		T1999		Difference-in-differences
	Change	SD	Change	SD	Change	SD	(T1998- C2003)	t-stat	(T1999- C2003)	t-stat
Population between 6 and 14	3.6	17.9	−0.6	17.7	−1.2	17.8	−4.24	−2.20	−4.84	−2.29
Population over 15	10.4	37.1	1.2	31.0	0.7	29.6	−9.26	−2.40	−9.72	−2.39
% Population between 5 and 14 able to read	5%	0.19	4%	0.13	2%	0.13	−0.01	−0.65	−0.03	−1.37
% Population over 15 able to read	2%	0.12	3%	0.07	3%	0.07	0.02	1.29	0.01	0.76
% Population speaks indigenous language	0%	0.07	0%	0.06	−1%	0.09	−0.00	−0.30	−0.01	−1.07
% Population speaks indigenous language and not spanish	−13%	0.24	−17%	0.29	−16%	0.29	−0.04	−1.28	−0.03	−0.87
Inhabitant per house	−0.2	0.81	−0.5	0.56	−0.4	0.62	−0.29	−3.60	−0.22	−2.57
% Houses with electricity	7%	0.21	12%	0.33	12%	0.29	0.05	2.00	0.05	1.84
Observations	116		320		186

^*Sources: 2000 Census and 1995 Conteo Surveys.

Most previous evaluation studies of the Oportunidades program are based on the experimental design, but one previous study by Dias and Handa (2006) provides some evidence that matching estimators can replicate the experimental estimates. Diaz and Handa (2006) attempt to replicate the short-run estimates from Oportunidades’s initial experimental design on expenditure shares, school enrollment and child work using matching estimators. They use the Survey of Income and Expenditures in Mexico (ENIGH), a nationally representative cross-sectional survey, to construct a comparison group that was matched to beneficiary households in the ENCEL treatment group. For the indicators where similar survey questions are available (school enrollment and child work), Diaz and Handa are able to closely replicate the experimental design estimates using cross-sectional matching estimators, with insignificant differences between the experimental design estimates and those based on their matching analysis. For those based on expenditures, where the survey instruments vary substantially, the estimates are significantly different. This is suggestive evidence that matching methods can replicate estimates based on randomized designs in the context of schooling and Oportunidades. It is particularly notable that Diaz and Handa were able to replicate results using only cross-sectional matching, presumably subject to greater bias than the difference-in-difference matching estimators that we primarily use here.

Section 4: Methodology

As described in the introduction, we evaluate the impacts of participation in the Oportunidades program using two different approaches: (i) difference and difference-in-difference comparisons between the original randomized treatment (T1998) and control (T1999) groups, which have by now both been incorporated into the program but which have 1.5 years difference in exposure duration, and (ii) difference and difference-in-difference comparisons between the original treatment group (T1998) and a new matched comparison group (C2003) that had not been exposed to the program. In both contexts, we use only the sample of program-eligible individuals.¹⁶, ¹⁷

Usually, difference-in-difference estimators are implemented using before and after information on the same individuals. In the current context, however, many of the children in our sample were not in school pre-program, and it is more meaningful to implement the difference-in-difference estimators using different children pre and post program initiation but holding the age constant over time. We use this approach for both the differential exposure estimates and for the matching estimates. For the oldest group of children (e.g. those age 6 to 8 pre-program), for whom longitudinal difference-in-difference estimators are feasible, we compare estimates using the age-constant strategy to those obtained using longitudinal estimators.

4.1. Differential exposure estimates: comparison of original randomized treatment (T1998) and control (T1999) groups, accounting for attrition

Comparison of T1998 and T1999 using difference and difference-in-difference estimates

We present first difference and difference-in-difference treatment effect estimates based on the original randomized treatment and control groups for children of different ages. These estimates exploit the fact that the treatment group (T1998) received the program1.5 years earlier than the control group (T1999) to evaluate the effects of differential exposure between the two groups on education outcomes, measured in 2003. As noted in Sections 1 and 2, our prior is that the magnitude of the impacts may depend critically on child ages in 1997, prior to the initiation of the program for the T1998 group. In particular, we hypothesize that there may be substantial effects of treatment for those children who in 1997 were (a) exposed to the nutritional supplements and growth monitoring for infants (aged 0-2 years in 1997 and therefore 6-8 years in 2003) or (b) were aged 6-8 years in 1997 and therefore 12-14 years in 2003 and had attained the critical age for making the schooling decision regarding enrolling in lower secondary school. We also hypothesize that there may be other important differences in effects by age because, for example, those T1998 children who entered the third (or higher) grade in 1998 or 1999 received two years of direct scholarship treatment that the same schooling (and, approximately, birth) cohort in T1999 did not receive. On the other hand, those T1998 children who entered the third grade in or after 2000 (children approximately aged 3 to 5 years in 1997) received the same direct scholarships for school attendance as the T1999 children in the same schooling cohort (though the former may have received other benefits, such as those due to the cash transfers discussed in Section 2, for two years longer). That is, we hypothesize that children aged 3 to 5 are likely to show lower effects of the program, given there are no major differences in terms of nutritional interventions or educational grants for this age group. For each of the outcome measures and for both pre-program and post-program-initiation data, we estimate a linear regression of the outcome variable on an indicator of whether the individual resided in an original treatment or control locality. The additional covariates include parental age, education, indigenous status, and household characteristics (number of rooms, electricity, type of floor and water/sewage system).¹⁸ The difference-in-difference estimates are constructed by taking the difference of program impacts “before” and after program initiation.

As discussed above, we do not have pre-program educational information for those aged 0 to 5 years pre-program (6 to 11 years after), because children below age five years were not in school. While the experimental design should ensure no significant pre-program differences between the T1998 and T1999 groups, we nevertheless allow for the possibility of pre-program differences between T1998 and T1999 using the group of children aged 6 to 14 years in 1997. This allows us to carry out difference-indifference estimators, on the assumption that differences in the educational outcomes of children 6 to 14 years in 1997 are representative of pre-program differences of children 6 to 14 years in 2003. We will use a similar age-constant differencing strategy below in the matching analysis.

One concern in evaluating longer-term impacts of the 1.5 years difference in program exposure is that of sample attrition of the original evaluation ENCEL sample. Sample attrition can be particularly problematic if it is correlated with program participation. For the purpose of this study, we are concerned with sample attrition of individuals who were in the baseline sample in 1997 but not in the 2003 follow-up sample.¹⁹ Table 4 (panel A) summarizes some statistics regarding sample attrition in this period for the original treatment (T1998) and original control (T1999) groups, focusing first on all youth in the community and then on those eligible for the program. 23% of the individuals aged 0 to 8 years in 1997 were not in the sample six years later, which certainly is a large enough proportion to raise concerns about attrition. As seen in Table 4, most attrition is due to household rather than individual attrition. There are, however, not large or statistically significant differences at the 10% level in overall attrition between the T1998 and T1999 samples, The proportion lost to follow-up is about the same for girls (21% in T1998, 19% in T1999) as for boys (20% in both T1998 and T1999); only for girls is there a statistically significant difference between T1998 and T1999 for overall attrition at the 10% level. So on an overall aggregate level it appears that sample attrition is not significantly associated with treatment at least for boys, though attrition is higher at the 10% significance level for the T1998 than the T1999 group for girls.

Table 4.

Proportion attriting by 2003 of original ENCASEH sample: individuals aged 0 to 8 years in 1997

	Treatment (T1998)		Control (T1999)		P>|Z|
	N	Mean	N	Mean
A. Total proportion attriting (individual or household)
0 to 8 years (all)	19,493	0.232	12,055	0.229	0.564
0 to 8 years (eligible)	14,610	0.205	8,783	0.199	0.236
By gender
Boys 0 to 8 years (eligible)	7,434	0.203	4,393	0.203	0.993
Girls 0 to 8 years (eligible)	7,168	0.208	4,378	0.194	0.068
B. Proportion due to individual attrition
0 to 8 years (all)		0.052		0.050	0.504
0 to 8 years (eligible)		0.041		0.045	0.238
By gender
Boys 0 to 8 years (eligible)		0.038		0.045	0.096
Girls 0 to 8 years (eligible)		0.045		0.044	0.961
C. Proportion due to household attrition (individual not found because household -HH- moves)
0 to 8 years (all)		0.181		0.180	0.802
0 to 8 years (eligible)		0.164		0.154	0.051
By gender
Boys 0 to 8 years (eligible)		0.165		0.158	0.375
Girls 0 to 8 years (eligible)		0.163		0.149	0.047

Notes: The last column gives the significance level for mean differences between T1998 and T1999 based on t-tests.Source: Authors’ calculations with 1997 ENCASEH and 2003 ENCEL data.

Overall attrition of individuals aged 0 to 8 years in 1997 includes: (i) individuals who have separated from households that are still in the sample in 2003 and (ii) individuals who are in households that are no longer in the sample in 2003. Of the 23 percent of the sample attritting, a majority, 18% are individuals in households that left the sample. There are some significant although overall small differences if individual and household attrition are considered separately: at the 10% level, higher individual attrition among the T1999 group for boys and higher household attrition among the T1998 group for girls. So, while the overall treatment-control differences are not significant for boys, greater disaggregation indicates some differences.

Appendix Table B estimates the probability of being lost to follow-up for individuals 0 to 8 years old in 1997 in eligible households from the T1998 and T1999 groups — again, for total attritors, individual attritors and household attritors - and shows that a number of the pre-program individual, parental and housing characteristics interact significantly with treatment (i.e., being in the T1998 group) to affect attrition. To account for possible attrition biases, we employ a weighting method that is equivalent to a matching on observables approach. That is, we carry out difference-in-difference regression estimates where both the treatment and control group observations are weighted to adjust for differences in the distribution of the X characteristics arising over time because of attrition. Using the dimension reduction theorem of Rosenbaum and Rubin (1983), we implement the reweighting estimator using as the weights the ratio of the univariate densities of the propensity score. Through this procedure, each individual observed post-program-initiation receives a weight equal to the ratio of the density of his/her probability of attriting with respect to the post-program-initiation distribution divided by the density estimated with respect to the pre-program (and pre-attrition) distribution. Effectively, this procedure reweights the post-program-initiation observations to have the same distribution of X as they did prior to the attrition. The key assumption that justifies application of this procedure is that attrition is random conditional on X, within each of the groups.²⁰ Details and derivations are provided in Behrman, Parker and Todd (2008).

4.2 Matching estimates

To estimate impacts of longer-run exposure to the program against the benchmark of no program, we compare the original treatment group (T1998) with the comparison group (C2003) that was drawn from rural areas that had not yet been incorporated into the program as of 2003. Because the C2003 group was not selected at random, we use matching methods to take into account differences in observed characteristics between the T1998 and C2003 samples. For each individual in the treatment group (T1998), these methods select an individual from the outside comparison group (C2003) that is comparable in terms of observed characteristics.²¹

The households living in localities where the program was not yet available at the time of the collection of the C2003 data were unlikely to have been affected in any way by the existence of the program. However, because they live in different geographic areas from the treatment group sample, they may experience different local area effects (labor market conditions, quality of schooling, quality of health clinics, prices) that may also be relevant determinants of outcomes of interest (schooling, work, achievement scores). The difference-in-difference matching methods that we implement control for fixed locality characteristics. These methods compare the change in outcomes in the treatment group (post-program-initiation minus baseline) to the change in outcomes in the control group. The C2003 sample was not incorporated into the main sample until 2003. The respondents were asked retrospective questions with regard to demographics, poverty, schooling and work in the baseline year 1997, which provides the pre-program information needed for the difference-in-difference matching estimators.

Matching estimators were first developed and are widely used in the statistics literature (e.g. Rosenbaum and Rubin, 1983). They have more recently been applied and extended in the economics literature (e.g., Heckman, Ichimura and Todd, 1997). To describe the estimators that we use, we need to introduce some notation. Let Y₁ denote the outcome for persons who receive the treatment and Y₀ the outcome without treatment. Let Δ = Y₁ − Y₀. The evaluation problem arises because Y₁ and Y₀ can never be observed simultaneously for the same individual and thus Δ, the estimator of interest, can never be estimated directly. Let D = 1 if persons participate in the program and D = 0 if not. X denotes other characteristics used as conditioning variables and P(X) = Pr(D = 1|X) , denotes the conditional probability of participating in the program, conditional on X. The matching literature refers to P(X) as the propensity score.

The key parameter of interest in our evaluation is the mean impact of treatment-on-the-treated (TT) (where the treated are defined as those persons participating in the program that we observe in the data in 2003).

$$TT=E(\Delta \mid X,D=1)=E(Y_1-Y_0\mid X,D=1)=E(Y_1\mid X,D=1)-E(Y_0\mid X,D=1)$$

The cross-sectional matching estimator assumes:

$$\left(\mathit{CS}.1\right)E(Y_{0t}\mid P(X),D=1)=E(Y_{0t}\mid P(X),D=0)$$

$$\left(\mathit{CS}.2\right)0<\mathrm{Pr}(D=1\mid X<1)$$

at some post program-initiation time period t and for some subset of characteristics X. Under these conditions, an estimator for TT is

$$\left(\mathit{CS}.3\right){\Delta }_{D=1}=(1∕n_1)\sum _i{Y}_{1i}\left(P\right(X_i\left)\right)-E(Y_{0i}\mid P(X_i),D=0)$$

where the sum is over n₁, the number of treated individuals with X values that satisfy CS.2.²² E(Y_0i|P(X_i), D = 0) represents the matched outcome for each treated individual, which can be estimated nonparametrically by nearest neighbor, kernel or local linear regression.

The difference-in-difference matching estimator requires longitudinal or repeated cross-sectional data on program participants and nonparticipants. Let t and t’ be two time periods, one before the program start date and one after. Y_0t is the outcome observed at time t. Conditions needed to justify the application of the estimator are:

$$\left(\mathit{DID}.1\right)E(Y_{0t}-Y_{0t^{\prime }}\mid P(X),D=1)=E(Y_{0t}-Y_{0t^{\prime }}\mid P(X),D=0)$$

$$\left(\mathit{DID}.2\right)0<\mathrm{Pr}(D=1\mid X)<1)$$

where t is a post-program-initiation time period and t’ a pre-program time period. The difference-indifference matching estimator, based on longitudinal data, is

$$\left(\mathit{DID}.3\right){\Delta }_{D=1}=(1∕n_{1t})\sum _i\left[Y_{1i}\right(P\left(X_i\right))-Y_{0i{t}^{\prime }}(P\left(X_i\right)\left)\right]-\left[E\right(Y_{0it}\mid P\left(X_i\right),D=0)-E(Y_{0i{t}^{\prime }}\mid P\left(X_i\right),D=0\left)\right]$$

where n_1t is the number of treated observations and the summation is over the participants.²³ The first term in brackets is the change in outcomes for the program participant and the second term is the matching estimate of the change in outcomes in the no-treatment state based on the control group data.

The propensity score matching estimators are estimated in two stages. In the first stage, P(X) is estimated using a logit model and a set X consisting of pre-program (1997) household and locality level characteristics.24 In the second stage, the matched outcomes are constructed, i.e. E(Y_0i|P(X_i), D = 0) for the cross-sectional estimator and, additionally, E(Y_0i|P(X_i), D = 0) for the difference-in-difference estimator. We restrict analysis to those eligible for the program under the original eligibility criteria. The model estimates the determinants of participating where participants are those eligible individuals living in treatment (T1998) communities and those who do not participate are those eligible individuals living in comparison (C2003) communities. As mentioned earlier, take up rates of the program in rural areas are nearly universal.

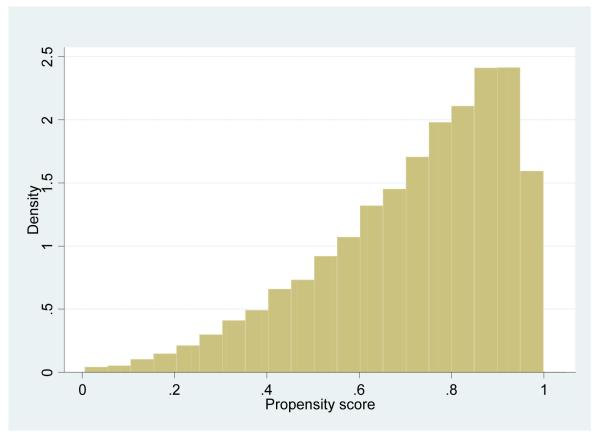
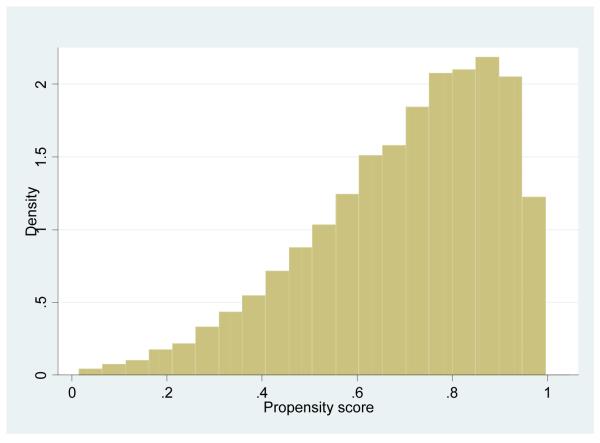
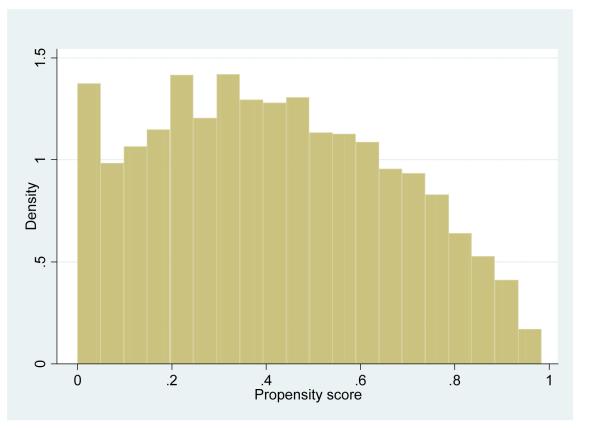
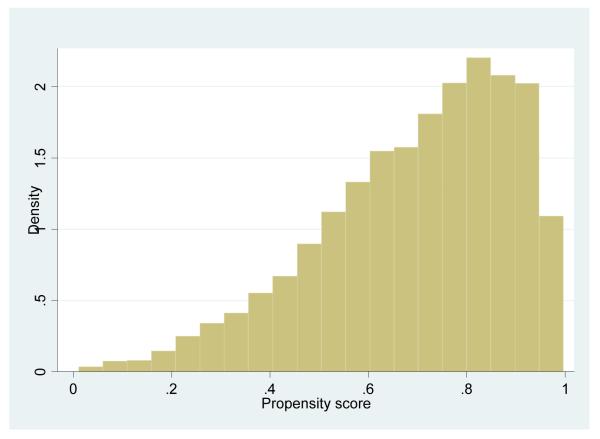
The variables used for the matching include demographic characteristics of the households in 1997, grades of schooling completed of household head and spouse in 1997, whether the household head and spouse spoke an indigenous language in 1997, whether the household head and spouse were employed in 1997, a number of household characteristics and consumer and production durables in 1997, the Oportunidades’ puntaje score for program eligibility, and state of residence in 1997. We use only preprogram information to avoid conditioning on any information that arguably could have been affected by the program. Nevertheless, pre-program information for the C2003 group relies on retrospective information, which for some variables such as income may be subject to recall biases. Unfortunately, only the C2003 group was applied the retrospective questionnaire; if such a questionnaire had been applied for the other groups we would have been able to judge the reporting bias by comparing retrospective information with information reported in 1997. We carry out however several different sets of estimates varying the variables used to calculate the propensity scores. First, we exclude variables from the propensity scores likely to be particularly subject to recall biases, including household income and the eligibility index which uses income as one of the criteria. We then experimented with a number of different matching specifications including some using only 2003 characteristics which are unlikely to have changed since pre-program (e.g. household age, parental schooling attainment, etc). The results are not fundamentally changed, in the Appendix (Figures C.1. to C.4.) we present graphs showing the distributions of the propensity scores for different specifications.²⁵

Table 5 gives the estimated logit model, for which the variables are jointly significant at the 0.1% level (according to a Chi² test) and which has fairly good predictive power (pseudo R squared = 0.26). The estimated relation is then used to generate propensity scores, which are estimated at a household level. Figure 1a and 1b gives the distribution of propensity scores in the original treatment group (T1998) and the distribution of propensity scores in the C2003 comparison group.

Table 5.

Logit model for probability of program participation D=1 Program eligible households in treatment group 1998 D=0 Program eligible households in new comparison 2003 communities

Variable	Coef.	Std. Err.	Variable	Coef.	Std. Err.
Age of Household head	0.001	0.003
Age of Spouse	−0.012	0.003	Blender	−0.082	0.069
Gender of Household head	1.185	0.114	Refrigerator	0.390	0.116
Hh head speaks indigenous lang.	0.356	0.086	Gas stove	0.905	0.090
Spouse speaks indigenous lang.	0.503	0.093	Gasheater	0.275	0.160
Grades of schooling HH head	0.019	0.011	Radio	0.276	0.047
Grades of schooling spouse	−0.062	0.011	Television	0.212	0.058
Employed HH head	−0.748	0.086	Video	0.493	0.179
Employed spouse	−0.741	0.068	Washer	0.692	0.192
Children 0 to 5	−0.671	0.031	Car	−0.435	0.238
Children 6 to 12	−0.410	0.032	Truck	0.26	0.163
Children 13 to 15	0.179	0.039	Guerrero state	0.816	0.121
Children 16 to 20	0.153	0.031	Michoacan state	1.06	0.106
Women 20 to 39	0.226	0.070	Puebla state	0.830	0.108
Women 40 to 59	−0.254	0.060	Queretaro state	0.568	0.106
Women 60+	−0.564	0.058	Hidalgo state	0.371	0.104
Men 20 to 39	−0.061	0.045	Morelos state	−0.685	0.100
Men 40 to 59	−0.865	0.065	Missing grades of schooling HH head	−0.802	0.190
Men 60+	−1.224	0.075	Missing grades of schooling spouse	−2.834	0.241
# Rooms	0.383	0.032	Missing age HH head	0.367	0.791
Electricity in HH	−0.397	0.052	Missing age spouse	−2.884	1.134
Water in HH	−0.651	0.050	Missing indig HH head	3.626	1.271
Dirt floor	−0.901	0.064	Missing working HH head	0.408	1.082
Roof material (inferior)	0.322	0.055	Missing working spouse	2.184	0.536
Wall material (inferior)	0.185	0.061	Missing water	−0.153	0.712
Own animals	0.293	0.051	Missing electricity	−1.532	0.712
Own land	0.487	0.047	Missing rooms	−0.356	0.363
Score	2.63	0.141	Missing own animals	−1.270	0.650
Score squared	−0.177	0.020	Missing own land	2.61	0.930
Constant	−4.553	0.322
Number of obs	13357
LR chi2(58)	4799		Pseudo R2	0.264
Prob > chi2	0.000		Log likelihood	6679

Notes: Authors’ calculations from ENCASEH97 and ENCEL2003 data. The sample used for matching and the impact analysis is ricted to program eligible households in both the treatm ent and new comparison communities. Variables used to predict participation are all pre-program data (1997). HH stands for household. Excluded state is Veracruz.

Figure 1a.

Distribution of Propensity score: Treatment98

Figure 1b.

Distribution of Propensity score: New Comparison Group

The distributions between the two groups are clearly different in a way that is consistent with poorer localities receiving benefits earlier as tended. Nevertheless, there is adequate support in the sense of a number of households in C2003 that have propensity scores similar to those in T1998 throughout the distribution. In implementing the matching estimators, we match on propensities scores and in addition match on the child’s age and sex. That is, eight-year-old boys in the T1998 group are matched only with eight-year—old boys in the C2003 comparison group living in households with similar propensity scores.

There are many variants of matching methods available in the literature. We have explored a number of alternatives including nearest-neighbor, kernel and local-linear matching with a range bandwidths and found that the empirical results are quite robust to these alternatives.²⁶ We report estimates here based on the nearest-neighbor method as well as on local-linear regression. Abadie and Imbens (2006) demonstrate that bootstrap standard errors in nearest-neighbor matching are inconsistent. For the case of nearest- neighbor estimates, they propose a variance estimator (Abadie and Imbens, 2002) that we use in this paper to calculate standard errors for nearest-neighbor matching. The critique of Abadie and Imbens does not apply for local-linear matching, for which we generate standard errors using bootstrapping.

As in the previous section, we implement age-constant difference-in-difference estimators, using children aged 6 to 14 years in the “before” period (1997) and the same age group in the “after” period (2003). For the oldest group (those aged 6 to 8 years in 1997), for whom we observe educational outcomes at baseline, we can compare the age-constant difference-in-difference estimates to longitudinal difference-in-difference matching estimates.

With respect to attrition, we only observe post-program-initiation outcomes for individuals who chose to remain in the communities and did not attrit. The difference-in-difference matching estimators are justified under the assumption that attrition is determined by observables that are controlled in the matching, or that attrition is determined in part by time-invariant unobservables that are on average eliminated through the differencing procedure. These assumptions, however, are not easily tested or verified. An additional exercise we carried out is to use the sample of youth age 6 to 14 years pre-program who did not attrit by 2003 to estimate pre-program differences between T1998 and C2003. The estimates obtained using this more restrictive preprogram group are very similar to those reported here.²⁷

5. Program Impact Estimates on Education of Children Age 0-8 Years in 1997

We begin with program impacts on the age at starting school (Tables 6a and 6b). If infants and very young children have better nutrition and health, they tend to develop more rapidly, both physically and cognitively, and therefore may be sufficiently mature to enter school when younger. Studies have found significant effects of pre-school nutrition on age at starting school in countries as varied as Ghana, Pakistan, the Philippines and Zimbabwe (see Alderman et al. 2001; Alderman, Hoddinott and Kinsey 2006; Glewwe and Jacoby 1995; Glewwe, Jacoby and King 2000; Glewwe and King 2001). If starting school earlier permits completing a given level of schooling when younger and expanding the number of post-schooling years in which to reap any productivity gains from schooling, the impact over the life-cycle can be considerable (see Glewwe and Jacoby 1995).

Table 6a.

Estimated impacts of program on age of entry to primary school: experimental sample T1998 vs. T1999

Age in 2003	Impact	Standard error	T1999 progression, % impact
Girls
7-8	−0.052	0.031*	6.11, 0.9%
9-11	0.028	0.085	6.30, 0.4%
7-11	−0.002	0.070	6.23, 0.0%

Boys
7-8	0.027	0.085	6.10, 0.4%
9-11	−0.000	0.010	6.38, 0%
7-11	0.008	0.037	6.27, 0.%

Table 6b.

Estimated impacts of program on age of entry to primary school: nearest-neighbor difference matching T1998 vs. C2003

Age in 2003	Impact	Standard error	T1999 progression, % impact
Girls
7-8	−0.080	0.045*	6.11, −1.3%
9-11	−0.033	0.047	6.30, −0.5%
7-11	−0.050	0.034	6.23, −0.8%

Boys
7-8	0.019	0.052	6.10, 0.3%
9-11	−0.025	0.048	6.38, −0.4%
7-11	−0.009	0.036	6.27, −0.1%

^†Difference-in-difference estimator, imposing common support (trimming=2%), 3 neighbors. Standard errors (parentheses) based on Abadie and Imbens, 2002.

For Mexico the potential gains from lowering the age of starting school are perhaps less than in many countries because the vast majority of children are in school at age six, the legal starting age. But it still is of interest to explore whether there is some evidence of a significant program impact on age of starting school, assuming that children starting school earlier reflects that they are developmentally more prepared. We explore this question for children aged 1 to 5 years in 1997 or 6 to 11 years in 2003.²⁸ Both sets of estimates (Tables 6a and 6b) indicate a significant impact of the program on reducing the age at starting school for girls. The matching estimates, whose impacts reflect the impact of 5.5 years of benefits, show slightly larger reductions on the age at entry to primary (−0.08 years) versus those based on the differential exposure of 1.5 years estimates (−0.05). These results are thus consistent with some potential effects on reducing age at entry although the overall magnitude is relatively low. For boys, there are no significant impacts of the program on age at entry for both sets of estimators.

It is useful to compare the impacts on age of entry to primary school for those children aged 7 to 8 years in 2003 with impacts for those children aged 9 to 11 years for the estimates of 1.5 years of differential exposure. As discussed above, children 7 to 8 years in 2003 would have been eligible to receive nutritional supplements whereas children aged 9 to 11 years would largely have been excluded. Thus, comparing differential exposure impact estimates for these two groups of children can provide an approximation of the impact of the nutritional supplement. It is notable that there are no significant impacts of differential program exposure on age at starting school for girls aged 9 to 11 years in 2003. A triple-difference estimator provides an impact estimate of the nutritional supplements on the age of entry for girls to primary school of 0.05, although given the large standard errors for the estimated impacts for 9 to 11 year olds in 2003, this difference is not statistically significant.

We now turn to program impacts on progressing on time through school grades (Tables 7a and 7b): Children who progress through school on time are defined to be those who progress one grade each year starting at age seven years. Progressing on time thus reflects both potential enrollment and continuation/passing rates.²⁹ Here we focus on the age groups of those 3 to 8 years in 1997 or 9 to 14 years after the program was started. The proportions who progress on time by this definition are considerably less than 1.0. For example for the C2003 group, the proportions for youth aged 12 to 14 years in 2003 are 0.65 for girls and 0.61 for boys (see Table 7b). The 1.5 year differential exposure to Oportunidades impacts, while all positive as would be expected, shows no statistically significant impacts at conventional significance levels.

Table 7a.

Estimated impacts on progressing on time; Difference-in-difference regression estimates: T1998 vs. T1999

Age in 2003	Pre- program difference	After- program- initiation difference	Impact: Difference- in- difference regression	C2000 progression, % impact
Girls
9-11	−0.002 (0.017)	0.001 (0.027)	0.003 (0.024)	0.84, 0.3%
12-14	0.017 (0.003)	0.026 (.020)	0.023 (0.028)	0.66, 3.5 %
9-14	0.01 (0.013)	.015 (0.013)	0.014 (0.018)	0.75, 1.9 %

Boys
9-11	0.025 (0.019)	0.012 (0.019)	−0.013 (0.027)	0.77,−1.6 %
12-14	0.009 (0.020)	0.041 (0.022)	0.032 (0.030)	0.60,5.3 %
9-14	0.015 (0.014)	0.027 (0.014)	0.012 (0.020)	0.68, 1.8%

Table 7b.

Estimated impacts on progressing on time: Difference-in-difference regression estimates: T1998 vs. T1999

Age in 2003	Pre- program difference	After- program- initiation difference	Impact: Difference- in- difference matching	C2003 progression, % impact
Girls
9-11	−0.081 (0.02)	−0.015 (0.02)	0.066 (0.03)	0.84, 8.0%
12-14	−0.094 (0.003)	0.055 (.020)	0.149 (0.04)	0.66, 22.9%
9-14	−0.087 (0.017)	.020 (0.016)	0.107 (0.02)	0.75, 14.5 %

Boys
9-11	−0.131 (0.019)	0.02 (0.02)	0.151 (0.03)	0.77, 19.6%
12-14	−0.087 (0.028)	0.08 (0.02)	0.167 (0.040)	0.60, 27.3%
9-14	−0.011 (0.017)	0.049 (0.016)	0.160 (0.020)	0.68, 23.0%

^†Difference-in-difference estimator, imposing common support (trimming=2%), 3 neighbors. Standard errors (parentheses) based on Abadie and Imbens, 2002.

The matching comparisons between T1998 and C2003, suggest important effects (presumably due to the greater time receiving program benefits) with significant and substantial impacts for both boys and girls. The impacts for the older groups (12 to 14 years in 2003) suggest increases in progression rates of about 11 percent overall for girls and 16 percent overall for boys. Higher impacts for the older group presumably reflect the (positive) program effect on the transition decision between primary and secondary school that under normal grade progression occurs around the age of 12 or 13 years (Table 7b).

We now turn to program impact estimates on grades of schooling completed (Tables 8a and 8b). The differential exposure results show some significant impacts of greater exposure to the program for both boys and girls, with a point estimate of an increase of 0.05 grades completed, mainly concentrated on the older group as would be expected. Nevertheless, taking into account the pre-program differences, the difference-in-difference estimates are not statistically significant (Table 8a).

Table 8a.

Estimated impacts on grades of schooling; Difference-in-difference regression estimates: T1998 vs. T1999

Age in 2003	Pre- program difference	After- program- initiation difference	Impact: Difference- in- difference regression	T1999 grades of schooling, % impact
Girls
6-8	0.008 (0.031)	0.22 (0.032)	0.014 (0.05)	1.00,1.4%
9-11	−0.015 (0.052)	−.016 (0.046)	−0.001 (0.06)	3.36,−0.0%
12-14	−0.053 (0.078)	0.06 (0.074)	0.113 (0.09)	5.69, 2.0%
6-14	−0.016 (0.034)	0.023 (0.033)	0.049 (0.08)	3.57, 1.4%

Boys
6-8	0.027 (0.031)	0.036 (0.032)	0.009 (0.05)	0.95,0.9%
9-11	0.00 (0.053)	0.043 (.048)	0.043 (0.06)	3.19, 1.3%
12-14	0.046 (0.079)	0.138 (.074)	0.092 (0.09)	5.49, 1.7%
6-14	0.027 (0.034)	0.078 (0.033)	0.051 (0.06)	3.42, 1.5%

Table 8b.

Estimated impacts on grades of schooling: Nearest-neighbor matching ^° T1998 vs. C2003 Difference-in-difference matching using children of same age pre-program

Age in 2003	Pre- program difference	After- program- initiation difference	Impact: Difference- in- difference matching	C2003 grades of schooling, % impact
Girls
6-8	−0.18	−0.223	−0.04	1.42, −2.8%
9-11	−0.31 (0.052)	−.038 (0.06)	0.27 (0.08)	3.33, 8.2%
12-14	−0.35 (0.111)	0.013 (0.093)	0.49 (0.14)	5.64, 8.6%
6-14	−0.28 (0.038)	−0.039 (0.049)	0.24 (0.06)	3.44, 6.9%

Boys
6-8	−0.17 (0.021)	−0.16 (0.075)	0.007 (0.08)	1.10,0.7%
9-11	−0.41 (0.051)	−0.027 (.064)	0.40 (0.08)	3.18, 12.3%
12-14	−0.169 (0.104)	0.352 (.089)	0.52 (0.14)	5.49, 9.5%
6-14	−0.25 (0.045)	0.067 (0.044)	0.32 (0.07)	3.32, 9.5%

^°Difference-in-difference estimator, imposing common support (trimming=2%), 3 neighbors. Standard errors (parentheses) based on Abadie and Imbens, 2002.

Table 8b shows matching estimates based on difference-in-difference matching using as the pre-program group children of the same age pre-program. First, it is noteworthy that there are significant differences in schooling pre-program between the two groups, indicating that the C2003 group has higher years of completed schooling in the absence of the program. Using simple difference matching of post-program-initiation schooling would thus likely under-estimate the potential impacts of the program.

The difference-in-difference matching estimates that compare the T1998 groups receiving 5.5 years of benefits to the C2003 group that never received benefits show strong and significant increases in completed years of schooling, increasing in absolute terms with age. Whereas there are no significant effects for children aged 6 to 8 who had not yet begun to receive the education grants, children aged 12 to 14 years in 2003 accumulate about 0.5 grades for both boys and girls. These increases represent notable increases in the level of completed schooling for the age groups, on average representing an increase of 8 to 9 percent of grades of current completed schooling.

To judge the plausibility of these results, a useful comparison can be made between the T1999 and the C2003 groups. This compares beneficiaries receiving about 4 years of program benefits to those never receiving benefits and for cumulative indicators such as years of schooling, would be expected to yield smaller impacts than those found comparing the T1998 to the C2003 group. In particular, we would expect impacts that are about 25 to 30 percent smaller. The results of this exercise on grades of completed schooling are presented in Table 8c. The T1999-C2003 comparison does show smaller impacts on years of schooling as expected, both for boys and girls and in particular about one third less than for the T1998-C2003 comparison. For instance, the overall results show increases in schooling for boys of 0.32 grades for the T1998-C2003 comparison versus 0.25 grades for the T1999-C2003 comparison.

Table 8c.

Estimated impacts on grade of schooling: Nearest-neighbor matching ^° T1999 vs. C2003 Difference-in-difference matching using children of same age pre-program

Age in 2003	Pre- program difference	After- program- initiation difference	Impact: Difference- in- difference matching	C2003 grades of schooling, % impact
Girls
6-8	−0.19 (0.022)	−0.033 (0.122 )	0.15 (0.13)	1.42, 10.2%
9-11	−0.32 (0.056)	−0.071 (0.070)	0.25 (0.09)	3.33, 7.5%
12-14	−0.31 (0.107)	0.09 (0.10)	0.40 (0.16)	5.64, 7.1%
6-14	−0.27 (0.038)	−0.10 (0.06)	0.17 (0.07)	3.44, 5.0%

Boys
6-8	−0.20 (0.022)	−0.17 (0.103)	0.038 (0.11)	1.10, 2.7%
9-11	−0.42 (0.056)	−0.024 (.079)	0.40 (0.10)	3.18, 11.9%
12-14	−0.21 (0.107)	0.07 (0.104)	0.28 (0.16)	5.49, 4.9%
6-14	−0.28 (0.04)	−0.035 (0.076)	0.25 (0.09)	3.32, 7.7%

^°Difference-in-difference estimator, imposing common support (trimming=2%), 3 neighbors. Standard errors (parentheses) based on Abadie and Imbens, 2002.

Finally, Table 9 presents a couple of alternative estimations. First, recall that we have used children of the same age group pre-program to estimate before program differences. In the first two rows of Table 9, we now carry out results using longitudinal matching (e.g. using the same children between 1997 and 2003) and compare these results with estimates based on age-constant difference-in-difference matching. These comparisons are only possible for the oldest age group of our study (e.g. those aged 12 to 14 years in 2003) for whom we observe preprogram education indicators. Table 9 presents the results for progressing on time and grades of completed schooling for this age group. In general, the longitudinal difference-in-difference matching estimates show smaller program effect estimates. This largely reflects that the before group differences are lower between the1998 and C2003 group when longitudinal matching is done, given that children age 6 to 8 years have just begun to enter school and little time has passed for potential differences to have manifested themselves between the T1998 and C2003 groups.

Table 9.

Comparing longitudinal difference-in-difference matching with difference-in-difference matching using children of same age pre-program Nearest-neighbor matching and local-linear matching^† T1998 vs. C2003

	Years of education		Progressing on time
Age in 2003	Longitudinal difference- in-difference matching	Same age difference- in- difference matching:	Longitudinal difference- in-difference matching	Same age difference- in- difference matching:
Nearest neighbor
Girls
12-14	0.20 (0.13)	0.52 (0.14)	0.091 (0.029)	0.15 (0.05)
Boys
12-14	0.54 (0.12)	0.50 (0.14)	0.082 (0.028)	0.17 (0.04)
Local linear Bandwidth=0.01				0.14 (0.047)
Girls 12-14	0.23 (0.20)	0.60 (0.19)	0.074 (0.04)
Boys 12-14	0.49 (0.16)	0.63 (0.20)	0.105 (0.03)	0.17 (0.054)
Local linear Bandwidth=0.2
Girls
12-14	0.29 (0.20)	0.63 (0.18)	0.064 (0.037)	0.140 (0.05)
Boys
12-14	0.54 (0.18)	0.50 (0.18)	0.094 (0.04)	0.165 (0.05)
Local linear: Bandwidth=0.4
Girls
12-14	0.30 (0.18)	0.62 (0.20)	0.062 (0.036)	0.142 (0.050)
Boys
12-14	0.58 (0.17)	0.50 (0.19)	0.086 (0.032)	0.160 (0.05)

^†Difference-in-difference estimator, imposing common support (trimming=2%), 5 neighbors. errors (parentheses) computed using bootstrapping with 200 repetitions. Longitudinal difference-in-difference matching using the same children over time to estimate impacts. Same aged difference-in-difference matching uses as pre-program measures those based on children who pre-program were the same age as children post-program-initiation.

Up until now, we have reported estimated based on nearest-neighbor matching using standard errors developed by Abadie and Imbens (2002, 2006). In Table 9, we use a local-linear matching estimator and provide impact estimates for years of schooling and progressing on time for a wide range of different bandwidths (0.01, 0.2 and 0.4), and estimating standard errors using bootstrapping with 200 repetitions.³⁰ The results are quite similar to those based on nearest-neighbor matching. We also estimate bootstrap errors taking into account potential correlations between individuals in each community, these bootstrap errors are slightly larger than those estimated without clusters but overall do not substantially change the significance levels of the estimates and are not reported here.

5. Summary and Conclusions

Previous evaluations of the educational impacts of Oportunidades have focused on the short-run impacts for children at least of school age (and possibly of sufficient age to be eligible for the scholarship program that commences in the third grade of primary level). In this paper we focus instead on the medium-term impacts on children who were for the most part too young to be eligible for the scholarship program, indeed, for the most part too young to be in school, at the time of the initiation of the rural program: children 0-8 years old in 1997 or 6-14 years old in 2003. The oldest group of children in the age range considered were eligible immediately or soon after the initiation of the program for direct scholarship support, and the youngest group of children in this age range were still not eligible for scholarship support by 2003. On the other hand, the youngest children in this age range were eligible for the nutrient supplements for infants and children under 24 months of age, which other studies suggest may have important benefits for their education when they became of school age. This is an important example of alleged synergies, or interactions, among various components of human capital that are key to the advocacy of integrated human capital investment programs, such as Oportunidades and many other programs with similar multi-faceted human capital enrichment aims.

This paper contributes to the available empirical evidence primarily by exploring the medium-term impact of the program package, including the nutritional components, for infants and young children on subsequent school performance. The evidence thus far is consistent with some initial impacts of the early nutritional intervention on early school outcomes. In particular, those aged 1 to 2 years in 1997 (7 years in 2003) show a reduction in the age at entering school, and we have provided suggestive evidence that this partially reflects the effect of the nutritional supplements. The age group 3 to 5 years in 1997 most likely did not benefit from the early nutritional intervention and also by 2003 would have only recently begun to be eligible themselves to receive Oportunidades scholarship grants. Nevertheless, the matching estimates show important increases in grades of completed schooling and progressing on time, consistent with families anticipating the receipt of grants for these children or possible income effects through program receipt. As expected, those aged 6 to 8 years in 1997 (12 to 14 years in 2003) show the largest increases in schooling indicators. This group was eligible to receive grants for a majority of the program’s duration and it is likely this and the conditionality aspect of the grants that explain the larger impacts of the program for this age group.

In summary, the matching estimates show a consistent and important improvement in educational indicators even for younger children who are not yet eligible or are only beginning to be eligible for the educational grants at the time the program initiated. Although limited by the fact that infants in 1997 are only beginning to enter school by 2003, the impact estimates are also consistent with positive effects of the nutritional intervention on later schooling indicators. The group aged 6 to 8 years pre-program show important and plausible increases in schooling levels, most likely attributable to the scholarship grants. The differential exposure estimates, based on only on a year and a half of difference in program receipt, show much smaller impacts and generally insignificant impacts of the program.

The results are encouraging, but it is clear that continued evaluation is needed. Most of the children studied here were still in primary school age in 2003 and thus received the Oportunidades scholarship grants for only a few years. Providing estimates of the eventual total effect of the program on their schooling necessitates their continued follow-up. This would seem particularly urgent and relevant for the youngest age group, e.g. infants at the start of the program in 1997. Further evaluation will permit the analysis of whether the apparent initial synergies between health and education observed here continue to be observed over time.

Appendix A. Construction of Variables

Sample construction

The analysis uses children aged 0 to 8 in 1997 and therefore 6 to 14 in 2003. In practice, there are inconsistencies in the ages reported, e.g. not all youth reported to be age 0 to 8 in 1997 are within the range of 6 to 14 in 2003 (or even slightly outside the range). An additional concern arises over whether age inconsistencies over time as well as in other indicators might reflect errors in id numbers resulting in individuals “matching” incorrectly.

To correct some errors and insure that we are correctly matching individuals over the six-year period, we deleted from the sample any individual who was more than two years off in 2003 with respect to what would be his or her “correct” age according to that reported in 1997. Additionally we eliminated individuals who reported changing gender between the periods.

We also deleted from the sample individuals who reported impossible changes in the schooling grade attainment over time. That is, we eliminated individuals reporting negative changes in schooling or those reporting they had completed more than 8 grades of schooling over the six-year period.

Definition of outcome indicators

Grades of completed schooling is constructed for both 1997 and 2003 using information on the level and grade. Years in preschool or kindergarten were not counted. Primary school education was allowed to have a maximum of six grades, lower secondary school was allowed a maximum of three additional grades, and upper secondary (i.e., high school) a further additional three grades. Further, we constrained the number of grades of completed schooling a child could have in the following way: children six year old could have at most 1 year of completed schooling, children seven years old could have at most 2 years of completed schooling etc. For schooling in 2003, we carried out the following corrections: For cases which were inconsistent with this rule (e.g. suggesting a child had more schooling than should be possible given his/her age), we used the grade they were currently attending in school and/or the grade they had attended in the previous year to correct the information on years of completed schooling. For the cases in which inconsistencies remained or where they were no longer attending school, we defined grades of schooling to be missing for these individuals and they were dropped from the sample.

Progressing through school on time is defined as 1 if the difference between age and schooling grade attainment is less than or equal to 7, for those children at least 8 years old. Note that the legal age for entering school is age 6 before the beginning of the school year so that many children may actually be close to 7 when starting school but be considered to be on time.

Age at entry is unfortunately not directly asked in the 2003 or 1997 data used here. We construct an indicator of age at entry based on the retrospective information available in the 2003 data on school enrollment and grade repetition/failure.

Appendix B. Attrition Model

Table B1.

Probability of attriting between 1997 and 2003 as a function of characteristics in 1997: Children 0 to 8 in 1997 eligible for benefits in 1997

	All attritors		Individual attritiona		Household attritionb
	(1)	(2)	(1)	(2)	(1)	(2)
T1998 = 1; T1999 = 0	−0.006	0.022	0.003	0.039	−0.01	−0.02
	[0.005]	[0.036]	[0.003]	[0.020]*	[0.005]*	[0.032]
Interactions
T1998*age		0.006		0.002		0.004
		[0.004]		[0.002]		[0.004]
T1998*gender		0.015		0.009		0.006
		[0.011]		[0.005]		[0.010]
T1998*indigenous		0.038		0.004		0.032
		[0.023]*		[0.010]		[0.021]
T1998*schooling		−0.019		−0.005		−0.014
		[0.011]*		[0.005]		[0.010]
T1998*enrolled		−0.026		−0.003		−0.021
		[0.018]		[0.008]		[0.016]
T1998*father schooling		0.004		0.001		0.003
		[0.003]		[0.001]		[0.002]
T1998*father age		−0.001		0.001		−0.001
		[0.001]		[0.000]		[0.001]
T1998*father indigenous		−0.05		0.019		−0.068
		[0.038]		[0.028]		[0.029]**
T1998*father bilingual		0.108		0.021		0.081
		[0.046]**		[0.027]		[0.041]**
T1998*mother schooling		0.003		−0.003		0.005
		[0.002]		[0.001]**		[0.002]**
T1998*mother age		−0.003		−0.002		−0.001
		[0.001]***		[0.000]***		[0.001]
T1998*mother indigenous		0.046		−0.027		0.1
		[0.034]		[0.007]***		[0.036]***
T1998*mother bilingual		−0.087		0.012		−0.088
		[0.018]***		[0.013]		[0.014]***
T1998*rooms		0		−0.001		0.001
		[0.001]		[0.000]		[0.001]
T1998*electricity		0.025		0.002		0.02
		[0.013]**		[0.006]		[0.011]*
T1998*water		0.027		−0.001		0.027
		[0.014]**		[0.006]		[0.013]**
T1998*dirt floor		0.031		−0.007		0.04
		[0.014]**		[0.005]		[0.013]***
Observations	23393	22756	23393	22756	23393	22756

Standard errors in brackets

^* significant at 10%;

^**significant at 5%;

^*** significant at 1%

^aIndividual attrition refers to individuals who attrit but original household stays in sample.

^bHousehold attrition refers to individuals attriting because entire household attrits.

Figure C1a.

T1998 Propensity score w/o HH Income and scores

Figure C1b.

C2003 Propensity score w/o HH Income and scores

Figure C2a.

T1998 Propensity score w/o HH Income, scores and durables

Figure C2b.

C2003 Propensity score w/o HH Income, scores and durables