A Unified Approach to Nonparametric Comparison of Receiver Operating Characteristic Curves for Longitudinal and Clustered Data

Abstract

We present a unified approach to nonparametric comparisons of receiver operating characteristic (ROC) curves for a paired design with clustered data. Treating empirical ROC curves as stochastic processes, their asymptotic joint distribution is derived in the presence of both between-marker and within-subject correlations. A Monte Carlo method is developed to approximate their joint distribution without involving nonparametric density estimation. The developed theory is applied to derive new inferential procedures for comparing weighted areas under the ROC curves, confidence bands for the difference function of ROC curves, confidence intervals for the set of specificities at which one diagnostic test is more sensitive than the other, and multiple comparison procedures for comparing more than two diagnostic markers. Our methods demonstrate satisfactory small-sample performance in simulations. We illustrate our methods using clustered data from a glaucoma study and repeated-measurement data from a startle response study.

1. INTRODUCTION

Receiver operating characteristic (ROC) curves are commonly used to evaluate and compare diagnostic markers in various fields, such as signal detection and medicine (Green and Swets 1966; Zhou, McClish, and Obuchowski 2002; Pepe 2003). The ROC curve of a diagnostic marker is a plot of the true positive rate (sensitivity) against the false-positive rate (1 – specificity) at different threshold values. It has the appealing property of describing the discrimination capacity of a diagnostic marker without linking it to any specific threshold. This enables direct comparisons of diagnostic markers even if they are on different measurement scales.

The most popular nonparametric methods for comparing ROC curves are based on some summary indexes, such as the area under the ROC curve (AUC) and the partial area under the ROC curve (pAUC) (see Hanley and McNeil 1982, 1983; McClish 1987; DeLong, DeLong, and Clarke-Pearson 1988; and Wieand, Gail, Barray, and James 1989 for independent data, and Obuchowski 1997; Emir, Wieand, Su, and Cha 1998; and Emir, Wieand, Jung, and Ying 2000 for clustered data). Although simple to use, these summary indexes are not without limitations; for example, a large value of the AUC or pAUC does not necessarily imply high sensitivity at a prespecified specificity. Many medical applications require comparisons of sensitivities of diagnostic markers at a prespecified specificity that is of clinical relevance. Confidence bands for the difference of two ROC curves also are desirable in practice for comparing sensitivities of two diagnostic markers over a prespecified range of specificities. In addition, interest may lie in estimating the set of specificities with differential sensitivity. Unfortunately, very few nonparametric comparison procedures beyond the use of AUC and pAUC have been rigorously developed in the literature. The problems can become more complicated when a paired design is used in which both markers are performed on the same study subjects and when there are multiple measurements for each marker from repeated-measurement or clustered data studies. In such situations, the between-marker and within-subject correlations must be accounted for. Some examples of a paired design with clustered data are given in Section 5.

The purpose of this article is to develop a unified approach to the analysis of ROC curves that allows a variety of non-parametric comparisons in the presence of between-marker and within-cluster correlations. We first derive the asymptotic distribution theory for correlated empirical ROC processes, taking into account of both between-marker and within-cluster correlations. This extends the work of Hsieh and Turnbull (1996) and Li, Tiwari, and Wells (1996b), who derived the asymptotic distribution of a single empirical ROC curve. The variance–covariance functions of the limiting ROC processes are shown to involve unknown densities that are difficult to estimate nonparametrically. By extending an idea of Keaney and Wei (1994), we propose to approximate the joint distribution of the empirical ROC processes by some Gaussian random processes whose distribution can be calculated by computer Monte Carlo simulations without involving density estimation. We provide a theoretical justification for this approach by proving that the Monte Carlo Gaussian processes have the same limiting distribution as the original empirical ROC processes. These results allow us to approximate the distribution of any continuous functional of the empirical ROC curves. This provides a general framework that enables various ROC curve comparisons. As examples, we apply the developed theory to obtain confidence bands for the difference of two ROC curves over a given range of specificities. We also derive nonparametric tests and confidence intervals for comparing weighted areas under the ROC curves that include AUCs, pAUCs, and sensitivities at a fixed specificity as special cases. In addition, we apply the intersection-union test concept (cf. Berger and Boos 1999; Berger and Hsu 1996) to obtain confidence intervals for the set of specificities at which one diagnostic test is more sensitive than the other. We also extend our theory to deal with multiple comparison problems involving more than two diagnostic markers.

We note that Uno, Cai, Tian, and Wei (2007) described a similar perturbation-resampling method to evaluate an ROC curve for censored data that include uncensored binary outcomes as a special case. As pointed by a referee, it may be possible to extend their method to correlated ROC curves and to clustered data. But our work is the first to clearly adapt these ideas to analyses of correlated ROC curves with clustered data, and we describe additional measures, such as confidence intervals, for the set of specificities with differential sensitivity.

The rest of the article is organized as follows. Section 2 gives the general asymptotic distribution theory for empirical ROC curves. Section 3 applies the developed theory to derive a number of inferential procedures for comparing ROC curves. Section 4 presents a simulation study to evaluate our methods’ performance. Section 5 illustrates our methods using a cluster data set from an ophthalmology study and a repeated-measurement data set from a neuroscience study. Section 6 gives some closing remarks.

2. LARGE–SAMPLE DISTRIBUTION THEORY FOR RECEIVER OPERATING CHARACTERISTIC CURVES

For simplicity, we consider only two diagnostic tests in this section.

2.1 The Receiver Operating Characteristic Curve

Let X^(v) denote the continuous outcome of the vth diagnostic marker for which a value greater than a cutoff value t indicates a positive test result, v = 1, 2. The sensitivity and specificity are then given by 1 − G^(v)(t) and F^(v)(t), where F^(v) and G^(v) are the cumulative distribution functions of X^(v) for the healthy and diseased populations, v = 1, 2. The ROC curve for the vth diagnostic test is defined by

$$RO{C}^{(v)}(p)=1-G^{(v)}\{F^{{(v)}^{-1}}(1-p)\},p\in [0,1],$$ (1)

where F⁻¹(p) = inf(t: F(t) ≥ p) for any function F. Equivalently, this is the plot of sensitivity against 1 − specificity, as the cutoff value t varies. Clearly, the closer to the upper left corner of the unit box, the greater the discriminating power.

2.2 The Data

Assume that there are a total of n subjects in the study. Suppose that we observe $X_{ij}^{(v)}\sim F^{(v)},j=1,\dots ,m_i^{(v)}$, representing the measurements of the vth marker from $m_i^{(v)}$ healthy units within subject i, and $Y_{ij}^{(v)}\sim G^{(v)},j=1,\dots ,n_i^{(v)}$, the measurements of the vth marker from $n_i^{(v)}$ diseased units within subject i, i = 1, …, n and v = 1, 2. Assume further that measurements from different subjects are independent and measurements within a subject are possibly correlated. These types of data commonly arise from clustered data or repeated-measurement studies. Our data setting allows for both between-marker and within-subject correlations. We also allow different markers to have different numbers of measurements per subject.

2.3 The Estimators

Let $M^{(v)}={\sum }_{i=1}^n{m}_i^{(v)}$ and $N^{(v)}={\sum }_{i=1}^n{n}_i^{(v)}$. Define the empirical ROC curves

$${\widehat{\mathit{ROC}}}^{(v)}(p)=1-{\widehat{G}}^{(v)}\{{\widehat{F^{(v)}}}^{-1}(1-p)\},v=1,2,$$ (2)

where ${\widehat{F}}^{(v)}(t)={\sum }_{i=1}^n{\sum }_{j=1}^{m_i^{(v)}}I(X_{ij}^{(v)}\le t)/M^{(v)}$ and ${\widehat{G}}^{(v)}(t)={\sum }_{i=1}^n{\sum }_{j=1}^{m}I(X_{ij}^{(v)}\le t)/N^{(v)}$.

2.4 The Joint Limiting Distribution of ( ${\widehat{\mathit{ROC}}}^{(1)}(p),{\widehat{\mathit{ROC}}}^{(2)}(p)$)

For any interval I, let D(I) denote the cadlag space of all right-continuous functions on I that have left-side limits, equipped with supremum norm || · ||_∞. The following lemma is needed to establish the limiting distribution of (ROC⁽¹⁾(p), ROC⁽²⁾(p)).

Lemma 1

Assume that as n → ∞, $n^{-1}{\sum }_{i=1}^n{m}_i^{{(v)}^k}\to {\lambda }_k^{(v)}$, and $n^{-1}{\sum }_{i=1}^n{n}_i^{{(v)}^k}\to {\gamma }_k^{(v)}$ for some positive constants ${\lambda }_k^{(v)}$ and ${\gamma }_k^{(v)}$, v = 1, 2 and k = 1, 2, 3. Then

$$\sqrt{n}\left(\begin{array}{c}{\widehat{F}}^{(1)}(t)-F^{(1)}(t)\\ {\widehat{F}}^{(2)}(t)-F^{(2)}(t)\\ {\widehat{G}}^{(1)}(t)-G^{(1)}(t)\\ {\widehat{G}}^{(2)}(t)-G^{(2)}(t)\end{array}\right)\stackrel{d}{\to }\left(\begin{array}{c}{W}_{F^{(1)}}(t)\\ W_{F^{(2)}}(t)\\ W_{G^{(1)}}(t)\\ W_{G^{(2)}}(t)\end{array}\right)\text{as}n\to \infty ,$$ (3)

in D(ℝ)⁴ = D(ℝ) × ··· × D(ℝ), where ℝ = (−∞, ∞), (W_F⁽¹⁾(t), W_F⁽²⁾(t), W_G⁽¹⁾(t), W_G⁽²⁾(t))′ is a vector of mean-0 Gaussian processes defined in (A.1) of the Appendix.

The joint limiting distribution of ( ${\widehat{\mathit{ROC}}}^{(1)}(p),{\widehat{\mathit{ROC}}}^{(2)}(p)$) is given next.

Theorem 1

Assume that the assumptions of Lemma 1 hold. Assume further that for v = 1, 2, F^(v) and G^(v) have derivatives F^(v)′ and G^(v)′ that are positive and continuous on [F^(v)−1(a) − ε, F^(v)−1(b) + ε], for some 0 < a < b < 1 and ε > 0. Then, as n → ∞,

$$\sqrt{n}\left(\begin{array}{c}{\widehat{\mathit{ROC}}}^{(1)}(p)-RO{C}^{(1)}(p)\\ {\widehat{\mathit{ROC}}}^{(2)}(p)-RO{C}^{(2)}(p)\end{array}\right)\stackrel{d}{\to }\left(\begin{array}{c}{Z}^{(1)}(1-p)\\ Z^{(2)}(1-p)\end{array}\right),$$ (4)

in D[1 − b, 1 − a] × D[1 − b, 1 − a], where for v = 1, 2, Z^(v)(p) = − s^(v)(p) · W_F^(v)(F^(v)−1(p)) + W_G^(v)(F^(v)−1(p)), s^(v)(p) = G^(v)′ (F^(v)−1(p))/F^(v)′ (F^(v)−1(p)). Recall that W_F⁽¹⁾(t), W_F⁽²⁾(t), W_G⁽¹⁾(t), and W_G⁽²⁾(t) are the limiting Gaussian processes in (3).

The foregoing theorem allows us to obtain the limiting distribution of any continuous functional of ( ${\widehat{\mathit{ROC}}}^{(1)}(p),{\widehat{\mathit{ROC}}}^{(2)}(p)$). For simplicity, hereinafter we focus on the difference function of the two ROC curves.

Corollary 1

Let D(p) = ROC⁽¹⁾(p) − ROC⁽²⁾(p) and $\widehat{D}(p)={\widehat{\mathit{ROC}}}^{(1)}(p)-{\widehat{\mathit{ROC}}}^{(2)}(p)$. Then, as n → ∞,

$$\sqrt{n}(\widehat{D}(p)-D(p))\stackrel{d}{\to }U(p)=Z^{(2)}(1-p)-Z^{(1)}(1-p).$$

2.5 Approximate the Limiting Process U(p)

Note that the result of Corollary 1 cannot be readily used to make inference for D(p). For instance, to construct simultaneous confidence bands for D(p) over [p₁, p₂], we need to know the distribution of sup_p∈[p1,p2] |U(p)|, which depends on some unknown quantities and is intractable. Variance estimation also is problematic, because it involves density estimation. Next, we study how to approximate the distribution of U(·) without using density estimation.

As a building block, we first describe a standard Monte Carlo method for approximating the empirical distributions. For v = 1, 2, define

$$W_{F^{(v)}}^{\ast }(t)=\frac{\sqrt{n}}{M^{(v)}}\sum _{i=1}^n{\eta }_i\sum _{j=1}^{m_i^{(v)}}\{I(X_{ij}^{(v)}\le t)-{\widehat{F}}^{(v)}(t)\}$$

and

$$W_{G^{(v)}}^{\ast }(t)=\frac{\sqrt{n}}{N^{(v)}}\sum _{i=1}^n{\eta }_i\sum _{j=1}^{n_i^{(v)}}\{I(X_{ij}^{(v)}\le t)-{\widehat{G}}^{(v)}(t)\},$$

where the η_i’s are iid standard normal random variables. Then, conditional on the observed data,

$$\begin{array}{l}(W_{F^{(1)}}^{\ast }(t),W_{F^{(2)}}^{\ast }(t),W_{G^{(1)}}^{\ast }(t),W_{G^{(2)}}^{\ast }(t))\\ \stackrel{d}{\to }(W_{F^{(1)}}(t),W_{F^{(2)}}(t),W_{G^{(1)}}(t),W_{G^{(2)}}(t))\end{array}$$ (5)

in D(ℝ)⁴ for almost all data realizations, where the limiting processes in (5) are defined in (3). This can be proven by observing that, conditional on the data, the left side is a Gaussian random field whose covariance function converges to that of the right side.

A naive method for approximating the limiting process U is to replace (W_F^(v)(t), W_F^(v)(t)) with ( $W_{F^{(v)}}^{\ast }(t),W_{G^{(v)}}^{\ast }(t)$) and then replace s^(v)(p) and F^(v)(t), v = 1, 2, by their corresponding sample estimates. But estimating s^(v)(p) nonparametrically is difficult. Keaney and Wei (1994) presented a novel method to approximate the distribution of a median survival time without requiring density estimation. We extend their idea to approximate the process U(p).

Note that the distribution of $\sqrt{n}\{{\widehat{F}}^{(v)}(F^{{(v)}^{-1}}(p))-p\}$ can be estimated by that of $W_{F^{(v)}}^{\ast }(F^{{(v)}^{-1}}(p))$. Define ξ^(v)*(p) by $\sqrt{n}\{{\widehat{F}}^{(v)}({\xi }^{(v)\ast }(p))-p\}=W_{F^{(v)}}^{\ast }({\widehat{F}}^{(v)-1}(p))$, or

$${\xi }^{(v)\ast }(p)={\widehat{F}}^{(v)-1}(p+n^{-1/2}{W}_F^{\ast }({\widehat{F}}^{(v)-1}(p))).$$ (6)

Then it can be shown that the conditional distribution of the process $\sqrt{n}\{{\xi }^{(v)\ast }(p)-{\widehat{F}}^{(v)-1}(p)\}$ given the data is asymptotically equivalent to $\sqrt{n}\{{\widehat{F}}^{(v)-1}(p)-F^{(v)-1}(p)\}$.

Similarly, define

$${\zeta }^{(v)\ast }(t)={\widehat{G}}^{(v)}(t)-n^{-1/2}{W}_G^{(v)\ast }(t).$$ (7)

Then it is easy to see that the distribution of $\sqrt{n}\{{\widehat{G}}^{(v)}(t)-G^{(v)}(t)\}$ can be estimated by the conditional distribution of $\sqrt{n}\{{\zeta }^{(v)\ast }(t)-{\widehat{G}}^{(v)}(t)\}$ given the data.

Finally, let Q^(v)*(p) = ζ^(v)*(ξ^(v)*(p)), ROC^(v)*(p) = 1 − Q^(v)*(1 − p), and D^*(p) = ROC^(1)*(p) − ROC^(2)*(p). We then have the following theorem.

Theorem 2

Assume that the conditions of Theorem 1 hold. Then, for every subsequence {n_j} of {n}, there is a further subsequence {m_k} ⊂ {n_j} such that, conditional on the data,

$$\sqrt{n}(D^{\ast }(p)-\widehat{D}(p))\stackrel{d}{\to }U(p)$$

in D[p₁, p₂] along the subsequence {m_k}, for almost all data realizations, where [p₁, p₂] ⊂ (1 − b, 1 − a) and U(p) is the limiting process defined in Theorem 1.

Although the foregoing result is established along subsequences, it leads to the following corollary for any continuous functional of $\sqrt{n}(D^{\ast }-\widehat{D})$ along the entire sequence {n}.

Corollary 2

Assume that the conditions of Theorem 1 hold. Let T: D[p₁, p₂] → ℝ be a continuous mapping from D[p₁, p₂] to the real line ℝ. Let $H_n^{\ast }(t)=P(T(\sqrt{n}(D^{\ast }-\widehat{D}))\le t\mid \mathit{data})$. Then, as n → ∞,

$$H_n^{\ast }t\to H(t)\equiv P(T(U)\le t)$$

uniformly in t on any compact interval for almost all data realizations.

Corollary 2 allows us to approximate the distribution of $T(\sqrt{n}(\widehat{D}-D))$ by that of $T(\sqrt{n}(D^{\ast }-\widehat{D}))$ given the data. Some useful examples of T include T₁(f) = f(p₀) for a fixed p₀, $T_2(f)={\int }_{p_1}^{p_2}f(p)dp$, and T₃(f) = sup_{p∈[p1, p2]}|f(p)|, which can be used to compare sensitivities at a prespecified specificity p₀, compare partial areas under the curve (pAUC) and construct simultaneous confidence bands for D(p).

3. RECEIVER OPERATING CHARACTERISTIC CURVE ANALYSIS

In this section we apply the theory developed in the previous section to derive a number of inferential procedures for comparing ROC curves. Specifically, we develop statistical tests for comparing weighted areas under ROC curves, construct confidence bands for the difference of two ROC curves, estimate the set of specificities at which one test is more sensitive than the other, and discuss multiple comparison procedures for more than two diagnostic markers.

3.1 Comparing the Weighted Areas Under Receiving Operating Characteristic Curves

Let $\mathrm{\Delta }={\int }_0^{1}D(p)dw(p)$ be the difference between the weighted areas under the two ROC curves, where w(p) is a prespecified weight function. Note that Δ is the difference between two sensitivities for a fixed specificity p₀ if w(p) is a degenerate distribution function at p₀, the difference between the total AUCs if w(p) is the uniform distribution function on [0, 1], and the difference between the pAUCs if w(p) is the uniform distribution function on [p₁, p₂] ⊂ [0, 1] multiplied by p₂ − p₁.

Let $\widehat{\mathrm{\Delta }}={\int }_0^1\widehat{D}(p)dw(p)$. From Section 2, we see that the distribution of $\sqrt{n}(\widehat{\mathrm{\Delta }}-\mathrm{\Delta })$ can be approximated by the conditional distribution of $\sqrt{n}({\mathrm{\Delta }}^{\ast }-\widehat{\mathrm{\Delta }})$ given data. Therefore, a confidence interval for Δ can be computed as follows:

Step 1. Generate K(say K = 1,000) independent standard normal samples ${\eta }_1^{(k)},\dots ,{\eta }_n^{(k)}$, k = 1, …, K. For each k, compute ${\mathrm{\Delta }}_k^{\ast }={\int }_0^1{D}_k^{\ast }(p)dw(p)$, based on ${\eta }_1^{(k)},\dots ,{\eta }_n^{(k)}$. Let S_Δ be the sample standard deviation of { ${\mathrm{\Delta }}_k^{\ast }-\widehat{\mathrm{\Delta }}$, k = 1, …, K}.

Step 2. A 100(1 − α)% confidence interval for Δ is given by

$$\widehat{\mathrm{\Delta }}\pm z_{1-\alpha /2}{S}_{\mathrm{\Delta }},$$

where z_{1 − α/2} is the 1 − α/2 percentile of the standard normal distribution.

One-sided confidence intervals and hypothesis tests for Δ can be obtained similarly.

3.2 Confidence Bands for D(p) = ROC⁽¹⁾(p) − ROC⁽²⁾(p)

The following theorem is a direct consequence of Theorem 2 and Corollary 2.

Theorem 3

For 0 < α < 1 and [p₁, p₂] ⊂ [0, 1], let C_α be determined by

$$\underset{n\to \infty }{lim}P\left\{\underset{p\in [p_1,p_2]}{sup}\left|\frac{D^{\ast }(p)-\widehat{D}(p)}{S_D(p)}\right|\le C_{\alpha }\mid \mathit{data}\right\}=1-\alpha ,$$

where $S_D^2(p)$ is a consistent variance estimate of D̂(p). Then, as n → ∞,

$$\begin{array}{l}P\{\widehat{D}(p)-C_{\alpha }{S}_D(p)\le D(p)\le \widehat{D}(p)+C_{\alpha }{S}_D(p),\\ \text{for}\text{all}p\in [p_1,p_2]\}\to 1-\alpha .\end{array}$$

The confidence band can be computed as follows:

Step 1. Generate K₁(say K₁ = 500) independent standard normal samples ${\eta }_1^{(k)},\dots ,{\eta }_n^{(k)}$, k = 1, …, K₁. For each k, compute $D_k^{\ast }(p)$, based on ${\eta }_1^{(k)},\dots ,{\eta }_n^{(k)}$. Let S_D(p) be the sample standard deviation of { $D_k^{\ast }(p)-\widehat{D}(p)$, k = 1, …, K₁}

Step 2. Generate another K₂(say K₂ = 500) independent realizations $D_1^{\ast }(p),\dots ,D_{K_2}^{\ast }(p)$. Compute C_α as the 100(1 − α)th percentile of ${sup}_{p_1\le p\le p_2}\mid (D_1^{\ast }(p)-\widehat{D}(p))/S_D(p)\mid ,\dots ,{sup}_{p_1\le p\le p_2}\mid (D_{K_2}^{\ast }(p)-\widehat{D}(p))/S_D(p)\mid$.

Step 3. A 100(1 − α)% simultaneous confidence band for D(p) over [p₁, p₂] is

$$(\widehat{D}(p)-n^{-1/2}{C}_{\alpha }{S}_D(p),\widehat{D}(p)+n^{-1/2}{C}_{\alpha }{S}_D(p)),p\in [p_1,p_2].$$

3.3 Determine the Set of Specificities With Differential Sensitivity

All of the preceding results are focused on comparisons of ROC curves for a prespecified set of specificities. In practice, it often is of interest to find the set of specificities at which one test is more sensitive than the other. Specifically, let R = {p ∈ [0, 1]: ROC₁(p) > ROC₂(p)}. We wish to find an estimated set R̂ such that P(R̂ ⊂ R) = 1 − α.

Note that R is an unknown set of specificities, not a parameter. Next we outline a procedure for estimating R based on an idea of Berger and Boos (1999) and Berger and Hsu (1996) who studied the problem of estimating the onset and duration of a treatment effect. Our procedure is as follows:

Step 1. For each p, conduct a one-sided level α/2 test of H_0p: D(p) = 0 versus H_ap: D(p) > 0, as discussed in Section 3.1.

Step 2. Let p₀ be an a priori fixed starting value. If H_0p0 is accepted, then no confidence statement is made. If H_0p0 is rejected, then test sequentially downward from p₀, and let P₁ be the first p for which the hypothesis H_0p is accepted. Also test sequentially upward from p₀, and let P₂ be the first p for which the hypothesis H_0p is accepted. Consequently, R̂ =[P₁, P₂] is the largest interval containing p₀ for which H_0p is rejected for all p ∈ [P₁, P₂].

Theorem 4

Let R̂ = [P₁, P₂] be defined by the foregoing algorithm. Then, as n → ∞,

$$\begin{array}{l}P(\widehat{R}\subset R)=P(RO{C}^{(1)}(p)>RO{C}^{(2)}(p)\text{for}\text{all}{P}_1\le p\le P_2)\\ \ge 1-\alpha .\end{array}$$

The proof of this theorem is essentially the same as that of Berger and Boos (1999) and thus is omitted. Note that in Step 1, a one-sided hypothesis is tested at level α/2 instead of level α; this is necessary to achieve the overall confidence level of 1 − α for R̂. As argued by Berger and Boos (1999), the starting value p₀ should be chosen beforehand and in a region likely to produce significant results. A statistical approach that requires less knowledge is to repeat the method at k different starting points using level α/k for each one.

3.4 Multiple Comparisons of More Than Two Diagnostic Tests

In this section we illustrate how to extend our method to multiple comparisons of more than two ROC curves. Without loss of generality, we consider three diagnostic tests. Similar to Theorem 1, it can be shown that

$$\sqrt{n}\left(\begin{array}{c}{\widehat{D}}^{(12)}(p)-D^{(12)}(p)\\ {\widehat{D}}^{(13)}(p)-D^{(13)}(p)\\ {\widehat{D}}^{(23)}(p)-D^{(23)}(p)\end{array}\right)\stackrel{d}{\to }\left(\begin{array}{c}{U}^{(12)}(p)\\ U^{(13)}(p)\\ U^{(23)}(p)\end{array}\right),$$

where D^(ij)(p) = ROC^(j)(p) − ROC⁽ⁱ⁾(p), D̂^(ij)(p) is the sample estimate of D^(ij)(p), U^(ij)(p) = Z⁽ⁱ⁾(1 − p) − Z^(j)(1 − p), and Z^(v)(p) is as defined in Theorem 1 for v = 1, 2, 3.

As in Section 2.5, we construct D^(12)*(p), D^(13)*(p), and D^(23)*(p) so that the joint distribution of (U⁽¹²⁾, U⁽¹³⁾, U⁽²³⁾) is approximated by that of (U^(12)*, U^(13)*, U^(23)*) given the data, where U^(ij2)*(p) = D^(ij)*(p) − D̂^(ij)(p). This allows us to perform various multiple comparisons. The following algorithm can be used to construct joint confidence intervals for three pairwise comparisons of weighted areas under the curve: Δ⁽¹²⁾, Δ⁽¹³⁾, and Δ⁽²³⁾, where ${\mathrm{\Delta }}^{(ij)}={\int }_0^1{D}^{(ij)}(p)dw(p)$:

Step 1. Generate K₁(say K₁ = 500) realizations of Z^(12)* ≡ Δ^(12)* − Δ̂⁽¹²⁾, Z^(13)* ≡ Δ^(13)* − Δ̂⁽¹³⁾, and Z^(23)* ≡ Δ^(23)* − Δ̂⁽²³⁾ by generating K₁ independent standard normal samples. Compute their sample standard deviations S_Δ⁽¹²⁾, S_Δ⁽¹³⁾, and S_Δ⁽²³⁾

Step 2. Generate another K₂(say K₂ = 500) independent realizations of Z^(12)*, Z^(13)*, and Z^(23)* and let A_k be the maximum of $\mid \frac{Z^{(12)\ast }}{S_{{\mathrm{\Delta }}^{(12)}}}\mid ,\mid \frac{Z^{(13)\ast }}{S_{{\mathrm{\Delta }}^{(13)}}}\mid$, and $\mid \frac{Z^{(23)\ast }}{S_{{\mathrm{\Delta }}^{(23)}}}\mid$ for the kth realization, k = 1, …, K₂.

Step 3. Let C_α be the 100(1 − α)th percentile of A₁, …, AK₂. The 100(1 − α)% joint confidence intervals for Δ⁽¹²⁾, Δ⁽¹³⁾, and Δ⁽²³⁾ are given by

$$\begin{array}{l}{\widehat{\mathrm{\Delta }}}^{(12)}\pm C_{\alpha }{S}_{{\mathrm{\Delta }}^{(12)}},{\widehat{\mathrm{\Delta }}}^{(13)}\pm C_{\alpha }{S}_{{\mathrm{\Delta }}^{(13)}},\text{and}\\ {\widehat{\mathrm{\Delta }}}^{(23)}\pm C_{\alpha }{S}_{{\mathrm{\Delta }}^{(23)}}.\end{array}$$

Other multiple inferences, such as multiple confidence bands, can be obtained similarly.

4. SIMULATIONS

In this section we report a simulation study conducted to evaluate the finite-sample performance of our methods. We also study the consequence of ignoring the within-subject correlations.

We generated repeated measurements using a setting similar to Emir et al. (2000). A failure time was generated for each subject from an exponential distribution with an expected value of 4. A subject was classified as “healthy” before the failure and as “diseased” after the failure. We then generated ${\mathbf{X}}^{(1)}={\mathbf{Y}}_1\sqrt{\lambda }+{\mathbf{Y}}_2\sqrt{(1-\lambda )}$ and ${\mathbf{X}}^{(2)}={\mathbf{Y}}_1\sqrt{\lambda }+{\mathbf{Y}}_3\sqrt{(1-\lambda )}$, where Y_i = (Y_i1, …, Y_i4)′, i = 1, 2, 3, are iid multivariate normal random vectors with mean 0 and cov(Y_ij, Y_ik) = ρ^{|j − k|}, for j, k = 1, 2, 3, 4. The value for subject i for marker v at visit j is $X_{ij}^{(v)}$ if the subject is “healthy” at the jth visit and $X_{ij}^{(v)}+1$ if he or she is “diseased.” Note that λ and ρ measure the between-marker and within-marker correlations.

Table 1 reports the achieved significance level of our test for the equality of pAUCs over three intervals (.1,.3), (.1,.5), and (.05,.95) for various sample sizes and between-marker and within-marker correlations. Each entry is based on 500 simulations. It is observed that the achieved significance level agrees with the nominal level fairly well even for small samples (n_D = n_H = 30).

Table 1.

Achieved significance level of our method for two-sided test of equality of partial areas under the curves (pAUC_{(p1, p2)}) (nominal level =.05)

		Achieved significance level
(ρ, λ)	(nD, nH)	pAUC(.05,.35)	pAUC(.05,.55)	pAUC(.05,.95)
(0, 0)	(30, 30)	.07	.07	.06
	(50, 50)	.06	.05	.05
	(100, 100)	.05	.05	.06
(.25,.5)	(30, 30)	.05	.05	.04
	(50, 50)	.04	.05	.05
	(100, 100)	.04	.06	.04
(.50,.75)	(30, 30)	.05	.05	.06
	(50, 50)	.05	.04	.04
	(100, 100)	.05	.04	.04
(.75,.75)	(30, 30)	.05	.05	.06
	(50, 50)	.04	.04	.04
	(100, 100)	.04	.05	.05

NOTE: ρ and λ are measures of the within-subject and between-marker correlations, and (n_D, n_H) are the number of clusters for diseased and healthy subjects.

Next, we illustrate the consequence of ignoring the within-subject correlations. Table 2 reports the achieved significance levels of our method (designated method 1) compared with the method that treats the observations within each cluster as independent (designated method 2) for testing the equality of the AUCs. We set the between-marker correlation λ =.5 and vary the within-marker correlation ρ from.05,.75 to.99. It can be seen that the achieved significance level of our method is always close to the nominal level.05, whereas ignoring the correlations within the cluster can lead to an unreasonably high probability of type I error (e.g.,.39) as the within-subject correlation ρ and cluster size grow. Therefore, ignoring the correlations within the cluster may lead to seriously biased conclusions.

Table 2.

Achieved significance level of the proposed method (method 1) versus the method ignoring clustering (method 2) for testing the equality of the total areas under the two ROC curves [nominal level =.05, (n_D, n_H) = (100, 100), λ =.5]

		Achieved significance level
ρ	Cluster size	Method 1	Method 2
.05	4	.05	.04
	8	.06	.05
.75	4	.05	.13
	8	.06	.26
.99	4	.05	.22
	8	.04	.39

NOTE: ρ is a measure of within-subject correlation, and (n_D, n_H) are the number of diseased and healthy subjects.

5. EXAMPLES

5.1 Detection of Glaucomatous Deterioration

A visual field test is a technique for measuring an individual’s entire scope of vision. It maps the visual fields of each eye individually. Longitudinal visual field image data can be used for early diagnosis of glaucomatous progression. But reliable detection remains one of the most difficult challenges for clinicians, due to the complex structure and high level of noise in the longitudinal visual field image data. Together with researchers at UCLA’s Jules Stein Eye Institute, Jiang (2005) developed some outlier statistics to use as a diagnostic marker for detecting visual field deterioration in glaucoma patients based on Bayesian hierarchical modeling. Here we illustrate how to use our methods to compare the diagnostic power of different models in discriminating between stable and progressive eyes. Our data set comprises a visual field series of 188 eyes of 171 patients over 8 years of follow-up study; it is independent of the training sample used by Jiang (2005) for model building. Apparently these are clustered data, because some data are from both eyes of the same patient. A paired design is appropriate for ROC analysis, because both models are applied to the same set of eyes.

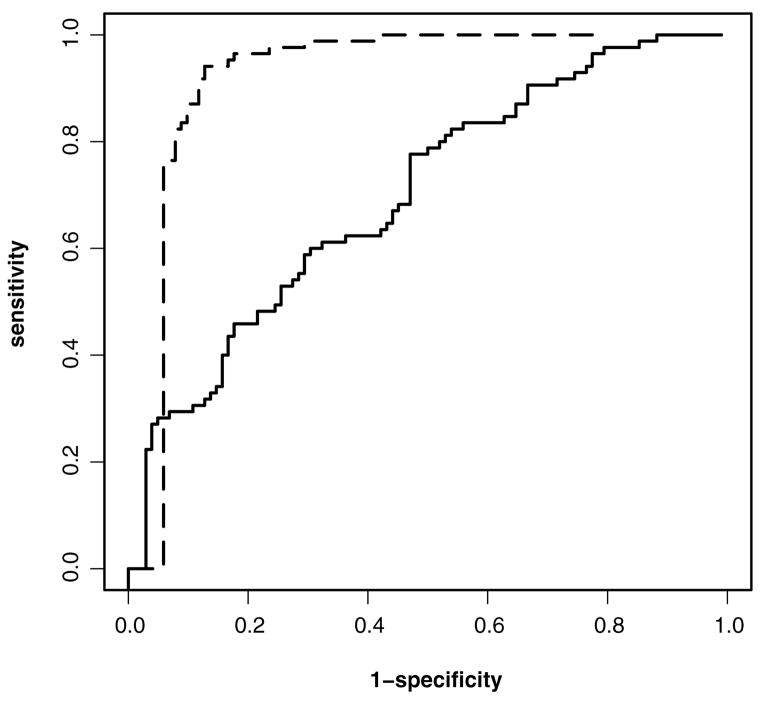
Figure 1 depicts the empirical ROC curves of the diagnostic markers based on two candidate models, referred to as models 1 and 2 here, which correspond to models 1 and 11 of Jiang (2005, p. 45). Figure 1 shows that the diagnostic marker based on model 2 has better power than model 1 for detecting glaucomatous progression. We performed a test for the equality of the total AUCs using the method in Section 3.1; the two-sided p value was.024, confirming a significant difference between the two diagnostic markers.

Figure 1.

Empirical ROC curves of two diagnostic markers for detecting glaucoma deterioration (——, model 2;— —, model 1).

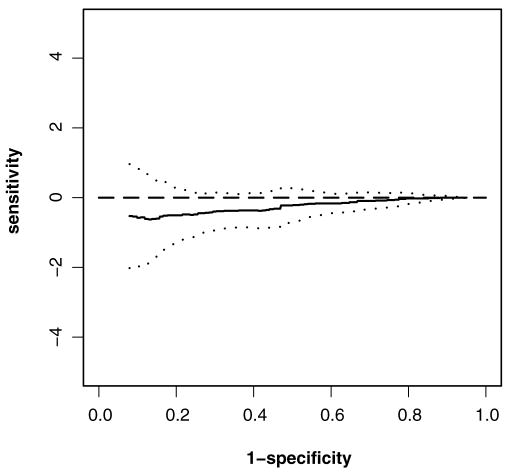
Figure 2 shows the confidence band for the difference function of the ROC curves between models 1 and 2 over the specificities.1–.9. Because the span of the confidence band over the specificities is too broad, it is too conservative to detect any significant difference.

Figure 2.

95% confidence band for the difference of the ROC curves between models 1 and 2 from.1 to.9 for the glaucoma data (——, difference; · · · ·, lower bound; · · · ·, upper bound).

Finally, we applied the method in Section 3.3 to estimate the range of specificities at which the diagnostic marker based on model 2 is more sensitive than that based on model 1. We had R̂ = [.34,.92]; therefore, with 95% confidence, model 2 had a higher sensitivity than model 1 at specificities between.34 and.92.

5.2 Acoustic Startle Response Data

The acoustic startle response in human studies is quantified by the startle blink response to a startling stimulus. It is typically measured and summarized by the orbicularis oculi electromyogram (ooEMG), a time series plot. But high variabilities make it difficult to evaluate the ooEMG and distinguish a normal response (healthy) from no response (diseased).

In this example we consider four diagnostic markers developed by researchers at UCLA’s Semel Institute for Neuroscience: the peak magnitude after the stimulus, the duration of the maximum magnitude above a certain threshold, the area under the maximum magnitude, and the ratio representing the amount exceeding a threshold. The data set comprises 37 participants from a total of 229 experiments. The maximum number of repeated experiments per person is 16. A detailed description of the study has been given by Waters and Ornitz (2008). Results of the same subject from different experiments are considered to be highly correlated; thus we adopt the clustered data setting. This is also a paired design or, more accurately, a block design, because each ooEMG yields values for all four markers.

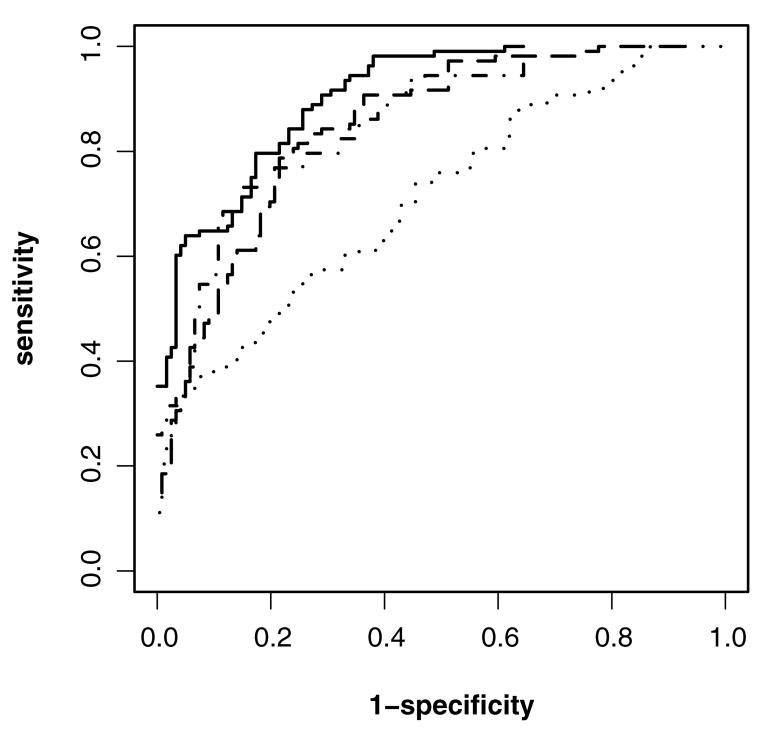
Figure 3 displays the empirical ROC curves for the four markers. We can see that ratio appears to be the best and peak the worst. We used the multiple comparison method outlined in Section 3.5 to construct 95% joint confidence intervals for six pairwise differences of the pAUC, pAUC_.05,.95, for these four markers. The results, summarized in Table 3, show that area, ratio, and duration are all significantly better than peak. No significant difference is found among area, ratio, and duration.

Figure 3.

Empirical ROC curves of four diagnostic markers for the acoustic startle response data (——, peak; · – ·, area; · · · ·, ratio; · – ·, duration).

Table 3.

Simultaneous 95% confidence intervals for the pairwise differences of pAUC_(.05,.95) of four tests for the acoustic response data

	Area	Ratio	Duration
Peak	(.03,.33)	(.05,.35)	(.01,.30)
Area		(−.03,.08)	(−.10,.06)
Ratio			(−.12,.03)

NOTE: pAUC_peak =.66, pAUC_area =.84, pAUC_ratio =.86, pAUC_duration =.81, and C_α = 2.62.

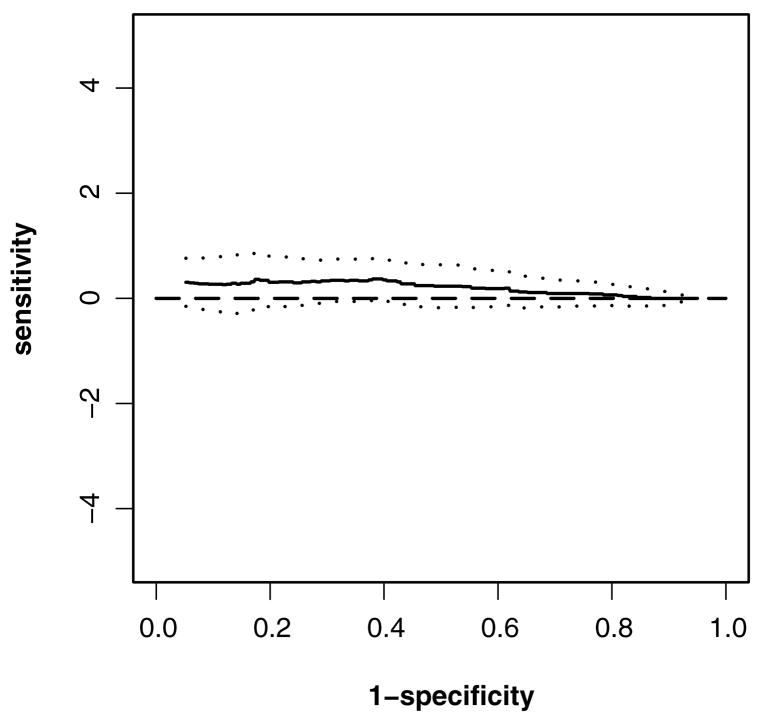
Figure 4 gives the 95% confidence band for the difference of ROC curves between the peak and area over specificities of.1–.9. The confidence bands again seem to be conservative.

Figure 4.

95% confidence band of the difference of the ROC curves between peak and area from.1 to.9 for the acoustic startle response data (——, difference; · · · ·, lower bound; · · · ·, upper bound).

We also applied the method in Section 3.3 to estimate the set of specificities at which area is more sensitive than peak. We found R̂ = [.38,.95]; therefore, with 95% confidence, area has a higher sensitivity than peak at specificities between.38 and.95.

6. DISCUSSION

The Monte Carlo resampling method is commonly used to approximate an empirical process, such as the empirical distribution process, that can be represented as the sum of iid random variables. But this article is the first to rigorously demonstrate that this method also can be extended to approximate quantile processes and ROC curves without the need to estimate density functions for a paired design. Clustered observations also are allowed. The result allows us to approximate the distribution of any continuous functional of correlated empirical ROC curves and thus provides a unified approach to the nonparametric comparison of ROC curves. Our method demonstrates satisfactory performance for both large and relatively small samples in simulations. We have developed software to implement the proposed procedures using R; this software can be downloaded at http://roc.cluster.googlepages.com/.

Note that much effort has been directed at approximating a quantile process without involving density estimation. For example, Li, Hollander, McKeague, and Yang (1996a) developed a nonparametric likelihood ratio method; Doss and Gill (1992) studied the bootstrap method, which was later adapted for ROC analysis by Li et al. (1996b); and Keaney and Wei (1994) introduced a Monte Carlo method for estimating a median survival time. But all of the earlier methods consider only iid observations and thus do not account for within-subject correlation for clustered data.

An alternative approach is to use the bootstrap method to approximate ROC processes by resampling the independent subjects. Although the bootstrap method has been commonly suggested in practice and is simple to use in principle, its consistency for the paired design with clustered data has not been established in the ROC analysis literature. For the upaired case where different markers are performed on different sets of subjects, Li et al. (1996b, 1999) showed that the bootstrap method is consistent in a sense that the bootstrapped ROC process has the same limiting process as the empirical ROC process. Extending their result to the paired design with clustered data does not appear to be trivial. Future work is needed to develop a theoretical justification for the bootstrap method for clustered data under the paired design.

APPENDIX: PROOFS

Proof of Lemma 1

Note that

$$\sqrt{n}\left(\begin{array}{l}{\widehat{F}}^{(1)}(t)-F^{(1)}(t)\hfill \\ {\widehat{F}}^{(2)}(t)-F^{(2)}(t)\hfill \\ {\widehat{G}}^{(1)}(t)-G^{(1)}(t)\hfill \\ {\widehat{G}}^{(2)}(t)-G^{(2)}(t)\hfill \end{array}\right)=\frac{1}{\sqrt{n}}\sum _{i=1}^n{\mathbf{V}}_i(t),$$

where

$${\mathbf{V}}_i(t)=\left(\begin{array}{l}\frac{n}{M^{(1)}}{\sum }_{j=1}^{m_i^{(1)}}\{I(X_{ij}^{(1)}\le t)-F^{(1)}(t)\}\hfill \\ \frac{n}{M^{(2)}}{\sum }_{j=1}^{m_i^{(2)}}\{I(X_{ij}^{(2)}\le t)-F^{(2)}(t)\}\hfill \\ \frac{n}{N^{(1)}}{\sum }_{j=1}^{n_i^{(1)}}\{I(X_{ij}^{(1)}\le t)-G^{(1)}(t)\}\hfill \\ \frac{n}{N^{(2)}}{\sum }_{j=1}^{n_i^{(2)}}\{I(X_{ij}^{(2)}\le t)-G^{(2)}(t)\}\hfill \end{array}\right),i=1,\dots ,n,$$

are independent random vectors. Applying the Cramer–Rao device and the Lyapunov central limit theorem, and following along the lines of the approach of Billingsley (1999) for empirical distribution processes, it can be shown that

$$\frac{1}{\sqrt{n}}\sum _{i=1}^n{\mathbf{V}}_i(t)\stackrel{d}{\to }\mathbf{W}(t)\text{in}D{(\mathbb{R})}^4,$$ (A.1)

where W(t) =(W_F⁽¹⁾(t), W_F⁽²⁾(t), W_G⁽¹⁾(t), W_G⁽²⁾(t))′ is a Gaussian process in D(ℝ)⁴ whose variance–covariance function is the limit of $\frac{1}{n}{\sum }_{i=1}^{n}cov({\mathbf{V}}_i(t),{\mathbf{V}}_i(t))$ as n → ∞.

Proof of Theorem 1

By (A.1), the compact differentiability of the inverse function and the functional delta method (see, e.g., Andersen et al. 1993), we have

$$\sqrt{n}\left(\begin{array}{c}{\widehat{F^{(1)}}}^{-1}-F^{{(1)}^{-1}}\\ {\widehat{F^{(2)}}}^{-1}-F^{{(2)}^{-1}}\\ \widehat{G^{(1)}}-G^{(1)}\\ \widehat{G^{(2)}}-G^{(2)}\end{array}\right)\stackrel{d}{\to }\left(\begin{array}{c}\frac{{\stackrel{\sim }{W}}_{F^{(1)}}(F^{{(1)}^{-1}})}{F^{(1{)}^{\prime }}(F^{{(1)}^{-1}})}\\ \frac{{\stackrel{\sim }{W}}_{F^{(2)}}(F^{{(2)}^{-1}})}{F^{(2{)}^{\prime }}(F^{{(2)}^{-1}})}\\ {\stackrel{\sim }{W}}_{G^{(1)}}\\ {\stackrel{\sim }{W}}_{G^{(2)}}\end{array}\right)$$ (A.2)

in D[a, b] × D[a, b] × D[F⁽¹⁾⁻¹(a), F⁽¹⁾⁻¹(b)] × D[F⁽²⁾⁻¹(a), F⁽²⁾⁻¹(b)], as n → ∞. This, along with lemma A.1 of Li et al. (1996a,b) and the functional delta method, implies that

$$\sqrt{n}\left(\begin{array}{l}{\widehat{G}}^{(1)}({\widehat{F^{(1)}}}^{-1}(p))-G^{(1)}(F^{{(1)}^{-1}}(p))\hfill \\ {\widehat{G}}^{(2)}({\widehat{F^{(2)}}}^{-1}(p))-G^{(2)}(F^{{(2)}^{-1}}(p))\hfill \end{array}\right)\stackrel{d}{\to }\left(\begin{array}{l}{Z}^{(1)}(p)\hfill \\ Z^{(2)}(p)\hfill \end{array}\right)$$ (A.3)

in D[a, b] where Z^(v), v = 1, 2 are as defined in Theorem 1.

Finally, combining (A.3) and the continuous mapping theorem proves the theorem.

Proof of Theorem 2

First, note that

$$\begin{array}{l}\sqrt{n}\{D^{\ast }(p)-\widehat{D}(p)\}=\sqrt{n}\{Q^{(2)\ast }(1-p)-{\widehat{Q}}^{(2)}(1-p)\}\\ -\sqrt{n}\{Q^{(1)\ast }(1-p)-{\widehat{Q}}^{(1)}(1-p)\},\end{array}$$

where for v = 1, 2, Q^(v)(p) = G^(v)(F^(v)−1(p)), Q̂^(v)(p) = Ĝ^(v)(F̂^(v)−1(p)), and Q^(v)*(p) = ζ^(v)*(ξ^(v)(p)) are as defined before Theorem 2. Moreover, by (A.3),

$$\sqrt{n}\left(\begin{array}{l}{\widehat{Q}}^{(1)}(p)-Q^{(1)}(p)\hfill \\ {\widehat{Q}}^{(2)}(p)-Q^{(2)}(p)\hfill \end{array}\right)\stackrel{d}{\to }\left(\begin{array}{l}{Z}^{(1)}(p)\hfill \\ Z^{(2)}(p)\hfill \end{array}\right)\text{in}D[a,b].$$ (A.4)

Thus, to prove Theorem 2, it suffices to show that for every subsequence {n_j} of {n}, there is a further subsequence {m_k} ⊂ {n_j} such that, conditional on the data,

$$\sqrt{n}\left(\begin{array}{l}{Q}^{\ast (1)}(p)-{\widehat{Q}}^{(1)}(p)\hfill \\ Q^{\ast (2)}(p)-{\widehat{Q}}^{(2)}(p)\hfill \end{array}\right)\stackrel{d}{\to }\left(\begin{array}{l}{Z}^{(1)}(p)\hfill \\ Z^{(2)}(p)\hfill \end{array}\right)\text{in}D[q_1,q_2],$$ (A.5)

along the subsequence {m_k} for almost all data realizations and a < q₁ < q₂ < b.

Here we prove only the convergence of a marginal process in (A.5), because the joint convergence is derived along the same lines. For simplicity, we also omit the superscript.

We first show that for any sequence δ_n(p) satisfying sup_{p∈ [q1,q2]} |δ_n(p)| = O(n^−1/2),

$$\underset{p\in [q_1,q_2]}{sup}\mid \sqrt{n}\{\widehat{Q}(p+{\delta }_n(p))-\widehat{Q}(p)\}+Q^{\prime }(p)\sqrt{n}{\delta }_n(p)\mid \stackrel{P}{\to }0.$$ (A.6)

Let $Z_n(p)=\sqrt{n}(\widehat{Q}(p)-Q(p))$. Then, by (A.4), $Z_n\stackrel{d}{\to }Z$ in D[a, b] as n → ∞. By the Skorohod–Dudley–Wichura representation theorem (cf. thm. 4 of Shorack and Wellner 1984), there exists a sequence $Z_n^{†}$, Z^† of random elements in D[a, b], defined in a common probability space, such that $Z_n^{†}\stackrel{d}{=}{Z}_n,Z^{†}\stackrel{d}{=}Z$, and $Z_n^{†}\stackrel{\parallel ·\mid {\mid }_{\infty }}{\to }{Z}^{†}$ almost surely in D[a, b] as n → ∞, where Z^† has continuous sample paths on [a, b] and ||·||_∞ represents the supremum norm. Because the sample paths of Z^† are continuous on a compact interval [a, b], they also are uniformly continuous on [a, b]. Thus

$$\begin{array}{l}\underset{p\in [q_1,q_2]}{sup}\mid Z_n^{†}(p+{\delta }_n(p))-Z_n^{†}(p)\mid \\ \le \underset{p\in [q_1,q_2]}{sup}\mid Z_n^{†}(p)-Z^{†}(p)\mid \\ +\underset{p\in [q_1,q_2]}{sup}\mid Z^{†}(p+{\delta }_n(p))-Z^{†}(p)\mid \\ +\underset{p\in [q_1,q_2]}{sup}\mid Z_n^{†}(p+{\delta }_n(p))-Z^{†}(p+{\delta }_n(p))\mid \\ \stackrel{a.s.}{\to }0,\end{array}$$ (A.7)

where the first and third terms converge to 0 because $Z_n^{†}\stackrel{\parallel ·\mid {\mid }_{\infty }}{\to }{Z}^{†}$ almost surely in D[a, b] and the second term goes to 0 because Z^† has uniformly continuous sample paths on [a, b]. Because $Z_n^{†}\stackrel{d}{=}{Z}_n$, (A.7) implies that as n → ∞,

$$\underset{p\in [q_1,q_2]}{sup}\mid Z_n(p+{\delta }_n(p))-Z_n(p)\mid \stackrel{P}{\to }0.$$ (A.8)

Moreover, by the mean value theorem, we have that $\sqrt{n}\{Q(p+{\delta }_n(p))-Q(p)\}=Q^{\prime }({\delta }_n^{\ast })\sqrt{n}{\delta }_n(p)$, where ${\delta }_n^{\ast }$ lies between p and p + δ_n(p). This, together with the fact that Q′(p) is uniformly continuous on a compact interval, implies that as n → ∞,

$$\underset{p\in [q_1,q_2]}{sup}\mid \sqrt{n}\{Q(p+{\delta }_n(p))-Q(p)\}-Q^{\prime }(p)\sqrt{n}{\delta }_n(p)\mid \to 0.$$ (A.9)

Combining (A.8) and (A.9) proves (A.6).

For the foregoing sequence δ_n(p), we also have

$$\begin{array}{l}\underset{p\in [q_1,q_2]}{sup}\mid {\widehat{F}}^{-1}(p+{\delta }_n(p))-F^{-1}(p)\mid \\ \le \underset{p\in [q_1,q_2]}{sup}\mid {\widehat{F}}^{-1}(p+{\delta }_n(p))-F^{-1}(p+{\delta }_n(p))\mid \\ +\underset{p\in [q_1,q_2]}{sup}\mid F^{-1}(p+{\delta }_n(p))-F^{-1}(p)\mid \\ \stackrel{P}{\to }0,\end{array}$$ (A.10)

where the convergence of the first term follows from the uniform consistency of F̂⁻¹ on [a, b] and the second term goes to 0 because F⁻¹ is uniformly continuous on [q₁, q₂].

By (A.6) and (A.10), for any subsequence {n_j} of {n}, there is a further subsequence {m_k} ⊂ {n_j} and a subsample space Ω₀ ⊂ Ω such that P(Ω₀) = 1 and, for every ω ∈ Ω₀,

$$\underset{p\in [q_1,q_2]}{sup}\mid \sqrt{n}\{\widehat{Q}(p+{\delta }_n(p))-\widehat{Q}(p)\}+Q^{\prime }(p)\sqrt{n}{\delta }_n(p)\mid (\omega )\to 0$$ (A.11)

and

$$\underset{p\in [q_1,q_2]}{sup}\mid {\widehat{F}}^{-1}(p+{\delta }_n(p))-F^{-1}(p)\mid (\omega )\to 0$$ (A.12)

along the subsequence {m_k}.

Next, we note from direct calculations that

$$\begin{array}{l}\sqrt{n}\{Q^{\ast }(p)-\widehat{Q}(p)\}=\sqrt{n}\{\widehat{Q}(p+n^{-1/2}{W}_F^{\ast }({\widehat{F}}^{-1}(p)))-\widehat{Q}(p)\}\\ -W_G^{\ast }({\widehat{F}}^{-1}(p+n^{-1/2}{W}_F^{\ast }({\widehat{F}}^{-1}(p)))).\end{array}$$

By (5) and the Korohod–Dudley–Wichura representation theorem (cf. thm. 4 of Shorack and Wellner 1984), there exists a sequence $(W_F^{\ast †},W_G^{\ast †}),(W_F^{†},W_G^{†})$ of random elements in D(ℝ) defined in a common probability space such that, conditional on the data,

$$(W_F^{\ast †},W_G^{\ast †})\stackrel{d}{=}(W_F^{\ast },W_G^{\ast }),(W_F^{†},W_G^{†})\stackrel{d}{=}(W_F,W_G),$$ (A.13)

and

$$(W_F^{\ast †},W_G^{\ast †})\stackrel{\parallel ·\mid {\mid }_{\infty }}{\to }(W_F^{†},W_G^{†})\text{almost}\text{surely}\text{in}D(\mathbb{R})$$ (A.14)

as n → ∞ for almost all data realizations, where $W_F^{†}$ and $W_G^{†}$ have continuous sample paths and ||·||_∞ is the supremum norm. Thus, conditional on the observed data,

$$\begin{array}{l}\underset{q_1\le p\le q_2}{sup}\mid W_F^{\ast †}({\widehat{F}}^{-1}(p))-W_F^{†}(F^{-1}(p))\mid \\ \le \underset{q_1\le p\le q_2}{sup}\mid W_F^{\ast †}({\widehat{F}}^{-1}(p))-W_F^{†}({\widehat{F}}^{-1}(p))\mid \\ +\underset{q_1\le p\le q_2}{sup}\mid W_F^{†}({\widehat{F}}^{-1}(p))-W_F^{†}(F^{-1}(p))\mid \\ \stackrel{a.s.}{\to }0,\end{array}$$ (A.15)

as n → ∞ for almost all data realizations, where the first term on the right side of the inequality converges to 0 because $W_F^{\ast †}\stackrel{\parallel ·\mid {\mid }_{\infty }}{\to }{W}_F^{†}$ almost surely in D(ℝ), and the second term goes to 0 because of the uniform consistency of F̂⁻¹ and the uniform continuity of $W_F^{†}(t)$ on any compact interval.

Finally, by combining (A.11)–(A.15), we can conclude that for every subsequence {n_j} of {n}, there is a further subsequence {m_k} ⊂ {n_j} such that, conditional on the data, $\sqrt{n}(Q^{\ast }-\widehat{Q})\stackrel{d}{\to }Z$ in D[_{q1, q2}], along the subsequence {m_k} for almost all data realizations and a < q₁ < q₂ < b. This concludes Theorem 2, as argued at the beginning of the proof.

Proof of Corollary 1

By Theorem 2 and the continuity of T(·), for every subsequence {n_j} of {n} there is another subsequence {m_k} ⊂ {n_j} such that, conditional on the data, $T(\sqrt{n}(D^{\ast }-\widehat{D}))\stackrel{d}{\to }T(U)$ along the subsequence {m_k}, for almost all data realizations.

We first show that as n → ∞,

$$H_n^{\ast }(t)\to H(t)\text{for}\text{every}t,$$ (A.16)

for almost all data realizations. This can be proved by contradiction. If for some t, $H_n^{\ast }(t)$ does not converge to H(t), then there exist an ε > 0 and a subsequence {n_j} of {n} such that $\mid H_{n_j}^{\ast }(t)-H(t)\mid \ge \epsilon >0$ for all n_j. This implies that no further subsequence of H_nj(t) converges to H(t), which contradicts the result in the first paragraph; thus (A.16) holds. The uniform convergence $H_n^{\ast }(t)$ to H(t) in t follows from (A.16) and the fact the $H_n^{\ast }(t)$ and H(t) are continuous nondecreasing distribution functions.