Partially Linear Models with Missing Response Variables and Error-prone Covariates

Summary

We consider partially linear models of the form Y = X^Tβ + ν(Z) + ε when the response variable Y is sometimes missing with missingness probability π depending on (X, Z), and the covariate X is measured with error, where ν(z) is an unspecified smooth function. The missingness structure is therefore missing not at random, rather than the usual missing at random. We propose a class of semiparametric estimators for the parameter of interest β, as well as for the population mean E(Y). The resulting estimators are shown to be consistent and asymptotically normal under general assumptions. To construct a confidence region for β, we also propose an empirical-likelihood-based statistic, which is shown to have a chi-squared distribution asymptotically. The proposed methods are applied to an AIDS clinical trial dataset. A simulation study is also reported.

1 Introduction

The partially linear model assumes that the response variable Y depends on variable X in a linear way but is related to another independent variable Z in an unspecified form:

$$Y=X^{\text{T}}\beta +\nu (Z)+\epsilon ,$$ (1.1)

where X is a p-vector covariate, Z is a scalar covariate, the function ν(·) is unknown, and the model error ε has mean zero conditional on (X, Z).

There is a substantial literature on kernel-based methods for partially linear models and their generalisations; see for example Engle et al. (1986), Speckman (1988), Robinson (1988), Severini & Staniswalis (1994), Zeger & Diggle (1994), Opsomer & Ruppert (1999) and Härdle et al. (2000), among many others. Liang et al. (1999) considered model (1.1) with error-prone X. Recently, missing-data issues have been considered, with Liang, et al. (2004) considering the case in which X in (1.1) is missing at random, while in Wang et al. (2004) the response Y is missing at random.

In this paper, we consider the missing response case, but in addition we allow some of the components of X to be measured with error. Our motivation is from AIDS clinical trials, where the response, variable viral load RNA, can be missing. In addition, the covariates, CD4 measurements, are measured with error. Measurement error in predictors causes a bias in the estimated regression coefficient. While Liang et al. (1999) considered the measurement error problem, they did not allow for missing responses.

We assume that we can observe a surrogate W related to X by

$$W=X+U.$$ (1.2)

If δ = 1 indicates that Y is observed and δ = 0 indicates that Y is missing, we assume that the measurement error U is independent of (Y, Z, X, δ) and with E(U) = 0, cov(U) = Σ_uu. We first assume that Σ_uu is known, and later extend the results to the general case.

It is important to stress that, under the setting considered in this paper, see (2.1) below, the missingness of Y is allowed to depend on (X, Z), but not otherwise on W. Since the true X is not observable, Y is therefore not missing at random. Since we will make no further assumption, such as on the distribution of X or on the missing data probabilities, what we are dealing with here is conceptually quite different from most studies of missing data in which missing at random or missing completely at random is assumed.

2 Estimation And Main Results

2.1 Known measurement error covariance matrix

As described previously, we assume that, if X were observed, the missing data mechanism would follow the missing at random mechanism in the sense that

$$\text{pr}(\delta =1\mid X,Z,Y)=\text{pr}(\delta =1\mid X,Z)=\pi (X,Z),$$ (2.1)

for some unknown π(X, Z). Since we also assume that the measurement errors U are independent of (Y, Z, X, δ), pr(δ = 1∣X, Z, Y, W) = π(X, Z). Furthermore, we assume that {(Y_i, W_i, Z_i, δ_i), i = 1, ⋯, n} are independent and identically distributed.

We use locally constant smoothers with fixed bandwidths for simplicity in presenting the derivations of the theoretical results: extensions to local polynomial estimation are straightforward, with no change in the limiting distribution of the estimator of β. In what follows, we write A^⊗2 = AA^T. Also, define m_x(z) = E(δX∣Z = z)/E(δ∣Z = z), m_w(z) = E(δW∣Z = z)/E(δ∣Z = z) and m_y(z) = E(δY∣Z = z)/E(δ∣Z = z). Let X̃_i = X_i − m_x(Z_i), W̃_i = W_i − m_w(Z_i), Ỹ_i = Y_i − m_y(Z_i), and denote cov(X̃δ) by Σ_X∣Z.

Note that δY = δX^Tβ + δν(Z) + δε. From our assumptions, it follows that E(δY∣Z) = E(δX^T∣Z)β + E(δ∣Z)ν(Z). If X is observed and m_x(z) and m_y(z) are known, one can obtain a least-squares-type estimator of β as

$${\left[\sum _{i=1}^n{\delta }_i{\{X_i-m_x(Z_i)\}}^{\otimes 2}\right]}^{-1}\left[\sum _{i=1}^n{\delta }_i\{X_i-m_x(Z_i)\}\{Y_i-m_y(Z_i)\}\right].$$

The expectation of the ith term in the second summation is E{π(X, Z)X̃Ỹ } = Σ_X∣Zβ. It is easily shown that this estimator is consistent and asymptotically normal(Wang et al., 2004).

The above formula cannot be applied directly when X is measured with error, and m_x(z) and m_y(z) are unknown. However, by our assumptions, E(δW∣Z) = E(δX∣Z). We thus propose an estimator of β that corrects for attenuation:

$${\widehat{\beta }}_n={(\sum _{i=1}^n{\delta }_i\left[\{W_i-{\widehat{m}}_w(Z_i){\}}^{\otimes 2}-{\sum }_{uu}\right])}^{-1}\left[\sum _{i=1}^n{\delta }_i\{W_i-{\widehat{m}}_w(Z_i)\}\{Y_i-{\widehat{m}}_y(Z_i)\}\right],$$ (2.2)

where m̂_w(z) and m̂_y(z) are nonparametric regression estimators. Let K(·) be a symmetric density function and h be a suitable bandwidth, and define K_h(z) = K(z/h)/h. These estimators take the form

$$\begin{array}{cc}{\widehat{m}}_w(z)=\frac{{\sum }_{i=1}^n{K}_h(Z_i-z){\delta }_i{W}_i}{{\sum }_{i=1}^n{\delta }_i{K}_h(Z_i-z)},& {\widehat{m}}_y(z)=\frac{{\sum }_{i=1}^n{K}_h(Z_i-z){\delta }_i{Y}_i}{{\sum }_{i=1}^n{\delta }_i{K}_h(Z_i-z)}\end{array}.$$ (2.3)

Remark 1

Alternative estimators are readily constructed, but generally suffer from complications. For example, since Y − E(Y∣Z) = {X − E(W∣Z) }^Tβ + ε, an obvious approach is to estimate E(W∣Z) and E(Y∣Z) using all the data. The former is easy: any nonparametric regression will do. However, the latter is problematic, because of the missing responses, the possibility that missingness depends on X and the fact that X is unobserved. There does not appear to be an easy way to estimate E(Y∣Z) consistently under the current conditions. Note that one of the most important features of the proposed approach is that, through use of the standard measurement error model (1.2), it can handle the not missing at random case with ease and still provide $\sqrt{n}$-consistent estimators, as shown in the theorems that follow.

Before presenting our first main result, we note that throughout the paper we make some general assumptions that are listed in the Appendix.

THEOREM 1. Assume that {(Y_i, W_i, Z_i, δ_i), i = 1, …, n} are independent and identically distributed. Under Assumptions A1-A7 in the Appendix, n^1/2(β̂_n − β) is asymptotically normally distributed with mean 0 and covariance matrix ${\sum }_{\beta }={\sum }_{X\mid Z}^{-1}\mathrm{\Gamma }{\sum }_{X\mid Z}^{-1}$, where

$$\mathrm{\Gamma }=E[\delta \{(\epsilon -U^{\text{T}}\beta )\stackrel{\sim }{X}{\}}^{\otimes 2}]+E(\delta U{U}^{\text{T}}{\epsilon }^2)+E[\delta \{(U{U}^{\text{T}}-{\sum }_{uu})\beta {\}}^{\otimes 2}].$$

The proof of Theorem 1 and those of Theorems 2 and 3 given below generally use a technique similar to that used by Liang et al. (2004) to prove their Theorems 1 and 2. We omit the details, which can be found in an earlier version of this article, available from the authors.

Remark 2

In typical nonparametric kernel regression, bandwidth selection plays a key role in the performance of nonparametric estimators in terms of their bias and variance. In partially linear models, β is of main interest, and ν(z) is a nuisance function. Based on Assumption A2, only the rate of order n^−1/5 is needed to lead to the same limit distribution for estimating β. In implementing our proposed estimation procedure, we adopt Ruppert et al.'s (1995) method of choosing the bandwidth. Our limited experience indicates that the numerical performance of the resulting estimators of β is stable around the selected bandwidth.

From the proof of Theorem 1, it is seen that Σ_β can be estimated via a standard sandwich method as follows. Let

$$\begin{array}{l}{\widehat{\sum }}_{X\mid Z}=n^{-1}\sum _{i=1}^n{\delta }_i[\{W_i-{\widehat{m}}_w(Z_i){\}}^{\otimes 2}-{\sum }_{uu}],\hfill \\ \widehat{\mathrm{\Gamma }}=n^{-1}\sum _{i=1}^n{\delta }_i{\left(\{W_i-{\widehat{m}}_w(Z_i)\}[Y_i-{\widehat{m}}_y(Z_i)-\{W_i-{\widehat{m}}_w(Z_i){\}}^{\text{T}}{\widehat{\beta }}_n]+{\sum }_{uu}{\widehat{\beta }}_n\right)}^{\otimes 2}\hfill \end{array}$$

and ${\widehat{\sum }}_{\beta }={\widehat{\sum }}_{X\mid Z}^{-1}\widehat{\mathrm{\Gamma }}{\widehat{\sum }}_{X\mid Z}^{-1}$. Then it is easily shown that Σ̂_β is a consistent estimator of Σ_β.

2.2 Estimated measurement error covariance matrix

The covariance matrix Σ_uu is generally unknown and needs to be estimated. The usual method of doing so (Carroll et al., 1995, Ch.3) is by partial replication, so that we observe W_ij = X_i + U_ij, j = 1, …, m_i. For notational simplicity, we assume that m_i ≡ 2. Extension to more general settings is straightforward; see Liang et al. (1999) for a related discussion. Let W̅_i be the sample mean of the replicates W_ij. A consistent, unbiased method-of-moments estimator for Σ_uu is

$${\widehat{\sum }}_{uu}=n^{-1}\sum _{i=1}^n\sum _{j=1}^2(W_{ij}-{\overline{W}}_i){(W_{ij}-{\overline{W}}_i)}^{\text{T}}.$$

The corresponding estimator of β is

$${\widehat{\beta }}_{n,2}={(\sum _{i=1}^n{\delta }_i\left[\{{\overline{W}}_i-{\widehat{m}}_{\overline{w}}(Z_i){\}}^{\otimes 2}-(1/2){\widehat{\sum }}_{uu}\right])}^{-1}\left[\sum _{i=1}^n{\delta }_i\{{\overline{W}}_i-{\widehat{m}}_{\overline{w}}(Z_i)\}\{Y_i-{\widehat{m}}_y(Z_i)\}\right],$$ (2.4)

where m̂_w̅(z) is the locally constant estimator of m_w(z) based on the data {(W̅_i, Z_i), i = 1, …, n}. We now present the following theorem.

THEOREM 2. Under the general conditions of Theorem 1, the estimator β̂_n,2 given in (2.4) is consistent and asymptotically normal with covariance matrix ${\sum }_{X\mid Z}^{-1}\mathrm{\Gamma }\ast {\sum }_{X\mid Z}^{-1}$, where

$$\mathrm{\Gamma }\ast =E[\delta \{(\epsilon -{\overline{U}}^{\text{T}}\beta )\stackrel{\sim }{X}{\}}^{\otimes 2}]+E(\delta {\overline{UU}}^{\text{T}}{\epsilon }^2)+E[\delta \{({\overline{UU}}^{\text{T}}-{\sum }_{uu}/2)\beta {\}}^{\otimes 2}].$$

By a straightforward but tedious derivation, Theorem 2 can be proved in a manner similar to Theorem 1.

The standard error estimators can also be derived. A consistent estimator of Σ_X∣Z in this case is defined as

$$n^{-1}\sum _{i=1}^n{\delta }_i\left[{\left\{{\overline{W}}_i-{\widehat{m}}_{\overline{w}}(Z_i)\right\}}^{\otimes 2}-(1/2){\widehat{\sum }}_{uu}\right].$$

The Γ* can be estimated as follows. Let

$$\begin{array}{r}\hfill R_i=\{{\overline{W}}_i-{\widehat{m}}_{\overline{w}}(Z_i)\}\left[Y_i-{\widehat{m}}_y(Z_i)-\{{\overline{W}}_i-{\widehat{m}}_{\overline{w}}(Z_i){\}}^{\text{T}}{\widehat{\beta }}_{n,2}\right]\\ \hfill +(1/2)\left\{{(W_{i1}-W_{i2})}^{\otimes 2}-{\widehat{\sum }}_{uu}\right\}{\widehat{\beta }}_{n,2}.\end{array}$$

Then a consistent estimator of Γ* is the sample covariance matrix of the R_iδ_i's (Liang et al., 1999).

3 Estimation of The Mean E(Y)

It is of interest to estimate the mean E(Y) = θ. Cheng (1994) studied this problem in the purely nonparametric regression case, while Wang et al. (2004) studied the partially linear model with X observed. Here we construct three estimators of θ when X is not observed. The methods are analogous to those of Wang et al. (2004) in the case in which X is observed. We obtain that the three estimators are asymptotically equivalent.

In a manner similar to Cheng (1994), we can construct two estimators of θ as follows:

$${\widehat{\theta }}_{n,\text{ave}}=n^{-1}\sum _{i=1}^n{\delta }_i{Y}_i+n^{-1}\sum _{i=1}^n(1-{\delta }_i)\{W_i^{\text{T}}{\widehat{\beta }}_n+{\widehat{\nu }}_n(Z_i)\},$$

$${\widehat{\theta }}_{n,\text{est}}=n^{-1}\sum _{i=1}^n\{W_i^{\text{T}}{\widehat{\beta }}_n+{\widehat{\nu }}_n(Z_i)\},$$

where ${\widehat{\nu }}_n(z)={\widehat{m}}_y(z)-{\widehat{m}}_w^{\text{T}}(z){\widehat{\beta }}_n$ is a nonparametric regression estimator of ν(z) based on the completely observed data of $\{(Z_i,Y_i-W_i^{\text{T}}{\widehat{\beta }}_n),i=1,\cdots ,n\}$. One can easily show that ν̂_n(z) − ν(z) = o_p(n^−1/3), in a way similar to Liang et al. (1999). This rate satisfies our assumption to establish the asymptotic normality of the estimators of θ.

Let $s_n(z)={\sum }_{i=1}^n{\delta }_i{K}_h(Z_i-z)/{\sum }_{i=1}^n{K}_h(Z_i-z)$, s(z) = E(δ∣Z = z) and P(Z, δ) = δ/s(Z). We define a third estimator of θ as

$${\widehat{\theta }}_{n,\text{wei}}=n^{-1}\sum _{i=1}^n\frac{{\delta }_i}{s_n(Z_i)}{Y}_i+n^{-1}\sum _{i=1}^n\left\{1-\frac{{\delta }_i}{s_n(Z_i)}\right\}\{W_i^{\text{T}}{\widehat{\beta }}_n+{\widehat{\nu }}_n(Z_i)\}.$$

Note that, if we try to substitute s_n(z) by an estimator of π(x, z), a problem arises because X is measured with error, so that the exact X is not available for estimating π(X, Z). In the following theorem, we establish the asymptotic normality of the three estimators, showing that they are asymptotically equivalent.

THEOREM 3. In addition to the assumptions of Theorem 1, assume that nh⁴ → 0. Then n^1/2(θ̂_n,● − θ) asymptotically has a normal distribution with mean 0 and variance $E[P(Z,\delta )\epsilon +\{1-P(Z,\delta )\}{U}^{\text{T}}\beta +E({\stackrel{\sim }{W}}^{\text{T}}){\sum }_{X\mid Z}^{-1}\delta \{\stackrel{\sim }{W}(\epsilon -U^{\text{T}}\beta )+{\sum }_{uu}\beta \}{]}^2+E\{X^{\text{T}}\beta +\nu (Z)-\theta {\}}^2$, where ● indicates “ave”, “est”, or “wei”.

4 Inference Based On Empirical Likelihood

Based on our estimators of the covariance matrix or its bootstrap version, one can give a confidence region for either β or θ = E(Y). Although we have confirmed that the estimator Σ̂_β given in §2 is consistent, its finite-sample behaviour may be affected by the need to plug in several estimated terms. Furthermore, the confidence region derived by this procedure is based on a normal approximation, which may be optimistic in small samples. An alternative method is to use the empirical likelihood principle, see Owen (2000), Qin (1994), Qin & Lawless (1994) and Chen (1994). In the remainder of this section, we assume that the ε_i are independent and identically distributed and independent of (W_i, Z_i). We need only to study the empirical-likelihood-based confidence interval for β since the case of θ is similar and simpler.

Let F be the distribution function which assigns probability p_i at points (W_i, Y_i, Z_i). Then ${\sum }_{i=1}^n{p}_i=1$ and p_i ≥ 0 for each i. Our semiparametric empirical likelihood ratio is defined as follows. Note that E[δ{W̃(Ỹ − W̃^Tβ) + Σ_uuβ }] = 0. The empirical likelihood ratio function for β may be defined as

$$ℛ(\beta )=max\left\{\prod _{i=1}^{n}n{p}_i\mid \sum _{i=1}^n{p}_i{\delta }_i\{{\stackrel{\sim }{W}}_i({\stackrel{\sim }{Y}}_i-{\stackrel{\sim }{W}}_i^{\text{T}}\beta )+{\sum }_{uu}\beta \}=0,p_i\ge 0,\sum _{i=1}^n{p}_i=1\right\},$$

if m_w(z) and m_y(z) are known. In our model setting, a modified empirical likelihood ratio function is defined as

$$\begin{array}{l}{ℛ}_n(\beta )=max\{\prod _{i=1}^{n}n{p}_i\mid \sum _{i=1}^n{p}_i{\delta }_i(\{W_i-{\widehat{m}}_w(Z_i)\}[Y_i-{\widehat{m}}_y(Z_i)-\\ \{W_i-{\widehat{m}}_w(Z_i){\}}^{\text{T}}\beta ]+{\sum }_{uu}\beta )=0,pi\ge 0,\sum _{i=1}^n{p}_i=1\}.\end{array}$$ (4.1)

THEOREM 4. Under Assumptions A1-A7, −2 log{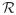_n(β)} converges in distribution to a chi-squared distribution with p degrees of freedom.

Based on this result, a confidence region of β can be given by {β : −2log{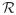_n(β)} ≤ c_α}, where c_α denotes the α quantile of the chi-squared distribution. When Σ_uu is unknown, we need replication data in the usual way. In the special case of m_i = 2, as in §2, we can then replace W_i by W̅_i and Σ_uuβ by 1/2Σ̂_uuβ. The resulting statistic still has the property given in Theorem 4. A justification of this last assertion can be easily obtained by using the fact that

$$E[\delta \{{\overline{W}}_{ir}({\stackrel{\sim }{Y}}_i-{\overline{W}}_{ir}^{\text{T}}\beta )+1/2{\widehat{\sum }}_{uu}\beta \}]=0,$$

where W̅_ir = W̅_i − m_w(Z_i).

We used software R in our numerical work described below. We developed our code using El. s, a function written by A. B. Owen, for implementing the proposed empirical likelihood method.

5 A Simulation Study

To evaluate the performance of the proposed methods, we conducted a small scale simulation experiment. We generated n = 100 and n = 500 observations from model (1.1), assuming that Y∣X, Z ∼ N{β₀ + β₁X + ν(Z), σ²(X, Z) } and that the probability of Y being observed equals pr(δ = 1∣Y, X, Z) = Φ {α₀ + α₁X + ν₁(Z) }, where Φ(·) is the standard normal cumulative distribution function. We also assumed that the measurement error follows W = X + U, where U ∼ N(0, 0.04). In our simulations, two replications for each X were obtained. We set α₀ = β₀ = 0, β₁ = 1, α₁ = 2, X ∼ Un(0, 1), Z ∼ Un(0, 1), independent of X, and ν(z) = 4{exp(−3.25z) − 4 exp(−6.5z) + 3 exp(−9.75z) }. We considered the following four cases.

• Case 1: Here ν₁(z) = 0.75z and σ²(x, z) = 0.25.

• Case 2: Here ν₁(z) = sin(z²) and σ²(x, z) = 0.25.

• Case 3: Here ν₁(z) = 0.75z and σ²(x, z) = 0.1{sin²(2πx³) + 0.5z + 0.3}. This case illustrated the effect of heteroscedastic error on the estimators and confidence intervals.

• Case 4: Here ν₁(z) = 0.75z and the error ε follows ${0.25}^2({\chi }_2^2-2)$, where ${\chi }_2^2$ is a chi-squared variable with 2 degrees of freedom. This case illustrated the effect of asymmetric error on the estimators and confidence intervals.

The reliability ratio, defined as var(X)/{var(X) + var(U)/2}, is 0.806 for all the 4 cases. In our nonparametric estimation procedure, we selected bandwidths as in Remark 2. We used the quartic kernel, K(u) = 15/16(1 − u²)²I_(|u|≤1). We generated 1, 000 datasets in each of the four cases. In each case, approximately 35% of the Y's are missing. To estimate the variance of U, we generated replicate samples of W. We computed the naive and correction-for-attenuation estimates of the parametric components, and their asymptotic and empirical-likelihood-based confidence intervals.

The results are given in Table 1(a). The column ‘Estimate’ gives the average of 1,000 estimated coefficients based on the naive and our proposed methods and the column ‘R²’ gives the coefficients of determination in the (Y, W, Z) naive and (Y, X, Z) analyses; for the latter, R² can be calculated directly when X is observable, as is the case in simulations, or can be estimated by 1−RSS/Syy, with $\mathit{\text{RSS}}={\sum }_{i=1}^n{\delta }_i[\{Y_i-W_i{\widehat{\beta }}_{n,2}-\widehat{\nu }(Z_i){\}}^2-{\widehat{\beta }}_{n,2}^2{\sigma }_{uu}^2]$ and $\mathit{\text{Syy}}={\sum }_{i=1}^n{\delta }_i{(Y_i-\overline{Y})}^2$. Our numerical experience indicates that the results of these two R²'s are generally close to each other. We present the estimated values of R² here and in our data analysis later. The columns ‘midpoint’ and ‘length’ give the average midpoint and length of the confidence intervals. The column ‘CI(ME)’ gives the confidence intervals using the empirical likelihood and normal approximation methods when the measurement errors are accounted for. The lower and upper values are the averages of 1,000 simulated corresponding lower and upper values. The column ‘Coverage (ME)’ gives the corresponding coverage probabilities of the 1,000 datasets.

Table 1.

Simulation study. Point estimates for β₁, with true value 1, together with the coefficients of determination (R²) and the 95% confidence intervals based on the empirical likelihood (EL) and normal approximation (Norm) methods. Also displayed are the averages of the lower and upper endpoints of the confidence intervals, their average midpoints, their average lengths, and the associated coverage probabilities for the simulated data (a) when X and Z are independent, and (b) when X and Z are strongly correlated.

		Estimate		R2		Confidence Interval		Midpoint		Length		Coverage
n	Case	Naive	ME	Naive	X observed	EL	Norm	EL	Norm	EL	Norm	EL	Norm
(a) X and Z are independent
100	1	0.649	1.027	0.464	0.525	(0.511, 1.624)	(0.438, 1.615)	1.072	1.027	1.114	1.177	93.7	94.3
	2	0.643	1.021	0.467	0.525	(0.500, 1.627)	(0.438, 1.605)	0.969	1.021	1.126	1.167	94.0	94.7
	3	0.655	1.042	0.861	0.915	(0.806, 1.318)	(0.740, 1.324)	1.082	1.042	0.522	0.544	95.7	92.7
	4	0.657	1.048	0.473	0.532	(0.505, 1.676)	(0.364, 1.733)	1.090	1.048	1.171	1.369	96.3	94.3
500	1	0.665	1.007	0.446	0.502	(0.793, 1.221)	(0.793, 1.221)	0.981	1.007	0.427	0.428	94.7	94.8
	2	0.658	0.997	0.445	0.501	(0.786, 1.217)	(0.777, 1.218)	1.006	0.997	0.432	0.441	95.8	94.5
	3	0.660	1.000	0.858	0.917	(0.913, 1.071)	(0.916, 1.083)	1.007	1.000	0.158	0.167	93.7	95.8
	4	0.663	1.003	0.446	0.502	(0.788, 1.144)	(0.785, 1.221)	0.990	1.003	0.363	0.436	94.8	94.9
(b) X and Z are strongly correlated
100	1	0.569	1.082	0.65	0.688	(0.306, 2.016)	(-0.001, 2.165)	1.061	1.082	1.71	2.166	92.7	97.0
	2	0.589	1.094	0.641	0.677	(0.357, 1.916)	(0.256, 1.931)	0.971	1.094	1.569	1.675	96.3	95.0
	3	0.568	1.088	0.879	0.922	(0.530, 1.907)	(0.044, 2.132)	1.019	1.088	1.377	2.088	94.6	96.7
	4	0.564	0.983	0.645	0.674	(0.261, 2.082)	(-0.296, 2.445)	1.172	0.983	1.821	2.741	94.7	97.7
500	1	0.586	1.013	0.631	0.665	(0.725, 1.227)	(0.720, 1.306)	1.026	1.013	0.522	0.586	94.8	94.2
	2	0.582	1.005	0.631	0.664	(0.716, 1.221)	(0.715, 1.296)	0.981	1.005	0.544	0.581	95.6	94.5
	3	0.582	0.991	0.912	0.942	(0.897, 1.062)	(0.892, 1.125)	0.993	0.991	0.168	0.233	98.6	95.3
	4	0.586	1.011	0.630	0.664	(0.728, 1.228)	(0.727, 1.295)	1.023	1.011	0.510	0.568	96.4	94.6

The results are generally in accord with the theory. The impact of the measurement errors on the estimates is substantial. When measurement errors are ignored, the estimators are significantly biased and attenuate to zero. For moderate sample size, the empirical-likelihood-based confidence intervals appear to be superior to those based on the normal approximation. The improvement is greater when the error is nonnormal or its variance is not constant.

At the referee's request, we repeated the procedure above except that X and Z are correlated. We used X = Z + e with e ∼ N(0, 0.06), so that the correlation coefficient of X and Z is 0.76, and the reliability ratio is about 0.877. The results are presented in Table 1(b). We can draw the same general conclusion as that from the case where X and Z are independent. The main difference is that the confidence intervals are generally much wider than in the independent X and Z case, as expected.

6 Analysis of A Dataset From An Aids Study

In this section we present an illustrative analysis of the pediatric AIDS clinical trial group PACTG 338 study. One of the purposes of this study is to investigate the effectiveness of antiretroviral medicines, and to see how increasing CD4 cell counts decrease the amount of HIV in the blood, the HIV viral load. We are interested in understanding the pathogenesis of HIV infection and in evaluation of antiretroviral therapies by characterising the relationship between viral load and CD4 cell counts. Our preliminary investigations suggested that viral load depends linearly on CD4 cell count but nonlinearly on treatment time; see Liang et al. (2004) for a related discussion. We therefore model the relationship between viral load and CD4 cell counts by model (1.1). Let Y_ij be the viral load and let X_ij be the CD4 cell count for subject i at treatment time Z_ij. The X_ij are measured with error (Liang et al., 2003). Here we treat Y_ij as measured without error except for being partially missing. The model we used is

$$\begin{array}{cc}{Y}_{ij}=X_{ij}\beta +\nu (Z_{ij})+{\epsilon }_{ij},& W_{ij}=X_{ij}+U_{ij}\end{array},$$

where W_ij are the observed CD4 cell counts. The first part of this model was applied by Zeger & Diggle (1994) to investigate the relationship between the CD4 cell count, Y_ij, and time, Z_ij, and other covariates, X_ij. If there is no correlation, this longitudinal model reduces to model (1.1).

The PACTG 338 study consists of 297 children, who were clinically stable and who had not had prior treatment with protease inhibitors. They were subjected to a regimen containing a 2- or 3-drug protease inhibitor containing regimen, i.e., ritonavir plus 1 or 2 nucleoside analogues, or to a dual nucleoside analogue regimen. There were 2287 observations, among which 404 (17.6%) viral load RNA values were missing. The ranges of viral load (log₁₀) and CD4 cell counts are (2.6, 6.21) and (51, 3284); the mean and median of CD4 cell counts are 824.55 and 746; the mean and median of HIV RNA levels are 3.518 and 3.346; and the specimens were obtained on weeks 0, 4, 8, 12, 24, 36, 48, 60, 72 and 84. See Nachman et al. (2000) for a detailed explanation of the study. The CD4 cell counts are used to follow response to HIV medications, as a measure of adherence to treatment and most importantly to guide decisions regarding opportunistic infection prophylaxis. Some patients may fail to go to clinical trial centres for a HIV viral load measurement when they feel that their immunity is strong enough or too weak. Therefore, the assumption that the missing RNA levels depend on true CD4 cell counts and not on measured counts and treatment time appears to be at least reasonable.

We ignored the correlation structure when computing the estimates, using the so-called working independence assumption. As pointed out in equation (2) of Lin & Carroll (2001), working independence has some model-robustness advantages over estimation methods that account for correlation, with a corresponding loss of efficiency. To reduce the marked skewness of CD4 cell counts, and make treatment times equal space, we take log-transformations of both variables. We used the same kernel function as in the simulation study in §5, and obtained a bandwidth of h = 0.124 in the same manner as described there. We assumed that the measurement errors U_ij were independent and normally distributed with mean zero and variance ${\sigma }_u^2$. In the absence of validation or replication data, as in Lin & Carroll (2000), we conducted a sensitivity analysis by taking ${\sigma }_u^2$ to be one quarter and one half of the variance of W.

We applied the methods proposed in §2 and 4, assuming ${\sigma }_u^2=0$, which naively ignores measurement error, ${\sigma }_u^2=0.068$ and ${\sigma }_u^2=0.135$. For β, we give estimated values, along with the normal approximation, bootstrap and empirical likelihood confidence intervals in the full-data part of Table 2. The bootstrap intervals were based on 200 replications. The R²'s shown in the table: are calculated as was described in §5 for the coefficient of determination in the (Y, X, Z) regression analysis if X were observed. The estimated values of β corresponding to ${\sigma }_u^2=0.068$ and ${\sigma }_u^2=0.135$ increased by 31.2% and 48.8% in absolute value, respectively, compared to the naive estimate, and the confidence intervals were widened accordingly. As expected, when the possibility of measurement errors was taken into account, we found a somewhat stronger negative association between viral load and CD4 cell counts. Whether or not there is correlation between within-subjects observations, the bootstrap method generally produces correct confidence intervals, while other two approaches can lead to incorrect, typically too optimistic, confidence intervals. However, in this special case, any correlation effect appears to be minimal since all three methods produced similar confidence intervals with the empirical-likelihood intervals being slightly shorter, as in the simulation studies, while the normal and bootstrap intervals are virtually identical.

Table 2.

AIDS study. Estimates of β, with the 95% confidence intervals (CI) based on the normal approximation (Norm), empirical likelihood (EL), and bootstrap methods. Also given are the estimated R²'s of the coefficient of determination for the (Y, X, Z) regression analysis if X were observed.

	${\sigma }_u^2=0$	${\sigma }_u^2=0.068$	${\sigma }_u^2=0.135$
Full data
Estimate of β	-0.125	-0.164	-0.186
R2	0.331	0.422	0.436
CI(Norm)	(-0.144, -0.106)	(-0.207, -0.121)	(-0.244, -0.128)
CI(EL)	(-0.132, -0.109)	(-0.183, -0.128)	(-0.221, -0.130)
CI(Boot)	(-0.143, -0.107)	(-0.205, -0.123)	(-0.245, -0.127)
Independent data
Estimate of β	-0.129	-0.159	-0.212
R2	0.138	0.162	0.214
CI(Norm)	(-0.190, -0.068)	(-0.236, -0.082)	(-0.320, -0.104)
CI(EL)	(-0.181, -0.068)	(-0.226, -0.076)	(-0.310, -0.114)

Since our approximate confidence intervals assumed working independence, which may well not be the case in the current data analysis, we also demonstrate how they perform for data that actually do satisfy the assumption of having independent observations. For this purpose, we took one observation from each child at random, and repeated the exercise 1,000 times. The results are presented in the independent-data part of Table 2. All the entries were computed in the same way as for the full data except that they are the averages of 1,000 estimates. Again, the two methods produced similar results with the empirical-likelihood intervals being slightly shorter.

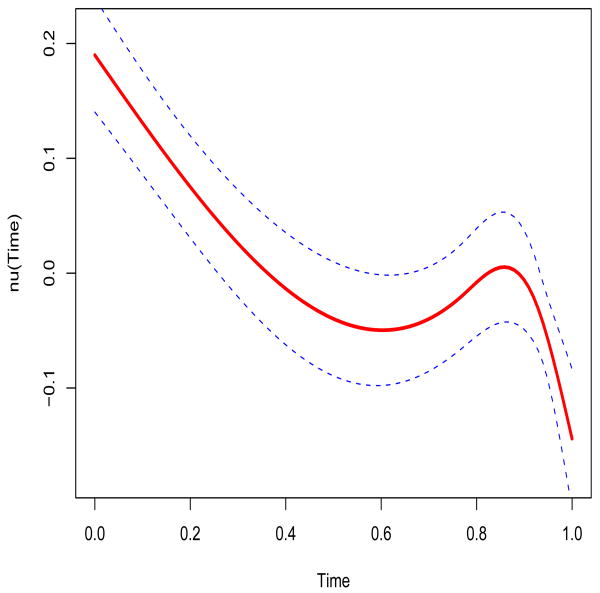
The curve of the estimated nonparametric function of treatment time and the corresponding confidence bands for the case of ${\sigma }_u^2=0$ are shown in Fig. 1. The results for the other cases of ${\sigma }_u^2=0.068$ and ${\sigma }_u^2=0.135$ are similar and are therefore not shown. The confidence bands were obtained by 200 bootstrap replications, in which patients were resampled. The plot indicates that the viral load RNA levels rapidly decrease after initial antiviral treatment, then become flat and even rebound a little bit and finally decrease rapidly.

Figure 1.

AIDS study. The solid curve represents the estimated values of ν(z) based on the complete observations, and the dotted lines are the confidence intervals.

7 Discussion

The point estimation methods and normal limit distributions are readily extended to longitudinal and repeated measures contexts, if one uses working independence, i.e. ignores the correlation structure when computing the estimator but uses it in computing asymptotic covariance matrices. However, as was suggested in our data analysis, how to employ the empirical likelihood procedure for correlated data appears to be a difficult issue, and is currently under our investigation.

The proposed estimators are based on the observed data, but exclude the observed covariates (W, Z) when Y is missing except that all the Ws are used to estimate Σ_uu when its estimation is desired. Although we have not derived the efficiency bound for the estimator of β, we conjecture that little gain, if any, can be obtained if we include those observations (W, Z) associated with missing Y's; see Bickel et al. (1993, p 146) for a related result.

Appendix

Technical details

• Assumption A1. The matrix E{π(X, Z)X̃X̃^T} is positive-definite, E(ε∣X, Z) = 0, and E(|ε|³∣X, Z) < ∞.

• Assumption A2. The bandwidths used in estimating m_w(z) and m_y(z) are of order n^−1/5.

• Assumption A3. The function K(·) is a bounded symmetric density function with compact support and satisfies ∫ K(u)du = 1, ∫ K(u)udu = 0 and ∫ u²K(u)du = 1.

• Assumption A4. The density function of Z, f_z(z), is bounded away from zero and has bounded continuous second derivatives.

• Assumption A5. The functions m_y(z) and m_w(z) have bounded and continuous second derivatives.

• Assumption A6. The probability function π(x, z) is bounded away from zero on the support of (X, Z), and has bounded continuous second partial derivatives.

• Assumption A7. The random variable U satisfies E(‖U‖³) < ∞.

We first point out the following facts, which can easily be shown by Assumptions A2-A5:

$${\widehat{m}}_w(z)-m_w(z)=o_p(n^{-1/4}),{\widehat{m}}_y(z)-m_y(z)=o_p(n^{-1/4}).$$ (A.1)

In the rest of the Appendix, we prove Theorem 4. We first present a lemma, whose proof can be found in Liang et al. (1999).

LEMMA A1. Assume that random variables a_i and b_i satisfy Ea_i = 0 and ‖b_i‖ = o_p(n^−1/4). Then

$$\sum _{i=1}^n{a}_i{b}_i{\xi }_i=o_p(n^{1/2}),$$

where ξ_i are independent variables with zero conditional mean and finite variance.

Proof of Theorem 4. Let

$${\mathrm{\Omega }}_i=\left(\{W_i-{\widehat{m}}_w(Z_i)\}[Y_i-{\widehat{m}}_y(Z_i)-\{W_i-{\widehat{m}}_w(Z_i){\}}^{\text{T}}\beta ]+{\sum }_{uu}\beta \right){\delta }_i.$$

A standard simplification as in Owen (2000, p 61) yields that

$$p_i=\frac{1}{n(1+a^{\text{T}}{\mathrm{\Omega }}_i)}\text{for}i=1,\dots ,n,$$ (A.2)

where a = (a₁, …, a_p)^T is the solution of the equation

$$n^{-1}\sum _{i=1}^n\frac{{\mathrm{\Omega }}_i}{1+a^{\text{T}}{\mathrm{\Omega }}_i}=0.$$ (A.3)

Mimicking the proof Theorem 3.2 of Owen (2000), we have

$$\Vert a\Vert =O_p(n^{-1/2}).$$ (A.4)

On the other hand, based on the assumptions, Theorem 1 and the strong law of large numbers, we have

$$\underset{1\le i\le n}{max}\Vert {\mathrm{\Omega }}_i\Vert =o_p(n^{1/2}).$$ (A.5)

Note that

$$n^{-1}\sum _{i=1}^n\frac{{\mathrm{\Omega }}_i}{1+a^{\text{T}}{\mathrm{\Omega }}_i}=n^{-1}\sum _{i=1}^n{\mathrm{\Omega }}_i(1-a^{\text{T}}{\mathrm{\Omega }}_i)+n^{-1}\sum _{i=1}^n\frac{{(a^{\text{T}}{\mathrm{\Omega }}_i)}^2{\mathrm{\Omega }}_i}{1+a^{\text{T}}{\mathrm{\Omega }}_i}.$$

The second term is o_p(n^−1/2) since |a^TΩ_i| = o_p(1) and

$$\sum _{i=1}^n{(a^{\text{T}}{\mathrm{\Omega }}_i)}^2{\mathrm{\Omega }}_i\le \Vert a\Vert \underset{1\le i\le n}{max}|a^{\text{T}}{\mathrm{\Omega }}_i|\sum _{i=1}^n{\Vert {\mathrm{\Omega }}_i\Vert }^2=O_p(n^{-1/2})o_p(1)O_p(n)=o_p(1).$$

It then follows from (A.3) that

$$a={\left(\sum _{i=1}^n{\mathrm{\Omega }}_i{\mathrm{\Omega }}_i^{\text{T}}\right)}^{-1}\sum _{i=1}^n{\mathrm{\Omega }}_i+o_p(n^{-1/2}).$$ (A.6)

A similar argument using ${\sum }_{i=1}^n{p}_i=1$ yields that

$$0=n^{-1}\sum _{i=1}^n\frac{a^{\text{T}}{\mathrm{\Omega }}_i}{1+a^{\text{T}}{\mathrm{\Omega }}_i}=n^{-1}\sum _{i=1}^n{a}^{\text{T}}{\mathrm{\Omega }}_i-n^{-1}\sum _{i=1}^n{(a^{\text{T}}{\mathrm{\Omega }}_i)}^2+o_p(n^{-1}).$$

Therefore, we have

$$\sum _{i=1}^n{a}^{\text{T}}{\mathrm{\Omega }}_i=\sum _{i=1}^n{(a^{\text{T}}{\mathrm{\Omega }}_i)}^2+o_p(1).$$ (A.7)

Consider 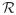_n(β). Using a Taylor expansion of log(1 + x) on x, we have

$$\begin{array}{l}-log\{{ℛ}_n(\beta )\}=\sum _{i=1}^{n}log(1+a^{\text{T}}{\mathrm{\Omega }}_i)\\ =\sum _{i=1}^n\{a^{\text{T}}{\mathrm{\Omega }}_i-(1/2)(a^{\text{T}}{\mathrm{\Omega }}_i{)}^2\}+Q_n.\end{array}$$

The remainder term Q_n is bounded by ${\Vert a\Vert }^2{max}_{1\le i\le n}|a^{\text{T}}{\mathrm{\Omega }}_i|{\sum }_{i=1}^n{\Vert {\mathrm{\Omega }}_i\Vert }^2=O_p(n^{-1})o_p(1)O_p(n)=o_p(1)$. Using (A.7) and (A.6), we have

$$\begin{array}{l}-2log\{{ℛ}_n(\beta )\}=\sum _{i=1}^n{a}^{\text{T}}{\mathrm{\Omega }}_i{\mathrm{\Omega }}_i^{\text{T}}a+o_p(1)\\ =(n^{-1/2}\sum _{i=1}^n{\mathrm{\Omega }}_i{)}^{\text{T}}(n^{-1}\sum _{i=1}^n{\mathrm{\Omega }}_i{\mathrm{\Omega }}_i^{\text{T}}{)}^{-1}(n^{-1/2}\sum _{i=1}^n{\mathrm{\Omega }}_i)+o_p(1).\end{array}$$

Write Ω̃_i = ({W_i − m_w(Z_i)}[Y_i − m_y(Z_i) − {W_i − m_w(Z_i)}^Tβ] + Σ_uuβ) δ_i. Then Ω̃_i − Ω_i can be expressed as

$$\begin{array}{l}{\stackrel{\sim }{W}}_i[\{{\widehat{m}}_y(Z_i)-m_y(Z_i)\}-\{{\widehat{m}}_w(Z_i)-m_w(Z_i){\}}^{\text{T}}\beta ]{\delta }_i\\ -\{{\widehat{m}}_w(Z_i)-m_w(Z_i)\}[\{{\widehat{m}}_y(Z_i)-m_y(Z_i)\}-\{{\widehat{m}}_w(Z_i)-m_w(Z_i){\}}^{\text{T}}\beta ]{\delta }_i\\ +\{{\widehat{m}}_w(Z_i)-m_w(Z_i)\}({\stackrel{\sim }{Y}}_i-{\stackrel{\sim }{W}}_i^T\beta ){\delta }_i.\end{array}$$

It follows from (A.1) that

$$\frac{1}{\sqrt{n}}\sum _{i=1}^n\{{\widehat{m}}_w(Z_i)-m_w(Z_i)\}[\{{\widehat{m}}_y(Z_i)-m_y(Z_i)\}+\{{\widehat{m}}_w(Z_i)-m_w(Z_i){\}}^{\text{T}}\beta ]{\delta }_i=o_p(1).$$

On the other hand, Lemma A1 implies that

$$\frac{1}{\sqrt{n}}\sum _{i=1}^n{\stackrel{\sim }{W}}_i[\{{\widehat{m}}_y(Z_i)-m_y(Z_i)\}+\{{\widehat{m}}_w(Z_i)-m_w(Z_i){\}}^{\text{T}}\beta ]{\delta }_i=o_p(1),$$

$$\frac{1}{\sqrt{n}}\sum _{i=1}^n\{{\widehat{m}}_w(Z_i)-m_w(Z_i)\}({\stackrel{\sim }{Y}}_i-{\stackrel{\sim }{W}}_i^{\text{T}}\beta ){\delta }_i=o_p(1).$$

These results imply that $n^{-1/2}{\sum }_{i=1}^n{\mathrm{\Omega }}_i$ and $n^{-1/2}{\sum }_{i=1}^n{\stackrel{\sim }{\mathrm{\Omega }}}_i$ asymptotically have the same normal distribution, and $n^{-1}{\sum }_{i=1}^n{\mathrm{\Omega }}_i{\mathrm{\Omega }}_i^{\text{T}}$ and $n^{-1}{\sum }_{i=1}^n{\stackrel{\sim }{\mathrm{\Omega }}}_i{\stackrel{\sim }{\mathrm{\Omega }}}_i^{\text{T}}$ and have the same limiting value. The proof is thus complete.