Probing the effect of amino-terminal truncation for Aβ_1–40 peptides

Abstract

We examine the effect of deletion of the amino-terminal (residues 1 to 9) on the structure and energetics of Aβ_1–40 peptides. To this end, we use replica exchange molecular dynamics to compare the conformational ensembles of Aβ_1–40 and amino-truncated Aβ_10–40 monomers and dimers. Overall, the deletion of the amino-terminal appears to cause minor structural and energetic changes in Aβ monomers and dimers. More specifically, our findings are as follows: (1) There is a small but discernible conversion of β-strand structure into helix upon amino-terminal deletion; (2) Secondary structure changes due to truncation are caused by missing side chain interactions formed by the amino-terminal; (3) The amino-terminal together with the central sequence region (residues 10–23) represents the primary aggregation interface in Aβ_1–40 dimers. The amino-truncated Aβ_10–40 retains this aggregation interface, which is reduced to the central sequence region. We argue that the analysis of available experimental data supports our conclusions. Our findings also suggest that amino-truncated Aβ_10–40 peptide is an adequate model for studying Aβ_1–40 aggregation.

Introduction

Currently accepted view postulates that the onset of Alzheimer’s disease is associated with the extracellular aggregation of Aβ peptides that involves oligomerization of individual Aβ chains and formation of amyloid fibrils.^1,2 Although Aβ amyloid fibrils show cytotoxic properties,³ it is believed that Aβ oligomers are the primary cytotoxic species.^4–6 Recently, it has been shown that synaptic structure and function can be impaired even by the smallest Aβ oligomers, dimers.⁷ Aβ peptides are produced by natural cleavage of the transmembrane amyloid precursor protein. They are released in a variety of lengths and, while the 40- or 42-residue species, Aβ_1–40 and Aβ_1–42, are the most common, other peptide fragments are also naturally present. Among them are amino-truncated species Aβ_x–40 and Aβ_x–42, where x is the first amino acid retained in the peptide fragment.^8,9 In particular, the peptides with x = 3,5,8,9,11 were reported. Importantly, it has been estimated that the amino-truncated species may constitute up to 60% of all Aβ aggregated peptides.⁸

In the past the impact of C-terminal truncation on Aβ amyloid formation has attracted significant experimental and computational attention, in part, because Aβ species, Aβ_1–39, Aβ_1–40, and Aβ_1–42, are the main constituents of Aβ fibrils.¹⁰ It is well established that Aβ_1–42 peptides are considerably more amyloidogenic than Aβ_1–40 and are capable of aggregating without detectable lag time.¹¹ It is also known that compared to Aβ_1–40 peptides two additional amino acids in Aβ_1–42 induce noticeable shift towards higher order oligomer assemblies.¹² Furthermore, single site mutagenesis at the positions 19–23 leads to different changes in the Aβ_1–40 and Aβ_1–42 oligomerization.¹³ These findings suggest that Aβ_1–40 and Aβ_1–42 aggregate via different pathways.

In comparison with the C-terminal, the role of the N-terminal in Aβ aggregation has been less studied and is not well understood.¹⁴ Several lines of experimental evidence suggest that in Aβ_1–40 fibrils roughly ten N-terminal residues form disordered structure.^15–18 Consequently, it is conceivable that the N-terminal is not important for fibril formation. Indeed, recent solid-state NMR studies did show that Aβ_1–40 and the truncated species Aβ_10–40 form very similar fibril structures.^17,19 Apparently minor role of the N-terminal in fibril assembly does not imply that it is also irrelevant in earlier stages of aggregation. Biophysical studies have revealed that progressive deletions of amino acids from the N-terminal (x = 1,4,8) affect the amount of Aβ deposits and their cytotoxicity.²⁰ On the other hand, the size distributions of Aβ_x–40 oligomers with x from 1 to 10 remain qualitatively similar and mostly include Aβ species from monomers to tetramers.¹³ These observations raise the question on the exact role, which the N-terminal plays in Aβ aggregation.

In silico studies, such as molecular dynamics (MD) simulations, can probe Aβ aggregation on a molecular level.²¹ In recent years several MD studies have explored the conformational properties of Aβ monomers and dimers.^22–26 In particular, explicit water replica exchange molecular dynamics (REMD) simulations have found several structured regions in generally disordered Aβ monomer.²³ Implicit solvent REMD also pointed out to generally random coil-like structure of Aβ monomer.²⁵ In our REMD simulations of Aβ monomers and dimers we used N-terminal truncated peptide Aβ_10–40.²⁷ We have showed that, although random coil dominates Aβ_10–40 conformational ensemble, significant populations of helix and β structure are also present. In particular, helix is most frequently formed in the sequence region 14–21 of Aβ_10–40 monomer, but is gradually replaced with β-strand conformers in Aβ_10–40 dimers and higher order aggregates. Furthermore, our simulations demonstrated that the primary aggregation interface in Aβ_10–40 dimers involves the sequence region 10–23, whereas the C-terminal was predicted to play minor role.²⁷ However, it is not a priori clear if these conformational properties and aggregation scenarios are applicable to full-length Aβ_1–40 peptides.

To answer the questions posed above we performed REMD simulations of Aβ_1–40 monomers and dimers and compared their structures and aggregation properties with those of Aβ_10–40.²⁷ We show that the deletion of the residues 1 to 9 in Aβ_1–40 does not qualitatively change the distribution of structures sampled by the monomer nor the aggregation interface in the dimer. However, the removal of the N-terminal does increase the helical propensity in Aβ monomers and dimers, while simultaneously reducing the fraction of β-structure. The analysis of REMD simulations indicate that these secondary structure changes are due to missing side chain interactions formed by the N-terminal with the central and C-terminal regions of Aβ peptides.

Model and Simulation Methods

Molecular dynamics simulations

To perform simulations of Aβ peptides we used CHARMM MD program²⁸ and all-atom force field CHARMM19 coupled with the SASA implicit solvent model.²⁹ The CHARMM19+SASA force field is not known for bias toward particular protein secondary structure. It has been used to fold polypeptides, which contain α-helices or β-sheets.^30,31 CHARMM19+SASA simulations were also employed for studying oligomerization of amyloidogenic peptides.^32,33

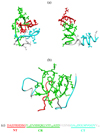
In this work, we use two versions of Aβ peptide - the full length wild-type Aβ_1–40 and the amino-truncated Aβ_10–40, in which nine N-terminal residues are removed (Fig. 1). To analyze monomeric peptide folding and aggregation we consider monomers and dimers of Aβ_1–40 and Aβ_10–40. The properties of Aβ_10–40 monomers and dimers were investigated in our previous study.²⁷ Here, by performing new simulations of Aβ_1–40 monomers and dimers and comparing them with those for Aβ_10–40 we evaluate the role of the N-terminal residues 1–9 in the ensemble of structures sampled by Aβ_1–40.

Fig. 1.

Representative snapshots of Aβ_1–40 (a) monomers and (b) dimers. (c) Sequence of Aβ_1–40 peptide. NT, CR, and CT regions in (a–c) are in red, green, and aqua, respectively. The turn between the CR and CT and Val40 (which is not part of the second fibril β-strand) are in grey. Two conformers of Aβ_1–40 monomer are shown, in which NT-CR and NT-CT side chain interactions are formed (left structure) or broken (right structure). Formation of these interactions induces β-structure in the CR and CT, while suppressing helix conformations. In Aβ_1–40 dimer (b) the aggregation interface predominantly involves the CR and NT regions, leaving the CT regions exposed to solvent.

Replica exchange simulations

To achieve exhaustive conformational sampling we used replica exchange molecular dynamics (REMD).³⁴ This method provides efficient sampling of rugged free energy landscapes governing protein folding and aggregation.^{26,32,33,35–39} To simulate Aβ_1–40 monomers and dimers we used 24 replicas distributed linearly in the temperature range from 300 to 530K. The exchanges were attempted every 80 ps in all neighboring replica pairs. The average acceptance rates were 62% (monomer) and 47% (dimer). In all, we produced four (monomer) and eight (dimer) REMD trajectories of the length 0.8µs each (per replica). Therefore, the cumulative simulation time for all replicas was about 76µs (monomer) and 152µs (dimer). The structures were saved every 40 ps. Between replica exchanges the system was evolved using NVT under-damped Langevin dynamics with the damping coefficient γ = 0.15ps⁻¹ and the integration step of 2fs. The initial equilibration intervals τ_eq were determined by monitoring the effective energy E_eff, which is the sum of potential and solvation energies. Consequently, the initial parts of REMD trajectories of the lengths up to 100 ns were excluded and the cumulative equilibrium simulation times were reduced to τ_sim = 66µs (monomer) and 128µs (dimer). Aβ systems were subject to spherical boundary condition with the radius R_s=90Åand the force constant k_s = 10kcal/(molŲ). For dimers the concentration of Aβ peptides was of an order of mM.

Computation of structural probes

To characterize intra- and interpeptide interactions we computed the number of side chain contacts. A contact is formed, if the distance between the centers of mass of side chains is less than 6.5Å. This cut-off approximately corresponds to the onset of hydration of side chains as the separation distance between them increases. Backbone hydrogen bonds (HBs) between NH and CO groups were assigned according to Kabsch and Sander.⁴⁰ Secondary structure in Aβ peptides was determined by evaluating their dihedral angles (ϕ, ψ).^41,42 To this end, the grid with the spacing of 18° was superimposed on the Ramachandran plot. The β-strand conformations are enclosed by the vertices of the polygon (−180°,180°), (−180°,126°), (−162°,126°), (−162°,108°), (−144°,108°), (−144°,90°), (−50°,90°), (−50°,180°); helix structures are confined to the polygon (−90°,0°), (−90°,−54°), (−72°,−54°), (−72°,−72°), (−36°,−72°), (−36°,−18°), (−54°,−18°), (−54°,0°). (Note that these definitions do not distinguish α-helix, 3₁₀-helix, or π-helix.) Using these definitions the fractions of residues in helix and β-strand conformations, H and S, can be computed in any structure. As an alternative it is possible to use the program STRIDE for secondary structure assignment.⁴³ However, we showed in our previous study²⁷ that, because STRIDE defines β-structure using HBs, it may underestimate the formation of extended β-like conformations in disordered systems such as Aβ dimers and monomers. Consequently, in this work we assign secondary structure using (ϕ, ψ) angles.

Throughout the paper angular brackets < ‥ > indicate thermodynamic averages. Because Aβ dimers include two indistinguishable peptides, we report averages over two peptides. The distributions of states produced by REMD were analyzed using multiple histogram method.⁴⁴

Cluster analysis of Aβ monomers

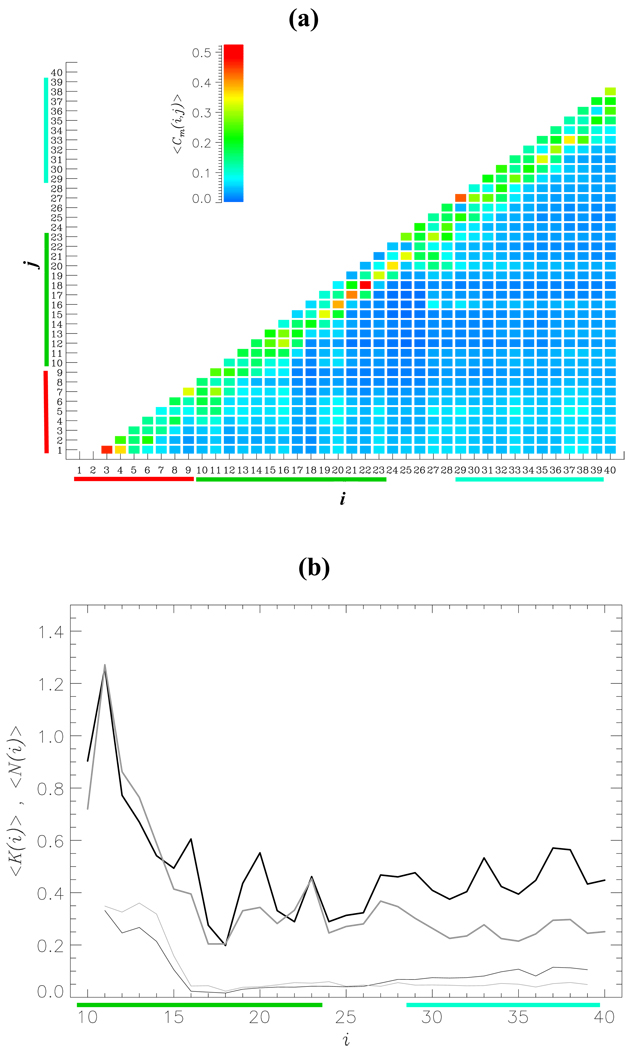
In order to probe the conformational ensemble sampled by Aβ_1–40 monomers we applied cluster analysis. Because the details of this method can be found elsewhere,⁴⁵ we present here only its short outline. We used 7000 Aβ_1–40 structures collected with the period of five REMD steps from the equilibrated REMD simulations at 360K. Because successive structures are, on an average, separated by several replica exchanges, they are statistically independent. Aβ conformations were clustered based on the distribution of side chain contacts. To this end, a structure k was represented by a vector D⃗(k) with 780 binary components, each given by the element of the contact map C_m(i, j). If the residues i and j (j>i + 1) form a contact, then C_m(i, j) = 1, and C_m(i, j) = 0, otherwise. The vector D⃗_cl representing the cluster is computed as the average of the vectors D⃗(k), where k are the indeces of structures assigned to the cluster. The peptide structural clusters were defined with the cut-off radius R_c = 7.3, which is equal to the maximum Euclidian distance between the cluster and a structure. To select R_c we scan its values in the range from 5 to 15. Small R_c lead to the appearance of numerous structurally similar clusters, whereas large R_c result in merging structurally distinct clusters.

Convergence of REMD simulations

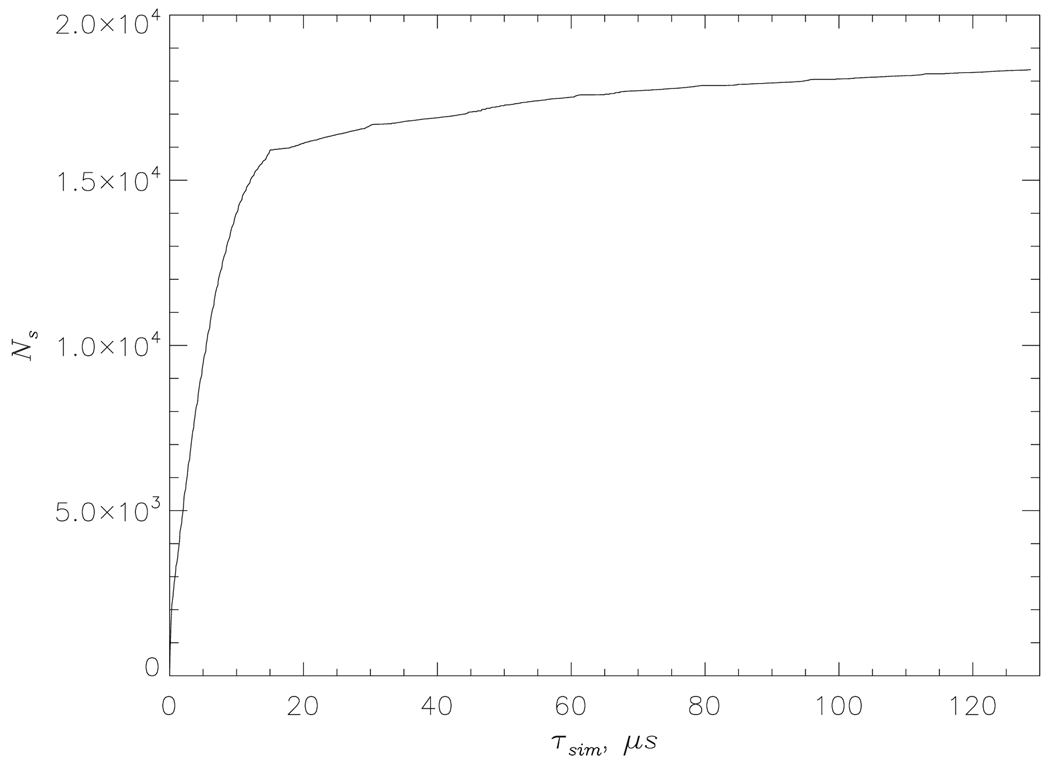
To evaluate the quality of REMD sampling we consider the number N_s of the unique states (E_eff,N_d), which were sampled in the course of Aβ_1–40 dimer simulations at least once. Each state (E_eff ,N_d) is defined by the effective energy E_eff and the number of interpeptide HBs, N_d. Fig. 2 shows N_s for Aβ_1–40 dimer as a function of the cumulative equilibrium simulation time τ_sim. At τ_sim ≳ 80µs N_s approximately levels off suggesting convergence of REMD. To further test the reliability of REMD we divided the Aβ_1–40 dimer simulations into two equal subsets and analyzed them independently. The thermodynamic quantities from the two subsets differed by no more than 6% (with respect to the numbers of HBs and side chain contacts) or 2% (with respect to secondary structure fractions). The errors for Aβ_1–40 monomers are smaller than those for the dimers. The error analysis for Aβ_10–40 monomers and dimers was reported earlier.²⁷

Fig. 2.

The number N_s of the new states (E_{e f f}, N_d) in Aβ_1–40 dimer not previously sampled in REMD as a function of the cumulative equilibrium simulation time τ_sim.

Testing the reliability of implicit solvent model

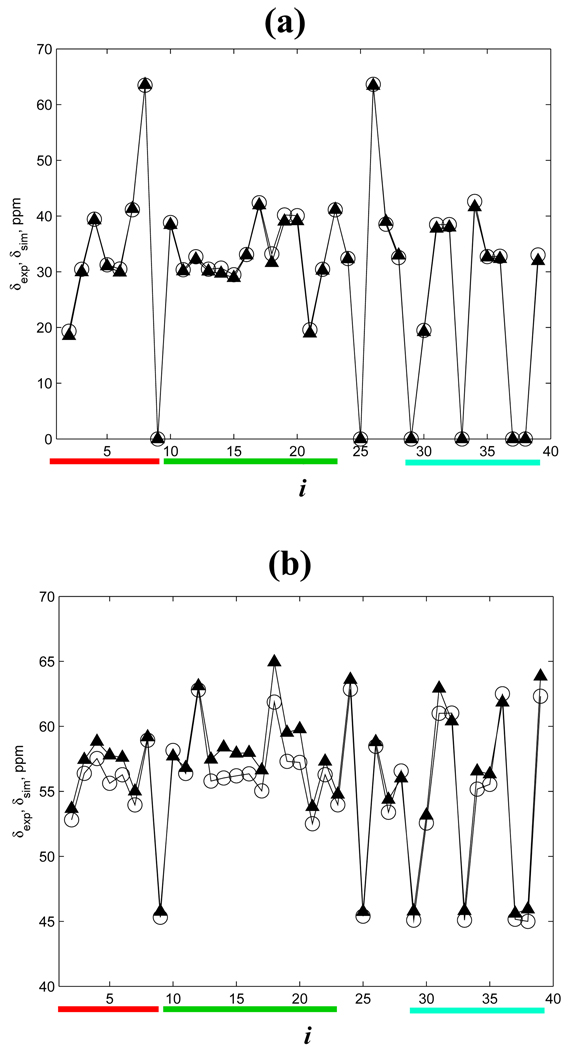
To test the implicit solvent model used in our study we computed the chemical shifts δ_sim(i) using the REMD sampling of Aβ_1–40 monomer and the program SHIFTS.⁴⁶ We choose to analyze C_α and C_β chemical shifts because of their sensitivity to α-helix and β-strand structures.⁴⁷ Fig. 3 shows the comparison of δ_sim(i) with the corresponding experimental chemical shifts δ_exp(i) measured by Zagorski and coworkers for Aβ_1–40-Met^red monomers at 278K.⁴⁷ It is seen that the C_β experimental and simulation chemical shifts are in perfect agreement (the correlation factor 0.999). The consistency of C_α δ_sim(i) and δ_exp(i) is also reasonably good (the correlation factor of 0.987). Some discrepancy between δ_sim(i) and δ_exp(i) for the residues 4–7 and 12–20 suggests that our simulations somewhat overestimate the helix fraction for these residues.^27,48 However, the overall agreement of the experimental and in silico distributions of chemical shifts suggests that the implicit solvent model reproduces the conformational ensemble of Aβ_1–40 monomers.

Fig. 3.

Experimental δ_exp(i) (open circles) and simulation δ_sim(i) (triangles) chemical shifts in Aβ_1–40 monomer as a function of residue number i: (a) C_β atoms, (b) C_α atoms. Chemical shifts of Gly C_β atoms are set to zero. The red, green, and aqua bars represent the NT, CR, and CT regions in this figure and in Fig. 4,Fig. 5,Fig. 7.

Results

Using REMD we investigated the distribution of structures sampled by Aβ_1–40 monomers and dimers (Fig. 1). We have previously showed that the amino-truncated Aβ_10–40 peptides dock to amyloid fibrils and assume ordered β-sheet conformations at the locking temperature T_l ≈ 360K.³³ Consequently, we report the structural properties of Aβ_1–40 monomers and dimers and compare them with those of Aβ_10–40 at the temperature 360K. The REMD simulations of Aβ_10–40 were published by us earlier.²⁷ Following the allocation of β-structure in Aβ_1–40 amyloid fibril,¹⁷ we distinguish three sequence regions in Aβ_1–40 - the N-terminal (residues 1 to 9, denoted as NT); the central region (residues 10 to 23, CR), which corresponds to the first fibril β-strand; and the C-terminal (residues 29 to 39, CT), which corresponds to the second fibril β-strand (Fig. 1). In what follows the changes in Aβ_1–40 secondary structure or free energy refer to the differences with respect to the truncated peptide Aβ_10–40.

Comparison of Aβ_1–40 and Aβ_10–40 secondary structure

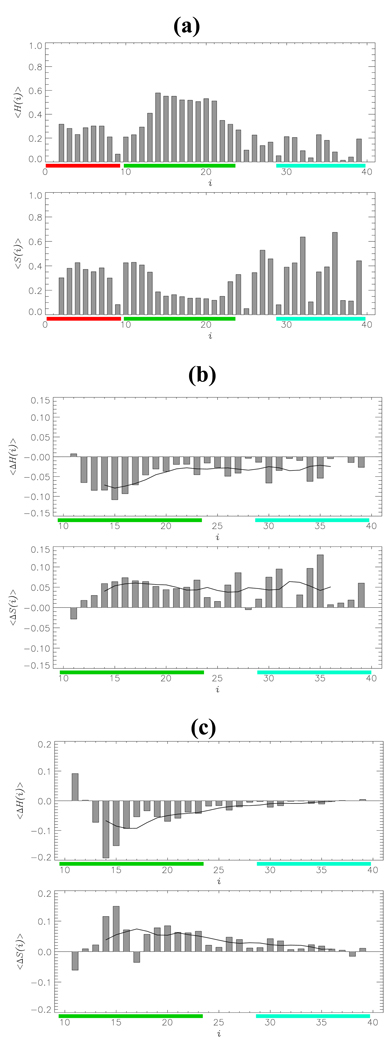
Using the REMD sampling we computed the distribution of secondary structure as described in Model and Simulation Methods. On an average, the fractions of residues in the β-strand and helix conformations in Aβ_1–40 monomer are < S >= 0.30 and < H >= 0.27. Fig. 4a shows the fractions of helix < H(i) > and β-strand < S(i) > structure formed by individual residues i in Aβ_1–40 monomer. It is seen that the helical conformations tend to localize in the central region CR (residues 14–21), in which the average helical fraction is < H(CR) >= 0.43. Elsewhere in Aβ_1–40 monomer the helical structure is less frequent (in the NT region, < H(NT) >= 0.25; in the CT, < H(CT) >= 0.12). The β-strand conformations are frequently observed in the NT (< S(NT) > = 0.32) and CT (< S(CT) >= 0.34) regions, but are less probable in the CR (< S(CR) >= 0.23).

Fig. 4.

(a) Thermal distributions of the fractions of helix < H(i) > and β-strand < S(i) > structures formed by individual residues i in Aβ_1–40 monomer. The average fraction of β-strand marginally exceeds that of helix states. (b,c) Changes in secondary structure < ΔS(i) > and < ΔH(i) > for residues i in Aβ_1–40 monomer (b) and dimer (c) with respect to Aβ_10–40 species. Black curves represent the smoothed < ΔS(i) > and < ΔH(i) > profiles obtained with the sliding window of seven residues. In the monomer, changes are spread through the sequence, whereas in the dimer they tend to localize within the CR region.

Compared to Aβ_10–40 monomer the fraction of β-strand structure in Aβ_1–40 is increased by <ΔS>=<S>Aβ_1–40 − <S>Aβ_10–40 =0.06 (from 0.24 to 0.30), while the helix fraction is decreased by <ΔH>=<H>Aβ_1–40 − <H>Aβ_10–40 =−0.05 (from 032 to 0.27). Fig. 4b demonstrates the changes in secondary structure, which occur in Aβ_1–40 monomer compared to Aβ_10–40, <ΔS(i)>=<S(i)>Aβ_1–40 − <S(i)>Aβ_10–40 and <ΔH(i)>=<H(i)>Aβ_1–40 − <H(i)>Aβ_10–40. The largest decrease in helical population < ΔH(CR) >= −0.08 occurs in the CR region, whereas in the CT it is smaller (< ΔH(CT) >= −0.03). In contrast, the increase in β-structure fraction is spread throughout Aβ_1–40 monomer (< ΔS(CR) >= 0.06 and < ΔS(CT) >= 0.05). Overall, the largest increase in < S(i) > occurs at the positions 14–23,26,27,30,31,34,35,39, whereas the largest decrease in < H(i) > is seen at 12–18,23,26,27,30,34,35. Two further observations follow from Fig. 4b. First, the secondary structure changes < ΔS(i) > and < ΔH(i) > are anticorrelated (the correlation coefficient is −0.6). Second and, more importantly, the window-averaged profiles of < ΔS(i) > and, to a lesser degree, of < ΔH(i) > suggest that the changes in secondary structure caused by the inclusion of the NT are not localized within the CR region, but extend over entire Aβ_1–40 sequence.

The structural changes in Aβ_1–40 dimer are similar to those observed for the monomer. The fraction of β-structure < S > is increased from 0.37 (Aβ_10–40) to 0.40 (Aβ_1–40, < ΔS >= 0.03), while the corresponding decrease in helical fraction is from 0.21 to 0.18 (< ΔH >= −0.03). As a result, the amount of β-structure in Aβ_1–40 dimer exceeds that of helix by a factor of 2. The changes in secondary structure for individual residues are shown in Fig. 4c. The largest changes < ΔS(i) > and < ΔH(i) > are observed in the CR region, where < ΔS(CR) >= 0.05 and < ΔH(CR) >= −0.06. In contrast, the secondary structure changes in the CT region are minor (< ΔS(CT) >= 0.01 and < ΔH(CR) >≈ 0.0). As in Aβ monomers the changes in β-strand and helix structure are anticorrelated (the correlation coefficient is −0.8). Consequently, there appears to be a direct interconversion of helix and β-strand structures, which bypasses the random coil conformations.

The analysis of the secondary structure in Aβ dimers suggests that the changes tend to localize in the CR region adjacent to the NT, while being relatively weak in the CT region, which is separated from the NT by 20 amino acids. This finding contrasts that seen in Aβ monomer, in which changes in secondary structure are spread across the entire Aβ_1–40 sequence (compare (b) and (c) in Fig. 4).

Distribution of intrapeptide interactions in Aβ_1–40

One may expect that the differences in conformational ensembles sampled by Aβ_1–40 and Aβ_10–40 are related to the interactions formed by the NT. To explore this possibility we computed the thermal map < C_m(i, j) > of contacts formed between the residues i and j in Aβ_1–40 monomer (Fig. 5a). This figure shows that a large fraction of contacts are local (|i– j| ≤ 6). From the contact map it follows that the total number of side chain contacts is < C_m >= 48.9 and about 56% of them falls into the local category. It is also clear that the NT region forms long range interactions with the CR and CT regions. Indeed, the thermal probability of the NT to form long range (|i– j| > 6) side chain contacts with the 10–40 sequence fragment is 0.97. To directly assess the role of the NT interactions in Aβ_1–40 monomer we plot in Fig. 5b the number of contacts formed by the NT with the residues 10 ≤ i ≤ 40, < K_m(i) >. The total number of contacts formed between the NT and the residues 10–40 is < K_m >= 15.1. Because most of the side chain contacts in Aβ_1–40 monomer are local, the largest values of < K_m(i) > are observed within the CR region, although significant number of contacts is also formed with the CT. Specifically, from Fig. 5b we compute that the overall number of contacts, which the NT forms with the CR and CT, are < K_m(CR) >= 7.8 and < K_m(CT) >= 5.0, respectively. In contrast, it follows from Fig. 5b that the number of hydrogen bonds (HB) between the NT and the residues 10–40 < N_m > is only 2.7.

Fig. 5.

(a) The thermal contact map < C_m(i, j) > displays the probabilities of forming side chain contacts between amino acids i and j in Aβ_1–40 monomer. < C_m(i, j) > is obtained by averaging over the canonical ensemble generated by REMD and is color coded according to the scale shown. The contact map indicates that the NT region forms interactions with the CR and CT regions. (b) The numbers of intrapeptide side chain contacts < K(i) > and HBs < N(i) > formed by the NT with the residues i (10 ≤ i ≤ 40) are shown by thick and thin curves, respectively. The data for monomer and dimer are in black and gray. Compared to side chain contacts the NT region forms few HBs with the rest of Aβ_1–40 sequence.

Fig. 5b also compares the intrapeptide interactions formed by the NT in Aβ_1–40 monomers and dimers. The number of intrapeptide contacts formed by the NT with the residues 10 ≤ i ≤ 40 in the dimer, < K_d(i) >, is similar to < K_m(i) > in the CR region, but is noticeably smaller in the CT. In fact, the overall numbers of contacts, which the NT forms with the CR and CT regions in the dimer, are < K_d(CR) >= 7.2 and < K_d(CT) >= 2.8, respectively. The total number of intrapeptide contacts between NT and the residues 10–40 in the dimer is < K_d >= 11.8. As for Aβ_1–40 monomer the total number of intrapeptide HBs between the NT and the residues 10–40 in the dimer < N_d > is small (2.6).

Effect of Aβ_1–40 amino-terminal deletion on the free energy landscape

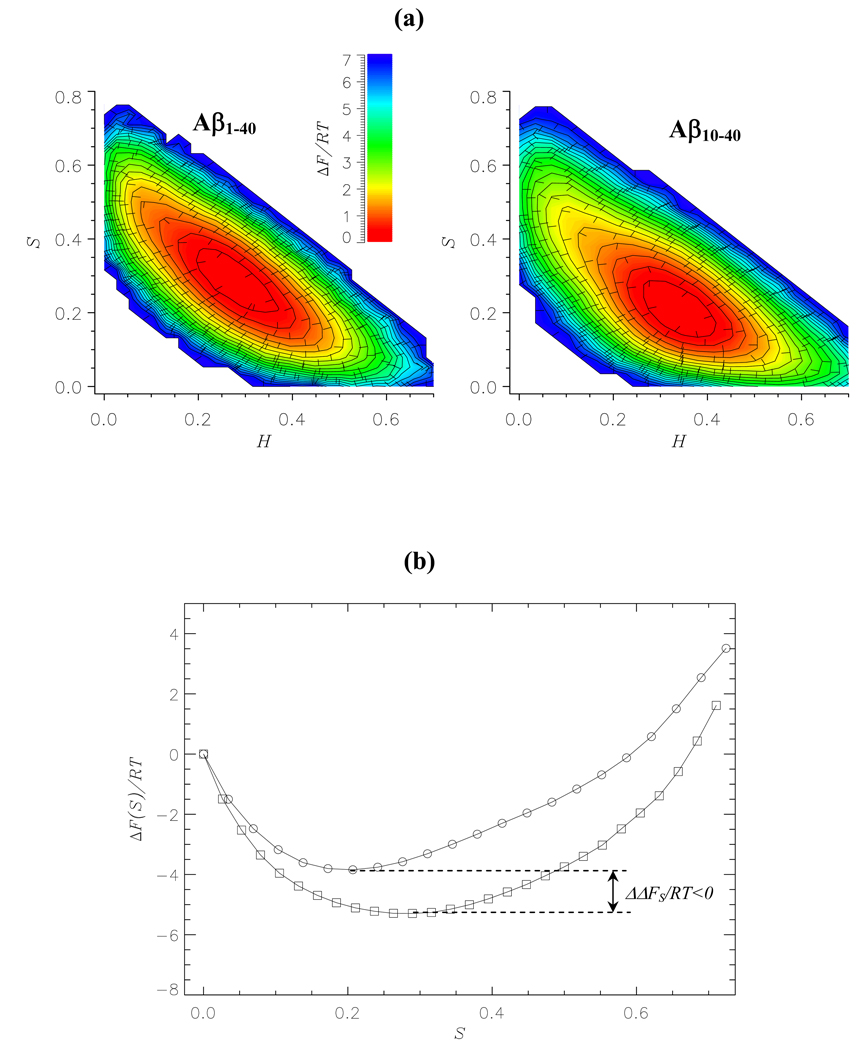
To further assess the impact of the NT region we used REMD simulations to compute the free energy contour plot ΔF(S,H) for Aβ_1–40 monomer as a function of β-strand S and helix H fractions. Fig. 6a shows that compared to Aβ_10–40 monomer the Aβ_1–40 free energy basin becomes broader and shifts from the region of H ~ 0.35 and S ~ 0.2 to H ~ 0.25 and S ~ 0.3. This shift in free energy is consistent with the changes in the strand and helix populations, < ΔS > and < ΔH >, described above. To provide a quantitative estimate of free energy change we plot in Fig. 6b the free energies of Aβ_10–40 and Aβ_1–40 monomers as a function of S. Addition of nine amino-terminal residues to Aβ_10–40 decreases the free energy of β-structure by ΔΔF_S = ΔF_S(Aβ_1–40)–ΔF_S(Aβ_10–40) = −1.9RT and shifts its minimum from S ~ 0.17 to ~ 0.27. Difference in free energy of the helix structure is less than RT. The changes in free energy landscape for Aβ_1–40 dimers are similar to those for the monomers. For example, the free energy minimum of the β-structure in the dimer deepens by ΔΔF_S = −1.6RT (data not shown). Therefore, the NT region in Aβ_1–40 appears to stabilize β-structure by decreasing its free energy.

Fig. 6.

(a) Two-dimensional projections of the free energy ΔF(H,S) as a function of the helix and strand fractions, H and S: Aβ_1–40 monomer (left panel); Aβ_10–40 monomer (right panel). The minima in free energy are set to zero. The values of ΔF(H, S) are color coded according to the scale. (b) One-dimensional profiles of the free energy ΔF(S): Aβ_1–40 monomers (squares); Aβ_10–40 monomers (circles). The states with zero strand contents are set to have zero free energy. The plots in (a) and (b) demonstrate that β-strand structure is stabilized in Aβ_1–40 compared to Aβ_10–40. ΔΔF_S is the free energy difference between the β-strand states in Aβ_1–40 and Aβ_10–40. β-strand states are operationally defined to have free energies less than −2RT.

Aβ_1–40 aggregation interface

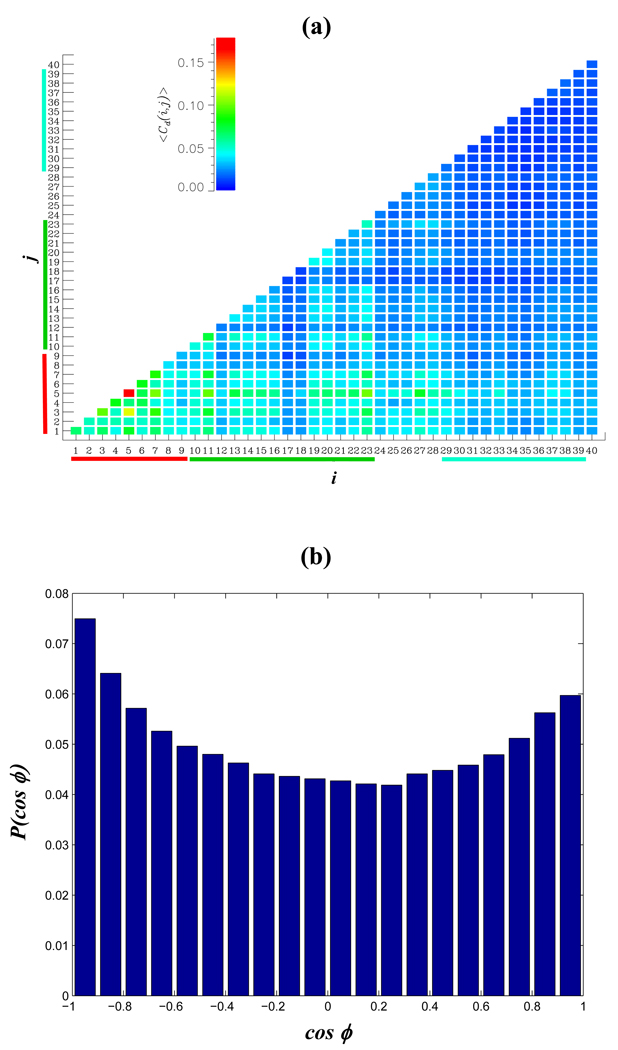
To probe the aggregation interface in Aβ_1–40 dimer, we used REMD simulations to compute the thermal map < C_d(i, j) > of interpeptide contacts between the residues i and j. Fig. 7a shows that the distribution of interpeptide contacts is highly uneven. Most frequently, they are formed by the NT and CR regions, whereas the CT is relatively rarely involved in dimer formation (as illustrated in Fig. 1b). From Fig. 7a we compute that the numbers of interpeptide side chain contacts formed by the NT, CR, and CT regions are < C_d(NT) >= 15.1, < C_d(CR) >= 16.8, < C_d(CT) >= 9.0 or 1.7, 1.2, and 0.8 per residue, respectively. The total number of interpeptide contacts is < C_d >= 46.9. More detailed description of the aggregation interface can be inferred from the Table 1a. The largest number of interpeptide contacts is formed between the CR regions followed by the NT-CR and NT-NT interactions. The least frequent contacts are formed by the CT regions.

Fig. 7.

(a) The thermal contact map <C_d(i, j) > visualizes the probabilities of forming interpeptide side chain contacts between the residues i and j in Aβ_1–40 dimer. The aggregation interface in the dimer involves primarily the NT and CR regions, whereas the CT region is weakly engaged in interpeptide interactions. < C_d(i, j) > is color coded according to the scale. (b) The orientation of the CR regions in Aβ_1–40 dimer is given by the probability distribution P(cosϕ), where ϕ is the angle between the CRs. Antiparallel aggregation interface is weakly preferred.

Table 1.

Aggregation interfaces in Aβ dimers^{‡ †}

(a) Numbers of interpeptide side chain contacts < Cd(s1,s2) > in Aβ1–40 dimer
	NT	CR	CT
NT	4.7	5.3	3.3
CR		6.2 (0.41)	3.6 (0.24)
CT			1.9 (0.12)

(b) Numbers of interpeptide side chain contacts < Cd(s1,s2) > in Aβ10–40 dimer
	CR	CT
CR	8.3 (0.41)	4.8 (0.24)
CT		2.3 (0.11)

^‡s1 and s2 denote sequence regions NT, CR, or CT. Due to exhaustive REMD sampling < C_d(s1,s2) >≈< C_d(s2,s1) >.

^†numbers in parenthesis indicate the fractions of (s1,s2) contacts computed with respect to the total number of interpeptide contacts formed by the CR and CT regions in the 10–40 fragment of the dimer.

To probe the orientation of Aβ_1–40 peptides in the dimer we considered the vectors R⃗(k) = r⃗_Cα (23, k) − r⃗_Cα (10, k), where r⃗_Cα (23, k) and r⃗_Cα (10, k) are the radius-vectors of C_α atoms of the residues Asp23 and Tyr10 in the peptide k(=1,2). By definition, R⃗(k) describes the orientation of the CR region. This region was selected, because the fraction of ordered structure (helix or strand) in the CR is high (~ 0.7) and, consequently, this region is relatively rigid. More importantly, the CR forms the largest number of contacts < C_d (CR) > in the aggregation interface. Fig. 7b displays the distribution P ( cosϕ), where ϕ is the angle between R⃗(1) and R⃗(2) The distribution P(cosϕ), which is weakly bimodal, shows a slight preference of Aβ_1–40 peptides to form antiparallel aggregation interface. The probability of antiparallel orientation (i.e, of cosϕ < 0) is 0.53.

The Aβ_1–40 aggregation interface emerging from Fig. 7a can be compared with that for Aβ_10–40 dimer.²⁷ At T = 360K used in this study the numbers of interpeptide side chain contacts formed by the CR and CT Aβ_10–40 regions are < C_d(CR) >= 16.1 and < C_d(CT) >= 8.6 or 1.2 and 0.8 per residue, respectively. Table 1b shows that most of interpeptide contacts are formed between the CR regions, whereas the contacts between CT terminals are almost four-fold less frequent. We also note that Aβ_10–40 dimer forms an antiparallel aggregation interface with almost the same probability (0.60)²⁷ as reported above for Aβ_1–40.

We have also computed the thermal distribution of interpeptide HBs for Aβ_1–40 dimers (data not shown). The numbers of HBs formed by the NT, CR, and CT regions are 2.5, 2.3, and 1.5, respectively. The largest number of interpeptide HBs are formed between the NT regions (0.9) followed by those formed between the NT and CR (0.7) and between the CR regions (0.7). The smallest number of HBs is formed between the CTs (0.3). The total number of interpeptide HBs in Aβ_1–40 dimer is 7.0. Two conclusions can be drawn from these computations. First, the distribution of interpeptide HBs is qualitatively similar to that of side chain contacts. Second, backbone HBs appear to play minor role in the dimer aggregation interface as the number of side chain contacts exceeds that of HBs by about a factor of seven.

Discussion

Aβ_1–40 and Aβ_10–40 peptides have similar conformational ensembles

In this study we investigated the impact of the amino-terminal on the conformational ensembles of Aβ peptides. The role of the NT region was inferred from the comparison of the secondary structure, interactions, and free energy landscapes of full-length Aβ_1–40 and amino-truncated Aβ_10–40 peptides. We showed that compared to Aβ_10–40 the fraction of β-structure in Aβ_1–40 monomer increases 25% (< ΔS >= 0.06), whereas the helix fraction decreases about 16% (< ΔH >= −0.05). These structural changes are consistent with those observed in the free energy landscape (Fig. 6).

With respect to Aβ_10–40 the secondary structure changes in Aβ_1–40 monomer occur in both the CR and CT regions (Fig. 4b). For example, the β fractions in the CR and CT increase 35% (< ΔS(CR) >= 0.06) and 17% (< ΔS(CT) >= 0.05), respectively. The helix fractions in the CR and CT decrease 16% (< ΔH(CR) >= −0.08) and 20% (< ΔH(CT) >= −0.03), respectively. In Aβ_1–40 dimers the inclusion of the NT also enhances β-strand structure (by 8% or < ΔS >= 0.03) and reduces the probability of helix conformers (by 14% or < ΔH >= −0.03). However, these changes mainly occur near the NT (Fig. 4c). Within the CR region the β-strand fraction increases 14% (< ΔS(CR) >= 0.05), while the helix fraction decreases 19% (< ΔH(CR) >= −0.06). In contrast, in the CT region the changes in helix and β-strand fractions are negligible (less than 3% or ≤ 0.01).

The changes in secondary structure can be rationalized by considering the number of contacts formed by the NT with the residues 10 ≤ i ≤40 in Aβ_1–40 monomer and dimer. In the monomer the NT forms with the CT about two-thirds of the contacts which it forms with the CR (< K_m(CT) >= 5.0 vs < K_m(CR) >= 7.8). However, in Aβ_1–40 dimer the NT forms with the CT only one-third of the contacts which it forms, on an average, with the CR (< K_d(CT) >= 2.8 vs < K_d(CR) >= 7.2). By comparing the changes in the secondary structure and the distribution of intrapeptide contacts one may suggest the two are related. Because the NT in Aβ_1–40 monomer forms large number of contacts with both the CR and CT regions, the changes in secondary structure propagate the entire Aβ sequence (data above and Fig. 4b and Fig. 5b). In contrast, in Aβ_1–40 dimer the NT tends to form most interactions with the CR region, which, in turn, experiences the largest change in secondary structure (data above and Fig. 4c and Fig. 5b). Furthermore, in Aβ_1–40 dimer the number of NT-CT contacts is twice smaller than in the monomer. Accordingly, the changes in the strand and helix fractions in the dimer CT region are negligible compared to those in the monomer CT.

To further probe the relation between the NT interactions and the changes in secondary structure, we clustered Aβ_1–40 monomer conformations as described in Model and Simulation Methods. We found that 80% of structures can be grouped into four large clusters (Table 2). The structural clusters differ with respect to the numbers of contacts between the NT and CR, K(NT –CR), and between the NT and CT, K(NT –CT), and with respect to the fractions of β-strand and helix in the CR (S(CR) and H(CR)) and CT (S(CT) and H(CT)) regions. In Table 2a the clusters are arranged in the descending order of K(NT –CR), which ranges from 8.0 in CL1 to 6.7 in CL4. Importantly, the fraction of helix H(CR) monotonically increases from 0.41 (CL1) to 0.54 (CL4), while the strand fraction S(CR) reveals a two-fold decrease, from 0.27 (CL1) to 0.13 (CL4). Similarly, Table 2b lists the clusters in the descending order of the number of NT-CT contacts, K(NT –CT). An almost two-fold decrease in K(NT –CT) from 5.8 (CL1) to 3.0 (CL4) results in two-fold monotonic increase in the helix fraction H(CT), from 0.10 (CL1) to 0.20 (CL4). Simultaneously, the strand fraction shows a matching reduction from 0.37 (CL1) to 0.18 (CL4). As follows from Table 2b the formation of NT-CT contacts results in the decrease in the monomer radius of gyration from 15.4 Å(CL4) to 14.1 Å(CL2). In summary, Table 2 demonstrates that with the increasing number of contacts formed by the NT the helix fractions in the CR and CT reveal monotonic decrease, while the β-strand fractions show an almost perfect opposite trend. As illustration to cluster analysis two representative monomer conformers with formed and broken NT interactions are shown in Fig. 1a. Taken together the findings presented above suggest that the interactions of the NT with the CR and CT regions are responsible for the changes in their secondary structure.

Table 2.

Structural clusters of Aβ_1–40 monomer

(a) InteractionsbetweentheNT and CR regions‡
cluster	p†	K(NT – CR)	H(CR)	S(CR)
CL1	0.31	8.0	0.41	0.27
CL2	0.18	7.4	0.46	0.22
CL3	0.19	7.0	0.53	0.12
CL4	0.12	6.7	0.54	0.13

(b) Interactions between the NT and CT regions‡
cluster	p†	K(NT – CT)	H(CT)	S(CT)	Rg, Å
CL1	0.19	5.8	0.10	0.37	14.3
CL2	0.31	5.4	0.10	0.38	14.1
CL3	0.12	4.2	0.14	0.33	15.0
CL4	0.18	3.0	0.20	0.18	15.4

^‡although both tables list the same cluster distribution, the clusters are relabeled according to the changes in K(NT – CR) in (a) and in K(NT – CT) in (b)

^†the fraction of structures included in the cluster

It is important to note that the analysis of intrapeptide interactions indicates that the number of HBs formed by the NT with other sequence regions is six-fold smaller than the number of respective side chain contacts (< N_m >= 2.7 vs < K_m >= 15.1). Similar result is obtained for Aβ dimer. Thus, it appears that the secondary structure changes in Aβ are driven mostly by side chain interactions rather than backbone HBs.

As a result of the NT interactions, the β-content in Aβ_1–40 monomers exceeds the helical one (0.30 vs 0.27), but most of Aβ_1–40 residues still adopt disordered random coil conformations (their fraction is 0.43). (For comparison, in the Aβ_10–40 monomer the fractions of strand, helix, and coil structures are 0.24, 0.32, 0.44 at 360K, respectively.²⁷) The distribution of Aβ_1–40 secondary structure obtained by us is consistent with previous experimental and simulation studies, which did not identify a stable native fold in Aβ monomer.^23,25,47

In summary, we traced the differences in the structural ensembles of Aβ_1–40 and Aβ_10–40 to the side chain interactions formed by the amino-terminal. However, because structural changes are relatively small (not to exceed 35%) and both peptides retain overall random coil structure, we conclude that there are no qualitative differences in the conformational ensembles sampled by Aβ_1–40 and Aβ_10–40. This conclusion finds support in the comparison of chemical shifts computed from simulations²⁷ and obtained experimentally.⁴⁷ In our previous simulations of Aβ_10–40 we computed the chemical shifts for C_α and C_β atoms and showed that are in good agreement with the experimental shifts measured by Zagorski and coworkers for Aβ_1–40 monomer.⁴⁷ This result implies that the truncation of the amino-terminal from Aβ_1–40 does not lead to qualitative changes in the structural properties of the peptide. In other words, the conformational ensembles of Aβ_10–40 and Aβ_1–40 appear to be qualitatively similar. Because the overall structural changes in the dimer are smaller than in the monomer and tend to affect the sequence region adjacent to the NT, we propose that in higher order oligomers the impact of the NT deletion should further diminish.

Aβ_1–40 and Aβ_10–40 peptides have similar aggregation interfaces

Using REMD simulations we mapped the aggregation interface in Aβ_1–40 dimer. The results suggest that the aggregation interface primarily involves the NT and CR regions, whereas the CT is relatively rarely engaged in dimer formation. For example, the number of interpeptide contacts per residue formed by the NT region is twice larger than that for the CT (1.7 vs 0.8). Similarly, the number of interpeptide contacts per residue in the CR is 50% more than in the CT (1.2 vs 0.8). Table 1a also shows that the number of interpeptide contacts between the CR regions exceeds that between the CTs by a factor of 3. Qualitatively similar distribution of interpeptide interactions is obtained for Aβ_10–40 dimer,²⁷ for which the number of contacts (per residue) formed by the CR regions is larger than that formed by the CTs 50%. Table 1b also shows that the CT-CT contacts are almost four-fold less frequent than those between the CRs.

To provide direct comparison of the involvement of the 10–40 fragment in aggregation, we included in Table 1 the fractions of contacts computed with respect to the total number of interpeptide contacts formed by the CR and CT regions in the 10–40 dimer fragment, <C_d(CR+CT) >. In Aβ_1–40 and Aβ_10–40 dimers <C_d(CR+CT) > are 15.3 and 20.2, respectively. Table 1 shows that these contact fractions are remarkably similar for Aβ_1–40 and Aβ_10–40. These findings indicate that the distributions of contacts along the sequence and between sequence regions in Aβ_1–40 and Aβ_10–40 dimers are similar. In both cases, most interpeptide contacts are formed by the aminoterminal regions - the NT and CR regions in Aβ_1–40 and the CR region in Aβ_10–40. Additionally, both Aβ_1–40 and Aβ_10–40 dimers show a tendency to form antiparallel aggregation interface (Fig. 7b). Consequently, we surmise that the deletion of the amino-terminal in Aβ_1–40 does not qualitatively change the aggregation interface in Aβ dimers.

It is important to compare our results with those obtained by Caflisch and coworkers.⁴⁹ These authors explored the aggregation profile along Aβ_1–42 sequence using seven- and 11-mer overlapping fragments of this peptide and performing MD simulations of oligomer assembly. An aggregationprone region was identified as 12–22 with other sequence regions revealing much lower aggregation propensity. Qualitatively similar suggestion was recently put forward by Derreumaux and coworkers.⁵⁰ These reports are consistent with our findings that the CT region may not represent the primary aggregation interface.

Comparison with experimental data

It is important to compare our computational predictions with available experimental data. There are indications that the NT region plays a minor role in Aβ fibril structure. Solid-state NMR, paramagnetic resonance, and electron cryomicroscopy studies revealed that the NT region in Aβ_1–40 fibril is disordered.^16–18 Proteolysis experiments also suggested that the NT region in Aβ_1–40 fibril is exposed to solvent and is not buried in the fibril core.¹⁵ Furthermore, solid-state NMR studies of Aβ_1–40 and the amino-truncated Aβ_10–40 showed that both form very similar fibril structures.^17,19 It is worth noting that the fibril structure for Aβ_1–42 peptide also reveals disordered N-terminal region (residues 1 to 17).⁵¹

However, the NT region does affect, at least to some extent, the Aβ_1–40 aggregation pathway.²⁰ It was found that the amino-truncated Aβ_8–40 demonstrates enhanced aggregation as its sedimentation increases about 50% within 7 days compared to Aβ_1–40. An opposite trend was observed for Aβ_4–40, for which the amount of sediments decreases roughly in half. Similar conclusions follow from the experimental study, which investigated the aggregation of several Aβ mutants.⁵² While the wild-type Aβ_1–40 aggregates with the average lag time t_l,0 = 4.8h, the mutant A2T shows no discernible time lag upon aggregation (t_l = 0). An opposite trend is reported for the mutant H6R, for which t_l is increased two-fold. Interestingly, the changes in t_l caused by the NT mutations are comparable with those seen for well-studied E22G (“Arctic”, t_l = 0) or D23N (“Iowa”, t_l ≈ 1.4t_l,0) mutants.

The involvement of the NT region in aggregation has been demonstrated by photo-induced cross-linking experiments on Aβ wild-type and amino truncated oligomers.¹³ The Aβ_1–40 oligomer size distribution predominantly shows monomer, dimer, trimer, and tetramer species. Similar distributions were observed for Aβ_x–40 oligomers with x = 3 and 5, although minor subpopulations of higher order oligomers did emerge. The distribution for Aβ_10–40 reveals a shift to smaller oligomers (monomers to trimers) due to partial depletion of the tetramer and higher order oligomer populations. Dramatic changes in the oligomer size distribution occur only with the deletion of Tyr10 (x = 11), for which no species larger than dimers are observed. The comparison of the deletions of N- and C-terminal amino acids demonstrates that the length of the C-terminal rather than of the N-terminal exerts the largest effect on oligomerization pathway.¹³

Taken together the experimental studies mentioned above indicate that the NT region is involved in Aβ_1–40 aggregation. These results are consistent with our current findings suggesting that Aβ_1–40 aggregates primarily using its amino-terminal and central sequence region (Fig. 7a and Table 1a). However, the experimental oligomer size distribution seems to suggest that the removal of the NT region (residues 1 to 9) does not qualitatively change the aggregation pathway. ¹³ This observation also agrees well with our conclusion that the aggregation interfaces in Aβ_1–40 and Aβ_10–40 dimers are similar (Table 1). As follows from our simulations the dimer assembly is mainly driven by side chain interactions rather than by backbone HBs. This observation is consistent with those made for other amyloidogenic peptides. It has been shown using explicit water MD that initial stages in oligomerization of the peptide NFGAIL primarily involve side chain interactions.⁵³

Finally, our REMD simulations show that the interactions formed by the NT region introduce a small but discernible bias toward β-structure in Aβ_1–40 conformational ensemble as revealed by the computations of secondary structure and free energy landscapes. Currently, we are not aware of secondary structure studies of amino-truncated Aβ_x–40 peptides. However, our observations are consistent with the CD measurements, which have been performed on the aggregated fragments Aβ_x–42 and compared with the data for the full-length Aβ_1–42.²⁰ It was found that the aggregated assemblies of full-length and truncated peptides are dominated by β-structure and no qualitative secondary structure differences between them have been detected.

Conclusions

We examined the effect of the deletion of the amino-terminal (residues 1 to 9) on the structure and energetics of Aβ_1–40 peptides. Using REMD simulations and comparing the conformational ensembles for the full length Aβ_1–40 and amino-truncated Aβ_10–40 monomers and dimers we arrived at the following conclusions: (1) There is a small but discernible conversion of β-strand structure into helix upon amino-terminal deletion; (2) The secondary structure changes due to amino-terminal truncation are caused by missing side chain interactions formed by the aminoterminal; (3) The amino-terminal together with the central sequence region (residues 10–23) represents the primary aggregation interface in Aβ_1–40 dimers. Strikingly, the amino-truncated peptide Aβ_10–40 retains this aggregation interface, which is reduced to central sequence region. Overall, the deletion of the amino-terminal in Aβ_1–40 monomers and dimers causes relatively minor structural and energetic changes. The analysis of available experimental data appears to support this conclusion. Based on our findings and on the studies of Aβ fibril structures^17,19 we suggest that amino-truncated Aβ_10–40 peptide represents an adequate model for studying Aβ_1–40 aggregation.