Abstract
Many ion channels show low basal activity which is increased hundreds fold by the relevant gating factor. A classical example is the activation G protein activated K+ channels (GIRK) by Gβγ subunit dimer. The extent of activation (relative to basal current), Ra, is an important physiological parameter, usually readily estimated from whole cell recordings. However, calculation of Ra often becomes non-trivial in multichannel patches, because of extreme changes in activity upon activation, from a seemingly single-channel pattern to a macroscopic one. In such cases calculation of the net current flowing through the channels in the patch, Ī, before and after activation may require different methods of analysis. To address this problem, we utilized neuronal GIRK channels activated by purified Gβγ in excised patches of Xenopus oocytes. Channels were expressed at varying densities, from a few to several hundreds per patch. We present a simple and fast method of calculating Ī using amplitude histogram analysis, and establish its accuracy by comparing with Ī calculated from event lists.This method allows the analysis of extreme changes in Ī in multichannel patches, that would be impossible using the standard methods of idealization and event list generation.
Keywords: ion channel, Kir3, patch clamp, G protein, amplitude histogram
Introduction
Single channel recordings yield important information about ion channels. The analysis of single channel recordings is based either on time-course fitting or event list analysis (Bauer et al., 1987; Jackson, 1992). Event list analysis requires implementation of idealization criterion (the most popular one is the so-called “50 % threshold crossing”) and subsequent transformation of recorded data into list of dwell times which are classified as open and closed events (Sachs et al., 1982). In a patch containing a single channel, open probability (Po) can be calculated from the above list. In addition, histograms of open and closed times distributions can be generated and fitted with exponential functions. These procedures render valuable information about minimal number of channel's open and closed states and about the rates of transitions between the states, based on assumptions of a Markov process (Colquhoun and Hawkes, 1977; Vivaudou et al., 1986; Bauer et al., 1987; Colquhoun and Hawkes, 1995; Blunck et al., 1998; Traynelis and Jaramillo, 1998). However, such analysis becomes more and more complex with the increase of number of channels in the patch, until it becomes impossible for recordings in which nearly-macroscopic activity is observed. In this case single open and closed events cannot be detected. Several methods for analysis of such high activity recordings exist (Colquhoun and Hawkes, 1977; Hosoya et al., 1996). For instance, fitting of power density spectra obtained from the recording with Lorenzian functions renders information about the number of states that the channel assumes and the transition rates between them (Colquhoun and Hawkes, 1977; Hosoya et al., 1996). However, with multi-channel recordings, the extraction of kinetic parameters using such methods becomes time-consuming and requires a great deal of correction in order to overcome problems such as erroneous shortening of closed times (Colquhoun and Hawkes, 1981). Therefore, multi-channel recordings are rarely employed for detailed kinetic analysis. Yet, analysis of average currents (Ī ) or total open probability (NPo, where N denotes the number of channels) in such recordings is often unavoidable, for instance when effects of channel modulators are being studied. In these recordings, NPo may change dramatically from a low-NPo, seemingly single-channel behavior, to a macroscopic one, or vice versa. Consequently, reliable and sufficiently simple methods of calculation of NPo and Ī in multi-channel recordings are needed. A classical example of extreme changes in NPo is demonstrated by the G protein activated potassium channels (GIRK), which are activated by Gβγ subunits of heterotrimeric G proteins (Dascal, 1997). When studied in excised patches of cardiac cells, neurons, or heterologous expression systems such as Xenopus oocytes, GIRK channels usually show low basal NPo which is increased several tens to hundreds fold after addition of purified Gβγ protein (Grigg et al., 1996; Jelacic et al., 1999; Yakubovich et al., 2000).
We have previously used estimates of Ī and NPo from idealized event lists before activation by Gβγ, and from amplitude histograms after activation, and calculated the activation ratio, Ra, as the ratio of these estimates (Peleg et al., 2002). This method is fast and apparently solves the problem of calculating Ra upon extreme changes in Ī and NPo, but its validity has not been so far tested rigorously. In the present work we describe the method in full, test the applicability of the calculations of average currents from amplitude histograms under different conditions and channel activity levels, and demonstrate it applicability in a wide range of NPo values of the GIRK channel. We show that calculation of Ī, NPo and Ra under different experimental conditions can be done directly without the estimation of number of channels in multi-channel patches and thus renders important quantitative measure of the effect under study (in this case, channel activation by Gβγ).
Materials and Methods
Electrophysiology
All experiments were carried out in accordance with the Tel Aviv University Institutional Animal Care and Use Committee (permits no. 11-99-47 and 11-05-064). Xenopus laevis frogs were maintained and operated, and oocytes were collected, defolliculated, and injected with RNA as described. Oocytes were injected with 10–100 pg/oocyte RNA of GIRK1 and GIRK2 subunits to obtain low density of channels in the patch, and with 1–2 ng RNA to obtain high density (Peleg et al., 2002). After RNA injection, oocytes were incubated for 3 to 5 days at 20–22°C in ND96 solution (96 mM NaCl, 2 mM KCl, 1 mM MgCl2, 1 mM CaCl2, 5 mM HEPES, pH 7.5), supplemented with 2.5 mM Na Pyruvate and 50 µg/ml gentamycine. All experiments were done at 20–22°C. Patch clamp experiments were done as described (Schreibmayer et al., 1996; Yakubovich et al., 2000). Currents were recorded at −80 or −120 mV, filtered at 2 kHz, and sampled at 5 or 10 kHz. Patch pipettes had resistances of 0.8 – 2.5 MΩ. Pipette solution contained, in mM: 144 KCl, 2 NaCl, 1 MgCl2, 1 CaCl2, 1 GdCl3, 10 Hepes/KOH, pH 7.5. GdCl3 completely inhibited the stretch-activated channels. Bath solution contained, in mM: 130 KCl, 2 MgCl2, 1 EGTA, 2 Mg-ATP, 10 Hepes/KOH, pH 7.5. After seal formation, the patches were excised and exposed to air to prevent the formation of closed membrane vesicles at the tip. Purified recombinant Gβ1γ2 was prepared and used as described (Schreibmayer et al., 1996; Yakubovich et al., 2000). Stock solutions of Gβγ were diluted into 50 µl of the bath solution to a final concentration of 200 or 400 nmol/L, added to the 500 µl solution in the bath, and stirred.
Analysis of event lists
Event lists were generated from recordings of GIRK channel activity using Clampfit 9 (Molecular Devices Corp., Sunnyvale). For the generation of event lists we utilized the “50 % crossing” criterion (see below). Event lists were imported utilizing custom software into Matlab 7.2 (Mathworks inc.). The open probability (Po) for the low activity recordings and the NPo (where N stays for the number of channels in patch) for intermediate activity recordings were calculated according to:
| (1) |
where x denotes the opening level (e.g. in case of 2 channels open together n is equal to 2) , no is the number of openings, Φ is the total recording time, is the duration of single opening.
Amplitude histograms and calculation of delimiters
Amplitude histograms were created either in Clampfit 9 (Molecular Devices Corp., Sunnyvale), Excel (Microsoft), or Matlab 7.2 (Mathworks inc.) utilizing equal width linear bins. Analysis of recordings demonstrating low to intermediate level of activity (see Results for definitions) required implementation of a delimiter. The delimiter (del) is an amplitude value above which all the currents are defined as channel openings and below it as background current. It is clear that absolute discrimination between channel openings and background current is impossible and every way of calculation of delimiter will lead to misclassification of events. We utilized several methods to calculate the delimiter. The first method is based on “50% crossing criterion”:
| (2) |
where i1 is the amplitude of the single opening of the channel as observed in the record and the b̅ is the midpoint (average) amplitude of the baseline current. In a simple case, i1 and b̅ values are obtained from visual inspection of the amplitude histogram. The peak which corresponds to the lowest current amplitude is defined as b̅ and the second peak as i1. When b̅ is equal or is offset to 0 Eqn. (2) reduces to:
| (3) |
where IΛ is the single opening amplitude (Colquhoun and Hawkes, 1995). Alternatively, i1 and b̅ can be estimated by fitting the amplitude histogram to a sum of Gaussian functions according to:
| (4) |
where f(x) is the number of points in a bin with current amplitude x, while μi ,σI and Ai are respectively the mean, standard deviation and the total number of points belonging to the ith component (consequently, μ1=b̅ and μ2= i1).
The second method of defining the delimiter is described in detail in the work of Howe et al. (Howe et al., 1991). This method takes into account the fact that imposition of any kind of delimiter leads to misclassification of certain number of points. Namely, some points of the record, which contain no channel openings, are defined as belonging to an opening, and vice versa. Such misclassification results from random fluctuations of the amplitudes of channel openings, baseline and also the effects of sampling and filtering. Consequently, delimiter is defined as the amplitude that minimizes the total area which is misclassified, i.e. erroneously defined as either the noise or the open channel amplitude. Thus, del according to Howe et al. is a solution of quadratic equation of the form
| (5) |
| (6) |
| (7) |
| (8) |
while μi, σI and Ai are defined as above in Eqn. (4).
Calculation of average current
Average current was calculated either from raw data, amplitude histogram or event list. In each case a delimiter (see above) is introduced. In general the average current is calculated according to:
| (9) |
where Ī is the average channel current value, id is the amplitude of an acquisition point (for i>del only) – points with amplitude above the delimiter, and l is the number of points in the recording. Eqn. (9) allows the calculation of average current directly from raw data if del is known or estimated.
Average current based on amplitude histogram is calculated according to:
| (10) |
where fi is the number of points in the bin with amplitude i > del.
Simulation and analysis of simulated data
In order to simulate single channel data we utilized 2 state scheme:
| Scheme 1 |
where α and β are, respectively, the opening and closing transition rates (in s−1).
According to this scheme the open probability (Po) and frequency of openings (fo) can be calculated according to:
| (11) |
| (12) |
We calculated the α and β values for Po of .05 and 0.5 and fo of 10, 100. Single channel data was generated utilizing QUB software (Qin et al., 1996,1997, 2000a, b). We assumed that b̅ is 0 and the IΛ is 1 pA, with standard deviation of both equal to 0. Simulated data was imported to Matlab 7.2 (Mathworks inc.) and processed there. In particular, in order to simulate the random fluctuations of the current, we utilized the algorithm shown in the attached ASCII file (see Supplementary material). This algorithm introduces a noise component which is normally distributed with a mean of zero and a given standard deviation. The ratio of the current amplitude to the standard deviation of noise (defined as signal to noise ratio (SNR)) was simulated as 10, 5 and 2.5.
Results
Presentation of the problem
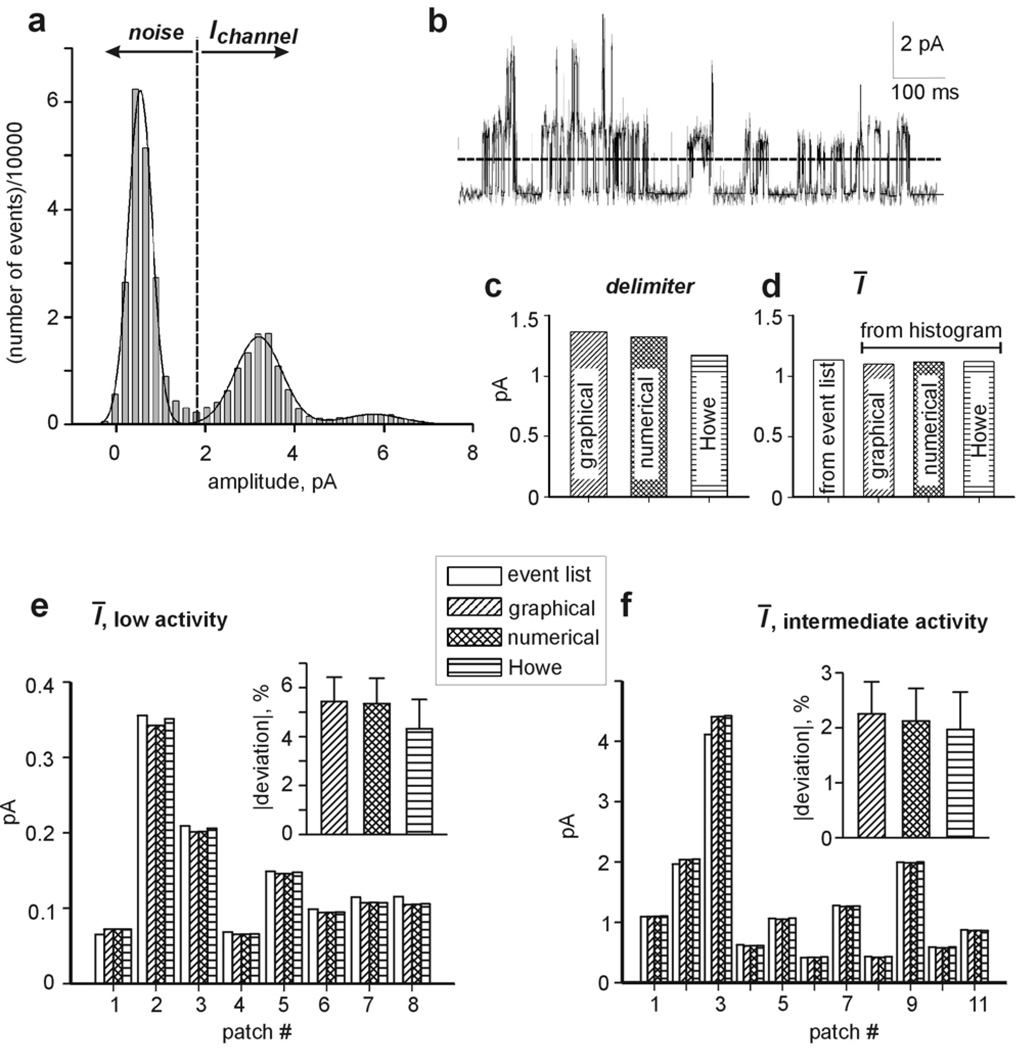
We recorded the activity of non-stimulated or Gβγ-stimulated GIRK1/2 channels (composed of GIRK1 and GIRK2 subunits) in cell-attached or excised patches of Xenopus oocytes. In general, 3 types of activity can be observed in such recordings. In patches containing one to three channels, single openings and closures can be readily discerned, and a complete kinetic analysis is often possible (e.g. Fig. 2b). With increase in channel density, overlaps corresponding to simultaneous openings of several channels can be observed, although single openings are occasionally seen (not shown). In high channel density patches, neither single channel openings nor closures can be observed and so-called “pseudomacroscopic” behavior is observed (Fig. 1c).
Fig. 2.
Analysis of Ī from amplitude histograms of GIRK1/2 activity in the presence of Gβγ. a shows an amplitude histogram of a 1 min interval of recording from an excised patch with intermediate density of GIRK1/2. Solid line corresponds to the fit of histogram with Gaussian (3 components according to equation 3, A1=6.4×104 , A2=1.6×104 , A3= 1870, μ1=.53, μ2=3.19, μ3=5.77, σ1=.38, σ2=.74, σ3=.94). The vertical dotted line represents the position of the delimiter determined from the above fit. A representative stretch of this record in shown in b, where the solid line delineates idealized data, and dashed line shows the 50 % crossing amplitude utilized for idealization. c compares the net values of delimiters (after subtraction of the baseline current) calculated using the three methods (graphical, numerical from Gaussian fit, and by Howe et al. (Howe et al., 1991)) The threshold for the calculations utilizing 50 % crossing criterion (from event list) was set as the graphical delimiter value. d presents a comparison of Ī calculated from the amplitude histogram using delimiters shown in C, and Ī calculated from the from event list (left bar). e and f demonstrate the application of the methods illustrated in a–d to calculate Ī in 8 single channel patches where no overlaps were observed during entire recording time (e) and 11 patches demonstrating intermediate level of activity (f). In each patch the results are presented in the same way as in d. Insets show the average absolute deviation of Ī values calculated from the histograms using 3 different delimiters, from Ī derived from the event list.
Fig. 1.
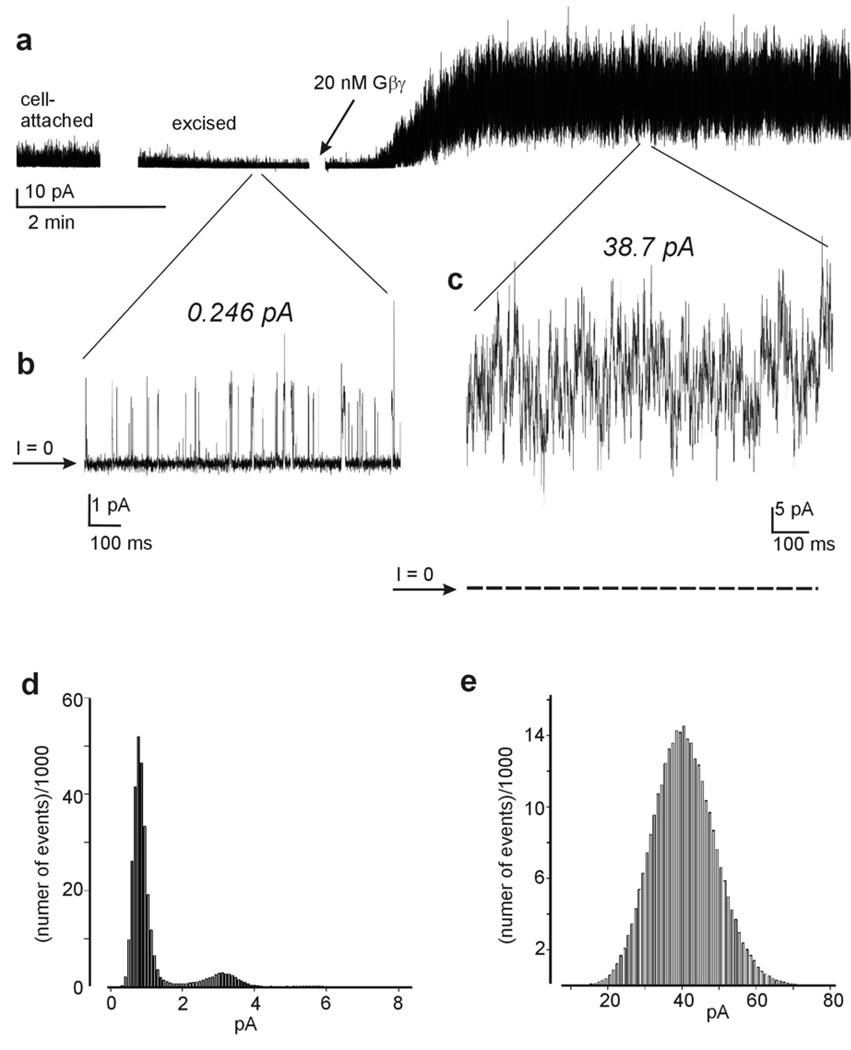
A representative recording of activation of GIRK1/2 channels by Gβγ. a, the complete record, starting with recording in the cell-attached mode, then excision into bath solution, and finally the addition of 20 nM Gβγ. Periods of excision/air exposure and addition of Gβγ were accompanied by large electrical noise and are blanked. b, c zoom on two selected stretches of the record at higher resolution. Zero current level is indicated by arrow, and by a dotted line in the right trace. The numbers above recordings are the calculated values of Ī. Low to intermediate activity is observed before addition of Gβγ (b), and high level activity is observed after the addition of 20 nM Gβγ (c). d and e show amplitude histograms corresponding to the record shown in b and c, respectively.
Typically, two or even all three types of activity are often observed in a single recording in a complete experiment, as shown in Figure 1a. A relatively high level of basal activity is observed in the cell-attached mode. After excision into GTP- and Na+-free solution, the activity runs down by 80–90% (Peleg et al., 2002), to a level where the creation of an event list is often possible (Fig. 1b). However, following the addition of 20 nM Gβγ a pseudo-macroscopic current ensues which cannot be analyzed in this way (Fig. 1c). Figures 1d and 1e, respectively, show amplitude histograms of representative 20–60 s intervals of activity in excised configuration before (Fig. 1b) and after (Fig. 1c) addition of 20 nM Gβγ. It can be seen that low to intermediate activity recordings render amplitude histograms with several peaks of which the leftmost peak corresponds to b̅ (the background or “leak” current), and the next peak to i1. On the other hand, high activity recordings render amplitude histogram with a single peak.
It is clear that trace idealization and event list analysis are applicable for calculation of total open probability (NPo) or of the net average current in recordings of Figure 1b, but impossible for recordings of the kind shown in Figure 1c. Moreover, quantitative description of activity changes such as Ra (fold activation by Gβγ) which occur on a wide amplitude scale, such as demonstrated in Figure 1a, are impossible utilizing solely event list analysis.
Analysis procedure
Calculation of the net average current flowing through the open channels ( Ī ) for low to intermediate activity level recordings involves 3 steps. The first step is the detection of baseline (leak) current value. This can be achieved in several ways. The simplest way is a graphical estimation (e.g. using cursors on the display screen). A numerical calculation of the average current value of a sufficiently long closed period also yields a good estimation of the baseline current value, assuming that no baseline drift is observed. A more accurate estimate is obtained by creating an amplitude histogram of the record and selecting the first (corresponding to the lowest current) peak either graphically or by fitting the amplitude histogram with a sum of Gaussian functions (see Fig. 2a). After estimation of the baseline current value, the latter can be subtracted from all amplitude values in order to offset the baseline to zero.
The second step is the calculation of the delimiter (See Fig. 2b). As described in Methods, the delimiter is a current value which discriminates between the open and closed events. All amplitude points above the delimiter are assigned as belonging to open events distribution, while the points below the delimiter represent closed states of the channel; any non-zero point below the delimiter is thus assigned to noise.
The third step is the calculation of Ī, which can be calculated either from the analysis of the event list, or from the amplitude histogram, or directly from the raw data without the creation of histograms, as will be explained below.
Calculation of average currents
The total average current ( Īt ) is given by:
| (13) |
where b̅ is the mean value of the background (leak) current and Ī is the average current flowing via open channels.
Having calculated Ī by subtracting b̅ from the total current, one can calculate the activation ratio (Ra) which we define as the ratio of net current flowing through the channels after perturbation (e.g. activation by agonist or another activator, such as Gβγ in the case of GIRK) to the basal current before perturbation:
| (14) |
where subscripts a and b denote the values of Ī before and after the perturbation, respectively.
Note that Ī is directly proportional to Po according to:
| (15) |
where the IΛ is the single channel amplitude and the N is the number of the channels carrying the current (Neher and Stevens, 1977; Traynelis and Jaramillo, 1998; Alvarez et al., 2002). From this equation, it can be directly deduced that, in a common case, when the perturbation involves mainly changes in channel open probability (Po) rather than single channel current (IΛ) or the number of channels (N), Ra reflects the change in Po:
| (16) |
An example of a standard calculation of the average current in a low/intermediate NPo record is shown in Figure 2. Initially, an amplitude histogram is created (Fig. 2a). Then the amplitude values of the two leftmost peaks is determined graphically (the positions of the peaks were set by eye), and the delimiter is calculated by halving the difference between the two amplitude values, according to equations (2) and (3). This delimiter can be utilized to create an event list from the record. A representative 1 s interval with superimposed idealized data is shown in Figure 2b.
We have also estimated the delimiter either numerically or according to Howe et al. (Howe et al., 1991) (see Methods). To do this, we used equations (2) or (5)–(8), respectively, after fitting the amplitude histogram to Gaussian function (in the case shown in Fig. 2a, with 3 Gaussian components). The delimiters calculated in these ways, and that determined graphically as explained above, were almost identical (Fig. 2c). The average single channel current, IΛ, was 2.2 pA in this recoding.
Subsequently, average current (Ī ) values were calculated from the amplitude histogram using equations (9), (10) and (13), assuming that the first peak in the amplitude histogram represented the background current. The estimates of the average current by this method, obtained with the delimiters calculated in either of the three ways described above, were practically identical. We find that a simple visual (graphical) estimation of the delimiter from histograms of the type shown in Fig. 2a, gives results practically indistinguishable from those obtained with sophisticated numerical methods. Most importantly, all estimates of Ī obtained from the histogram were also indistinguishable from the average current calculated in the classical way from the event list (Fig. 2d).
To confirm the accuracy of the method of calculation of Ī based on amplitude histogram analysis, we analyzed 8 low and 11 intermediate activity recordings of Gβγ-activated GIRK1/2 channels, utilizing the above procedures. The results of these analyses are shown in Figure 2e, f. In all cases, the histogram-based method gave similar estimates of Ī, independently of the method chosen to calculate the delimiter. The absolute values of deviation of Ī obtained from amplitude histograms from that calculated from the standard event list were small for low-activity patches (∼ 5.5 ± 1 %) and even smaller (∼2%) for patches with intermediate activity (insets in Figs. 2e, f). Interestingly, in patches with low activities the current values estimated from histograms were usually slightly lower, when compared to the event list method. The reasons for this tendency have not been investigated, as the differences were small and did not affect the main conclusion (see below). In patches with intermediate activity the current values estimated by all methods were practically indistinguishable. We conclude that the histogram method provides reliable estimates of total current in a wide range of channel activity levels except in records with extermely low NPo (see below).
Analysis of recordings demonstrating pseudomacroscopic behavior
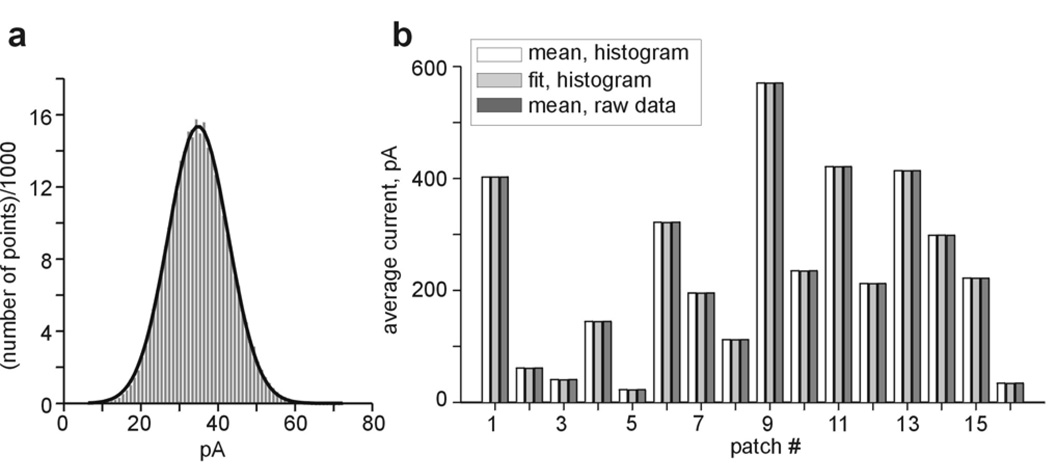
Several specific problems have to be faced while analyzing recordings with pseudomacroscopic behavior (Fig. 1c). Imposition of a delimiter is quite useless, since current amplitudes of each point represent simultaneous opening of several channels and will exceed any delimiter calculated utilizing the methods described above. In addition, the amplitude of the baseline current cannot be estimated from amplitude histogram since no actual baseline is observed. In such cases, the baseline value can be extracted from the analysis of a low to intermediate level activity period of the same recording (such as a stretch of record of basal activity in the excised patch before the addition of Gβγ in Fig. 1). A less satisfactory approximation, applicable in cases of high stability in different recordings from the same day under same recording conditions and with similar seal resistances, is to extract an average background noise level from patches with fewer channels. In our hands, when GIRK channel was expressed at high density, basal average currents after patch excision often reached amplitudes above 20 pA, whereas in lowdensity patches basal activity of 0.5–3 pA were observed. The latter easily allowed the calculation of the baseline which usually did not exceed 2 pA in our experiments. In records of pseudomacroscopic currents, two additional methods of calculation of average current can be utilized: (1) averaging all amplitudes (raw data) in the selected record without building an amplitude histogram (i.e. amplitudes of all points within the selected section of the record are summarized and divided by the number of points in the segment); (2) fitting the amplitude histogram with Gaussian function (1 component), as exemplified in Fig. 3a. The position of the peak of the histogram on the X-axis, determined graphically or from Gaussian fit, corresponds to the total average current. Ī is obtained by subtracting the baseline current estimated from low-density patches as explained above. Figure 3b compares these two methods to the previously analyzed method of calculating the average current from the amplitude histogram, in 16 different patches of Gβγ-activated GIRK1/2 expressed at high levels. It is clear that all three methods yield very close results.
Fig. 3.
Comparison of different methods of calculation of average current in patches with pseudomacroscopic behavior (Ī >20 pA). a exemplifies a 1-component Gaussian fit (solid line) to an amplitude histogram of a 1 min segment from the recording shown in Fig. 1c (close to the end of record). b compares the values of Ī calculated in 16 representative high-activity patches using three different methods: mean value of the amplitude histogram, Gaussian fit of the histogram and mean of raw data.
It must be emphasized that for Po values close to 1 the form of amplitude histogram becomes progressively asymmetrical due to the properties of binomial distribution and thus fitting it with a single Gaussian is inappropriate. In GIRK channels, where Po is usually below 0.1 even at saturating doses of Gβγ, this problem is never encountered.
Analysis of simulated data
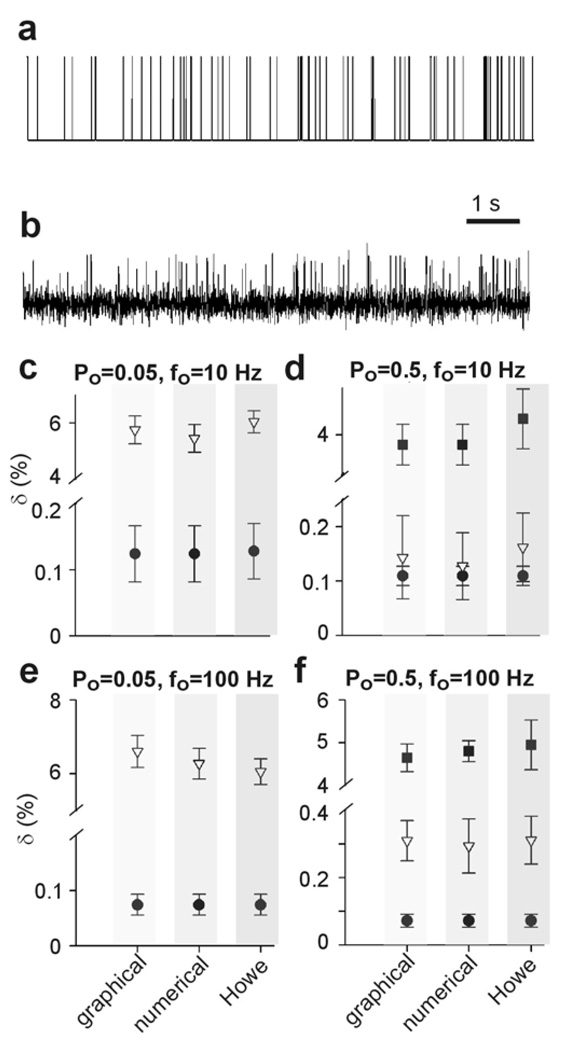
In order to test the limits of the method proposed above we utilized simulated data. We tested several factors which can influence the accuracy of implementation of the method. In particular, we tested the influence of Po, frequency of openings and signal to noise ratio (SNR). An example of simulated data with and without noise component is shown in Figure 4a and b. The presence of simulated data without the noise component made the estimation of Po straightforward.
| (17) |
where Po, s− is open probability of simulated data before the imposition of noise component, to,tot is total open time and Φ is the total recording time. For each record we calculated the Po,s− and also the Po,s+ value (the latter stays for the open probability after noise component imposition and consequently was estimated utilizing the method described above). The δ value was defined as
| (18) |
Fig. 4.
Analysis of simulated data. a shows a representative 10 s interval of simulated activity, α= 10 s−1 , β = 200 s−1 , b̅ =0, IΛ = 1, no noise component imposed, b shows the same record as in A but with a superimposed noise component with mean 0 and standard deviation of 0.2. c, calculation of differences between Po,s+ and Po,s−, δ (%), for Po =0.05 and fo = 10 Hz. d, calculation of δ (%) for Po =0.5 and fo = 10 Hz. e, calculation of δ (%) for Po =0.05 and fo = 100 Hz. f, calculation of δ (%) for Po = 0.5 and fo = 100 Hz. Each point is an average of 5 simulations (10 s each). Filled circles are for SNR of 10, inverted triangles for SNR of 4, filled squares for SNR of 2.5.
It can be seen in Figure 4 that the major contributing factor to the extent of deviation between the Po,s− and Po,s+ is the signal to noise ratio (SNR). For all open probabilities the δ value changes up to 60 fold for a 4 fold change of SNR. Additionally, assuming adequate sampling rate, the fo has almost no effect on δ (for the simulation we have chosen the sampling rate of 400–4000 Hz, respectively, in order to provide at least 2 sampling points for each opening event). Furthermore, there was no significant difference between the δ values calculated by either of the 3 methods of estimation of delimiter described in the present work.
Discussion
In this work we present a simple and reliable method to assess very large changes in channel activity in multichannel patches through the calculation of average current, Ī. We demonstrate that Ī can be calculated with high accuracy from amplitude histograms, or (at very high channel densities) directly from raw data. The procedure is very simple and does not require the use of any special software. Most importantly, we have shown that the calculation of average current from amplitude histograms renders results very similar (within 2–6 %) to those obtained using the standard procedure of generation of event lists. The accuracy of calculation of average current from amplitude histograms or raw data was demonstrated here using records that showed low to intermediate channel activity, where calculation of Ī both from event lists and from amplitude histograms was possible. This finding allows the combined or alternative use of calculations of average current from event list and/or from amplitude histograms. In our analyzes of activation of GIRK by Gβγ, such combined use of the two methods was indispensable in recordings that contained segments where the channel population behaved either in a pseudo single channel manner (basal activity), where the event list was often the only way to accurately calculate NPo, or in a pseudomacroscopic manner (after activation) where the construction of an event list was impossible. This pattern is frequently observed in patch clamp recordings of GIRK channel activity in Xenopus laevis oocytes (Fig. 1), cardiac cells (Schreibmayer et al., 1996; Nemec et al., 1999) and neurons (Grigg et al., 1996) upon activation by agonist or Gβγ. Similar kind of analysis has been previously implemented for description of GIRK channel activation by Gβγ and sodium (Ho and Murrell-Lagnado, 1999; Peleg et al., 2002; Rishal et al., 2003; Ivanina et al., 2004) but its validity has not been explicitly tested.
Both methods mentioned above are directly related to integration of current amplitudes. It must be emphasized that integration of current amplitude requires manipulation of vast amount of unprocessed data and consequently demands much more computer power and more specialized software than the analysis of amplitude histograms which can be easily and rapidly processed by any spreadsheet analysis program. Average current values and sum of current amplitudes are directly proportional to open probability. However, while the ratio of average currents is equal to activation ration assuming constant single channel current amplitude and number of channels in patch, the same generally does not hold true for the ratio of sum of current amplitudes. Indeed, same number of sample points is required for this. Consequently, simple integration of current amplitudes without calculation of average imposes limitation of length of stretches of activity which can be utilized for the calculation of the activation ratio.
Calculations of average current from amplitude histograms or from raw data are subject to several limitations. Our data clearly indicate that there is a lower limit to NPo below which the simplified methods become inaccurate. The calculation of Ī from raw data is only valid when the baseline current is negligible compared to the current flowing via the channels, and is therefore usually applicable only for very large currents. Calculation from amplitude histograms is much more accurate but it still cannot be applied to patches with very low NPo. Thus, as shown in Fig. 2, estimation of Ī in patches of intermediate density with currents of 0.5 – 4 pA (NPo approximately between 0.25 and 2) deviated from estimates of Ī obtained from event lists by less than 3%. However, for patches with average currents of 0.07 – 0.4 pA (NPo of 0.03 – 0.2), this deviation reaches 4–8%. Thus, in records with NPo below 0.03, calculation of NPo and Ī from amplitude histograms may become unreliable, and the use of event lists is recommended.
Analysis of simulated data has demonstrated that the most important factor which can influence the results of analysis based on amplitude histogram is the SNR (signal to noise ratio). This is quite an intuitive conclusion since the peak separation on the amplitude histogram is strongly dependent on SNR. The results of simulation thus support the conclusions drawn from the analysis of real data, that low Po significantly hampers implementation of the methods based on amplitude histogram for single-channel recordings. Indeed, differences between Po,s+ and Po,s− (δ) below 10 % were observed for Po,s− ∼ 0.05 and SNR of 4. On the other hand, δ above 30 % were calculated for SNR of 1 and same Po,s− (data not shown). The same would be true for the accuracy of calculation of average current in single channel records using the histogram method. However, it must be noted that an absolute level of noise (e.g. 0.5 pA RMS) that can make the histogram-based analysis of a single channel recording inaccurate, will become tolerable to negligible in multichannel recordings (since the signal increases, and thus SNR decreases).
Additionally, unstable data with high extent of drifting will lead to smearing of the histogram and subsequent miscalculation of delimiter (Molleman, 2003). This limitation can be overcome by selection of data segments in which the time dependent variation is minimal. Additionally, changes of baseline current value can occur during the recording, thus hampering the baseline subtraction based on estimation of the baseline from the periods of low channel activity. Despite the fact that this notion must be kept in mind, it was demonstrated above that baseline currents generated by stable recording sets are relatively low comparing to the open channel current, and subtraction of an estimated baseline applied to recordings with high channel activity (>20 pA) yields negligible effects. Furthermore, baseline current values can be instantly accessed during or at the end of periods of high channel activity, e.g. by adding an inhibitor.
The choice and calculation of delimiter introduced only minor inaccuracies, at least in the case of heterologously expressed GIRK channels (Fig. 2). In fact, a simple graphical estimation of the delimiter proved to be as reliable as two sophisticated numerical methods and thus can be recommended as the default method for the analysis of average current.
While we present only results with GIRK channel, it is clearly possible to generalize and extend the use of the proposed methods to any other ion channel. This is particularly useful when single channel recordings are unavailable, for example in cells or cell areas where the density of a certain type of channel in the plasma membrane is high, and/or when there is no intention to conduct in-depth kinetic analysis calculations of single channel parameters. Calculations of average current are highly suitable for the analysis of robust changes in channel activity caused by activators, inhibitors, or blockers of ion channels, to provide essential, physiologically relevant information such as relative efficiency of such agents, extent of activation (Ra) or inhibition compared to basal activity.
Supplementary Material
Acknowledgements
This work was supported by grants from NIH (GM68493 (N.D.) and GM60419 (C.W.D.)) and US-Israel Binational Science Foundation (01-122, N.D. and C.W.D). The authors report no conflicts of interest.
Contributor Information
Daniel Yakubovich, Department of Physiology and Pharmacology, Sackler School of Medicine, Tel Aviv University, Tel Aviv 69978, Israel.
Ida Rishal, Weizmann Institute of Science, Rehovot, Israel.
Carmen W. Dessauer, Department of Integrative Biology and Pharmacology, Medical School, University of Texas, Houston, TX 77030, USA
Nathan Dascal, Department of Physiology and Pharmacology, Sackler School of Medicine, Tel Aviv University, Tel Aviv 69978, Israel.
References
- Alvarez O, Gonzalez C, Latorre R. Counting channels: a tutorial guide on ion channel fluctuation analysis. Adv Physiol Educ. 2002;26:327–341. doi: 10.1152/advan.00006.2002. [DOI] [PubMed] [Google Scholar]
- Bauer RJ, Bowman BF, Kenyon JL. Theory of the kinetic analysis of patch-clamp data. Biophys J. 1987;52:961–978. doi: 10.1016/S0006-3495(87)83289-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Blunck R, Kirst U, Riessner T, Hansen U. How powerful is the dwelltime analysis of multichannel records? J Membr Biol. 1998;165:19–35. doi: 10.1007/s002329900417. [DOI] [PubMed] [Google Scholar]
- Colquhoun D, Hawkes AG. Relaxation and fluctuations of membrane currents that flow through drug-operated channels. Proc R Soc Lond B Biol Sci. 1977;199:231–262. doi: 10.1098/rspb.1977.0137. [DOI] [PubMed] [Google Scholar]
- Colquhoun D, Hawkes AG. On the stochastic properties of single ion channels. Proc R Soc Lond B Biol Sci. 1981;211:205–235. doi: 10.1098/rspb.1981.0003. [DOI] [PubMed] [Google Scholar]
- Colquhoun D, Hawkes AG. The principles of the stochastic interpretation of ion-channel mechanisms. In: Sakmann B, Neher E, editors. Single-Channel Recording. New-York: Plenum Press; 1995. pp. 397–482. [Google Scholar]
- Dascal N. Signalling via the G protein-activated K+ channels. Cell Signal. 1997;9:551–573. doi: 10.1016/s0898-6568(97)00095-8. [DOI] [PubMed] [Google Scholar]
- Grigg JJ, Kozasa T, Nakajima Y, Nakajima S. Single-channel properties of a G-protein-coupled inward rectifier potassium channel in brain neurons. J Neurophysiol. 1996;75:318–328. doi: 10.1152/jn.1996.75.1.318. [DOI] [PubMed] [Google Scholar]
- Ho IH, Murrell-Lagnado RD. Molecular mechanism for sodium-dependent activation of G protein-gated K+ channels. J Physiol. 1999;520(Pt 3):645–651. doi: 10.1111/j.1469-7793.1999.00645.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hosoya Y, Yamada M, Ito H, Kurachi Y. A functional model for G protein activation of the muscarinic K+ channel in guinea pig atrial myocytes. Spectral analysis of the effect of GTP on single-channel kinetics. J Gen Physiol. 1996;108:485–495. doi: 10.1085/jgp.108.6.485. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Howe JR, Cull-Candy SG, Colquhoun D. Currents through single glutamate receptor channels in outside-out patches from rat cerebellar granule cells. J Physiol. 1991;432:143–202. doi: 10.1113/jphysiol.1991.sp018381. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ivanina T, Varon D, Peleg S, Rishal I, Porozov Y, Dessauer CW, et al. Gα1 and Gαi3 differentially interact with, and regulate, the G protein-activated K+ channel. J Biol Chem. 2004;279:17260–17268. doi: 10.1074/jbc.M313425200. [DOI] [PubMed] [Google Scholar]
- Jackson MB. Ion channels. Single-channel analysis. Methods Enzymol. 1992;207:729–746. doi: 10.1016/0076-6879(92)07053-q. [DOI] [PubMed] [Google Scholar]
- Jelacic TM, Sims SM, Clapham DE. Functional expression and characterization of G-protein-gated inwardly rectifying K+ channels containing GIRK3. J Membr Biol. 1999;169:123–129. doi: 10.1007/s002329900524. [DOI] [PubMed] [Google Scholar]
- Molleman A. Patch clamping: an introductory guide to patch clamp electrophysiology. J. Wiley; 2003. [Google Scholar]
- Neher E, Stevens CF. Conductance fluctuations and ionic pores in membranes. Annu Rev Biophys Bioeng. 1977;6:345–381. doi: 10.1146/annurev.bb.06.060177.002021. [DOI] [PubMed] [Google Scholar]
- Nemec J, Wickman K, Clapham DE. Gβγ binding increases the open time of IKACh: kinetic evidence for multiple Gβγ binding sites. Biophys J. 1999;76:246–252. doi: 10.1016/S0006-3495(99)77193-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Peleg S, Varon D, Ivanina T, Dessauer CW, Dascal N. Gαi controls the gating of the G protein-activated K+ channel, GIRK. Neuron. 2002;33:87–99. doi: 10.1016/s0896-6273(01)00567-0. [DOI] [PubMed] [Google Scholar]
- Qin F, Auerbach A, Sachs F. Estimating single-channel kinetic parameters from idealized patch-clamp data containing missed events. Biophysical Journal. 1996;70:264–280. doi: 10.1016/S0006-3495(96)79568-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Qin F, Auerbach A, Sachs F. Maximum likelihood estimation of aggregated Markov processes. Proceedings of the Royal Society of London. Series B: Biological Sciences. 1997;264 doi: 10.1098/rspb.1997.0054. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Qin F, Auerbach A, Sachs F. A direct optimization approach to hidden Markov modeling for single channel kinetics. Biophysical Journal. 2000a;79:1915–1927. doi: 10.1016/S0006-3495(00)76441-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Qin F, Auerbach A, Sachs F. Hidden Markov modeling for single channel kinetics with filtering and correlated noise. Biophysical Journal. 2000b;79:1928–1944. doi: 10.1016/S0006-3495(00)76442-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rishal I, Keren-Raifman T, Yakubovich D, Ivanina T, Dessauer CW, Slepak VZ, et al. Na+ promotes the dissociation between Gα-GDP and Gβγ, activating G-protein-gated K+ channels. Journal of Biological Chemistry. 2003;278:3840–3845. doi: 10.1074/jbc.C200605200. [DOI] [PubMed] [Google Scholar]
- Sachs F, Neil J, Barkakati N. The automated analysis of data from single ionic channels. Pflugers Arch. 1982;395:331–340. doi: 10.1007/BF00580798. [DOI] [PubMed] [Google Scholar]
- Schreibmayer W, Dessauer CW, Vorobiov D, Gilman AG, Lester HA, Davidson N, et al. Inhibition of an inwardly rectifying K+ channel by G-protein α-subunits. Nature. 1996;380:624–627. doi: 10.1038/380624a0. [DOI] [PubMed] [Google Scholar]
- Traynelis SF, Jaramillo F. Getting the most out of noise in the central nervous system. Trends Neurosci. 1998;21:137–145. doi: 10.1016/s0166-2236(98)01238-7. [DOI] [PubMed] [Google Scholar]
- Vivaudou MB, Singer JJ, Walsh JV., Jr An automated technique for analysis of current transitions in multilevel single-channel recordings. Pflugers Arch. 1986;407:355–364. doi: 10.1007/BF00652618. [DOI] [PubMed] [Google Scholar]
- Yakubovich D, Pastushenko V, Bitler A, Dessauer CW, Dascal N. Slow modal gating of single G protein-activated K+ channels expressed in Xenopus oocytes. J Physiol. 2000;524(Pt 3):737–755. doi: 10.1111/j.1469-7793.2000.00737.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.