HIGH-RESOLUTION SPATIAL MAPPING OF SHEAR PROPERTIES IN CARTILAGE

Abstract

Structural properties of articular cartilage such as proteoglycan content, collagen content and collagen alignment are known to vary over length scales as small as a few microns (Bullough and Goodfellow, 1968; Bi et al., 2006). Characterizing the resulting variation in mechanical properties is critical for understanding how the inhomogeneous architecture of this tissue gives rise to its function. Previous studies have measured the depth-dependent shear modulus of articular cartilage using methods such as particle image velocimetry (PIV) that rely on cells and cell nuclei as fiducial markers to track tissue deformation (Buckley et al., 2008; Wong et al., 2008a). However, such techniques are limited by the density of trackable markers, which may be too low to take full advantage of optical microscopy. This limitation leads to noise in the acquired data which is often exacerbated when the data is manipulated. In this study, we report on two techniques for increasing the accuracy of tissue deformation measurements. In the first technique, deformations were tracked in a grid that was photobleached onto each tissue sample (Bruehlmann et al, 2004). In the second, a numerical technique was implemented that allowed for accurate differentiation of optical displacement measurements by minimizing the propagated experimental error while ensuring that truncation error associated with local averaging of the data remained small. To test their efficacy, we employed these techniques to compare the depth dependent shear moduli of neonatal bovine and adult human articular cartilage. Using a photobleached grid and numerical optimization to gather and analyze data led to results consistent with those reported previously (Buckley et al., 2008; Wong et al., 2008a) but with increased spatial resolution and characteristic coefficients of variation that were reduced by up to a factor of 3. This increased resolution allowed us to determine that the shear modulus of neonatal bovine and adult human tissue both exhibit a global minimum at a depth z of around 100 μm and plateau at large depths. The consistency of the depth dependence of |G*| (z) for adult human and neonatal bovine tissue suggests a functional advantage resulting from this behavior.

Introduction

Measuring the depth-dependent mechanical properties of articular cartilage with a high spatial resolution can help elucidate the functional benefits resulting from the tissue’s complex structure. As such, recent studies have investigated the depth-dependent compressive and shear properties of this tissue (Guilak et al., 1995; Schinagl et al., 1996; Wang et al., 2002; Chahine et al., 2004; Wong et al., 2008a; Wong et al., 2008b; Buckley et al., 2008) using particle image velocimetry (PIV) and other feature-tracking algorithms. Unfortunately, the spatial resolution in these techniques is limited by the density of trackable markers (i.e., cells or cell nuclei). For example, in adult human articular cartilage, where cells are particularly sparse, the depth-dependent shear modulus G(z) has been reported to an accuracy of ~350 μm (Wong et al., 2008a; Wong et al., 2008b). However, near the surface, structural properties can vary over much smaller length scales (Bi et al., 2007).

Here, we describe two techniques for improving measurement resolution in G(z). To increase the spatial accuracy of local displacement measurements, we used grid-resolution automated tissue elastography (GRATE). This technique builds on pioneering efforts for measuring deformation in intervertebral disk under flexion (Bruehlmann et al., 2004) and entails tracking the displacement of gridlines photobleached onto the sample. Since the gridlines are continuous, measurement resolution is limited by diffraction rather than the density of trackable markers. To reduce noise inherent in processing the extracted displacement data, we employ weight-averaged noisy differentiation (WAND). This numerical technique addresses amplification of noise associated with differentiation of discrete experimental data and draws from previously described methods (Anderssen and Bloomfield, 1974; Muller et al., 1987; Anderssen et al., 1996; Carlsson et al., 1992; Anderssen and Hegland, 1999; Chartrand, 2005).

We applied these procedures to neonatal bovine and adult human articular cartilage tested in a tissue deformation imaging stage (TDIS) (Buckley et al., 2008; Michalek et al., 2009). We found that these techniques substantially improve the resolution and accuracy of the measured shear modulus profiles.

Methods

Sample Preparation: Adult Human Tissue

Three 6 mm diameter cylindrical explants of thickness 2–3 mm were harvested from frozen adult human tibial plateus (Musculoskeletal Transplant Foundation). After dissection, samples were bisected into hemi-cylinders and placed into PBS until thawed. Prior to mechanical testing, hemi-cylinders were placed into PBS with 7 μg/mL 5-dichlorotriazinylaminofluorescein (5-DTAF) for 2 hours (Bruehlmann et al, 2004; Michalek et al., 2009). 5-DTAF modifies amines in proteins and fully stains the extracellular matrix. Shear modulus profiles obtained using carboxyfluorescein diacetate, succinimidyl ester (CFDA-SE), a cellular stain, were consistent with those obtained using 5-DTAF, verifying that matrix proteins are not mechanically altered by this stain (data not shown).

Sample Preparation: Neonatal Bovine Tissue

Three 6 mm diameter cylindrical explants of thickness 3–4 mm were harvested from patellofemoral grooves of 1–3 day old calves. Prior to mechanical testing, samples were placed into PBS and 7 μg/mL 5-DTAF for 2 hours.

Mechanical Testing

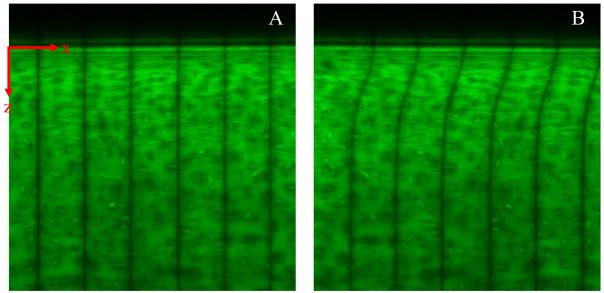
Cartilage hemi-cylinders were placed between two glass shearing plates of a TDIS. Sandblasted protrusions ~10 μm in diameter on the moving plate gripped the surface and prevented slip (Supplementary Section 1). Results were consistent with those obtained using smooth glass (data not shown). The opposing face of the tissue was adhered to the stationary plate using cyanoacrylate glue. For all experiments, the compressive strain on the hemi-cylinder was 10%. After positioning the device onto an inverted Zeiss LSM 510 confocal microscope, five lines spaced by 50 μm were photobleached onto the hemi-cylinder along the z axis (Figure 1A) using a 488 nm laser. Samples were imaged (Figure 1B) during sinusoidal shear with frequency f = 100 mHz and a shearing plate peak-to-peak displacement amplitude of 32 μm.

Figure 1.

Confocal micrographs of 5-DTAF-stained human articular cartilage with vertical photobleached lines (A) before and (B) during application of shear. The photobleached lines are spaced by 50 μm.

Data Analysis: PIV

For PIV, the displacement amplitude at a given depth u₀(z) was determined using software adapted from MatPIV (Sveen and Cowen, 2004; Buckley et al., 2008) with a window size of 317 × 20 μm².

Data Analysis: GRATE

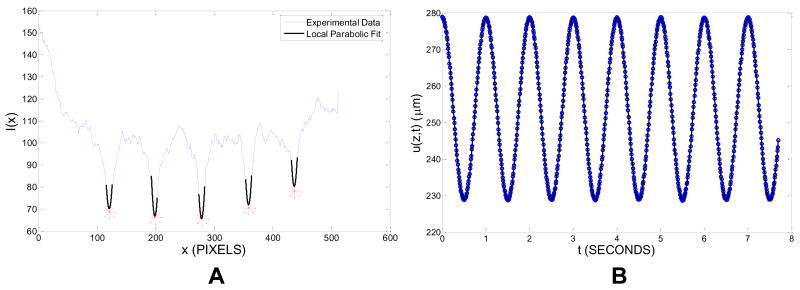
For GRATE, custom MATLAB (The Mathworks, Inc., Natick, MA) software was used to determine u₀(z). For an image taken at time t, this software first plots I(x), the average intensity across vertical regions of width w=20 μm centered at a depth z, versus horizontal location x (Fig. 2A). It then determines m_n(z,t), the locations of the five local minima of I(x) corresponding to the five photobleached lines indexed by n. To better determine these minima, a parabola is fit to I(x) over 11 pixel-wide regions centered at m_n(z,t). The locations M_n(z,t) of the minima of these parabolic fits give the photobleached line locations. The mean photobleached line location u(z,t) is the average of M_n(z,t) over all lines. u(z,t) is then plotted as a function of time, yielding a sinusoidal curve (Fig. 2B). Both the displacement amplitude u₀(z) and the displacement phase angle δ_u(z) are obtained by fitting a cosine to u(z,t).

Figure 2.

(A) Mean intensity I(x) at depth z for a sheared sample of articular cartilage at time t (blue). Also shown are local parabolic fits near each photobleached line location (black) and the calculated photobleached line locations (red stars). (B) Mean photobleached line location u(z,t) at depth z vs. time t for a sheared sample of articular cartilage (blue circles) and sinusoidal fit (black solid line).

Data Analysis: Obtaining |G*| (z) from u₀(z)

For a dynamically sheared inhomogeneous material, the shear strain amplitude γ₀(z) is given by

$${\gamma }_0=\sqrt{{\left[\frac{d}{dz}(u_{0}cos{\delta }_u)\right]}^2+{\left[\frac{d}{dz}(u_{0}sin{\delta }_u)\right]}^2}$$ (1)

if the stress is assumed to be uniform with z. This relation reduces to du₀/dz in the limit where δ_u(z) = 0. To obtain γ₀, differentiation of u₀ cos δ_u and u₀ sin δ_u was performed numerically using either five-point linear least-squares fitting (5PLSQ) (Supplementary Section 2) or WAND (see below). The complex shear modulus profile is given by:

$$\mid G^{\ast }\mid (z)=\frac{{\tau }_0}{{\gamma }_0(z)},$$ (2)

where τ₀ is the measured stress amplitude.

Data Analysis: WAND

WAND addresses the amplification of noise associated with differentiation of discrete experimental data. To differentiate a function f sampled at depths z_i such that f_j = f(z_j), we employ the finite difference derivative operator:

$$\text{D}(z_i)\equiv \sum _{j\ne i}{w}_j\frac{f_i-f_j}{z_i-z_j}$$ (4)

where the weights w_j satisfy

$$\sum _{j\ne i}{w}_j=1\text{and}{w}_j\ge 0.$$ (5)

D smoothes the measurement error in the differentiated series by using a weighted average of the standard finite-difference derivative between z_i and data points in its neighborhood. We determine w_j using the CVXopt Python package to calculate

$$\underset{\overrightarrow{w}}{argmin}({\overline{\sigma }}_i)\text{s}.\text{t}.100{\overline{\text{e}}}_{\text{i}}<{\overline{\sigma }}_i$$

which minimizes the propagated experimental error σ̄_i while ensuring that the smoothing (or truncation) error ē_i remains 100 times smaller (Supplementary Section 3).

Results

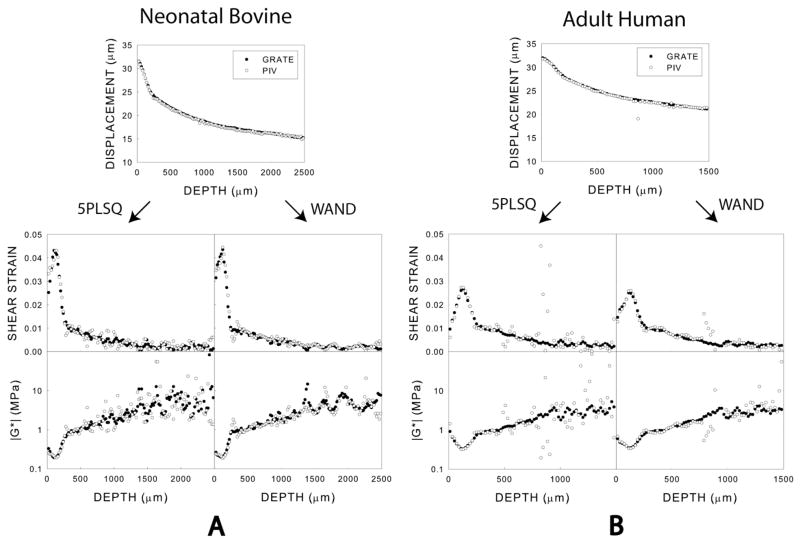
For representative samples of adult human and neonatal bovine articular cartilage, GRATE displacement and shear modulus profiles were consistent with those obtained using PIV (Fig. 3A,B). However, using GRATE decreased scatter in these profiles. WAND further smoothed shear strain and shear modulus profiles in both PIV and GRATE data, particularly the former.

Figure 3.

Depth dependence of peak-to-peak displacement amplitudes and complex shear moduli for single representative samples of (A) neonatal bovine and (B) adult human articular cartilage subject to shear at 100 mHz and analyzed using 5PLSQ and WAND.

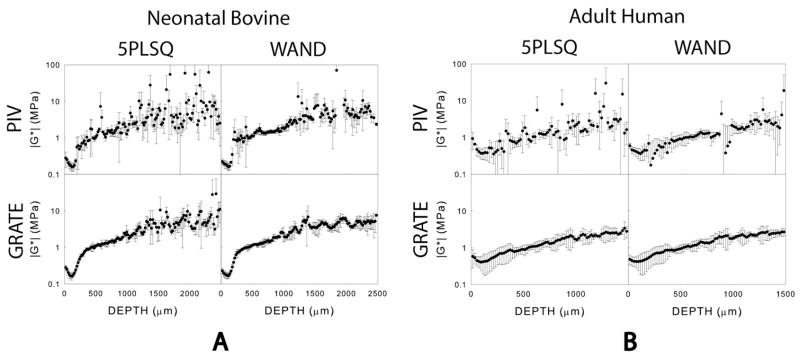
In both neonatal bovine (n=3) and adult human (n=3) articular cartilage, the standard deviation of the local shear modulus was substantially lower when WAND was used instead of 5PLSQ and when GRATE was used instead of PIV (Fig. 4A,B). We define c_V as the ratio of the mean standard deviation of |G*| (z) to the mean value of |G*| (z) over the range 0<z<1000 μm. In neonatal bovine tissue, c_V was nearly 0.5 for data analyzed with PIV and 5PLSQ. However, c_V was 0.26 when PIV and WAND was employed, 0.14 when GRATE and 5PLSQ were used and 0.15 when GRATE and WAND were used. Similarly, in adult human tissue, c_V was reduced from 0.70 to 0.58 when implementing WAND instead of 5PLSQ on images analyzed with PIV. c_V was lowest (0.36) when both GRATE and WAND were used.

Figure 4.

Depth dependence of complex shear moduli for n=3 samples of (A) neonatal bovine and (B) adult human articular cartilage subject to shear at 100 mHz and analyzed using PIV and GRATE.

The shear modulus of adult human cartilage |G*| (z) depended strongly on z (Fig. 3). In particular, the shear stiffness displayed a global minimum of 0.4 MPa at a depth z~100 μm. The shear modulus profile for neonatal bovine articular cartilage exhibited similar features.

Discussion

In this study, we combined GRATE and WAND to measure the spatially-dependent shear stiffness of articular cartilage with a spatial resolution of less than 20 μm. Given the same set of images, GRATE yields displacement profiles with reduced scatter and higher spatial resolution than PIV, leading to more accurate shear modulus profiles. In addition, we demonstrated that strain profiles obtained using PIV can be smoothed using WAND, yielding shear modulus profiles with substantially reduced scatter and a resolution that approaches the separation between markers. These techniques should also be applicable for mapping shear modulus profiles in other soft biological tissues with small-scale inhomogeneities.

By performing GRATE and WAND on samples of adult human articular cartilage, we found that |G*| (z) exhibits a global minimum at a depth z~100 μm. A similar qualitative behavior was observed in bovine neonatal tissue. The fact that the general shape of the shear modulus profile is maintained across different species implies that such a depth-dependent mechanical response is phylogenetically conserved and therefore may have an important as yet undiscovered functional benefit.