Abstract
We propose a feature vector approach to characterize the variation in large data sets of biological sequences. Each candidate sequence produces a single feature vector constructed with the number and location of amino acids or nucleic acids in the sequence. The feature vector characterizes the distance between the actual sequence and a model of a theoretical sequence based on the binomial and uniform distributions. This method is distinctive in that it does not rely on sequence alignment for determining protein relatedness, allowing the user to visualize the relationships within a set of proteins without making a priori assumptions about those proteins. We apply our method to two large families of proteins: protein kinase C, and globins, including hemoglobins and myoglobins. We interpret the high-dimensional feature vectors using principal components analysis and agglomerative hierarchical clustering. We find that the feature vector retains much of the information about the original sequence. By using principal component analysis to extract information from collections of feature vectors, we are able to quickly identify the nature of variation in a collection of proteins. Where collections are phylogenetically or functionally related, this is easily detected. Hierarchical agglomerative clustering provides a means of constructing cladograms from the feature vector output.
Introduction
Recent advances in biotechnology have allowed sequencing of millions of proteins from a wide spectrum of organisms and this information is rapidly becoming accessible to any researcher with an internet connection. For instance, the UniProtKB database currently contains over 7 million protein sequences and is updated every three weeks [1]. Current protein alignment methods are often slow and require assumptions about relatedness and evolutionary mechanisms [2]. In order to make use of the vast amount of protein data available, a method for quickly delineating large numbers of proteins into related types is necessary. As a solution, we propose a method for quantifying the frequency and position of amino acids within a protein, and demonstrate the ease, rapidity and usefulness of this technique for uncovering phylogenetic and functional relationships within protein families, using protein kinase C (PKC), hemoglobin and myoglobin as examples.
One of us (S.Y.) previously designed three types of parameters for use in clustering amino acid sequences [3]. Here, we reconceptualize these parameters, making them more statistical in character and more applicable to measuring protein similarity. The new parameters measure the degree to which the distribution of amino acids in a particular protein deviates from a theoretical protein containing an equal number of residues but undergoing neutral evolution. This measure allows us not only to characterize the extent to which the distribution of amino acids in a protein deviates from the expected but also the distance between proteins. Our theoretical model of the distribution of amino acids in a protein assumes that for any given amino acid, the locations of residues of that amino acid are distributed uniformly and the number of residues is distributed binomially.
In contrast to previous methods of constructing distance measures to determine protein relatedness [4], our method does not require performing multiple sequence alignment. Instead, this method creates measures of protein relatedness based on the distribution of amino acids in the proteins. Differences in these measures are then used to determine the difference between two proteins. In doing so, this method requires no assumptions about the way in which certain amino acids may be inserted or deleted. This allows us to look at protein difference in an abstract way, without making assumptions about the mechanisms by which these differences may arise.
Results
Implementation of the Feature Vectors
The selection pressure to which proteins are subjected affects both the number of residues in the protein [5] and the identity and location of these residues. By using a feature vector, which is an ordered list of numbers that characterize the distribution of amino acids in a protein, we can describe this selection pressure. Our method uses a feature vector constructed with three types of parameters (Fig. 1). The three types of parameters can be described as compositional, centrodial and distributional. Compositional parameters (type I) measure the extent to which the proportion of amino acids deviate from the expected. Centroidial parameters (type II) measure the extent to which amino acids tend to be in a particular region of the protein. Distributional parameters (type III) measure the extent to which amino acids cluster along the length of the protein. All parameters are adjusted for the length of the protein. From simulation of parameter distributions, it can be seen that, for some range of protein lengths and frequencies of amino acids, individual parameters have an approximately Gaussian distribution over large data sets (data not shown). The distance between feature vectors is measured as Euclidean distance.
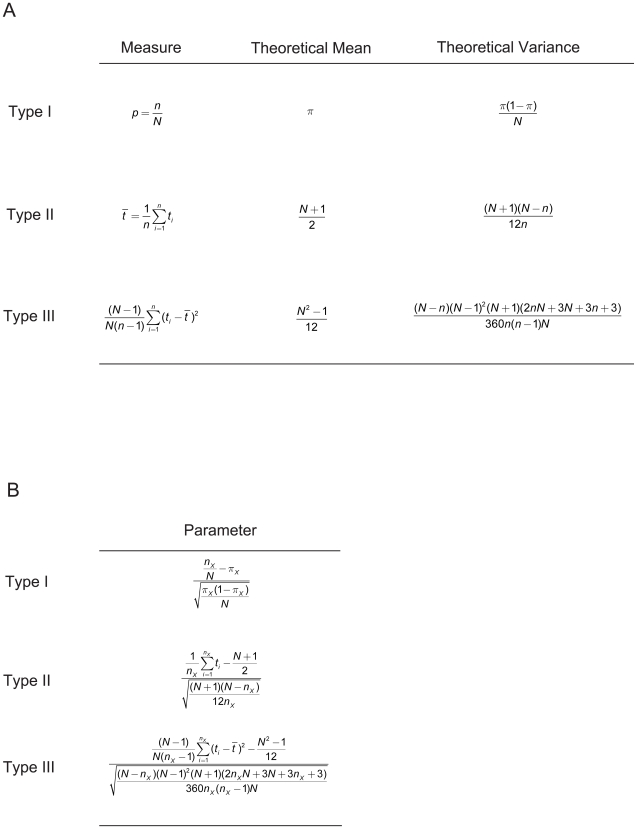
Figure 1. Calculation of the Protein Feature Vectors.
(A) Intermediate calculations necessary to compute three component parameters of the feature vector, parameters are computed as (measure − mean)/sqrt(variance); (B) sample parameters of Types I–III for an amino acid of type X, the full 60-dimentional feature vector for a given protein will include parameters for all amino acid types in that protein (3 parameters for each of 20 amino acid types).
To describe any protein using the feature vector method, we must first compute parameters of type I, II and III for each of the twenty amino acids which occur in proteins (Supplement S1). The parameter for each amino acid can be computed based on the information in figure 1A, by subtracting the theoretical mean from the measure and dividing by the square root of the theoretical variance. As an example, the formula for a parameter of type I for glycine (G) is:
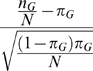 |
Here, πG is the probability of glycine occurring in a theoretical dataset of proteins under neutral evolution. This probability is set by the user and can vary for a given dataset. For the current analyses, we use by the number of genetic codons for glycine divided by 64. Alternatively, one can set πG to the frequency of glycine in the total dataset of proteins. The variable nG is the number of glycines in the protein and N is the length of the protein.
The following 9 steps detail the specifics of computing the parameters for the feature vector method and of using the feature vectors to categorize and analyze proteins. C++ and Mathematica (Wolfram Research, Urbana-Champaign, IL) code for steps 1–8 is available in the supplementary online materials (Sample Code S1 and S2). Step 9, performing a principle component analysis (PCA), can be done using Matlab software (Mathworks, Natwich, MA) or similar statistical software. Matlab code is provided in the supplementary online materials (Sample Code S3).
1. Count the number of amino acids of each type and note the length of the protein. We denote the length of protein as N and the number of amino acids of each type as nA, nR, nN, nD, nC, nE, nQ, nG, nH, nI, nL, nK, nM, nF, nP, nS, nT, nW, nY and nV. Use these numbers to compute the proportion of amino acids in the protein, the type I measure (fig. 1A): pA, pR, pN, pD, pC, pE, pQ, pG, pH, pI, pL, pK, pM, pF, pP, pS, pT, pW, pY and pV. (Where, A = Alanine, R = Arginine, N = Asparagine, D = Aspartic acid, C = Cysteine, E = Glutamic, Q = Glutamine, G = Glycine, H = Histidine, I = Isoleucine, L = Leucine, K = Lysine, M = Methionine, F = Phenylalanine, P = Proline, S = Serine, T = Threonine, W = Tryptophan, Y = Tyrosine, V = Valine).
2. For each amino acid, find the indices of the positions in the protein sequence which contain that amino acid (we count the first position as one and not zero).
3. Use the indices from step 2 to compute the mean position of each amino acid, the type II measure: mA, mR, mN, mD, mC, mE, mQ, mG, mH, mI, mL, mK, mM, mF, mP, mS, mT, mW, mY and mV. The type II theoretical mean is calculated as the average of all possible positions in a protein of length N.
4. Using the indices from step 2 compute the unbiased variance, type III measure, of the set of indices of each amino acid: vA, vR, vN, vD, vC, vE, vQ, vG, vH, vI, vL, vK, vM, vF, vP, vS, vT, vW, vY and vV. The type III theoretical mean is calculated as half of one less than the square of the length.
5. The type I theoretical mean is the a priori estimate of the probability of the occurrence of each amino acid: πA, πR, πN, πD, πC, πE, πQ, πG, πH, πI, πL, πK, πM, πF, πP, πS, πT, πW, πY and πV, This value was taken to be the number of codons corresponding to a particular amino acid divided by the total number of coding codons, although it could also more appropriately be taken as the rate of occurrence of amino acids in the population from which the sample proteins were selected. Use the type I mean to compute the type I theoretical variance of index positions given the observed number of amino acids.
6. Compute the type II theoretical variance in the mean and the type III theoretical variance of the variance given the observed number of amino acids as shown in figure 1A.
7. Normalize the measures computed in steps 1, 3 & 4 by subtracting the theoretical means, computed in steps 3, 4 & 5, and dividing by the square root of the theoretical variances, computed in steps 5 & 6.
8. Assemble the parameters into a 60 dimensional vector.
9. Using principle components analysis (PCA) or some other means of high dimensional data analysis, search for clusters or patterns in the protein data.
This method can be adapted for use in analyzing DNA or RNA sequences. To create a feature vector for a given DNA sequence, one need only create parameters of types I, II and III for each nucleic acid type, and then combine these parameters into a feature vector. The resulting DNA feature vector will be 12-dimensional, with 3 types of parameter for each of 4 types of nucleic acid, compared to the 60-dimensional protein feature vector (Tables S1, S2, and S3 contain feature vectors for our PKC, hemoglobin and myoglobin datasets, respectively).
To demonstrate the utility of this method, we applied our feature vector method to an exhaustive set of 128 proteins from the PKC family and a set of 904 hemoglobins and 150 myoglobins. The UniProt KB accession numbers for these proteins are provided in the supplementary online materials (see Tables 1– 4 for accession numbers; see Data Set S1 for additional information).
Table 1. NCBI or SwissProt/UniProt Accession Numbers for Protein Kinase C dataset.
| NP_001006133 | P09215 | P87253 | Q5R4K9 | Q7SY24 | Q9UVJ5 |
| NP_001008716 | P09216 | P90980 | Q5TZD4 | Q7SZH7 | Q9Y792 |
| NP_001012707 | P09217 | Q00078 | Q62074 | Q7SZH8 | Q9Y7C1 |
| O01715 | P10102 | Q02111 | Q62101 | Q7T2C5 | XM_391874 |
| O17874 | P10829 | Q02156 | Q64617 | Q86XJ6 | XP_001066028 |
| O19111 | P10830 | Q02956 | Q69G16 | Q86ZV2 | XP_001116804 |
| O42632 | P13677 | Q04759 | Q6AZF7 | Q873Y9 | XP_001147999 |
| O61224 | P16054 | Q05513 | Q6BI27 | Q8IUV5 | XP_001250401 |
| O61225 | P17252 | Q05655 | Q6C292 | Q8J213 | XP_234108 |
| O62567 | P20444 | Q15139 | Q6DCJ8 | Q8JFZ9 | XP_421417 |
| O62569 | P23298 | Q16974 | Q6DUV1 | Q8K1Y2 | XP_540151 |
| O76850 | P24583 | Q16975 | Q6FJ43 | Q8K2K8 | XP_541432 |
| O94806 | P24723 | Q19266 | Q6GNZ7 | Q8MXB6 | XP_583587 |
| O96942 | P28867 | Q25378 | Q6P5Z2 | Q8NE03 | XP_602125 |
| O96997 | P34885 | Q28EN9 | Q6P748 | Q90XF2 | XP_683138 |
| P04409 | P36582 | Q2NKI4 | Q6UB96 | Q91569 | XP_849292 |
| P05126 | P36583 | Q2U6A7 | Q6UB97 | Q91948 | XP_851386 |
| P05129 | P41743 | Q3UEA6 | Q75BT0 | Q99014 | XP_851861 |
| P05130 | P43057 | Q498G7 | Q76G54 | Q9BZL6 | |
| P05696 | P63318 | Q4AED5 | Q7LZQ8 | Q9GSZ3 | |
| P05771 | P68403 | Q4AED6 | Q7LZQ9 | Q9HF10 | |
| P05772 | P68404 | Q4R4U2 | Q7QCP8 | Q9HGK8 |
Table 2. SwissProt/UniProt Accession Numbers for Hemoglobin dataset – Part 1.
Table 3. SwissProt/UniProt Accession Numbers for Hemoglobin dataset – Part 2.
Table 4. SwissProt/UniProt Accession Numbers for Myoglobin dataset.
Visualization of the Feature Vectors
The feature vector is high dimensional. PCA is a popular method of reducing the number of variables in a vector. This method provides a linear transformation of the variables of the feature vector into a new set of uncorrelated variables. In so doing, it captures the dominant variations in the data set. The first two principal components contain more information than any other pair of linearly constructed variables and thus are used in our analysis [6]. This allows us to easily visualize the key elements of the data without loss of much information.
An alternative method for visualizing the patterns emerging from the feature vector method of analysis is to create a dendrogram using agglomerative hierarchical clustering. We use agglomerative hierarchical clustering with complete linkage [7] to provide a more detailed view of the data, and of the relationships between groups within the data. In order to demonstrate the utility and flexibility of the feature vector method, we provide one dendrogram as part of the PKC analysis.
Identification of Protein Sub-Types
Kinases are proteins which modify other proteins by phosphorylation, the covalent addition of phosphate groups [8]. The PKC family is a large multigene family of serine/threonine kinases [8]. Six main groups of PKCs can be identified by domain architecture: conventional, novel, atypical, PKCμ-like, fungal PKC1, and PKC-related kinases [9]. The first three of these groups can be further categorized into subtypes [9]. In general, the PKC domain architecture (fig. 2A) consists of a regulatory region and a catalytic domain [10]. The regulatory region contains several functional domains of varying types [10]. True PKCs are classified as conventional, novel or atypical based on the functional domains present in the regulatory regions of the PKCs (fig. 2A). Briefly, conventional PKCs contain subtypes α, βI, βII and γ; novel PKCs contain subtypes θ, ε, δ and η; and atypical PKCs contain λ\ι and ζ [9]. The catalytic domain is more conserved and more commonly used for differentiating between families of protein kinases [11]. However, it is also useful in characterizing the PKCμ-like kinases, which contain markedly different catalytic regions from the rest of the protein kinase C members [12].
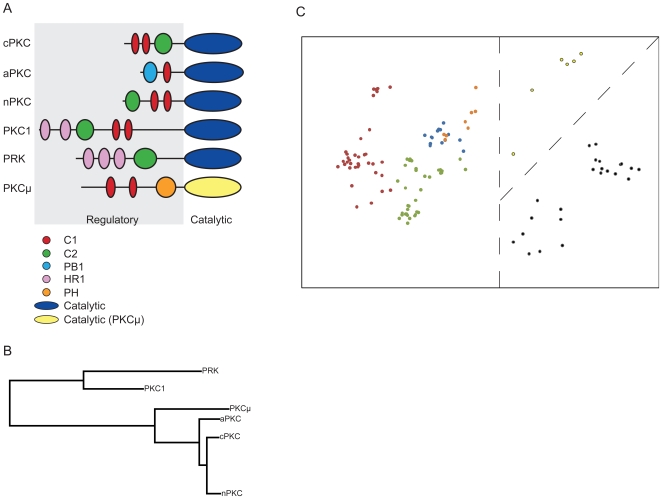
Figure 2. Analysis of the Protein Kinase C (PKC) family using the feature vector method.
(A) Structural architecture types of PKCs used in analysis, showing regulatory domains – C1, C2, PB1, HR1 and PH – and catalytic domains. cPKC – conventional PKCs, aPKC – atypical PKCs, nPKC – novel PKCs, PKC1 – fungal PKC1s, PRK – PKC-related kinases, PKCμ – PKCμ-like PKCs; (B) agglomerative hierarchical clustering dendrogram of PKC feature vectors for structural architecture types; (C) principle component analysis (PCA) of PKC feature vectors, coded by known architectural type of proteins – red dots: cPKCs; blue dots: aPKCs; green dots: nPKCs; black dots: PKC1s; orange dots: PKCμ; yellow dots: PRKs; dashed lines indicate dividing surfaces for identifying major clusters in the data set.
The dendrogram created by agglomerative hierarchical clustering of the PKC feature vectors (fig. 2B) successfully recreates the phylogenetic relationships between PKC architectural types and highlights the degree of difference between PKC-related kinases, PKC1s and other PKCs.
By running a PCA on the feature vector values for each PKC protein, we were able to quickly visualize the six architecture types of PKCs in our dataset. Figure 2C shows the PCA output for PKCs. A dashed line marking a clear dividing surface is added to this figure to demonstrate divisions in the data that warrant further analysis. Fungal PKC1s are clearly separated from other PKCs and can be identified as an important, distinct grouping (fig. 2C). In addition, PKC-related kinases and true PKCs are located in distinct clusters (fig. 2C). Finally, conventional PKCs and novel PKCs are resolved into distinct clusters (fig. 2C).
A similar identification of hemoglobin structure was also possible (fig. 3). Hemoglobins are large proteins which function in oxygen transport [13]. Each hemoglobin molecule contains 2 alpha chains and 2 beta chains, subunits which are identifiable by structural characteristics [13]. Alpha hemoglobins lack a specific alpha-helix, the D helix, that is present in beta hemoglobins [14]. Many organisms have several distinct hemoglobins, an adult form and embryonic or fetal forms created by combining different alpha and beta hemoglobin units [13]. There are more types of embryonic and fetal alpha hemoglobins than beta hemoglobins, and thus alpha hemoglobins are presumed evolutionarily older [13]. In protein databases, alpha and beta chain hemoglobins belonging to a given species are typically recorded in separate entries and so are separate in our data set also.
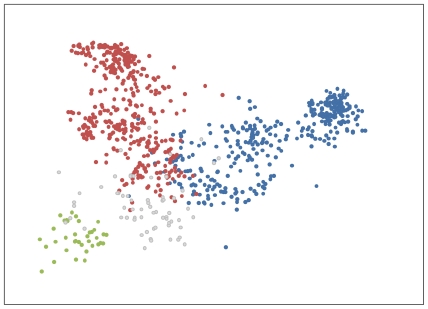
Figure 3. Analysis of hemoglobin proteins using the feature vector method.
PCA results of hemoglobin feature vectors, coded by known protein type – red dots: beta-chain hemoglobins; blue dots: alpha-chain hemoglobins, including fetal alpha-type proteins; green dots: leghaemoglobins; grey dots: other hemoglobins.
Using the feature vector method, the PCA identifies the difference between alpha chain hemoglobins, beta chain hemoglobins and leghaemoglobins, a type of monomeric hemoglobin chain found in plants [15], as the main features of the protein set (fig. 3). A range of other types of hemoglobins occur in the dataset in small numbers, but are not well resolved into distinct clusters due to their rarity in the data (see below). These proteins include the non-symbiotic plant hemoglobins, also called truncated or 2-on-2 hemoglobins [16]; the lamprey/hagfish hemoglobins [17]; bacterial hemoglobins; and erythrocruorins, which are large extracellular hemoglobins found in annelid worms and arthropods [18].
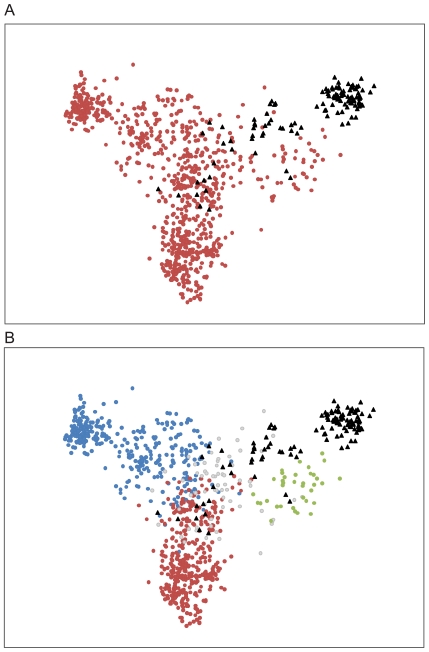
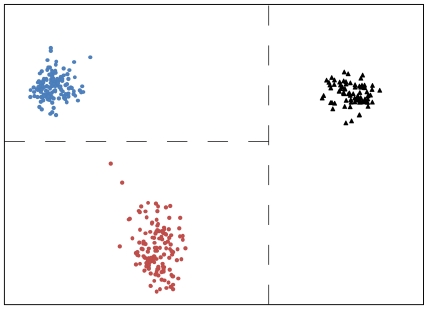
The feature vector method is able to store large amounts of information about the proteins in the dataset. When the 150 myoglobins are added to the hemoglobin dataset, the feature vector is able to distinguish these two types of proteins (fig. 4A), while retaining information about structural relationships within the hemoglobin family (fig. 4B). Myoglobins are single chain hemoproteins and share a common ancestor with hemoglobins, more than 500 million years ago [19]. Structurally, myoglobins are similar to leghaemoglobins, but functionally these proteins are quite different, with leghaemoglobins having significantly higher oxygen affinity and a broad range of functions within plant nodules [15], [19], [20]. The feature vector method, combined with PCA for visualization, clearly separates the majority of myoglobins from hemoglobins (fig. 4A), while preserving the ability to identify structural relationships between alpha and beta hemoglobins and leghaemoglobins (fig. 4B).
Figure 4. Identification of protein type as myoglobin and hemoglobin by feature vector analysis.
(A) PCA results of hemoglobin and myoglobin feature vectors, coded by known protein family – red dots: all hemoglobins; black triangles: myoglobins; (B) PCA results of hemoglobin and myoglobin feature vectors, coded by known protein type with hemoglobins identified by subtype – red dots: beta-chain hemoglobins; blue dots: alpha-chain hemoglobins, including fetal alpha-type proteins; green dots: leghaemoglobins; grey dots: other hemoglobins; black triangles: myoglobins.
When analyzing a large and varied protein dataset, some protein types may occur infrequently. These rare protein types are more difficult to cluster using PCA due to the limited amount of information available to the algorithm. As a result, these rare proteins cluster near the center of the PCA output, creating ‘noise’ in the analysis (fig. 3). By limiting the hemoglobin dataset to only adult alpha and beta chain mammalian hemoglobins and mammalian myoglobins, the most frequent protein types present in the dataset, the ability of the feature vector method to create clear separation between different groups of proteins is readily apparent (fig. 5). As in previous figures, dashed lines indicating decision surfaces are used to highlight clusters warranting further analysis.
Figure 5. Use of the feature vector method allows unequivocal protein identification when data is limited to large, well-defined protein types.
PCA results of adult alpha and adult beta mammalian hemoglobins and mammalian myoglobin feature vectors, coded by known protein type to demonstrate the ability of the feature vector to produce perfect separation of types – dashed lines indicate dividing surfaces for identifying clusters in the data; red dots: beta-chain mammalian hemoglobins; blue dots: alpha-chain mammalian hemoglobins, excluding fetal proteins; black triangles: mammalian myoglobins.
Discussion
The feature vector method described here is intended to measure the distance between protein sequences in a way that makes numerical comparisons easy and allows identification of similarity within large numbers of proteins that are not too distantly related. Using PKCs and hemoproteins as examples, we demonstrated the effectiveness of this method. When groups are completely distinct, perfect separation can be achieved; where there are gradual changes in the sequences of proteins, the feature vector performs well in conjunction with principal components analysis. Importantly, this method does not attempt to characterize differences as functional or non-functional, nor does it seek to identify key single point mutations. Rather, the goal is to provide a rapid understanding of the patterns of relatedness in large datasets of protein sequences.
Although protein kinase C was one of the first protein kinases discovered [21], categorizing members of this family is particularly challenging [22], [23]. Our method successfully reproduces the traditional classification of PKCs and clusters family members on the basis of these classifications [24]. Previous work analyzing relationships among multiple PKCs or among the larger kinase superfamily has been limited by the maximum dataset size [23], [24], [25], in a way that our method is not. The statistical feature vector method is particularly useful as a simple way of identifying subgroups in non-mammalian PKCs, an area where little is known. In the future, more detailed visualization techniques may suggest new relationships which could be explored experimentally.
Mammalian hemoglobins are also well understood, in terms of classification [16]. However, research is increasingly identifying hemoglobin-like proteins outside of mammals, including bacterial hemoglobins and non-symbiotic hemoglobins in plants [16]. As the number of hemoglobins identified in these organisms increases, the feature vector method will provide a simple tool for identifying structural groupings within these proteins.
The feature vector method provides one of the most definitive ways of classifying various types of proteins. This method provides an advantage over other classification programs in ease of use and, unlike other methods, the feature vector is not constrained to a single protein family or superfamily [23]. We have shown the usefulness of this method in PKCs and hemoproteins, and we anticipate that it will perform equally well when applied to other protein families providing a simple, rapid tool for sorting through the increasingly large datasets of proteins now available to researchers.
In the future, the utility of this method can be increased by applying new, and more specific, visualization tools to the analysis of the feature vector output, such as K-means, agglomerative hierarchical clustering, artificial neural networks and self-organizing maps. For a given data set, the patterns of variation in sequences can be learned by neural networks, or other methods, to provide a more accurate classification or clustering than can be achieved with less flexible methods like principal components analysis.
Methods
Datasets
We used three online protein sequence databases to create our protein datasets: Uniprot KB, UniprotKB/Swissprot, and NCBI Entrez-Protein. UniprotKB (www.uniprot.org) is an online repository of protein sequences; UniprotKB/Swissprot (http://ca.expasy.org/sprot/) builds upon this repository through annotation of protein sequences. Information available in UniprotKB/Swissprot includes citations for related publications, species name, protein family, domain structure and detail on protein variants and structure. NCBI Entrez-Protein (http://www.ncbi.nlm.nih.gov/protein/) is an online protein sequence database curated by the National Center for Biotechnology Information (NCBI).
The protein kinase C dataset of 127 protein sequences was downloaded from the NCBI Entrez-Protein and UniProtKB/SwissProt databases. The hemoglobin and myoglobin datasets, of 904 and 150 protein sequences respectively, were downloaded from the UniProtKB database. In order to ensure that sequences were not fragments or labeled incorrectly by protein family, sequences were analyzed using the SMART domain recognition software on the UniProtKB website. In addition, for all sequences the family classification was confirmed and the subfamily classification was assigned based on peer-reviewed journal articles which were obtained through the SwissProt database reference listings and based on notations on the UniProtKB entries where detailed information from articles was not available.
Supporting Information
Sample Parameter Calculations. This file works through the calculations of the parameters for Alanine in a short, hypothetical protein, and demonstrates the construction of the feature vector for this protein.
(0.05 MB PDF)
Feature vectors computation in C++. Computation of the feature vectors for a protein data set in C++.
(0.01 MB TXT)
Feature vector computation in Mathematica. Computation of the feature vector for a single protein in Mathematica.
(0.00 MB TXT)
PCA code for Matlab. Principle component analysis code for Matlab.
(0.00 MB TXT)
Protein Kinase C Feature Vectors. This file contains the set of all feature vectors for the PKC proteins in our dataset.
(0.16 MB XLS)
Hemoglobin Feature Vectors. This file provides the set of all feature vectors for the Hemoglobins in our dataset.
(1.03 MB XLS)
Myoglobin Feature Vectors. This file provides the set of all feature vectors for the Myoglobins in our dataset.
(0.17 MB XLS)
Protein datasets. Accession numbers and taxonomic information for Protein Kinase C (PKC), Hemoglobin and Myoglobin dataset. Each protein dataset is provided as a separate worksheet.
(0.16 MB XLS)
Acknowledgments
The authors would like to thank Dr. Changchuan Yin for providing valuable comments on the manuscript.
Footnotes
Competing Interests: The authors have declared that no competing interests exist.
Funding: The authors have no support or funding to report.
References
- 1.The UniProt Consortium. The Universal Protein Resource (UniProt). Nucleic Acids Res. 2008;36:D190–D195. doi: 10.1093/nar/gkm895. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Wang L, Jiang T. On the complexity of multiple sequence alignment. J Comput Biol. 1994;1:337–348. doi: 10.1089/cmb.1994.1.337. [DOI] [PubMed] [Google Scholar]
- 3.Liu L, Ho Y, Yau S. Clustering DNA sequences by feature vectors. Mol Phylogenet Evol. 2006;41:64–69. doi: 10.1016/j.ympev.2006.05.019. [DOI] [PubMed] [Google Scholar]
- 4.Casari G, Sander C, Valencia A. A method to predict functional residues in proteins. Nat Struct Biol. 1995;2:171–178. doi: 10.1038/nsb0295-171. [DOI] [PubMed] [Google Scholar]
- 5.Lipman DJ, Souvorov A, Koonin EV, Panchenko AR, Tatusova TA. The relationship of protein conservation and sequence length. BMC Ecol Biol. 2002;2:20. doi: 10.1186/1471-2148-2-20. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Jolliffe IT. New York, NY: Springer Science+Business Media; 2004. Principle Component Analysis, 2nd Ed. Springer Series in Statistics. pp. 80–85. [Google Scholar]
- 7.Everitt BS, Landau S, Leese M. New York: Oxford University Press; 2001. Cluster Analysis, 4th Ed. pp. 59–67. [Google Scholar]
- 8.Karp G. New York: John Wiley & Sons, Inc; 1999. Cell and Molecular Biology: concepts and experiments. 2nd ed.669 [Google Scholar]
- 9.Nishikawa K, Toker A, Johannes F-J, Songyang Z, Cantley LC. Determination of the specific substrate sequence motifs of protein kinase C isozymes. J Biol Chem. 1997;272:952–960. doi: 10.1074/jbc.272.2.952. [DOI] [PubMed] [Google Scholar]
- 10.Hofmann J. Protein kinase C isozymes as potential targets for anticancer therapy. Curr Caner Drug Targets. 2004;4:125–146. doi: 10.2174/1568009043481579. [DOI] [PubMed] [Google Scholar]
- 11.Hanks SK, Hunter T. The eukaryotic protien kinase superfamily: kinase (catalytic) domain structure and classification. FASEB J. 1995;9:576–596. [PubMed] [Google Scholar]
- 12.Rykx A, De Kimpe L, Mikhalap S, Vantus T, Seufferlein T, et al. Protein kinase D: a family affair. FEBS Lett. 2003;546:81–86. doi: 10.1016/s0014-5793(03)00487-3. [DOI] [PubMed] [Google Scholar]
- 13.Chapman BS, Tobin AJ. Complete amino acid sequences of the major early embryonic α-like globins of the chicken. J Biol Chem. 1980;255:9051–9059. [PubMed] [Google Scholar]
- 14.Whitaker TL, Berry MB, Ho EL, Hargrove MS, Phillips GN, Jr, et al. The D-helix in myoglobin and in the β subunit of hemoglobin is required for the retention of heme. Biochemistry. 1995;34:8221–8226. doi: 10.1021/bi00026a002. [DOI] [PubMed] [Google Scholar]
- 15.Kundu S, Trent JT, III, Hargrove MS. Plants, humans and hemoglobins. TRENDS Plant Sci. 2003;8:387–393. doi: 10.1016/S1360-1385(03)00163-8. [DOI] [PubMed] [Google Scholar]
- 16.Vinogradov SN, Hoogewijs D, Bailly X, Arredondo-Peter R, Gough J, et al. A phylogenomic profile of globins. BMC Evol Biol. 2006;6:31–48. doi: 10.1186/1471-2148-6-31. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Qiu Y, Maillett DH, Knapp J, Olson JS, Riggs AF. Lamprey hemoglobin. Structural basis of the Bohr effect. J Biol Chem. 2000;275:13517–13528. doi: 10.1074/jbc.275.18.13517. [DOI] [PubMed] [Google Scholar]
- 18.Royer WE, Jr, Strand K, van Heel M, Hendrickson WA. Structural hierarchy in erythrocruorin, the giant respiratory assemblage of annelids. Proc Natl Acad Sci USA. 2000;97:7107–7111. doi: 10.1073/pnas.97.13.7107. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Ordway GA, Garry DJ. Myoglobin: an essential hemoprotein in striated muscle. J Exp Biol. 2004;207:3441–3446. doi: 10.1242/jeb.01172. [DOI] [PubMed] [Google Scholar]
- 20.Downie JA. Legume haemoglobins: symbiotic nitrogen fixation needs bloody nodules. Curr Biol. 2005;15:R196–198. doi: 10.1016/j.cub.2005.03.007. [DOI] [PubMed] [Google Scholar]
- 21.Mellor H, Parker PJ. The extended protein kinase C superfamily. Biochem J. 1998;332:281–292. doi: 10.1042/bj3320281. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Coussens L, Parker PJ, Rhee L, Yang-Feng TY, Chen E, et al. Multiple, distinct forms of bovine and human protein kinase C suggest diversity in cellular signalling pathways. Science. 1986;233:859–866. doi: 10.1126/science.3755548. [DOI] [PubMed] [Google Scholar]
- 23.Martin DMA, Miranda-Saavedra D, Barton GJ. Kinomer v. 1.0: a database of systematically classified eukaryotic protein kinases. Nucleic Acids Res. 2009;37:D244–D250. doi: 10.1093/nar/gkn834. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Hanks SK, Quinn AM, Hunter T. The protein kinase family: conserved features and deduced phylogeny of the catalytic domains. Science. 1988;241:42–52. doi: 10.1126/science.3291115. [DOI] [PubMed] [Google Scholar]
- 25.Kruse M, Gamulin V, Cetkovic H, Pancer Z, Muller IM, et al. Molecular evolution of the metazoan protein kinase C multigene family. J Mol Evol. 1996;43:374–383. doi: 10.1007/BF02339011. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Sample Parameter Calculations. This file works through the calculations of the parameters for Alanine in a short, hypothetical protein, and demonstrates the construction of the feature vector for this protein.
(0.05 MB PDF)
Feature vectors computation in C++. Computation of the feature vectors for a protein data set in C++.
(0.01 MB TXT)
Feature vector computation in Mathematica. Computation of the feature vector for a single protein in Mathematica.
(0.00 MB TXT)
PCA code for Matlab. Principle component analysis code for Matlab.
(0.00 MB TXT)
Protein Kinase C Feature Vectors. This file contains the set of all feature vectors for the PKC proteins in our dataset.
(0.16 MB XLS)
Hemoglobin Feature Vectors. This file provides the set of all feature vectors for the Hemoglobins in our dataset.
(1.03 MB XLS)
Myoglobin Feature Vectors. This file provides the set of all feature vectors for the Myoglobins in our dataset.
(0.17 MB XLS)
Protein datasets. Accession numbers and taxonomic information for Protein Kinase C (PKC), Hemoglobin and Myoglobin dataset. Each protein dataset is provided as a separate worksheet.
(0.16 MB XLS)