Non-contact measurement of linear external dimensions of the mouse eye

Abstract

Biometric analyses of quantitative traits in eyes of mice can reveal abnormalities related to refractive or ocular development. Due to the small size of the mouse eye, highly accurate and precise measurements are needed to detect meaningful differences. We sought a non-contact measuring technique to obtain highly accurate and precise linear dimensions of the mouse eye. Laser micrometry was validated with gauge block standards. Simple procedures to measure eye dimensions on three axes were devised. Mouse eyes from C57BL/6J and rd10 on a C57BL/6J background were dissected and extraocular muscle and fat removed. External eye dimensions of axial length (anterior-posterior (A-P) axis) and equatorial diameter (superior-inferior (S-I) and nasal-temporal (N-T) axes) were obtained with a laser micrometer. Several approaches to prevent or ameliorate evaporation due to room air were employed. The resolution of the laser micrometer was less than 0.77 microns, and it provided accurate and precise non-contact measurements of eye dimensions on three axes. External dimensions of the eye strongly correlated with eye weight. The N-T and S-I dimensions of the eye correlated with each other most closely from among the 28 pair-wise combinations of the several parameters that were collected. The equatorial axis measurements correlated well from the right and left eye of each mouse. The A-P measurements did not correlate or correlated poorly in each pair of eyes. The instrument is well suited for the measurement of enucleated eyes and other structures from most commonly used species in experimental vision research and ophthalmology.

INTRODUCTION

The vertebrate eye is a precision optical sensor, with optically clear media bounded by smooth optical surfaces (Fernald, 2006; Pepose and Applegate, 2005). During development, the ocular dimensions of the eye can grow at different rates producing eyes of abnormal size, such as microphthalmia or macrophthalmia. In addition, the axial length of the eye is matched to the optical power of the eye in a process called emmetropia. The vertebrate eye can accurately grow to match the ocular power of the eye (Zhu et al., 2005). A mismatch of the length of the eye and optical power results in refractive errors such as hyperopia and myopia.

Measurements of the dimensions (linear distances) of the eye have helped to understand how the eye works and maintains clarity in the visible spectrum (Zhu et al., 2005) (Wallman and Winawer, 2004). We were interested in measuring the linear dimensions of the mouse eye (axial length, and equatorial diameter). These linear measurements inform us about eye growth (Carson et al., 2004; Finlay, 2008; Martins et al., 2008; Zuber et al., 1999), emmetropization (Zhou et al., 2008), and genes that regulate fundamental visual pathways influencing the size of ocular structures (Collinson et al., 2001; Puk et al., 2009a; Puk et al., 2009b; Schaeffel et al., 2004; Steele et al., 2000; Troilo and Wallman, 1991).

Opportunities to solve key biological problems have arisen by using genetically altered mice, especially in vision sciences (Everett et al., 1994; Jablonski et al., 2005; Kao, 2006; Kerscher et al., 1995; Le et al., 2006; Lyon et al., 2000; Peachey and Ball, 2003; Pierce, 2001; Schippert et al., 2007; Schweers and Dyer, 2005), but simple and rapid technologies to measure small phenotypic changes caused by subtle genotypic changes in mice need to keep pace. Determining ocular dimensions can pose a challenge in an eye of ~3.0 mm diameter, such as the mouse, since traditional devices for large eyes can have resolutions of about 0.05 mm, including, for example, A-scan ultrasound and calipers used with chickens (Irving et al., 1992). Additionally, optical modeling of the mouse eye has predicted that a 6 micron change in axial length would result in a 1 diopter shift in refractive error (Schmucker and Schaeffel, 2004b). This predicts the need for one hundred fold better precision than the human eye in which a 0.5 mm change in axial length results in 1 diopter of refractive shift (Atchison and Smith, 2000).

While several groups have measured mouse eye size (Glickstein and Millodot, 1970; Martins et al., 2008; Puk et al., 2006; Shupe et al., 2006; Zhou et al., 2001; Zhou and Williams, 1999a, b) and eye weight (Barathi et al., 2008; Shupe et al., 2006) and lens size and lens weight (Augusteyn, 1998; Shupe et al., 2006), there are difficulties in achieving extremely high levels of accuracy and precision with the rapidity and throughput needed for large mouse studies, including mutant screens, crossbreeding, and transgenic technologies. Similar eye measurement problems arise in mutant screens and breeding experiments with small fish, cf., zebrafish, or during mammalian embryonic development when the eye is quite small and rapidly growing.

Prior work in vision research used biometrics instrumentation from four categories to measure eyes in many models:

1. Calipers or micrometers (Barathi et al., 2008; Guggenheim et al., 2004; Irving et al., 1992; Prashar et al., 2009; Zhou and Williams, 1999b);

2. Image analysis of histological sections or gross images of eyes with corresponding images of calibration standards (Kröger and Fernald, 1994; Schmucker and Schaeffel, 2004b; Zuber et al., 1999);

3. MRI (Atchison et al., 2004; Chen et al., 2008; Goodall et al., 2009; Molokhia et al., 2009; Singh et al., 2006) or CT scan images (Berkowitz et al., 2004; Crow et al., 1982; Gumpenberger and Kolm, 2006; Tkatchenko et al., 2009);

4. Interferometric techniques including OCT (Gumpenberger and Kolm, 2006), partial coherence interferometry (PCI) or optical low coherence interferometry (OLCI)(Schmucker and Schaeffel, 2004a; Liu et al., 2004; Molokhia et al., 2009; Nickla et al., 1998; Peachey and Ball, 2003; Wilson et al., 2006), or ultrasound-based (Guggenheim et al., 2004; Gumpenberger and Kolm, 2006; McFadden et al., 2006; Nickla et al., 1998).

While these techniques all work well for their intended purpose, in the different context of screening tiny mouse or fish eyes, they are slow and delicate.

Advances in manufacturing and industrial metrology now offer another method to measure small or fine structures with high accuracy and precision without contacting the object. For example, there are necessities to measure the diameter of wire or single optical fibers during production while the object is still extremely hot and moving quickly along a line of processing steps. The required measurements and production standards in this setting frequently require submicron resolution. An instrument that can perform such high-resolution measurements is the laser (aka, optical) micrometer (Figure 1). We sought to determine the utility of the instrument in establishing external eye dimensions under experimental and control conditions. We tested the efficacy of the laser micrometer on one of the more challenging small eyes that is commonly used in vision research, the mouse eye, for which the previously mentioned four measurement techniques can be problematic. Because the instrument makes large numbers of measurements per second (e.g., about 2400 measurements per second) and because the instrument is designed to interface with a computer, sending data for storage in real-time, the instrument is ideal for obtaining measurements in a high throughput environment where many eyes are being studied nearly at once. The instrument is simple, fast, and easy to operate, lending itself to routine use in the laboratory by many different personnel.

Figure 1.

Components of the laser micrometer. Components consist of an emitter head and a receiver head mounted on a rail, and a controller interfaced with a computer.

In this study, we sought to validate the repeatability and reproducibility of laser micrometer-based mensuration of the mouse eye. We studied eye size and weight, and body weight in C57BL/6J and rd10 mice (Pde6b^rd10/rd10 on C57BL/6J background)(Chang et al., 2002; Chang et al., 2007) that leads to blindness and retinal degeneration. Measurements of eye size using the laser micrometer were assessed for dependence and variability corresponding to eye and body weight.

METHODS

Animal Care

Protocols were approved by the Emory Institutional Animal Care and Use Committee and used in accordance with ARVO guidelines. Wild-type C57BL/6J and rd10 on the same C57BL/6J background, up to 800 days old, were housed at 23 °C in Emory University Division of Animal Resources facilities. They were provided standard mouse chow (Lab Diet 5001; PMI Nutrition Inc., LLC, Brentwood, MO) and water ad libitum. They were maintained on a 12 h:12 h light-dark cycle. Mice were euthanized by CO₂ gas asphyxiation. Breeders were genotyped at the rd1 (Pittler et al., 1993) and rd10 (Chang et al., 2007) loci, and only mice of the correct genotypes were used in experiments.

Dissection

After euthanization, an orientation mark was placed on each eye at the most superior point of the cornea with a Sharpie pen. The left or right eye was enucleated, then about 5 min later the fellow eye was removed, as noted. The eye was removed with forceps capturing about 3 mm of optic nerve, which was used as a handle for subsequent manipulations. In some cases but not routinely, 0.25% (W/V) Rose Bengal (R-3877; Sigma-Aldrich, St. Louis, MO) in dPBS (Dulbecco's phosphate buffered saline; Invitrogen, Carlsbad, CA) was used to stain tissues (muscles and fat) adhering to the globe. The excised eye was stained for 30 s, and then rinsed serially through 5 or 6 changes of fresh dPBS, making it easier to detect when all extraocular structures were removed. Extraorbital fat and muscles were removed under a dissecting microscope with Dumont #5 forceps (World Precision Instruments cat # 500085) and iridectomy scissors. As a final step in dissection, the optic nerve was cut close to the sclera. This remnant of the optic nerve was sufficient to grasp the eye with Dumont #7 forceps (World Precision Instruments cat# 501206) while measurements were made without introducing errors.

Instrumentation

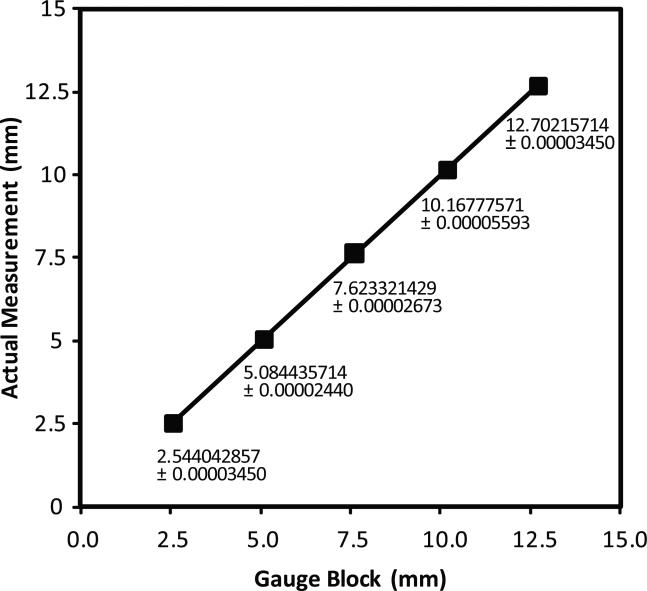
A model 7030M-laser micrometer with an LS-7601 controller and LS-H1W software (Keyence America Corp, Itasca, IL) was used in these experiments (Figure 1). Two identical instruments were used. Software from the manufacturer (Keyence) was used to interface the micrometer with a personal computer running Windows XP professional and Microsoft Office 2003 (Microsoft Corp., Redmond, WA). Workshop Grade (±0.00005 inch accuracy; labeled in English measurement units, converted to metric hereafter) gauge blocks were used to verify factory calibration of the Keyence laser micrometers. Five gauge blocks with widths of 0.254, 0.508, 0.762, 1.016, and 1.27 cm were measured seven times each. Averages and standard deviations were calculated. Linear regression was conducted (Figure 2).

Figure 2.

Laser micrometer calibration assessment. The laser micrometer was calibrated against gauge blocks. Workshop grade gauge blocks with fixed widths of 0.254, 0.508, 0.762, 1.016, and 1.27 cm (0.1, 0.2, 0.3, 0.4, and 0.5 inch thickness in English units as stamped on the gauge blocks) were measured 7 times at 23 °C and the standard's value is shown as the independent variable on the X-axis. The average of the 7 measurements is shown as the dependent variable on the Y-axis. Numbers indicate actual measurements with their standard deviations; the error bars of the standard deviations cannot be seen on the graph because they are so small. A linear least squares fit line was applied. Slope, intercept, and coefficient of determination (R²) were calculated and graphed in Microsoft Excel 2003 and calculations verified in Plainstat. These data show a resolution of 0.7679 microns and a coefficient of determination of 0.999999726.

For measurement of the mouse globe, the mouse eye, held by the stump of the optic nerve with Dumont #7 forceps, was passed into the laser plane. A video camera is built into the receiver head of the laser micrometer, and a 2D shadow of the eye is observed on the controller. A box surrounding the measurement area is projected onto the video image of the eye, and obvious errors in detecting extraneous objects in the beam, such as the forceps or fingers, are immediately apparent. Those measurements were not collected. The measurement being detected (a green vertical line bisecting the box) was viewed on a video image of the mouse eye. Once the eye was centered in the beam, the measurement was recorded and manually entered into an Excel spreadsheet.

A video recording of the dissection (Figure 3A-D) and measurement (Figure 3E-I) techniques of a single mouse eye is shown in Figure 3. The removal of the eye from the mouse takes a few seconds, while the dissection to remove the fat and extraorbital muscle takes 3-5 min. The measurement of the linear dimensions on three axes, axial (anterior-posterior; A-P), nasal-temporal (N-T), and superior-inferior (S-I), takes a few seconds each. The durability and compact size of the micrometer heads and rail allows them to be quickly repositioned from a vertically oriented plane of the LED light to horizontal in 2 or 3 seconds. The dimensions were collected and entered into the computer for each eye in less than 30 seconds. Rapid, simple, and easy operation to collect the three dimensions without contacting the globe is demonstrated in the Video Supplements.

Figure 3.

Video of the dissection and measurement techniques. Video 3A presents the dissection, and Video 3B illustrates the measurement technique. Representative images at different stages of the dissection and measurement process are illustrated in the static images in Figure 3. Panel A, removal of the eye; Panel B, removal of fat and extraocular muscle; Panel C, a representative eye following removal of fat and muscle and the optic nerve (note the orientation ink mark on the cornea identifying superior); Panel D, grasping the remnant of the optic nerve with forceps; Panel E, measurement of the A-P dimension; Panel F, re-orienting the micrometer heads and rail; Panel G, measurement of the N-T dimension (note the position of the #7 forceps handle and the ink mark indicating superior); Panel H, turning the mouse eye 90 degrees to measure the S-I axis (note the orientation of the #7 forceps handle relative to the ink mark on the superior point of the cornea and the centering coordinates on the laser micrometer rail).

Each individual eye was placed in a pre-weighed airtight screw cap tube (VWR; 2.0 ml conical bottom (cat# 16466-044) and lid (16466-080)) or tared VWR weighing dish. A Denver A-160 analytical balance with 0.1 mg resolution was used for measuring the weight of the tube alone and then with the whole eye. A 0.1 g resolution pan balance (Escali, model P115WR; Minneapolis, MN) was used to weigh the whole mouse following sacrifice.

Fixation after evaporation

Eyes were allowed to evaporate through three cycles of measurement, weighing the eyes and measuring the length of each of the three axes. During this time, the eye lost about 1 mg of weight and about 50 microns on each axis. At this point the eyes were fixed in 10% Buffered Formalin Phosphate (Fisher Cat # SF100-4, Pittsburgh, PA) for 1h. After fixation, each eye was blotted with a kimwipe to remove excess liquid. Three more sets of measurements were made with the laser micrometer and the analytical balance.

Statistics

Values are reported in metric units even though the gauge blocks are in English inch standards. Averages, standard deviations, and linear regressions were calculated using Excel 2003 or 2008 (Microsoft). Multiple linear regressions, pair-wise correlations, and other statistics were calculated in the program Plainstat <www.plainstat.com>. As per the software manufacturer's literature, the analyses are as described in standard references (Glantz, 1997). When summarized in the text or figure captions, average values are presented with standard deviations.

RESULTS

The essential components of a laser micrometer are illustrated in Figure 1. A Gallium nitride LED emitter head produces a green beam that is accurately collimated in a plane about 5 cm wide, of which the central 3 cm can be used for measurements. An object in the beam casts a shadow such that no signal from the LED is received at the measuring head. The measurement area is displayed on the video image on the controller, bounded by a box. A green line indicates the measurement extent and plane. Once the object is centered in the detection beam, the measurement was captured.

To validate the measurements from the laser micrometer, gauge blocks of known widths were measured (Figure 2). Workshop grade gauge blocks (±1.27 micron accuracy) from 0.254 to 1.27 cm widths in 0.254 cm size increments were measured with two laser micrometers of the same model. Measurements were repeated 7 times. The gauge blocks themselves were checked with a separately traceable recently inspected micrometer (Mitutoyo 293-185; Kawasaki, Japan). Figure 2 illustrates the linear regression data from one of the laser micrometers; the measurements from the second were essentially the same (data not shown). The adjusted R² was 0.999999726, the slope of the line was 0.999983015 (suggesting a minimal scaling error), and the intercept was 4.476 microns (suggesting a minimal offset error).

We determined the resolution of the instrument empirically from this calibration curve. “Resolution” is defined as the smallest difference of the independent variable (in this case, the known width of the gauge blocks) that can be resolved. That is, resolution is the ratio of the “standard error of the estimate” (Glantz, 1997) divided by the “slope” of the regression line relating the actual measurement of the dependent variable (displayed as the ordinate) to the independent variable (the known widths of the gauge blocks, displayed as the abscissa). The standard error of the estimate was 0.7679 microns, and the slope was 0.999983. Therefore, the resolution of the laser micrometer was 0.7679 microns. This measured resolution is at the detection limit of the present gauge blocks, given that the gauge blocks were certified as accurate to only ±1.27 microns. Thus, the resolution of the instrument could be less than 0.7679 microns. The manufacturer of the laser micrometer claims a resolution of 0.15 microns and an accuracy of less than 2 microns. With higher-grade gauge blocks we could test resolution to lower limits, but at this time we cannot because of their extraordinary expense.

Two of the hallmarks of a useful test measure are repeatability and reproducibility. We assessed repeatability with gauge blocks across consecutive tests with the same protocol and after multiple cycles of powering the laser micrometer on and off. We assessed reproducibility across two different model LSM-7030M laser micrometers, different operators, different locations, different days, and two slightly different measuring protocols (either manually holding the gauge blocks or positioning the gauge blocks perpendicular to the beam with draftsman's triangles). Under all these circumstances, we obtained indistinguishable accuracies and precisions of the laser micrometers (data not shown).

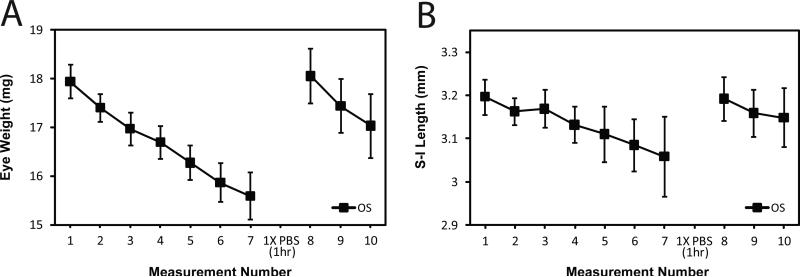
A complication of the measurement of the mouse eye is the drying out of the excised tissue in just a few minutes in room air. When measurement intervals were about 3 minutes apart, changes were observed in both weight (Figure 4A) and length (Figure 4B), suggesting effects of drying. In this experiment, we excised eyes, removed extraocular muscle and fat, measured eyes on three axes, and weighed them. Seven cycles of measurements were repeated at about 3 minute intervals. During this brief period of time, eyes lost about 13% of their weight with similar reductions of length measurements on all three axes (S-I, Figure 4B; N-T and A-P data not shown). Immediately thereafter, eyes were placed in dPBS for one hour to rehydrate. They were blotted dry and again repeatedly measured for lengths on the three axes and weighed as before. During rehydration, weight and eye dimensions were restored to their initial values. Thereafter, the trend was for evaporative loss of weight and eye dimensions with the same slope as before in exposure to room air.

Figure 4.

Repeated measurements of the same eye during evaporation. Eye weight and eye dimensions were lost quickly with time following excision. C57BL/6J mice were sacrificed at P60 (N=10 mice; 10 eyes). The left eye (OS) was enucleated first, fat was trimmed from whole eye globe, eye weight taken, and then lengths on three axes were measured. Each eye was measured 7 times, placed in 1X dPBS for 1 h, and then measured again 3 more times. Average time to reach measurement 7 was 13 .0 min ± 1.60 min. Average time from measurement 8 to measurement 10 was 4.30 min ± 0.833 min. Error bars represent standard deviations. Panel A: Eye weights over time. Panel B: Superior-inferior length over time. Regardless of axes or weight, the same pattern of evaporation and full rehydration emerged.

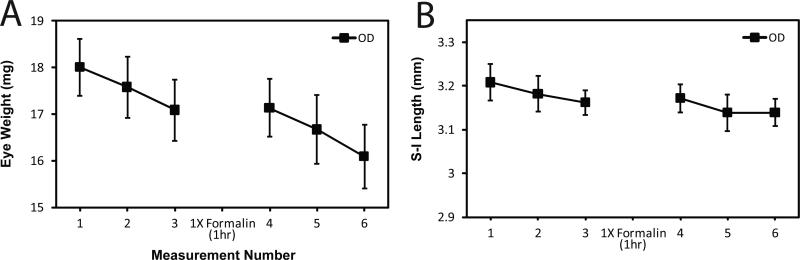
To determine the effects of fixation on evaporation and rehydration, we measured the loss of weight and length on each of three axes before and after fixation (Figure 5). We fixed the eyes after the third set of measurements of eye weight and size, a point at which the eyes had lost about 1 mg of weight and about 50 microns of length on each axis. Fixation by soaking the eye in neutral buffered formalin did not allow any restoration of eye weight or dimensions. This suggests that fixation quickly crosslinked tissue and prevented rehydration. Thus, it is important to note that fixation locks or holds the tissue at the weight, size, and dimensions of the eye at the time the eye is deposited in the formalin fixative. We have not tested other fixatives nor have we deliberately over-fixed the tissue to examine for potential loss in size or weight. The fixation process did not block further loss of weight or size by evaporation in the fourth through sixth measurements (Figure 5).

Figure 5.

Repeated measurements before and after fixation. Eyes were weighed and axis lengths measured over time before and after fixation with 10% buffered formalin. C57BL/6J mice were sacrificed at P60 (N=10). The left eye (OS) was enucleated first; fat was trimmed from whole eye globe; eye weight was taken; and then axis lengths were measured. After 3 measurements, the eye was placed in 10% buffered formalin for 1 h. The eye was then re-weighed 3 more times. Average time to reach measurement 3 was 4.73 min ± 0.467 min. Average time from measurement 4 to 6 was 4.60 min ± 0.699 min. Error bars represent standard deviations. Panel A: Eye weights over time. Panel B: Superior-inferior over time. Regardless of axes or weight, the same initial pattern of evaporation as before emerged. However, eyes could not be rehydrated after fixation with formalin.

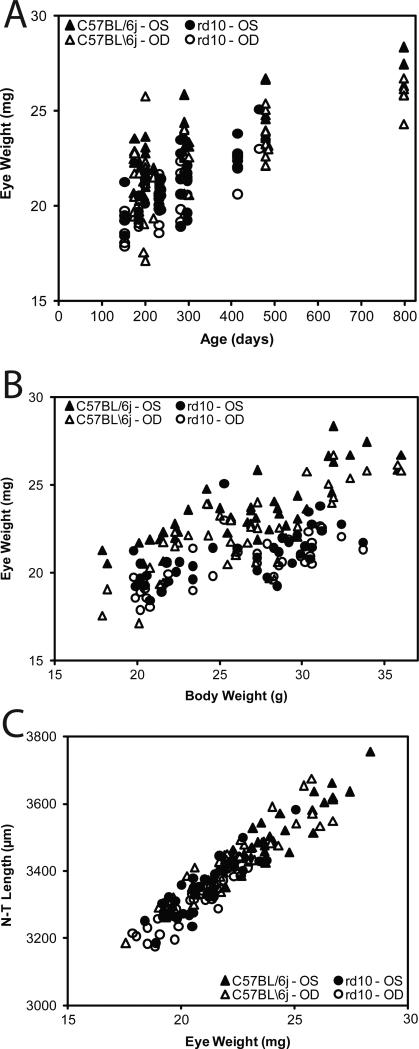
With increasing mouse age from P150 to P800, there was a general trend of increased body weight (Y = 0.0161X + 21.4; R² = 0.34601474; data not shown). In Figure 6A, we show the strong positive correlation of increased eye weight with increasing age (Y = 0.00968X + 18.9; R² = 0.54889351). As shown in Figure 6B, eye weight and body weight correlated (Y = 0.311X + 13.7; R² = 0.41930223). There is an association of increasing length measurements on all three axes with mouse age (for example, linear regression relates the N-T dimension (Y) to age (X) as follows; Y = 0.457X + 3,252; R² = 0.43719217; data not shown). There was a close correlation (Y = 49.6X + 2,306; R² = 0.88157034) of N-T length measurement to eye weight (Figure 6C). Similar results were found comparing the A-P and S-I length to eye weight (data not shown). The equatorial diameters of the S-I and N-T axis correlated closely with each other: S-I versus N-T (Y = 0.917X + 284; R² = 0.75232553). Neither S-I versus A-P (Y = 0.516X + 1,744; R² = 0.22243449) nor N-T versus A-P (Y = 0.649X + 1,293; R² = 0.31868911) correlated as closely as the equatorial diameters (S-I and N-T).

Figure 6.

Relationships among, body weight, eye weight, axis lengths, and age in normal and mutant mice. Mice were sacrificed at various ages. The left eye was enucleated first, fat was trimmed from the globe and eye weight and lengths on three axes were measured. This was repeated for the right eye. The time between left eye removal and right eye measurements was about 5 min. Panel A: Eye weight compared to age. Panel B: Eye weight compared to body weight. Panel C: N-T lengths compared to eye weight. C57BL/6J wild type mice are identified by triangles and rd10 by circles. Left eyes are represented by filled symbols and right eyes by open symbols.

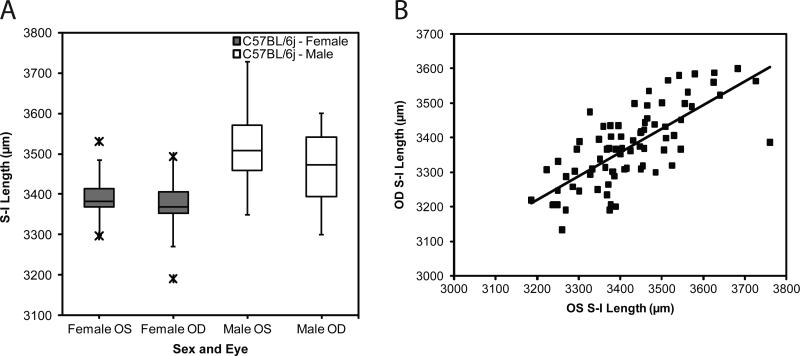
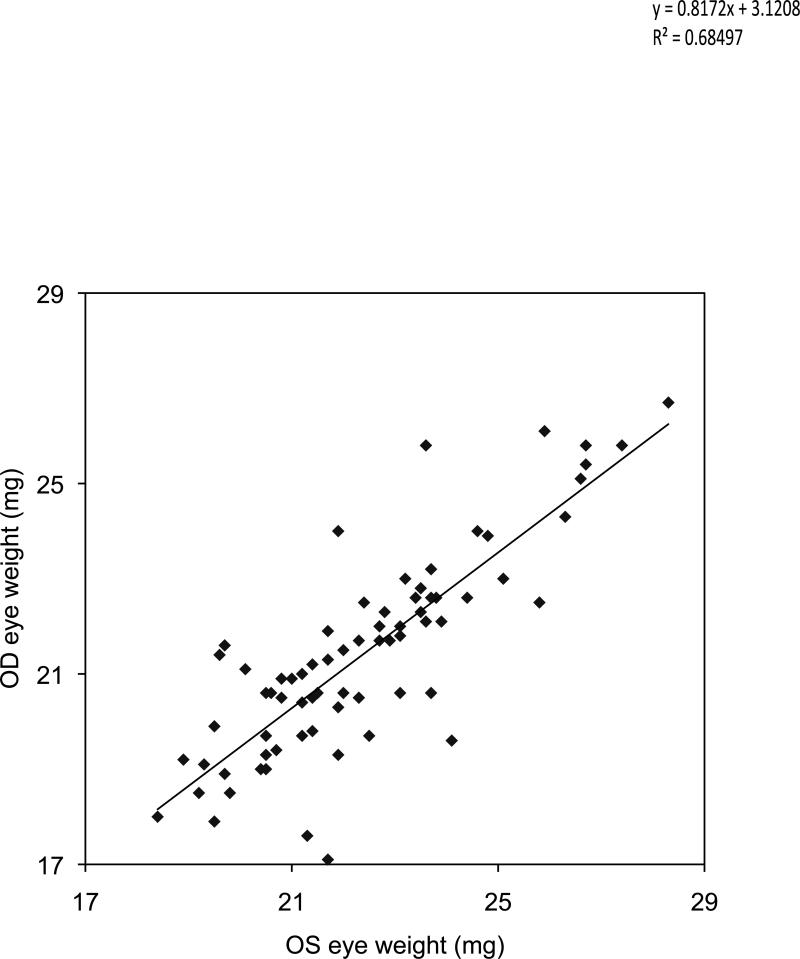
The left eye was compared to the right eye in individual mice. On the S-I axis there was a close correlation (R² = 0.618; Figure 7B) of the left and right eye dimension, but there was a consistent difference (based on paired t-test, P<0.01) with the right eye dimension and weight being slightly smaller (Figure 7A). Similar results were found on the N-T axis. The A-P axis did not exhibit a correlation (R² = 0.06835) of the OD and OS lengths in the same mouse (data not shown). The eye weight of the first enucleated eyes (OS) was generally larger than the second (OD) eye in each mouse (Figure 8). On average, the OS weighed 22.37 mg and the OD eye 21.40, for a significant difference of 1 mg, (P<0.0001; paired t-test). There was a tight correlation in weight within each pair of eyes per mouse, illustrated in Figure 8. The coefficient of determination was 0.685, and the linear regression line was:

$$\mathrm{OD}\text{eye weight}=0.8172\times \mathrm{OS}\text{eye weight}+3.121.$$

The slope of < 1 illustrates the loss in weight of the right eye over 5 min, even though the right eye was still in the mouse carcass.

Figure 7.

Left eye compared to right eye in individual mice. Mice of both sexes and strains (C57BL/6J and rd10) mice were sacrificed at various ages. The left eye was enucleated first, fat was trimmed from whole eye globe, and lengths of the three axes measured. This was repeated for the right eye. The time between left eye removal and right eye measurements was about 5 min. Panel A. S-I length in the left and right eye by sex. A box and whisker plot identify quartiles, and the average is shown as a horizontal line in the rectangle. Values indicated by X's were classified as outliers and were excluded. Panel B. Correlation of S-I length in left and right eye pairs.

Figure 8.

Comparison of the OS and OD eye weight in each mouse. The OS eye was removed first and dissected to remove extraocular fat and muscle. The eye axes were measured and the eye weighed. The right eye was left in the mouse uncovered until all measurements were collected from the left eye. A least squares linear regression was conducted, and the coefficient of determination was 0.685. The regression equation was Y = 0.8172 X + 3.121. These show a tight relationship between the size of the left and right eye of each mouse, but the right eye was lower in weight by about 1 mg on average. This is attributable to evaporation before the right eye was processed.

To test if evaporation between enucleation of the first and second eyes from one mouse was the cause of the difference in weight and size, we removed the right eye first and then the left in seven mice. The data showed that this order of enucleation did not show a difference (OD compared to OS) in eye weight, equatorial dimensions, or volume by paired t-tests. We found this result surprising. Next, returning to the original order of enucleation, we asked whether hydration with eye drops would prevent evaporation in the right eye in the 5 min time interval between first (OS) and second eye (OD) enucleation. By keeping the OD eye covered with eye drops while still in the carcass (during the 5 min interval after OS removal), there were no subsequent differences between the OS and OD eye in eye weight, lengths of the three axes, or eye volume by paired t-tests. Thus, the eye drops prevented weight and size loss in the right eye. These experiments highlight the need to either remove both eyes simultaneously, or to cover the second eye with eye drops to moisturize the globe during the period of time between the first eye's removal from the mouse and the excision of the second eye.

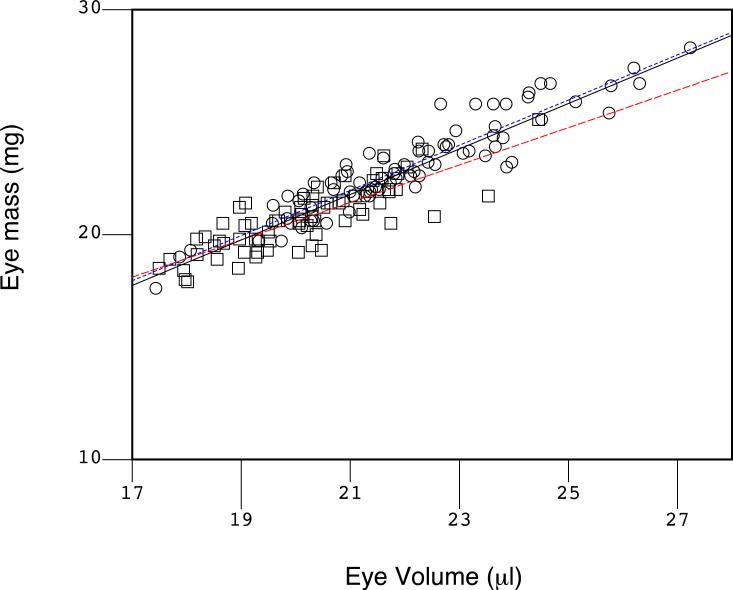
The density of the mouse eye was assessed. The volume of the eye was approximated as a prolate spheroid. The volume (V) of the prolate spheroid was based on measurements of the lengths of the three axes and was calculated as V = (4/3)πa²b, where “a” is the short axis radius and “b” is the long axis radius. We approximated “a” as the average of the S-I and N-T radii, and “b” as the A-P radius. This volume was plotted against the measured weight of each eye (Figure 9). In Figure 9, the slope of the least squares linear regression line indicated a density of (1.013 mg/μl), and the coefficient of determination (R²) was 0.852, indicating the tight accuracy and precision of the measurement techniques and low natural variation in density of the mouse eye.

Figure 9.

Density of the mouse eye. The volume of the eye was approximated as a prolate spheroid and plotted on the X-axis against the measured weight of the eye on the Y-axis. A least squares linear regression was conducted (black line; pooled data), and the slope of the line indicated the density of the eye as 1.013 mg/μl. The coefficient of determination (R² = 0.852) suggests that both measurements tools, the laser micrometer and the analytical balance, were accurate and precise, and there was little variation in the density of the eye. Deviations would indicate significant problems in eye growth. The rd10 mice are indicated by squares and WT C57BL/6 with circles. Regression lines for each group are illustrated (red for rd10 and blue dashes for C57BL/6). These two groups were not different based on the slope and the intercept of the regression lines. However, based on a coincidence test (Glantz, 1997), there is an improvement (F=7.607, P<0.001) by fitting the two sets of data to two lines (blue dots for the C57BL/6; red dashes for the rd10) over a fit of the pooled data to a single regression line (black solid line).

The rd10 mutation contributed to a slightly smaller eye size and weight (Figure 9), and a slight trend (red dashed line) to a slightly lower density when compared to the regression line of the WT C57BL/6J mice (blue dotted line). The two strains are identified by circles (WT C57BL/6) and squares (rd10). There was a clustering of smaller eye volumes and eye weights in the rd10 mice partly due to a tighter age range of younger rd10 mice in the sample, and there was a wider distribution of sizes and weights and ages in the WT C57BL/6J mice, as indicated by the coefficients of determination (R² of 0.869 for C57BL/6J and 0.666 for rd10). A coincidence test (Glantz, 1997) of the regression lines indicated a difference in the two trend lines (F=7.607, P<0.001), though slopes of the lines, 1.005 and 0.830, respectively, were not different; P=0.805) and the intercepts of the regression lines (0.869 and 3.993, respectively) were not significantly different either (P=0.788). This suggests at most a slight trend towards a smaller eye in rd10 compared to C57BL/6.

Table 1 summarizes pair-wise correlations among the various factors that we measured, including the correlation coefficient, coefficient of determination, t-statistic, and p-value for each pair. Tight correlations were found among several pairs, especially between N-T eye diameter and S-I eye diameter (pair 26), and eye weight with N-T and S-I diameters (pairs 27 and 28), and with body weight and sex (pair 14), and eye weight and age (pair 7). No correlations were found with strain and body weight or sex (pairs 8 and 9). Although not among the tightest of correlations (ranging from −0.56 to −0.59), the rd10 strain had marginally smaller eye weights and equatorial diameters than the wild type C57BL/6J counterparts (see pairs 11-13, Table 1) consistent with the graphical representation in Figure 9.

Table 1. Pair-wise Correlation Summary.

Pair-wise correlations of measurements were conducted. Eight characteristics (age, strain, body weight, sex, anterior-posterior (Ant-Post) eye length, nasal-temporal (Nas-Temp) eye diameter, superior-inferior (Sup-Inf) eye diameter, and eye weight) were compared. Coefficients of determination (R-SQ) over 0.5 (accounting for 50% or more of the variation) are indicated in Yellow (pair 7 (Age with eye weight), pair 14 (body weight and sex), and pairs 26-28; pairs of nasal-temporal eye diameter, superior-inferior eye diameter, and eye weight). Almost all of the correlations (26 of the pairs) are significant (P<0.01) except pairs 8 and 9 (strain with body weight, and strain with sex; both shown in Red). All these correlations matched with expectations. “r” refers to the coefficient of variation, and “t” to the t-statistic.

Pair	Item 1	Item 2	Count	r	R-SQ	t	p-level
1	Age	strain	150	−0.3346	0.11196	−4.31959	0.00003
2	Age	Body Weight	150	0.59195	0.35040	8.93498	0.00000
3	Age	Sex	150	−0.3227	0.10414	−4.14773	0.00006
4	Age	Ant-Post (um)	150	0.57028	0.32522	8.44577	0.00000
5	Age	Nas-Temp (um)	150	0.66406	0.44097	10.80481	0.00000
6	Age	Sup-Inf (um)	150	0.63445	0.40252	9.98538	0.00000
7	Age	Eye weight (mg)	150	0.74291	0.55192	13.50181	0.00000
8	strain	Body Weight	150	−0.0630	0.00398	−0.76860	0.44335
9	strain	Sex	150	0.08322	0.00693	1.01592	0.31133
10	strain	Ant-Post (um)	150	−0.2216	0.04912	−2.76499	0.00642
11	strain	Nas-Temp (um)	150	−0.5998	0.35987	−9.12164	0.00000
12	strain	Sup-Inf (um)	150	−0.5586	0.31210	−8.19437	0.00000
13	strain	Eye weight (mg)	150	−0.5641	0.31829	−8.31273	0.00000
14	Body Weight	Sex	150	−0.8392	0.70431	−18.7754	0.00000
15	Body Weight	Ant-Post (um)	150	0.38331	0.14693	5.04881	0.00000
16	Body Weight	Nas-Temp (um)	150	0.62621	0.39214	9.77126	0.00000
17	Body Weight	Sup-Inf (um)	150	0.63259	0.40017	9.93658	0.00000
18	Body Weight	Eye weight (mg)	150	0.65054	0.42320	10.42055	0.00000
19	Sex	Ant-Post (um)	150	−0.2757	0.07603	−3.48975	0.00064
20	Sex	Nas-Temp (um)	150	−0.4912	0.24134	−6.86155	0.00000
21	Sex	Sup-Inf (um)	150	−0.5231	0.27372	−7.46847	0.00000
22	Sex	Eye weight (mg)	150	−0.5072	0.25731	−7.16076	0.00000
23	Ant-Post (um)	Nas-Temp (um)	150	0.56856	0.32326	8.40809	0.00000
24	Ant-Post (um)	Sup-Inf (um)	150	0.47713	0.22765	6.60483	0.00000
25	Ant-Post (um)	Eye weight (mg)	150	0.60359	0.36432	9.20985	0.00000
26	Nas-Temp (um)	Sup-Inf (um)	150	0.86832	0.75399	21.29780	0.00000
27	Nas-Temp (um)	Eye weight (mg)	150	0.93934	0.88237	33.31862	0.00000
28	Sup-Inf (um)	Eye weight (mg)	150	0.87354	0.76307	21.83254	0.00000

The data set was further explored to validate already known relationships and to find new ones. Such validations serve to check the consistency of the laser micrometer with other measurement tools. Multiple linear regressions were performed to predict the value of a dependent variable. Independent variables that were tested included age, sex, strain, body weight, eye weight, A-P length, S-I eye diameter, and N-T diameter of the eye, omitting the dependent variable. During multiple linear regression, those independent variables that were not significant at P<0.05 were eliminated, and the regression recalculated. A Y-intercept term was allowed, as there is no reason a priori to assume a regression passing through the origin. Three examples are given below. Multiple regression analyses were conducted to predict N-T and S-I equatorial diameters:

$$\mathrm{N}\text{-}\mathrm{T}\left(\text{length in}\mu \mathrm{m}\right)=1997\text{-}18.40\times \text{Strain}+0.1685\times \mathrm{S}\text{-}\mathrm{I}\text{length}+38.84\times \text{Eye weight},$$

where the categorical or nominal value of “strain” was arbitrarily taken as “2” for rd10 and “1” for the wild type counterpart, C57BL/6J. This model accounts for about 89% of the variation in N-T length.

$$\mathrm{S}\text{-}\mathrm{I}\text{length}\left(\mu \mathrm{m}\right)=1339+0.4288\times \mathrm{N}\text{-}\mathrm{T}\text{length}+27.43\times \text{Eye weight}.$$

This model accounts for about 78% of the variation in S-I length.

Third, among the several potential independent variables listed above, the two equatorial lengths best predicted eye weight:

$$\begin{array}{cc}\hfill & \text{Eye weight}\left(\mathrm{mg}\right)=\text{-}31.96+0.002522\times \text{Age}+0.01224\times \mathrm{N}\text{-}\mathrm{T}\text{length}+0.003410\times \mathrm{S}\text{-}\mathrm{I}\hfill \\ \hfill & \text{length}.\hfill \end{array}$$

This model accounts for 91% of the variation in eye weight.

DISCUSSION

Here, we introduce the laser micrometer to the vision sciences community, and we find that for the purpose of measuring the exterior linear dimensions of the eye, the laser micrometer is remarkably fast, easy, and accurate. Its noncontact operation does not distort the shape of the eye, and the rapidity of the measurements allows the eye to be processed subsequently for myriad experimental purposes. Due to the portability, ruggedness, and minimal maintenance needs of the instrument, one can serve a full floor or department quite readily. The accuracy and precision are in the 0.1-micron range according to the manufacturer's specifications. Operating costs are negligible. Its chief drawback is the initial purchase cost, about $8,400 for the model we used.

The necessity for high accuracy and precision in making a measurement can vary widely depending on the types of hypotheses posed, but most vision related experiments concern some aspects of focus or defocus or light scatter, and knowledge of focus to <1 diopter is often necessary. This sets a boundary on linear measurement accuracies. Given that for practical purposes of measuring eye dimensions in the mouse, an accepted assumption is that a 6 micron change in axial A-P length corresponds to about 1 diopter of refractive change (Schmucker and Schaeffel, 2004b), so that a resolution of <6 microns should in general be sufficient for most vision sciences laboratory measurements of length, such as those needed in most myopia or optical aberrations experiments, quantitative trait locus experiments (Prashar et al., 2009; Wagner et al., 2008; Williams et al., 1998; Zhou et al., 2001; Zhou and Williams, 1999a), and mutational analyses (Glaser et al., 1994; Hill et al., 1992, 1991; Jablonski et al., 2005; Puk et al., 2006) in mice or other species (Dirani et al., 2009; Yeh et al., 2007). The measured resolution of the laser micrometer was 0.7679 microns. (The actual resolution of the instrument is less than this, as we were limited by the precision of our gauge blocks).

While the laser micrometer is simple and easy to use, care must be taken to assure the collection of valid data. Considerations include:

1. The laser micrometer measures the shadow cast by an object. If an object does not refract light, if it is so clear that it casts no shadow, then the laser micrometer will not work. However, the laser micrometer is routinely used to measure optical fibers and clear plastic films. An alternative is to sparingly powder coat the object so that it becomes sufficiently opaque.

2. The laser micrometer measures external dimensions. Deep pits in the external surface can be missed.

3. The dimensions measured represent those of the dead eye, excised from the orbital socket, and stripped of extraocular tissue with no blood flow. The eye lacks normal supporting tissues. Distortions, stresses, and strains placed on the shape of the eye that occur in vivo when in the orbital socket. The eye, as measured in the laser micrometer, dangles from the optic nerve stump and is subjected to 1× g as it is suspended. While most eyes exhibit some rigidity, there may be strain that slightly lengthens the vertical dimension. It is possible to mount the eye in other orientations (other than suspending from its optic nerve), to pressurize the eye to a normal or high IOP and then measure the shape and size of the eye as a function of IOP, or to measure the eye suspended in a clear liquid of equal density to the eye.

4. Length and weight measurements change with time following excision from the mouse due to evaporation in normal room air (Figure 4, Figure 5). Evaporative water loss was a significant problem, but weight and size were fully restored to normal levels by soaking the eye in dPBS for an hour indicating that a straightforward reversible evaporative mechanism was at work. The amount of weight loss due to evaporation is large enough to be a concern, but there are several simple solutions and precautions to prevent evaporation or ameliorate its effects: 1. The measurements can be made rapidly following excision. 2. Measurement timing can be standardized. 3. The eye can be dissected in a suitable aqueous buffer and kept in a 100% humidified chamber or a buffered solution between excision and measurement. 4. An eye remaining in the deceased mouse even for as little as 5 minutes ought to be covered with eye drops to maintain hydration. We showed that covering second eye (OD) with eye drops prevented dehydration, and OS and OD weights and volume then were the same by paired t-tests.

We were able to obtain novel data through the use of the laser micrometer. We were able to rapidly measure lengths on 3 axes within a few seconds for each eye. This allowed novel correlations (Table 1) and volume calculations. The results (Table 1) showed close correlations among the body weight, eye weight, age, and these three ocular dimensions.

There was a general trend towards larger ocular dimensions and eye weight with age (from 150 to 800 days of age) and with body weight. Our mice were up to P800, which is longer than any other studies, and the trends of earlier studies extrapolated as far as P800 hold up well with our actual measurements (Shupe et al., 2006; Zhou and Williams, 1999a, b).

The A-P length (averaging 3,495 ±129 microns) was almost always greater than the equatorial diameter. If we model the eye as a sphere with a 100 micron corneal bulge, it would add 100 microns, on average, to the A-P length, which is consistent with the length that we found. The S-I and N-T dimensions (averaging 3,396 ±119 microns and 3,394 ±113 microns, respectively) were always very close and the averages differed by only 2 microns. Eye mass averaged 21.92 ±2.14 mg with a body weight of 26.35 ±4.48 g, for a group of mice averaging 309 ±164 days old.

In Figure 9, we estimated the density of the mouse eye based on volume estimates and weights. The slope of the linear regression of volume and weight provided the density. The relatively small variation (the coefficient of determination, R², was 0.852) from the line indicated that eye growth is generally normal. Technical variation in the weight and length measurements contributed some of this variation, but by in large the eyes deviated little from the line regardless of age, sex, or strain of mice. This might provide a baseline for a quantitative trait: Deviations from linearity (a high or low density) might be a sign of a misshapen eye due to abnormal mouse eye growth, and we consider that a distorted shape is a marker of eye disease. In Figure 9, we observed a larger variation in eye density in the rd10 mice and a slight change in the regression lines of rd10 and WT C57BL/6J mice.

In mice, age, body weight, and brain weight together account for 75% of the variation in eye weight by multiple linear regression (Zhou and Williams, 1999a, b). Similarly, in chickens, eye size strongly correlates with body size (Prashar et al., 2009). Our data were similar. Multiple linear regression models of N-T and S-I were built that account for 89% and 78% of the variability, respectively. A-P length was less well predicted (about 39% of the variability was accounted for in our best multiple regression, and 61% comes from unknown factors). We did not control, measure, or vary these factors, which may include genetics or environment that may contribute to emmetropia.

It is significant that the left and right eye of each mouse closely correlate in the length of the S-I axis (Figure 7B). The same is true for the measurement of the N-T axis, showing the same tight correlation. More profound is that despite these two tight correlations, the A-P axes of the right and left eye in the same mouse do not correlate well (R² = 0.06835). This is telling: Hypotheses and mechanisms to explain eye growth and emmetropia must account for tight coupling of the equatorial diameters of the left and right eye, and at the same time must explain how the A-P lengths of each eye are largely independent of each other in the same mouse.

One could argue that in most of our data, the right and left eyes were excised from one mouse at different times, so any OS-OD comparisons are not relevant. However, the right eye was removed within 5 minutes of the left, reducing artifactual differences caused by the sequential dissections. Also, the tight correlation (OD to OS compared) on the N-T axis and S-I axis argue against this criticism. It, however, is possible that evaporation on the A-P axis is subject to erratic and variable rates of dehydration across the OD and OS eye pair. This argument may imply a difference in water vapor permeability between the right and left eye or between different surface structures of the eye (c.f., cornea versus sclera).

In general, our linear measurements and eye weights are in agreement with previous results for the C57BL/6J mouse and other strains of mice (Barathi et al., 2008; Guggenheim et al., 2004; Prashar et al., 2009; Zhou et al., 2001; Zhou and Williams, 1999a, b). However, measurements with the laser micrometer appear to be a significant improvement because: 1. They are more accurate and precise, and eye shape is less distorted compared to methods that require contact with soft tissue. 2. Measurements were done quickly and easily on all three axes. 3. We were able to obtain eye length measurements up to P800, and regardless of the optical clarity of the cornea or lens. 4. Laser micrometer measurements are direct. No calculations or assumptions are necessary, and no internal standards involved. 5. The laser micrometer is very durable and holds its calibration over long periods of time. 6. In a genetic model, the rd10 mouse, we were able to determine that the eye was trending to slightly smaller than WT, corresponding to initial reports of hyperopia in these mice (Faulkner et al., 2008). However, our data do not speak to a causal relationship between the rd10 mutation and the slightly smaller eye.

Table 2 summarizes comparisons of the laser micrometer to other measuring devices. The table highlights the utility and simplicity of the laser micrometer. We suggest that the laser micrometer would be useful in many active areas of research in vision and ophthalmology: Myopia (Cottriall and McBrien, 1996; Luft et al., 2003; Troilo, 1992; Wallman and Winawer, 2004; Young, 2009) is a clear and obvious subject where accurate measurement of eye dimensions is known to be critical. Developmental biology (Carson et al., 2004; Guggenheim et al., 2004; Martins et al., 2008) is another obvious application to quantify eye and lens (Augusteyn, 1998) growth. Eye size changes may be critical in high-tension glaucoma research. Zoological comparisons of eye size would be helped with highly accurate measures of eye dimensions. Mouse models of genetic eye diseases such as keratoconus clearly would benefit from highly accurate measurements of external eye dimensions. It is interesting that we detected very small variations between the rd10 and the WT C57BL/6J mice by mensuration. We speculate that we will find further evidence of myopia or hyperopia in retinal degenerations in many different mouse models of retinitis pigmentosa and allied retinal diseases.

Table 2.

Comparison of several measuring devices to the laser micrometer.

Device Type	Contact?	Precision	Cost (USD)	Training	Live?	Measurement Time	Eye Size	Maintenance; Operating cost	Quirks
Laser Micrometer	No	0.15 μ	8,400.	minimal	No	seconds	0.5-25 mm	None
Micrometer Calipers	Yes	1-100 μ	200.	moderate	No	minutes	0.5-25 mm	None
PCI/OCT	No1	3-20 μ	40,000 to 150,000.	heavy	Yes	minutes	P2	High	Head-post. Anesthesia. Calibration Required. Only optical axis measured. Optical clarity needed.
MRI/CT	No1	252μ	>500,000.	heavy	Yes	minutes	3-25 mm	High	Anesthesia
Image Analysis	Depends3	4-100μ	1,000. to 2,000.4	moderate	No	minutes	1-25 mm	Low	Calibration required

¹Eye drops or hydrogels are placed in contact with the eye to prevent dehydration during anesthesia and the procedure.

²Purpose built for the species under study.

³Contact of the eye with a holder is usually required.

⁴Camera equipment and image analysis software costs. Assumes that microscopes, histological, and other equipment are already available.

In summary, the laser micrometer proved to be an efficient, precise, and repeatable method to obtain useful information of the 3D size and shape of the mouse eye. The technique is readily applicable to almost all enucleated eyes routinely used in vision research. It is particularly apropos when a non-contact measurement is required, given that the eye is soft and could deform if measured with a contact method. The laser micrometer tested here should work equally well with eyes from other animals up to and including the size of the human eye. For eyes larger than human, larger laser micrometers are available with nearly the same resolution. For substantially smaller eyes than mouse, there are smaller laser micrometers with even higher accuracies and precisions.