Selection-Fusion Approach for Classification of Datasets with Missing Values

Abstract

This paper proposes a new approach based on missing value pattern discovery for classifying incomplete data. This approach is particularly designed for classification of datasets with a small number of samples and a high percentage of missing values where available missing value treatment approaches do not usually work well. Based on the pattern of the missing values, the proposed approach finds subsets of samples for which most of the features are available and trains a classifier for each subset. Then, it combines the outputs of the classifiers. Subset selection is translated into a clustering problem, allowing derivation of a mathematical framework for it. A trade off is established between the computational complexity (number of subsets) and the accuracy of the overall classifier. To deal with this trade off, a numerical criterion is proposed for the prediction of the overall performance. The proposed method is applied to seven datasets from the popular University of California, Irvine data mining archive and an epilepsy dataset from Henry Ford Hospital, Detroit, Michigan (total of eight datasets). Experimental results show that classification accuracy of the proposed method is superior to those of the widely used multiple imputations method and four other methods. They also show that the level of superiority depends on the pattern and percentage of missing values.

1. Introduction

Missing value is a common problem in real-world data processing and pattern recognition. Management of missing values becomes critical when the number of available samples is small [1]. Modifying an algorithm primarily designed to work on complete datasets to work on incomplete datasets is a challenge. In general, an appropriate strategy based on the ultimate processing goal may be developed. However, in the case of datasets with a small number of samples, not only the final goal but also the percentage and the distribution of missing values should be considered in algorithm development [2-3].

Traditional missing value management methods are based on the preprocessing of the data independent of the final goal and the associated processing scheme. In these methods, the missing values are estimated or the deficient samples are removed [1]. Although in this approach the data processing algorithm does not need to change, the data is not efficiently used, especially when a large portion of the samples have missing features. Modern missing value management methods are designed for specific applications and associated processing schemes where missing value management is integrated into the processing scheme [4]. These algorithms either apply multiple data processing stages, e.g., multiple imputations or somehow avoid the unknown values in the processing scheme, e.g., decision trees.

Although modern algorithms are shown to be successful in different applications, their proposed solutions are not designed to deal with a high percentage of missing features or a large number of systematic missing values that are frequent scenarios in some data categories such as medical datasets [1]. The main challenge arises from insufficient statistical power after the missing values are imputed. In this situation, the following questions arise.

• How to measure the complexity of the missing values?

• How to work with the missing values when imputation of the missing values is inappropriate?

• How to manage the missing values when the same features are missing in the test and training samples?

This paper proposes a new approach, named selection-fusion, based on the subspace classification method. In the proposed approach, missing value management is integrated not only in the training but also in the testing of the classifier. To this end, a set of classifiers are trained on the subspaces of the original feature space and then clustered using a distance metric. The best classifiers in each cluster, depending on the testing data, are combined to construct the overall classifier and estimate the final output.

The proposed approach is compared with the multiple imputations method as the most similar incomplete data processing method. Our major contributions can be summarized as follows.

• As part of the algorithm, we define a quantitative measure for the complexity of the missing values. Based on this measure, the usefulness of the algorithm for a particular dataset can be evaluated.

• We consider missing values in both of the training and the testing datasets without filling the missing values.

• We show that the proposed approach can be efficiently implemented for the support vector machine classifiers.

The rest of the paper is organized as follows. In the next section, we review the state-of-the-art for incomplete data processing. Details of the proposed selection-fusion method and its application to missing value management are described in Section 3. In this section, we address the above three challenges using multi-classifier fusion. We describe how each classifier is selected and how the results are combined to boost up the performance. The experimental results are presented in Section 4. We highlight the application areas of the new method and also discuss its limitations in Section 5 and conclude the paper in Section 6.

2. Related Work

In a missing value problem, considerable portions of the data fields may be incomplete. To describe the seriousness of the data deficiency, the primary question in a typical missing value problem is “the missing value pattern.” For example, in Pneumonia data described in [6], on average 6.3% of the feature values are missing while one individual feature is missing for 61% of the cases. On the other hand, in C-Section problem [6], only 1.2% of the feature are missing, while 27.9% of the cases have at least one missing feature. However, these figures do not provide clear ideas about the complexity of these problems. In fact, despite a smaller percentage of the missing values, the second problem is more complicated than the first.

To describe the complexity of a missing value pattern, some statistical models are used in the literature. Missing completely at random (MCAR) and missed at random (MAR) are the models most frequently used in the database literature. Although due to their simplicity, they are not always realistic models for the real-world problems, they provide relative measures of complexity. The missing value for a random variable X is MCAR if the missing probability is independent of the actual value of X or the values of the other features. The missing value is called MAR if the missing probability is independent of the value of X after controlling the other variables. Missing values due to equipment malfunction is an example of the MCAR well-described pattern. However, in many real-world applications, MAR is a more realistic model than MCAR [2].

Generally speaking, there are five classes of well-established strategies to deal with the missing values: 1) discard the incomplete samples (e.g., pairwise deletion [2]); 2) avoid the missing features by dynamic decisions (e.g., decision trees such as CART [7]); 3) recover unknown values from the similar samples (e.g., Expectation Maximization (EM) [8]); 4) insert possible values for the missing features, classify after each insertion and combine the classification results (e.g., Multiple Imputations (MI) [9]); and 5) design multiple classifiers on the subsets of the data and combine the classification results (e.g., ensemble classifiers [17]).

Discarding the incomplete samples and filling the missing values are very simple but undesirable methods for a dataset with a small number of samples and a large percentage of missing values. The former approach may discard significant amount of information when the number of samples is limited and the latter approach may add considerable distortion to the data when the percentage of the missing values is high.

Recovering the missing values form the other samples, also called single imputation, is the traditional approach for the treatment of incomplete datasets with a small number of samples. Many single imputation methods have been proposed over the years. Decision tree imputation [7], nearest neighbor imputation [10], and mean value substitution [11-12] are examples of classical imputation methods. These methods are only valid under specific assumptions such as MCAR assumption for the mean value substitution approach or dense sampling for the nearest neighbor imputation approach. Bayesian missing value treatment is a modern approach that replaces the missing values with the most probable values [8].

From the classification point of view, there is a common problem in all traditional missing value treatment methods: they provide a solution independent of the ultimate goal. Multiple imputations (MI) method [1,9] is an alternative solution that uses Monte Carlo simulation to generate more than one imputation of the missing values. However, the MI usually implies several assumptions on the data distribution such as joint normality [13] and regression relationships [14]. Application of MI is particularly favorable when the number of samples is relatively small (100 cases or less). Markov Chain Monte Carlo (MCMC) method is a successful MI method for datasets with a small number of samples [13-15].

Recently, ensemble classifiers technique has been shown to be a valuable tool for missing value management. In this approach, the results of multiple weak classifiers are combined to boost-up the performance. Different groups have shown effectiveness of this approach for general classification problems [16-17]. Recently, it has also been applied to the missing value problem [18]. Despite its advantages, this approach suffers from two major limitations in its application to the missing value problem: 1) lack of mathematical framework for the selection of the weak classifiers; and 2) handling of the missing values in the testing data. In this paper, we overcome both of these limitations.

From the performance point of view, the most effective ensemble approach in the literature utilizes fusion. In this approach, outputs of a set of inaccurate classifiers are combined to generate highly accurate classification results. A simple implementation of this idea, also known as selection-fusion (SF), trains each classifier on a random subset of data [19]. This implementation is shown to be effective for small datasets and improve the performance compared with traditional methods. However, in the large datasets, since the number of possible classifiers increases quickly, this implementation of fusion would not work well. A systematic method to find an optimal set of classifiers, as proposed in the paper, solves the problem using a manageable number of classifiers. In addition, when there are missing values in the data, as is the case in this paper, random selection of the subsets is inapplicable.

In general, both of the testing and training datasets may have missing values. When a feature is missing in the testing data, filling the missing value is the most common approach [19-20]. The advantage of the filling method has been mostly discussed under certain conditions like the MCAR model and a sufficient sample size. Apparently, the performance degrades if these assumptions are invalid [21-22]. Dealing with the missing value in the testing phase may be completely different from the training phase. In the statistical methods, these two phases are not necessarily separated. However, in the classification and machine learning methods, they are separated.

In summary, the conventional missing value treatment algorithms either estimate the unknown values or remove the deficient samples. Estimation of the unknown values needs particular assumptions about the data distribution. Obviously, any unrealistic assumptions may bias the results. On the other hand, removal of samples form the training pool reduces the statistical power of the classification process. Therefore, both approaches are suboptimal.

3. Proposed Method

3.1. Classification of a Dataset with Missing Values

We use the ensemble classifiers idea to overcome the limitations discussed in the previous section. We use a pool of classifiers each trained using a portion of the original data called a subset. In other words, a subset is a collection of the samples that have complete data for a specific subset of features. As such, each subset is identified by a set of samples and a set of features. The subsets are selected such that each subset has no missing values and a collection of the subsets includes all of the samples in the original data. By training multiple classifiers using the data in the individual subsets, a set of completely trained but weak classifiers are constructed. If the subsets are selected properly, the results of the weak classifiers may be combined to build a strong classifier. This step is called fusion (See Figure 1).

Fig. 1.

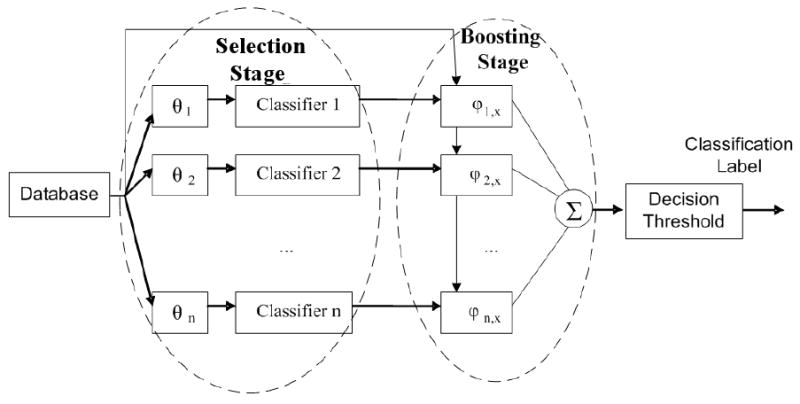
Selection-fusion approach: Overall view of the proposed two stage classification approach. In the selection stage, a set of classifiers are trained on different feature spaces (subsets). In the fusion stage, the results of the classifiers of the selection stage are combined.

Selection of the subsets is the most challenging part of the proposed selection-fusion algorithm. Each subset is defined as a set of samples and a set of features from the original data. Since a large number of samples are always desirable for classifier training, given a feature set, it is desirable to find the largest number of samples for each subset. We refer to such subsets as the complete subsets. Each subset of the original features corresponds to an empty or a unique complete subset. Therefore, there are at most 2^n(F)-1 non-empty complete subsets for a data with n(F) features.

There is a trade off between the set of features and the set of samples in a subset. Adding a new feature may cause removal of some samples from the subset and vice versa. On one hand, a small sample size does not allow efficient training of the classifier. On the other hand, a small number of features limit the classifier accuracy. However, by balancing the feature set versus the sample set, the performance of the classifier may be optimized.

Moreover, the fusion performance depends not only on the performance of the individual classifiers but also on the diversity of the classifiers. The performance of the final classifier will depend on the way the subsets are selected and the way the results of the weak classifiers are combined. Variation in the performance of the classifiers that are combined can improve the performance of the ensemble classifiers [5]. For example, in the case of two primary classifiers, if the first one works significantly better in one part of the feature space and the second one works significantly better in another part of the feature space, classifier aggregation has the potential to improve the classification performance by selecting the first classifier in the former part of the feature space and the second classifier in the latter part of the feature space. Of course, achieving this limit needs additional information on the relative performance of the classifiers which is not always available. In other words, good performance is achieved when the individual classifiers are trained on specific but disjoint parts of the feature space. It is also desirable to have at least one good classifier for each part of the feature space.

To formulate the missing values, assume S represents the original data and n(S) represents the total number of samples. Define a n(S)×n(F) binary matrix M whose elements are:

$${\mathbf{\text{M}}}_{i,j=}\{\begin{array}{ll}0,& \begin{array}{l}\text{the}j\text{th feature is missing}\\ \text{in the}i\text{th sample}.\end{array}\\ 1,& \text{otherwise}.\end{array}$$ (1)

and a 1×n(F) binary vector θ whose ith element is 1 if the set includes the ith feature. Also, define S_θ to refer to the complete subset from S associated with the θ subset. A simple scenario with just one missing value (the ith sample and the jth feature) is demonstrated in Figure 2. In this case, two complete subsets cover all of the samples.

Fig. 2.

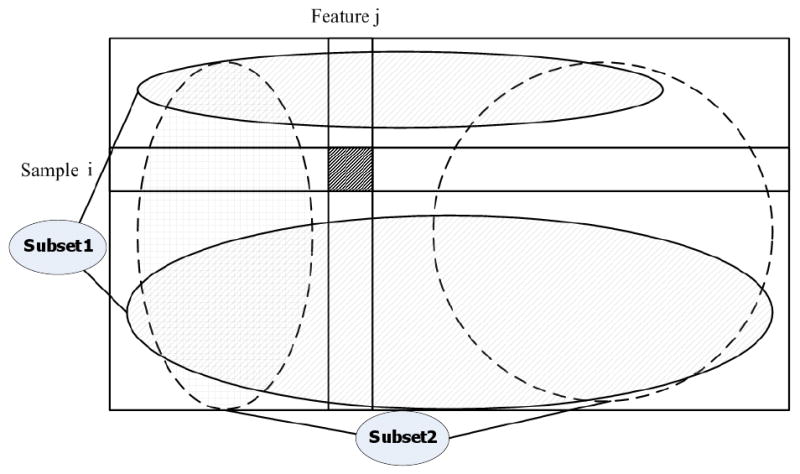
Subsets in the feature space: In the very simple case of just one missing value, two subsets can be used to cover all of the samples.

Since there are multiple classifiers, a notation is needed to distinguish different classifiers. To this end, Γ(x; Ω) is used to show the result of a classifier trained by Ω dataset for a test sample x. Here, Γ is a function from the sample space to the class label space (R^n(F) → N) where N is the set of natural numbers. When a feature is missed in x, Γ imputes the missed value with the average value of the feature. In the case that all features used by Γ are missed, the output is set to an out-of-range value so that it is discarded later. Although the proposed approach can be extended to the multiclass classification, for the sake of simplicity, we present the method as applied to the two-class classification.

Selection of the subsets and combination of the results are nontrivial problems as they directly impact the performance of the ultimate classifier. These two problems are addressed in the following sections.

3.2. Selection of the Subsets

Generally speaking, it is desirable to cover the entire data with as few subsets as possible. Each subset should be large enough (with enough number of samples) to train a classifier. Also, the classifiers need enough features in each subset to make a good decision about the class labels. Obviously, certain subsets such as those with all features but a small number of samples or those with a small number of features even with a large number of samples are not desirable.

Using the above notations, the proposed selection-fusion classification is formulated as follows: In the first step (selection step), a set of m feature subsets {θ₁,…, θ_m} corresponding to a set of complete subsets {S_θ1,…,S_θm} is selected. After training a classifier for each subset, the results are denoted by {Γ(x; S_θ1),…, Γ(x; S_θm)}. Using these class labels in the fusion step, a decision is made about the most likely class label for each data sample.

It has been shown that for a constant average performance, the maximum achievable performance in the ensemble classification is achieved when the variance of the results of the primary classifiers are at a maximum [5]. In other words, the best performance is obtained when $\text{∑}_{i,j,k}{[\Gamma (x_j,{\theta }_k)-\Gamma (x_j,{\theta }_i)]}^2$ is maximized under the constraint that $\text{∑}_{i,j}Er[y_j,\Gamma (x_j,{\theta }_i)]$ is a constant where Er[.] is the error function and y_j is the correct class label for x_j. The lowest achievable error for the ultimate selection-fusion classifier is $\text{∑}_j\underset{i}{min}(Er[y_j,\Gamma (x_j,{\theta }_i)]$ if meta information is available about the best primary classifier for a test data. However, since the best classifier for a specific test sample is not predictable, this limit is not achievable.

Based on the above, the proposed method starts with a pool of complete subsets represented by B = [θ̑₁ … θ̑_n(B)]^T. The pool size, n(B), can be relatively large even close to 2^n(F)-1 (maximum number of complete subsets). Having this set of subsets, each element of a so-called co-accordance binary matrix A is defined as:

$$A_{i,j=}\{\begin{array}{ll}1,& j\text{th sample is in}{S}_{{\theta }_i}\\ 0,& j\text{th sample is not in}{S}_{{\theta }_i}\end{array}$$ (2)

where A is a binary matrix that shows the inclusion of particular samples in particular subsets. The diversity of two subsets relates to the number of their common samples. The more common samples they have, the less diversity they have. On the other hand, independencies of the samples and a small number of common samples result in high diversity. Next, a symmetric similarity matrix C is defined as:

$$C=A{A}^T$$ (3)

Here, C includes the number of common samples between each two subsets. To generate a similarity metric, a normalized version of C is defined as:

$${\overline{C}}_{i,j}=\frac{C_{i,j}}{max(C_{i,i},C_{j,j})}$$ (4)

The similarity between each two subsets is a scalar between 0 and 1 and the self similarity of each subset is 1. From the maximum variance rule for ensemble classification, the choice of the subsets should maximize the diversity between each pair of the subsets. This choice is a difficult NP-complete problem [12] and is not well-studied [10]. To translate this problem into a well-studied clustering problem, a dual difference matrix D is defined as:

$$D_{i,j}=\frac{1-{\overline{C}}_{i,j}}{1+{\overline{C}}_{i,j}}$$ (5)

Using this distance measure, the selection problem can be solved from a different point of view: the well-known clustering methods. Each cluster is a collection of similar subsets with small distances or almost identical information. The kth cluster is represented by a set of subset indices Λ_k. By selecting the best subset from each cluster, a set of subsets that satisfies the maximal diversity criterion while maximizing the overall performance can be obtained.

3.3. Quality Measure for the Selection Step

Now that subset selection is translated into a clustering problem, we apply the well-known k-means clustering algorithm. Then, to evaluate the quality of the resulting clusters, we apply the following Cluster Validity Index (CVI):

$$\mathit{\text{CVI}}=E_k\left\{\frac{\text{∑}_{i,j\in {\Lambda }_k}{D}_{i,j}}{\text{∑}_{\begin{array}{l}i\in {\Lambda }_k\\ j\notin {\Lambda }_k\end{array}}{D}_{i,j}}\right\}$$ (6)

where E_k(.) represents expectation over k and Λ_k is a set showing subsets in the kth cluster.

In the clustering context, this cluster validity index shows whether there are significant clusters in the data or not. When clusters are completely separated, CVI is very small, near 0. In the worse case, when there are no distinct clusters, CVI is around 1. In our application, this index shows whether a specific collection of subsets represents a complex or simple missing value pattern. Simple missing value patterns correspond to well-separated subset clusters and consequently smaller CVI. We use 1/CVI on a linear scale to generate a clear separation when CVI is small. The more samples per feature are found by the clustering algorithm, the better the generalization of the classifiers would be. Thus, there is a direct relationship between the quality of the clustering results and the ultimate performance of the classification process.

Once the subsets are chosen, a classifier is needed for each subset. Selection of the best classifier for each subset is discussed in [8,10]. In this work, as a widely-used and generally well-performed method, we use the support vector machine (SVM) classifier in all of the experiments. Note that the focus of this paper is not on the optimal classifier design for the subsets.

3.4. Fusion Step

Similar to the traditional multiple imputations approach, the fusion step in the selection-fusion algorithm combines the results of the individual classifiers to boost-up the overall classification accuracy. In multiple imputations, the results are combined in a simple fashion:

$${\Gamma }_{\mathit{\text{MI}}}(x)=\frac{1}{q}\sum _{i=1}^q\Gamma (x;I_i)$$ (7)

where I_i is the ith imputation of the incomplete data and q represents the number of imputations. The number of required imputations is estimated by the Rubin's imputation efficiency law quantified by [12]:

$$\mathit{\text{efficiency}}=\frac{1}{{(1+\gamma /q)}^{0.5}}$$ (8)

where γ is the fraction of the missing values in the data. The efficiency is a value between 0 and 1 and shows the performance of q imputations compared with the infinite number of imputations. When q is small compared with γ, increasing q improves the efficiency. However, when q is large enough, its further increments do not improve the efficiency considerably. This criterion may be used to select appropriate number of imputations.

The fusion step in the proposed selection-fusion method is different. Here, the distribution of the missing values in the feature space is used to improve the performance. In contrast to the multiple imputations where all imputations have the same weight, in the proposed approach, the classification accuracy of each classifier for a given testing sample is used to weigh the outputs. Since a subset of samples and features, not the whole data, is involved in the training of each classifier, a specific subset may be advantageous depending on the sample being tested. Thus, in the fusion step, the aggregation step is the weighted combination:

$${\Gamma }_{BB}(x)=\frac{1}{\text{∑}_{i}1/{\phi }_{i,x}}\sum _{i=1}^{n(B)}\frac{1}{{\phi }_{i,x}}\Gamma (x;S_{{\theta }_i})$$ (9)

where φ_i,x is the relative inaccuracy or expected error of Γ(x;S_θi) estimated at x which depends on the accuracy of Γ(.;S_θi) around x and the number of features used in the classifier.

Two factors are important in determining the classifier's expected error φ_i,x for a specific sample: 1) general accuracy of the classifier; and 2) similarity between the features of the samples in the training set and those of the testing sample. Thus, the local accuracy of the classifier should be calculated for each individual testing sample based on two factors: 1) the number of samples in the training set that are in the neighborhood of the testing sample; and 2) the similarity between the subset features (θ_i) and the existing features for the testing sample.

Now, we explain our approach to estimate the similarity between the training and testing samples. If all features are identically informative, the similarity between the missing value patterns in a subset and the testing sample can be characterized by ${\widehat{\theta }}_{x_j}^T{\theta }_i$ where θˆ_xj and θ_i are the feature sets available for the testing sample x_j and the ith subset, respectively. To take the relative quality of the features into account, the similarity is written as ${\theta }_{x_j}^T\mathbf{\text{K}}{\theta }_i$ where K is a diagonal matrix to weigh the features based on their information level.

We calculate φ_i,x using:

$${\phi }_{i,x}={(\Gamma (x;S_{{\theta }_i})-Y(x))}^{2}f({\theta }_{x_j}^T\mathbf{\text{K}}{\theta }_i)$$ (10)

where Y(x) is the label of x. When there is no ranking of the features, K is equal to the identity matrix. Here, f is a non-increasing function that calculates the effect of similarity between the feature spaces of the classifier and the testing sample. For simplicity, we define f(u) as 1/u. When there are no common features, f removes the effect of the classifier from aggregation. On the other extreme, when all features are present, f does not change the error measure.

Equation (10) can be calculated for the training data. However, for a testing sample, it needs to be estimated since Y(x) is unknown. To estimate φ_i,x easily, we use all of the training samples in the vicinity of the testing sample:

$${\stackrel{\sim }{\phi }}_{i,x^{\prime }}=\frac{1}{{\eta }_{x^{\prime }}}\sum _{x\in \mathit{\text{Training}}}\mathit{\text{dis}}(x,x^{\prime }){\phi }_{i,x}$$ (11)

where

$${(\mathit{\text{dis}}(x,x^{\prime }))}^2={\Vert x-x^{\prime }\Vert }^{2}f({\theta }_x^T\mathbf{\text{K}}{\theta }_{x^{\prime }})$$ (12)

$${\eta }_{x^{\prime }}=\sum _{x\in \mathit{\text{Training}}}\mathit{\text{dis}}(x,x^{\prime })$$ (13)

Note that the distance between the two samples is modulated by their common features through the second term in Equation (12).

3.5. Pruning Step

In the previous sections, the primary assumption was that when the number of common samples between the training sets of different classifiers is small, they would have a different performance. However, this assumption is not always true as discussed below. We use a pruning step to deal with this issue.

Our observations show that in addition to the desirable subsets, a few useless subsets may be generated at the end of the selection process due to the simplified assumptions about the diversity. In some cases, these subsets have poor performance for almost any testing dataset. In other cases, different subsets do not have additional information and their corresponding classifiers have almost identical outputs.

For the former case, assume a problem with three features where the first two features are more informative than the last one. Also, assume that the first feature is missing in the first half and the second feature is missing in the second half of the samples. A clustering algorithm in this case will obtain three clusters: 1) with just the third feature; 2) with the third and first features; 3) with the third and second features. However, since the third feature is not very informative, the subset from the first cluster will not contribute significantly in the fusion step due to its poor performance, despite its large number of samples. In fact, the remaining two subsets are sufficient for this scenario.

For the latter case, assume the above scenario but this time just the third feature is missing in the first half of the samples. There are two significant subsets in the data: one subset with all features (second half of samples) and one subset with the first and second features (all samples). These two subsets are certainly in two different clusters. Since the third feature is not informative, the two clusters represent the same information and combination of the two classifiers is not useful.

As described in the selection step, the CVI is a good performance measure if the diversity of the subsets is high. When two clusters are separated by a set of informative and relevant features, this is the case. However, when a large portion of the features are irrelevant, it is likely to get a couple of clusters with similar information separated by the unimportant features.

The pruning step is designed to solve the above problems by removing weak clusters and combining similar clusters. During the feature selection step, the irrelevant features are identified and the distance metric of the clusters with the irrelevant features [D_ij] are modified accordingly. The overall process, including the pruning step, is summarized in Figure 3. In the worst case, all clusters are combined after m-1 iterations. Although the pruning step does not always have a large impact on the performance, it may reduce the computational complexity.

Fig. 3.

Selection-fusion algorithm for missing value management: B is the set of all subsets, M is the missing value matrix as defined in Equation (1), A is the co-accordance binary matrix as defined in Equation (2), C is the subset similarity matrix as defined in Equation (3), D is the distance matrix as defined in Equation (5), CVI is the cluster validity index as defined in Equation (6), x_j is the testing sample, φ̃_i,xj is the fusion weight as defined in Equation (11), and Γ_BB(x) is the classification result for the testing sample x as defined in Equation (9).

One important remaining point about the proposed algorithm is the initial condition for the primary subset pool B. If we eliminate some of very unlikely subsets before running the algorithm, the execution time of algorithm will be reduced. As discussed, the primary subsets pool can be as large as 2^n(F)-1. However, for the sake of computational cost, we limit the size of the subsets pool. We reduce the size of the subsets pool by putting lower and upper bounds on the number of features in each subset. According to the discussion about the desirable subsets, the number of the features in each subset should be large enough to get a reliable determination of the class label. A lower bound can be obtained using a simple feature reduction technique; for details see [9-10].

4. Experimental Results

To support the hypotheses in the previous sections and to evaluate the proposed method and compare it with the previous methods, we have conducted a variety of experiments using a wide range of real-world datasets. Seven datasets from the University of California, Irvine and our epilepsy dataset (a total of eight datasets) have been used in these experiments. Details of the datasets are given in Table 1. The algorithms have been applied to the original data as well as datasets with additional missing values generated by randomly deleting some of the values from the datasets. All algorithms are run on Intel 3.0 GHz CPU with 2GB of RAM.

Table 1.

Specifications of the datasets used in the study.

Number	Name	Number of Samples	Original Missing Values Percentage	1/CVI	Number of Classes
1	Breast Cancer	699	9.6%	9.52	2
2	Pima Diabet	768	0.0%	0.00	2
3	Tic Tac Toe	958	0.0%	0.00	2
4	Sonar	208	7.2%	15.24	2
5	Votes	435	2.2%	6.85	2
6	Iris	150	0.0%	0.00	2
7	Wine	178	0.0%	0.00	2
8	HBIDS	55	8.3%	18.26	2

In the comparison study, the proposed method is compared with five well-known missing value management algorithms: 1) pairwise deletion; 2) decision tree (CART); 3) Expectation Maximization (EM) single imputation; 4) Multiple Imputations (MI) with EM; and 5) ensemble classifier (voting selection-fusion (SF) with random selections). The Support Vector Machine (SVM) is used for classification in all of the methods. Each dataset is divided into 6 equal parts, 1 part for the testing phase and 5 parts for the training phase. The training and testing parts are permuted and the experiments are repeated for cross-validation. The execution time of each permutation depends on the size of the dataset and the number of clusters, ranging from 125 sec for database number 1 (Breast Cancer) to 20 sec for database number 8 (HBIDS). All of the algorithms are run on the 8 datasets (Table 1). To evaluate the effect of the percentage of the missing values, some of the values are randomly removed from both of the testing and training datasets using the MAR missing value pattern. This is repeated 20 times and the means and standard deviations of the correct classification percentages are calculated and presented in Table 2.

Table 2.

Means and standard deviations of the correct classification percentages of the experiments done on 8 datasets using 6 different methods. Note that our proposed method with CVI outperforms other approaches when applied to the datasets with a small number of samples and a high percentage of missing values.

Additional missing value percentage	Pairwise deletion	Decision Tree (CART)	EM single imputation	Multiple imputations with EM	Voting selection-fusion with random selections	Proposed selection-fusion method with CVI
UCI Dataset 1: Breast Cancer
0%	94.7	94.7	94.7	95.9	95.3	92.4
10%	91.1±0.1	90.3±0.1	91.2±0.1	90.4±0.1	91.9±0.1	92.2±0.1
20%	84.4±0.3	89.7±0.1	90.8±0.1	89.1±0.2	82.8±0.2	90.1±0.1
30%	66.4±0.6	77.4±0.6	83.6±0.1	82.5±0.2	81.0±0.3	85.2±0.2
UCI Dataset 2: Pima Diabet
0%	76.5	76.6	76.1	77.3	74.8	75.1
10%	72.3±0.1	74.1±0.1	74.1±0.2	74.2±0.1	71.2±0.1	73.5±0.1
20%	69.7±0.1	71.4±0.1	72.2±0.1	70.3±0.1	67.2±0.1	71.8±0.1
30%	59.9±0.9	62.4±0.8	67.6±0.4	65.2±0.3	67.2±0.5	70.3±0.2
UCI Dataset 3: Tic Tac Toe
0%	99.3	99.3	99.3	98.9	98.9	98.3
10%	94.4±0.1	95.2±0.1	97.5±0.1	94.2±0.1	92.8±0.2	95.4±0.1
20%	83.6±0.1	86.5±0.1	90.6±0.1	94.2±0.1	87.6±0.1	90.3±0.2
30%	70.1±0.5	80.7±0.3	90.2±0.3	90.3±0.3	86.6±0.3	89.4±0.4
UCI Dataset 4: Sonar
0%	83.7	83.8	83.7	83.9	81.0	82.9
10%	78.8±0.1	77.1±0.1	79.0±0.1	80.1±0.1	77.9±0.1	81.3±0.1
20%	63.0±0.1	69.4±0.1	70.4±0.1	72.7±0.1	74.2±0.1	78.3±0.1
30%	58.3±0.2	65.3±0.3	62.7±0.3	69.1±0.1	71.2±0.2	76.9±0.2
UCI Dataset 5: Votes
0%	95.8	95.8	95.8	94.3	94.7	95.9
10%	88.4±0.2	91.2±0.1	89.2±0.1	93.5±0.1	91.6±0.1	92.2±0.1
20%	85.3±0.3	88.2±0.2	85.2±0.1	87.1±0.1	87.6±0.1	89.2±0.1
30%	71.2±0.4	77.3±0.2	84.6±0.2	86.3±0.2	81.4±0.2	89.1±0.3
UCI Dataset 6: Iris
0%	89.4	89.4	89.4	92.1	94.3	93.2
10%	74.2±0.1	75.2±0.2	78.3±0.2	81.3±0.1	81.2±0.1	81.4±0.1
20%	62.3±0.1	69.2±0.2	69.5±0.2	72.3±0.1	72.2±0.1	77.4±0.1
30%	53.1±0.2	62.4±0.3	65.1±0.3	69.5±0.1	69.5±0.2	75.1±0.3
UCI Dataset 7: Wine
0%	85.2	85.2	85.2	90.1	89.1	89.1
10%	72.6±0.1	74.5±0.2	78.1±0.1	82.5±0.1	78.2±0.2	81.3±0.1
20%	62.6±0.1	65.5±0.2	68.2±0.1	72.6±0.1	69.4±0.2	78.2±0.1
30%	59.3±0.2	62.3±0.3	65.7±0.3	64.3±0.1	62.2±0.2	72.4±0.2
HBIDS
0%	74.5±0.5	72.1±0.3	66.7±0.3	76.4±0.5	69.5±0.4	79.3±0.5
10%	72.2±1.7	65.7±1.9	62.1±1.2	68.2±1.0	62.1±0.9	76.4±0.8
20%	65.1±1.9	64.8±1.5	59.4±1.8	65.2±1.2	59.3±2.8	72.8±0.9

Generally speaking, the results show that the proposed algorithm outperforms the other methods when either the percentage of the missing values is large (more than 20%) or the number of samples in the dataset is small. On the other hand, the EM single imputation and MI with EM methods outperform the other methods when the number of the samples is large and the percentage of the missing values is small.

In particular, the proposed method outperforms the previous methods in their applications to the target problem of our research, i.e., epilepsy surgery candidate selection (HBIDS). This problem can be considered as a prototype of the common medical diagnosis problems such as breast cancer staging or leukemia genome expression, where a non-MAR missing value pattern and a small number of samples are the most common limitations for the recovery of the missing values. The human brain image database system (HBIDS) is developed for epilepsy patients at Henry Ford Hospital, Detroit, MI [23, 24]. The system will examine surgical candidacy among temporal lobe epilepsy patients based on their brain images and other data modalities. It is expected to discover relatively weak correlations between symptoms, medical history, treatment planning, outcome of the epilepsy surgery, and the brain images.

At the time of this investigation, the HBIDS contains a 40-dimensional feature space and 55 samples. Our examination of the database shows that the missing values do not follow the MAR or MCAR models [12, 24-28]. Thus, the missing value patterns are not easily predictable. Therefore, a complex probabilistic model is necessary. Also, there are a large number of missing values that are non-random. Moreover, the missing values may have dependencies in contradiction to the usual assumptions [13]. The complex probabilistic model and the large percentage of the missing values limit the performance of the previous methods like expectation maximization (EM) and multiple imputations (MI) [1, 12].

In the second experiment, the relationship between the proposed index (CVI) and the performance of the selection-fusion algorithm is evaluated. To this end, some of the samples are randomly removed from 3 of the datasets (Breast Cancer, Pima Diabet, HBIDS) to generate datasets with different patterns and percentages of the missing values. Then, the CVI and the accuracy of the four missing value treatment algorithms (SF, EM, MI, CART) are evaluated for each condition. The results are presented in Figure 4. This figure compares the accuracy of the four methods when 1/CVI changes from 1 to 40 for the 3 datasets. The results illustrate that although the relationship between the accuracy and the 1/CVI depends on the pattern of the missing values, our approach (SF) is always superior when 1/CVI is larger that 20. Also, as 1/CVI increases further, the superiority of the SF approach to the other methods becomes more pronounced.

Fig. 4.

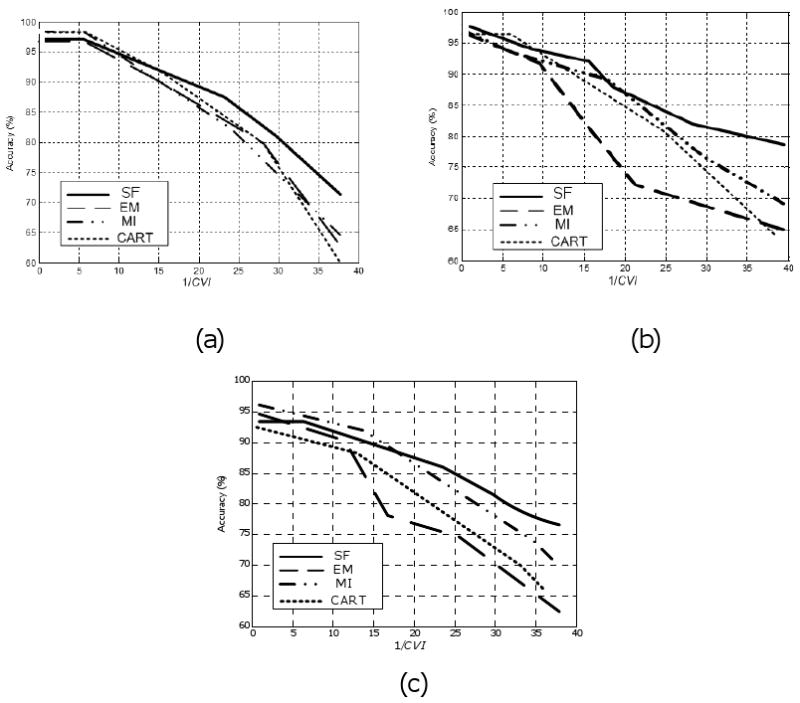
Performance of missing value management methods versus cluster validity index: (a)-(c) the results of the UCI Breast Cancer and Pima Diabet datasets, and the human brain image database system (HBIDS), respectively (refer to Table 1). The selection-fusion (SF), expectation maximization (EM), multiple imputations (MI), and CART methods are compared. 1/CVI increases as the percentage of missing values increases. Note the overall superiority of the SF method especially when 1/CVI is large.

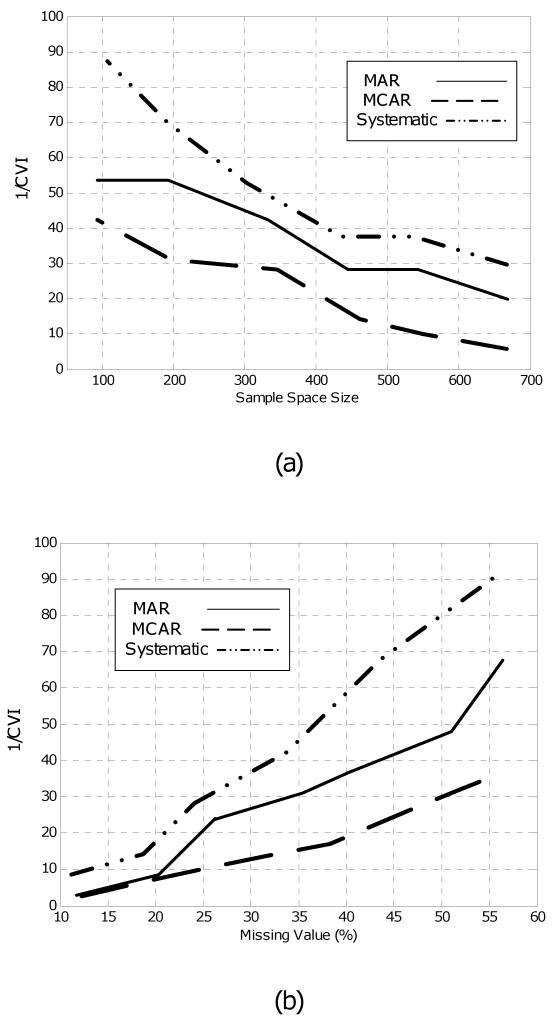
In the third experiment, to evaluate the effect of the number of samples in the dataset and the percentage of the missing values on the CVI, some of the features are removed from the Breast Cancer dataset, using the MAR, MCAR, and systematic missing value models. For each of the resulting datasets, 1/CVI is calculated and plotted in Figure 5 versus the number of the samples (sample space size) and the percentage of the missing values. The results show that the relationships between the 1/CVI and the missing value parameters depend on the pattern of the missing values, although it is always a monotone function. For example, a 1/CVI of 20 equals 23%, 25%, and 40% missing values for the systematic, MAR, and MCAR models, respectively (Figure 5.b). Thus, for example, for a dataset with the MAR missing value pattern, the selection-fusion algorithm is superior when more than 23% of the data is missing. Based on Figure 5.a, the same argument can be made for the sample size. Figure 5 also shows that the systematic missing value pattern is more sensitive to the percentage of the missing values and the sample size compared with the MAR and MCAR models. In the systematic pattern, the 1/CVI increases from 20 to 40 when the missing values increase about 10%, while in the MCAR model, this requires at least 20% more missing values.

Fig. 5.

(a) Effect of the sample size on the cluster validity index (CVI) of the UCI Breast Cancer dataset: In general, 1/CVI increases as the number of samples decreases. However, the rate of change depends on the missing value model. Here, MCAR, MAR, and systematic missing value are compared. (b) Effect of missing value percentage on CVI: In general, 1/CVI increases as the percentage of missing values increases. However, the rate of change depends on the missing value model. Note that when 1/CVI is large, classifiers with more diverse performance can be found. This is due to the fact that we select one classifier from each cluster and thus the distance between selected pairs of classifiers is large (i.e., they are diverse) when 1/CVI is large.

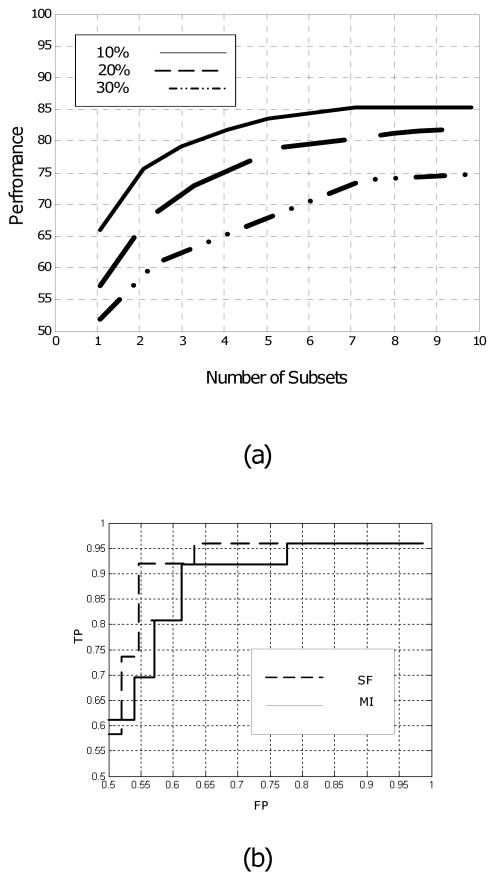
In the fourth experiment, the effect of the number of subsets on the performance of the proposed method is evaluated by applying the method to the original HBIDS dataset and additional datasets generated by randomly removing some of the features from the original dataset. The results are graphed in Figure 6.a. Note that with 10% missing values, 5 subsets yield the maximum performance. In this case, the performance does not improve much by increasing the number of subsets beyond 5. On the other hand, with 30% missing values, at least 8 subsets are required to get the maximum performance.

Fig. 6.

(a) Effect of the number of subsets on the performance of the method for the human brain image database system (HBIDS). This figure compares the performance for 10%, 20%, and 30% missing values. As a rule of thumb, 6 to 10 subsets are sufficient. Let alone how much data is missing, more than 10 subsets do not seem to improve the performance. (b) Receiver Operating Characteristic (ROC) curves for the surgery candidate selection problem. The selection-fusion (SF) and Multiple Imputation (MI) methods are compared. Note the superiority of SF.

In the fifth experiment, the performance of the proposed approach is compared with the multiple imputation method by estimating their Receiver Operating Characteristic (ROC) for the HBIDS dataset. The results graphed in Figure 6.b show that our approach has higher sensitivity and specificity. The area under the ROC curve of the proposed method for the dataset with 20% missing values is about 5% larger than that of the multiple imputations.

5. Discussion

Clustering is a well-established field and many of its results are applicable to the missing value problem. The optimal number of subsets in our application has a close relationship with the number of clusters in the clustering algorithms [11, 12]. When the number of clusters is unknown, the elbow criterion [12] is a common rule of thumb to determine the number of clusters. Also, as shown in the clustering literature, determining the number of clusters is an NP-Complete problem [12] but many fast suboptimal methods are proposed for it [11].

Since we use a weighted combination algorithm in the fusion step, the number of subsets may not be very important. However, more subsets are not always desirable because the number of parameters that need to be estimated in the fusion stage depends on the number of subsets. With a small number of subsets, the parameters can be estimated more reliably using a limited number of samples. In addition, although for the weak classifiers, the weight is small, accumulation of a large number of weak subsets may deteriorate the overall performance.

The sample size and the percentage of the missing values are two important parameters of the data but these parameters are not necessarily the most appropriate measures for the quantification of the complexity of the missing values. Our experimental results (Figure 4) show that the superiority of the selection-fusion method almost always improves as the CVI decreases. This confirms that this index describes the complexity of the missing value problem appropriately.

The relationship between the complexity of the missing value problem and the CVI is nonlinear and depends on parameters other than the sample size and the missing value percentage. However, our experiments using three databases show that the relationship is monotone (Figure 5). When the sample size decreases, the 1/CVI increases but the rate of its increase depends on the missing value pattern. When the data is MCAR, the CVI does not change as much as the other models as the sample size changes.

The impact of the diversity of the classifiers on the performance of the proposed method is also explored through the evaluation of the CVI (Figure 5). When 1/CVI is large, classifiers with more diverse performance can be found. This is due to the fact that we select one classifier from each cluster and thus the distance between the selected pairs of classifiers is large (i.e., they are diverse) when the 1/CVI is large. A large 1/CVI corresponds to a small sample size and a large missing value percentage. Thus, we can conclude that more missing values in the data for a fixed sample size produce more clusters and therefore more subsets (Figure 6.a). Comparing the performance of our approach with the multiple imputations in their applications to the HBIDS dataset shows that our approach has higher sensitivity and specificity (Figure 6.b).

A comprehensive analysis using 8 datasets with different sample sizes and different data models show that our selection-fusion approach is superior to the previous approaches when there are at least 20% missing values added with the MAR model. This difference is more pronounced in the Sonar, Iris, Wine, and HBIDS datasets. These four datasets have smaller sample sizes and therefore, the 1/CVI increases faster with the missing values. In particular, in the HBIDS dataset, the presence of systematic missing values makes the 1/CVI more sensitive to the large percentages of the missing values.

In summary, the proposed selection-fusion algorithm is applicable to the problems with a small CVI. This usually happens in the datasets with a small number of samples and a large percentage of missing values.

6. Conclusion

Evaluation of the proposed selection-fusion algorithm on different types of datasets shows that it can improve the classification performance on datasets with missing values. Our study shows that the estimation of the missing values by the EM method works fine when the percentage of the missing values is small. However, as the percentage of the missing values increases, its performance deteriorates such that in some cases (like HBIDS), the pairwise deletion approach may offer a superior solution. The selection-fusion approach maintains an acceptable performance when the percentage of the missing values is small, at the expense of more computational complexity in the classifier training and application.

The results of the surgery candidate selection problem (HBIDS) show that the selection-fusion algorithm outperforms the other approaches. Also, the results of the Sonar and some other UCI datasets agree with this observation. While the limitations in the surgery candidate selection such as a large percentage of the missing values, a non-MAR missing value pattern, and a small number of samples are the challenging problems in the medical record analysis, the proposed selection-fusion approach is an appropriate solution to these problems. The results show that the proposed approach outperforms the EM and MI methods in this type of missing value patterns with a small CVI. In addition, we observe that this index decreases when the sample size decreases or the percentage of the missing values increases. Based on these two observations, we conclude that the proposed missing value management method is most appropriate when the number of samples is small and the percentage of the missing values is large.

Biographies

Mostafa Ghannad-Rezaie, MS, was born in Tehran, Iran in 1981. He received BS degree in electrical engineering: communications and MS degree in electrical engineering: bioelectric from the University of Tehran, Tehran, Iran, in 2003 and 2005, respectively. Since 2005, he has been with the Department of Radiology, Henry Ford Health System, Detroit, Michigan, USA, where he is a Research Assistant. Since 2006, he has been graduate student in Department of Electrical and Computer Engineering, Wayne State University, Detroit, MI. His research interests include medical imaging, signal and image processing and analysis, and computational neuroscience.

Hamid Soltanian-Zadeh, PhD, was born in Yazd, Iran in 1960. He received BS and MS degrees in electrical engineering: electronics from the University of Tehran, Tehran, Iran in 1986 and MSE and PhD degrees in electrical engineering: systems and bioelectrical sciences from the University of Michigan, Ann Arbor, Michigan, USA, in 1990 and 1992, respectively. Since 1988, he has been with the Department of Radiology, Henry Ford Health System, Detroit, Michigan, USA, where he is currently a Senior Staff Scientist. Since 1994, he has been with the Department of Electrical and Computer Engineering, the University of Tehran, Tehran, Iran, where he is currently a full Professor and director of Control and Intelligent Processing Center of Excellence. Dr. Soltanian-Zadeh has active research collaboration with Wayne State University, Detroit, MI, USA and the Institute for studies in theoretical Physics and Mathematics (IPM), Tehran, Iran. His research interests include medical imaging, signal and image processing and analysis, pattern recognition, and neural networks. He has published over 500 papers in journals and conference records or as book chapters in these areas. He has served on the scientific committees of several international conferences and editorial boards of many scientific journals. He has also served on the study sections of the National Institutes of Health (NIH), National Science Foundation (NSF), American Institute of Biological Sciences (AIBS), and international funding agencies.

Hao Ying, PhD, received his PhD degree in biomedical engineering from The University of Alabama, Birmingham, Alabama in 1990.

He is currently a full Professor at the Department of Electrical and Computer Engineering, Wayne State University, Detroit, Michigan, USA. He is also Full Member of its Barbara Ann Karmanos Cancer Institute. He was on the faculty of The University of Texas Medical Branch at Galveston between 1992 and 2000. He was Adjunct Associate Professor of the Biomedical Engineering Program at The University of Texas at Austin between 1998 and 2000. He has published a research monograph/advanced textbook entitled Fuzzy Control and Modeling: Analytical Foundations and Applications (IEEE Press, 2000), 82 peer-reviewed journal papers, and 117 conference papers.

Dr. Ying is an Associate Editor for five international journals (Dynamics of Continuous, Discrete & Impulsive Systems Series B: Applications & Algorithms, International Journal of Fuzzy Systems, International Journal of Approximate Reasoning, Journal of Intelligent and Fuzzy Systems, and Advances in Fuzzy Systems). He is on the editorial board of three other international journals (Advances in Fuzzy Sets and Systems, Far East Journal of Mathematics, and The Open Cybernetics and Systemics Journal). He was a Guest Editor for four journals. He is an elected board member of the North American Fuzzy Information Processing Society (NAFIPS). He served as Program Chair for The 2005 NAFIPS Conference as well as for The International Joint Conference of NAFIPS Conference, Industrial Fuzzy Control and Intelligent System Conference, and NASA Joint Technology Workshop on Neural Networks and Fuzzy Logic held in 1994. He served as the Publication Chair for the 2000 IEEE International Conference on Fuzzy Systems and as a Program Committee Member for 27 international conferences. He was invited to serve as reviewer for more than 50 international journals, which are in addition to major international conferences, and book publishers.

Ming Dong, PhD, received his BS degree from Shanghai Jiao Tong University, Shanghai, P.R. China in 1995 and his PhD degree from the University of Cincinnati, Ohio, in 2001, both in electrical engineering. He joined the faculty of Wayne State University, Detroit, MI in 2002. He is currently an assistant professor of computer science and a scientific member of Developmental Therapeutics Program, Karmanos Cancer Institute. He is also the Director of the Machine Vision and Pattern Recognition Laboratory in the Department of Computer Science. His research interests include pattern recognition, multimedia analysis, and data mining. He is an associate editor of the Pattern Analysis and Applications Journal and is on the editorial board of International Journal of Technology Enhanced Learning.