Estimating replicate time shifts using Gaussian process regression

Abstract

Motivation: Time-course gene expression datasets provide important insights into dynamic aspects of biological processes, such as circadian rhythms, cell cycle and organ development. In a typical microarray time-course experiment, measurements are obtained at each time point from multiple replicate samples. Accurately recovering the gene expression patterns from experimental observations is made challenging by both measurement noise and variation among replicates' rates of development. Prior work on this topic has focused on inference of expression patterns assuming that the replicate times are synchronized. We develop a statistical approach that simultaneously infers both (i) the underlying (hidden) expression profile for each gene, as well as (ii) the biological time for each individual replicate. Our approach is based on Gaussian process regression (GPR) combined with a probabilistic model that accounts for uncertainty about the biological development time of each replicate.

Results: We apply GPR with uncertain measurement times to a microarray dataset of mRNA expression for the hair-growth cycle in mouse back skin, predicting both profile shapes and biological times for each replicate. The predicted time shifts show high consistency with independently obtained morphological estimates of relative development. We also show that the method systematically reduces prediction error on out-of-sample data, significantly reducing the mean squared error in a cross-validation study.

Availability: Matlab code for GPR with uncertain time shifts is available at http://sli.ics.uci.edu/Code/GPRTimeshift/

Contact: ihler@ics.uci.edu

1 INTRODUCTION

A typical microarray time-course expression dataset consists of measurements taken at a relatively small number of time points (e.g. 5 to 10), where at each time point microarray measurements are obtained on a small number (e.g. 3) of replicate samples. There has been considerable work in recent years in bioinformatics on the development of statistical techniques for accurately inferring expression profiles from such data, in the face of both measurement noise and biological variation across replicates (Bar-Joseph, 2004; Tai and Speed, 2006). In this article, we focus on a different source of variation that has received little attention to date, namely uncertainty about the precise biological time at which measurements were taken. We are specifically interested in the case where replicates that were measured at the same time point are in fact developing at different rates and correspond to different developmental times. The general intuition we pursue is that even though the underlying true expression profiles for each gene are masked by considerable noise, we can nonetheless infer time shifts for each replicate by analyzing all genes simultaneously.

As a motivating example, in this article, we use a time-series dataset of mRNA expression for the hair-growth cycle in the mouse, with microarray measurements for 6333 hair-cycle-related genes from 2 or 3 replicates at each of 9 time points, resulting in a total of 24 individual mice (Lin et al., 2004, 2009); see Figure 1. Hair follicles grow in repeated cycles, each of which can be coarsely broken down into three phases: anagen, catagen and telogen. These cycles have been well-characterized morphologically, but are understood incompletely at the molecular level. Time-course microarray data have been shown to be useful for automated, reliable identification of hair cycle-associated genes (Lin et al., 2004). However, in addition to the usual measurement noise, a significant source of variability arises from the fact that each sample in the time course is taken from a different individual, or replicate, and since each replicate develops at a slightly different rate, we can never obtain truly synchronous time points. From morphological observation, we find that after a few weeks, replicates which are of the same age (time since birth) may differ in the stage of hair follicle development by as much as 2–3 days. If the expression profile is changing rapidly over time, these developmental differences can result in major discrepancies among the replicates' observations, leading to poor estimates of the underlying expression patterns. Moreover, if the time interval between successive samples is relatively small, it is even possible for two replicates measured at successive time points to be in reverse order, i.e. the replicate measured at the later time point may be less developed than the earlier measurement. Figure 2 illustrates this point with images from two pairs of replicates at successive time points. If the estimated profiles are disturbed by such desynchronization, analysis tasks, such as estimating the underlying expression profiles and identifying periodically expressed genes, become more inherently difficult. These desynchronization effects have been previously discussed but not addressed in a systematic manner in existing literature (Erdal et al., 2004; Wichert et al., 2004). For datasets measuring multiple modalities (transcriptome and proteome, for example) or relatively short transient responses, we may expect timing and desyncronization effects to be more pronounced and methods of coping with these effects may become critical to analysis.

Fig. 1.

A schematic of the time points (numbered by days since birth for each mouse) where we profile the second hair growth cycle. The numbers in parentheses are the numbers of replicates profiled at that time point.

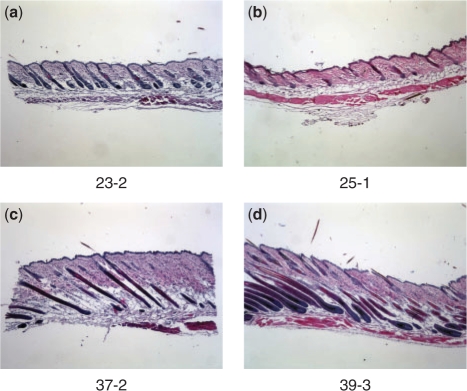
Fig. 2.

Histological sections from the back-skin of mice taken at different number of days since birth. 23-2 indicates a mouse that is 23 days old, and second in the set of replicates. The darker (somewhat vertically oriented) parts of the image correspond to hair follicles. For the pair of images in each row, the younger mouse (left image) appears to be developmentally ahead of the older mouse (right image), i.e. the mice have reversed orders of morphological development with respect to calender time. (a) and (b) show that 25-1 (which is in the Anagen I stage) is at an earlier stage (less follicle development) than 23-2 (in Anagen I/II). (c) and (d) show that the follicles in 39-3 (which is in the Catagen I/II stage) are less regressed (i.e. are less developed) compared with 37-2 (in Catagen II/III).

In this article, we describe a Gaussian process regression (GPR) approach that explicitly models desynchronization effects among replicates. GPR is a Bayesian non-linear regression technique, and has been previously applied in several contexts in bioinformatics (Gao et al., 2008; Kirk and Stumpf, 2009; Lawrence et al., 2007; Yuan, 2006). Rather than specifying predetermined shapes or other parametric assumptions, such as linear or polynomial regression, GPR is a semi-parametric method that uses the data themselves to represent the function, smoothed by an assumed covariance structure. Since we have little if any prior knowledge to determine what expression patterns to expect for different genes, it is reasonable to use GPR to automatically discover the shapes. We note in passing that our general approach for modeling desynchronization among replicates should be generally applicable to other statistical profile modeling methods such as splines (e.g. Bar-Joseph et al., 2003).

To consider replicate desynchronization, we assume that each replicate has an ‘ideal’ physiological age, and that the expression profile viewed with respect to the physiological age is shared across replicates. The observed age is then the ideal physiological age plus a time shift due to developmental drift. We model the time shift using a Gaussian prior, and use a maximum a posteriori (MAP) approach to estimate the time shifts and expression patterns simultaneously. We evaluate our method using the aforementioned hair-cycle dataset, comparing our predicted time shifts with morphological observations, and also using cross-validation to measure the predictive accuracy of the model. Our experiments indicate that the time-shift estimates from our model both agree with independent morphological evidence and provide more accurate prediction of expression profiles for out-of-sample replicates and genes. Our approach should be generally useful for reducing uncertainty and improving the quality of inferred profiles for time-course microarray data, as well as more specific tasks such as analysis of differential expression in time-course data (Storey et al., 2005).

Our method is substantially different from work on ‘aligning’ time-course datasets using techniques, such as dynamic time-warping algorithms (Aach and Church, 2001), continuous-time modeling of expression data by B-splines (Bar-Joseph et al., 2003; Kaminski and Bar-Joseph, 2007) and discriminative hidden Markov models (Lin et al., 2008). Those approaches focus on finding an optimal matching between two sequences by aligning the time points, provided that there are enough time points for matching to occur. Such methods, however, are not directly applicable to situations where each replicate is measured at only one time point, as in the aforementioned hair-cycle dataset. In contrast, the methodology we propose in this article can be applied whether each replicate is observed at a single time or at many.

Like any method of estimating expression profiles, we assume that the signals are sufficiently smooth to be estimated from the measurements. Furthermore, we assume that at least some signals are smooth compared with the temporal uncertainty, to allow the direction and magnitude of shifts to be estimated. Finally, we also assume that all genes are affected jointly by the time shift, which could be violated if some genes are influenced by external timing effects; in theory the model could be extended to include such effects. Our method is most similar to the general framework of total least squares (TLS) or error-in-variables (EIV) modeling in regression (Markovsky and Van Huffel, 2007; Van Huffel et al., 2007), which minimizes the weighted sum of errors on both dependent and independent variables; our model can be viewed as a Gaussian process (GP) version of TLS or EIV.

2 METHODS

We used Affymetrix Mouse Genome 430 2.0 DNA microarrays to profile mRNA expression of 45 101 probe sequences in mouse back skin in the second hair growth cycle (Lin et al., 2009). Nine representative time points were selected to measure the gene expression, shown in Figure 1. Two or three replicates were profiled at each time point, and we restricted our attention to 6333 genes that had been previously determined to be hair-cycle regulated (Lin et al., 2004). Expression values were normalized by taking logarithms and subtracting their mean value across the replicates and time points.

2.1 GPR

Let t_i, for i=1, 2, …, n be the collection of time points at which we measure the expression (Fig. 1). Let y^g,m(t) be the expression of the g-th gene from the m-th replicate at time t. For convenience, we write the data in vector form, defining y^g,m_j=y^g,m(t_j), and writing y^g=[y^g,1₁, y^g,2₁, y^g,1₂,…, y^g,2_n, y^g,3_n]^T and y=[y¹, y²,…, y^N].

Let us first suppose that there is no time shifting in the data. We model the expression profile y^g,m(t) as a GP, so that any finite number of y^g,m(t_i) have a jointly Gaussian distribution. Since the expression data of each gene have been normalized to have mean zero across time, we assume that the mean of this GP is zero, and the GP is determined by its covariance function. A common, reasonable choice of covariance function is the squared exponential (Rasmussen and Williams, 2006)

where σ_f² is the variance of any particular point y^g,m(t), and l is the length parameter. For two nearby time points, t_i≈t_i′, we have k(t_i, t_i′)≈σ_f², meaning the profile values are highly correlated. In contrast, when t_i is further away from t_i′, k(t_i, t_i′) decreases toward zero, making the profile values uncorrelated. The length parameter l determines how fast the correlation decays with time.

The microarray data are noisy due to measurement errors and biological factors—two measurements taken at the same physiological age will not be exactly equal. We therefore model each observation as a noisy observation of the underlying expression profile. This is equivalent to modifying the covariance function to

(1)

where δ(·; ·) is the Kronecker delta, equal to one if and only if t_i=t_i′ and m=m′. Then, the joint distribution of y^g is Gaussian,

(2)

where the covariance matrix K is given by

Notice that the last term in Equation (1) is non-zero only in the diagonal of K. This ensures that if σ_n²>0 then K is always non-singular.

We further assume that the expression profiles of different genes y^g are statistically independent, and share the same GP parameters: θ={l, σ_f, σ_n}. We can estimate the parameters by maximizing the log likelihood, which is given by

Using GPR, we can estimate the gene expression at any given time point t_*. For a given t_*, the conditional distribution of y^g(t_*), denoted y^g_*, given the observed data y^g, is also Gaussian:

where K_**=k(y^g_*, y^g_*) and

The minimum mean squared error estimate for y^g_* is the mean of this conditional distribution , and the estimate uncertainty is given by the conditional variance:

(3)

2.2 Modeling temporal uncertainty

Now suppose that each replicate has an ideal, physiological age, denoted , which corresponds to the degree of physiological development at the time at which the replicate is measured. Our observed age t_i, which is the nominal or temporal time at which the replicate is measured, can be treated as a noisy observation of :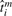

where τ^m_i is the time shift associated with the m-th replicate at time t_i; for convenience, we also write the vector τ=[τ¹₁, τ²₁,…, τ³_n]^T.

It is natural to model the τ^m_i using a Gaussian prior distribution,

To incorporate the time shifts into GPR, we still model the expression values using a GP as in Equation (2), but Equation (1) is replaced by

Thus, the expression profiles are GP with respect to the ideal, physiological ages 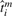, rather than the nominal or observed ages t_i.

We employ a MAP approach to estimate the τ^m_i and θ, by optimizing the posterior distribution over both. The posterior distribution is given by

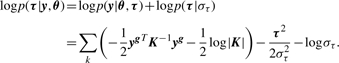(4)

Maximization of Equation (4) was carried out using the large-scale fminunc algorithm in MATLAB's non-linear optimization toolbox. This algorithm uses a trust-region-based Newton method, which iteratively optimizes a local quadratic approximation to the objective function in a small neighborhood around the current estimate. For more information, see the documentation (MathWorks, 2009).

Note that Equation (4) places a prior distribution on τ, but assumes no (informative) prior information about θ. The former reflects our intent that biological time be similar to the measurement time, i.e. we should not allow τ to take on arbitrary values. However, we have no specific prior information about the GP parameters θ; if additional information were available it could be included in Equation (4).

3 RESULTS

We estimate the time shifts and GP parameters by optimizing Equation (4) for the microarray data described in Section 2.1, and can compute the estimated profiles for each gene using Equation (3). When referring to the data, we use the notation ‘t_i-m’ to represent the m-th replicate measured at the i-th time point, t_i. For example, ‘23-1’ denotes the first replicate measured on the 23rd day.

Figure 3 shows example curves fit with and without time shifts. In general, the overall curve shapes are similar when estimated with and without time shifting, since the τ remain small. However, time shifts can refine the pattern, decrease random fluctuation and reduce uncertainty. Figure 3a–c shows three genes fit using GPR without time shifting. The curves display considerable random fluctuation and fitting errors. It is hard to discern meaningful patterns. Figure 3d–f fits the same genes, but including time shifts. The small fluctuations in Figure 3a–c are interpreted as arising from the time shifts; the estimated curves are smoother, highlighting the underlying patterns, and the estimated noise σ_n is decreased.

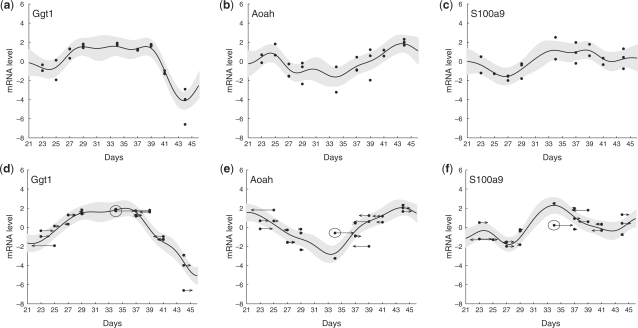
Fig. 3.

Examples of curve fitting using GPR with time shifts. The dots represent the gene expression of the replicates at their nominal time. Their time shifts are shown by arrows, whose end points indicate the shifted data. Curves show the estimated gene expression profiles, with pointwise 95% confidence intervals shaded. Here, we use σ_τ=1. (a–c), Curves fit to genes Ggt1, Pixna1 and S100a9 using GPR without time shifts. The estimated GP parameters are l=2.15, σ_n=0.41, σ_f=0.75. (d–f), The same genes as (a–c), including time shifts. The estimated GP parameters are l=2.50, σ_n=0.33, σ_f=0.86. Replicate 34-1 is circled for emphasis; its time shift in (e) and (f) greatly improves the apparent fit.

The changes in estimated parameters are quantified in Figure 4, which shows the estimated values of θ as σ_τ is increased. For σ_τ near zero, little or no time shifting occurs. As σ_τ increases, the length scale l also increases, suggesting that the random fluctuations are decreased in the shifted data. The noise σ_n decreases, indicating a better fit to the data, and σ_f increases, as we explain the variations within each time point as variation across time. Although this could indicate overfitting, we show later that time shifted profiles improve the predictive accuracy in cross-validation, suggesting that these changes do in fact reflect the underlying structure of the data. We also see that the parameter estimates are fairly stable across a wide range of σ_τ.

Fig. 4.

The estimated values of θ=[l, σ_n, σ_f]^T when using different values of σ_τ are plotted. The length scale l increases when σ_τ increases, and the value of θ changes little when σ_τ is sufficiently large. This suggests again that the result of the algorithm is insensitive to σ_τ.

We can also characterize the stability of our estimate using the Laplacian approximation to the posterior, characterized by a covariance matrix around the MAP estimate. We find that the primary direction of uncertainty is an equal shift of all τ (which yields the same expression profiles and is thus unobservable from the data); the second allows for an equal shift of replicates in days 23–29, which yields very similar profiles due to the large gap between day 29 and day 34. Ignoring these two directions, the estimates of τ are highly certain, each with a residual posterior standard deviation (SD) between 0.01 and 0.07 (compared with a minimum 2-day separation between measurement times).

It is important to note that the time shifts are optimized using the entire set of genes, i.e. they are not optimized individually for each gene. For example, 34-1 (the circled point in Fig. 2d–f ) is not strongly encouraged to shift by the profile in Figure 3d, since the expression profile is relatively flat during that period. Similarly, there is only a slight improvement obtained by the large time shift indicated by the arrow at datum 34-1 in Figure 3d. However, if we look at the gene in Figure 3e and f, the rightward time shift of 34-1 greatly reduces its distance from the profile, strongly suggesting that the time shift of 34-1 is preferred by these and similarly shaped genes. The time shifts integrate the information across all the genes, and can thus reflect the relative development stage of the entire system.

3.1 Comparing with observed morphology

To verify that the time shifts we learn correspond to actual differences in the developmental rates among the replicates, we can compare to estimates of the physiological age based on morphological observations. We had a domain expert independently estimate the developmental stage and rank the replicates in order of degree of development using only images from histological sections of the replicates taken at the time of measurement. We then compared this ranking with the replicate order predicted by our algorithm's estimates of biological time 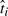, based solely on the gene expression measurements.

The rank correlation coefficient between these two global orderings was found to be 0.98, showing that they are in close correspondence. However, it is not immediately obvious how to measure the significance of this number. Both rankings rely on the nominal ordering of measurements indicated by their respective days, e.g. that measurements on day 23 are almost certainly earlier than measurements from day 34. It is difficult to know how much influence this implied ordering has on the rankings.

However, we can control for the implied ordering and assess the significance of our ranking quantitatively by comparing only the within-group orders, i.e. the relative ordering of replicates measured at the same time. These relative orders are listed in Table 1. For example, for day 23, both our expert and the algorithm ranked 23-1 as being at an earlier developmental stage than 23-2, so the order for both is [23-1, 23-2], abbreviated as [1, 2] on day 23. We can then compute the rank correlation coefficient ρ_i between the orderings at each time point, also shown in Table 1. We score the full ranking by simply taking the average score (correlation coefficient) at each time point, yielding .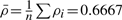

Table 1.

The within-group orders of the estimated time shifts from each of the expert and algorithm, and the rank correlation between the two orders

ti	23	25	27	29	34	37	39	41	44
Expert Orders	1,2	1,2	2,3,1	1,2,3	2,1	1,3,2	3,2,1	1,3,2	1,2,3
Algorithm Orders	1,2	1,2	3,1,2	1,2,3	2,1	3,1,2	2,3,1	1,3,2	1,3,2
ρi	1	1	−0.5	1	1	0.5	0.5	1	0.5

It is then possible to assess the significance of 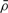, compared with the plausible null hypothesis that the ordering of replicates measured at the same day is uniformly random. We compute the P-value, or probability under the null hypothesis of obtaining a score as high or higher than the observed correlation, to be 0.0037. This shows that the expert ranking based on histology and the algorithm ranking based on expression are in fact in close correspondence.

However, this P-value may underestimate the quality of the algorithm ranking. We have controlled for the information from the measurement day by using within-group rankings, but this ignores any reordering of replicates across days. Both rankings occasionally reversed the ordering implied by the measurement day, ranking a replicate at an earlier day as being developmentally later than some replicate at the next time point. Quantifying the significance of these reversals is difficult, but we can discuss them anecdotally.

In the morphologically based ordering, there were only two instances in which replicates at successive time points appeared to be in reversed order of morphological development. These are replicates 25-1 and 23-2, in which the latter appears to be further developed in the Anagen stage of the hair cycle, and the pair 39-3 and 37-2, in which the latter appears to be in a later stage of the Catagen stage, as shown in Figure 2. Both of these order reversals were correctly predicted by the model, as shown in Figure 5. However, the model also predicts two other reversals (also at time points 37–39), which were not predicted by our expert. Without ground truth, the accuracy and significance of these reversals is difficult to quantify.

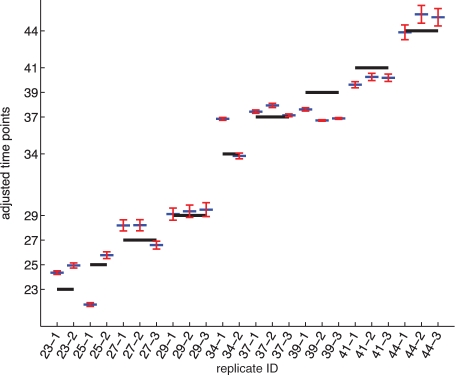
Fig. 5.

The estimated time shifts τ by maximizing Equation (4) when σ_τ=1. The x-axis represents the replicates and their measured time points; the y-axis represents the physiological ages 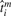. Longer lines show measurement times without shifting, whereas short lines show the estimated physiological ages of the replicates, with error bars indicating the maximal and minimal time shift values when σ_τis varied from 0.025 to 2.

Finally, we test the sensitivity of the algorithm's ordering to the choice of the parameter σ_τ, which controls how easy it is to shift each time away from its nominal value. Figure 5 shows the time shifts found using several different values of σ_τ. Although the values of τ_i do change with the variance σ_τ, the relative differences among the τ_i do not change significantly, especially among replicates measured at the same time point. This makes the rank correlation relatively stable and insensitive to σ_τ.

3.2 Predictive accuracy in cross-validation

Another way to measure whether the learned time shifts correspond to real developmental phenomena is to check whether they improve our ability to predict the expression levels of data not used in the learning process. We use cross-validation to maximize the amount of data on which we can make predictive measurements.

Specifically, we subdivide the data into two sets, training and test, in which the test set is made up of the intersection of a subset of genes and a subset of the replicates (Fig. 6a). Only the training dataset is used for learning the expression patterns of the genes and time shifts of the replicates, maximizing Equation (4) on the training set to obtain an estimate of θ and τ. Since the training set includes some genes for every replicate, we obtain an estimate of its time shift τ_i and thus its estimated biological time 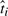. Similarly, since the training data include some replicate measurements for every gene in the training data, we can compute an estimate of the gene's profile and predicted expression level at the held-out replicates' times t_i using Equation (3). We then measure the mean squared error (MSE) between the predicted values and the measured expression levels for the test replicates and genes, to see if the time shifts improve our predictive accuracy.

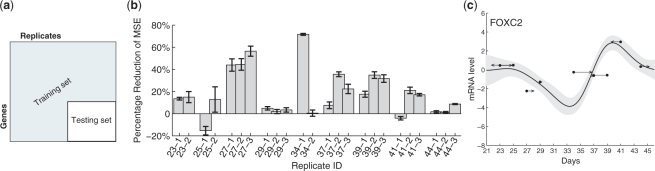
Fig. 6.

(a) Data partitioning for cross-validation. The testing data consists of the intersection of a subset of genes and of replicates; this allows us to predict the profile shape for all genes and time shift for all replicates while withholding unused data for testing. (b) Percent reduction in the average MSE when time shifts are included in the model. Results are grouped by replicate and found using cross-validation; see text. Most replicates have lower MSE (positive reduction) after introducing time shifts. (c) An example curve fit during cross-validation. The curve and time shifts are predicted using only the training data (data not shown); dots show the expression levels of the nine withheld test replicates (one at each time point) at their nominal times, and arrows show the estimated time shifts.

We use a cross-validation strategy for evaluating the predictions. First, we randomly partition the genes into 10 subsets. In each round of cross-validation, one of these subsets is used to define the testing set, and the other nine subsets are assigned to the training set. Similarly, we randomly select one replicate at each time point to define the test set; recall that the test set is defined as the intersection of the test genes and test replicates. We select 100 such groups for each subset of genes; each round of cross-validation consists of leaving out the all the data corresponding to the randomly selected replicates for the current partition of genes.

In each round of cross-validation, we predict the time shift and expression profile of each gene/replicate pair, and measure the error from the observed expression value. We compute the MSE for each replicate by averaging over all rounds in which that replicate was left out, and compare with the MSE for a prediction made without time shifts. The percentage reduction in MSE is shown for each replicate in Figure 6b. We can see that most replicates improve their MSE with time shifts; only two (25-1 and 41-1) show any increase, and these increases are relatively small. The average MSE over all replicates is 0.2042 with time shifts as compared with 0.2515 without, resulting in a 20% reduction of average MSE. Figure 6c shows an anecdotal example of the held-out measurements and their estimated time shifts compared with the profile learned on the training data.

Finally, to test whether the predictive accuracy is sensitive to the variance in time, we performed the same cross-validation study at various values of σ_τ. The results are shown in Figure 7. For very low σ_τ, time shifting is essentially disallowed and the MSE matches that of the model without time shifts. However, as σ_τ increases, the MSE drops rapidly, and is relatively stable over the rest of the interval. We conclude that beyond very low values (empirically σ_τ>0.1), the choice of σ_τ does not greatly influence the predictive accuracy.

Fig. 7.

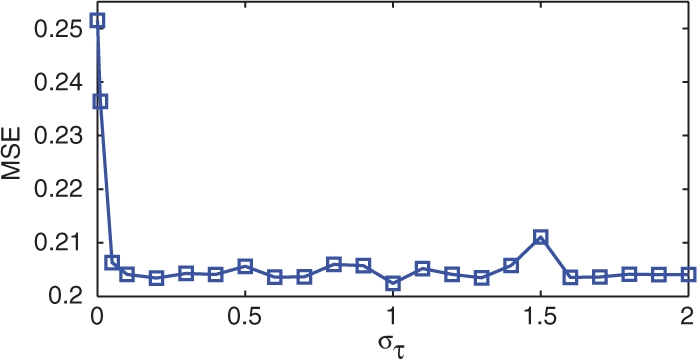
The average MSE found using cross-validation, as a function of the time-shift variance parameter σ_τ. Beyond very low values, the predictive performance is fairly insensitive to this parameter.

4 DISCUSSION AND CONCLUSION

We have argued that due to biological variation, time-course microarray data suffer from noise not only in the observed expression values, but also in the axis corresponding to the time of observation. Typical estimates of the expression profile assign all the uncertainty to the observation value, providing less accuracy and lower confidence in the resulting shapes. By introducing a model with uncertainty in the time axis, we can accurately infer the relative degree of development in each replicate and improve our estimates of the temporal expression profile.

The predictions of our GPR model show high consistency with human-generated estimates based on morphological observation (Table 1). Differences between the two estimation methods could be due to a number of factors. The expert ranking involves some subjective uncertainty, which can be hard to gauge; for example, the orientations of the histological sections are not always ideal, making morphological estimates more difficult. There is also always the possibility of human error in the data collection and processing.

As an example, we examined the three replicates on the 27th day, in which the ordering of the estimated time shifts from the model differs significantly from the expert's ordering based on morphological results (Table 1). We find that the keratin-associated protein expressions, an excellent marker for anagen progression, supports the hypothesis that replicate 27-4 is in fact more delayed in development as predicted by the algorithm.

In addition to not requiring histological sections, one advantage to the regression approach to estimating time shifts is that it provides a quantitative estimate of the amount of relative development, as compared with a subjective ordering. For the purposes of improving the estimated shapes of expression profiles, the proposed method also has the advantage that it works directly with the relevant measurements. While this carries some risk of overfitting, the predictive improvement seen in cross-validation suggests that the phenomena being identified are real effects in the expression data.

In terms of further improvements, in the general approach presented here, we modeled different gene expression profiles as independent GP sharing the same GP parameters and time shifts. While these assumptions give results that justify the inclusion of time shifts, there is still room to further refine and improve upon the model. For example, since different genes promote or inhibit one another in a regulation network and often share similar basic shapes, the assumption of independence is overly simple. One possible way to address this issue would be to group the genes into clusters, where each cluster shares an underlying shape or parameters. The grouping could be estimated simultaneously with the GP parameters, by modeling the data as a mixture model and using statistical estimation techniques such as the expectation–maximization method. There may also be temporal effects that are not shared by all genes or are unrelated to development, such as external effects, which would require further extension of the model.

Funding: National Institutes of Health–National Institute of Arthritis and Musculoskeletal and Skin Diseases (grant AR 44882 to B.A., including a BIRT revision award); National Science Foundation Grant (NSF IIS-0431085 to P.S.); National Library of Medicine–National Research Service (Award 5 T15 LM00744 to K.K.L.).

Conflict of interest: none declared.