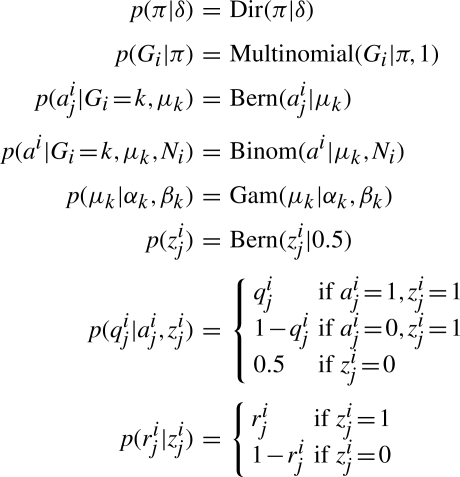SNVMix: predicting single nucleotide variants from next-generation sequencing of tumors

Abstract

Motivation: Next-generation sequencing (NGS) has enabled whole genome and transcriptome single nucleotide variant (SNV) discovery in cancer. NGS produces millions of short sequence reads that, once aligned to a reference genome sequence, can be interpreted for the presence of SNVs. Although tools exist for SNV discovery from NGS data, none are specifically suited to work with data from tumors, where altered ploidy and tumor cellularity impact the statistical expectations of SNV discovery.

Results: We developed three implementations of a probabilistic Binomial mixture model, called SNVMix, designed to infer SNVs from NGS data from tumors to address this problem. The first models allelic counts as observations and infers SNVs and model parameters using an expectation maximization (EM) algorithm and is therefore capable of adjusting to deviation of allelic frequencies inherent in genomically unstable tumor genomes. The second models nucleotide and mapping qualities of the reads by probabilistically weighting the contribution of a read/nucleotide to the inference of a SNV based on the confidence we have in the base call and the read alignment. The third combines filtering out low-quality data in addition to probabilistic weighting of the qualities. We quantitatively evaluated these approaches on 16 ovarian cancer RNASeq datasets with matched genotyping arrays and a human breast cancer genome sequenced to >40× (haploid) coverage with ground truth data and show systematically that the SNVMix models outperform competing approaches.

Availability: Software and data are available at http://compbio.bccrc.ca

Contact: sshah@bccrc.ca

Supplemantary information: Supplementary data are available at Bioinformatics online.

1 INTRODUCTION

1.1 Single nucleotide variants in cancer

Cancer is a disease of genetic alterations. In particular, single nucleotide variants (SNVs) present as either germline or somatic point mutations are essential drivers of tumorigenesis and cellular proliferation in many human cancer types. The discovery of germline mutations established important gene functions in cancer; however, the contribution of single germline alleles to the population burden of cancer is relatively low. In contrast, determination of tumorigenic mechanisms has focused on somatic mutations. The somatic mutational landscape of cancer has to date largely been derived from small-scale or targeted approaches, leading to the discovery of genes affected by somatic mutations in many diverse cancer types. More comprehensive studies using Sanger-based exon resequencing suggest that the mutational landscape will be characterized by relative handfuls of frequently mutated genes and a long tail of infrequent somatic mutations in many genes (Jones et al., 2008; Stratton et al., 2009).

Considering this, unbiased sequencing surveys of tumor transcriptomes or genomes are expected to reveal mutations in these commonly affected cancer genes as well as many novel mutations in genes with no previous implication in cancer. Next-generation sequencing (NGS) technology (Shendure and Ji, 2008) has now emerged as a practical, high-throughput and low-cost sequencing method enabling the full and rapid interrogation of the genomes and transcriptomes of individual tumors for mutations. As such, NGS has presented an unprecedented opportunity for SNV discovery in cancer. Recent studies involving deeply sequencing the tumor genomes from acute myeloid leukemia patients (Ley et al., 2008; Mardis et al., 2009) and a lobular breast cancer patient (Shah et al., 2009b) have revealed numerous novel somatic mutations in genes that had not been previously reported to harbor abnormalities. In addition, sequencing the transcriptomes of ovarian cancers with RNA-seq (Marioni et al., 2008; Morin et al., 2008; Mortazavi et al., 2008) led to the discovery of a defining mutation in the FOXL2 gene (previously not implicated in cancer) in granulosa cell tumors of the ovary (Shah et al., 2009a).

While these early studies have emerged as proof of principle that novel SNVs can indeed be discovered using NGS, the study of computational methods for their discovery in cancer is under-represented in the bioinformatics literature. The analysis of SNVs from cancer data, where altered ploidy and tumor cellularity impact the statistical expectations of SNV discovery; and transcriptome data, where the dynamic range of depth of sequencing is dependent on highly variable transcript expression present unique challenges. In this contribution, we describe a new statistical model for identifying SNVs in NGS data generated from cancer genomes and transcriptomes. We demonstrate how its novel features outperform other available methods. Additionally, we provide a ground truth dataset (with Sanger validated SNVs) and robust accuracy metrics that will permit future study of computational methods for SNV detection in cancer genomes.

1.2 NGS data preprocessing for SNV detection

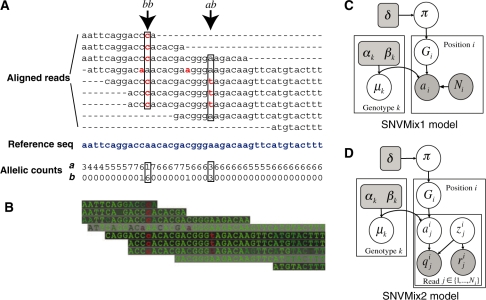
The data produced by NGS consists of millions of short reads ranging in length from approximately 30–400 nt (although this is steadily increasing with ongoing technology development). Here, we focus explicitly on the problem of inferring SNVs once these reads have been aligned to the genome. Numerous methods have been developed for short read alignment including Maq (Li,H. et al., 2008), BowTie (Langmead et al., 2009), ELAND (Illumina), SHRiMP (Rumble et al., 2009), BWA (Li and Durbin, 2009), SOAP (Li,R. et al., 2008) and Mosaik (http://bioinformatics.bc.edu/marthlab/Mosaik). We begin the discussion by describing two ways of preprocessing aligned data for input to SNV detection algorithms. The first method is shown in Figure 1A, where we show an example of aligned data where two SNVs are identified. The reads are positioned according to their alignment in the genome and the reference genome sequence is shown in blue. The first step involves transforming the aligned reads into allelic counts. This method assumes that the reads are correctly aligned and the nucleotide base calls are correct. Nucleotides that match the reference are shown in black, whereas nucleotides that do not match the reference are shown bolded in red. The figure illustrates how aligned data can be ‘collapsed’ into allelic counts. At each position i in the data, we can count the number of reads a_i that match the reference genome and the number of reads b_i that do not match the reference genome. In the case of rare third alleles, these reads are assumed to be errors. The total number of reads overlapping each position (called the depth) is given by N_i=a_i+b_i. In this context, given {a_i, b_i, N_i} for all i∈{1, 2,…, T} where T is the total number of positions in the genome, the task is to infer which positions exhibit an SNV.

Fig. 1.

(A) Schematic diagram of input data to SNVMix1. We show how allelic counts (bottom) are derived from aligned reads (top). The reference sequence is shown indicated in blue. The arrows indicate positions representing SNVs. The non-reference bases are shown in red. (B) Input data for SNVMix2 that consists of the mapping and base qualities. The darker the background for a read represents a higher quality alignment. The brighter colored nucleotides represent higher quality base calls. Therefore, high contrast nucleotides are more trustworthy than lower contrast nucleotides. (C) SNVMix1 shown as a probabilistic graphical model. Circles represent random variables, and rounded squares represent fixed constants. Shaded notes indicate observed data [the allelic counts and the read depth from (A)]. Unshaded nodes indicate quantities that are inferred during EM. G_i∈{aa, ab, bb} represents the genotype, N_i∈{0, 1,…,} is the number of reads and a_i∈{0, 1,…, N_i} is the number of reference reads. π is the prior over genotypes and μ_k is the genotype-specific Binomial parameter for genotype k. (D) SNVMix2 shown as a probabilistic graphical model. In comparison to SNVMix1, a_i is unobserved and we expand the input to consider read-specific information indexed by j where zⁱ_j=1 indicates that read j is correctly aligned, qⁱ_j is the base quality and rⁱ_j is the mapping quality.

The second method (Fig. 1B) relaxes the assumption that the base calls and the alignments are correct and instead considers two types of uncertainty related to determining a_i and N_i , namely the uncertainty encoded in the base call qⁱ_j∈[0, 1] which represents the probability that the stated base is correct for read j∈(1, …, N_i) at position i; and rⁱ_j∈[0, 1] representing the probability that read j aligns to its stated position in the genome. Note that although mapping quality is derived in part from base qualities, considering these quantities as independent allows us to encode the fact that base qualities are position specific, while mapping qualities are constant for all bases in the read. The input data for this method can be visualized as shown in Figure 1B: high mapping quality is shown as dark background and high base quality as bright foreground, high contrast positions indicate positions where the data are more trustworthy. We show in Section 2.4 how to explicitly model these uncertainties to perform soft probabilistic weighting of the data rather than thresholding the uncertainties to deterministically calculate the allelic counts. We will now describe how various authors have approached this problem given {a_i, b_i, N_i} and optionally, {qⁱ_1:Ni, rⁱ_1:Ni}.

1.3 Related work

A simple way to detect SNV locations would be to compute the fraction 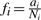, and then to call as SNVs those locations where f_i is below some threshold. In the example in Figure 1A, applying threshold of 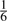would successfully discard all columns (including the two columns which have singleton non-reference reads, which may be due to base-calling errors), except the two containing the SNVs. A critical flaw with this approach is that it ignores the confidence we have in our estimate of f_i. Intuitively, we can trust our estimate more at locations with greater depth (larger N_i). This idea has been applied by Morin et al. (2008), wherein read depth thresholds of N_i ≥ 6 and b_i ≥ 2 reads supporting the variant allele were applied, with an additional requirement that the non-reference allele must be represented by at least 33% of all reads at that site. This should eliminate SNVs with weak supporting evidence, but it categorizes the data into two discrete classes—SNV or not, without explicitly providing confidence estimates on the prediction. Moreover, in transcriptome data, the number of reads representing a given transcript expected to be highly variable across all genes and thus determining a minimum depth can be difficult. We demonstrate (Section 3) that applying depth-based thresholds reduces sensitivity to finding real SNVs.

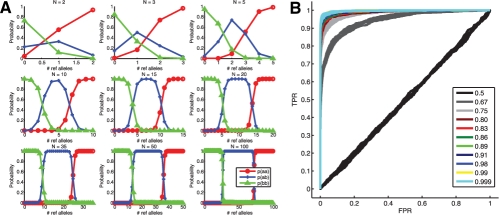
To overcome these limitations, we propose a probabilistic approach based on a Binomial mixture model, called SNVMix1, which computes posterior probabilities, providing a measure of confidence on the SNV predictions. The model infers the underlying genotype at each location. We assume the genotype to be in one of three states: aa = homozygous for the reference allele, ab = heterozygous and bb = homozygous for the non-reference allele; the latter two genotypes constituting an SNV. In Figure 2, we show how the posterior probability of each of these three states increases with more depth, which demonstrates the theoretical qualities of our approach. Two other approaches: Maq (Li,H. et al., 2008) and SOAPSNP (Li,R. et al., 2008) have proposed using Binomial distributions to model genotypes; however, these were developed in the context of sequencing normal genomes, not cancer genomes. Both set parameters for the model assuming expected distributions for normal allelic ratios, and apply post-processing heuristics to reduce false positives. In our application, we are interested in cancer genomes and transcriptomes, both of which may not follow expected distributions due to tumor-normal admixtures in the sample, within sample tumor heterogeneity, copy number changes and other factors. We use the expectation maximization (EM) algorithm to find a maximum a posteriori (MAP) estimate of the parameters given some training data, allowing the model to adapt to genomes and transcriptomes that may deviate from the assumed distributions for normal genomes and thus model the data more accurately.

Fig. 2.

(A) Theoretical behavior of SNVmix at depths of 2, 3, 5, 10, 15, 20, 35, 50 and 100. The plots show how the distribution of marginal probabilities changes with the number of reference alleles given the model parameters fit to a 10× breast cancer genome dataset. (B) ROC curves from fitting SNVMix2 to synthetic data with increasing levels of certainty in the base call.

Previous studies have employed stringent thresholding for removing poor quality bases and/or reads (Ley et al., 2008; Morin et al., 2008). We propose that this may throw out informative data, and we extend SNVMix1 to explicitly encode base and mapping qualities by using them to probabilistically weight the contribution of each nucleotide to the posterior probability of a SNV call. In addition, we explore how to optimally combine thresholding and probabilistic weighting in order to obtain more accurate results. We show (Section 3) how this extended model, which we call SNVMix2, confers an increased specificity in our predictions.

The statistical models we propose in this contribution provide posterior probabilities on SNV predictions, removing the need for depth thresholds and use an EM learning algorithm to fit the model to data removing the need to set model parameters by hand. We also show how to explicitly model base and mapping qualities, and explore how quality thresholds can be used in combination with probabilistic weighting. We show that these attributes of the model result in increased accuracy compared with Maq's SNV caller and depth threshold-based methods. We evaluate the model based on real data derived from 16 ovarian cancer transcriptomes sequenced using NGS, and a lobular breast cancer genome sequenced to >40x coverage (Shah et al., 2009b). For all cases, we obtained high-density genotyping array data for orthogonal comparisons. Finally, we demonstrate results on 497 positions from the breast cancer genome that were subjected to Sanger sequencing and thus constitute a ‘ground truth’ dataset for benchmarking.

2 METHODS

2.1 SNVMix model specification

SNVMix1 is shown as a probabilistic graphical model in Figure 1C. The conditional probability distributions for the model are given in Figure 3 and the description of all random variables is listed in Table 1. The input is composed of allelic counts from aligned data and the output of inference is the predicted genotypes. Consider G_i=k, k∈{aa, ab, bb}, to be a Multinomial random variable representing the genotype at nucleotide position i, where aa is homozygous for the reference allele, ab is heterozygous and bb is homozygous for the non-reference allele. At each position, we have an observed number of aligned reads N_i. We let aⁱ_j∈{0, 1} represent whether or not read j∈{1,…, N_i} matches the reference at position i. We let a_i (no j index) be the total number of reads that match the reference at i. We assume the following likelihood model for the data:

(1)

where μ_k is the parameter of a Binomial distribution for genotype k. μ_k models the expectation that for a given genotype k, a randomly sampled allele will be the reference allele. Intuitively, we should expect μ_aa to be close to 1, μ_ab to be close to 0.5 and μ_bb to be close to 0. Thus, the key intuition is that for genotype k=aa, the Binomial distribution defined by μ_aa should be highly skewed toward the reference allele. Similarly, μ_bb would be skewed toward the non−reference allele. For μ_ab, the distribution would be much more uniform. We impose a prior on the genotypes, G_i|π∼ Multinomial(G_i|π, 1) where π(k) is the prior probability of genotype k. Given knowledge of all the parameters, θ=(μ_1:3, π), we can use Bayes' rule to infer the posterior over genotypes, γ_i(k)=p(G=k|a_i, N_i, θ), where:

(2)

Fig. 3.

Conditional probability distributions of SNVMix model.

Table 1.

Description of random variables in SNVMix1 and SNVMix2

Parameter	Description	Value
δ	Dirichlet prior on π	(1000,100,100)
π	Multinomial distribution over genotypes	Estimated by EM (M-step)
Gi	Genotype at position i	Estimated by EM (E-step)
aij	Indicates whether read j at position i matches the reference	Observed in SNVMix1, latent in SNVMix2
zij	Indicates whether read j aligns to its stated position	Latent
qij	Probability that base call is correct	Observed (SNVMix2 only)
rij	Probability that alignment is correct	Observed (SNVMix2 only)
μk	Parameter of the Binomial for genotype k	Estimated by EM (M−step)
α	Shape parameter of Beta prior on μ	(1000,500,1)
β	Scale parameter of Beta prior on μ	(1,500,1000)

Our approach to inference involves learning the parameters θ by fitting the model to training data using MAP EM (see below). We demonstrate that this produces better results than Maq, which uses fixed parameters (Section 3).

2.2 Prior distributions

We assume that π is distributed according to a Dirichlet distribution parameterized by δ, the so−called pseudocounts. We set δ to be skewed toward π_aa assuming that most positions will be homozygous for the reference allele. μ_k is conjugately distributed according to a Beta distribution: μ_k∼Beta(μ_k|α_k, β_k). We set α_aa=1000, β_aa=1; α_ab=500, β_ab=500 and α_bb=1, β_bb=1000 assuming that μ_aa should be skewed towards 1, μ_ab should be close to 0.5 and μ_bb should be close to 0.

2.3 Model fitting and parameter estimation

We fit the model using the EM algorithm. We initialize μ_k and π(k) to their prior means. The EM algorithm iterates between the E-step where we assign the genotypes using Equation 2 and the M-step where we re-estimate the model parameters. At each iteration, we evaluate the complete data log-posterior and the algorithm terminates when this quantity no longer increases. The M-step equations are standard conjugate updating equations:

(3)

where I(G_i=k) is an indicator function to signal that G_i is assigned to state k at position i, and:

(4)

2.4 Modeling base and mapping qualities

The model shown in Figure 1C assumes that aⁱ_j is observed (it is a shaded node in the graph), and thus assumed correct. However, each nucleotide's contribution to the allelic counts has uncertainty associated with it in the form of base and mapping qualities. We propose a soft (or probabilistic) weighting scheme, which will down-weight the influence of low-quality base and mapping calls, but not discard them altogether. To model this, we change aⁱ_j to be an unobserved quantity as shown in Figure 1D, and instead observe the soft evidence on them in the form of probabilities, which we represent by the observed base qualities qⁱ_j∈[0, 1]. Similarly, we introduce unobserved binary random variables zⁱ_j∈{0, 1} representing whether read j is correctly aligned, and soft evidence in the form of probabilities which we represent by the observed mapping qualities rⁱ_j∈[0, 1]. The conditional probability distributions for p(qⁱ_j|aⁱ_j, zⁱ_j) and p(rⁱ_j|zⁱ_j) are given in Figure 3. Thus, the input data is now q^1:T, r^1:T and the corresponding likelihood for each location i can be obtained by marginalizing out a, z as follows:

(5)

(6)

(7)

As before, given the model parameters μ, π, we can infer the genotype at each position by modifying Equation (2) as follows:

(8)

The updating equations are unchanged in the M-step of EM. The model-fitting algorithm changes only in the E-step by using Equation (2) instead of Equation (2). We have specified how to encode base and mapping uncertainty into the model, obviating the need for thresholding these quantities. We call this version of the model SNVMix2.

In Figure 2, we show the theoretical behavior of this model using simulated data with varying base qualities. The model performs equally well for datasets where the mean certainty of the base calls is ∼80% and higher. This suggests that thresholding base calls at Phred Q20 [99% certainty (Morin et al., 2008)] or Q30 [99.9% certainty (Ley et al., 2008)] may be overly stringent.

2.5 Implementation and running time

The model and inference algorithm is implemented in C and supports both SAMtools (Li et al., 2009) and Maq pileup format. Running EM (SNVMix2) on 14 649 positions for the 40× breast cancer genome took 36 s. Predicting genotypes for the whole 40× genome took 11 min and 38 s. (The Maq step cns2snp took 19 min and 9 s.) A script to choose optimal base and mapping quality thresholds, given ground truth [or orthogonal single nucleotide polymorphism (SNP) array] data, is provided in the software package.

2.6 Datasets

We used three datasets to evaluate our models. The first (Supplementary Dataset 1A and B) consists of 16 ovarian cancer transcriptomes sequenced using the Illumina GA II platform, RNA-Seq paired end protocol. (Note that this data has been generated as part of an ongoing study to profile ovarian carcinoma subtypes, and the full datasets will be available as part of forthcoming manuscripts. However, all SNV data referenced in this manuscript is available as Supplementary Materials). For each of these cases, we obtained Affymetrix SNP 6.0 high-density genotyping arrays from the corresponding DNA. We examined coding positions in the transcriptome data for which there was a corresponding high-confidence (>0.99) genotyping call from the array predicted using the CRLMM algorithm (Lin et al., 2008). This resulted in an average of approximately 9000 positions from each case and a total of 144 271 positions. These data were used in the cross-validation experiment, described below. The second dataset (Supplementary Dataset 2A–D) consisted of 497 positions from a lobular breast tumor genome predicted as SNVs using SNVMix1 model from data generated using the Illumina GA II platform. These positions were predicted to be non-synonymous protein-coding changes and were subsequently sequenced using Sanger capillary-based technology. Of these, 305 were confirmed as SNVs and 192 were not confirmed. These 497 positions were considered as the ground truth dataset used for sensitivity and specificity calculations. In addition, we also generated Affymetrix SNP 6.0 array data for this case and considered 14 649 positions (Supplementary Dataset 3A–D) that matched the coding positions and CRLMM prediction criteria outlined above. All NGS data were aligned to the human genome reference (NCBI build 36.1) using Maq's map tool (v0.6.8). Thus, for all comparisons between Maq and SNVMix, we used the same baseline set of aligned data.

2.7 Accuracy metrics

While comparing with the SNP array data, we defined a true positive (TP) SNV as an ab or bb CRLMM genotype. A true negative (TN) SNV was defined as an aa genotype from the SNP array. For the Sanger validated positions, a TP was an SNV that was confirmed by Sanger sequencing, whereas a TN was a position that was not confirmed. To evaluate our models against these data, we computed p(SNV_i)=γ_i(ab)+γ_i(bb) and standard receiver operator characteristic (ROC) curves. The area under the ROC curve (AUC) was computed as a single numeric metric of accuracy that effectively measures the trade-off between sensitivity and specificity. As an additional measure, we computed the F-statistic: 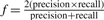, where precision is measured as the proportion of predictions that were true and recall is the proportion of true SNVs that were predicted.

2.8 Benchmarking experiments

To evaluate the effect of estimating parameters, we designed a 4-fold cross-validation study. We permuted the 144 271 positions with matched array-based genotype data from the ovarian cancer data, and divided the positions into four equal parts. We fit the model to three parts (training data) using EM and used the converged parameters to calculate p(SNV_i) for each of the remaining positions (test data). We repeated this 10 times and computed the AUC for each of the 16 cases. We also computed AUC from the results predicted by Maq v0.6.8 and compared the AUC distributions across the 16 cases to SNVMix1 and SNVMix2. These data also allowed us to determine the range of converged parameter estimates across the folds and 10 replicates. We also tested the effect of depth-based thresholding by running SNVMix1 on the 14 649 positions from the breast cancer genome. To simulate the thresholding, we set p(SNV_i)=0 at locations where N_i was below some threshold, chosen from the set {0, 1,…, 7, 10}. We compared SNVMix1, SNVMix2 and Maq on this data as well. Finally, we evaluated the true positive rate (TPR) and false positive rate (FPR) on the 497 ground truth positions from this case for SNVMix1, SNVMix2 and Maq.

3 RESULTS

3.1 Depth heuristics reduce sensitivity

We first determined the effect that depth thresholding had on 14 649 positions probed using an Affymetrix SNP 6.0 array from genome data from the lobular breast cancer by calculating ROC curves and corresponding AUC values (Section 2) from the output of SNVMix1 at different cutoff values. The most accurate results were obtained when no depth thresholding was applied. At a threshold of 0, the AUC was 0.988 (the highest) and at a threshold of 10 reads, the AUC was 0.614 (the lowest). At a FPR of 0.01, the TPR decreased with increasing number of reads required for the threshold without exception, suggesting that depth-thresholding under the SNVMix1 model reduces overall sensitivity without increasing specificity, and should therefore be avoided. AUC for thresholds of 1, 3, 5 and 7 reads were 0.971, 0.893, 0.782 and 0.707, respectively.

3.2 Estimating parameters in transcriptome data by model fitting confers better accuracy

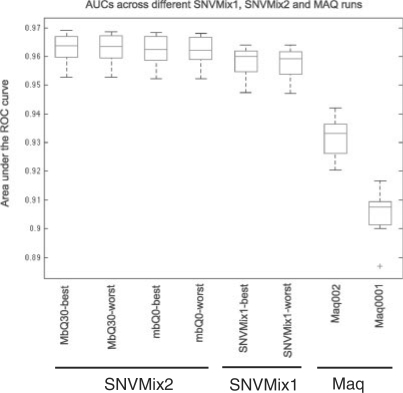
Figure 4 shows the AUC distribution over 16 ovarian cancer transcriptomes (Section 2) for the best and worst cross-validation runs of SNVMix2 and SNVMix1 as well as the results from the Maq SNV caller with the two recommended settings of the r parameter (0.001 and 0.02). Both runs of SNVMix1 were statistically significantly better than the Maq runs [analysis of variance (ANOVA) test, P<0.0001], with mean AUC of 0.9557 ± 0.0100 and 0.9552 ± 0.0100, compared with 0.9290 ± 0.0120 and 0.9032 ± 0.0119 for the Maq runs. Furthermore, SNVMix2 without quality thresholds offers a slight performance improvement over SNVMix1. Although the improvement of SNVMix2 over SNVMix1 is not statistically significant, it is noteworthy that no thresholds of any kind were applied to the data and thus probabilistic weighting can eliminate the need for arbitrarily thresholding the data (see below).

Fig. 4.

Distribution of AUC over 16 ovarian cancer transcriptomes comparing accuracy of SNV detection for two Maq runs, the best and worst SNVMix1 runs in the cross-validation experiment (middle) and best and worst runs for SNVMix2 (mbQ0 = no quality thresholding, MbQ30 = keeping only reads with mapping qualities > Q30). SNVMix1 and SNVMix2 runs were statistically more accurate than both Maq runs (ANOVA, P < 0.0001). SNVMix2 runs were better than SNVMix1, but not statistically significantly.

3.3 Evaluation of models on a deeply sequenced breast cancer genome with ground truth SNVs

We evaluated performance of the models on a lobular breast cancer sample sequenced to >40× haploid coverage (Shah et al., 2009b). In addition, we compared results obtained from the same genome at 10× coverage. We first trained the model using 14 649 protein coding positions for which we generated matching Affymetrix SNP6.0 calls. We computed the AUC for SNVMix1, SNVMix2 and Maq. Table 2 shows that the highest AUCs were obtained with SNVMix2 on the 40× genome, followed by SNVMix2 on 10× genome (AUCs of 0.9929 and 0.9905, respectively). Both of these were higher than results achieved for SNVMix1 (AUC of 0.9880) and Maq (0.9824 for 40× and 0.9115 for 10×—both for the r=0.001 parameter setting). After fitting the model to the 14 649 positions, we evaluated the performance using 497 candidate mutations originally detected using SNVMix1 at 10×, which were validated using Sanger amplicon sequencing (Section 2). These consisted of 305 true SNVs (variants seen in the Sanger traces) and 192 that could not be confirmed in the Sanger traces. Table 2 shows the sensitivity, precision and F-measure results of SNVMix2, SNVMix1 and SNVMix2 combined with base and mapping quality thresholding at both 10× and 40× coverage at a p(SNV) (Section 2) threshold determined using a FPR ≤ 0.01. We did not include a comparison to Maq at these 497 positions since the results would be biased toward the SNVMix1 model that led us to identify them in the first place. SNVMix2 and SNVMix1 showed similar F-measure at both 10× and 40× reinforcing that the probabilistic weighting confers equal accuracy without having to select arbitrary quality thresholds. In addition, both SNVMix2 and SNVMix1 had higher accuracy at 40× and 10× (Table 2). Interestingly, all the models had increased false negative rates in the 40× genome in comparison with the 10× genome. Upon further review of the SNVMix2 positions predicted at 10×, but not at 40×, we examined that the majority (9 out of 13) were marginally below threshold and significant probability mass was indeed on the P(ab) state (>0.99) and would have been predicted with even a slightly less stringent threshold. Three out of the remaining four appear to be the result of DNA copy number amplifications that are skewing the allelic ratios involved. We elaborate on this point in Section 4.

Table 2.

Comparison of accuracy of SNVMix1, SNVMix2 and SNVMix combined with base and mapping quality thresholding

Model	Run	Train AUC	TP	FP	TN	FN	Sens	Prec	F-measure
SNVMix1	10×	0.9880	305	192	0	0	1.0000	0.6137	0.7606
	40×	0.9924	293	107	85	12	0.9607	0.7325	0.8312
SNVMix2	10×	0.9905	299	162	30	6	0.9803	0.6486	0.7807
	40×	0.9929	290	107	85	15	0.9508	0.7305	0.8262
SNVMix2+thresholding	mQ50_bQ20 (10×)	0.9882	287	88	104	18	0.9410	0.7653	0.8441
	mQ50_bQ15 (40×)	0.9928	287	71	121	18	0.9410	0.8017	0.8658

While the SNVMix2 model eliminates the need for thresholding through probabilistic weighting, we explored the effect of applying thresholds to the SNVMix2 input in order to identify a practical balance between pure weighting and thresholding. We compared the results of thresholding mapping qualities at (Q0, Q5, Q10, Q20, Q30, Q40 and Q50) and concomitantly thresholding base qualities at (Q0, Q5, Q10, Q15, Q20 and Q25) and running SNVMix2 on the resulting data from both 10× and 40× genomes. As shown in Table 2, thresholding the mapping qualities at Q50 and base qualities at Q20 (mQ50_bQ20) at 10× performed better than all other 10× runs (F−measure 0.8441). For the 40× data, thresholding the mapping qualities at Q50 and base qualities at Q15 (mQ50_bQ15) performed best over all runs (F-measure 0.8658). (See Supplementary Table S1 for all results from runs in increments of Q1 base quality thresholds.) This suggests that previously reported base quality thresholds may be too stringent. Furthermore, when used with stringent mapping quality thresholds, the SNVMix2 model can effectively use the base qualities by probabilistic weighting to confer higher accuracy. These results indicate that treating mapping and base qualities separately as opposed to taking a minimum over the two (as in Maq) has advantages.

4 DISCUSSION

We have described two statistical models based on Binomial mixture models to infer SNVs from aligned NGS data obtained from tumors. We demonstrated that a probabilistic approach to modeling allelic counts obviates the need for depth-based thresholding of the data, and how fitting the model to real data to estimate parameters is superior to Maq, which uses fixed parameter settings on the assumption that the data come from a normal human genome. In addition, we extended the basic Binomial mixture to model mapping and base qualities by using a probabilistic weighting technique. This eliminates the need to employ arbitrary thresholds on base and mapping qualities and instead lets the model determine the strength of contribution of each read to the inference of the genotype. Finally, we showed that even further gains in accuracy can be obtained by combining moderate thresholding and probabilistic weighting of the base and mapping qualities. Importantly, gains in accuracy by the SNVMix models were shown in both transcriptome and genome data.

4.1 Dependence on alignments

Our results will be highly dependent on the accuracy of alignments as well as the consistency and accuracy of mapping qualities reported by the aligner. Results in Table 2 showed that the combined approach of stringent thresholding on mapping quality and modeling the uncertainty of the remaining reads gave the highest accuracy. Given that the most gain was obtained in precision, it suggests that false positive predictions may indeed be reduced with more accurate alignments. As read lengths increase with technology development and mapping algorithms improve, we expect that the input to SNVMix will be of higher quality, which should yield more accurate results. Moreover, alignment using Maq presents a drawback with regard to SNVMix2's model. When a short read can be aligned to more than one position in the genome with the same mapping quality, this read is dropped, being assigned a mapping quality of zero. SNVMix2's design would be able to leverage the read's quality amongst the distinct coordinates and still use the information it conveys to predict SNVs. The performance of this will be evaluated in future work.

4.2 Limitations, extensions and future work

As stated earlier, a major objective in cancer genome sequencing is to discover somatic mutations. If sequence data from tumor and normal DNA from the same patient is available, candidate somatic mutations can be identified as positions for which p(SNV) is high in the tumor and 1−p(SNV) is high in the normal data. If only tumour data is available, we recommend filtering against dbSNP and performing targeted validation on the remaining positions in both tumor and normal DNA as described previously (Shah et al., 2009b). Moreover, the models we have presented assume identically and independently distributed genotypes. As such, the common prior over genotypes π can be indexed by position (i.e. π_i) and thus could encode information about what variants are known for each position i in the genome.

We noticed that some positions missed by SNVMix1 at 40× were in what we believe are allele-specific copy number amplifications. Future work will involve incorporating copy number data directly into the model to consider such situations where the resultant allelic bias is expected to mask variants present in the unamplified allele. These results will be presented in a forthcoming manuscript. In a similar vein, due to regulatory mutations or epigenetic changes, transcriptomes can show preferential expression of one allele and thus our model will be insensitive to instances of extensively skewed allelic expression. Further extensions of the model to consider these factors will be explored.

Finally, we recently demonstrated that intra-tumor heterogeneity can be seen using ultra-deep targeted sequencing (Shah et al., 2009b). The allelic frequencies of SNVs in rare clones in the tumor population will likely result in false negative predictions at conventional sequencing depths (i.e. between 20× and 40×), and confound the estimation of the false negative rates of prediction. Future investigation of all of these problems will be necessary if the goal of sequencing studies is to characterize all mutations present in the heterogeneous mixture of genomes that make up a tumor.

Funding: The project is supported by the Canadian Institutes for Health Research (CIHR). SPS is supported by the Michael Smith Foundation for Health Research (MSFHR) and the Canadian Breast Cancer Foundation. RG is supported by MSFHR and CIHR.

Conflict of Interest: none declared.