Prediction of human functional genetic networks from heterogeneous data using RVM-based ensemble learning

Abstract

Motivation: Three major problems confront the construction of a human genetic network from heterogeneous genomics data using kernel-based approaches: definition of a robust gold-standard negative set, large-scale learning and massive missing data values.

Results: The proposed graph-based approach generates a robust GSN for the training process of genetic network construction. The RVM-based ensemble model that combines AdaBoost and reduced-feature yields improved performance on large-scale learning problems with massive missing values in comparison to Naïve Bayes.

Contact: dargenio@bmsr.usc.edu

Supplementary information: Supplementary material is available at Bioinformatics online.

1 INTRODUCTION

Biological pathways that organize functional associations between different genes, proteins and small molecules are central to understanding cellular function. A variety of high-throughput experimental data, such as DNA microarray, ChIP-chip technology and systematic two-hybrid analysis (Lee et al., 2002; Rual et al., 2005; Stears et al., 2003), have the potential to provide a system-level perspective of cellular processes and may contribute to systematic drug discovery (Stoughton and Friend, 2005). Moreover, the broad availability of indirect biological data sources, such as Gene Ontology and protein localization information, also contain information that can be used to understand cellular processes (Loging et al., 2007). Understanding biological pathways at the whole-genome level, however, remains a major challenge.

Several computational approaches have been applied to construct biological networks using different individual data sources (Basso et al., 2005; Papin et al., 2005). However, the results are often contradictory and not super imposable in any obvious way due to the intrinsic error rate of each data set and limited coverage (Zhong and Sternberg, 2006). This limitation has motivated more recent work addressing the problems of integrating heterogeneous functional genomic and proteomic data to construct biological network. Results from these studies suggest that the combination of multiple sources can provide a more unified view of prediction with large coverage and high reliability. Several rigorous statistical models and machine learning approaches have been applied to generate reliable integrated predictions, such as Bayesian modeling, Decision Tree and Random Forest (Jansen et al., 2003; Lee et al., 2004, Qi et al., 2006). Bayesian modeling (Naïve Bayes and Fully Connected Bayes) is the most popular method used to predict protein–protein and genetic interactions (Jansen et al., 2003; Troyanskaya et al., 2003; Rhodes et al., 2005). Correlation among data sets, however, can cause prediction bias in Naïve Bayes models. Fully Connected Bayes models (Jansen et al., 2003), in contrast, can capture the interdependence among data sources by directly calculating joint probabilities; however, it results in higher computational costs and requires bin size adjustment of each data dimension to obtain reasonable results, especially for high-dimension data. Moreover, the model prior is generally arbitrarily set to be the proportion of total number of positive and negative examples in the chosen benchmarks (Jansen et al., 2003; Rhodes et al., 2005).

Kernel-based models have demonstrated very competitive computational performance due to their ability to model non-linear systems and high-dimension data. The Support Vector Machine (SVM) has recently been successfully applied to predict protein–protein interactions and protein complex relationships in Yeast and Escherichia coli using heterogeneous data (Ben-Hur and Noble, 2005; Qiu and Noble, 2008; Yellaboina et al., 2007). The Relevance Vector Machine (RVM) approach (Tipping, 2001), another powerful kernel-based model, uses a Bayesian learning framework to produce sparse decision models. RVM is similar to SVM in many respects and has been reported to yield nearly identical performance, but surpasses SVM in several aspects, including automatic prevention of over fitting and generation of much sparser models (Bowd et al., 2005; Tipping, 2001). The RVM has been applied to several biological tasks including the classification and diagnosis of cancers (Krishnapuram et al., 2004; Van Holsbeke et al., 2007) and the identification of non-coding regions in genomes (Down and Hubbard, 2004). Thus, RVM may be a useful approach for integrating multiple heterogeneous data for constructing genetic networks.

Three major problems, however, confront the use of RVM in constructing a human genetic network from diverse genomic data. First, a robust gold-standard negative (GSN) set is needed for training. A noisy gold-standard will impair training and cause prediction bias. Major methods reported in previous protein interaction studies to define GSN (Ben-Hur and Noble, 2006; Jansen and Gerstein, 2004; Jansen et al., 2003; Qi et al., 2006) are not suitable for defining GSN for construction of a functional genetic network, which is not only composed of physical interactions but broader functional gene–gene relationships in pathways. Second, the size of the training data derived from human KEGG pathways is large. As with most of the kernel-based approaches, the computational cost associated with RVM for large-scale problems is a challenge (Tipping and Faul, 2003). Third, most biological datasets contain many missing data values and the number will dramatically increase as more data types are included.

The work reported herein addresses each of the three aforementioned challenges and is organized as follows. A graph-based method to define an accurate GSN is first presented to reduce noise in our negative training set (Section 2.1). Next, Sections 2.2 and 2.3 present the proposed RVM-based approach that combines two ensemble models, AdaBoost and reduced-feature to simultaneously address the other two problems of large-scale learning and massive missing data values. The data features and performance evaluation are presented in Section 2.4. Finally, all the results of experiments for the proposed approach are presented in Section 3.

2 METHODS

2.1 Gold-standard datasets for training

2.1.1 Gold-standard positive

In order to construct a genetic network to reveal the tendency for genes to operate in the same pathways, we derive the gold-standard positive (GSP) set from the KEGG pathway, as has been reported in previous studies (Franke et al., 2006; Lee et al., 2004). Two genes can be considered to constitute a positive pair if they have at least one KEGG pathway membership. Using the version of the KEGG pathway on DEC 2008, 498 989 positive interactions among 4882 genes are generated.

2.1.2 GSN via a graph-based approach

Unlike GSP, identification of a GSN set for training and testing is challenging because of the difficulty in specifying gene pairs that do not function together in the same pathway. Three methods have been reported to generate a GSN. In the first method, two genes are defined as a negative pair if they do not function together in any KEGG pathway (Franke et al., 2006; Lee et al., 2004). This method will generate a large number of negative interactions (in our case, 11 415 704 negative interactions), but most of them represent potentially positive interactions. For instance, if two genes are defined as a negative pair but share the same positive interacting partners (i.e. they share same pathway partners), it is possible that they may function together in some unknown pathway (Fig. 1a). In the second approach, which is often used to predict protein–protein interactions, a random set of protein pairs (after filtering the positive examples) can be defined as the GSN. This method is justified because the fraction of the positive pairs in the total set of protein pairs is small (Ben-Hur and Noble, 2005; Qi et al., 2006). However, this method is not suitable for defining the GSN for predicting a functional genetic network, which is not only composed of protein–protein interactions but also broader functional genetic relationships in pathways. The third approach generates negative examples based on different cellular compartments (Jansen and Gerstein, 2004; Jansen et al., 2003). This strategy is also often applied to predict protein–protein interactions, but is not applicable to construction of a genetic network because a pathway is composed of proteins located in different compartments.

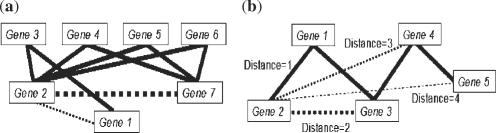
Fig. 1.

Two genes are linked together with solid lines if they function together in the present KEGG pathways (positive examples) while those connected with dotted lines do not function together. (a) illustrates potential positive examples. It would be more likely that genes 7 and 2 function together in some unknown pathways than genes 1 and 2, because the former pair shares more pathway partners. The width of the dotted line reflects the probability that a linkage exists. (b) Illustrates ideal negative examples. It would be less likely for genes 2 and 5 to function together in some unknown pathways than genes 2 and 3 or genes 2 and 4.

To overcome these limitations, we present a graph-based approach to define the GSN. The central concept is to find the most distant functional relationship between any two genes based on the defined GSP. A network is first derived based on the GSP, in which any two genes which share at least one KEGG pathway are linked together. It is then further assumed that two genes are increasingly less likely to function together in the same pathway as the topological distance between them increases in this network (Fig. 1b). Here, Dijkstra's algorithm (Dijkstra, 1959) is used to calculate the shortest topological distance between any gene pair in the network. The topological distance between a gene pair is then used to represent their functional relationship in the KEGG pathways. The N most distant gene pairs in the network (excluding an infinite relationship) can be defined as our robust GSN. For a balanced learning process, N is taken equal to the size of the GSP. Some newly discovered pathways are now isolated (i.e. genes in these pathways are infinite-distant from other genes in the KEGG network), but these could be potentially found to connect to other existing pathways in the future (the result in the Section 3.1 illustrates this point). Therefore, infinite-distant gene pairs are excluded from the GSN.

2.2 RVM and kernels

2.2.1 RVM

Assume that a genetic network is developed based on a set of N training examples, { x_n, t_n}_n=1^N, where x_n ∈ R^d (d is the number of features, Table 1) represents a vector of gene pair scores for the nth training example, and t_n ∈ {0, 1} is a label vector indicating the classes to which the nth example belongs (1 and 0 denote interacting and non-interacting pairs). Correspondingly, X={x_n}_n=1^N and T={t_n}_n=1^N denote the training and label set. A RVM classification model can take the form of a linear combination of basis functions, formed by a kernel function centered at the different training points.

(1)

where W=[w₁, w₂,…, w_N] is a vector consisting of the linear combination weights, and K is a design matrix whose i-th column is formed with the value of the kernel function, k(x_i, x_n), at the nth training point. Moreover, Y={y_n}_n=1^N is the output prediction vector corresponded to the label vector T. Given an input x_i, a gene pair is assigned as interacting (i.e. t_i^*=1) if y_i(x_i)≥0 and as non−interacting (i.e. t_i^*=0) otherwise. Then, RVM uses a sparse Bayesian learning framework in which an a priori parameter structure is based on the automatic relevance determination theory for removing irrelevant data points. Hence, the number of kernel linear combinations in Equation (1) will be reduced to M (M ≪ N) and a sparse model for decision is produced. This advantage of RVM (Bowd et al., 2005; Tipping, 2001) can greatly reduce the prediction time of the proposed ensemble framework in Section 2.3. A more extensive explanation of RVM is provided in the work of Tipping (Tipping, 2001), and its MATLAB implementation is also available from http://www.relevancevector.com.

Table 1.

Data features

Data type	No. of genes	Data source
Literature	26 475	Entrez gene
Functional annotation	14 667	Ashburner et al. (2000)
	16 015
	16 507
Protein domain	15 565	Ng et al. (2003)
Protein–protein interaction and genetic interaction	8787	Entrez Gene
	2166	Vastrik et al. (2007)
	6982	Gary et al. (2003)
	9295	Keshava Prasad et al. (2009)
	6279	Shannon et al. (2003)
Gene context	11 303	Bowers et al. (2004)
Protein phosphorylation	5490	Linding et al. (2008)
Gene expression profile	19 777	Obayashi et al. (2008)
Transcription regulation	937	Ferretti et al. (2007)

2.2.2 Kernel used

The radial basis kernel, denoted K_RB, is used as a pair wise kernel to present the similarity between any gene pair and any other gene pair, given a dataset that has been assigned a measure between any two genes (such as Pearson correlation of gene expression and co-citation score). However, for graph-structure datasets (genetic interaction, protein–protein interactions and protein phosphorylation), we first employ the diffusion kernel (Kondor and Lafferty, 2002), denoted K_D, to capture in-directed gene–gene relationships before applying the radial basis kernel to calculate pair–pair similarities (Qiu and Noble, 2008).

2.2.3 Kernel combinations

Heterogeneous datasets, {D₁, D₂,…, D_n}, are to be integrated and m datasets among them are graph-structure data features, while the remaining n–m are from other heterogeneous data. In this work, we consider four kernel combinations in the RVM-based model, denoted KC1–KC4. In KC1, the graph-structure data features are first pre-computed using the diffusion kernel, and then the pairwise kernel values of each data set are calculated using the radial basis kernel separately before they are added together. The final summed kernel matrix, which is the input to the RVM model, is as follows:

(2)

KC2 concatenates all the data sets together to form a single data matrix after applying the diffusion kernel to the graph structure data. The pairwise kernel values are later directly computed based on the data matrix.

(3)

In KC3, the kernel matrix of each data feature is used to train an individual model, and the resulting values from all the models are averaged to generate a final result. Finally, to evaluate the performance of diffusion kernel in RVM-based model, we also consider a KC4 scenario, in which the diffusion kernel is not applied to the graph-structure data features. The gene pairwise kernel values of all data are directly calculated using the radial basis kernel separately before summing.

(4)

In Section 3.3, the performance of all combination approaches using the RVM-based model is evaluated.

2.3 The RVM-based ensemble framework

Ensemble methods that attempt to build up highly accurate models by combining many diverse base models represent a major development in machine learning in the past decade (Opitz et al., 1999; Polikar, 2006). A diversity of base models is typically achieved by using different training data sets, which allows each base model to be able to generate different discriminant boundaries. The combination of these base models is expected to improve the learning performance and the generalization performance. More recently, numerous ensemble-based approaches have been proposed to address missing value and large-scale problems (Polikar, 2006). We now focus on how the ensemble framework can address the two remaining problems for prediction of human genetic networks.

2.3.1 AadaBoost for large-scale learning

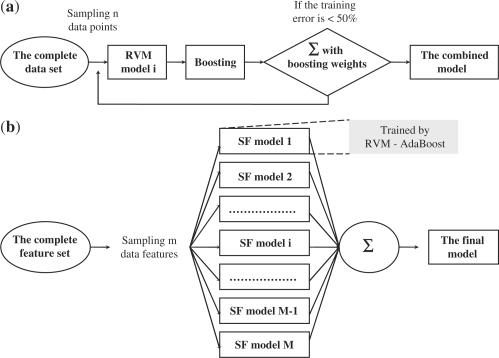
AdaBoost (Freund and Schapire, 1999), a popular ensemble method, is first combined with RVM to address the problem of large-scale learning. The main concept of RVM-AdaBoost (as detailed in the Supplementary Data S3) is to sample many small training sets from the original large training set (Fig. 2a). Each RVM base model, which is trained from each small training set with low computational cost, is much weaker than it would be if it were trained with the whole data set. As a sufficient number of base models are generated, most of the distinct aspects of the complete training set can be captured and represented in the final combined model.

Fig. 2.

(a) RVM-AdaBoost. (b) RVM-based double ensemble model.

2.3.2 Reduced-feature model for missing values

There are two major causes for missing values in our data. First, no individual dataset covers all gene pairs since different types of data contain complementary pathway information (Table 1). Second, most biological datasets are corrupted and noisy, as is the case with gene expression data. Therefore, missing values are common in heterogeneous biological data, and more gene pairs will have missing data as more datasets are integrated. When using RVM to build a prediction system, proper treatment of biological datasets with a large number of missing values is a critical issue for classification learning since missing data values in both training and testing set can affect prediction accuracy. Missing data problems have been well-studied in machine learning. Widely used approaches such as data deletion, which results in information lose, and simple imputation methods, which are problematic for large-scale missing data sets, would not be appropriate for our application. An alternative method, namely the reduced-feature model, is an ensemble based approach that combines many base models corresponding to various patterns of data features. These base models are trained only using a subset of all the data features. This reduced-feature modeling has been shown to be more robust to missing data than other imputation approaches (Saar-Tsechansky and Provost, 2007), and it also reduces computational costs because of its lower-dimensional learning than the complete modeling. Thus, we will adopt reduce-feature modeling for the problem of massive missing values in our application. Additional investigation of missing values problems will be illustrated in the Section 3.4.

2.3.3 The RVM-based double ensemble

In this work, AdaBoost and reduced-feature are combined as outlined below and illustrated in Figure 2:

1. Generate M feature sets by sampling m features M times from the complete set of data features without replacement.

2. Train M base models (SF models in Fig. 2b) with these M feature sets using RVM-AdaBoost, which is the first level ensemble.

3. An ensemble of all base models is then generated through averaging of the outputs from all base models. This is the second level ensemble.

2.4 The data features and performance evaluation

Fourteen datasets, as summarized in Table 1, are integrated in our study. Overall, these data sets can be divided into eight categories. The Supplementary Data S1 describes the source of these data sets and presents preprocessing details. As shown in the Table 1, different data features contain significantly varying degrees of coverage. These biological datasets present different types of pathway information and thus yield massive missing values in our training and prediction phase.

Ten-fold cross-validation testing is used to access performance of models to be presented in Sections 3.2 and 3.3 based on precision–recall curve and the area under ROC curve (AUC). Other measures of prediction performance, including classification error, F-measure and G-mean, are detailed in the Supplementary Data S2. However, the gold-standard set in our work consists of many replicated data points (i.e. many interactions with same data feature scores). This produces dependence between testing and training data in cross-validation. Cross-validation testing is not able to reveal much difference in the generalization performance of different models. Therefore, two curated pathway datasets, Biocarta and NCI-nature pathways are used to serve as independent testing examples. Biocarta and NCI-nature pathway contain 18 574 and 69 123 interactions different from the KEGG pathways. The classification errors of the two independent testing sets are calculated for all cases to evaluate the generalization performance. Finally, average values and standard derivations of all the performance measures are reported.

3 RESULTS

3.1 Performance of the graph-based GSN approach

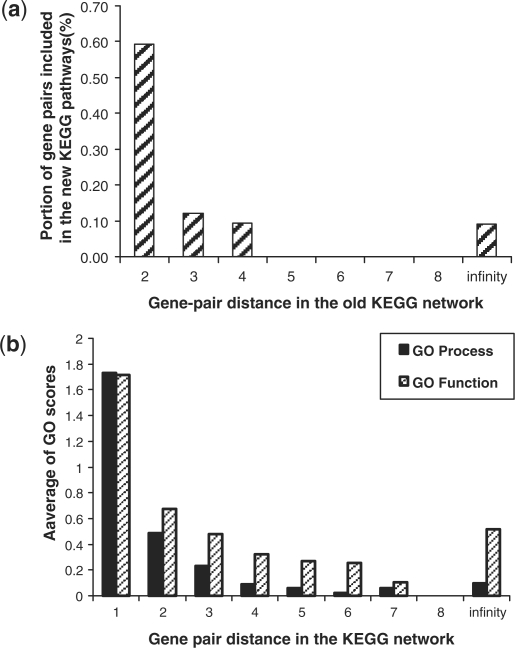
The negative gold-standards generated by existing methods (Franke et al., 2006; Lee et al., 2004) for genetic network prediction contains a significant portion of potential positive interactions. To illustrate this, an old version of the KEGG pathways (downloaded on July, 2007) is compared with the new KEGG pathways (downloaded on Dec, 2008). We first define a GSP and GSN based on the old KEGG pathways; that is, the GSP is composed of gene pairs that share at least one old KEGG pathway, and the GSN is composed of any two genes that do not share any old KEGG pathways but both of them are involved in at least one KEGG pathways. The result is that 19 285 gene pairs included in the GSN are found to appear in some new KEGG pathways.

In order to determine if the graph-based approach presented in the Section 2.1 can define a more robust GSN, a network composed of all interactions in the old KEGG pathway is derived first. The shortest topological distance of those gene pairs without any linkage between them in the network is determined using Dijkstra's algorithm (Dijkstra, 1959). Then, we calculate the portion of gene pairs with specific topologic distances (≤2) that do not function together in the old KEGG pathways, but are found to function together in the new KEGG pathways. The results presented in Figure 3a show that more gene pairs with lower topological distances in the network are included in new KEGG pathways. Genes in isolated pathways (newly discovered pathways) are indicated as having an infinite-distant from other genes in the KEGG network, but these newly discovered pathways may be found to connect to other pathways in the future. Therefore, infinite-distant gene pairs would have a little higher probability to be positive than others with high distance (≥5). This approach was also evaluated using the two independent data sets, the NCI-nature pathways and Biocarta pathways, with similar results to those shown in Figure 3a.

Fig. 3.

(a) Proportion of gene pairs with specific topologic distances in the old KEGG network that function together in the new KEGG pathways. (b) GO scores of gene pairs with specific topologic distances in the old KEGG network.

To evaluate whether any two genes with a more distant KEGG relationship have a lower functional relationship, the Gene Ontology functional information was mapped to each gene pair. The GO functional relationship score of a gene pair is determined by identifying the shared GO process or function term as described in the Supplemental Data S1. A higher score represents a closer functional relationship.Figure 3b confirms that the greater distance between any two genes in this network, the lower the functional relationship between them (they have a lower chance to function together in the same pathway). It should be emphasized that the Gene Ontology was not used to determine the GSN.

3.2 Combining heterogeneous data

The RVM-Adaboost (Fig. 2a) is the first level ensemble model embedded in our framework (Fig. 2b) for training the gold-standard set (GSP and GSN defined in the Section 2.1) with the size of almost 1 million. Based on analysis of synthetic data (Supplementary Tables S1 and S2), RVM-AdaBoost is able to reduce the run-time relative to RVM alone. At a data set size of 1000, the computation time for RVM-AdaBoost is ∼2.5-fold less than that of RVM alone. As the data set size is increased to 3000, the runtime of RVM-AdaBoost is ∼20-fold less than RVM alone. Based on these synthetic data results, therefore, we expect the reduction in computation time of RVM-AdaBoost relative to RVM alone to become greater as N increases. RVM-AdaBoost can approach the result achieved from the complete data set with reduced computation cost both in the training and prediction phase (i.e. fewer vectors will be included in the final model) by choosing a moderate sampling size. We selected a sampling size of 500 and a maximum number of boosting iterations of 20 for the RVM-AdaBoost models as sufficient for genetic network construction in this work (details in the Supplementary Data S4).

To evaluate the performance of RVM-AdaBoost in the construction of a genetic network, it is necessary to first determine which of the kernel combination approaches introduced in the Section 2.2 should be incorporated. Hence, the prediction performance of models with several different kernel combinations has been evaluated. To accommodate missing values in data features in kernel combination methods KC1, KC3 and KC4, the element values of each kernel matrix are replaced with zeros corresponding to row or column with missing values to indicate no similarity measure among them. In KC2, the missing values in each dataset have to be first imputed with the average value of each data feature before concatenating all the data sets to form a single data matrix. The pairwise kernel values are later directly computed based the imputed data matrix before the training process.

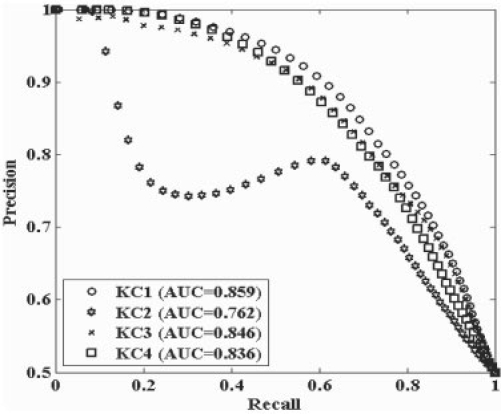
The work of Pavlidis (Pavlidis et al., 2001) investigated the kernel combination approaches denoted here as KC1–KC3 for use with SVM models, while the following presents our evaluation of the methods for use with RVM-based models.Figure 4 presents the performance based on 10-fold cross validation of the three kernel combination methods using precision–recall curves, while Table 2 lists the classification errors for the two independent testing sets for the models. Based on the 10-fold cross-validation testing, the results indicate that the KC1 combination method outperforms the other methods. Pavlidis (Pavlidis et al., 2001) also concluded that the KC1 method (their intermediate combination approach) when incorporated in a SVM model perform better than the other two combination methods in predicting yeast protein function. The KC2 and KC3 methods can not preserve the different semantic associations within data type as well as KC1, and hence produce inferior prediction performance. Moreover, the imputation implemented in KC2 may cause biased results (the effect of imputation will be illustrated in Section 3.3). In contrast, the KC1 method can subsequently sum up the kernel values of each data feature to represent different semantic association, and hence improve the performance progressively. However, we also find that KC3 has better generalization performance based on the classification error of the two independent sets. This latter point is not discussed in the work by Pavlidis (Pavlidis et al., 2001). The KC3 method is a type of reduced-feature ensemble model (the number of sub feature set is 1) that trains a base model using a subset of all the data features. The reduced-feature ensemble model can generate better generalization performance than models trained by whole data features. The reduced-feature models are investigated further in Section 3.3.

Fig. 4.

Precision–recall curves of models with different kernel combinations based on 10-fold cross-validation testing.

Table 2.

Performances of models with different kernel combinations using independent testing sets

Combination	Number of vectors	Biocarta error (%)	NCI_nature error (%)
KC1	121.±39.2	23.6±2.44	24.6±2.83
KC2	981.±153.	47.2±3.47	53.7±2.16
KC3	40.6±5.19	15.2±9.73	16.0±10.8
KC4	92.8±20.35	33.3±2.15	35.4±2.40

Next, to demonstrate the performance of the diffusion kernel in RVM-based model, we also compare results of KC1 to those of KC4, which does not employ a diffusion kernel to the graph-structure data features. The results in Table 2 and Figure 4 taken together show that KC1 outperforms KC4, indicating that the diffusion kernel can capture indirect gene–gene relationships from graph structure-data features to improve the prediction of pathway relationship.

Therefore, the KC1 kernel combination approach incorporated in the RVM-based model will be used in all the results shown below. With this method, the model performance increases progressively as more datasets are integrated, thus allowing the model to include complementary pathway information, such as protein–protein interactions, protein phophorylation and transcription regulation (Supplementary Figure S3).

3.3 Performance of RVM-based double ensemble model with missing values

Several additional approaches for dealing with missing values using RVM-based models are considered here using the kernel combination method KC1 (see Section 2.2). In the first scenario, denoted M1, the element values of kernel matrices are replaced with zeros corresponding to a row or column with missing values to indicate no similarity measure among them (methods denoted KC1 in Section 3.3). This scenario attempts to keep the data structure of complementary pathway information, but does not impute a value on the original missing data feature. In the second scenario (denoted M2), the missing values in each dataset are first imputed with the average value of each data feature. The kernel matrices are then computed based on the imputed data features. In the M1 and M2 model scenarios, RVM-AdaBoost (Fig. 2a) is applied to generate the discriminant result. The third scenario (M3) is the double ensemble model (Fig. 2b) that combines RVM, AdaBoost and the reduced-feature approach. The method of dealing missing values in the base model of M3 is same as the M1. The number of reduced-feature models in the M3 ensemble structure is set at 14, equal to the number of total data features, in order to allow comparison with the M1 model. The number of randomly chosen features in each base model is set to m=log₂(k+1)≈4 as in Random Forest (a three-based ensemble approach) (Breiman, 2001), where k=14 is the total number of our data features. (The results in the Supplementary Data S6 show that this rule is also applicable to the RVM-based model.) To further evaluate the performances of the RVM-based models in all the scenarios, we compare them with the baseline model, Naïve Bayes (denoted as NB in the Table 3), which is also the most popular approach used in prediction of genetic and protein interactions (Franke et al., 2006; Jansen et al., 2003; Rhodes et al., 2005; Troyanskaya et al., 2003). The prior odds of the Naïve Bayes model is set to one, which is determined based on the proportion of total number of positive and negative examples in the benchmarks (Jansen et al., 2003; Rhodes et al., 2005).

Table 3.

Performances of different models with missing values using independent testing sets

Model	Number of vectors	Biocarta error (%)	NCI_nature error (%)
NB	–	41.5±0.08	48.6±0.08
M1	121.±39.2	23.6±2.44	24.6±2.83
M2	104.±19.7	34.7±2.22	38.1±2.53
M3	366.±34.2	14.3±4.01	13.9±4.54

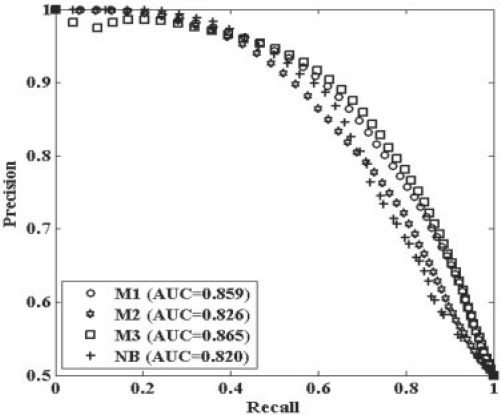
In Figure 5, the performance based on 10-fold cross-validation of all the models is also presented using precision–recall curves. Table 3 lists the average values and standard derivations of the performance measures of independent testing for all three approaches. Performances of the RVM-based models all surpass Naïve Bayes in the 10-fold validation testing. This indicates that RVM-based ensemble model can yield significant learning performance even as the data contain massive missing vales. Among the three scenarios, M2 is inferior to the other scenarios, especially based on its poor independent testing error. M2 differs from M1 and M3 mainly due to its imputation of missing values. Most imputation methods are based on the assumption of missing at random and missing completely at random, however, the assumption is not applicable to genetic network construction. Many missing values are actually caused by data complementariness due to different molecular relationships in pathways. For this reason, imputation may cause bias in the result.

Fig. 5.

Precision–recall curves of models with different ways for dealing with missing values based 10-fold cross-validation testing.

The M1 method shows comparable performance to M3 in 10-fold cross-validation testing, but results in a higher independent testing error. Both of M1 and M3 use the same method for handling the missing values. However, the reduce-feature structure of M3 can include base-models corresponding to training data with different patterns of missing values, and thus generate better performance. In addition, M3 may benefit from its double ensemble structure. The model diversity in M3 not only comes from sampling subsets of data points, but also from sampling subsets of data features. The higher variety of base models in M3 can help yield much lower generalization errors (details are in the Supplementary Data S6).

We also find the number of vectors increases when applying the reduced-feature model (M3). However, the reduced-feature model has an important advantage: it is a lower-dimensional learning problem compared to the complete-feature learning, and thus can reduce computation costs both in the training and testing phases. Although more base models are included in the M3 ensemble structure, the number of vectors is still small compared to the total number of the training data points. The sparseness of RVM plays an important role on the reduction of the number of vectors.

4 CONCLUSION

In this work, a graph-based approach is first presented to construct a more robust GSN than previous methods. Through validations using old and new KEGG pathways as well as the Gene Ontology, it has been shown that a robust GSN can be constructed by choosing the N most distant KEGG pathway relationships. The high values of F-measure and G-Mean (supplementary material S5) in all our results also indicate that our models can yield good classification performance on both positive and negative examples. This suggests that the proposed graph-based GSN is sufficiently robust that the overlap between GSP and GSN is small.

With moderate sampling size, the RVM-based model with only a few vectors is able to significantly reduce both training and prediction time. It will be of interest to compare the performance of RVM-AdaBoost with SVM-AdaBoost (Do and Fekete, 2007; Li et al., 2005) in future applications, especially with respect to prediction time that is dominated by the number of vectors in the final assembled model. This can clarify the advantage of RVM-based ensemble models on sparseness. The KC1 kernel combination approach in Section 2.2 has been shown to be an effective kernel integration approach in RVM-based model, which can retain the semantic association within each dataset and subsequently sum up kernel values of each dataset to improve the performance progressively. Through this method, it is observed that the model performance increases progressively as more datasets are integrated (Supplementary Data S5), thus allowing the model to predict complementary pathway information.

We have also addressed the ability of the RVM-based models to classify the biological dataset with a large number of missing values. We find that the RVM-based model can yield significant performance even with massive missing data values, as shown by comparison with the Naïve Bayes baseline model. Among the three model scenarios, the double ensemble model (M3) can generate a much lower generalization error than the others because it includes base-models corresponding to training data with different patterns of missing values. Our results also indicate that naïve imputation may not be suitable for complementary pathway data since each gene pair is only able to be presented in some types of genomic and proteomic data.

In summary, the graph-based approach presented can generate robust GSN for the training process of genetic network construction. The RVM-based ensemble model also yields significant performance improvement even if it does not achieve the optimal results generated by the RVM model trained from the complete dataset. Finally, based on the results presented, the RVM-based ensemble model is a computationally practical and effective approach that can be used on large-scale and high-dimension problems even with massive missing data values..

Funding: National Institute of Health grant P41-EB001978, US Department of Defense grant W81XWH-07-1-0580, and National Institute of Health's Child Health Research Career Development Award Program K12-CA60104.

Conflict of Interest: none declared.