Abstract
Under physiological conditions of loading, articular cartilage is subjected to both compressive strains, normal to the articular surface, and tensile strains, tangential to the articular surface. Previous studies have shown that articular cartilage exhibits a much higher modulus in tension than in compression, and theoretical analyses have suggested that this tension-compression nonlinearity enhances the magnitude of interstitial fluid pressurization during loading in unconfined compression, above a theoretical threshold of 33% of the average applied stress. The first hypothesis of this experimental study is that the peak fluid load support in unconfined compression is significantly greater than the 33% theoretical limit predicted for porous permeable tissues modeled with equal moduli in tension and compression. The second hypothesis is that the peak fluid load support is higher at the articular surface side of the tissue samples than near the deep zone, because the disparity between the tensile and compressive moduli is greater at the surface zone. Ten human cartilage samples from 6 patellofemoral joints, and ten bovine cartilage specimens from 3 calf patellofemoral joints were tested in unconfined compression. The peak fluid load support was measured at 79%±11% and 69%±15% at the articular surface and deep zone of human cartilage, respectively, and at 94%±4% and 71%±8% at the articular surface and deep zone of bovine calf cartilage, respectively. Statistical analyses confirmed both hypotheses of this study. These experimental results suggest that the tension-compression nonlinearity of cartilage is an essential functional property of the tissue which makes interstitial fluid pressurization the dominant mechanism of load support in articular cartilage.
Introduction
The contribution of interstitial fluid pressurization to the functional response of articular cartilage has long been recognized (Mansour and Mow, 1976; McCutchen, 1962; Mow et al., 1980; Zarek and Edward, 1963). With the development and application of porous media theories for the modeling of cartilage (Frank and Grodzinsky, 1987b; Lai et al., 1991; Lanir, 1987; Mow et al., 1980), it has been shown that fluid pressurization is responsible for increasing the stiffness of cartilage under dynamic loading, which allows it to sustain physiological levels of stress in the range of 2 to 12 MPa. It has also been hypothesized that this interstitial pressurization is the primary mechanism imparting low friction and wear to the tissue (Ateshian, 1994; Forster and Fisher, 1996; McCutchen, 1962; Mow and Lai, 1980; Walker et al., 1968).
Theoretical and computational analyses of the contact response of cartilage under various loading conditions have predicted that more than 90% of the load transmitted across articular layers is supported by the pressurized interstitial fluid, with the remainder contributed by the collagen-proteoglycan solid matrix (Ateshian et al., 1994; Ateshian and Wang, 1995; Macirowski, 1994). Since this fluid pressure is a hydrostatic stress, and since cartilage has been shown to be nearly incompressible at physiological levels of pressures (Bachrach, 1998), it has become evident that the interstitial fluid shields the solid matrix from excessive deformations.
Direct measurements of interstitial fluid pressurization in cartilage have been reported in confined compression (Oloyede and Broom, 1991; Oloyede and Broom, 1993; Soltz and Ateshian, 1998; Soltz and Ateshian, 2000a) and have been shown to agree well with predictions from the linear biphasic theory of Mow et al. (Mow et al., 1980). In this configuration of confined compression, a cylindrical tissue sample is confined within a chamber of the same diameter, with impermeable side wall and bottom surface, and is loaded with a free-draining porous permeable indenter. The interstitial fluid pressure, measured at the bottom impermeable surface, has been observed to reach 100% of the total applied load under dynamic loading or in the initial response to creep loading, before subsiding to zero after several thousand seconds. These experimental findings, in very good agreement with theoretical predictions, result from the confined nature of the loading; however confined compression with a free-draining indenter is not representative of physiological loading conditions because of the large tissue strains induced at the interface with the porous indenter which would not occur in situ at the contact interface of two articular layers.
Unconfined compression, where a tissue sample is loaded with smooth impermeable platens, has been a commonly used alternative testing configuration for articular cartilage and may be considered more physiologic than confined compression because the impermeable loading platens restrict fluid flow in a similar manner to subchondral bone, and because no artificially elevated strain gradients occur along the axial loading direction (though higher strains and fluid fluxes do occur at the radial edge of the sample). A confounding question which initially arose upon the solution of the unconfined compression problem with the linear biphasic theory was the prediction that the interstitial fluid pressurization could support no more than 33% of the applied load (Armstrong, 1984). This finding would suggest that the mechanism of interstitial fluid pressurization, while still present, was not primordial in the functional response of the tissue.
Interestingly however, it was later shown that a much higher fluid load support could be predicted from theory if the modeling equations accounted for the large disparity between the tensile and compressive moduli of cartilage (Cohen et al., 1998; Soltz and Ateshian, 2000b; Soulhat, 1999). The increased fluid pressurization predicted from such models was confirmed experimentally in our recent study, where the interstitial fluid pressure of cartilage samples loaded in unconfined compression was measured at the center of the articular surface side of the cylindrical specimens (Soltz and Ateshian, 2000b). Because of the inhomogeneity of the pressure field along the radial dimension of the specimens however, experimental measurement of the interstitial fluid pressure at the specimen center was insufficient to predict the total contribution of interstitial pressurization to the load support across the entire loaded face of the sample.
In the present study an experimental methodology is introduced which allows measurement of the total fluid load support in unconfined compression. Therefore, the first hypothesis of this study is that the peak fluid load support in unconfined compression is significantly greater than the 33% theoretical limit predicted for porous permeable tissues modeled with equal moduli in tension and compression. The second hypothesis is that the peak fluid load support is higher at the articular surface side of the tissue samples than near the deep zone, because the disparity between the tensile and compressive moduli is greater at the surface zone (Armstrong and Mow, 1982; Kempson et al., 1968; Roth and Mow, 1980; Schinagl et al., 1996).
Materials and Methods
Cylindrical cartilage samples (6 mm diam.) were harvested from two different sources for this study and analyzed as distinct groups. In Group I, eleven cartilage samples were harvested from visually normal or mildly fibrillated regions of the femoral condyles and retropatellar surface of six human cadaver knee joints (4 males, ages 37, 43, 45, 58; 2 females, ages 30, 61; thickness 1.49±0.23 mm). In Group II, eleven cartilage samples were harvested from the femoral surface of three 2–4 month-old healthy bovine calf knee joints (thickness 1.96±0.07 mm) obtained from a local abattoir. Using a sledge microtome (model 1400; Leitz, Rockleigh, NJ), approximately 0.5–1 mm of tissue was removed from the deep zone to produce a surface parallel to the articular side. The harvested samples were then stored at −80°C until ready for use.
The testing apparatus was similar to that used in our earlier study (Soltz and Ateshian, 1998), where a stepper micrometer (model 18500, Oriel Instruments, Stratford, CT, step size 0.7–1.2 µm) provides displacement actuation, and is connected in series with a linear variable differential transformer (LVDT, model HR 100, Schaevitz Sensors, Hamptons, VA) for measuring displacements, and a uniaxial load cell (model GM, Sensotec, Columbus, OH, load limit 44.50±0.09 N) for measuring the total reaction force across the loading platens. Measurements of interstitial fluid pressure were performed using a piezoresistive microchip pressure transducer (NPC1210-100G-3N, Lucas NovaSensor, Fremont, CA; range 0–690 kPa gauge pressure).
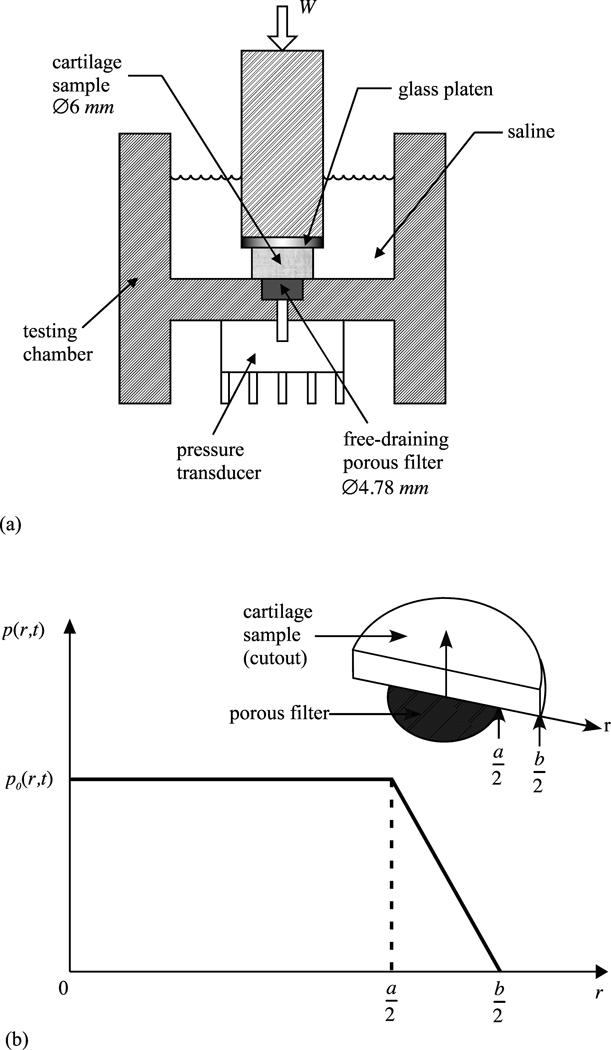
The testing chamber (Figure 1a) represents the primary modification to the previously reported apparatus. To measure the load supported by interstitial fluid pressurization, a 4.78 mm diam.×1.50 mm deep recess was created at the bottom of the testing chamber to hold a free-draining porous filter consisting of 4 stacked layers of stainless steel wire mesh (McMaster-Carr, Type 316 SS woven wire cloth, 60×60 mesh, .0075” wire dia., 30.5% open area, catalog no. 9319T575) such that the top sheet remained flush with the bottom surface of the testing chamber. A 1 mm diameter hole at the center of the recess communicated with the 1 mm diam.×1 mm deep well of the piezoresistive pressure transducer bonded to the chamber. No pathway existed for fluid to flow through the pressure transducer so that the bottom surface of the testing chamber was effectively impermeable to fluid flow, despite the presence of the free-draining porous filter. The 6 mm cartilage specimen was centered on top of the 4.78 mm porous filter such that the pressure measured by the transducer represented the average value over all but a narrow annular region of the specimen surface facing the transducer. To estimate the load supported by interstitial fluid pressurization over the entire specimen surface, a trapezoidal pressure profile was assumed (Figure 1b) whereby the spatially averaged pressure measured over the 4.78 mm diam. footprint decreased linearly to zero across the annular region. The relationship between the measured pressure p0 and the total load supported by the interstitial fluid pressure was thus given by
where a = 4.78 mm and b = 6 mm.
Figure 1.
(a) Testing chamber for unconfined compression. The cylindrical cartilage sample (diameter b = 6 mm) is flush against a recessed free-draining porous filter (diameter a = 4.78 mm) communicating with a piezoresistive microchip pressure transducer. (b) The non-uniform pressure distribution at the interface of the cartilage and filter is averaged into a single time-varying value p0(t) measured by the pressure transducer over the footprint of the porous filter. In the annular region a/≤r≤b/2 the pressure is assumed to drop linearly to zero, producing a trapezoidal pressure profile p(r,t) along r.
Two types of displacement control tests were employed in this study. In each group, ten specimens were loaded by imposing a relatively rapid ramp displacement on the top platen to reach 20% compression in 100 s, immediately followed by unloading at the same rate. This triangular displacement profile test (Experiment 1) was used to determine the peak fluid load support achievable in these specimens during the loading phase. For the remaining eleventh specimen in each group, a more standard stress-relaxation test was performed (Experiment 2), where the top platen was displaced by 10% of the specimen thickness over 500 s, then maintained constant until stress-relaxation equilibrium was reached. This test was used to verify whether the fluid load support does indeed subside to zero at equilibrium, as observed in previous studies. In both groups, each of the eleven samples was tested twice, once with its articular surface facing the pressure transducer, and then with the surface nearer to the deep zone facing the transducer. The ordering of these two tests on each specimen was randomized.
Ideally, pressure transducers are assumed to have infinite impedance, i.e., any amount of pressurization is instantaneously detectable by the transducer. In practice, all pressure transducers have a finite impedance which means that a certain amount of pressurized fluid must enter the transducer before a reliable voltage signal can be detected. (This impedance can be severely degraded by the presence of air bubbles because of the compressibility of air, so that particular care must be taken to avoid trapping air bubbles between the sample and the transducer during setup.) Because of the very low permeability of articular cartilage, it takes a finite amount of time (typically tens of seconds under creep loading, (Soltz and Ateshian, 1998)) for a sufficient amount of interstitial fluid from a loaded tissue sample to flow into the pressure transducer cavity and overcome its intrinsic compliance before a reliable pressure measurement can be made. Such delays in pressurization have been observed in the studies of Oloyede and Broom (Oloyede and Broom, 1991; Oloyede and Broom, 1993) and our own (Soltz and Ateshian, 1998), even when there is no filter separating the cartilage specimen from the pressure transducer. In contrast, the total load W measured across the specimen using the load cell registers a signal within a negligible amount of time upon initiation of loading. This means that the direct calculation of fluid load support, defined by the ratio Wp/W, would be unduly biased toward a low value in the early time response of the experiment because of this fundamental limitation.
To help circumvent this problem, the following tare loading protocol was used in the current study: For Experiment 1, a very small tare load (0.044 N) was first applied across the specimen to ensure proper contact with the loading platens; upon reaching equilibrium, the top loading platen was displaced at a relatively rapid rate (5 µm/s) while simultaneously monitoring W and Wp. When either of the conditions Wp/W =40% or W =13.34 N was first met, Experiment 1 proper was initiated. For Experiment 2, a compressive tare load of 4.45 N was first applied and maintained constant while monitoring Wp/W. The fluid pressure initially rose and then slowly decreased toward zero, and Experiment 2 was initiated when Wp/W decreased to approximately 21±11%. These tare loading protocols, determined by trial and error from the observation of the onset of a linear response of Wp versus W, served to prime the transducer to minimize the unavoidable impedance effect. The evaluation of the fluid load support in Experiments 1 and 2, so as to account for this tare loading, was performed as described in the Results section.
The results of Experiment 1 were used to test both hypotheses of this study. A T-statistic was used to test the hypothesis that Wp/W>33% with α =0.05, independently performed for measurements at the articular surface and near the deep zone, for bovine and human specimens. A one-tailed paired Student t-test with repeated measures was used to test the hypothesis that Wp/W measured at the articular surface is greater than that measured at the surface near the deep zone (using repeated measures), with α=0.05. The results of Experiment 2 were used to verify that the experimental time-response of the fluid load support over the duration of a standard stress-relaxation test qualitatively agree with the behavior predicted from theory, when properly accounting for the biphasic nature of cartilage and the large disparity between its tensile and compressive moduli (Soltz and Ateshian, 2000b).
Results
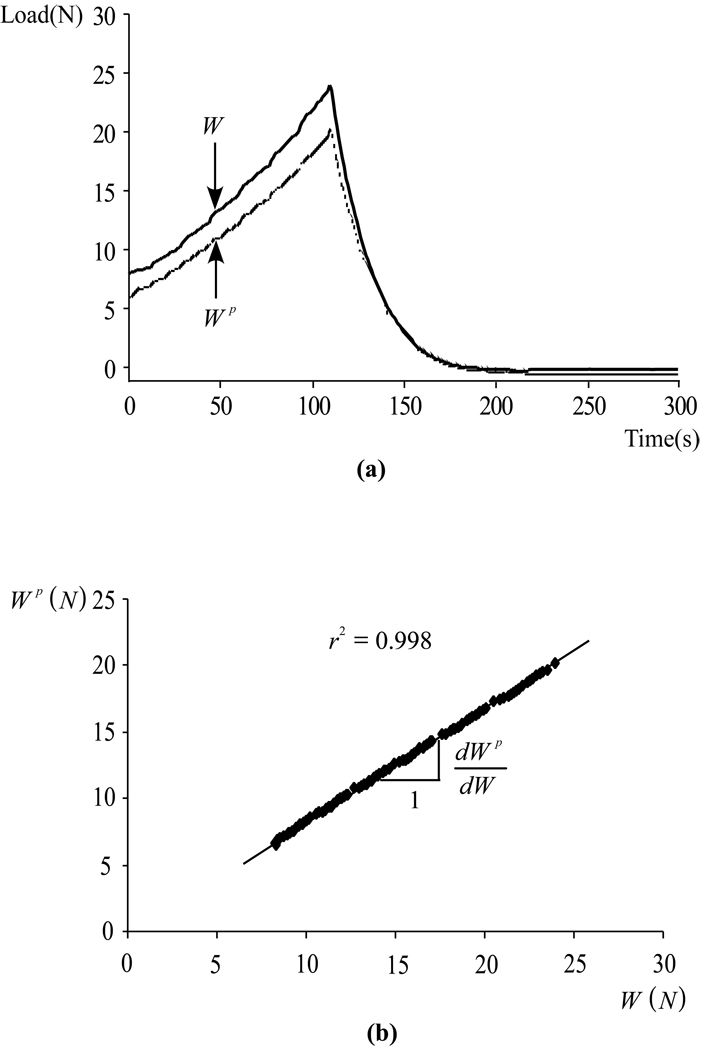
The raw data for the total load, W, and the load supported by interstitial fluid pressurization, Wp, from a typical human specimen in Experiment 1 is presented in Figure 2a as a function of time, starting from the completion of the rapid tare loading. Both W and Wp are observed to rise in magnitude with a concave profile during the compressive phase of loading, and to reduce in magnitude during the unloading phase. The peak magnitude of W averaged 38.2±9.8 N for human specimens and 37.4±3.7 N for bovine specimens, corresponding to peak average stresses of 1.35±0.35 MPa and 1.32±0.13 MPa, respectively. In some specimens, the corresponding peak fluid pressure exceeded the range of the pressure transducer in the latter portion of the loading phase; for these cases, only the data prior to reaching the peak range was used in the subsequent analysis. Because of loading platen lift-off during the unloading phase (i.e., because the platen recedes faster than the tissue can recover), W reduces to zero at the end of the unloading ramp, while Wp becomes slightly negative (subatmospheric pressure) because the tissue is re-imbibing the fluid lost during the loading phase; only the loading phase data was used in the subsequent analysis.
Figure 2.
(a) Typical response for the total load, W(t), and the load supported by interstitial fluid pressure, Wp(t), for a human Specimen in Experiment 1, with the articular surface facing the pressure transducer. Both W(t) and Wp(t) rise during the compressive phase of loading (0 ≤ t ≤ s) conducted at a constant strain rate (20% over 100 s), and reduce to zero during the unloading phase when the platen recedes at the same rate (100 ≤ t ≤ 200 s), because loading platen lift-off typically occurs during unloading. (b) Plot of Wp(t) versus W(t) during the loading phase (0 ≤ t ≤100 s), using the same data set as in (a). Linear regression on the data provides the slope dWp/dW which remains nearly constant during the entire loading phase.
The direct calculation of the ratio Wp/W cannot be used to reliably estimate the fluid load support because of the impedance of the pressure transducer which causes a significant delay in the rise of Wp relative to W during tare loading as mentioned above. However, when plotting the same data as Wp against W during the compressive phase of loading, it can be noted that the observed response is very nearly linear over most of the loading phase, Figure 2b, with only a small initial nonlinear response. The slope of this linear response, dWp/dW, which is a measure of how much Wp increases with increasing W irrespective of their initial values, can thus be used to calculate the fluid load support for this test. Standard linear regression was employed to evaluate this slope and the results are shown in Table 1 for all specimens in both groups, and for measurements at the articular surface and near the deep zone (a total of 40 tests). The correlation coefficient of the linear regression analysis is also provided in each case.
Table 1.
Experiment I. Summary of results, including specimen source, thickness, fluid load support dWp/dW, and coefficient of determination r2 for the linear regression evaluation of dWp/dW. Data are presented for Group I (human specimens from 6 patellofemoral joints) and Group II (bovine specimens from 3 2–4 months calf knee joints). See Results section for description of the assumed equivalence of dWp/dW and Wp/W.
| Group I : Human Specimens |
Thickness (mm) |
Articular Surface | Deep Zone | |||
|---|---|---|---|---|---|---|
| dWp/dW | r2 | dWp/dW | r2 | |||
| Female(30) | F3 | 1.85 | 97% | 0.996 | 59% | 0.984 |
| F5 | 1.71 | 76% | 0.996 | 41% | 0.998 | |
| Male(37) | F9 | 1.41 | 90% | 0.998 | 76% | 0.998 |
| Female(61) | F6 | 1.28 | 82% | 0.996 | 81% | 0.998 |
| F10 | 1.25 | 85% | 0.998 | 84% | 0.998 | |
| Male(43) | F13 | 1.21 | 87% | 0.998 | 77% | 0.992 |
| F16 | 1.25 | 76% | 0.996 | 88% | 0.998 | |
| Male(58) | P4 | 1.65 | 65% | 0.996 | 53% | 0.988 |
| Male(45) | F7 | 1.65 | 69% | 0.998 | 74% | 0.998 |
| F11 | 1.60 | 65% | 0.998 | 61% | 0.998 | |
| Average | 1.49 | 79% | 0.997 | 69% | 0.995 | |
| STD(±) | 0.23 | 11% | 0.001 | 15% | 0.005 | |
| Group II : Bovine Specimens |
Thickness (mm) |
Articular Surface | Deep Zone | ||
|---|---|---|---|---|---|
| Wp/W | r2 | Wp/W | r2 | ||
| F1 | 2.15 | 97% | 0.998 | 72% | 0.996 |
| F2 | 1.94 | 88% | 0.998 | 71% | 0.998 |
| F3 | 1.94 | 99% | 0.992 | 62% | 0.998 |
| F5 | 1.94 | 98% | 0.994 | 69% | 0.998 |
| F6 | 1.94 | 91% | 0.996 | 75% | 0.998 |
| F7 | 1.94 | 95% | 0.994 | 80% | 0.996 |
| F8 | 1.94 | 92% | 0.998 | 85% | 0.998 |
| F9 | 1.94 | 96% | 0.998 | 64% | 0.996 |
| F10 | 1.94 | 96% | 0.996 | 70% | 0.998 |
| F11 | 1.94 | 89% | 0.994 | 60% | 0.998 |
| Average | 1.96 | 94% | 0.996 | 71% | 0.997 |
| STD(±) | 0.07 | 4% | 0.002 | 8% | 0.001 |
For Group I (human specimens), the mean±standard deviation of the peak fluid load support was 79%±11% at the articular surface and 69%±15% near the deep zone, whereas for Group II (bovine specimens) it was 94%±4% at the articular surface and 71%±8% near the deep zone. All four values exhibited a T-statistic greater than the critical t-distribution value of t0.05=1.833 for nine degrees of freedom (ν = n − 1, with n = 10 specimens), indicating that the peak fluid load support was significantly greater than 33% in all cases. In both groups, the fluid load support was significantly greater at the articular surface than near the deep zone, with p<0.05 for Group I and p<0.0001 for Group II.
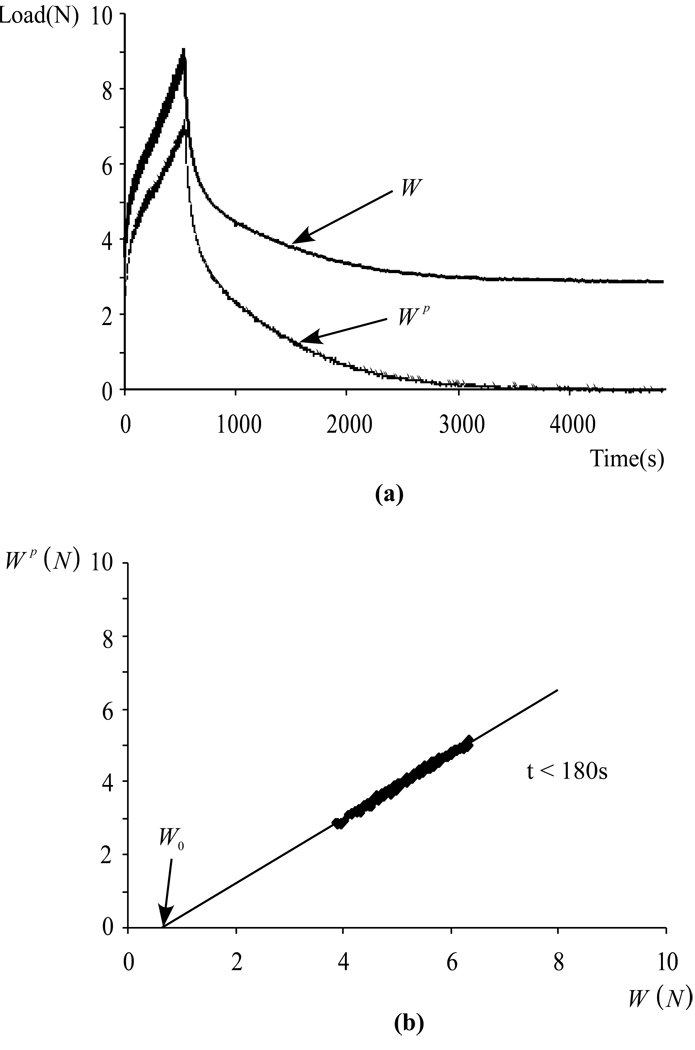
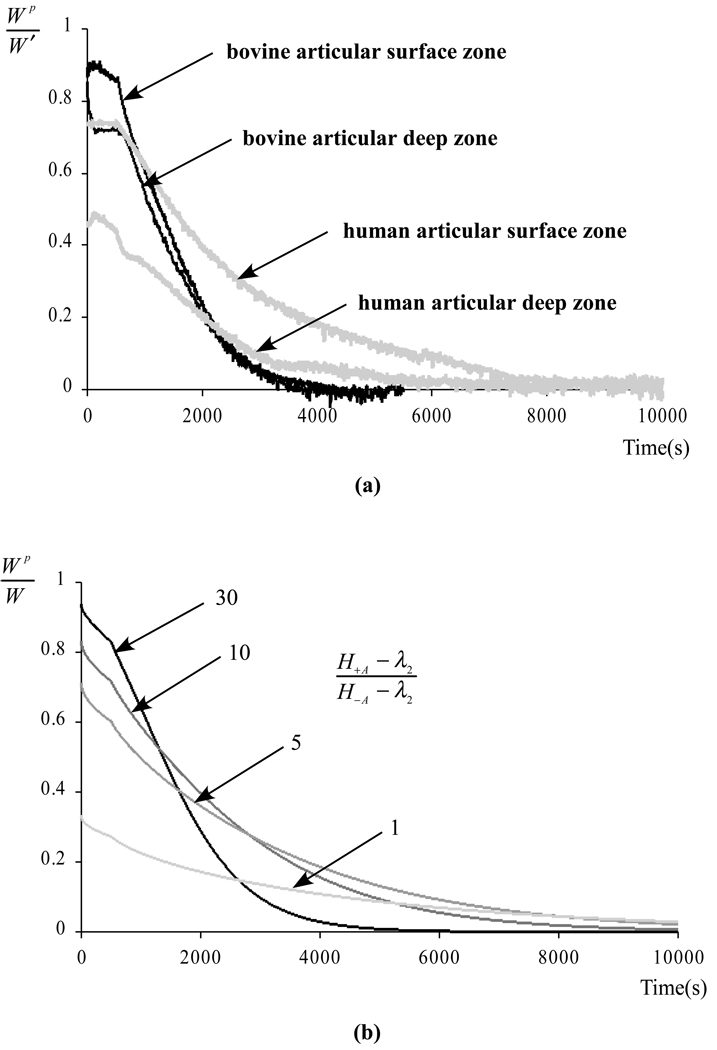
For the tests of Experiment 2, reporting dWp/dW alone is not as informative because this slope varies very significantly over the much longer duration of these tests, whereas it remained virtually constant over the 100 s loading duration of Experiment 1. Nevertheless, a very similar concept can be used to estimate the fluid load support. The raw data for a typical test is displayed in Figure 3a, showing (as designed in the testing protocol) that neither W(t) nor Wp(t) starts at zero at the initiation of the test following tare loading. For the first 180 s of the test, plotting Wp(t) versus Wp(t) as presented in Figure 3b shows a similar behavior as for Experiment 1 (Figure 2b). By extending the best-fit line of the linear region of this curve down to where it intersects the horizontal axis W(t), we get an estimate W0 of the value of the load when the transducer impedance was overcome, and the corresponding time t0 when W0 = W(t0) Then the fluid load support can be calculated from Wp(t)/W'(t), where W'(t) = W(t) − W0(t). This methodology can be viewed as a generalization of that employed for Experiment 1, since dWp/dW = dWp/dW'. Plots of Wp/W' are presented in Figure 4a for all four tests of Experiment 2. For purposes of comparison, the fluid load support Wp/W predicted for unconfined compression from the recently described biphasic-CLE theory (Soltz and Ateshian, 2000b), using the same loading protocol as Experiment 2, is presented in Figure 4b for different ratios of the tensile and compressive moduli.
Figure 3.
(a) Typical response for W(t) and Wp(t), for a bovine Specimen in Experiment 2, with the articular surface facing the pressure transducer. Both W(t) and Wp(t) rise during the compressive phase of loading (0 ≤ t 500 s) conducted at a constant strain rate (10% over 500 s). For t > 500 s the applied deformation is maintained constant and W(t) relaxes to its equilibrium value while Wp(t) reduces to zero. (b) Plot of Wp(t) versus W(t) during the early portion of the loading phase (0 ≤ t ≤ 180 s), using the same data set as in (a). Linear regression on the linear portion of the data provides the slope dWp/dW and the load W0 where the compliance is approximately overcome.
Figure 4.
(a) Fluid load support Wp/W' as a function of time (W'(t) = W(t) − W0) for the four tests of Experiment 2. (b) Theoretical fluid load support Wp/W predicted from the biphasic-CLE theory for the same loading protocol as in (a), using typical material properties H−A =0.64 MPa, λ2=0.48 MPa, k=0.6×10−15 m4/N.s (Soltz and Ateshian, 2000b), and varying the ratio of the tensile to compressive moduli H+A − λ2/H−A − λ2 from 30 down to 1.
Discussion
The objective of this study was to verify from experiments that interstitial fluid pressurization supports most of the load transmitted across articular layers even in the case of unconfined compression, despite earlier theoretical predictions that placed a ceiling of 33% on the fluid load support in this testing configuration. The results presented in Table 1 evidently support this hypothesis, showing that the peak fluid load support in the first 100 s of loading averages 79% for human cartilage and 94% for bovine cartilage, at the articular surface. Furthermore, the hypothesis that the fluid load support is greater at the articular surface than near the deep zone is also verified, for both human and bovine tissue.
Because of the technical challenges faced in measuring interstitial fluid load support experimentally, particularly with regard to transducer impedance which causes delays in the measurement of the fluid pressure, it was necessary to verify that the measurements acquired in this study were consistent with theoretical predictions. The results presented in Figure 4a show that measurements of the interstitial fluid load support in a standard stress-relaxation test are consistent with the theoretical predictions of Figure 4b, with the fluid load support starting at its highest value and decreasing almost linearly during the ramp phase of loading, then decreasing slowly to zero during the relaxation phase. As derived in our earlier studies (Huang et al., 2001; Soltz and Ateshian, 2000b), the peak fluid load support is dependent on the ratio of the tensile and compressive moduli of the tissue according to the formula
where H−A is the aggregate modulus in compression and H+A is the corresponding modulus in tension; λ2 is the “off-diagonal” modulus (λ2<H−A). The decrease in fluid load support with decreasing H+A − λ2/H−A − λ2 can be observed in the theoretical predictions of Figure 4b, including in the limiting case of H+A − λ2/H−A − λ2 = 1 which yields a peak fluid load support of 33% as also confirmed from the above equation. The physical explanation behind this theoretical prediction is premised on the recognition that cartilage is subjected to both compressive strains (in the axial loading direction, normal to the articular surface) and tensile strains (in the radial and circumferential directions, tangential to the articular surface), in unconfined compression as well as in physiological loading conditions. If the solid matrix compressive modulus is much lower than the tensile modulus, the tissue will strongly resist radial and circumferential expansion upon rapid axial loading, and the only way that the tissue can maintain its volume is for the interstitial fluid to pressurize substantially to prevent large compressive strains in the axial direction.
It is therefore reasonable to attribute the reduction in the peak value of Wp/W' in the experimental data of Figure 4a to differences in the ratio H+A − λ2/H−A − λ2. Thus a peak fluid load support of 94% suggests that the ratio of H+A − λ2 to H−A − λ2 is greater than 30 to 1 near the articular surface of bovine cartilage, whereas 79% fluid load support suggests a ratio of 7.5 to 1 near the articular surface of human patellofemoral joint cartilage. Near the deep zone, the corresponding ratios are 4.9:1 in bovine cartilage and 4.4:1 in human cartilage. The depth-dependent differences in the ratio of tensile to compressive moduli are consistent with literature findings that demonstrate a decreasing tensile modulus and an increasing compressive modulus from the superficial to the deep zone of cartilage (Akizuki et al., 1986; Guilak et al., 1995; Kempson et al., 1968; Schinagl et al., 1996). For comparison, our recent experimental study of human patellofemoral joint cartilage (Krishnan et al., 2001), where the tensile and compressive modulis are determined within the same sample using confined and unconfined compression stress-relaxation tests (Soltz and Ateshian, 2000b), reported ratios for H−A − λ2 of 36:1 and 9.4:1 in the superficial and deep zone of patellar cartilage, respectively, and 67:1 and 8.5:1 in the superficial and deep zone of femoral cartilage, respectively. The lower ratios extrapolated from the fluid load support measurements of this study may indicate that the fluid pressurization remains underestimated in our experimental protocol, or that the specimens used in the current study have greater degeneration. Nevertheless, these results confirm that the disparity in tensile and compressive moduli of cartilage is an essential functional property of the tissue, without which the interstitial fluid could not contribute as significantly to load support and dynamic stiffening.
We believe that the greater interstitial fluid load support at the articular surface represents a functional optimization which promotes a low friction coefficient for cartilage. In our recent studies (Ateshian et al., 1998), we have proposed that the time-dependent friction coefficient of cartilage, μeff, is a function of the interstitial fluid load support as described by
where μeff is the friction coefficient at equilibrium, when Wp/W = 0, and φ is the fraction of the porous contact area where solid-to-solid friction occurs. This model embodies the hypothesis that hydrostatic pressurization of the interstitial fluid reduces the friction occurring at the interface of contacting collagen-proteoglycan solid matrices by shifting most of the load support to the fluid phase (Ateshian, 1997; Forster and Fisher, 1996; McCutchen, 1962). To illustrate the significance of this model, if two contacting articular layers each have 80% water content (or equivalently 20% solid content) then the solid-to-solid contact area fraction is at most φ = 0.2 × 0.2 = 0.04 (and possibly lower if synovial fluid is temporarily trapped between the articular surfaces). With a peak fluid load support of 94%, this means that the smallest achievable friction coefficient is ten times smaller than the equilibrium coefficient, e.g., μeff =0.03 versus μeff =0.3, in good agreement with friction experiments. It is likely that μeff can be further reduced by a boundary lubricant such as lubricin, superficial zone protein, or phospholipids (Flannery et al., 1999; Hills, 2000; Jay et al., 2001; Schumacher et al., 1999; Swann et al., 1985), but according to the above model the primary mechanism of lubrication is governed by the interstitial fluid pressurization.
It is also likely that the differences observed in the peak fluid load support between the human and bovine cartilage is related to difference in tissue integrity, with the human adult cartilage more likely to exhibit some signs of degeneration than the immature bovine cartilage. The results of Table 1 indicate that some human cartilage specimens did exhibit fluid load support in excess of 90% though the majority were significantly below that. This observation motivates future studies where the potential correlation between tissue degradation and peak fluid load support is investigated. It also suggests that loss of interstitial fluid pressurization associated with tissue degradation might significantly increase the frictional response of the tissue. Hence, the impaired functional properties of osteoarthritic cartilage may result from the loss of matrix macromolecules which renders the tissue unable to effectively restrain radial and circumferential expansion, and thereby achieve sufficient fluid pressurization.
It is important to emphasize that the pressure measurements reported in this study correspond to the interstitial fluid pressure of cartilage over and above the Donnan osmotic pressure resulting from the negative fixed-charge density of the proteoglycans (Maroudas, 1979). This measured pressure is equivalent to the pressure variable p which appears in the biphasic theories employed in this study (Mow et al., 1980; Soltz and Ateshian, 2000b). The total pressure, inclusive of Donnan osmotic effects, cannot be measured directly in cartilage, even with a hypothetical pressure probe sufficiently small to be inserted into its pores (e.g., a smaller version of the micropipette servonulling pressure transducer of Wiederhielm et al., 1964), because that would require the proteoglycans to flow into the probe's pressure chamber to contribute a Donnan pressure against the transducer's sensing surface. In cartilage, proteoglycan flow is considered very limited, with diffusion times of days or weeks. The fact that the osmotic pressure contribution is not being measured directly should not be construed as a limitation. In principle, the Donnan pressure component of the total pressure in cartilage can be estimated from the measurement of fixed-charge density and tissue dilatation (Maroudas, 1979). The theoretical relationship between the pressure terms inclusive and exclusive of Donnan osmotic effects, and the implications for interstitial fluid load support and frictional response, are described in detail in our recent study (Ateshian et al., 2003).
The potential limitations of the current study are primarily of a technical nature. Despite the fact that the true, time-dependent, spatial distribution of the interstitial pressure could not be determined, its net resultant contribution to the total load could be measured correctly over the 4.78 mm diameter footprint and extrapolated conservatively over the entire 6 mm diameter face of the specimen. Because of transducer impedance the interstitial fluid load support could not be measured instantaneously but could be deduced from finding the slope of the experimental response over 100 s; thus, it is possible that the current study has underestimated the actual peak fluid load support in the tested specimens. The peak stresses applied on the tissue could not exceed the upper limit of the pressure transducer (0.69 MPa), which is on the low end of physiological contact stresses; however theory suggests that interstitial fluid load support might be further enhanced at higher loads because the tensile modulus of cartilage increases nonlinearly with increasing strain at a rate which exceeds the concomitant increase in compressive modulus. On the positive side, the tests of Experiment 1 demonstrated that useful data can be extracted from short tests of cartilage (200 s) when acquiring measurements of both the total load and the load supported by interstitial fluid pressurization.
Table 2.
Experiment II. Summary of results, including specimen source, thickness, peak fluid load support (maximum value of Wp/W'), and coefficient of determination r2 for the linear regression evaluation of W0, where W' = W − W0. Data are presented for one bovine and one human cartilage specimen, for interstitial fluid pressure measurements at the articular surface and the deep zone.
| Species | Thickness (mm) |
Articular Surface | Deep Zone | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Wp/W' | r2 | t0 (s) | W0 (N) | Wp/W' | r2 | t0 (s) | W0 (N) | ||
|
Bovine (3 months) |
1.94 | 90% | 0.990 | 5 | 0.664 | 71% | 0.980 | 81 | 2.737 |
|
Human (Male, 45) |
1.50 | 74% | 0.994 | 0 | 0.985 | 53% | 0.908 | 8 | 1.236 |
Acknowledgments
This study was supported by the National Institute of Arthritis and Musculoskeletal and Skin Diseases (NIH) AR43628, AR46532, AR46568.
Appendix A
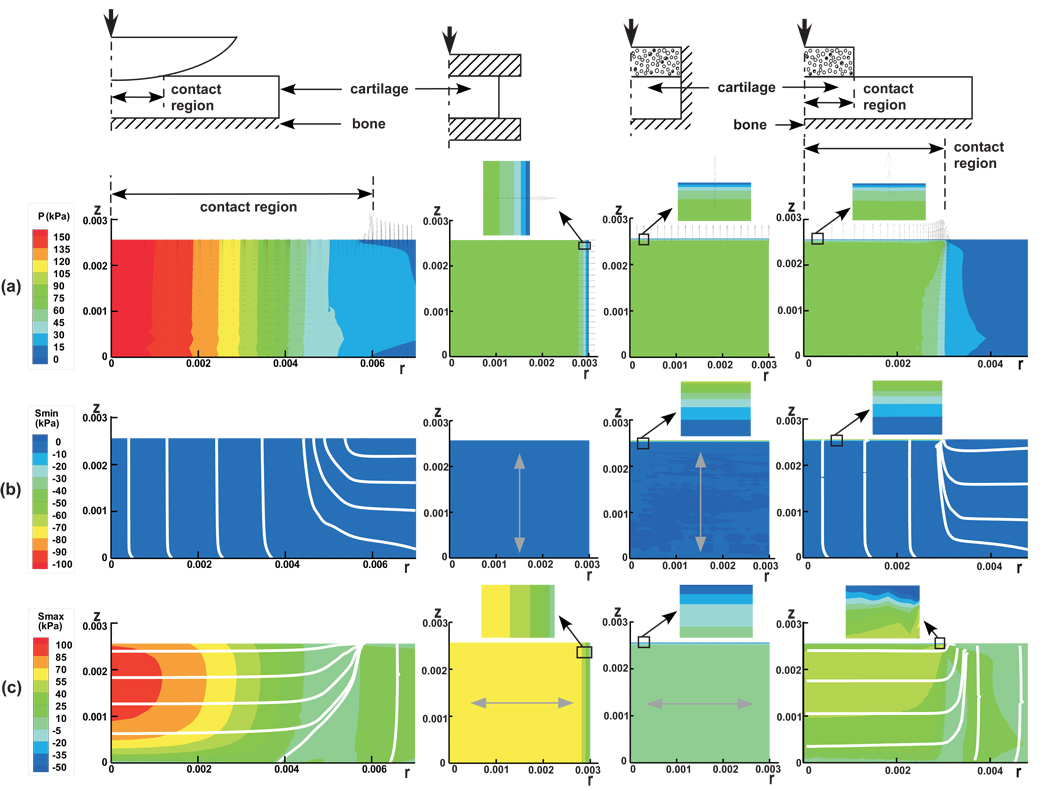
A finite element analysis, employing a custom-written finite element code which accounts for tension-compression nonlinearity in articular cartilage using the biphasic-CLE theory (Soltz and Ateshian, 2000b), was performed on the following configurations: (a) Physiologic contact, represented by a cylindrical cartilage layer (radius=25 mm) bonded to a rigid impermeable bony substrate and loaded with a rigid, impermeable, frictionless spherical indenter (radius=500 mm); (b) unconfined compression of a cylindrical cartilage plug (radius=3 mm) using rigid, impermeable, frictionless platens, representative of the experimental loading configuration presented in the above study; (c) confined compression of a cylindrical cartilage plug (radius=3 mm) in a rigid, impermeable chamber with frictionless side walls, using a porous free-draining rigid flat indenter of the same diameter as the sample; and (d) indentation of a cylindrical cartilage layer (radius=25 mm) bonded to a rigid impermeable bony substrate, using a rigid porous free-draining flat indenter (radius=3 mm). In all cases, the cartilage thickness was 2.56 mm, and the material properties were the same as the average bovine cartilage properties obtained in our earlier experimental study (Soltz and Ateshian, 2000b; see Figure 4). Only the short-time response after one second of load application was examined, as this represents a physiological loading duration (Ateshian et al., 1994). In all cases, the load was applied such as to reproduce an average surface contact traction of 64 kPa, which represents 10% of the compressive aggregate modulus of the tissue, in order not to exceed the small strain modeling assumption of this analysis. For the physiological contact configuration, the contact area radius at 1 s was 6.1 mm and the normal approach was 0.031 mm.
In a biphasic material, the total stress σ in the tissue is given by σ = −pI + σe, where p is the interstitial fluid pressure, I the identity tensor, and σe the effective (or elastic) stress tensor resulting from the strain in the solid matrix. Finite element results presented in Figure 5 include (a) contour plots of p superposed with the relative interstitial fluid flux field given by w = −k grad p (where k is the hydraulic permeability); (b) the principal minimum value of σe, along with its corresponding principal directions; and (c) the principal maximum value of σe, along with its principal directions.
Figure 5.
Testing configuration and results for finite element analyses of contact analysis of a spherical indenter on a cartilage layer (physiologic contact condition), unconfined compression and confined compression of a cylindrical cartilage sample, and indentation of a cartilage layer with a flat porous permeable probe. Results include (a) the interstitial fluid pressurization, with arrows indicating the relative interstitial fluid flux; (b) the minimum principal effective stress, with lines and arrows indicating their principal direction; and (c) the maximum principal effective stress, with lines and arrows indicating their principal directions.
In the model representative of physiological contact, the following observations can be made: (a) p is nearly uniform through the thickness of the articular layer (z − direction) and decreases to zero in the radial r − direction. Under the contact region, the fluid flux is oriented radially; there is no fluid flux occurring across the contact interface, but elevated fluid flux occurs normal to the articular surface at the edge of the contact region. (b) The principal minimum effective stress is entirely compressive throughout the articular layer; its magnitude is much smaller than that of the interstitial fluid pressure (which explains why Wp/W is close to 100%) or the maximum effective stress; its principal direction under the contact region is along the axial direction. (c) The principal maximum effective stress is tensile everywhere and highest under the contact region, but reduces in magnitude at the cartilage-bone interface; its magnitude is significantly greater than that of the minimum effective stress; under the contact region, it is oriented principally in the radial direction.
In comparison to this physiological environment, the unconfined compression problem also shows a uniform interstitial fluid pressure through the thickness of the tissue, while confined compression and indentation exhibit a boundary layer at the articular surface where the interstitial fluid pressure (and fluid load support) is zero. The fluid flux in unconfined compression is oriented radially and exhibits its maximum value at the radial edge of contact with the loading platen, similarly to the physiologic contact configuration, whereas confined compression and indentation exhibit fluid flux axially across the contact interface, where the flux magnitude is greatest.
In unconfined and confined compression, and in indentation, the principal minimum effective stress is compressive everywhere and directed axially, just as in physiologic contact; however, in confined compression and indentation, all of the applied traction at the articular surface is supported by the solid matrix, leading to an elevated compressive effective stress in a narrow boundary layer, which is not found in either unconfined compression or physiological contact.
Finally, unconfined compression and indentation exhibit tensile maximum effective stresses which are oriented radially under the loading platen/indenter, just as physiological contact, whereas confined compression has a compressive maximum effective stress (i.e., there is no tension in the solid matrix of cartilage in confined compression); a boundary layer with high gradients in maximum stresses is also observed at the articular surface in confined compression and indentation, which is not found in unconfined compression or physiological contact.
Based on this comparison of three common testing configurations against physiological contact conditions, it becomes evident that there are significantly greater analogies in the response of cartilage between unconfined compression and physiological contact, than with confined compression or loading with a flat porous indenter.
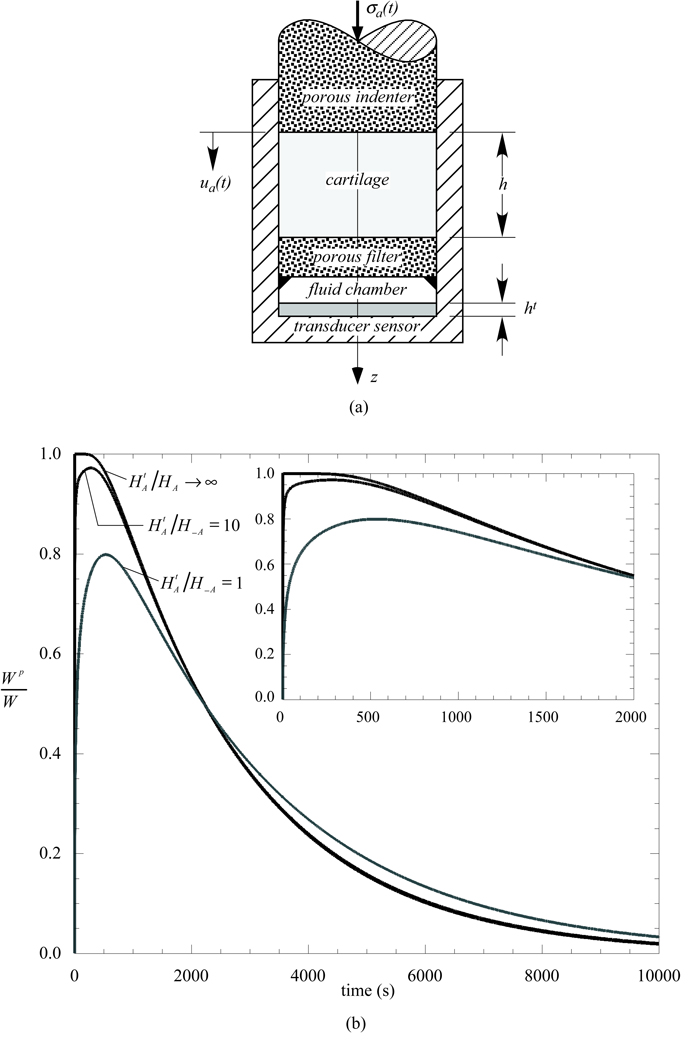
Appendix B
Using the testing configuration of confined compression for simplicity, it can be shown from theory that there exists a delay in pressurization when taking into account the impedance of the pressure transducer. Consider a cylindrical cartilage plug placed within a confining chamber and resting on a rigidly fixed porous free-draining platen, atop a fluid layer representing the pressure transducer chamber, and a compressible elastic substrate representing the transducer's sensing surface (Figure 6a). The cartilage is modeled with the linear biphasic theory (Mow et al., 1980), which also corresponds to the biphasic-CLE theory for this testing configuration where no tensile strains exist. Load is applied via a porous free-draining indenter either in creep or in stress-relaxation. It can be shown that the governing equations for this problem reduce to
| (1) |
| (2) |
| (3) |
| (4) |
| (5) |
where u(z,t) is the axial displacement of the cartilage, ν(t) is the velocity of the interstitial fluid flowing out of the cartilage into the pressure transducer chamber, and ε(t) is the axial normal strain in the transducer's sensing surface. H−A, k and h are the compressive aggregate modulus, permeability and thickness of the cartilage, respectively; and ht are the aggregate modulus and thickness of the transducer sensing surface, respectively. The boundary condition in creep is an applied constant stress σa(t) = σ0H(t) (where H(t) is the Heaviside step function), whereas in stress-relaxation it is a prescribed ramp-and-hold displacement ua(t) = H(t0 − t)V0t + H(t − t0)V0t0 (where V0 is the ramp velocity). The fluid load support Wp/W is evaluated at the interface between the cartilage and the porous filter above the pressure transducer.
Figure 6.
Theoretical analysis of confined compression of a biphasic cylindrical cartilage plug, taking into account pressure transducer impedance. (a) Schematic of loading configuration. (b) Theoretical prediction of interstitial fluid load support for various ratios of the pressure transducer sensor and cartilage compressive aggregate moduli ().
These equations can be solved numerically using standard finite difference methods. Using the representative cartilage biphasic properties given in Figure 4 and assuming h = 1.5 mm, ht = h/10 and σa = −64 kPa, the fluid load support for the creep response is presented in Figure 6b for various choices of . It is evident from this result that the compliance of the pressure transducer has a significant influence on the fluid load support under creep loading conditions. The greater the compliance (i.e., the smaller ), the greater the delay in interstitial fluid pressurization, as more fluid has to flow into the pressure transducer chamber before pressurization can occur. Even the peak value of Wp/W is affected by transducer compliance. With decreasing transducer compliance, the response approaches the instantanenous pressurization predicted in the absence of a transducer (or a transducer with infinite impedance).
In contrast, in stress-relaxation (results not shown), there is no delay in pressurization observed, regardless of the choice of . This can be explained on physical grounds by the fact that the applied ramp displacement on the tissue sample forces fluid to flow into the pressure transducer chamber at a rate which matches the rise in pressurization. These findings are in excellent agreement with our previous experimental results in confined compression (Soltz and Ateshian, 1998) where a delay in pressurization was observed in creep but not in stress-relaxation.
In the current experimental study, the unconfined compression testing configuration is somewhat different from the confined compression analysis presented above, and the fluid flow and pressurization response is two-dimensional and more complex (instead of the one-dimensional analysis of confined compression). Nevertheless, the above analysis proves from theory that delays in pressurization can be caused by transducer impedance, as is believed to occur in the experimental configuration presented in this study.
References
- Akizuki S, Mow VC, Muller F, Pita JC, Howell DS, Manicourt DH. Tensile properties of human knee joint cartilage: I. Influence of ionic conditions, weight bearing, and fibrillation on the tensile modulus. J Orthop Res. 1986;4:379–392. doi: 10.1002/jor.1100040401. [DOI] [PubMed] [Google Scholar]
- Armstrong CG, Mow VC. Variations in the intrinsic mechanical properties of human articular cartilage with age, degeneration, and water content. J Bone Joint Surg Am. 1982;64:88–94. [PubMed] [Google Scholar]
- Armstrong CG, Lai WM, Mow VC. An analysis of the unconfined compression of articular cartilage. J Biomech Eng. 1984;106:165–173. doi: 10.1115/1.3138475. [DOI] [PubMed] [Google Scholar]
- Ateshian GA. A theoretical formulation for boundary friction in articular cartilage. J Biomech Eng. 1997;119:81–86. doi: 10.1115/1.2796069. ASME. [DOI] [PubMed] [Google Scholar]
- Ateshian GA, Lai WM, Zhu WB, Mow VC. An asymptotic solution for the contact of two biphasic cartilage layers. J Biomech. 1994;27:1347–1360. doi: 10.1016/0021-9290(94)90044-2. [DOI] [PubMed] [Google Scholar]
- Ateshian GA, Wang H. A theoretical solution for the frictionless rolling contact of cylindrical biphasic articular cartilage layers. J Biomech. 1995;28:1341–1355. doi: 10.1016/0021-9290(95)00008-6. [DOI] [PubMed] [Google Scholar]
- Ateshian GA, Wang H, Lai WM. The role of interstitial fluid pressurization and surface porosities on the boundary friction of articular cartilage. J Tribology. 1998;120:241–251. ASME. [Google Scholar]
- Ateshian GA, Soltz MA, Mauck RL, Basalo IM, Hung CT, Lai WM. The role of osmotic pressure and tension-compression nonlinearity in the frictional response of articular cartilage. Transport in Porous Media. 2003;50:5–33. [Google Scholar]
- Bachrach NM, Mow VC, Guilak F. Incompressibility of the solid matrix of articular cartilage under high hydrostatic pressures. J Biomech. 1998;31:445–451. doi: 10.1016/s0021-9290(98)00035-9. [DOI] [PubMed] [Google Scholar]
- Cohen B, Lai WM, Mow VC. A transversely isotropic biphasic model for unconfined compression of growth plate and chondroepiphysis. J Biomech Eng. 1998;120:491–496. doi: 10.1115/1.2798019. [DOI] [PubMed] [Google Scholar]
- Flannery CR, Hughes CE, Schumacher BL, Tudor D, Aydelotte MB, Kuettner KE, Caterson B. Articular cartilage superficial zone protein (SZP) is homologous to megakaryocyte stimulating factor precursor and is a multifunctional proteoglycan with potential growth-promoting, cytoprotective, and lubricating properties in cartilage metabolism. Biochemical & Biophysical Research Communications. 1999;254:535–541. doi: 10.1006/bbrc.1998.0104. [DOI] [PubMed] [Google Scholar]
- Forster H, Fisher J. The influence of loading time and lubricant on the friction of articular cartilage. Proc Inst Mech Eng [H] 1996;210:109–119. doi: 10.1243/PIME_PROC_1996_210_399_02. [DOI] [PubMed] [Google Scholar]
- Frank EH, Grodzinsky AJ. Cartilage electromechanics--II. A continuum model of cartilage electrokinetics and correlation with experiments. J Biomech. 1987b;20:629–639. doi: 10.1016/0021-9290(87)90283-1. [DOI] [PubMed] [Google Scholar]
- Guilak F, Ratcliffe A, Mow VC. Chondrocyte deformation and local tissue strain in articular cartilage: a confocal microscopy study. J Orthop Res. 1995;13:410–412. doi: 10.1002/jor.1100130315. [DOI] [PubMed] [Google Scholar]
- Hills BA. Boundary lubrication in vivo. Proceedings of the Institution of Mechanical Engineers Part H - J Eng Med. 2000;214(1):83–94. doi: 10.1243/0954411001535264. [DOI] [PubMed] [Google Scholar]
- Huang CY, Mow VC, Ateshian GA. The role of flow-independent viscoelasticity in the biphasic tensile and compressive responses of articular cartilage. J Biomech Eng. 2001;123:410–417. doi: 10.1115/1.1392316. [DOI] [PubMed] [Google Scholar]
- Jay GD, Tantravahi U, Britt DE, Barrach HJ, Cha CJ. Homology of lubricin and superficial zone protein (SZP): products of megakaryocyte stimulating factor (MSF) gene expression by human synovial fibroblasts and articular chondrocytes localized to chromosome 1q25. J Orthop Res. 2001;19:677–687. doi: 10.1016/S0736-0266(00)00040-1. [DOI] [PubMed] [Google Scholar]
- Kempson GE, Freeman MA, Swanson SA. Tensile properties of articular cartilage. Nature. 1968;220:1127–1128. doi: 10.1038/2201127b0. [DOI] [PubMed] [Google Scholar]
- Krishnan R, Park S, Soltz MA, Pawluk RJ, Ateshian GA. Depth-dependent tensile and compressive properties of human patellofemoral joint cartilage; 2001 Summer Bioengineering Conference; 2001. pp. 847–848. ASME, BED. [Google Scholar]
- Lai WM, Hou JS, Mow VC. A triphasic theory for the swelling and deformation behaviors of articular cartilage. J Biomech Eng. 1991;113:245–258. doi: 10.1115/1.2894880. [DOI] [PubMed] [Google Scholar]
- Lanir Y. Biorheology and fluid flux in swelling tissues. II. Analysis of unconfined compressive response of transversely isotropic cartilage disc. Biorheology. 1987;24:189–205. doi: 10.3233/bir-1987-24211. [DOI] [PubMed] [Google Scholar]
- Macirowski T, Tepic S, Mann RW. Cartilage stresses in the human hip joint. J Biomech Eng. 1994;116:35720. doi: 10.1115/1.2895693. [DOI] [PubMed] [Google Scholar]
- Mansour JM, Mow VC. The permeability of articular cartilage under compressive strain and at high pressures. J Bone Joint Surg Am. 1976;58:509–516. [PubMed] [Google Scholar]
- Maroudas A. Physicochemical properties of articular cartilage. In: Freeman MAR, editor. Adult Articular Cartilage. 2nd ed. Tunbridge Wells, England: Pitman Medical; 1979. pp. 215–290. [Google Scholar]
- McCutchen CW. The frictional properties of animal joints. Wear. 1962;5:1–17. [Google Scholar]
- Mow VC, Lai WM. Recent developments in synovial joint biomechanics. SIAM Review. 1980;22:275–317. [Google Scholar]
- Mow VC, Kuei SC, Lai WM, Armstrong CG. Biphasic creep and stress relaxation of articular cartilage in compression: Theory and experiments. J Biomech Eng. 1980;102:73. doi: 10.1115/1.3138202. [DOI] [PubMed] [Google Scholar]
- Oloyede A, Broom ND. Is classical consolidation theory applicable to articular cartilage deformation. Clin Biomech. 1991;6:206–212. doi: 10.1016/0268-0033(91)90048-U. [DOI] [PubMed] [Google Scholar]
- Oloyede A, Broom N. Stress-sharing between the fluid and solid components of articular cartilage under varying rates of compression. Connect Tissue Res. 1993;30:127–141. [PubMed] [Google Scholar]
- Roth V, Mow VC. The intrinsic tensile behavior of the matrix of bovine articular cartilage and its variation with age. J Bone Joint Surg Am. 1980;62:1102–1117. [PubMed] [Google Scholar]
- Schinagl RM, Ting MK, Price JH, Sah RL. Video microscopy to quantitate the inhomogeneous equilibrium strain within articular cartilage during confined compression. Ann Biomed Eng. 1996;24:500–512. doi: 10.1007/BF02648112. [DOI] [PubMed] [Google Scholar]
- Schumacher BL, Hughes CE, Kuettner KE, Caterson B, Aydelotte MB. Immunodetection and partial cDNA sequence of the proteoglycan, superficial zone protein, synthesized by cells lining synovial joints. J Orthop Res. 1999;17:110–120. doi: 10.1002/jor.1100170117. [DOI] [PubMed] [Google Scholar]
- Soltz MA, Ateshian GA. Experimental verification and theoretical prediction of cartilage interstitial fluid pressurization at an impermeable contact interface in confined compression. J Biomech. 1998;31:927–934. doi: 10.1016/s0021-9290(98)00105-5. [DOI] [PubMed] [Google Scholar]
- Soltz MA, Ateshian GA. Interstitial fluid pressurization during confined compression cyclical loading of articular cartilage. Ann Biomed Eng. 2000a;28:150–159. doi: 10.1114/1.239. [DOI] [PubMed] [Google Scholar]
- Soltz MA, Ateshian GA. A conewise linear elasticity mixture model for the analysis of tension-compression nonlinearity in articular cartilage. J Biomech Eng. 2000b;122:576–586. doi: 10.1115/1.1324669. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Soulhat J, Buschmann MD, Shirazi-Adl A. A fibril-network reinforced model of cartilage in unconfined compression. J Biomech Eng. 1999;121:340–347. doi: 10.1115/1.2798330. [DOI] [PubMed] [Google Scholar]
- Swann DA, Silver FH, Slayter HS, Stafford W, Shore E. The molecular structure and lubricating activity of lubricin isolated from bovine and human synovial fluids. Biochem J. 1985;225:195–201. doi: 10.1042/bj2250195. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Walker PS, Dowson D, Longfield MD, Wright V. Boosted lubrication in synovial joints by fluid entrapment and enrichment. Ann Rheum Dis. 1968;27:512–520. doi: 10.1136/ard.27.6.512. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wierderhelm CA, Woodbury JW, Kirk S, Rushmer RF. Pulsatile pressures in the microcirculation of frog's mesentary. Am J Physiol. 1964;207:173–176. doi: 10.1152/ajplegacy.1964.207.1.173. [DOI] [PubMed] [Google Scholar]
- Zarek JM, Edward J. The stress-structure relationship in articular cartilage. Med Electron Biol Eng. 1963;1:497–507. [PubMed] [Google Scholar]