AQUASOL: An efficient solver for the dipolar Poisson–Boltzmann–Langevin equation

Abstract

The Poisson–Boltzmann (PB) formalism is among the most popular approaches to modeling the solvation of molecules. It assumes a continuum model for water, leading to a dielectric permittivity that only depends on position in space. In contrast, the dipolar Poisson–Boltzmann–Langevin (DPBL) formalism represents the solvent as a collection of orientable dipoles with nonuniform concentration; this leads to a nonlinear permittivity function that depends both on the position and on the local electric field at that position. The differences in the assumptions underlying these two models lead to significant differences in the equations they generate. The PB equation is a second order, elliptic, nonlinear partial differential equation (PDE). Its response coefficients correspond to the dielectric permittivity and are therefore constant within each subdomain of the system considered (i.e., inside and outside of the molecules considered). While the DPBL equation is also a second order, elliptic, nonlinear PDE, its response coefficients are nonlinear functions of the electrostatic potential. Many solvers have been developed for the PB equation; to our knowledge, none of these can be directly applied to the DPBL equation. The methods they use may adapt to the difference; their implementations however are PBE specific. We adapted the PBE solver originally developed by Holst and Saied [J. Comput. Chem. 16, 337 (1995)] to the problem of solving the DPBL equation. This solver uses a truncated Newton method with a multigrid preconditioner. Numerical evidences suggest that it converges for the DPBL equation and that the convergence is superlinear. It is found however to be slow and greedy in memory requirement for problems commonly encountered in computational biology and computational chemistry. To circumvent these problems, we propose two variants, a quasi-Newton solver based on a simplified, inexact Jacobian and an iterative self-consistent solver that is based directly on the PBE solver. While both methods are not guaranteed to converge, numerical evidences suggest that they do and that their convergence is also superlinear. Both variants are significantly faster than the solver based on the exact Jacobian, with a much smaller memory footprint. All three methods have been implemented in a new code named AQUASOL, which is freely available.

INTRODUCTION

Electrostatic interactions play a major role in the stabilization of biomolecules; as such, they remain a major focus of theoretical and computational studies in biophysics. Theoretical modeling of electrostatics interactions is in principle simple. The interaction between two isolated charges in a medium with uniform dielectric property can be described by Coulomb’s law. When more than two charges interact, the total electrostatic energy of the system is derived as the sum of all pairwise Coulomb interactions (superposition principle). Applications of these simple principles imply that the positions of all charges be known. While this seems to be a simple requirement, it is unfortunately difficult to meet when modeling solvated large molecular systems. This is mostly due to the inherent difficulties in accounting for the mobile solvent molecules and ions that surround the solutes. Explicit representation of the solvent provides an accurate treatment of electrostatics, but it increases the size of the system under study by orders of magnitude.¹ In addition, interactions involving solvent need to be averaged over relatively long time intervals before results become meaningful. As a response to these problems, there has been a continuous effort to develop simplified models that are computationally tractable and that remain physically accurate. Most of these models include the solvent implicitly, reducing the solute-solvent interactions to their mean field characteristics, which are expressed as functions of the solute degrees of freedom alone. They treat the solvent as a dielectric continuum and are therefore referred to as continuum dielectric models. The Poisson–Boltzmann theory provides a framework for calculating the electrostatics solvation free energy of a solute in such a dielectric continuum; many numerical solvers have been developed for solving the corresponding elliptic, second order partial differential equation (PDE) (the PB equation). The PB equation is not however the panacea to all electrostatics problems; it is just a mean field approximation, with known limitations. In addition, the PB solvers are still too slow to be included in routine biomolecular simulations. Many improvements have been proposed to the PB equation, either on the theoretical side or on the scientific computing side. These two approaches however often seem exclusive of each other; faster solvers often rely on simplification of the equations, while new theoretical models result in more complicated equations that cannot be solved with the current solvers. This paper addresses specifically this false segregation issue between correctness and speed and ease of use; we show that it is possible to derive a robust and fast solver for even the most complicated modified Poisson–Boltzmann equations developed so far. We first briefly review the current computational and theoretical developments around the PB model.

Exact, closed form solutions of the Poisson–Boltzmann equation exist only for simple geometries of the solute, i.e., a sphere,² a plane (the Gouy–Chapman solution)^{3, 4} or a cylinder.⁵ In both cases however, the corresponding equations are cumbersome as they involve slow converging infinite series. Furthermore, these solutions cannot be extended to more complicated shapes such as those adopted by large macromolecules. Recently, Onufriev and co-workers⁶ developed an approximate analytical solution to the linearized PB equation for such molecule, using a regularized expression for the solution of PB on a sphere, and introducing the concept of electric shape of a molecule, which they identify to be an ellipsoid. Such an approach however loses all the fine details of the molecule of interest. While this might not be important if the goal is to get a single number for the total electrostatic energy of the molecule, it is definitely an issue if one is interested in molecular interactions. For solutes of arbitrary shape, the PB equation can be solved numerically and efficiently using finite difference methods, as pioneered by Warwicker and Watson⁷ and further developed by Honig and co-workers.^{8, 9, 10, 11} Several programs that solve either the linearized version of PBE, or directly the nonlinear PBE, with a variety of scientific computing techniques are now available (see Refs. ^{12, 13, 14} for recent reviews), among which the multigrid methods seem to be the fastest ones^{15, 16, 17} (with the exception of some specialized solvers).^{18, 19} It is noteworthy that most of these programs have been tailored to the PB equation and cannot be used to solve other nonlinear second order PDEs. The successes of the applications of these techniques in biology^{14, 20} boosted the interest for Poisson–Boltzmann in biology in general, including its potential use in molecular simulations. Some approximations however are needed to meet the computing time requirements of the latter. The boundary element methods for example are viable alternatives to finite difference methods that can be implemented efficiently into molecular dynamics packages.²¹ These methods rely on the linearization of the Debye–Hückel term that accounts for counterions around the solute; it is known however that this approximation is not valid for highly charged systems.²² Boschitsch and Fenley²³ proposed a correction to the BME methods to account for the nonlinearity in the PB equation. Clearly, we need a more general framework for solving PB equations, especially in light of the recent theoretical modifications.

Despite its success, PBE is only a mean-field approximation to the multibody problem of solvent-solute electrostatics interactions. It is based on several approximations that proved to be limitations in some cases. For example, PBE does not include effects due to ion size or ion-ion correlations in its treatment (for reviews, see Grochowski and Trylska).²⁴ Solutions have been proposed to account for at least ion size using either a single size²⁵ or two different sizes,²⁶ yielding a size-modified Poisson–Boltzmann (SMPB) equation. In addition, the PB method contains a very rough approximation that consists in using a constant and somewhat arbitrary value for the dielectric constant of the protein (usually set at 2–4), which abruptly jumps to 80 at the interface between the protein and the solvent. This approximation overemphasized the definition of this interface, usually set to the molecular surface of the solute, leading to dependency of the numerical solution of the PBE to the positioning of the solute in the grid used by the solver. Several solutions have been proposed to alleviate this problem. Roux and co-workers introduced an intermediate boundary dielectric region in which the dielectric permittivity grows smoothly from its value in the solute to its value in bulk water.²⁷ Similarly, the program ZAP proposed by Nicholls and co-workers uses a Gaussian representation of the atoms of the solutes and defines a smooth dielectric permittivity based on the molecular function that accounts for all the individual Gaussians representing the atoms.²⁸ While these approaches reduce the importance of the solute interface, they introduce a (smooth) dielectric response that only depends on the geometry of the molecule. Because of strong polarization effects in the vicinity of charges, it is expected however that these simple geometric models are bound to be erroneous close to the interface. We recently developed an extension to the PB equation in which the solvent is described as an assembly of interacting dipoles on a lattice gas to account for the nonuniform dielectric property of the solvent.^{29, 30, 31} Here we describe how we solve the corresponding equations, dubbed dipolar Poisson–Boltzmann–Langevin (DPBL) equations.

This paper is organized as follows. First, we provide an overview of the PB equation and two of its recent modifications, the SMPB and DPBL equations. The following section describes three variants of the truncated Newton solver originally developed by Holst³² and Holst and Saied¹⁶ for the PB equation and their applications to the DPBL equation. The first variant is a direct adaptation of the truncated Newton solver that uses the correct Jacobian of the discretized equations. The second variant uses a truncated, quasi-Newton solver based on an approximate Jacobian. The third variant solves the DPBL self-consistently, using an iterative scheme where each iteration solves a PB-like equation. The following section describes our implementation of these solvers in our software package, AQUASOL. AQUASOL is heavily based on the package MG developed by Michael Holst and freely available at http://www.fetk.org. Note that MG is the scientific computing core of APBS.³³ The next section provides examples of the usefulness of DPBL for understanding protein and nucleic acid solvation, as well as numerical examples of the convergence of our three Newton-based solvers of the DPBL equation. We conclude the paper by noting that the self-consistent Newton solver for the DPBL equation is the faster of the three methods we describe, has a small memory footprint, and is the easiest to implement and can readily be adapted in any existing PBE solvers; it is the method of choice in AQUASOL.

CONTINUUM ELECTROSTATICS: MODIFIED POISSON EQUATIONS

We are interested in computing the electrostatics contribution W_el to the solvation free energy of a set of solutes in a solvent, using a model in which this solvent is considered implicitly. The solutes are described by a constant charge density ρ_f and a solvent accessibility function γ(r) that is zero for points inside their envelopes and one otherwise. The envelope or “interface” for a solute can be taken as its molecular surface, accessible surface or skin surface (for review, see Ref. 34). In this section, we review the Poisson–Boltzmann approach for computing W_el as well as a few its recent extensions.

The Poisson–Boltzmann model

The fundamental equation of electrostatics is given by Gauss’s law:

$$\mathbf{\nabla }\cdot \mathbf{D}\left(\mathbf{r}\right)=4\pi \rho \left(\mathbf{r}\right),$$ (1)

which relates spatial variation of the displacement field D with position r to the charge density distribution ρ. In general, the displacement field is defined as

$$\mathbf{D}={ϵ}_0\mathbf{E}+\mathbf{P},$$ (2)

where E is the electric field, ϵ₀ is the vacuum permittivity, and P is the polarization density of the material considered.

In a region of material with uniform susceptibility, χ, the polarization density P is given by P=ϵ₀χE. Taking into account the boundaries of the solutes and setting the electric field as the gradient of and electrostatic potential (E(r)=−∇ϕ(r)), Eq. 1 becomes

$$\mathbf{\nabla }\cdot \left(\left({ϵ}_0+\gamma \left(\mathbf{r}\right){ϵ}_0\chi \right)\mathbf{\nabla }\varphi \left(\mathbf{r}\right)\right)=-4\pi \rho \left(\mathbf{r}\right).$$ (3)

The charge density is the sum of all charges q_i at positions r_i of the solutes and of the ions in the solvent,

$$\rho \left(\mathbf{r}\right)={\rho }_s\left(\mathbf{r}\right)+{\rho }_{\text{ion}}\left(\mathbf{r}\right)=e_c\sum _{i=1}^M{q}_i\delta \left(\mathbf{r}-{\mathbf{r}}_{\mathbf{i}}\right)+{\gamma }_{\text{ion}}\left(\mathbf{r}\right)e_c\sum _{i=1}^m{c}_i{z}_i{e}^{-\beta z_i{e}_c\varphi \left(\mathbf{r}\right)},$$ (4)

where e_c is the charge of the electron, c_i and z_i are the bulk concentration and valence of ion specie i, respectively, and β=1∕k_BT, where k_B is the Boltzmann constant, and T the temperature. γ_ion(r) is an indicator function for the presence of absence of ions, equal to 1 if ions can be present at position r, and 0 otherwise [usually γ_ion(r) is set equal to γ(r) though sometimes an ion-excluded zone is defined in the neighborhood of the solvent, the so-called Stern zone]. Note that in this formulation, ions are not represented explicitly. Instead, the ions are considered to be in thermal equilibrium with each other and relatively free to move. Thus they obey Boltzmann statistics and their number density follows a Boltzmann distribution. Replacing Eq. 4 into Eq. 3 we obtain the Poisson–Boltzmann equation in its standard form:

$$\mathbf{\nabla }\cdot \left(\left({ϵ}_0+\gamma \left(\mathbf{r}\right){ϵ}_0\chi \right)\mathbf{\nabla }\varphi \left(\mathbf{r}\right)\right)+{\gamma }_{\text{ion}}\left(\mathbf{r}\right)4\pi e_c\sum _{i=1}^m{c}_i{z}_i{e}^{-\beta z_i{e}_c\varphi \left(\mathbf{r}\right)}=-4\pi e_c\sum _{i=1}^M{q}_i\delta \left(\mathbf{r}-{\mathbf{r}}_{\mathbf{i}}\right).$$ (5)

Size modified Poisson–Boltzmann equation

The Poisson–Boltzmann equation has two limitations with respect to how it treats ion atmosphere: it does not consider ion size explicitly, nor does it account for ion-ion correlations. Traditional Poisson–Boltzmann solvers define an ion-excluded layer around the solute, the so-called Stern layer, as a first-order approximation of the effects of ion size on ion-protein interactions. The Stern layer however cannot capture the effects of mixture of mobile ions of different sizes, nor does it take into account interactions between the ions. Differential ion size however does play a role in electrostatics interactions; this was recently shown for DNA in solutions containing competing cations.³⁵ Coalson and co-workers^{36, 37, 38} as well as Orland and co-workers²⁵ developed an attractive solution to the problem of the influence of ion size using a lattice field theory. This solution was recently generalized by Chu et al.²⁶ to deal with ions with two different sizes; it is referred to as the SMPB theory which we describe below. Note that Chu et al.²⁶ have shown that the SMPB theory accurately describes the effect of size on ion binding on DNA for monovalent ions but not for divalent ions. The relative failure for divalent ions is most likely related to the fact that SMPB does not account for ion-ion correlation (except through their steric interactions); there is still a need for further theoretical developments to treat ions correctly within the PB formalism.

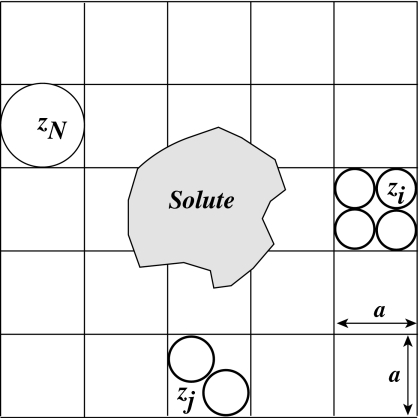
In the SMPB model, the hard core repulsion between solvated ions is approximated with an excluded term in the free energy density of a lattice gas model of the ionic solution. The domain around the charged biomolecule is treated as a lattice (see Fig. 1). This three dimensional lattice contains N uniformly sized cuboids, of size a³, with a being the lattice spacing. Let us suppose that the solution contains N_ion species of ions, with ion i having a valence z_i and a bulk concentration c_i. Note that electroneutrality imposes that ${\sum }_{i=1}^{\text{Nion}}{z}_i{c}_i=0$. We assume that ion specie one corresponds to the largest ion, i.e., its volume is a³, where a is the lattice spacing. The volume of ion i is set to a³∕k_i, where k_i is a dimensionless parameter, for all i in 2,…,N_ion. The lattice site at position r contains at most one ion or type 1 and at most k_i ions of type i. Enumerating all possible configurations of occupancy of this site, for integral values k_i, the grand canonical partition function is

$$\mathcal{Z}\left(\mathbf{r}\right)={\lambda }_1{e}^{-\beta z_1{e}_c\varphi \left(\mathbf{r}\right)}+\sum _{i=2}^{N_{\text{ion}}}\left(\sum _{j=0}^{k_i}\left(\begin{array}{c}{k}_i\\ j\end{array}\right){\left({\lambda }_i{e}^{-\beta z_i{e}_c\varphi \left(\mathbf{r}\right)}\right)}^j\right)={\lambda }_1{e}^{-\beta z_1{e}_c\varphi \left(\mathbf{r}\right)}+\sum _{i=2}^{N_{\text{ion}}}{\left(1+{\lambda }_i{e}^{-\beta z_i{e}_c\varphi \left(\mathbf{r}\right)}\right)}^{k_i},$$ (6)

where λ_i=e^{−μ_i∕k_BT} is the fugacity of ion type i and μ_i its chemical potential. μ_i and λ_i are independent of the electrostatics potential; they are derived by considering the mean number of each ion type in the bulk part of the solvent,

$${\mathcal{N}}_A{c}_i{a}^3=\frac{1}{\beta }{\left(\frac{\delta \text{\hspace{0.17em}ln}\left(\mathcal{Z}\right)}{\delta {\mu }_i}\right)}_{\varphi =0}.$$ (7)

There are as many equations of type 7 as there are types of ions. Note that in the case of ions of two different sizes, the corresponding system of equation can be solved analytically.²⁶ In the generic case, however, the system is solved numerically.

Figure 1.

Illustration of the lattice gas model for the SMPB equation. Each lattice cell may be empty or occupied by one or several ions of the same type. The lattice size a sets the size of the species with the largest radius, z_N, while the parameters k_i and k_j (in this example k_i=4 and k_j=2) set the relative sizes of the smaller ions with valence z_i and z_j, respectively.

The free energy functional for the whole lattice includes the electrostatic energy, the energy of the fixed charges, and the logarithm of the partition function Z defined in Eq. 6,

$$\beta \mathcal{F}=-\frac{\beta }{2}\int d\mathbf{r}\left({ϵ}_0+\gamma \left(\mathbf{r}\right){ϵ}_0\chi \right){\left|\mathbf{\nabla }\varphi \left(\mathbf{r}\right)\right|}^2+\beta \int d\mathbf{r}{\rho }_f\left(\mathbf{r}\right)\varphi \left(\mathbf{r}\right)-\frac{1}{a^3}\int d\mathbf{r}{\gamma }_{\text{ion}}\left(\mathbf{r}\right)\text{ln}\left(\mathcal{Z}\left(\mathbf{r}\right)\right).$$ (8)

Setting δF∕δϕ=0, we find that ϕ must satisfy the equation

$$\mathbf{\nabla }\cdot \left(\left({ϵ}_0+\gamma \left(\mathbf{r}\right){ϵ}_0\chi \right)\mathbf{\nabla }\varphi \left(\mathbf{r}\right)\right)+{\gamma }_{\text{ion}}\left(\mathbf{r}\right)\frac{4\pi e_c}{Z\left(\mathbf{r}\right)}\left\{{\lambda }_2{z}_2{e}^{-\beta z_2{e}_c\varphi \left(\mathbf{r}\right)}+\sum _{i=2}^{N_{\text{ion}}}\left(k_i{z}_i{\lambda }_i{e}^{-\beta z_i{e}_c\varphi \left(\mathbf{r}\right)}{\left[1+{\lambda }_i{e}^{-\beta z_i{e}_c\varphi \left(\mathbf{r}\right)}\right]}^{k_i-1}\right)\right\}=-4\pi e_c\sum _{i=1}^{N_{\text{ion}}}{q}_i\delta \left(\mathbf{r}-{\mathbf{r}}_{\mathbf{i}}\right).$$ (9)

This is the SMPB equation. Note that although Eq. 9 was derived for integral values of k_i, the continuity of the grand partition function allows us to choose any real values of k_i.

Dipolar Poisson–Boltzmann equation

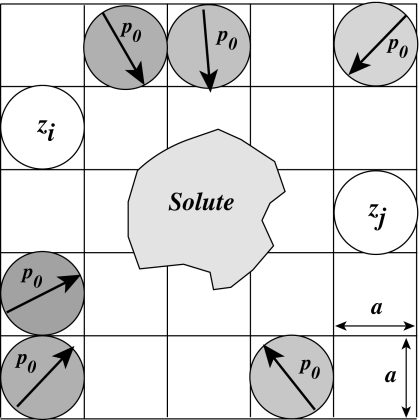
The PB model assumes a linear dielectric response of the solvent to the presence of the charges of the solute, leading to a continuum dielectric with a dielectric susceptibility χ that is independent of the electrostatic potential; this assumption however does not take into account the strong, nonuniform dielectric response of water molecules around charges.^{39, 40, 41, 42} We recently proposed a simple formalism based on statistical thermodynamics that allows us to circumvent this limitation.^{29, 30, 43} In this formalism, we represent the solvent as an assembly of freely orientable dipoles of constant modulus p₀ and bulk concentration c_dip. These dipoles as well as all counterions are distributed on a lattice surrounding the solutes to simulate the excluded volume effects (see Fig. 2). Note that this formalism is a generalization of the Langevin dipoles-protein dipoles model advocated by Warshel and co-workers,^{44, 45} with the key additional feature that the dipoles are now allowed to have a variable density at each lattice site.

Figure 2.

Illustration of the lattice gas model for the DPBL equation. Each lattice cell may be empty, occupied by one ion or occupied by a water dipole of constant magnitude p₀ but variable orientation. This example shows multiple sites occupied by water dipoles and two sites occupied by ions with valence z_i and z_j. The lattice size a sets the size of the ions and dipoles.

Each site in this lattice can contain at most one dipole or one ion. If it is empty, its energy is 0. The energy of one dipole of constant magnitude p₀ at position r is obtained as the Boltzmann-weighted average of the interaction −p₀⋅E over all orientations of p₀, where E is the local electric field. The energy of one ion of charge z_ie_c at the same position is z_ie_cϕ(r). Following the formalism introduced by Borukhov et al.,²⁵ the grand canonical partition function Z(r) for the lattice site at position r is then given by, after enumeration of its possible occupancies (empty, one dipole, or one ion),

$$\mathcal{Z}\left(\mathbf{r}\right)=1+{\lambda }_{\text{dip}}\gamma \left(\mathbf{r}\right)\frac{\text{sinh}\left(u\left(\mathbf{r}\right)\right)}{u\left(\mathbf{r}\right)}+{\gamma }_{\text{ion}}\left(\mathbf{r}\right)\sum _{i=1}^{N_{\text{ion}}}{\lambda }_i{e}^{-\beta z_i{e}_c\varphi \left(\mathbf{r}\right)},$$ (10)

where N_ion is the number of ion types, λ_dip and λ_i are the fugacities of the dipoles and ions, respectively, andu(r)=βp₀|∇ϕ(r)|. The fugacities are derived from the bulk concentration of the dipoles and ions:${\lambda }_{\text{dip}}=\left({\mathcal{N}}_A{c}_{\text{dip}}{a}^3\right)∕\left(1-{\mathcal{N}}_A{\sum }_{i=1}^{N_{\text{ion}}}{c}_i{a}^3-{\mathcal{N}}_A{c}_{\text{dip}}{a}^3\right)$ and ${\lambda }_i=\left({\mathcal{N}}_A{c}_i{a}^3\right)∕\left(1-{\mathcal{N}}_A{\sum }_{i=1}^{N_{\text{ion}}}{c}_i{a}^3-{\mathcal{N}}_A{c}_{\text{dip}}{a}^3\right)$.

Using the same approach described above for the SMPB equation, the free energy functional for the whole lattice is given by

$$\beta \mathcal{F}=-\frac{\beta }{2}\int d\mathbf{r}{ϵ}_0{\left|\mathbf{\nabla }\varphi \left(\mathbf{r}\right)\right|}^2+\beta \int d\mathbf{r}{\rho }_f\left(\mathbf{r}\right)\varphi \left(\mathbf{r}\right)-\frac{1}{a^3}\int d\mathbf{r}\text{\hspace{0.17em}ln}\left(\mathcal{Z}\left(\mathbf{r}\right)\right).$$ (11)

Setting δF∕δϕ=0, we find that ϕ must satisfy the equation

$$\mathbf{\nabla }\cdot \left(\left({ϵ}_0+\gamma \left(\mathbf{r}\right){ϵ}_0\chi \left(\mathbf{r},\varphi \left(\mathbf{r}\right)\right)\right)\mathbf{\nabla }\varphi \right)+{\gamma }_{\text{ion}}\left(\mathbf{r}\right)\frac{4\pi e_c}{a^3\mathcal{Z}\left(\mathbf{r}\right)}\sum _{i=1}^{N_{\text{ion}}}{\lambda }_i{c}_i{z}_i{e}^{-\beta z_i{e}_c\varphi \left(\mathbf{r}\right)}=-4\pi e_c\sum _{i=1}^M{q}_i\delta \left(\mathbf{r}-{\mathbf{r}}_{\mathbf{i}}\right),$$ (12)

where χ(r,ϕ(r)) is the dielectric susceptibility given by

$$\chi \left(\mathbf{r},\varphi \left(\mathbf{r}\right)\right)=\frac{\beta p_0^2{\lambda }_{\text{dip}}{F}_1\left(u\left(\mathbf{r}\right)\right)}{a^3{ϵ}_0\mathcal{Z}\left(\mathbf{r}\right)},$$ (13)

with F₁(x)=(sinh(x)∕x²)((1∕tanh(x))−(1∕x))=(sinh(x)∕x²)L(x) where L(x) is the Langevin function. This is the DPBL equation.

NUMERICAL SOLUTIONS TO THE DIPOLAR POISSON–BOLTZMANN–LANGEVIN EQUATION

The general form of the family of Poisson–Boltzmann-like equations described in the previous section is

$$\mathbf{\nabla }\cdot \left(ϵ\left(\mathbf{r},\varphi \left(\mathbf{r}\right)\right)\mathbf{\nabla }\varphi \left(\mathbf{r}\right)\right)+H\left(\mathbf{r},\varphi \left(\mathbf{r}\right)\right)=f\left(\mathbf{r}\right).$$ (14)

The function ϵ describes the dielectric permittivity at any position,

$$ϵ\left(\mathbf{r},\varphi \left(\mathbf{r}\right)\right)={ϵ}_0+\gamma \left(\mathbf{r}\right){ϵ}_0\chi \left(\mathbf{r},\varphi \left(\mathbf{r}\right)\right).$$ (15)

In the special cases of the PB and SMPB equations [Eqs. 5, 9, respectively], χ is constant and ϵ only depends on the position r. In the more general case of the DPBL Eq. 12, χ is given by Eq. 13 and ϵ depends nonlinearly on the position r, on the electrostatic potential ϕ(r), and on the magnitude u(r)=|∇ϕ(r)| of the electric field at position r. The function H is the Helmholtz source term that account for the ionic atmosphere in the solvent surrounding the solute. H is a nonlinear function of r and ϕ(r) for the PB and SMPB equations, and of r, ϕ(r), and u(r) for the DPBL equation. The fixed charges of the solutes have been denoted as the generic function f. The infinite domain of Eq. 14 is usually truncated to a finite domain Ω with boundary δΩ, which requires knowledge of the boundary conditions on δΩ that are provided either from a known analytical solution or from an approximation.

Several programs that solve either the linearized version of PBE, or directly the nonlinear PBE, are available with a variety of scientific computing techniques (see Refs. ^{12, 13} for recent reviews). To our knowledge, all these programs have been tailored to the PB equation, i.e., they assume for example that the coefficient function ϵ only depends on position. While these methods can easily be adapted to solve the SMPB equation (recent versions of APBS for example contains such a functionality, see http://www.poissonboltzmann.org/apbs), they cannot be used without significant modifications to solve the more general second order PDE given by Eq. 14. In the following, we describe three numerical methods for solving the DPBL equation, which generalize the methods proposed by Holst and Saied¹⁶ for solving the nonlinear PB equation. While these methods are general enough that they can solve all three types of equations described above, we will focus on their application to the DPBL equation.

Discrete DPBL equation: A nonlinear system of equations

The DPBL model expresses the electrostatic potential ϕ in the domain Ω in which the solutes of interest are surrounded by solvent that may contain electrolytes as the solution of a second order differential equation given by Eq. 12. As this PDE cannot be solved analytically (except maybe for simple cases such a single solute with spherical or cylindrical geometry), it is discretized on a mesh. Appendix A reviews this process using the box method on a Cartesian, nonuniform three dimensional (3D) mesh that is relevant to the DPBL equation; it leads to an algebraic system of nonlinear equations,

$$F\left(\mathbf{\varphi }\right)=A\left(\mathbf{\varphi }\right)\mathbf{\varphi }+H\left(\mathbf{\varphi }\right)-g=0,$$ (16)

where F(ϕ)=(F₁(ϕ),…,F_N(ϕ))^T, ϕ=(ϕ₁,…,ϕ_N)^T, A is the stiffness matrix whose coefficients are nonlinear functions of ϕ, and N is the number of interior vertices in the mesh (see Appendix A). The different functions F_i are defined in Eq. A8.

Inexact Newton methods for solving the discrete DPBL equations

Newton’s methods are probably the most popular methods for solving nonlinear system of equations. These are iterative methods that are derived from classical Newton’s method for one dimensional problem. Assume we know that ϕ is “close” to the true solution ϕ_min of the nonlinear system of equation F(ϕ)=0. We can estimate the behavior of F in the neighborhood of ϕ using a first-order Taylor expansion,

$$F\left(\mathbf{\varphi }+\mathbf{h}\right)=F\left(\mathbf{\varphi }\right)+F^{\prime }\left(\mathbf{\varphi }\right)\mathbf{h}+O\left({\mathbf{h}}^2\right),$$ (17)

where F^′ is the Jacobian of F (i.e., the matrix of partial derivatives of F). By neglecting terms of order h² and by setting F(ϕ+h)=0, we obtain a set of linear equations for the correction vector h that moves the function F closer to zero, namely, F^′(ϕ)h=−F(ϕ). This system is also referred to as the Newton or Jacobian system. The correction h (also referred to as Newton direction) is then added to the approximate solution ϕ and the process is iterated until convergence. Each Newton step is then defined as follows:

$$F^{\prime }\left({\mathbf{\varphi }}^n\right){\mathbf{h}}^n=-F\left({\mathbf{\varphi }}^n\right),$$ (18)

$${\mathbf{\varphi }}^{n+1}={\mathbf{\varphi }}^n+{\mathbf{h}}^n.$$

When the number of equations and variables is large, the Newton linear system of equations defined in Eq. 18 is solved iteratively. Finding the exact (or at least accurate) solution of this system may however be very time consuming. The inexact Newton methods were designed to circumvent this problem [for review, see Refs. ^{46, 47}]. They are based on the rationale that it is often preferable to compute only an approximate (inexact) Newton direction; the number of Newton iterations may then be higher, but this is usually compensated by the fact that the amount of work per iteration is smaller. There are two types of inexact Newton methods, the truncated methods that use the exact Jacobian but only solve the Newton system approximately with loose stopping criteria, and the quasi-Newton methods that use an approximate Jacobian. The latter approach is popular for cases for which computing the exact Jacobian is costly. Note that these two options can be combined.

A key element to the success of inexact Newton methods is the definition of the level of accuracy that is required to maintain rapid convergence of the overall Newton approach. Holst and Saied derived conditions that this level of accuracy must satisfy to guarantee global and superlinear convergence of the Newton method applied to the PB equation.¹⁶ It leads to the following algorithm (corresponding to their algorithm 7):¹⁶

Algorithm 1.

Truncated Newton method for solving the PB equation (from Holst and Saied [16])

Initialize ϕ0=0

forn=0,… until convergence do

(1) Compute exact Jacobian matrix F′(ϕn)

(2) Solve iteratively the Jacobian system F′(ϕn)hn=−F(ϕn)+rn until:

(a) ∥rn∥<∥F(ϕn)∥

and

(b) ∥rn∥≤C∥F(ϕn)∥p+1, C>0,p>0

(3) Update: ϕn+1=ϕn+αnhn

(4) Check for convergence: if $\frac{\parallel F({\mathbf{\varphi }}^{n+1}\phantom{)}\parallel }{\parallel F\left({\mathbf{\varphi }}^0\right)\parallel }<TOL$, stop

end for

In this algorithm condition (a) in step (2) is the necessary and sufficient condition for the truncated direction hⁿ to be a descent direction,¹⁶ while condition (b) ensures local Q-order (1+p) (i.e., superlinear) convergence.⁴⁶ The damping parameter α_n is obtained by solving the equation ∥F(ϕⁿ+α_nhⁿ)∥≤∥F(ϕⁿ)∥ using line search. The existence of such an α_n is guaranteed as long as hⁿ is a descent direction.^{16, 48}

We derived three extensions of this algorithm for the purpose of solving the DPBL equation:

• Variant 1: Newton27. Newton27 is a direct application of algorithm 1 to the DPBL equation. It uses the exact Jacobian matrix that can be computed analytically (see Appendix B). As such, it is guaranteed to be globally convergent, with superlinear behavior. It is named Newton27 as each row of the exact Jacobian contains 27 nonzero elements.

• Variant 2: Newton7. Newton7 implements a quasitruncated Newton method to solve the DPBL equation. It varies from algorithm 1 in that, in step 1, an approximate Jacobian is computed and subsequently used in step 2. This approximate Jacobian only includes the stiffness matrix of the nonlinear system of equation (i.e., the matrix of coefficients ϵ) and ignores its derivatives with respect to the electrostatic potential (see Appendix B). This approximate Jacobian is much faster to compute and has a much smaller memory footprint [O(4N) compared to O(14N) for the exact Jacobian], which is significant for large meshes. As it is an approximation, however, conditions (a) and (b) of step 2 do not guarantee any more global convergence and local superlinear convergence. It is named Newton7 as each row of the approximate Jacobian contains seven nonzero elements.

• Variant 3: NewtonSC. This variant uses a self-consistent approach. The idea is to apply algorithm 1 directly on a set of PB like equations that converge toward the DPBL equation. This leads to the following algorithm:

Algorithm 2.

Self-Consistent Newton method for solving the DPBL equation

Initialize ϕ0=0

forn=0,… until convergence do

(1) Set ϵn(r)=ϵ(r,ϕn)

(2) Set Zn(r)=Z(r,ϕn)

Define $H_n\left(\mathbf{r},\psi \right)={\gamma }_{\text{ion}}\left(\mathbf{r}\right)\frac{4\pi e_c}{a^3{\mathcal{Z}}_n\left(\mathbf{r}\right)}\sum _{i=1}^{N_{\text{ion}}}{\lambda }_i{c}_i{z}_i{e}^{-\beta z_i{e}_c\psi \left(\mathbf{r}\right)}$

(3) Solve the PB-like PDE:

∇⋅(ϵn(r)∇ψ(r))+Hn(r,ψ(r))=f(r)

for ψ, using algorithm 1

(4) Update ϕ:

ϕn+1=λψ+(1−λ)ϕn

(5) Check for convergence: if $\frac{\parallel F({\mathbf{\varphi }}^{n+1}\phantom{)}\parallel }{\parallel F\left({\mathbf{\varphi }}^0\right)\parallel }<TOL$, stop

end for

Step (1) of this algorithm sets the diffusion coefficients ϵ_n independent of the electrostatic potential. Similarly, step (2) defines a Helmholtz-like term H_n whose value at position r only depends on the value of the electrostatic potential at that position. The PDE in step (3) is then a PB equation that can be solved directly by algorithm 1 without modification. The update in step (4) is a typical trick for self-consistent methods that remove oscillations in the convergence behavior.

Similar to the reasoning behind inexact Newton methods, there is no need to solve the PDE in step (3) exactly. As its solution vector ψ is used as a correction for the solution of the DPBL equation (step 4), it is appropriate to use an approximation; the number of total iterations may then be higher, but this is compensated by the fact that the amount of work per iteration is smaller. The algorithm is then fully defined by the number n_N of Newton iterations used for solving the PDE in step (3) and the damping factor λ in step (4).

Solving the Jacobian systems

We finish this section by looking at the core element of any Newton methods, i.e., how to solve the Newton or Jacobian system. There are many direct methods available for solving linear systems of the form Jϕ=f such as Gauss, LU decomposition, Jacobi, etc. These methods however becomes impractical as the size of the system (number N of unknowns) increases, as their computational complexities and memory requirements are usually O(N³). Such systems are usually solved using methods that iteratively improve an estimate w of the solution. There are two measures of w as an approximation of ϕ. One is the error, defined as

$$\mathbf{\varphi }=\mathbf{w}+\mathbf{e},$$

and the second is the residual r that measures how well w satisfies the linear system,

$$\mathbf{r}=\mathbf{f}-J\mathbf{w}.$$

From these two definitions we derive a key relationship between the error and the residual,

$$J\mathbf{e}=\mathbf{r}.$$ (19)

Iterative methods for solving linear systems of equations therefore proceed as follows: for a given estimate w of the solution, compute the residual r, find the corresponding error e by solving Je=r, update accordingly w, and repeat until either the norm of the residual or of the error becomes small enough. Among those, the Jacobi techniques and the Gauss–Seidel technique are well adapted to solving systems coming from the discretization of PDEs.⁴⁹ These types of solvers quickly reduce local (high frequency) errors in the solution, but perform poorly however on global (or low frequency) errors in the solution. The key to the success of multilevel methods is to notice that a low frequency phenomenon on a fine mesh can be transformed into a high frequency phenomenon on a coarser mesh. The idea is to first run a few iterations of the solver on the fine mesh to remove high frequency errors (the so-called smoothing process), to restrict the corresponding residual on a coarser grid, to solve for the correction on this coarser grid using the same smoothing solver, and finally to interpolate this correction back to the fine mesh and apply it to the current estimate. This strategy was first implemented by Holst and Saied¹⁵ to solve the linearized Poisson–Boltzmann equation and later adapted as a preconditioner for the Newton method for solving the nonlinear Poisson–Boltzmann.¹⁶ We rely on their implementation in their software package MG.

COMPUTATIONAL CONSIDERATIONS

AQUASOL is a generic package written in FORTRAN designed to solve the dipolar Poisson–Boltzmann equation and accessorily the Poisson–Boltzmann and SMPB equations, as those can be considered as special cases of the former. AQUASOL implements the three variants Newton27, Newton7, and NewtonSC of the inexact Newton method originally developed by Holst and Saied¹⁶ to solve the nonlinear system of equations that results from the discretization of the DPBL equation on a Cartesian nonuniform mesh.

AQUASOL is mostly inspired from and in fact uses many routines from the FORTRAN package MG developed by Michael Holst and freely available at http://www.fetk.org. Note that there is a more recent version of MG, named PMG, written in C∕C++ and that is available at the same site. MG is also available as part of APBS (Ref. ³³ see also http://www.poissonboltzmann.org/apbs), a popular package for solving the PB equation on biomolecular systems.

In this section, we describe the particulars of AQUASOL, focusing on the parts that were added to MG, as well as the modifications required by each of the three solvers that were implemented. Note that AQUASOL differs significantly from AQUA, a software package available in APBS that is only an optimized version of MG.

Setting up the mesh

The coordinates of the atoms of the solute(s) as well as their vdW radii and partial charges are read from a single file under the PQR format used by APBS. For large biomolecules, PQR files can be readily generated from the correspondent PDB⁵⁰ files using the service PDB2PQR.⁵¹ The PQR file may contain several molecules.

AQUASOL starts by building a regular mesh around the solutes (note that the solvers included in AQUASOL can handle both uniform and nonuniform meshes). The mesh is positioned such that its center matches with the center of the solute. The user provides the number of points and the mesh spacing in each direction. When solving DPBL equations, AQUASOL checks that there is at least a distance of 2l_B (l_B being the Bjerrum length in water at 300 K, i.e., approximately 7 Å) from any point on the surface of the solute to the closest face of the mesh; if this condition is not met, the mesh size is adjusted accordingly.

AQUASOL offers two options for representing the interface between the interior and exterior of the solutes, namely, their accessible surface or their molecular surface. The accessible surface is obtained as the envelope of the hydrated spheres representing the atoms, whose radii are the vdW radii increased by R_probe=1.4 Å, where R_probe is the radius of a water molecule.⁵² We map the accessible surface on the regular mesh as follows. All mesh vertices are initially labeled as 0. The procedure then loops over each atom and labels as 1 each mesh point that is interior to its hydrated sphere. This method is not optimal as it will visit some mesh vertices several times but is fast enough for this application. The molecular surface is the lower envelope obtained by rolling a water probe of radius R_probe on the vdW surface of the molecule. It is computed as follows. First, mesh vertices are labeled with 0 or 1 based on the accessible surface as described above. AQUASOL then loops over each atom, placing uniformly points on the surface of its hydrated sphere at a density of 10 points∕Ų. It uses the rapid method of Le Grand and Merz⁵³ based on Boolean logic to select those that are accessible; any mesh vertex with a label of 1 that is within R_probe of one of these accessible points is then reverted to a label of 0. At the end of the procedure, all points whose label stayed as 1 are inside the molecular surface. AQUASOL repeats the calculation of the solute interface four times: first for the regular mesh and then for the three meshes whose generic points are {i+1∕2,j,k}, {i,j+1∕2,k}, and {i,j,k+1∕2}, respectively. These four maps are stored for subsequent use in computing the scalar fields γ and γ_ion that are needed for computing the stiffness matrix A (see Appendix A).

Computing the charge densities on all vertices of the mesh

Classical treatment of electrostatics assigns a point charge to each atom, usually located at the center of the sphere representing this atom. The mesh considered in AQUASOL is Cartesian; as such, the centers of the atoms of the solute(s) will most likely not coincide with its vertices. One step in setting up the PDE solver described above is therefore to project the atomic charges on the vertices of the mesh. The most common approach to perform this task is trilinear interpolation. A point charge is positioned in the mesh by defining the cell to which it belongs. The charge is then distributed over all eight vertices of this cell, with the fraction of the charge on each vertex given by a trilinear function based on the distance between the vertex and the actual charge. Bruccoleri proposed an alternate method for computing the charge density on the mesh, the sphere charging model.⁵⁴ This method assumes a spherical distribution of charges. Given the position of an atom relative to the mesh, we identify all mesh points that fall within the van der Waals radius of that atom. If there are eight or more such points, then the atom’s charge is evenly divided and added to the charges assigned to these points. If there are less than eight points, then the trilinear interpolation is used. Both methods have been implemented in AQUASOL, with the trilinear interpolation method used by default. Note that both approaches introduce nonphysical energies coming from the interactions between the partial charges representing an actual point charge. These energies can be removed by subtracting potentials calculated in vacuo.

Implementing the three variants of the Newton method

MG includes an implementation of the inexact Newton method given in algorithm 1 that is specific to the PB equation. Specifically, it uses the fact that the matrix of diffusion coefficients A is independent of the electrostatic potential. The Jacobian matrix at each iteration can then be computed efficiently, as it only requires the (low cost) computation of the derivatives of the Helmholtz term H.

The two variants Newton27 and Newton7 designed to solve the DPBL equation cannot use the same simplification. Newton27 uses the exact Jacobian, computed from the analytical derivatives of the Jacobian system given in Appendix B, while Newton7 uses an approximate Jacobian, also given in Appendix B. Both the exact and approximate Jacobian matrices depend on the electrostatic potential. These two variants therefore require that the full Jacobian matrix be recomputed at each step (instead of only being updated). Consequently, AQUASOL includes a modified version of MG that accounts for this difference, as well as all routines required to compute the exact and approximate Jacobians given in Appendix B.

The third variant NewtonSC was much easier to implement and required no modification of the Newton solver implemented in MG. It is based on algorithm 2 whose implementation only requires routines for computing the dielectric permittivity maps (step 2) and Helmholtz term (step 3) at each iteration; it solves the PB-like equation by a direct call to the driver for the inexact Newton solver available in MG. As such, NewtonSC is very attractive as it can be implemented with minimal programming cost in any Poisson–Boltzmann solver currently available.

Solving the Jacobian system

AQUASOL uses the linear multilevel solver developed by Holst and Saied¹⁵ and available in MG with the following features:

• Smoothing. The red-black Gauss–Seidel algorithm is used for pre- and postsmoothing. The number of iterations for both smoothing operations is set to 2 on the finest mesh and 2 on the coarse meshes. Note that the Gauss–Seidel algorithm is guaranteed to converge if the matrix is either diagonally dominant, or symmetric and (semi-) positive definite. While this is the case for Jacobian matrix corresponding to the PB and SMPB equations, as well as for the approximate Jacobian matrix used by the variant Newton7 for the DPBL equation, it is not guaranteed to be true for the exact Jacobian of DPBL used in the variant Newton27. The following strategy was consequently implemented in Newton27 to circumvent possible problems of convergence. The multigrid linear solver starts with the exact Jacobian matrix; if the residual at the end of its first iteration is larger than the initial residual, the procedure is deemed to diverge and the solver switches to the inexact, 7-stencil Jacobian. While this safeguard option was not necessary on most of the cases tested so far, it prevented divergence in a few difficult cases (see next section).

• Restriction and interpolation. Special care must be taken for both operations in the presence of discontinuities in the coefficients of the PDE; we have consequently used the 3D Galerkin coarsening procedure of Holst,³² directly from the MG package.

Availability of AQUASOL

A full version of AQUASOL (including source code and binaries for Linux) is available upon request to P. Koehl (koehl@cs.ucdavis.edu) under a lesser GPL open source license.

RESULTS AND DISCUSSION

We evaluate and compare the three solvers implemented in AQUASOL for solving the DPBL equations on two test cases that are typical of applications in computational biology, namely, the analyses of the electrostatics component of the solvation of a protein and a DNA molecule. First, The C-terminal fragment of the L7∕L12 ribosomal protein (PDB code 1CTF) was chosen, as it is a pet protein in many computational biology studies. Second, the B-DNA Dickerson–Drew dodecamer (PDB code 1BNA) was chosen as an example of the family of highly charged nucleic acids.

The relative pros and cons of the PB and DPBL equations have been described in detail;^{12, 13, 25, 26, 29, 30, 31, 43, 55} here we focus on the properties of the PDE solvers, namely, convergence rate, computing time, and memory requirements. As the emphasis of the paper is on solving the DPBL equation, we show first that the increased complexity of the equation is a small price to pay compared to the wealth of information derived from its solution, in particular the possibility to look at hydration.

Protein and DNA hydration

In the DPBL formalism, the solvent is represented as an assembly of freely orientable dipoles of constant modulus p₀ and fixed bulk concentration c_dip. The local concentration of these dipoles however vary and is defined by the corresponding local electric field E. The solution of the DPBL equation provides the electrostatic potential at each position in the mesh; the local dipole (water) density is then defined by

$${\rho }_{\text{dip}}\left(\mathbf{r}\right)=\frac{1}{a^3}\frac{{\lambda }_{\text{dip}}\text{\hspace{0.17em}sinh}u}{u\mathcal{Z}\left(\mathbf{r}\right)},$$ (20)

where u=βp₀∥E(r)∥ and Z(r) is given by Eq. 10. Once the solvent density map is known, it can be used to place a collection of water molecules around the solute molecule. First we sort the ρ_dip(r) values obtained from Eq. 20 in descending order. Water molecules are placed by walking down the list until the desired number of water molecules is reached; each time a water molecule is placed, we eliminate points within 1.5 A of this position from the list. We use the local electrostatic field to orient the dipole. As an illustration of the usefulness of the DPBL equation, we give two examples where the knowledge of the water density profile clearly correlates with known molecular properties.

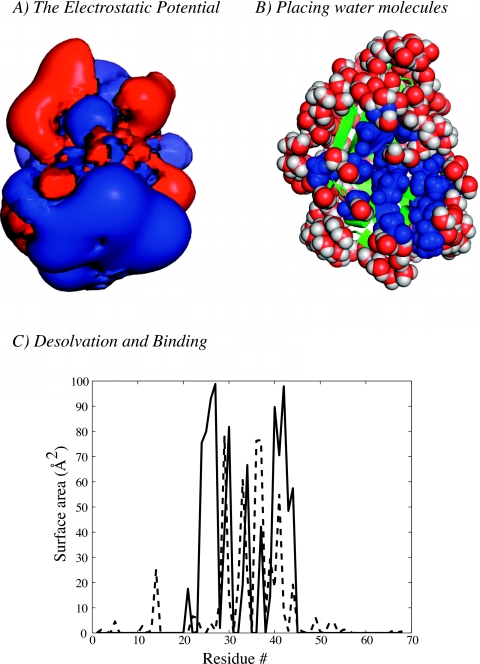
The first example is the C-terminal domain of the L7∕L12 ribosomal protein from Escherichia coli, whose structure was derived by x-ray crystallography at 1.7 Å resolution (PDB code 1CTF). This protein is known to form a homodimer in solution.⁵⁶ We solved for the electrostatic potential around the assymetric unit of 1CTF using the DPBL equation. The protein was immerged in a 65×65×65 regular grid, with 1.1 Å spacing in each direction. The lattice size for the dipoles and ions was set to 2.8 Å (i.e., the diameter of a water molecule), and p₀ was set to 3.0 D, its accepted value in liquid phase.⁵⁷ Monovalent counterions at 0.1M were added. We derived the solvent density map around the asymmetric unit of 1CTF and placed 200 water molecules based on this density map. These water molecules are organized relatively uniformly around the protein, except for one region with a strong desolvation; this region is found to match with the dimerization zone for 1CTF, derived from the structure of the dimer (see Fig. 3).

Figure 3.

Analyzing protein hydration: application to 1CTF. 1CTF is a small globular α+β protein shown in cartoon mode (green). Its electrostatic potential was computed from the DPBL equation using a mesh of size 65×65×65 with uniform spacing of 1.1 Å in each direction. (a) Visualizing the potential. We show two isosurfaces at +1k_BT∕e_c and −1k_BT∕e_c of the electrostatic potential derived as solution of the DPBL equation on the mesh. (b) Adding water molecules. The electrostatic potential map is used to derive the water dipole density map (see text for details), which is subsequently used to place water molecules around the proteins. The top 200 water molecules corresponding to the highest water density points are represented in CPK mode. These molecules are positioned relatively uniformly around the protein, except for one patch. Interestingly, this patch corresponds to the dimerization zone for 1CTF. This is illustrated by coloring in blue all residues whose accessible surface area is reduced by more than 10% between the monomer and the dimer (the structure of the monomer is taken from the PDB file 1CTF); the structure of the dimer was downloaded from the PQS server (http://www.ebi.ac.uk/pdbe/pqs/). Note that the same procedure can be used to place ions around the solute. They are omitted here, for sake of clarity. (c) Desolvation and binding. We compare the difference in accessible surface area between the monomer alone and the monomer as part of the dimer (solid line), with the accessible surface area of the 1CTF monomer in the presence of the top 200 water molecules (dashed line). The two curves correlate well. Panels (a) and (b) of this figure were generated using pymol (http://www.pymol.org).

The second example is the so-called Dickerson–Drew DNA dodecamer; its crystal structure provided the first detailed picture of a right-handed DNA duplex.^{58, 59} This structure and those of related dodecamers served as bases to study the interdependence of base sequence and structure, DNA backbone flexibility, solvation, bending and bendability, drug binding, and the effects of packing forces and crystallization conditions on DNA structure. Of particular interest to us is the study of the hydration of the dodecamer. Based on 72 bound water molecules observed in the electron density maps, Drew and Dickerson⁶⁰ identified three different hydration patterns in B-DNA:

• Water molecules that hydrate the oxygens of the backbone phosphate.

• A “spine of hydration” deep in the minor groove of the DNA duplex.

• Hydration in the major groove is confined to water bound to exposed N and O of the bases.

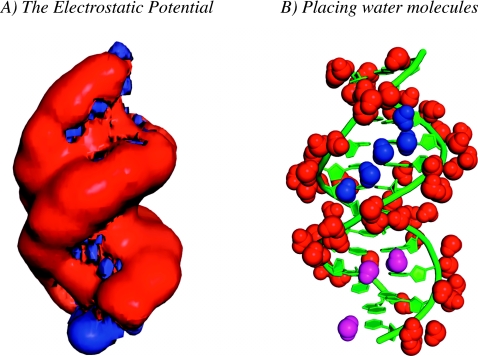
We solved for the electrostatic potential around the Dickerson–Drew DNA dodecamer (PDB structure 1BNA) using the DPBL equation. The DNA was placed in a 65×65×65 regular grid, with 1.2 Å spacing in each direction. The lattice size for the dipoles and ions was set to 2.8 Å (i.e., the diameter of a water molecule), and p₀ was set to 3.0 D, its accepted value in liquid phase.⁵⁷ Monovalent counterions at 0.1M were added. We derived the solvent density map around the asymmetric unit of 1BNA and placed 72 water molecules based on this density map, as a parallel to Drew and Dickerson studies. The positions of these water molecules match remarkably well with the experimental observations (see Fig. 4).

Figure 4.

DNA solvation. The Drew–Dickerson dodecamer adopts a right handed double helix structure (green). Its electrostatic potential was computed as the solution of the DPBL equation on a mesh of size 65×65×65 with uniform spacing of 1.2 Å in each direction. (a) Visualizing the potential. We show two isosurfaces at +1k_BT∕e_c and −3k_BT∕e_c of the electrostatic potential derived as solution of the DPBL equation on the mesh. (b) DNA hydration. The electrostatic potential map is used to derive the water dipole density map (see text for details), which is subsequently used to place water molecules around the proteins. The top 72 water molecules corresponding to the highest water density points are represented in CPK mode. We distinguish three types of water molecules: those that bind nonspecifically to the oxygens of the phosphate (shown in red), those that form a spine of hydration that sits at the bottom of the minor groove (shown in blue), and those found in the major groove (shown in magenta). Similar to the protein case (see Fig. 3, ions are omitted for sake of clarity). This figure was generated using pymol (http://www.pymol.org).

Solving the DPBL equation: Numerical comparison of the three Newton variants implemented in AQUASOL

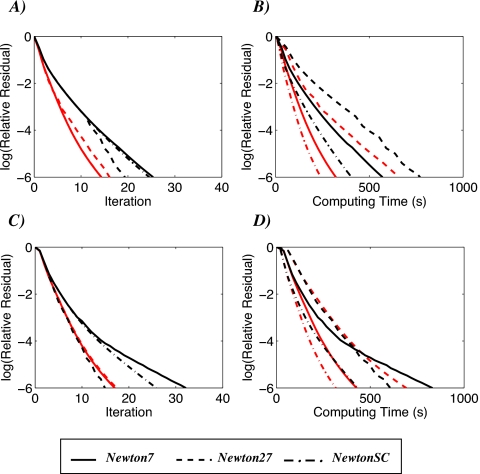
The three nonlinear Newton variants presented above are investigated numerically when applied to the DPBL equation on the two test sets described above, i.e., the protein molecule 1CTF and the DNA molecule 1BNA. A first set of comparison is performed on Cartesian uniform meshes of size 257×257×257. All calculations use a lattice size for the dipoles and ions of 2.8 Å (i.e., the diameter of a water molecule), with p₀, the intensity of the dipole moment set to 3.0 D. Monovalent counterions with an ionic strength of 0.1M are added. The interface between the solute and the solvent is taken to be either the molecular surface or the solvent accessible surface. Computing times shown in the plots include preprocessing time. The electrostatic potential is initialized at zero for all methods. The same stopping criteria is used [steps (4) and (5) of algorithms 1 and 2, respectively], with TOL set to 1.0e−6. While this is not the most appropriate stopping criterion for nonlinear iterations, it allows us to compare the method as they produce solutions with similar qualities. All computations are performed on an Intel Xeon 5560 2.8 GHz eight-core processor with 16 Gbyte of memory; the program is compiled without any parallel option. Results are presented in Fig. 5.

Figure 5.

Comparison of Newton7, Newton27, and NewtonSC for solving the DPBL equation. The relative residual computed as ∥F(ϕ_n)∥∕∥F(ϕ₀)∥ is plotted vs the number of iterations [panels (a) and (c)] as well as vs the computing time, given in seconds [panels (b) and (d)]. Panels (a) and (b) correspond to the protein test case, while panels (c) and (d) relate to the DNA test case. All calculations are performed on a 257×257×257 Cartesian grid. The interface between the solute and the solvent is set to either the accessible surface (red curves) or the molecular surface of the molecule (black curves).

The convergence of our solvers is sensitive to the definition of the surface of the molecule that serves as an interface: calculations based on the accessible surface are usually faster than those based on the molecular surface (red versus black curves on Fig. 5). This is expected for two reasons. First, the molecular surface may include self-intersection that leads to severe singularities; such singularities may result in convergence problem. Second, and more importantly, the accessible surface area is an expanded surface of the molecule. As such, it defines a larger solvent-excluded region around the charges than can be seen as a pseudo-Stern layer for the water dipole, thereby reducing the effect of steric interactions between the dipole and the solute. Note that the DPBL formalism is designed to take into account the steric interactions between the solvent dipoles and between these dipoles and the ions, but not between the dipoles or the ions and the solute.

The convergence behavior observed for Newton27 was fully predictable; it is a direct application of the truncated Newton method and as such is expected to converge globally and superlinearly. Holst and Saied¹⁶ gave formal proofs that justify these two properties; their proofs, while originally developed for the PB equation, make no assumptions on the nature of the diffusion coefficients and therefore apply directly to the DPBL equation. There is however a significant difference between the PB and DPBL equations that may adversely affect the convergence of Newton27 for the latter. The global convergence of algorithm 1 is guaranteed if we can solve approximately the Jacobian system F^′(ϕⁿ)h=−F(ϕⁿ) at any iteration n with a residual rⁿ that satisfies ∥rⁿ∥<∥F(ϕⁿ)∥. Michael Holst has shown that for elliptic equations with smooth coefficients a red∕black Gauss–Seidel algorithm or a Jacobi algorithm combined with a multigrid technique solves this problem efficiently.³² In the more complicated case however of the PB equation applied on large biomolecules with interface problem at the molecular surface boundary, this simple procedure may fail. Special care is needed for the coarsening steps of the multigrid techniques, and Holst designed a Galerkin coarsening procedure that restores good convergence property for solving the Jacobian system. The exact Jacobian matrix for the DPBL equation is more complicated and more prone to discontinuities at the molecular surface interface. In the DNA case tested above, the Gauss–Seidel red-black algorithm coupled with a multigrid technique that uses the Galerkin procedure diverge during the second and third Newton iterations; using the harmonic averaging proposed by Holst and Saied¹⁵ did not solve the problem. The solution we implemented in Newton27 for the DPBL equation is pragmatic; if at any Newton step of algorithm 1 the linear solver fails on the exact Jacobian, we temporarily switch to the approximate Jacobian to derive an approximate descent direction. Numerous numerical experiments (those presented here and others) indicate that this restores good convergence for the difficult cases encountered. Ultimately, we need a more robust iterative solver for the exact Jacobian system derived from the DPBL equation. We did not pursue this direction as the two other variants implemented in AQUASOL proved to be robust and more efficient than Newton27.

Newton7 is the quasitruncated Newton version of algorithm 1 applied to the DPBL equation. While it is not theoretically guaranteed to converge, the numerical experiments shown in Fig. 5 as well as extensive testing on other test cases not shown here indicate that it does, albeit not always globally, especially at the initial steps when the current solution is usually a poor estimate. It requires more iterations than Newton27 to reach convergence, but its iterations are faster to compute.

NewtonSC is the most efficient of the three Newton variants implemented in AQUASOL. For the examples shown in Fig. 5, we used n_N=1 and λ=1. The convergence rate for NewtonSC is very similar to the one observed for Newton7; the former is however consistently faster than both Newton27 and Newton7. The speedup compared to Newton27 is related to the fact that it does not compute the exact Jacobian associated with the DPBL equation. It is faster than Newton7 as it makes full use of the PBE specific code implemented in the software package MG.

In addition to the three Newton variants described here, we also tested the full approximation scheme (FAS) method that implements a fully nonlinear multilevel method.⁴⁹ The FAS method is found to be significantly slower (a factor of 4 at least for a mesh with 257³ vertices) than all three Newton methods. There are two factors that explain this difference. First, the FAS method computes explicitly the coarse grid Jacobians by finite difference, while the Newton methods proceed by simple restrictions. Second, FAS uses nonlinear procedures for smoothing, which are much slower than the linear smoothing routines used in the Newton iterations. We did not explore further the use of other fully nonlinear multigrid methods.

Differences in solving the PB, SMPB, and DPBL equations

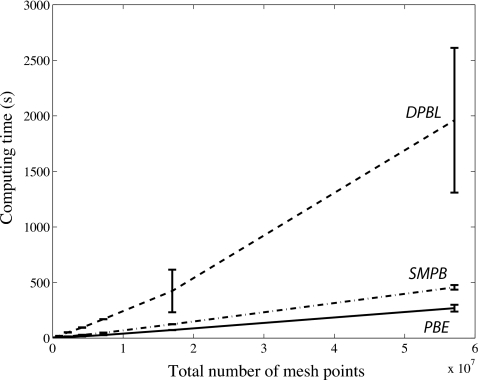
The PB, SMPB, and DPBL equations belong to the same class of PDEs whose discretization leads to the general nonlinear system of equation given by Eq. 16. There is however a significant difference to take into account: the stiffness matrix A is independent of the electrostatic potential ϕ for the PB and SMPB equations, but highly nonlinear in ϕ for the DPBL equation. The Newton7 variant implemented in AQUASOL is “exact” if applied on the PB and SMPB equations, in that the approximate Jacobian is then exact. In Fig. 6 we compare the performance of this specialized Newton’s method applied to solving the PB and SMPB equations with the performance of the NewtonSC method for solving the DPBL equation (the average behavior between the protein test case and the DNA test case is shown). It takes approximately ten times longer to solve the DPBL equation than to solve the PB equation. This difference is not unexpected: many of the convenient time-saving tricks that apply to the PB equation (see Ref. 16) are obsolete for the DPBL equation. It remains that there is room for improvement if the DPBL equation is to replace the PB equation for routine analysis.

Figure 6.

Solving the PB, SMPB, and DPBL equations. The computing time required to reach a residual error lower than TOL=1.e−6 is plotted vs the number of points in the mesh. The mean and standard deviation for each mesh size are computed over the CTF and DNA test cases. All calculations are performed with the molecular surface defining the interface of the solute, in presence of 0.1M of monovalent ions, with the intensity of the dipole moment set to 3.0 D. The lattice is set at 2.8 Å.

CONCLUSION

We described three nonlinear multigrid methods for solving the DPBL equation, a modified Poisson–Boltzmann equation whose solution describes the electrostatic potential around the solute of interest as well as provide water density maps around the same solute. These three methods are derived from a truncated Newton method proposed by Holst and Saied for solving the Poisson–Boltzmann equation.¹⁶ Our numerical results indicate that the self-consistent method which we dubbed NewtonSC is the best compromise for solving DPBL as it is fast, robust, and has a low storage requirement. It is also the easiest to implement and can be adapted with low implementation cost to any PB solvers to allow them to solve the DPBL equation.

Newton-like methods are robust and efficient solvers for elliptic PDEs and it can be shown theoretically that they are guaranteed to converge if the coefficients of the PDE are smooth. For nonlinear systems with possible discontinuities in the coefficient, however, this guarantee is contingent to finding a good initial approximation. In that respect, we have shown that the quasi-Newton method Newton7 is more robust than Newton27 that uses the exact Jacobian of the nonlinear system of equations resulting from the discretization of the DPBL equation.

The solution of the DPBL equation is more informative than the solution of the PB equation; solving the former however is approximately ten times costlier in computing time than solving the latter, even with the fast NewtonSC method described here. While most of this difference is inherent to the nature of the equations themselves, we believe that there is still room for improvement. We are currently investigating approaches such as the Jacobian-free Newton–Krylov methods⁶¹ in hope of substantial speedup.

AQUASOL is a software package designed as a specialized solver for DPBL equation; it can be used however for solving the PB and SMPB equations as those can be considered as special cases of the former. It is heavily based on the MG software package developed by Michael Holst, which also serves as a base for the software package APBS. AQUASOL currently uses Cartesian meshes and a finite volume approach to discretize the nonlinear PDE resulting from the DPBL formalism. While working on a Cartesian mesh offers some numerical advantages (the setup is usually easy and the Jacobian matrices used in the Newton-like solvers are usually highly sparse), there are two main issues that are left untreated.¹⁴ First, the point charges do not match with vertices of the mesh and consequently need to be projected. All current methods apply fractional projections, leading to self-interactions between the different partial charges generated. This effect is usually removed by subtracting the result of a calculation with vacuo dielectric; it still remains a subject of concern. Second, and probably more important, Cartesian meshes provide only an approximate position for the molecular surface of the solutes. This leads to discontinuities in the coefficients of the discrete equations, as well as in difficulties in enforcing a continuity condition of the electric displacement on the molecular surface. As a result, we usually observe low accuracy of the solution potential at the surface and low convergence rate.⁶² Possible solutions to these problems include reducing the mesh spacing to improve resolution as well as application of improved and robust solvers. While we have taken both options into account while developing AQUASOL (i.e., special care was taken to limit the AQUASOL memory usage to allow for large meshes, the discretization scheme allows for nonuniform meshes to give the possibility to increase resolution at the interface, and AQUASOL strives to fast convergence by adopting an inexact Newton solver), it remains that these are workarounds that treat the symptoms related to the use of Cartesian meshes rather than the problems at the root. There has been recently significant interest from applied mathematicians to develop PB solvers with interface methods that specifically deal with the continuity and accuracy issues at the molecular surfaces. Methods such as the jump condition capturing finite difference scheme,^{63, 64} and the matched interface and boundary^{62, 65, 66} seem very promising and we are currently investigating ways to incorporate them in AQUASOL.

Finite element methods represent a viable alternative to the finite difference methods discussed above. They allow for non-Cartesian meshes that provide better approximation of the geometry of the solutes. They also provide more flexibility for local mesh refinement as well as for handling nonlinear equations.¹⁴ Finite elements methods have been applied both to the linearized PB equation⁶⁷ and to the nonlinear PB equation.¹⁷ Recently, Holst and colleagues⁶⁸ established its rigorous solution and approximation theory, resulting in the first rigorous convergence result for any numerical methods applied to PBE. We plan to either extend AQUASOL to include a finite element solver for the DPBL equation that will take into account these theoretical results, or to adapt the NewtonSC strategy in an existing finite element solver.

APPENDIX A: DISCRETIZING THE DPBL EQUATION

The box method (also called finite volume method) is one of the standard approaches for discretizing PDEs on general meshes. We follow the implementation of Holst³² of this method; it is designed for nonuniform Cartesian meshes, i.e., the mesh lines need not be uniformly spaced. This has the advantage that the mesh can be adapted to the geometry of the system considered to represent more accurately the solute-solvent interface. The box method is well known; for a full description we refer the reader to Holst’s thesis³² as well as to Holst and Saied.¹⁶ The purpose of the following section is simply to introduce notation and equations relevant to our system.

The DPBL model expresses the electrostatic potential ϕ in a domain Ω that includes the solutes of interest as the solution of a second order differential equation, 

$$\mathbf{\nabla }\cdot \left(ϵ\left(\mathbf{r},\varphi \left(\mathbf{r}\right)\right)\mathbf{\nabla }\varphi \left(\mathbf{r}\right)\right)+H\left(\mathbf{r},\varphi \left(\mathbf{r}\right)\right)-f=0,$$ (A1)

where ϵ is the dielectric permittivity, 

$$ϵ\left(\mathbf{r},\varphi \left(\mathbf{r}\right)\right)={ϵ}_0+\gamma \left(\mathbf{r}\right)\frac{\beta p_0^2{\lambda }_{\text{dip}}{F}_1\left(u\left(\mathbf{r}\right)\right)}{a^3\mathcal{Z}\left(\mathbf{r}\right)},$$ (A2)

with u(r)=p₀e_c∇ϕ(r) and

$$\mathcal{Z}\left(\mathbf{r}\right)=1+{\lambda }_{\text{dip}}\gamma \left(\mathbf{r}\right)\frac{\text{sinh}\left(u\left(\mathbf{r}\right)\right)}{u\left(\mathbf{r}\right)}+{\gamma }_{\text{ion}}\left(\mathbf{r}\right)\sum _{i=1}^{N_{\text{ion}}}{\lambda }_i{e}^{-\beta z_i{e}_c\varphi \left(\mathbf{r}\right)}.$$ (A3)

H accounts for the ion atmosphere in the solvent surrounding the solute,

$$H\left(\mathbf{r},\varphi \left(\mathbf{r}\right)\right)={\gamma }_{\text{ion}}\left(\mathbf{r}\right)\frac{4\pi e_c}{a^3\mathcal{Z}\left(\mathbf{r}\right)}\sum _{i=1}^{N_{\text{ion}}}{\lambda }_i{c}_i{z}_i{e}^{-\beta z_i{e}_c\varphi \left(\mathbf{r}\right)},$$ (A4)

and f accounts for the fixed charges of the solutes. The functions γ(r) and γ_ion(r) are witness functions set to 1 if r is in a region where solvent and ions are present, respectively, and 0 otherwise.

The domain Ω on which Eq. A1 is discretized as a rectangular mesh characterized by vertices r_ijk at position (x_i,y_j,z_k). There are Nx+2, Ny+2, and Nz+2 possible values for x, y, and z. We define the mesh spacings as 

$$h_i=x_{i+1}-x_i,h_j=y_{j+1}-y_j,h_k=z_{k+1}-z_k,$$ (A5)

which are not required to be equal or uniform.

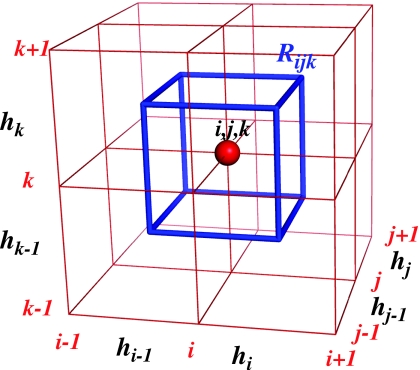
We build a three-dimensional parallelepiped R_ijk centered at each mesh point r_ijk of sizes 0.5(h_i+h_i−1), 0.5(h_j+h_j−1), and 0.5(h_j+h_j−1) along the directions i, j, and k, respectively (see Fig. 7). The volume of R_ijk is given by

$$\text{Vol}\left(R_{ijk}\right)=V_{ijk}=\frac{\left(h_{i-1}+h_i\right)\left(h_{j-1}+h_j\right)\left(h_{k-1}+h_k\right)}{8}.$$ (A6)

The surface areas of the faces of R_ijk along x, y, and z are given by 

$$S_{jk}=\frac{\left(h_{j-1}+h_j\right)\left(h_{k-1}+h_k\right)}{4},S_{ik}=\frac{\left(h_{i-1}+h_i\right)\left(h_{k-1}+h_k\right)}{4},$$ (A7)

$$S_{ij}=\frac{\left(h_{i-1}+h_i\right)\left(h_{j-1}+h_j\right)}{4},$$

respectively.

Figure 7.

Geometry of the mesh near a vertex r_ijk.

Integrating Eq. 14 inside the region R_ijk gives the resulting discrete equation (see Holst’s thesis³² for details) 

$${ϵ}_{i-1∕2.j,k}\left(\frac{{\varphi }_{ijk}-{\varphi }_{i-1,j,k}}{h_{i-1}}\right)S_{jk}+{ϵ}_{i+1∕2.j,k}\left(\frac{{\varphi }_{ijk}-{\varphi }_{i+1,j,k}}{h_i}\right)S_{jk}+{ϵ}_{i.j-1∕2,k}\left(\frac{{\varphi }_{ijk}-{\varphi }_{i,j-1,k}}{h_{j-1}}\right)S_{ik}+{ϵ}_{i.j+1∕2,k}\left(\frac{{\varphi }_{ijk}-{\varphi }_{i,j+1,k}}{h_j}\right)S_{ik}+{ϵ}_{i.j,k-1∕2}\left(\frac{{\varphi }_{ijk}-{\varphi }_{i,j,k-1}}{h_{k-1}}\right)S_{ij}+{ϵ}_{i.j,k+1∕2}\left(\frac{{\varphi }_{ijk}-{\varphi }_{i,j,k+1}}{h_k}\right)S_{ij}+V_{ijk}\left(H_{ijk}-f_{ijk}\right)=0.$$ (A8)

f_ijk is the value of the fixed (solute) charge density at position r_ijk. H_ijk=H(r_ijk,ϕ(r_ijk)) depends on the values ϕ_ijk and u_ijk [see Eq. A4]. In this equation, the modulus of the electric field u_ijk is given by

$$u_{ijk}=p_0{e}_c\sqrt{{\left(\frac{{\varphi }_{i+1,j,k}-{\varphi }_{i-1,j,k}}{h_{i-1}+h_i}\right)}^2+{\left(\frac{{\varphi }_{i,j+1,k}-{\varphi }_{i,j-1,k}}{h_{j-1}+h_j}\right)}^2+{\left(\frac{{\varphi }_{i,j,k+1}-{\varphi }_{i,j,k-1}}{h_{k-1}+h_k}\right)}^2}.$$ (A9)

The different coefficients ϵ are evaluated at the center of the faces of R_ijk based on Eq. A2. To compute these coefficients we need the values of the different scalar fields γ(r), γ_ion(r), ϕ, and u at positions {i+h_i∕2,j,k}, {i−h_i−1∕2,j,k}, {i,j+h_j∕2,k}, {i,j−h_j−1∕2,k}, {i,j,k+h_k∕2}, and {i,j,k−h_k−1∕2} in the mesh. The values of γ and γ_ion are precomputed once during setup, based on the geometry of the solutes (see Sec. 4 above). The values of the electrostatic potential ϕ at midpoints along each mesh direction are computed using linear interpolation:

$${\varphi }_{i\pm 1∕2,j,k}=\frac{{\varphi }_{i,j,k}+{\varphi }_{i\pm 1,j,k}}{2},$$ (A10)

$${\varphi }_{i,j\pm 1∕2,k}=\frac{{\varphi }_{i,j,k}+{\varphi }_{i,j\pm 1,k}}{2},$$

$${\varphi }_{i,j,k\pm 1∕2}=\frac{{\varphi }_{i,j,k}+{\varphi }_{i,j,k\pm 1}}{2}.$$

Finally, the moduli of the electric field at the centers of the six faces of R_ijk are computed using bilinear interpolation. For the faces perpendicular to the x direction, we have

$$u_{i\pm 1∕2,j,k}=p_0{e}_c\sqrt{{\left({\mathbf{\nabla }}_x{\varphi }_{i\pm 1∕2,j,k}\right)}^2+{\left({\mathbf{\nabla }}_y{\varphi }_{i\pm 1∕2,j,k}\right)}^2+{\left({\mathbf{\nabla }}_z{\varphi }_{i\pm 1∕2,j,k}\right)}^2},$$

with

$${\nabla }_x{\varphi }_{i+1∕2,j,k}=\frac{{\varphi }_{i+1,j,k}-{\varphi }_{i,j,k}}{h_i},{\nabla }_x{\varphi }_{i-1∕2,j,k}=\frac{{\varphi }_{i,j,k}-{\varphi }_{i-1,j,k}}{h_{i-1}},$$ (A11)

$${\nabla }_y{\varphi }_{i\pm 1∕2,j,k}=\frac{{\varphi }_{i,j+1,k}+{\varphi }_{i\pm 1,j+1,k}-{\varphi }_{i,j-1,k}-{\varphi }_{i\pm 1,j-1,k}}{2h_{j-1}+2h_j},$$

$${\nabla }_z{\varphi }_{i\pm 1∕2,j,k}=\frac{{\varphi }_{i,j,k+1}+{\varphi }_{i\pm 1,j,k+1}-{\varphi }_{i,j,k-1}-{\varphi }_{i\pm 1,j,k-1}}{2h_{k-1}+2h_k}.$$

The values of u at the centers of the faces perpendicular to the y and z directions can be derived in the same way.

There is one nonlinear Eq. A8 for each of the (Nx+2)∗(Ny+2)∗(Nz+2) vertices in the mesh. The boundary conditions impose the values of the electrostatic potential on the outer faces of the mesh; therefore, there remains only N=Nx∗Ny∗Nz such equations, with N unknowns, i.e., the values of the electrostatic potential ϕ at these vertices. After proper ordering of these vertices we obtain a single nonlinear algebraic system of equations of the form

$$F\left(\mathbf{\varphi }\right)=A\left(\mathbf{\varphi }\right)\mathbf{\varphi }+H\left(\mathbf{\varphi }\right)-\mathbf{g}=0,$$ (A12)

where A(ϕ) is the “stiffness matrix,” H(ϕ) is the nonlinear term resulting from the ion atmosphere in the solvent and the vector g consists of the component Vol(R_ijk)f(r_ijk) for each mesh vertex. Each row of the matrix A corresponds to one point in the mesh. The row associated with the point r_ijk contains seven nonzero values given by

$$A_{ijk}={ϵ}_{i+1∕2,j,k}\frac{S_{jk}}{h_i}+{ϵ}_{i-1∕2,j,k}\frac{S_{jk}}{h_{i-1}}+{ϵ}_{i,j+1∕2,k}\frac{S_{ik}}{h_j}+{ϵ}_{i,j-1∕2,k}\frac{S_{ik}}{h_{j-1}}+{ϵ}_{i,j,k+1∕2}\frac{S_{ij}}{h_k}+{ϵ}_{i,j,k-1∕2}\frac{S_{ij}}{h_{k-1}},$$ (A13)

$$A_{i\pm 1,j,k}=-{ϵ}_{i\pm 1∕2,j,k}\frac{S_{jk}}{h_{i\pm }},$$

$$A_{i,j\pm 1,k}=-{ϵ}_{i,j\pm 1∕2,k}\frac{S_{ik}}{h_{j\pm }},$$

$$A_{i,j,k\pm 1}=-{ϵ}_{i,j,k\pm 1∕2}\frac{S_{ij}}{h_{k\pm }},$$

where h_i+=h_i, h_i−=h_i−1, h_j+=h_j, h_j−=h_j−1, h_k+=h_k, and h_k−=h_k−1. These seven values relate to the point itself and its six direct neighbors, forming a stencil of size 7. In the simple case of the Poisson equation, the stiffness matrix is constant and H(ϕ)=0; the system of equations is linear. In the cases of the PB and SMPB equations, the stiffness matrix is also constant while H(ϕ) is a vector that is nonlinear in ϕ. In the general case of the DPBL equation, A contains the nonlinear functions of ϕ. It is not difficult to show that A is symmetric in all three cases.

APPENDIX B: JACOBIAN OF THE NONLINEAR SYSTEM OF EQUATION

The exact Jacobian

The Newton method solves iteratively the system of nonlinear equations F(ϕ)=0 using the iteration

$${\mathbf{\varphi }}^{n+1}={\mathbf{\varphi }}^n-F^{\prime }{\left({\mathbf{\varphi }}^n\right)}^{-1}F\left({\mathbf{\varphi }}^n\right),$$ (B1)

where F^′(ϕ) is the Jacobian matrix of partial derivatives,

$$F^{\prime }\left(\mathbf{\varphi }\right)=\left[\frac{\delta F_{ijk}\left(\mathbf{\varphi }\right)}{\delta {\varphi }_a}\right],$$ (B2)

where ϕ_a stands for the electrostatic potential at any mesh position a and F_ijk corresponds to the nonlinear equation derived at position r_ijk in the mesh, given by Eq. A8.

From Eq. A12, we get

$$F^{\prime }\left(\mathbf{\varphi }\right)=A\left(\mathbf{\varphi }\right)+B\left(\mathbf{\varphi }\right)+H^{\prime }\left(\mathbf{\varphi }\right),$$ (B3)

where B is a perturbation matrix whose jth column is given by

$$B_j=\frac{\delta A}{\delta {\mathbf{\varphi }}_j}\mathbf{\varphi }.$$

In Appendix A we described how to compute the stiffness matrix A. We describe now how to obtain the two other terms B and H^′ needed to build F^′.

The derivative of the Helmholtz term H

The Helmholtz term H(ϕ) in Eq. A12 is a diagonal matrix corresponding to the contribution of the ionic atmosphere in the solvent. Its generic term H_ijk at position r_ijk is computed using Eq. A4.

Let ϕ_abc be the electrostatic position at position r_abc with a∊{i−1,i,i+1}, b∊{j−1,j,j+1}, and c∊{k−1,k,k+1}. Using Eq. A4, we get

$$\frac{\delta H_{ijk}}{\delta {\varphi }_{abc}}={\delta }_{ijk;abc}\left(-{\gamma }_{\text{ion}}\left({\mathbf{r}}_{ijk}\right)\frac{4\pi \beta e_c^2}{a^3{\mathcal{Z}}_{ijk}}\sum _{i=1}^{N_{\text{ion}}}{\lambda }_i{c}_i{z}_i^2{e}^{-\beta z_i{e}_c{\varphi }_{ijk}}\right)-\frac{H_{ijk}}{{\mathcal{Z}}_{ijk}}\frac{\delta {\mathcal{Z}}_{ijk}}{\delta {\varphi }_{abc}},$$ (B4)

with

$$\frac{\delta {\mathcal{Z}}_{ijk}}{\delta {\varphi }_{abc}}={\lambda }_{\text{dip}}\gamma \left({\mathbf{r}}_{ijk}\right)F_1\left(u_{ijk}\right)\frac{\delta u_{ijk}}{\delta {\varphi }_{abc}}-{\delta }_{ijk,abc}{\gamma }_{\text{ion}}\left({\mathbf{r}}_{ijk}\right)\beta e_c\sum _{i=1}^{N_{\text{ion}}}{\lambda }_i{z}_i{e}^{-\beta z_i{e}_c{\varphi }_{ijk}},$$ (B5)

where δ_ijk;abc=1 if {i,j,k}={a,b,c} and 0 otherwise and u_ijk and its derivatives can easily be computed from Eq. A9.

Note that the derivatives δu_ijk∕δϕ_abc are nonzero only if r_abc is in direct contact with r_ijk. This means that there are only seven nonzero terms in each row of the matrix H^′(ϕ), corresponding to a stencil of size seven.

The perturbation matrix B

Each column j of B is the product of the derivative of the stiffness matrix A with respect to ϕ_j with the field vector ϕ. We show how to compute the different derivatives of A.

From Appendix A, it is clear that the elements of the stiffness matrix corresponding to the mesh point r_ijk depend only on the values of the electrostatic potential at the 27 vertices in the direct neighborhood of this point (see Fig. 7). Let ϕ_abc be the electrostatic potential at position r_abc, with a∊{i−1,i,i+1}, b∊{j−1,j,j+1}, and c∊{k−1,k,k+1}. There are seven nonzero values [see Eqs. A13] in the row of A corresponding to position r_ijk; their derivatives with respect to ϕ_abc are

$$\frac{\delta A_{ijk}}{\delta {\varphi }_{abc}}=\frac{S_{jk}}{h_i}\frac{\delta {ϵ}_{i+1∕2,j,k}}{\delta {\varphi }_{abc}}+\frac{S_{jk}}{h_{i-1}}\frac{\delta {ϵ}_{i-1∕2,j,k}}{\delta {\varphi }_{abc}}+\frac{S_{ik}}{h_j}\frac{\delta {ϵ}_{i,j+1∕2,k}}{\delta {\varphi }_{abc}}+\frac{S_{ik}}{h_{j-1}}\frac{\delta {ϵ}_{i,j-1∕2,k}}{\delta {\varphi }_{abc}}+\frac{S_{ij}}{h_k}\frac{\delta {ϵ}_{i,j,k+1∕2}}{\delta {\varphi }_{abc}}+\frac{S_{ij}}{h_{k-1}}\frac{\delta {ϵ}_{i,j,k-1∕2}}{\delta {\varphi }_{abc}},$$ (B6)

$$\frac{\delta A_{i\pm 1,j,k}}{\delta {\varphi }_{abc}}=-\frac{S_{jk}}{h_{i\pm }}\frac{\delta {ϵ}_{i\pm 1∕2,j,k}}{\delta {\varphi }_{abc}},$$

$$\frac{\delta A_{i,j\pm 1,k}}{\delta {\varphi }_{abc}}=-\frac{S_{ik}}{h_{j\pm }}\frac{\delta {ϵ}_{i,j\pm 1∕2,k}}{\delta {\varphi }_{abc}},$$

$$\frac{\delta A_{i,j,k\pm 1}}{\delta {\varphi }_{abc}}=-\frac{S_{ij}}{h_{k\pm }}\frac{\delta {ϵ}_{i,j,k\pm 1∕2}}{\delta {\varphi }_{abc}}.$$

Equations B6 require the derivatives of the dielectric coefficients ϵ with respect to the 27 different ϕ_abc. The derivatives of the coefficients ϵ_i±1∕2,j,k are derived from Eq. A2,

$$\frac{\delta {ϵ}_{i\pm 1∕2,j,k}}{\delta {\varphi }_{abc}}=\gamma \left({\mathbf{r}}_{i\pm 1∕2,j,k}\right)\frac{\beta p_0^2{\lambda }_{\text{dip}}}{a^3{\mathcal{Z}}_{i\pm 1∕2,j,k}}\frac{\text{sinh}\left(u_{i\pm 1∕2,j,k}\right)-3u_{i\pm 1∕2,j,k}{F}_1\left(u_{i\pm 1∕2,j,k}\right)}{u_{i\pm 1∕2,j,k}^2}\frac{\delta u_{i\pm 1∕2,j,k}}{\delta {\varphi }_{abc}}-\gamma \left({\mathbf{r}}_{i\pm 1∕2,j,k}\right)\frac{\beta p_0^2{\lambda }_{\text{dip}}{F}_1\left(u_{i\pm 1∕2,j,k}\right)}{a^3{\mathcal{Z}}_{i\pm 1∕2,j,k}^2}\frac{\delta {\mathcal{Z}}_{i\pm 1∕2,j,k}}{\delta {\varphi }_{abc}},$$ (B7)

where u_i±1∕2,j,k and its derivatives are computed from Eq. A11, and Z_i±1∕2,j,k and its derivatives are computed with analogs of Eqs. A4, B5, respectively. Similar expressions are obtained for the derivatives of the coefficients ϵ_i,j±1∕2,k and ϵ_i,j,k±1∕2.

Note that since A is symmetric and H is diagonal, it is clear that the Jacobian matrix is symmetric; this implies that we only need to compute and store 14 values for each value ϕ_ijk, namely, the derivatives of F_ijk with respect to ϕ_ijk, ϕ_i+1,j,k, ϕ_i−1,j+1,k, ϕ_i,j+1,k, ϕ_i+1,j+1,k, ϕ_{i−1,j−1,k+1}, ϕ_i,j−1,k+1, ϕ_{i+1,j−1,k+1}, ϕ_i−1,j,k+1, ϕ_i,j,k+1, ϕ_i+1,j,k+1, ϕ_{i−1,j+1,k+1}, ϕ_i,j+1,k+1, and ϕ_i+1,j+1,k+1.

The inexact Jacobian

In the simpler cases of the PB and SMPB equations, the stiffness matrix is constant, and H_ijk only depends on ϕ_ijk. This property makes the Newton method very attractive for solving the corresponding nonlinear systems of equations; the Jacobian matrix can be computed at very low computing cost as all its off-diagonal elements are constant and can be precomputed once during setup and only its diagonal terms need to be updated at each step. In addition, there are only seven nonzero elements in F^′(ϕ), and since the matrix is symmetric only four of these need to be computed and stored (see Holst and Saied for details).¹⁶

Computing the exact Jacobian for the DPBL equation is more demanding; it needs to be performed at each iteration and the memory footprint is large as it requires space for 14 values for each interior point in the mesh. To reduce the computational cost and the memory footprint required by the exact Jacobian matrix, we propose to build an approximation that neglects the perturbation matrix B as well as the off-diagonal elements of the derivatives of H,

$$F_{\text{approx}}^{\prime }\left(\mathbf{\varphi }\right)=A\left(\mathbf{\varphi }\right)+H_{\text{approx}}^{\prime }\left(\mathbf{\varphi }\right),$$ (B8)

where the only nonzero elements in $H_{\text{approx}}^{\prime }$ are given by

$$\frac{\delta H_{\text{approx};ijk}}{\delta {\varphi }_{ijk}}=-{\gamma }_{\text{ion}}\left({\mathbf{r}}_{ijk}\right)\frac{4\pi \beta e_c^2}{a^3{\mathcal{Z}}_{ijk}}\sum _{i=1}^{N_{\text{ion}}}{\lambda }_i{c}_i{z}_i^2{e}^{-\beta z_i{e}_c{\varphi }_{ijk}}.$$ (B9)

Since A is a symmetric matrix obtained with a stencil of size seven, $F_{\text{approx}}^{\prime }$ is also a symmetric matrix with seven nonzero elements per row, out of which only four need to be stored.