A shared random effect parameter approach for longitudinal dementia data with non-ignorable missing data

SUMMARY

A significant source of missing data in longitudinal epidemiologic studies on elderly individuals is death. It is generally believed that these missing data by death are non-ignorable to likelihood based inference. Inference based on data only from surviving participants in the study may lead to biased results. In this paper we model both the probability of disease and the probability of death using shared random effect parameters. We also propose to use the Laplace approximation for obtaining an approximate likelihood function so that high dimensional integration over the distributions of the random effect parameters is not necessary. Parameter estimates can be obtained by maximizing the approximate log-likelihood function. Data from a longitudinal dementia study will be used to illustrate the approach. A small simulation is conducted to compare parameter estimates from the proposed method to the ‘naive’ method where missing data is considered at random.

1. INTRODUCTION

Many prospective epidemiological studies on elderly individuals rely on using follow up waves, usually several years apart, for the examination of a particular disease status, such as dementia or Alzheimer’s disease. These cohort studies are often complicated by the presence of missing data. Many study subjects die before the next examination wave. Some refuse further participation in the study and some move out of the study area. The latter two sources of missing data may perhaps be minimized or eliminated by aggressive operational measures. However, for studies on elderly subjects, death is an inevitable source of missing data which cannot be eliminated by operational improvement. For those deceased subjects, disease status prior to death is not ascertained. Under the assumption of missing completely at random (MCAR) or missing at random (MAR) of the missing data mechanism, using the terminology of Little and Rubin [1], valid inference may still be derived provided appropriate likelihood or Bayesian approaches are taken and all covariates contributing to missing data process are included in the model [2]. However, most medical studies following subjects with various diseases in cohort studies have found that these subjects are more likely to die than non-diseased subjects. Hence there are reasons to suggest the data missing by death are probably non-ignorable, indicating that the missing by death may somehow relate to disease status. Estimation procedures without adjusting for this type of missing data may lead to biased conclusions.

Statistical inference on non-ignorable missing data has mostly concentrated in two areas: the selection model approach and the pattern mixture model approach. In the selection model approach, first proposed by Diggle and Kenward [3], the missing data mechanism was modelled to depend on the missing outcome variable as well as covariates. Gao and Hui [4] extended the selection model approach from continuous outcomes to binary outcomes for estimating the incidence of dementia adjusting for missing data due to death. One difficulty with using the selection model approach is that parameter estimates obtained from the selection model, especially in the model for missing data, are sometimes difficult to interpret.

The pattern mixture model approach, on the other hand, models the probability of missing data first, then appends to the joint likelihood disease outcome models conditional on the missing data status. One problem with the pattern mixture model approach is that the modeling of disease to be dependent on survival status does not seem to follow the chronological order of these events. Pros and cons of these two approaches for non-ignorable missing data have been thoroughly discussed by Little [5].

The shared random effect parameter approach has a very intuitive appeal to biomedical researchers who generally believe that there may be some latent quantity underlying a person’s susceptibility to both disease and death. This latent quantity may represent genetic or environmental risk factors yet to be identified. A shared random effect parameter approach has been used by Lancaster and Intrator [6] on joint modelling of medical expenditures and survivals, Pulkstenis et al. [7] and Ten Have et al. [8] on comparing pain relievers accounting for informative drop out in the form of re-medication, to name just a few recent publications. Most authors have chosen models in specific forms for both disease outcome and missing data mechanism so that the joint likelihood function will have closed form expression after integrating over the random effect parameters, with the exception of Ten Have et al. [8] where numerical approximations are used to derived maximum likelihood estimates with logistic model assumptions for the disease outcome.

In this paper I propose to use the shared random effect parameter models for the analysis of longitudinal dementia data with missing data by death. Maximum likelihood estimation with Laplace approximation can be used for parameter estimation. We illustrate the proposed models and estimation procedure with a small simulation study which uses data from the Indianapolis Dementia Project.

2. NOTATIONS AND GENERAL MODELS

Let y_ij be a binary variable denoting disease status ascertained from the ith subject at the jth examination wave, i =1,…,N, j =1,…,J_i. y_ij = 1 indicates diagnosed disease and y_ij =0 non-disease. Let D_ij be the variable for survival status for the ith subject at the jth examination wave. D_ij = 1 indicates the ith subject died before the jth wave. We restrict our methodology to situations where the examination waves are approximately equally spaced. Let X_ij be the set of covariates associated with the fixed effect for disease outcome and Z_ij be the set of covariates associated with the fixed effect for death. Let γ_i be a m × 1 vector of unobserved random effects contributing to the probabilities of disease and death. γ_i can be thought of as a measure of ‘physical toughness’ of the person to disease and death. Let W_ij and U_ij be the set of covariates associated with the random effect in the disease model and the death model, respectively.

We assume a general disease model for the disease outcome: Let

$$p_{ij}=\mathrm{Prob}(y_{ij}=1\mid y_{ij-1}=0;{\mathbf{X}}_{ij},{\mathbf{W}}_{ij})=\eta ({\mathbf{X}}_{ij}\beta +{\mathbf{W}}_{ij}{\Sigma }^{1∕2}{\gamma }_i),j\ge 2$$ (1)

where β is the fixed effect parameter. We assume that γ_i follows a distributional function H(γ_i), with E(γ_i)=0 and Var(γ_i)=I_m, where I is a m × m identity matrix, and Σ′Σ is a positive definite variance–covariance matrix. In other words we define the conditional probability of new disease to relate linearly to fixed and random effects by some link function η. The quantity p_ij has the epidemiological interpretation of disease incidence.

We also define the following model for death:

$${\pi }_{ij}=\mathrm{Prob}(D_{ij}=1\mid D_{ij-1}=0,{\mathbf{Z}}_{ij},{\mathbf{U}}_{ij})=\xi ({\mathbf{Z}}_{ij}\alpha +{\mathbf{U}}_{ij}{\Delta }^{1∕2}{\gamma }_i),j\ge 2$$ (2)

where α is the fixed effect parameter and γ_i is as defined in the disease model. Δ′Δ is a positive definite variance–covariance matrix.

The above disease and death models are in the most general forms.

Assuming that y_ij and D_ij are independent given γ_i, the joint likelihood function of y and D is

$$L=\int f(\mathbf{y}\mid \gamma )g(\mathbf{D}\mid \gamma )\mathrm{d}H\left(\gamma \right)$$ (3)

The derivation of maximum likelihood estimates from the joint likelihood function above usually requires high dimensional integration over the distributions of the random effect parameters, with the exception of some specific forms of link functions where closed form expression is available. Pulkstenis et al. (1998) used a log–log link for the binary outcomes and a log–log link for the drop-out model. A closed form expression for the likelihood function was achieved for these specific models.

In general, the Laplace method can be used to approximate the integral in the likelihood function (3). We consider here the situation where γ~N(0, I). An alternative approximation, used by Ten Have et al. (1998), is a binomial approximation to the normal distribution in the above likelihood function.

With the normal distribution assumption for γ, and letting κ(y, D/γ)=f(y/γ)g(D/γ), the likelihood function can be rewritten as

$$L=\frac{1}{\sqrt{2\pi }}\int {\mathrm{e}}^{\log \kappa -\frac{1}{2}{\gamma }^{\prime }\gamma }\mathrm{d}\gamma$$ (4)

We can expand $\log \kappa -\frac{1}{2}{\gamma }^{\prime }\gamma$ at ${\widehat{\gamma }}_0$ by Taylor series to the 2nd order, where ${\widehat{\gamma }}_0$ maximizes $\log \kappa -\frac{1}{2}{\gamma }^{\prime }\gamma$

$$\begin{array}{cc}\hfill L\approx & \frac{1}{\sqrt{2\pi }}\int \exp \{\left(\log {\kappa }_{{\gamma }_0}-\frac{1}{2}{\widehat{\gamma }}_0^{\prime }{\widehat{\gamma }}_0\right)+\left({\phantom{\mid }\frac{\partial \log \kappa }{\partial \gamma }\mid }_{{\widehat{\gamma }}_0}-{\widehat{\gamma }}_0\right)(\gamma -{\widehat{\gamma }}_0)\phantom{\}}\hfill \\ \hfill & \phantom{\{}+\frac{1}{2}{(\gamma -{\widehat{\gamma }}_0)}^{\prime }\left({\phantom{\mid }\frac{{\partial }^2\log \kappa }{\partial {\gamma }^2}\mid }_{{\widehat{\gamma }}_0}-I\right)(\gamma -{\widehat{\gamma }}_0)\}\mathrm{d}\gamma \hfill \\ \hfill =\mathrm{e}& {}^{\log {\kappa }_0-(1∕2){\widehat{\gamma }}_0^{\prime }{\widehat{\gamma }}_0}{\left({\phantom{\mid }I-\frac{{\partial }^2\log \kappa }{\partial {\gamma }^2}\mid }_{{\widehat{\gamma }}_0}\right)}^{-(1∕2)}\hfill \end{array}$$ (5)

Notice that the first order term in the Taylor series expansion in (5) is zero because the first derivative of $\log \kappa -\frac{1}{2}{\gamma }^{\prime }\gamma$ is zero at ${\widehat{\gamma }}_0$. The remaining terms in the integral was evaluated by taking expectations with respect to a normal variate having mean ${\widehat{\gamma }}_0$ and variance ${(I-({\partial }^2\log \kappa ∕\partial {\gamma }^2\left){\mid }_{{\widehat{\gamma }}_0}\right)}^{-1}$. The approximate log-likelihood function is therefore

$$l=\log L\approx \log {\kappa }_0-\frac{1}{2}{\widehat{\gamma }}_0^{\prime }{\widehat{\gamma }}_0-\phantom{\mid }\frac{1}{2}\log {\mid I-\frac{{\partial }^2\log \kappa }{\partial {\gamma }^2}\mid }_{{\widehat{\gamma }}_0}\mid$$ (6)

Similar approximation approaches have been used by Solomon and Cox [9], Breslow and Lin [10] and Lin [11] in approximating the likelihood function of random effect generalized linear models. Notice that the random effect γ is no longer present in the approximate log-likelihood function. We can then derive maximum likelihood estimates of β, α, Σ, and Δ using a Newton–Raphson algorithm.

In summary three steps are involved in parameter estimation from the shared random effect models:

1. obtain ${\widehat{\gamma }}_0$ by maximizing:

   $$\log f(\mathbf{y}\mid \gamma )+\log g(\mathbf{D}\mid \gamma )-\frac{1}{2}{\gamma }^{\prime }\gamma$$
2. substitute ${\widehat{\gamma }}_0$ in the approximate log-likelihood function:

   $$l^{\ast }=\log f(\mathbf{y}\mid \gamma )\mid {\widehat{\gamma }}_0+\log g(\mathbf{D}\mid \gamma )\mid {\widehat{\gamma }}_0-\frac{1}{2}{\widehat{\gamma }}_0^{\prime }{\widehat{\gamma }}_0-\phantom{\mid }\frac{1}{2}\log {\mid I-\frac{{\partial }^2\log \kappa }{\partial {\gamma }^2}\mid }_{{\widehat{\gamma }}_0}\mid$$

3. maximize l* to obtain $\widehat{\beta }$, $\widehat{\alpha }$, $\widehat{\Sigma }$ and $\widehat{\Delta }$.

3. THE INDIANAPOLIS DEMENTIA STUDY

The Indianapolis dementia study is an on-going prospective epidemiological study on dementia and Alzheimer’s disease [12, 13]. The study subjects are African Americans age 65 and over living in Indianapolis. The primary aim of the study is to estimate the prevalence and incidence rates of dementia and Alzheimer’s disease and identify potential risk factors. The study is designed to have one baseline wave and three follow up waves two years apart. Data are currently available on two follow up waves. At study baseline 2212 subjects participated in the study providing exposure history on potential risk factors. One risk factor that has generated considerable interest in the dementia field is the level of education. Low education has been suggested by numerous studies to be a risk factor for dementia. However, there are inconsistencies in the reported strength of this association between cross-sectional and prospective studies with stronger associations reported by cross-sectional studies. Evidence from cross-sectional studies are sometimes dismissed because education has been shown to influence performance on neuropsychological tests used in the diagnosis of dementia. Longitudinal studies, where cognitive changes within subjects are considered as evidence of cognitive decline instead of comparisons made between subjects cross-sectionally, are believed to yield more valid answer to the association between low education and dementia. One problem with many longitudinal studies, however, is that subjects with low education also die earlier than the ones with high education, thus raising the possibility of non-ignorable missing data. In the Indianapolis dementia study, a total of 551 subjects died during the course of the study before the 2nd follow up wave yielding incomplete responses on disease status. Among the subjects with low education defined as having 6 years or less schooling in this population, 34 per cent died before the second follow up compared to 23 per cent in the high education group. Analyses ignoring deceased subjects are likely to find a weaker association between education and dementia.

Since the data from the Indianapolis dementia study is complicated by complex sampling schemes to ascertain disease status at each examination wave, we conducted a simulation study to investigate the performance of the Laplace approximation on parameter estimation from the shared random effect models.

4. A SIMULATION STUDY

The probability of incident dementia, p_ij, can be modeled by a logistic function:

$$\mathrm{logit}{p}_{ij}={\mathbf{X}}_{ij}\beta +{\mathbf{W}}_{ij}{\Sigma }_{{\gamma }_i},i=1,\dots ,N,j=1,\dots ,J_i$$

We assume that the ith subject has J_i non-missing observations on disease status y.

The joint probability of disease outcomes can be written in terms of conditional probabilities:

$$\begin{array}{cc}\hfill f(y_{i1},\dots ,y_{i{J}_i})=& f\left(y_{i1}\right)f(y_{i2}\mid y_{i1}),\dots ,f(y_{i{J}_i}\mid y_{i{j}^{\prime }},j^{\prime }<J_i)\hfill \\ \hfill =& p_{i1}^{y_{i1}}{(1-p_{i1})}^{(1-y_{i1})}{\left[p_{i2}^{y_{i2}}{(1-p_{i2})}^{(1-y_{i2})}\right]}^{(1-y_{i1})}\dots \hfill \\ \hfill & \times {\left[p_{iJ}^{y_{i{J}_i}}{(1-p_{i{J}_i})}^{(1-y_{i{J}_i})}\right]}^{\prod _{j^{\prime }=1}^{J_i-1}(1-y_{i{j}^{\prime }})}\hfill \end{array}$$ (7)

We will also use a logistic regression model for death:

$$\mathrm{logit}{\pi }_{ij}={\mathbf{Z}}_{ij}\alpha +{\mathbf{U}}_{ij}\Delta {\gamma }_i$$

Hence the probability function for death is

$$g\left(D_{ij}\right)=\prod _{j=2}^{J_i}p{\left(D\right)}_{ij}^{D_{ij}}{(1-p(D{)}_{ij})}^{(1-D_{ij})}$$

Covariates from the Indianapolis dementia study were used for the simulation. We used a logistic regression model with random intercept and random slope for disease for the simulation. Specifically, we used the following disease model:

$$\mathrm{logit}{p}_{ij}={\beta }_0+{\beta }_1\text{age}+{\beta }_2\text{Female}+{\beta }_3\text{Low education}+{\sigma }_1{\gamma }_1+(\text{age}-65){\sigma }_2{\gamma }_2$$ (8)

Here the variance covariance matrix for γ is

$${\Sigma }^{\prime }\Sigma =\left[\begin{array}{cc}{\sigma }_1^2\hfill & 0\hfill \\ 0\hfill & {\sigma }_2^2\hfill \end{array}\right].$$

The covariate age used in the disease model is the age of the participant at each examination wave.

We also used a logistic regression model with random intercept and random slope for the death model:

$$\mathrm{logit}p(D{)}_{ij}={\alpha }_0+{\alpha }_1\text{age}+{\alpha }_2\text{Female}+{\alpha }_3\text{Low education}+{\delta }_1{\gamma }_1+(\text{age}-65){\delta }_2{\gamma }_2$$ (9)

The variance–covariance matrix for γ is

$${\Delta }^{\prime }\Delta =\left[\begin{array}{cc}{\delta }_1^2\hfill & 0\hfill \\ 0\hfill & {\delta }_2^2\hfill \end{array}\right]$$

Regression coefficients in the simulation were chosen so that the percentages of diseased and died in the simulated datasets are similar to those observed in the Indianapolis dementia data. Parameter estimates from 100 simulations are presented in Table I. For comparison purposes, we also included in Table I the so-called ‘naive’ estimates where two separate logistic regression models are fit, one for the dementia outcome and one for the survival outcome. The ‘naive’ approach assumes that the missing data by death is not related to the disease model and is shown here to underestimate the education effect on disease. The parameter estimate for education from the shared random effect model approach corrected some of the downward bias of the naive estimate, but still slightly underestimates the true parameter.

Table I.

Parameter estimates using Laplace approximation for the shared random effect parameter models (n = 100). Empirical standard errors calculated from the 100 simulated datasets are included in the parentheses.

Parameters	True value	‘Naive’ estimate	SREP estimate
Disease model
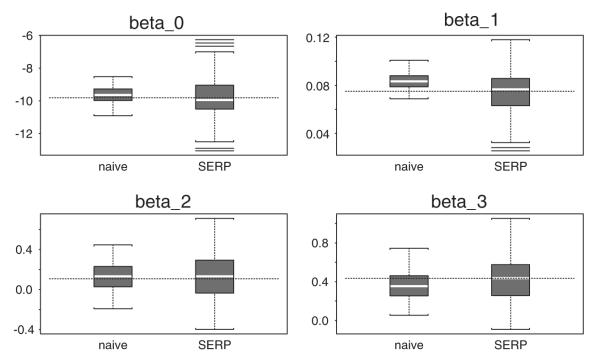
β0 (intercept)	−9.8057	−9.6096 (0.0518)	−9.8028 (0.1341)
β1 (age)	0.0750	0.0836 (0.0007)	0.0742 (0.0018)
β2 (female)	0.1069	0.1317 (0.0148)	0.1360 (0.0236)
β3 (low education)	0.4346	0.3547 (0.0141)	0.4271 (0.0224)
σ1	0.2	—	0.2743 (0.0012)
σ2	0.2	—	0.2952 (0.0014)
Death model
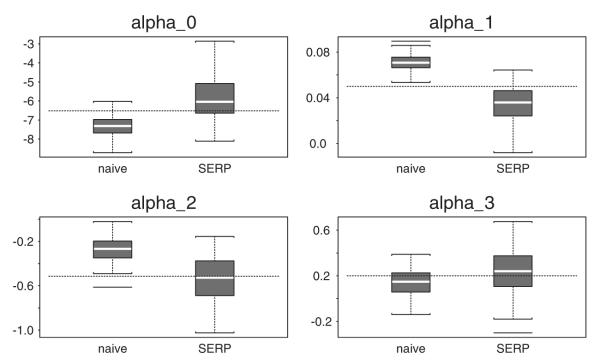
α0 (intercept)	−6.5100	−7.3345 (0.0515)	−5.8938 (0.1075)
α1 (age)	0.0500	0.0708 (0.0006)	0.0350 (0.0014)
α2 (female)	−0.5147	−0.2757 (0.0109)	−0.5318 (0.0198)
α3 (low education)	0.2000	0.1348 (0.0109)	0.2342 (0.0192)
δ1	0.2	—	0.2644 (0.0019)
δ2	0.2	—	0.2938 (0.0020)

In Figures 1 and 2 we present box plots of the parameter estimates from the two methods. The white line in each box plot is the median of the estimates and the dotted line represents the true parameter values. As is shown by these figures, the variability in the parameter estimates given by the shared random effect parameter models is much larger than those of the naive estimates.

Figure 1.

Parameter estimates for the disease model.

Figure 2.

Parameter estimates for the death model.

4. DISCUSSION

In this paper I propose to use the shared random effect parameter models for the joint modeling of disease status and missing data by death in longitudinal dementia studies. The two models assume a common latent quantity attributing to the probabilities of both disease and death, while allowing the distribution of this random effect to differ between the two models by including separate variance–covariance parameters in the models. While the conceptualization of the models is straightforward, parameter estimation for the general model is challenging. There are three approximation methods for avoiding the high dimensional integration in the joint likelihood function. Some of the methods have the additional assumption of normality of the random effect distribution. The first is the Gaussian quadrature points where the integration over the normal distribution is approximated by summing over selected quadrature points with probability weights attached. The method of quadrature points can be computationally intensive if either the number of random effects is large, the number of observations is large, or there are many quadrature points. The second method is the binomial approximation used by Ten Have et al. [8] which has essentially the same computational challenges as the Gauss quadrature method. The third method is the Laplace approximation used in this paper. The Laplace method is applicable to any parametric distributions, although in this paper we considered only the normal distribution. The Laplace approximation is attractive in that it offers the approximate likelihood function in an algebraic form so that standard techniques for deriving maximum likelihood estimates such as the Newton–Raphson algorithm can be used. However, results from our limited simulation indicate less than satisfactory performance for the Laplace method on some parameter estimates. Two sources of potential errors are suspected. One is in the accuracy of the estimation of the expansion point ${\widehat{\gamma }}_0$. Another is in whether Taylor series to the second order is accurate enough to approximate the target function. More extensive simulations are needed to investigate the properties of the approximate maximum likelihood estimates from the Laplace approximation. It is also interesting to compare parameter estimates from the Laplace approximation to those obtained by Gauss quadrature points or the binomial approximation in more extensive simulations.

The modelling framework used here bears resemblance to generalized random effect models used for longitudinal data where a single random effect is introduced in all observations from the same subject to induce a pattern of correlation. The difference between the longitudinal data setting and our modelling is that the observations in the longitudinal setting all belong to a single response variable and are generated random outcomes from similar stochastic processes, while in our models we have two distinct stochastic processes linked by two related, but different, random effects. In the cases of longitudinal data of the generalized linear models the penalized quasi-likelihood (PQL) proposed by Breslow and Clayton [14] has been shown to adequately estimate the fixed effect parameters in large samples. It is to be noted that the PQL uses the Laplace method for approximating the quasi-likelihood function.

The current paper has focused narrowly on parameter estimation from the shared random effect parameter models. More research is needed for variance estimation, hypothesis testing regarding model parameters and model diagnostics. Although my motivation is rooted in the dementia data, the methodology is applicable to a wide variety of problems with non-ignorable missing data.