Computer-based analysis of the binding steps in protein complex formation

Abstract

Computer models were used to examine whether and under what conditions the multimeric protein complex is inhibited by high concentrations of one of its components—an effect analogous to the prozone phenomenon in precipitin tests. A series of idealized simple “ball-and-stick” structures representing small oligomeric complexes of protein molecules formed by reversible binding reactions were analyzed to determine the binding steps leading to each structure. The equilibrium state of each system was then determined over a range of starting concentrations and K_ds and the steady-state concentration of structurally complete oligomer calculated for each situation. A strong inhibitory effect at high concentrations was shown by any protein molecule forming a bridge between two or more separable parts of the complex. By contrast, proteins linked to the outside of the complex by a single bond showed no inhibition whatsoever at any concentration. Nonbridging, multivalent proteins in the body of the complex could show an inhibitory effect or not depending on the structure of the complex and the strength of its bonds. On the basis of this study, we suggest that the prozone phenomenon will occur widely in living cells and that it could be a crucial factor in the regulation of protein complex formation.

In the precipitin reaction widely used by immunologists, increasing amounts of soluble antigen are added to a series of tubes each containing a fixed amount of antibody-containing serum. As the antigen increases, the quantity of precipitate also increases up to a maximum and then declines. The basis for this phenomenon, for which the term “prozone” was originally used (1, 2), is well understood and depends on the fact that the precipitates are made from a three-dimensional lattice of antigen and antibody molecules (3). Macroscopic precipitates form only when antibody and antigen are in optimal proportions, and if either molecule is present in excess, small soluble complexes are produced instead. With excess antigen, for example, the soluble complexes consist of antibody molecules surrounded by multiple molecules of antigen.

There is reason to think that a similar effect may occur in the formation of multimeric protein complexes in living cells. Many if not most protein molecules in a living cell are part of multiprotein assemblies held together by noncovalent bonds, such as multimeric enzymes and receptor complexes (4–8). Such complexes have a definite structure and composition, and their formation depends in part on a series of diffusion-limited binding reactions influenced by the concentrations of participating protein molecules and their binding affinities for each other. Thus, if one species is present at much higher levels than the others, we might anticipate that something similar to the prozone phenomenon could operate. That is, we might find that formation of the structurally complete complex would be suppressed at the expense of smaller, incomplete clusters of proteins. Because the function of most protein complexes depends on their having a complete complement of proteins, a prozone effect, if it existed, could lead to anomalous or unexpected phenotypes when particular proteins are expressed at high levels, for example by genetic manipulations.

Theoretical work by Goldberg and others provides equations that predict the quantity of antibody–antigen precipitate for given starting concentrations of antigen and antibody (9, 10). However, these calculations embody a number of simplifying assumptions, such that all bonds are equal in strength and that intra-aggregate reactions yielding cyclical structures do not occur, that do not apply to small oligomeric clusters of proteins. Indeed, there is at present no easy route by which one could decide how much protein complex of defined structure will be produced from a mixture of its component proteins. Even if all of the binding steps leading to that complex and their individual K_d values were known, which is almost never the case, these would still give rise to a series of nonlinear binding equations for which no general analytical solution exists.

We have examined this issue using a theoretical computer-based approach. Customized computer routines were used (i) to deduce the binding steps leading to one of a number of idealized structures, each representing a small oligomeric complex of proteins, and (ii) to calculate, by numerical integration or other approximation method, the equilibrium concentration of each structure for a range of starting concentrations of its constituent proteins. The results of this study were analyzed, in particular, to determine when and to what extent the prozone phenomenon may be expected to occur during protein complex formation.

METHODS

The assembly of protein molecules into multimeric assemblies by diffusion-limited binding reactions was analyzed by means of a custom-written computer program, here referred to as oligo-d. In this program, the user specifies a set of protein species, each of which has one or more binding sites. The proteins are then allowed to come together in combinatorial fashion and to make bonding relationships permitted by the specificity of their binding sites. By giving precedence to closed structures, which maximize the number of bonds formed, the program avoids unwanted polymerization and terminates with a oligomeric complex of defined structure. The list of binding reactions and intermediate complexes generated in this process may then be used to calculate the steady state of the system. A graphical version of the oligo-d program is described elsewhere (11) and is available from http://www.zoo.cam.ac.uk/zoostaff/levin/index.htm.

Binding Steps.

The oligo-d algorithm builds an oligomeric complex from a starting list of protein species each with a set of binding sites. For example, a simple starting set might be A (1, 1) and B (2, 20) where 1, 2, and 20 are numbers designating binding sites. A set of bonding rules then controls the specificity and strength of the binding sites so that, for example, 1 and 2 pair together with a designated strength and binding site 20 undergoes homophilic binding with another 20, again with a designated strength. The program then takes pairs of molecules iteratively from the list and compares their binding sites. If sites on the two proteins match, and if other criteria specified below are fulfilled, then a new oligomeric complex is made containing the two proteins. The new species is added to the list, and a new binding reaction is formulated. Thus, if protein A and protein B are tested, binding sites 1 and 2 will associate through noncovalent bonds to produce the complex AB and create the association reaction: A + B <=> AB. Similarly, two B molecules will associate to form the complex BB through the association reaction B + B <=> BB. The two new complexes, AB and BB, will be added, in this case, to the list of oligomeric species and be included in subsequent iterations of the pairwise binding test.

Both AB and BB have remaining nascent binding sites through which they can add other proteins; AB has unfilled sites (1, 20), and BB has unfilled sites (2, 2). Continuation of the combinatorial process will therefore generate larger complexes through additional binding reactions. In fact, like most collections of proteins operating under the rules so far described, A, B, AB, and BB would generate an indefinitely large number of polymeric species, such as BAB, ABBAB, BABBAB, and so on. The problem of unwanted polymer formation is avoided by, in effect, forcing the assembly of proteins to close back on itself wherever possible. Once a bond has formed between two species, then the program examines the product made and completes any further bonds that are possible. Each protein aggregate also is tested to see if a smaller, more compact oligomer already in the list of species can be made with the same proteins, and, if it can, the new, larger complex is discarded. The biochemical justification for this step is that most protein complexes in a cell do have a compact, defined structure so that other factors must exist, not included by our simple ball-and-stick representation, that add extra stability to such configurations. Most bonding interactions between real proteins have specific spatial orientations, for example, that can constrain them into a compact, closed structure.

Pairwise matching of species and formation of bonds and reaction steps where possible continue until the list of species no longer increases in length. The “target oligomer” is the largest oligomer formed at this stage—that with no remaining unfilled bonds. At this stage, a list of oligomeric species and binding reactions leading to the target oligomer is displayed as illustrated in Fig. 1. The validity of the sets of binding reactions produced can be confirmed by inspection although this can be a tedious process for larger complexes. These sets also have been checked by means of a second, graphical program for the analysis of oligomer formation, which uses a different algorithm (11).

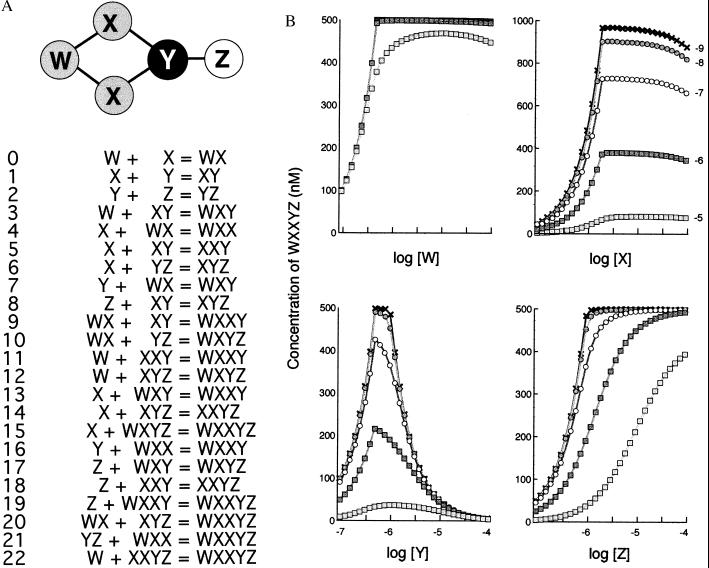
Figure 1.

(A) The WXXYZ oligomer. Topological structure of the oligomer together with the binding reactions by which it assembles from proteins W, X, Y, and Z. (the significance of different levels of gray in the structure are explained later). (B) Equilibrium concentrations of WXXYZ oligomer for different concentrations of W, X, Y, or Z. The binding reactions shown in A were solved by numerical integration for various starting concentrations and K_ds. Initial concentrations of test proteins were as indicated on the abscissa and otherwise were held constant at 1 μM (X). Each bond in the WXXYZ oligomer was assigned the same strength, corresponding to a K_d value of 10⁻⁵ M (open squares), 10⁻⁶ M (filled squares), 10⁻⁷ M (open circles), 10⁻⁸ M (filled circles), or 10⁻⁹ M (crosses).

Assigning K_ds.

Once a complete set of binding reactions has been created, then their dissociation constants (K_ds) are calculated from the strengths of individual bonds and the starting concentrations of the proteins. (For convenience, bond strengths are represented in the program as the number of hydrogen bonds they contain; if we assume that each hydrogen bond has a bond strength of 1.4 kcal/mol, then N such bonds will give a protein–protein binding affinity of N × 1.4 kcal/mol corresponding to a K_d of 10^−N M.) To relate the results to the conditions inside a living cell, bonds were usually assigned K_d values in the range of 10⁻⁴ to 10⁻¹⁰ M, which is the same as for enzyme–substrate complexes, and starting concentrations ranged from 0.1 μM to 0.1 mM corresponding to typical values for cytosolic enzymes (12, 13).

Equilibrium Concentrations.

Each initial protein species is then assigned a starting concentration, and the equilibrium state of the system is calculated by numerical integration. oligo-d uses a customized algorithm that traverses the list of reactions, solving each individual reaction in turn (as if run in isolation to equilibrium). This procedure is repeated until each reaction is within a specified concentration (the sum of starting concentrations divided by 10⁻¹⁰) of equilibrium. A fortuitous aspect of this study is that the accuracy of the results can be checked easily by calculating the apparent binding constant from the steady-state concentrations and comparing these to the K_d values initially assigned. In every case reported here, K_d values for all reactions were within 0.1% of the value specified by the user; the accuracy with which the concentration of major species, such as the target complex, was estimated was considerably greater than that.

RESULTS

oligo-d was used to explore the influence of protein concentrations and dissociation constants (K_ds) on the formation of a range of small complexes of arbitrary design. The results may be illustrated with reference to a pentameric oligomer WXXYZ produced by 23 binding reactions involving a total of 15 different molecular species (Fig. 1A). The range of possible K_ds and protein concentrations for even this small structure is enormous, and the survey initially was limited to situations in which each bond had the same binding strength, in the range 10⁻⁵ to 10⁻¹⁰ M. Each type of protein in the complex was then varied in turn, from a concentration of 10⁻⁷ to 10⁻⁴ M and the amount of final WXXYZ oligomer predicted by means of the oligo-d program (Fig. 1B). It may be seen that, under these conditions, protein Y showed a dramatic inhibitory effect. Thus, with bond K_ds of 10⁻¹⁰ M and starting concentrations of 1 μM, 490 nM of the WXXYZ complex is produced whereas if protein Y is then increased to 10 μM, leaving all other parameters unchanged, then only 50 nM of WXXYZ is produced, a reduction of ≈90%. Reducing the strengths of the bonds (increasing their K_ds) reduced the sharpness of this prozone effect (as well reducing the total yield of complex); conversely, K_d values below 10⁻¹⁰ M produced an even steeper fall in complex concentration as Y increased (not shown).

None of the other proteins in the WXXYZ complex showed a pronounced prozone effect. Protein Z displayed a particularly simple set of hyperbolic curves, each rising asymptotically to the maximum concentration of complex and with no evidence of inhibition. Proteins W and X had a similar profile but both showed a slight negative slope at certain K_d values. As suggested from this observation, when the test was extended to very high concentrations (>10 mM) of W and X, then significant suppression of complex was obtained with each protein (not shown).

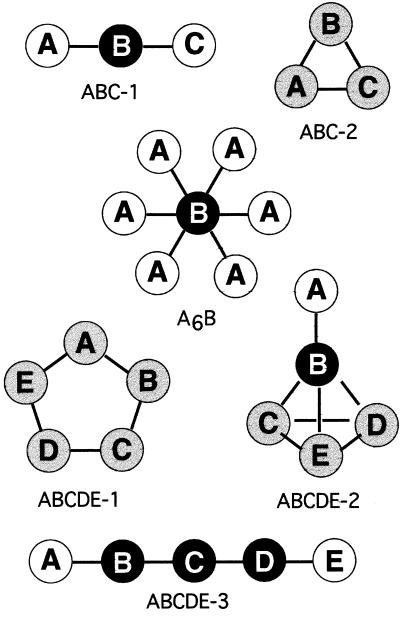
A similar procedure was repeated for more than 30 simple oligomeric structures, including linear, branched, and cyclic structures. For each structure, a series of binding reactions was generated by the program and then used to predict the steady-state concentration of the oligomer for a range of starting concentrations and K_d values (Fig. 2). A marked prozone effect, comparable to that shown by protein Y in Fig. 1, was found in some but not all oligomers tested. Examination of the geometry of these different complexes revealed that the strongest effect was produced by proteins that form a single link or bridge between two separable parts of the complex (indicated by black filled circles in Fig. 2). The effect was especially sharp for complexes such as A₆B in Fig. 2, in which many proteins were attached to a single multivalent core protein. Conversely, if a bridge consisted of two or more molecules of the same protein in parallel (as in protein X in the WXXYZ complex shown in Fig. 1), then a much higher concentration was required to produce inhibition.

Figure 2.

Representative examples of protein complexes examined for a prozone effect. Each oligomer comprises a set of proteins linked by dissociable bonds (black lines). Binding reactions leading to each of the oligomers were analyzed by means of the oligo-s program for a range of physiologically relevant starting concentrations and K_d values. This revealed that the black proteins show pronounced inhibition, the white proteins never show inhibition, and that gray proteins can show inhibition with certain sets of K_d values.

Fig. 2 also shows the proteins for which no diminution of concentration could be detected, even at the highest concentrations tested (indicated by white filled circles). In every case, these were proteins that laid on the outside of the complex, being linked to it through a single bond.

The majority of proteins in the complexes (gray circles) were like proteins W and X in Fig. 1 in that they failed to show a marked drop in concentration under the range of conditions tested, but significant inhibition could be obtained by going to very high concentrations (high, that is, compared with those normally present in a cell). We also found that, in many cases, gray proteins could produce a prozone effect if the bond strengths in the complex were altered. To examine more closely the conditions under which this third category of proteins would show a prozone effect, the cyclic oligomeric complex ABCD was selected for a more thorough investigation (Fig. 3A). In this case, bond strengths in the complex were changed individually, rather than coordinately as above, and varied according to one of two procedures. In the first procedure, each bond was assigned a strength that it preserved in all complexes so that, for example, the K_d of reaction 0 (A + B = AB) was automatically the same as that for reaction 4 (A + BC = ABC). This rule implies that the protein complex can be adequately represented by a simple ball-and-stick model and that conformational or other changes do not take place during the binding reactions.

Figure 3.

(A) The ABCD oligomer. Topological structure of the oligomer together with the binding reactions by which it assembles from proteins A, B, C, and D. Note that all four proteins are colored gray here to indicate that they do not show a pronounced prozone effect under the usual conditions of concentration and K_d values. (B) Equilibrium concentrations of ABCD oligomer for different concentrations of A. The binding reactions shown in A were solved by numerical integration for various starting concentrations and K_ds. Initial concentrations of protein A were as indicated on the abscissa, and B, C, and D were held constant at 1 μM. For one curve (crosses), K_d values were obtained by assigning the same strength, corresponding to a K_d value of 10⁻⁷ M to each bond in the ABCD oligomer. For the other two curves (open squares, filled squares), K_d values were selected by the optimization procedure described in the text using different target values.

In the second procedure, sets of K_ds were “trained” to give desired dose–response curves by a process analogous to the evolution, or more accurately, the selective breeding of a novel species, using an algorithm described (14). This entails making a set of random “mutational” changes in the K_d values, with each set being followed by a selection step (note that because of thermodynamic constraints, only 9 of the total of 18 K_ds leading to ABCD can be varied independently). In this second procedure, the strength of binding between two proteins could change depending on their association with other components of the complex. It therefore includes implicitly the possibility of conformational or other changes occurring during the binding steps.

Three representative curves obtained with ABCD illustrate the wide range of responses to increasing concentrations of protein A that can be obtained simply by changing the K_d values (Fig. 3B). Because of symmetry, identical curves also could be obtained by varying proteins B, C, or D. The curves ranged from no detectable inhibition to a very strong inhibition at even modest doses of protein A and were representative of features we have observed in other complexes. Sets of K_d values generated by the first of the two procedures mentioned above, in which bond strengths are preserved in different binding reactions, typically showed little or no prozone effect, at least over the range of concentrations tested here. Conversely, the sets of K_d values that showed a strong prozone effect were in most cases selected by optimization and contained bond strengths that changed with different binding reactions. This would arise, for example, if the addition of each protein to a complex produced a conformational change in the constituent proteins resulting in altered binding affinities for subsequent addition or if the first binding either enhanced or inhibited a second association for steric reasons.

DISCUSSION

In this study we have analyzed the suppression of protein complex by disproportionately high concentrations of their components. The basis of this suppression was the same as in the familiar antibody–antigen prozone effect, namely, the accumulation of small, incomplete complexes. As they build up in concentration, these small complexes sequester other proteins that are not present in high concentrations and thereby prevent them from participating in other binding reactions, including, in some cases, reactions that are essential for complex formation. But although the general principle is clear, the extent to which it applies to a given protein in a specific complex is difficult to predict, because it depends crucially on the precise structure of the complex and its bond strengths. It seems unlikely that one could obtain a universal formula, comparable to the equations derived by Goldberg and colleagues for antibody–antigen reactions (9), which would apply to all situations. The only sensible route to this information at present is an empirical one: that of setting up the multiple binding reactions leading to a particular complex and then determining their steady-state equilibrium point by reiterated approximation.

Our experience of analyzing 30 or so small oligomeric complexes enabled us to identify three categories of protein subunits from the standpoint of a possible prozone phenomenon. The first, represented by the black circles in Fig. 2, is a protein that forms a single bridge or link between two or more separable parts of the structure. Proteins in this category may be expected to show a pronounced inhibition of complex formation for even modest increases in concentration over a wide range of bonds strengths in the physiological (micromolar) range. The effect is stronger the higher the number of bonds to the bridging protein whereas it is markedly reduced if the bridge consists of two or more molecules of the protein in parallel. The second category of proteins (white circles in Fig. 2) is one on the outside of the complex and linked to it through a single bond; it is readily apparent that such proteins will not show a prozone effect under any conditions.

The third and most abundant category of protein molecules is one that forms multivalent links within the body of the structure of the complex but without forming a link between separable parts (gray circles in Fig. 2). In this case, the reactions driven by high concentrations of the protein lead to small complexes that can usually close up into the complex structure, thereby reducing the prozone effect. Thus, if one compares the two small trimeric complexes ABC-1 and ABC-2 in Fig. 2, the first one shows a pronounced suppression by high concentration of B whereas the second, ABC-2, shows very little effect. Similarly, we expect that the majority of proteins in the body of most large proteins complexes will fail to suppress complex formations when present at high concentrations.

However, it is not a universal rule, and, as we found for the small ABCD complex (Fig. 3), internal proteins can indeed produce a prozone effect if they are bonded with suitable strengths to their neighbors. In most cases, we were able to obtain a strong prozone effect only when the strengths of individual bonds (such as that between A and B) were allowed to vary freely within thermodynamic limits, which may suggest that inhibitory effects with such proteins will depend on conformational or cryptic steric effects occurring as proteins add to the complex. However, it was surprisingly easy to shape the dose–response curve, by means of an optimization routine, to a wide variety of forms, and we wonder what limits there are to such a procedure. Would it be possible, for example, in a large complex with many reactions, to obtain a dose–response curve that showed not one maximum but two or more?

Although we have focused, in this study, on the disruption of protein complexes, our analysis also speaks to the opposite process. The successful formation of a complete, or “correct,” complex will generally be favored by having a closed, multiple-bonded topology and strong binding interactions (low K_ds). Conformational changes also could push the binding steps toward completion if they made successive additions of proteins to the complex more favorable.

It is difficult to make general statements about the disruption of protein complexes in vivo. Multimeric proteins assemble in a living cell by a variety of routes, often requiring a sequence of stages. Sometimes they move between different intracellular compartments, and they may undergo posttranslational modifications before completion (15). There is also a mechanism by which unwanted proteins in the cytosol are degraded by proteolysis, and this can include proteins that have failed to assemble correctly into a structural complex (16). However, these various processes do not substitute for binding reactions but rather exist with it concurrently. The diffusion-limited matching of complementary binding surfaces governed by the law of mass action is the basis for most specific interactions in a cell, and when it occurs, it will be influenced by the kinds of effects we have described.

A clear example of the inhibition of protein complex formation in a living cell arose recently in a study of dynactin, a multisubunit regulatory factor for cytoplasmic dynein. Overexpression of the 50-kDa subunit of dynactin results in the disruption of dynactin and suppresses mitosis (17). The authors suggest that the 50-kDa protein acts as a linker between two portions of the dynactin complex and inhibits complex formation by a process “analogous to that of antigen:antibody excess.”

A second possible example arose in earlier study of a membrane-associated protein complex in coliform bacteria, which participates in the chemotactic signaling pathway. Mutant bacteria, in which protein components of a complex associated with the chemotactic receptor Tar are expressed in elevated amounts, were found experimentally to have phenotypes in which the function of the receptor is much reduced or absent (18, 19). These mutant phenotypes, however, could be explained on the basis of binding reactions leading to the receptor complex (20, 21). Computer-based analysis predicted that, when specific proteins belonging to the Tar complex were present in elevated amounts, they would lead to an accumulation of incomplete protein oligomers at the expense of the fully active complex (22).

Any protein capable of inhibiting complex formation in the cell would be expected to be closely regulated in its synthesis. Consider, for example, a constellation of proteins built on a single macromolecular site, such as a signaling complex of kinases and phosphatases built on a scaffolding protein (5, 23) or proteins associated with the cytoplasmic domains of a growth factor receptor (7). Our experience with structures such as the A6B oligomer in Fig. 2 leads us to predict that the common core protein (B) will be the source of a large prozone effect and its rate of synthesis will therefore be crucial to the expression of the active complex as a whole. So long as the cell limits production of this one species, then dependent species (in this case A) may be made in large amounts without close regulation because they will not affect the amount of functional oligomer. Interesting to note, this situation is similar topologically to that of the many oligomeric complexes that associate with protein filaments or DNA molecules in which binding sites on the filament will dictate the final quantity of the functional cluster.

Whatever consequences the prozone effect might have for a normal, wild-type cell, it seems certain to have a major influence on the phenotype of cells and organisms in which specific genes have been expressed at higher than normal levels. A variety of routes are available, such as transfection and microinjection, by which genes may be introduced into cells or organisms in unusually large amounts. It must be anticipated that there will be many instances, as in the example of dynactin (17), in which an overexpressed gene will suppress complex formation and hence produce anomalous or unexpected phenotypes in the target cell or organism.