Systematic distortions of perceptual stability investigated using immersive virtual reality

Abstract

Using an immersive virtual reality system, we measured the ability of observers to detect the rotation of an object when its movement was yoked to the observer's own translation. Most subjects had a large bias such that a static object appeared to rotate away from them as they moved. Thresholds for detecting target rotation were similar to those for an equivalent speed discrimination task carried out by static observers, suggesting that visual discrimination is the predominant limiting factor in detecting target rotation. Adding a stable visual reference frame almost eliminated the bias. Varying the viewing distance of the target had little effect, consistent with observers under-estimating distance walked. However, accuracy of walking to a briefly presented visual target was high and not consistent with an under-estimation of distance walked. We discuss implications for theories of a task-independent representation of visual space.

Introduction

The apparent stability of the visual world in the face of head and eye movements has been a long standing puzzle in vision research. Much of the discussion of possible mechanisms has focused on methods of compensating for rotations of the eye such as saccades (reviewed by Burr, 2004), including evidence of neurons that appear to shift their retinal receptive field to compensate for eye position with respect to the head (e.g. Duhamel et al., 1997); changes in perceived visual direction around the time of a saccade (e.g. Ross et al., 2001); and descriptions of a ‘stable feature frame’ that could describe the visual direction of features independent of eye rotations (Feldman, 1985; Bridgeman et al., 1994; Glennerster et al., 2001).

There have been fewer proposals about the type of representation that observers might build when the head translates in space. This is a more difficult computational problem than for the case of pure rotations of the eye. For one thing, the depth of objects must be known in order to ‘compensate’ for a head translation. The visual system must maintain some representation of a scene that is independent of observer translation. Cullen (2004) provides a recent review of relevant neurophysiological evidence. However, there are few detailed proposals about what form the ‘stable’ representation might take. It could include the world-centred 3-D coordinates of points, in which case there must be a coordinate transformation from the binocular retinal images into this frame. There are suggestions that such a transformation may not be required and that a ‘piece-wise retinotopic’ map could be sufficient for navigation (e.g. Franz and Mallot, 2000) or perception of depth (Glennerster et al., 2001). However, these ideas have not yet been developed into a detailed model.

There have also been fewer psychophysical studies addressing the consequences of head movements than there have been for eye movements. This is due in part to the practical difficulties involved in psychophysical investigations using a moving observer. In studies where observers move their head, the focus has often been on the perception of surface structure or orientation (e.g. Rogers and Graham, 1982; Bradshaw and Rogers, 1996; Wexler et al., 2001b) but this is not the same as detecting whether an object moves relative to a world-based reference frame. A number of early studies investigated the perception of static objects as the observer moved. With no ability to move the object, they were limited in the measurements that could be made, but it was shown that mis-perceptions of the distance of a point of light induced by changes in convergence (Hay and Sawyer, 1969), convergence and accommodation (Wallach et al., 1972) or by presentation of the light in a dark room (Gogel and Tietz, 1973, 1974; Gogel, 1990) gave rise to perceptions of the light as translating in space with (or against) the observer as they moved, in a manner explicable from the observer's incorrect judgement of distance.

Using a far more ambitious experimental setup, Wallach et al. (1974) did succeed in yoking the movement of an object to the movement of the observer, though in this case it was rotation of the object rather than translation. A mechanical apparatus connected a helmet worn by the observer to the target object via a variable ratio gear mechanism, allowing the experimenter to vary the rotational gain of the target. Thus, with a gain of 1, the target object rotated so as to always present the same face to the observer, with a gain of −1 it rotated by an equal and opposite amount and with a gain of zero the ball remained stationary. They found that a gain of as much as ±0.45 was tolerated before observers reported that the object had moved.

Wexler and colleagues have also used the technique of yoking an object's movement to the observer's movement to study the perception of stability. Wexler (2003) varied the gain with which an object translated as the observer moved towards it. Subjects judged whether the object moved in the same direction as their head movement or in the opposite direction. Wexler was primarily interested in the difference in perception produced by active or passive movement of the observer. Overall in these papers, Wexler and colleagues have shown that active movement alters observers' perceptions by resolving ambiguities that are inherent in the optic flow presented to them (Wexler et al., 2001a,b; van Boxtel et al., 2003; Wexler, 2003).

Rather than vary the proprioceptive information about observer movement, we have, like Wallach et al. (1974), examined the role of visual information in determining the perception of an object as static in the world. We have expanded their original experiment using an immersive virtual reality system. The advantages of our apparatus are that (i) the observer is free to move as they would when exploring a scene naturally, (ii) we have greater flexibility to yoke movements of the target object to certain components of the observer's movement and not others, (iii) we can manipulate different aspects of the virtual environment. Wallach et al. (1974) concluded that: there is a “compensating process that takes the observer's change in position into account” and that this process “emerges from our measurements as rather a crude process”. They found no significant effect on performance of adding a visual background and no consistent bias in observers' perception of stability (though their psychophysical method was too crude to measure this properly). Our findings challenge all these conclusions. We find that large biases are one of the most striking aspects of people's perception of stability as they move round an isolated object.

Methods

Subjects

All subjects had normal visual acuity without correction. In experiments 1 and 2, subjects were naïve to the purposes of the experiment other than subject LT (author). Two subjects (JDS and PHF) had not taken part in psychophysical experiments before. In experiment 3, the three authors acted as subjects.

Equipment

The virtual reality system consisted of a head mounted display, a head tracker and computer to generate appropriate binocular images given the location and pose of the head. The Datavisor 80 (nVision Industries Inc, Gaithersburg, Maryland) head mounted display unit presents separate 1280 by 512 pixel images to each eye using CRT displays. In our experiments, each eye's image was 72° horizontally by 60° vertically with a binocular overlap of 32°, giving a total horizontal field of view of 112° (horizontal pixel size 3.4 arc min). The DV80 has a see-through mode that allows the displayed image to be compared to markers in the real world using a half-silvered mirror. This permits calibration of the geometry of the display for each eye, including the following values: horizontal and vertical resolution and field of view; the 3-D location of the optic centre (projection point) of each display relative to the reported location of the tracker and the direction of the principal ray (the vector normal to the image plane passing through the optic centre) for each eye's display. The calibration was verified by comparing the location of real world points with virtual markers drawn at these locations. The 3-D location of the points must be known in the coordinate frame used by the tracker. We used the ultrasound emitters of the tracking system. In the experiment, the head mounted display was sealed, excluding light from the outside.

The location and pose of the head was tracked using an IS900 system (Intersense Inc, Burlington, Massachusetts). This system combines inertial signals from an accelerometer in the tracker with a position estimate obtained from the time of flight of ultrasound signals. Four ultrasound receivers are attached to the tracker, while more than 50 ultrasound emitters placed around the room send out a timed 40kHz pulse sequence. The data are combined by the Intersense software to provide a six degrees of freedom estimate of the tracker pose and location and are polled at 60Hz by the image generation program. Knowing the offset of the tracker from the optic centres of each eye, the position and pose of the head tracker allow the 3-D location of the two optic centres to be computed. These are used to compute appropriate images for each eye. Binocular images were rendered using a Silicon Graphics Onyx 3200 at 60 Hz.

We have measured the temporal lag between tracker movement and image display as 35 ms. This was done by comparing the position of a moving tracker with its virtual representation captured on a video camera. We have measured the spatial accuracy of the IS900 tracker as approximately 5 mm rms for speeds of movement used in our experiments (Gilson et al., 2003).

Stimulus and task

In the virtual scene, observers viewed a normal sized football (approximately 22cm diameter, see figure 1a) at a viewing distance of approximately 1.5m from the observer's starting position. Observers were prevented from approaching the target by a table placed between them and the target (but not visible in the virtual scene). The table was approximately 2m wide and guided their movement, ±1m from side to side. Lateral movement beyond this range caused the target ball to disappear. Observers were permitted to walk back and forth as many times as they wished but, after the first few trials, observers normally did so only once before making their response. Subjects were instructed to fixate the ball as they walked.

Figure 1. Different backgrounds.

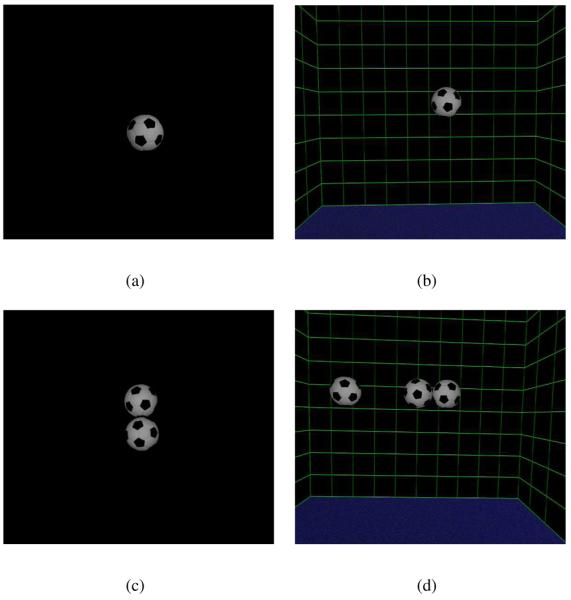
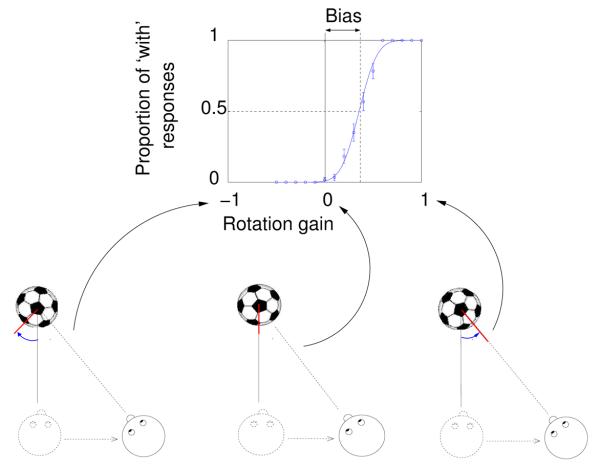
The central, target football rotated around a vertical axis as the observer moved. The gain of this yoked movement varied from trial to trial, as described in the text. Observers judged the direction of rotation, as ‘with’ or ‘against’ them, as illustrated in figure 2. The walls of the room and the other footballs shown in (b), (c) and (d) were static throughout. Results for the ‘target alone’ condition, (a), and the ‘rich cue’ scene, (d), are shown in figure 3. Results when the target was presented just with a background, (b), and when a static reference was presented adjacent to the target, (c), are shown in figure 5.

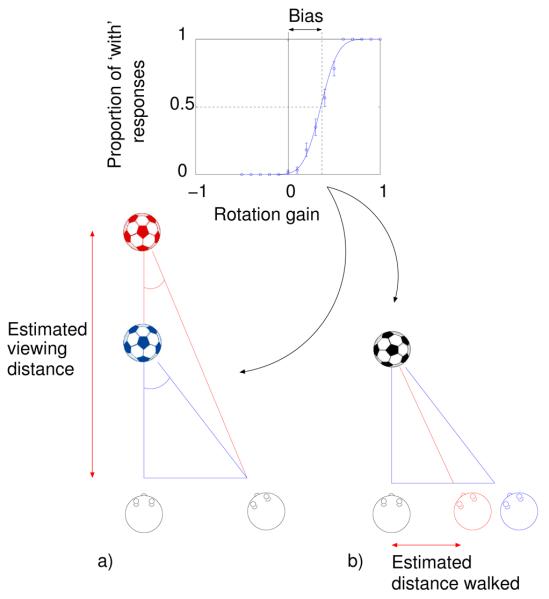
The target rotated about a vertical axis as the observer moved (its centre point remained fixed). The amount of rotation was linked to the observer's movement by different gains on each trial. When the gain was +1 the ball rotated so as to always present the same face to the observer (see figure 2), i.e. the ball moves ‘with’ the observer. A gain of −1 would give rise to an equal and opposite angular rotation, i.e. the ball moves ‘against’ the observer. When the gain was zero the ball remained static. Any vertical movement of the observer had no effect on the ball's rotation. The rotation of the ball depended only on the component of the observer's movement in a lateral direction, as shown by the arrows in figure 2.

Figure 2. An example psychometric function.

The proportion of trials on which the subject responded that the target ball had moved ‘with’ them as they moved is plotted against the rotation gain of the ball. As shown in the diagrams below, when the gain is 1 the ball rotates so as to always face the observer, when it is −1 the ball has an equal and opposite rotation and when the gain is 0 the ball remains static. The red line is included in order to illustrate the rotation of the ball. The bias, or shift in the 50% point, indicates the rotation gain at which the subject perceived the ball to be stationary as they moved. The threshold is the standard deviation of the fitted cumulative Gaussian.

The subject's task was to judge whether the ball moved ‘with’ or ‘against’ them as they moved. No feedback was provided. After the subject indicated their response, by pressing one of two buttons, the target football disappeared. It reappeared after a delay of 500 ms. The surface of the ball had no specular component since this would enable subjects to detect movement of the ball by judging the motion of features on the ball relative to the specular highlight. The ball had a random initial pose at the start of every trial to prevent subjects comparing the position of a particular feature from trial to trial.

Psychometric procedure

The first run or block of trials in each condition tested gains, presented in random order from the range −0.5 and 0.5 (increments of 0.1, i.e. 11 different gain values). A run consisted of 55 trials, with each gain value tested 5 times. The range of the next run was determined by the observer's bias on the previous run, following a semi-adaptive procedure for deciding the range of gain values to be tested during a run (Andrews et al., 2001). At least eight runs were performed for each scene so that the minimum number of trials per psychometric function was 440. For each scene, the observer's responses were plotted against the rotation gain of the target. A cumulative Gaussian curve was fitted to the data using probit analysis (Finney, 1971) to obtain the bias (or point of subjective equality) and the threshold (standard deviation of the fitted Gaussian). Error bars shown on the psychometric functions (figures 2 and 4) show the standard deviation of the binomial distribution. Error bars on the histograms of bias and threshold show 95% confidence limits of bias and threshold from the probit fit.

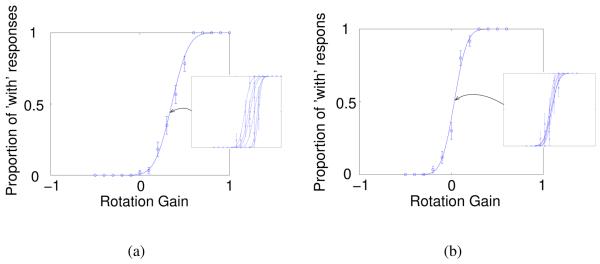
Figure 4. Thresholds raised by a drifting bias.

Psychometric functions for the data of subject LT shown in figure 3b for (a) the ‘target alone’ condition and (b) the ‘rich cue’ condition. These illustrate how thresholds for individual runs of 55 trials were similar across runs in both conditions (see insets). The values of the root mean square thresholds for the two conditions are plotted in figure 3b (subject LT). However, because the bias has drifted between runs in the ‘target alone’ condition, the psychometric function for the combined data in (a) has a shallower slope, i.e. a higher threshold, than in (b).

Experiment 1a: Detecting the movement of a yoked target

We examined the claim by Wallach et al. (1974) that the addition of a static environment around a yoked target did not affect subjects' perception of stability of the target. The static stimulus they used was a background of vertical stripes 40 cm behind the yoked target object. However, Wallach et al. (1974) did not use a forced choice procedure, measure psychometric functions or present data on individual subjects. We measured the bias and threshold of observers' responses when judging the direction of rotation of a yoked ball when the ball was presented alone or in the presence of a surrounding static scene. The static scene consisted of a virtual room with walls 1m from the ball and two other footballs close to the target ball (see ‘rich cue’ scene in figure 1d). For one observer, we measured performance for intermediate scenes, with static objects close to or distant from the yoked target (figure 1b and c).

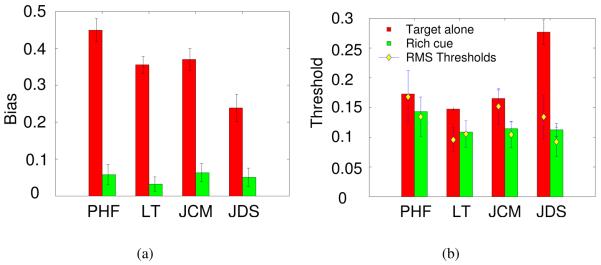
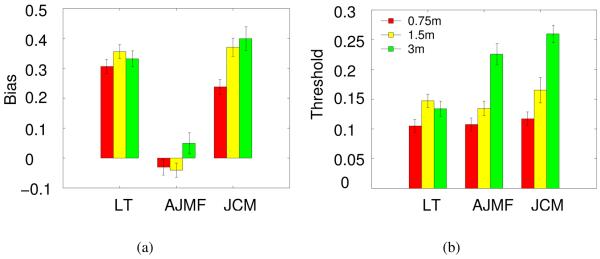
Figure 3a shows the biases and thresholds for observers in the ‘target alone’ and ‘rich cue’ conditions. All four subjects show a large positive bias when the ball was presented alone. That is, when subjects perceived the ball to be stationary it was in fact rotating to face them with a gain of 25-45%. Wallach et al. (1974) did not report this result, although their data are consistent with a small positive bias. Our data are also consistent with the direction and magnitude of bias found in a related experiment by Wexler (2003) (see discussion of experiment 2 and figure 9). Note that we did not find the large positive bias in all subjects. In a separate experiment manipulating viewing distance (experiment 2, figure 8) one subject had biases close to zero.

Figure 3. Results from experiment 1.

Biases (a) and thresholds (b) are shown for four observers when the yoked target football was presented alone (red) or in the ‘rich cue’ environment (green) which consisted of a static background and adjacent static objects (see figure 1a and d). Biases and thresholds are given as rotation gains (see figure 2) and hence have no units. The white diamonds show the average (root mean square) threshold for individual runs (see text and figure 4 for explanation).

Figure 9. Tests of the hypotheses in figure 7.

(a) Data from figure 8 re-plotted to show the estimated viewing distance that would account for the rotation perceived as static if other parameters were judged correctly (equation 1). (b) The same data re-plotted but now assuming that distance walked is mis-estimated. The ordinate shows estimated distance walked normalised by the true distance walked (x′/x, equation 2). The squares show, in corresponding colours for each subject, (a) estimated viewing distance and (b) estimated distance walked assuming that subjects make their judgement on the basis of a short translation rather than the ±1m maximum excursion (see text). The arrow in (b) shows the estimated distance walked derived from a related experiment by Wexler (2003).

Figure 8. Results of experiment 2.

The ‘target alone’ condition from experiment 1 (1.5m) repeated at 0.75 and 3m viewing distances. For subjects LT and JCM, the bias and thresholds for 1.5m viewing distance is re-plotted from figure 3. Figure 9a shows how the bias data here can be related to the two hypotheses illustrated in figure 7.

It is clear from figure 3a that a static background can have a dramatic effect on subjects' perception of stability. For all four subjects, biases for the ‘rich cue’ condition are around 5%, far lower than when the target is presented alone. This is perhaps not surprising, given that subjects can use the relative motion between the target and static objects as a cue, but it is contrary to the conclusion of Wallach et al. (1974). Figure 3b shows the corresponding thresholds for these judgements. As in the case of biases, for all four subjects, thresholds (shown by the histogram bars) are better in the ‘rich cue’ than the ‘target alone’ condition. However, the effect of the stable visual background on thresholds is considerably smaller than for biases.

It might be suggested that the 35 ms latency between head movement and visual display could be a cause of the large positive biases. We found this not to be the case. Two subjects repeated the ‘target alone’ condition with two different latencies, 50 ms and 10 ms. The 50 ms latency was the result of using a different (IS900 Minitrax) receiver. The 10 ms latency was achieved by using a predictive algorithm for head position supplied by the IS900 tracking system. We have confirmed the latency using the method described above. In one subject, the reduction in latency led to an increase in the bias (by 0.05), while in another subject there was a small decrease (by 0.01).

Different measures of threshold

The histogram bars and the diamonds in figure 3b show thresholds for the same data calculated by different methods, as follows. The first method is to fit a cumulative Gaussian to the entire data set for one condition (440 trials, see figure 4a). These thresholds are shown as bars in figure 3). The second method is to fit a cumulative Gaussian to the data for each individual run of 55 trials and calculate the average (root mean square) of the thresholds for all 8 runs. These thresholds are shown as diamonds. If there is a significant variation in the bias for different runs then the threshold according to the first method can be substantially larger than the second. This was the case in the ‘target alone’ condition for subject LT, as the inset to 4a shows: there was a systematic drift in the bias to progressively larger values across runs causing the averaged data to have a shallower slope than any of the individual runs. Note that this systematic drift in bias was due in part to the fact that the range of cues presented was varied according to the subject's responses on previous runs (see Methods). For all four subjects, the root mean square thresholds (diamonds) are lower than the thresholds obtained from the combined data (bars) in the ‘target alone’ condition, consistent with drifting biases in each case. There is less difference between the different threshold measures for the ‘rich cue’ condition, presumably because subjects used the relative motion between target and static background to help make their judgements.

Intermediate conditions

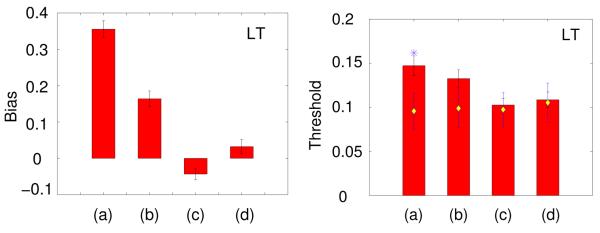
Figure 5 shows data for one subject for the conditions shown in figure 1b and 1c which provide more information than the ‘target alone’ but less than the ‘rich cue’ condition. When the reference football is adjacent to the target the bias is close to zero. This suggests that the most important components of the static environment shown in the ‘rich cue’ condition are likely to be the objects close to the target, as would be expected if relative motion is an important cue.

Figure 5. Other backgrounds.

Bias and thresholds in experiment 1 for one subject using all four types of background shown in figure 1. The labels (a) to (d) correspond to the labels of the conditions illustrated in figure 1. Data for the ‘target alone’, (a), and ‘rich cue’ conditions, (d), are re-plotted from figure 3. (b) shows data for the target football with a static room. (c) shows data for the target with an adjacent static football. The white diamonds show average thresholds across individual runs, as in figure 3. The asterisk (column (a), thresholds) shows data for a control condition in which the subject remained static, as described in the text.

Experiment 1b: Low level limits on performance

Wallach et al. (1974) described the range over which subjects perceived no rotation as ‘large’ but gave no indication of the range that might be expected. It is possible to ask whether observers' thresholds in this task are congruent with thresholds that would be measured for an equivalent visual task in which the observer does not move and is not asked to make a judgement about the allocentric pose of the object. The task in the walking experiment relies on observers making a speed discrimination judgement. We measured thresholds when this was the only element of the task.

Specifically, subjects were seated while wearing the head mounted display and saw a football presented alone at a viewing distance of 1.5m, as illustrated in figure 1a. On each trial, the subject saw the images that they would have seen had they moved along a circular path centred on the football and always facing towards it. The simulated observer's speed varied according to a cosine function, slowing down at either extremity of the path. The amplitude of the trajectory was ±45° around the circle. In fact, both subjects perceived the ball to rotate about a vertical axis rather than perceiving themselves to be moving around the ball. The simulated observer's location was static for 1s at the beginning of the trial, it moved through a single oscillation lasting 3s and then the ball disappeared until the subject made their response, triggering the next trial.

On different trials, the ball had different rotation gains relative to the simulated observer's translation, as in the previous experiment. The subject's task was to judge whether the rotation speed of the ball on a particular trial was greater or smaller than the mean rotation speed in the run. We again used a method of constant stimuli except that in a run of 130 trials the responses from the first 20 trials were discarded. This allowed subjects to view sufficient trials to judge the mean rotation speed. In this type of paradigm, subjects are known to be able to make comparisons of a stimulus relative to the mean of a set of stimuli with as much precision as when the standard is shown in every trial (McKee et al., 1990; Morgan et al., 2000)). We measured thresholds for this task for a range of different rotation gains.

As described above, a rotation gain of 1 means that the image of the ball does not change as the simulated observer moves, while a rotation gain of 0 means that the virtual ball is static. However, since subjects perceived themselves to be static, the ball would appear static for a gain of 1 and to rotate in the opposite direction for a gain of 0. In the case of a gain of 0, the maximum retinal speed generated by the ball would be 1 degree of visual angle per second. In fact, we used mean gains of 0.9, 0.8, 0.6, 0.2 and −0.6 in different runs, corresponding to retinal speeds of 0.1, 0.2, 0.4, 0.8 and 1.6 times the speeds of a ball with a gain of 0.

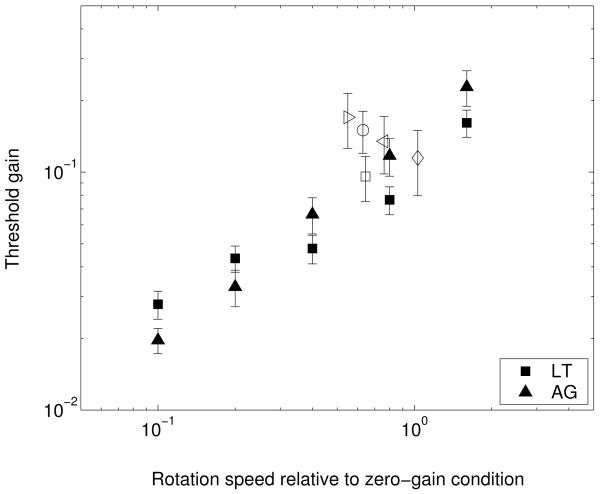
The results are shown in figure 6 for two observers (closed symbols). Thresholds rise with the mean rotation speed of the ball relative to the observer. The slope of the functions relating threshold to mean speed is 0.59 for subject LT and 0.89 for subject AG. The thresholds approach Weber's law (a slope of 1) at the highest speeds. Also shown, as open symbols, are the thresholds measured in the experiment where subjects walked to and fro viewing the target football with no background (re-plotted from figure 3b and, for subject AJMF, from figure 8). Each subject had a slightly different bias, and hence a different rotational gain at the point of subjective equality even if they walked at the same speed. We have used this rotational gain to plot their thresholds alongside the static observer data in figure 6.

Figure 6. Speed discrimination thresholds.

Results of experiment 1b showing the thresholds for determining whether a ball is rotating faster or slower than the mean speed across trials. Thresholds are given in terms of gain (no units) as in experiment 1a. Thresholds from experiment 1a are re-plotted as open symbols (see text). The abscissa shows rotation speeds in the image, where all rotation speeds are given relative to the situation in which the ball is stationary and the simulated observer moves round it (this corresponds to 1 on the abscissa). A gain of 1 would lead to no image motion and correspond to 0 on this axis. In general, rotation speed is (1 − g), where g is the rotation gain of the ball.

This control condition demonstrates that the thresholds for “constancy of object orientation” (as Wallach et al., 1974, described them) are similar in magnitude to those measured for a low-level speed discrimination task that is intrinsic to the judgement of object stability. Far from being a “crude”, active process, the detection of object motion that occurs while the observer is moving appears to be almost as precise as speed discrimination thresholds allow and hence noise from any subsequent stage of the task must be low.

Experiment 2: Mis-estimation of viewing distance or distance walked?

In experiment 1, when the target football was presented alone, all observers perceived a stationary football to be rotating ‘against’ them. In this experiment, we explored possible reasons for the bias, namely that subjects perceive the ball to be further away than it really is or under-estimate the distance that they have walked. Figure 7 illustrates how each of these mis-estimates could give rise to a positive bias.

Figure 7. Possible causes of bias in the ‘target alone’ condition.

A positive bias can be attributed to either a) an overestimate of distance to the target or b) an underestimate of the distance walked. In either case, the subject expects their view of the ball to change by a smaller amount than would be the case if their estimate was correct. Hence, the ball they see as stationary is one that rotates ‘with’ them.

The explanations illustrated in figure 7 rely on an assumption that the observer perceives the ball to be stationary (not translating). Several investigators have investigated situations in which stationary objects are perceived to translate as the observer moves their head back and forth (Hay and Sawyer, 1969; Wallach et al., 1972; Gogel and Tietz, 1973, 1974). The direction of perceived translation depends on whether the object is misperceived as closer or more distant than its true distance (Hay and Sawyer, 1969; Gogel and Tietz, 1973) consistent with subjects accurately estimating (i) the distance they moved their head and (ii) the angle of rotation around the object (the change in visual direction of the object). By contrast, in all the experiments described here, observers' subjective reports were that the target object appeared to be fixed in space (not translating). We have carried out other experiments, in which the ball translated laterally, yoked to the observer's translation. In those experiments (not reported here), observers did perceive the ball to be translating as they moved when the gain was non-zero (±0.5)¹. In the present experiment, given that the ball was perceived to remain in one location, possible interpretations of the point of subjective equality are illustrated in figure 7 and figure A1 in the Appendix².

If the cause of the bias is a mis-estimation of viewing distance, then one would expect the size of the bias to vary with viewing distance in a way that is consistent with previous experiments. These studies have generally found that close distances are over-estimated and far distances are under-estimated with a distance between the two, sometimes called the ‘abathic distance’ or ‘specific distance’, at which viewing distances are estimated correctly (Ogle, 1950; Gogel, 1969; Foley, 1980). The method is often indirect, so that the judgement the observer makes is one of shape rather than distance (e.g. Johnston, 1991; Cumming et al., 1991). Ogle (1950) found that the shape of an apparently fronto-parallel plane was convex at distances closer than about 5m and was concave at distances greater than this, corresponding to an overestimate of near and an underestimate of far distances. Johnston (1991) found a similar result using a different shape judgement, although in this case the ‘abathic distance’ was approximately 1m. There is other evidence that the absolute value of the abathic distance varies with the subject's task (see review by Foley, 1980). However, all these cases can be interpreted as showing a ‘compression of visual space’, i.e. an overestimate of near and an underestimate of far distances. We repeated the ‘target alone’ condition of the previous experiment at different distances to see whether the same type of distortion of space could explain our results.

Figure 8a shows the biases for viewing distances of 0.75, 1.5 and 3m. The definition of a gain of 1 still implied that the ball rotated to face the observer. Thus, for a given distance walked, a gain of 1 corresponds to a smaller rotation of the ball when the viewing distance is large. The biases for subjects LT and JCM are large and positive at all three viewing distances, as in experiment 1. (Their data for 1.5m is re-plotted from figure 3a, the ‘target alone’ condition in experiment 1.) By contrast, the biases for subject AJMF are close to zero. Despite this variability between subjects, figure 9 shows how all the data can be used to assess the hypotheses described above. It shows the biases in figure 8a converted into estimated viewing distance and estimated distance walked, calculated as described below.

Converting biases into distance estimates

The biases in figure 8a can be converted to an estimated viewing distance if one assumes that the observer estimates correctly the distance they walk and that they perceive the centre of the ball to be stationary in space (as discussed in Experiment 2). Estimated viewing distance, D′, is given by:

$$D^{\prime }=\frac{D\tan \theta }{\tan \left((1-\beta )\theta \right)}$$ (1)

where D is the true viewing distance, β is the bias, θ = arctan(x/D) and x is the lateral distance walked from the starting position (see Appendix for details). Estimated viewing distance, D′, is plotted against real viewing distance, D, in figure 9a. It is possible that observers make their judgements on the basis of a small head movement rather than the whole ±1m excursion in which case small angle approximations apply and the estimated viewing distance is given by D′ ≈ D/(1 − β). As figure 9a shows (square symbols), these values are only slightly different. The estimated viewing distances for AJMF are close to veridical, corresponding to the small biases shown in figure 8a. The larger positive biases for observers LT and JCM give estimated viewing distances that are greater than the true viewing distance and which increase with increasing viewing distance. This trend is the reverse of that expected from previous experiments (Ogle, 1950; Foley, 1980; Johnston, 1991).

The second possible explanation of biases in the ‘target alone’ conditions is that subjects mis-estimate the distance they have walked. The ratio of estimated lateral distance walked, x′, to real distance walked, x, is given by:

$$\frac{x^{\prime }}{x}=\frac{\tan \left((1-\beta )\theta \right)}{\tan \theta }$$ (2)

as shown in the Appendix. As before, if subjects use information from only a short head movement then the equation can be simplified. Here, x′/x ≈ (1 − β), shown by the squares in figure 9b.

Figure 9b shows estimated distance walked, x′/x, for the three conditions tested in experiment 2. Although there are differences between subjects, for each subject the extent to which distance walked is mis-estimated is almost constant across viewing distance. This makes mis-estimation of distance walked a plausible explanation of the biases. It has the advantage over the viewing distance hypothesis that it does not contradict results of earlier experiments.

In fact, the conclusion that subjects mis-estimate distance walked is consistent with data from a related experiment (Wexler, 2003). For the purposes of comparison, we have plotted the estimate of distance walked derived from Wexler's experiment in figure 9b (arrow). In Wexler's experiment, as in ours, observers judged whether an object moved ‘with’ or ‘against’ them as they moved, although in their case the target object translated rather than rotated. The target was presented alone and, as in our experiment, subjects displayed a large bias. Wexler (2003) found that for the conditions in which observers moved their head the underestimation of distance moved was about 40%, very close to the values found for subject LT and JCM.

Experiment 3: Walking to a virtual target

Walking to a remembered visual target requires an estimate of viewing distance and an estimate of distance walked. The task has been used on numerous occasions as a measure of the visual representation of space (Thomson, 1983; Elliott, 1987; Rieser et al., 1990; Steenhuis and Goodale, 1998; Sinai et al., 1998; Loomis et al., 1998, 1992; Ooi et al., 2001), including the effects of immersive virtual reality on distance perception (Witmer and Sadowski, 1998; Loomis and Knapp, 2003).

In our experiment, subjects (the three authors) viewed a football of the same size and type as in Experiments 1 and 2 placed at the observer's eye height at a distance of 0.75, 1.06, 1.5, 2.12 and 3 m from the observer. The football was only visible when the observer was within a viewing zone 0.5 m wide by 0.1 m deep. The viewing zone was narrow so that as soon as the observer moved forward the football disappeared. They were instructed to continue walking until they judged that a point midway between their eyes coincided with the location at which the centre of the football had been displayed. The subject then pressed a button on a handheld wand, the location of the subject's cyclopean point was recorded and the trial terminated.

We ran two conditions. In one, the football was presented alone, as in the target-alone condition in Experiment 1 and 2. Thus, once the subject had left the viewing zone they were in complete darkness until they pressed a button to end the trial. In the other condition, the ball was presented within a wire-frame room (like the one shown in figure 1b) which remained visible throughout the trial. In this case there were many visual references that subjects could use to tell them when they had reached the previous location of the ball. From trial to trial the location of the football was varied. Each of the 5 viewing distances were tested 5 times within a run. We ran 10 trials for each distance in each condition.

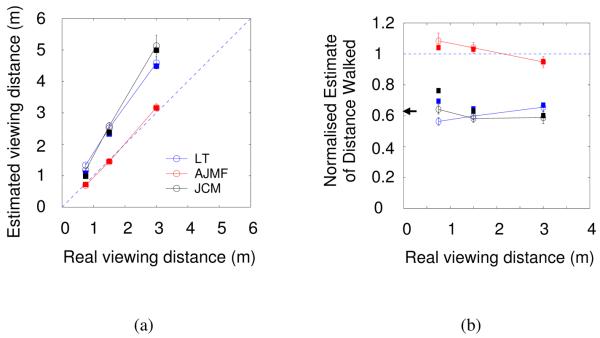
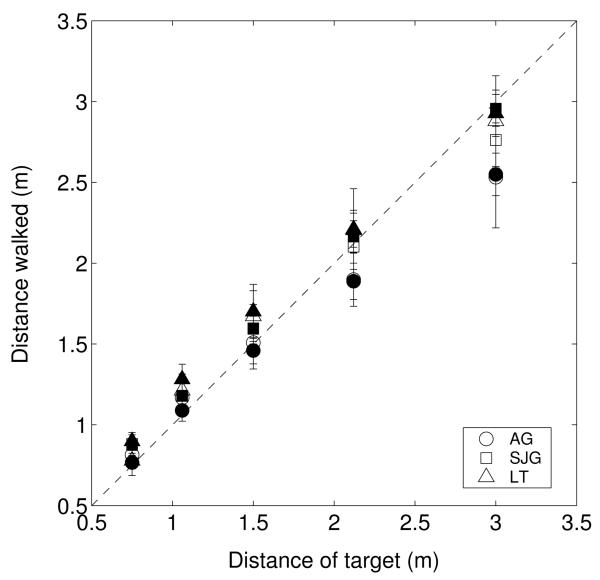
Figure 10 shows data for three subjects. Most of the data lie close to the dashed line indicating accurate walking. The regression slopes for the data shown in figure 10 are 0.92, 0.78, 0.88 (SJG, AG, LT) for trials in which a background was visible and 0.91, 0.74 and 0.83 when no background was present. Distances closer than 2m tend to be over-estimated (as measured by subjects' walking) while further distances are under-estimated. A three way ANOVA shows a significant effect of distance walked (understandably) and also of subject (F(2,299) = 48; p < 0.01). We found no significant effect of the background being present or absent (F(1,299) = 1.6; p > 0.2).

Figure 10. Estimated viewing distance measured by walking.

The distance subjects walked to reach the location where a target had been presented is plotted against the true distance of the target for three subjects. Solid and open symbols show results with and without a visible background. Error bars show s.e.m.

Philbeck and Loomis (1997) carried out a similar experiment, measuring walking distance to previously displayed visual targets at eye level in the dark and under full cue conditions. They found accurate walking under full cue conditions but much poorer performance in the dark. The reason that they found a large effect of removing the background while we did not is probably that their stimulus had a constant angular size while we used the same familiar football at all distances (as we did in our other experiments).

Figures 7 and 10 show radically different plots of estimated viewing distance against real viewing distance for the rotating football and walking tasks. To explain the data in figure 10, the hypothesis was raised that observers might under-estimate the distance they had walked, particularly for the more distant targets. By contrast, the data in Figure 10 from the walking experiment suggest, if anything, that for the more distant targets observers over-estimate the distance they have walked (they stop too early). The walking data are compatible, instead, with an abathic or specific distance hypothesis (Ogle, 1950; Gogel, 1969; Foley, 1980) in which near objects are perceived to be further than their true distance while distant objects are perceived to be closer.

The fact that very different patterns of estimated distance are observed for two tasks, despite similar cues being available, is evidence that the visual system does not use a common ‘perceived distance’ to underlie both tasks. (The converse logic has been used to argue for a common representation of distance, (e.g. Philbeck and Loomis, 1997; Foley, 1977).) Instead, different cues might be important in the two tasks. The issue of task-dependent judgements is taken up in the Discussion.

Discussion

We have examined people's perception of a set of images that, taken alone, are compatible with movement of the object, the observer or both. Extra-retinal information about vergence and proprioception could distinguish these in theory but we have found that subjects show large biases in their judgements, tending to see a static ball rotate away from them as they move round it (see figures 3 and 8). The ability to use relative motion between the target and static objects dramatically improved observers' biases (figure 4). Thresholds for the task are within the range expected given the sensory demands for this judgement (figure 6).

All of these conclusions contrast with those of Wallach et al. (1974) in their earlier study yoking target rotation to observer movement. First, they described the process responsible for ‘constancy of object orientation’ as ‘crude’, whereas we show that observers are about as good at the task as can be expected given that the judgement requires different speeds to be discriminated. Of course, thresholds for detecting that the ball moved are very much greater than if the observer had remained static. However, using an object-centred measure of thresholds rather than a retina-centred measure would be mis-leading, as has been pointed out in other contexts (e.g. Eagle and Blake, 1995).

Second, the psychometric procedure Wallach et al. (1974) used is not well suited to measuring bias, there is no consistent evidence for a bias in their data and the authors make no mention of a bias. By contrast, we find that when the target is presented alone, subjects' biases are the most striking feature of their responses (figure 3). Third, they found no significant effect of adding a static background and concluded that the process of compensating for movement of the observer was primarily driven by proprioceptive inputs. We found, instead, that relative motion between the target and objects that are static in the virtual world is an important cue that produces large changes in observers' perception of stability. The strong influence of reliable visual cues on the bias is perhaps not surprising and fits with cue combination models (Clark and Yuille, 1990; Landy et al., 1995; Ernst and Banks, 2002), but Wallach et al. (1974) described an active compensation process that was independent of visual cues.

We have considered two possible causes of the large biases that occur when the object is presented alone. One is an over-estimation of the distance of the target. The other is an under-estimation of the distance walked (see figure 7). Our results do not fit with previous results on a mis-estimation of distance which have shown, using a variety of tasks, that subjects tend to over-estimate near distances and under-estimate far distances, with a cross-over point at some ‘abathic’ distance (e.g. Foley, 1980; Johnston, 1991; Glennerster et al., 1996). In order to explain the biases in our experiment within the same framework, one would have to postulate a quite different pattern of estimated viewing distances: an expansion of visual space rather than a compression around an abathic distance (see figure 9a).

On the other hand, the explanation that subjects mis-estimate the distance that they walk fits both our data and that from a previous experiment (Wexler, 2003) in which observers judged whether an object was translating towards or away from them when that movement was yoked to their own head movement. For each subject in our experiment, the extent to which distance walked was mis-estimated remained constant across viewing distances (figure 8b). For two subjects, the mis-estimation was a factor of about 40%, very similar to the mean value found for subjects in Wexler's study.

The conclusion that subjects under-estimate the distance they have walked when carrying out the rotating object task seems at odds with the results we obtained when subjects walked to a previously displayed target (figure 10). Here, in line with data in similar studies (e.g. Witmer and Sadowski, 1998; Loomis et al., 1998; Loomis and Knapp, 2003), the direction of the biases in the walking task indicates, if anything, the reverse (an over-estimation of distance walked for more distant targets). However, walking to a remembered location is a quite different task from judging the visual consequences of moving round an object. There is no logical necessity that performance on one task should be predictable from the other. A purely task-dependent explanation of the rotation bias we have found makes it unnecessary to discuss the underlying cause in terms of mis-estimating object distance or distance walked. If it is not possible to generalise about a mis-estimation of walking distance to other tasks, then it may be more appropriate to describe the bias in terms that are much closer to the data (e.g. simply as a mis-estimate of the angle the observer walks round the target, angle θ in figure A1).

The extent to which performance in spatial tasks is task-dependent remains to be determined. There is some empirical evidence that supports the idea of a single representation underpinning performance in a number of different tasks (see reviews by Gogel, 1990; Loomis et al., 1996). On the other hand, there is psychophysical evidence for quite different performance in different tasks suggesting that either different representations of distance or different algorithms are used depending on the task with which the observer is faced (Glennerster et al., 1996; Bradshaw et al., 2000). There are also good theoretical reasons for using different information for different tasks (e.g. Schrater and Kersten, 2000).

Appendix

Here we give the derivations of equations 1 and 2 for ‘estimated viewing distance’ and ‘estimated distance walked’ plotted in figure 9.

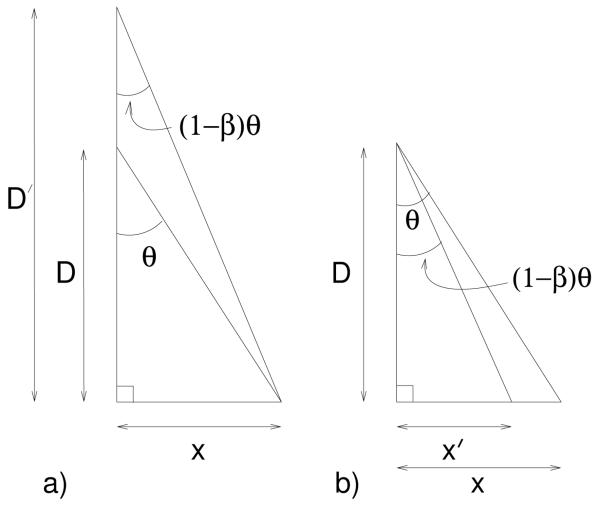
The estimated viewing distance of the yoked object can be calculated from the bias (the rotation gain at which the ball was perceived to be stationary) if it is assumed that the subject estimates correctly the distance they have walked. As can be seen from figure A1a, the distance walked, x, is given by

$$x=D\tan \theta$$ (A1)

where D is the real distance of the target ball at the start of the trial and θ is the angle between the line of sight to the ball at the start of the trial and the line of sight after walking laterally by distance x. When the ball rotates with a certain rotation gain, g, the angle through which the line of sight moves relative to the ball is θ(1 − g). For example, for a gain of 1 the view does not change; for a gain of 0 the line of sight moves through an angle θ. Let β be the bias, i.e. the gain at which observers perceive the ball to be stationary. As figure A1a illustrates, if observers perceive the ball to be at distance D′ and they perceive the distance they walk correctly as x, then:

$$x=D^{\prime }\tan \left((1-\beta )\theta \right).$$ (A2)

Equation 1 follows from equations A1 and A2.

Similarly, the estimated distance walked can be calculated from the bias if it is assumed that the subject estimates the viewing distance of the target correctly. As can be seen from figure A1b, the distance of the object D, is given by

$$D=\frac{x}{\tan \theta }=\frac{x^{\prime }}{\tan \left((1-\beta )\theta \right)}$$ (A3)

from which equation 2 follows.

Figure A1. Assumptions used in calculating estimated viewing distance and distance walked.

D is the real distance of the target ball at the start of the trial, θ is the angle between the line of sight to the ball at the start of the trial and the line of sight after walking laterally by distance x and β is the subject's bias. In (a), D′ is the estimated viewing distance of the target assuming x is judged correctly. In (b), x′ is the estimated distance walked assuming D is judged correctly. D′ and x′ are plotted in figure 9 for the conditions tested in experiment 2.