Humans ignore motion and stereo cues in favour of a fictional stable world

Summary

As a human observer moves through the world, their eyes acquire a changing sequence of images. The information from this sequence is sufficient to determine the structure of a 3-D scene, up to a scale factor determined by the distance that the eyes have moved [1, 2]. There is good evidence that the human visual system accounts for the distance the observer has walked [3, 4] and the separation of the eyes [5-8] when judging the scale, shape and distance of objects. However, using an immersive virtual reality environment we created a scene that provided consistent information about scale from both distance walked and binocular vision and yet observers failed to notice when this scene expanded or contracted. This failure led to large errors in judging the size of objects. The pattern of errors cannot be explained by assuming a visual reconstruction of the scene with an incorrect estimate of interocular separation or distance walked. Instead, it is consistent with a Bayesian model of cue integration in which the efficacy of motion and disparity cues is greater at near viewing distances. Our results imply that observers are more willing to adjust their estimate of interocular separation or distance walked than to accept that the scene has changed in size.

Results and Discussion

In order to study different sources of visual information about the 3-D structure of scenes, it is necessary to bring them under experimental control. Over the past 200 years, a number of ingenious devices and strategies have been used to isolate particular sources of information so that their influence on human behaviour can be assessed (such as Helmholtz' telestereoscope, which effectively increases the separation of the viewer's eyes [5]). A much more general approach is to generate a complete visual environment under computer control, using the technological advantages of virtual reality.

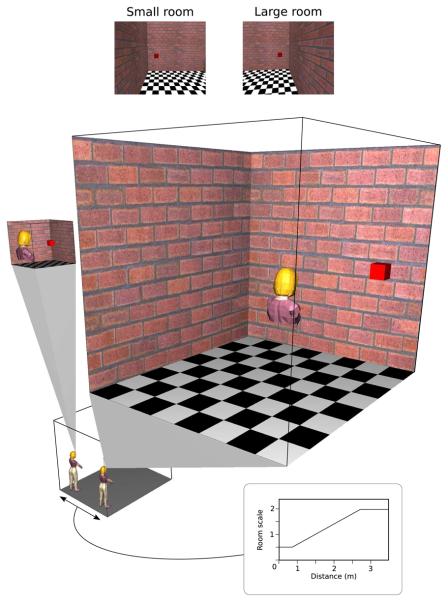
Figure 1 illustrates an observer in a virtual room whose scale varies as the observer walks from one side to the other. Subjects wore a head-mounted display controlled by a computer that received information about the location and orientation of the subject's head and updated the binocular visual displays to create an impression of a virtual 3-D environment with a floor, walls and solid objects. When the virtual room changed size, the centre of expansion was half way between the two eyes (the ‘cyclopean’ point), so that as objects became larger they also moved further away. Consequently, no single image could identify whether the observer was in a large or a small room (e.g. images at the top of Figure 1). Thus, the expansion of the room results in retinal flow similar to that experienced by an observer walking through a static room, although the relationship between distance walked and retinal change is altered.

Figure 1. An expanding virtual room.

Observers wearing a head mounted display occupied a virtual room whose size varied as they walked across it. Moving from the left to the right side of the real room caused the virtual room to expand by a factor of 4. The inset graph shows how the scale of the room changed with lateral distance walked. When the scale was 1, the room was 3 m wide and 3.5 m deep. Because the centre of expansion was a point midway between the eyes, any single image could not reveal the size of the room, as the example views illustrate. Observers reported no perceived change in the size of the virtual room despite correct and consistent information from stereopsis and motion parallax. In the experiment, observers compared the size of two cubes, one seen when the room was small and the other seen when the room was large.

None of the subjects we tested noticed that there had been a change in size of the room. If they reported anything, it was that their strides seemed to be getting longer or shorter as they walked to and fro. The phenomenon is remarkable because binocular and motion cues provide consistent information about the size and distance of objects and yet the information is apparently ignored. Subjects seem to ignore information both about vergence angle (to overrule stereopsis) and about stride length (to overrule depth from motion parallax).

We tested the consequences of subjects' ‘blindness’ to variations in the scale of the room by asking them to compare the sizes of objects viewed when the room was different sizes. On the left side of the room the subjects viewed a cube whose size they were to remember. As they walked to the right the cube disappeared. Then, in a region on the right hand side of the room, a second cube appeared and subjects were asked to judge whether it was larger or smaller than the first cube. The size of the virtual room varied with the subject's position, as shown in Figure 1. In the period when neither cube was visible, the room expanded gradually until it was four times larger in all dimensions than before. Using a forced-choice paradigm, we determined the size of the comparison cube (viewed when the room was large) that subjects judged to be the same as the size of the standard cube (viewed when the room was small).

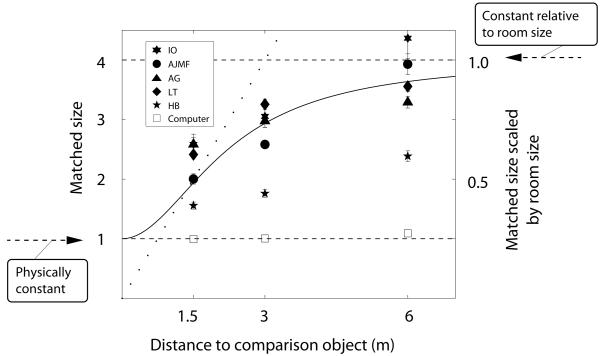
Subjects always mis-estimated the relative sizes of the cubes by at least a factor of 2 and sometimes as much as 4 (see Figure 2). The mis-estimation varied systematically with the viewing distance of the comparison cube: at far viewing distances, subjects' matches were close to the value predicted if they judged the sizes of the cubes relative to other objects in the room, such as the bricks forming the wall (a size ratio of 4), while at close viewing distances matches were more veridical. An important cue about distance is the height of the eye above the ground plane [9, 10]. This varies as the room expands whereas it is normally fixed which could be an important signal for stability of the room. However, removing the floor and ceiling gives rise to an equally strong subjective impression of stability and similar psychophysical data (see Supplemental Data).

Figure 2. Size matches in the expanding room.

The size of the comparison cube that subjects perceived to be the same size as the standard is plotted against the viewing distance of the comparison cube for five subjects. The standard cube was always presented at 0.75m. The ordinates show matched size relative to the true size of the standard (left) or relative to a cube 4 times the size of the standard (right), i.e. scaled in proportion to the size of the virtual room. Error bars show ±1 s.e.m. The fitted curve shows the output of a model in which cues indicating the true distance of the comparison cube are more reliable, and so have greater weight, at close viewing distances. The dotted line shows the predicted data if subjects matched the retinal size of the standard and comparison cubes. The open squares show the matched size computed from the images a subject saw on a typical trial. We used a 3D reconstruction package, as described in the text and Supplemental Data.

Stereo and motion parallax, if scaled by interocular separation or distance travelled, should indicate a veridical size match. Hence, it is rational to give more weight to these cues at close viewing distances because this is where they provide more reliable information [11-13]. The curve in Figure 2 shows that a model incorporating these assumptions provides a reasonable account of the data. The single free parameter in the model determines the relative weight given to cues signalling the true distance of the comparison object (e.g. from stereo or motion parallax) compared with cues that specify the size of the cube in relation to the features of the room.

The pattern of errors by human observers is quite different from that predicted by current computational approaches to 3D scene reconstruction. We used a commercially available software package [14, 15] to estimate the 3D structure of the scene and the path that the subject had taken. The input to the algorithm was the sequence of images seen by a subject (monocular input only) on a typical trial, giving separate 3D reconstructions of the room when the standard and comparison cubes were visible. The example in Figure S1 (Supplemental Data) shows the head movement during a typical trial and how the motion parallax information available to subjects can be used to reconstruct the scene. When combined with information about the actual distance the subject travelled, the algorithm also provides estimates of the size of the room for each sequence of images. The change in room size was recovered almost perfectly and hence the computed size matches, shown in Figure 2, are close to 1. If there were errors in the estimate of the distance that the subject travelled, then the size matches for all three comparison distances would have been affected equally, unlike the human data which shows quite different size matches at different distances.

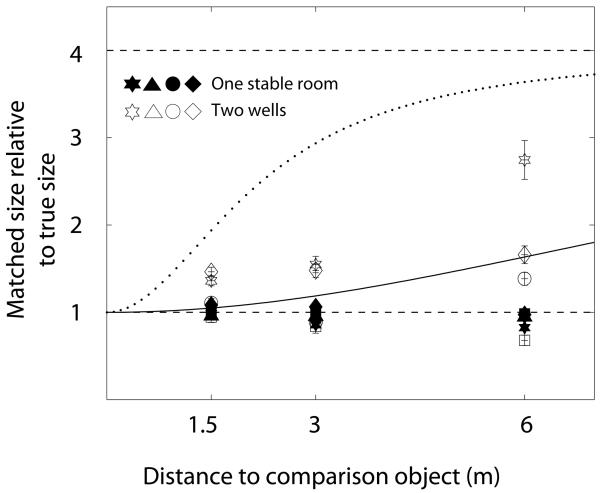
There is good evidence that information about the distance observers walk and their interocular separation are sufficiently reliable to signal the change in size of the room if these are the only cues. For example, stereo thresholds for detecting a change in relative disparity have a Weber fraction of 10-20% [16], far below the fourfold change in both relative and absolute disparities that occur in the expanding room. Erkelens and Collewijn [17] found insensitivity to smooth changes in absolute disparity for a large field stimulus in which relative disparities did not change. More direct evidence in Figure 3 shows that information from stereo and motion parallax was sufficient to signal the relative size of objects when these cues generate no conflict with texture or eye height information. Subjects initially viewed the standard cube in a small room, the same size as in the first experiment. Instead of the room expanding smoothly as they walked, subjects passed through the wall of the small room into a room that was four times larger, in which the comparison cube was visible. The walls of both rooms were featureless to avoid comparison of texture elements (such as bricks) but stereo and motion parallax information was still available from the vertical joins between the back and side walls. The floor and ceiling were also removed to avoid the height of the observer's eye above the ground being used as a cue to size of the room [10]. Thus, if observers looked up or down they appeared to be suspended in an infinite shaft or ‘well’. Figure 3 (open symbols) shows that size matching across different distances was better than with the smoothly expanding room. The limitation in the expanding room is therefore not due to the lack of motion and disparity information. In fact, in terms of the number of visible contours, there is much less stereo and motion information in this situation. Size matching is even more accurate in a room that remains static (Figure 3, closed symbols), as one would expect from many previous experiments on size constancy [9, 18, 19].

Figure 3. A static environment.

Size constancy is close to perfect when the comparison task is carried out in a room of constant size (closed symbols, subject symbols as in Figure 2). Size constancy is also significantly improved compared to the expanding room experiment (dotted curve re-drawn from Figure 2) when subjects walk from a featureless small ‘well’ (i.e. a room without a floor or ceiling) into a well that is four times the size (open symbols). The solid line shows the fit of equation 5. In this case, stereo and motion parallax information dominate.

Our results demonstrate that human vision is powerfully dominated by the assumption that an entire scene does not change size. An analogous assumption underlies the classic ‘Ames room’ demonstration [20]. In that illusion, the two sides of a room have different scales but appear similar because observers fail to notice the gradual change in scale across the spatial extent of the room. Our case differs from the ‘Ames room’ illusion because the observers receive additional information about the true 3D structure of the room through image sequences that are rich in binocular disparity and motion information. Nonetheless, the phenomenon is just as compelling. The human visual system does not appear to implement a process of continuous reconstruction using disparity and motion information, as used in computer vision [1, 2] (see Supplemental data). A data-driven process of this kind should signal the current size of the room equally well in the expanding room (Figure 2) or the two wells (Figure 3). Instead, our results are best explained within a Bayesian framework [21] in which a prior assumption that the scene remains a constant size influences the interpretation of 3D cues gathered over the course of many seconds.

Experimental Procedures

Psychophysics

Subjects (two of the authors and three naïve to the purposes of the experiment) viewed a virtual environment using an nVision datavisor 80 head mounted display (112° field of view including 32° binocular overlap, pixel size 3.4 arcmin, all peripheral vision obscured). For details of calibration, see [22]. Position and orientation of the head, determined with an InterSense IS900 tracking system, were used to compute the location of the left and right eyes' optic centres. Images were rendered at 60Hz using a Silicon Graphics Onyx 3200 computer. The temporal lag between tracker movement and corresponding update of the display was 48 - 50 ms. For the expanding room experiment, the dimensions of the virtual environment varied according to the observer's location in the real room. When the observer stood within a zone (0.5 m by 0.5 m, unmarked) near the left side of the room, the size of the virtual room was 1.5 m wide by 1.75 m deep. The standard object, a cube with sides of 5 cm, was always presented 0.75 m from the centre of the viewing zone. Subjects were instructed to walk to their right until the comparison cube appeared. They did this rapidly, guided by the edge of a real table (which they could not see in the virtual scene) that ensured they did not advance towards the cubes as they crossed the room. Leaving the first viewing zone caused the standard cube to disappear and the virtual room to start expanding. The centre of expansion was the cyclopean point, halfway between the subject's eyes. The expansion of the room was directly related to the lateral component of the subject's location between the two viewing zones, as shown in Figure 1. When the scale was 1, the virtual room was 3 m wide and 3.5 m deep. At this scale, the virtual floor was at the same level as the subject's feet. When subjects reached the viewing zone near the right hand side of the room, from where the comparison cube could be viewed, the size of the room was 6 m by 7 m. Room size was held constant within each viewing zone. The walls and floor were textured (see Figure 1). No other objects were presented in the room. The subject's task was to judge whether the comparison cube was larger or smaller than the standard, with the comparison cube size chosen according to a standard staircase procedure [23]. Psychometric functions for three viewing distances of the comparison cube were interleaved within one run of 120 trials. Data from 160 trials per condition were fitted using probit analysis [24] and the 50% point (point of subjective equality) shown in Figures 2 and 3. Error bars show standard errors of this value, computed from the probit fit. In the two-wells experiment, the walls were different shades of grey and an added black vertical line in each corner meant that the junctions between the back and side walls were clearly visible. These junctions extended without any visible end above and below the observer (as if the observer was in an infinitely deep well).

Model

Let R be the ratio of the size of the comparison object to the size of the standard object and $\hat{\mathit{R}}$ be the observer's estimate of this ratio. By definition, when the subject makes a size match in the experiment, $\hat{\mathit{R}}=1$. We consider two different types of cue contributing to $\hat{\mathit{R}}$. We assume one set of ‘physical’ cues (stereo and motion parallax given knowledge of the interocular separation and distance walked) provide an unbiased estimate, $\hat{\mathit{P}}$, in other words $\langle \hat{\mathit{P}}\rangle =\mathit{R}$ where $\langle \rangle$ indicates the mean value. $\hat{\mathit{T}}$ is the estimate provided by cues, such as the texture on the walls and floor, that signal the size of objects relative to the size of the room. The use of texture cues was suggested by Gibson [9]. Because the cubes are not resting on the ground surface, a cue such as relative disparity is required to identify the texture elements at the same distance as the cube. Since the room expanded fourfold between the subject viewing the standard and comparison objects, the average estimate of the size of the comparison object according to these ‘relative’ cues is four times smaller (i.e. $\langle \hat{\mathit{T}}\rangle =\mathit{R}/4$). (As a result, if a subject used only ‘relative’ cues, their match should be 4 times larger than if they used only ‘physical’ cues.)

If the noises on each of these estimates, $\hat{\mathit{P}}$ and $\hat{\mathit{T}}$, are independent and Gaussian with variances σ_P and σ_T and the Bayesian prior is uniform (all values of R between 1 and 4 are equally likely a priori) then the maximum-likelihood estimate [12, 13] of the size match is given by:

$$\widehat{R}=\widehat{P}{w}_P+\widehat{T}{w}_T=1$$ (1)

where

$$w_P=\frac{1∕{\sigma }_P^2}{1∕{\sigma }_P^2+1∕{\sigma }_T^2},w_T=\frac{1∕{\sigma }_T^2}{1∕{\sigma }_P^2+1∕{\sigma }_T^2}.$$ (2)

Substituting the average values of $\hat{\mathit{P}}$, $\hat{\mathit{T}}$ and $\hat{\mathit{R}}$ given above into equation 1 and re-arranging gives the predicted size match:

$$R=\frac{1}{w_P+w_T∕4}$$ (3)

We assume that noise on the texture- or room-based size estimate, $\hat{\mathit{T}}$, is independent of distance. For example, according to Weber's law, judging an object relative to the size of neighbouring bricks would lead to equal variability at all viewing distances when expressed as a proportion of object size. On the other hand, judging object size using an estimate of viewing distance introduces greater variability at larger viewing distances. Specifically, assuming constant variability of estimated viewing direction in each eye, the standard deviation of an estimate of viewing distance from vergence increases approximately linearly with viewing distance [11], (see also Figure 12 of [25]). From these assumptions,

$$\frac{{\sigma }_T^2}{{\sigma }_P^2}=\frac{k}{D^2}$$ (4)

where D is the viewing distance of the comparison object and k is a constant. From equations 2, 3 and 4, the expected value of the subject's size match is:

$$R=\frac{k+D^2}{k+D^2∕4}.$$ (5)

Figure 2 shows R plotted against D. The curve shows the best fit of equation 5, (k = 1.24). The same equation was fitted to the data on two static ‘wells’ shown in Figure 3. In this case, we assume that subjects may still use cues that signal cube size relative to the room, even in the absence of texture. Here, k = 33.6, indicating a dominance of cues signalling the physical size match.